齿轮载荷系数
齿轮载荷系数

齿轮载荷系数
标题:齿轮载荷系数及其在机械设计中的应用
简介:本文将详细介绍齿轮载荷系数的定义、计算方法以及在机械设计中的重要性。
通过了解齿轮载荷系数的相关知识,读者将能更好地理解齿轮传动的工作原理,并能在实际设计中合理选取载荷系数,提高齿轮传动的寿命和可靠性。
正文:
齿轮传动作为一种常见的动力传动方式,在机械设计中广泛应用。
齿轮的载荷系数是评估齿轮传动承载能力的重要参数,它描述了齿轮在工作过程中所受到的载荷与其承载能力之间的关系。
齿轮载荷系数是通过计算齿轮传动中的接触应力和弯曲应力得出的。
接触应力是指齿轮齿面接触区域的压力,而弯曲应力是指齿轮齿面曲线所受到的拉伸或压缩应力。
通过计算这两种应力,我们可以得到齿轮的载荷系数。
在机械设计中,选取合适的载荷系数是至关重要的。
如果载荷系数选择不当,齿轮传动可能会发生过载和疲劳破坏现象,从而影响整个机械系统的正常运行。
因此,在设计过程中,我们需要考虑齿轮的使用条件和工作环境,合理选择载荷系数,以确保齿轮传动的可靠性和寿命。
除了在设计中的应用,齿轮载荷系数还对齿轮制造和使用过程中的质量控制起着重要作用。
通过合理选择载荷系数,可以确保齿轮的制造精度和装配质量,从而提高整个齿轮传动系统的工作效率和稳定性。
总之,齿轮载荷系数在机械设计中具有重要的意义。
通过了解齿轮载荷系数的计算方法和应用,我们可以更好地理解齿轮传动的工作原理,合理选择载荷系数,提高齿轮传动的可靠性和寿命。
同时,在齿轮的制造和使用过程中,齿轮载荷系数也起到了重要的指导作用,帮助我们提高齿轮传动系统的工作效率和稳定性。
齿轮的载荷系数

02
03
利用数学统计方法和图表 分析手段,分析载荷系数 与各种因素之间的关系。
比较不同实验条件下的载 荷系数变化,找出影响载 荷系数的主要因素。
04
对实验结果进行误差分 析和不确定性评估,提 高数据可靠性。
结论与展望
总结实验研究成果,阐述载荷系数的变化规律和影响因 素。
展望未来齿轮载荷系数研究的发展方向和应用前景。
案例三
某型号齿轮的接触强度不足,导致齿面点蚀严重。通过增大载荷系数、优化几何参数和采用合适的热处理工 艺后,齿轮的接触强度得到提高,延长了使用寿命。
04 载荷系数与齿轮寿命关系
齿轮疲劳寿命概念
齿轮疲劳寿命是指齿轮在循环载荷作 用下,从开始使用到出现疲劳破坏所 经历的时间或循环次数。
疲劳破坏通常发生在齿轮的齿根部位, 表现为裂纹的萌生和扩展,最终导致 齿轮断裂或点蚀失效。
动态载荷分析
通过对齿轮传动系统进行 动力学建模,分析齿轮在 动态载荷作用下的响应, 得到动载荷系数。
振动与冲击考虑
在计算动载荷系数时,需 要考虑齿轮传动过程中产 生的振动和冲击对载荷的 影响。
阻尼与刚度影响
齿轮传动系统的阻尼和刚 度特性对动载荷系数也有 显著影响,需要在计算中 予以考虑。
有限元法应用
斜齿轮载荷系数特点
同时受径向和轴向载荷作用,载荷系数需同时 考虑两个方向力影响;
载荷分布不均匀,轮齿接触线为斜线,因此载 荷系数相对较高;
适用于高速、重载场合,需要选择较高的载荷 系数以保证安全性。
锥齿轮载荷系数特点
受径向、轴向和周向载荷作用,载荷系数需全面考虑 三个方向力影响;
载荷分布极不均匀,轮齿接触线为曲线,载荷系数较 高;
适用于相交轴传动,需选择较高的载荷系数并关注轮 齿的弯曲和接触强度。
锥齿轮承载能力计算方法载荷及一般影响系数
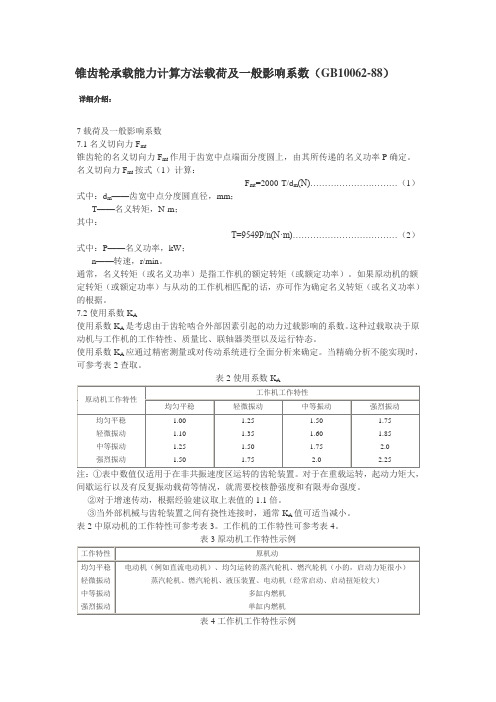
锥齿轮承载能力计算方法载荷及一般影响系数(GB10062-88)详细介绍:7载荷及一般影响系数7.1名义切向力F mt锥齿轮的名义切向力F mt作用于齿宽中点端面分度圆上,由其所传递的名义功率P确定。
名义切向力F mt按式(1)计算:F mt=2000.T/d m(N) (1)式中:d m——齿宽中点分度圆直径,mm;T——名义转矩,N·m;其中:T=9549P/n(N.m) (2)式中:P——名义功率,kW;n——转速,r/min。
通常,名义转矩(或名义功率)是指工作机的额定转矩(或额定功率)。
如果原动机的额定转矩(或额定功率)与从动的工作机相匹配的话,亦可作为确定名义转矩(或名义功率)的根据。
7.2使用系数K A使用系数K A是考虑由于齿轮啮合外部因素引起的动力过载影响的系数。
这种过载取决于原动机与工作机的工作特性、质量比、联轴器类型以及运行特态。
使用系数K A应通过精密测量或对传动系统进行全面分析来确定。
当精确分析不能实现时,可参考表2查取。
表2使用系数K注:①表中数值仅适用于在非共振速度区运转的齿轮装置。
对于在重载运转,起动力矩大,间歇运行以及有反复振动载荷等情况,就需要校核静强度和有限寿命强度。
②对于增速传动,根据经验建议取上表值的1.1倍。
③当外部机械与齿轮装置之间有挠性连接时,通常K A值可适当减小。
表2中原动机的工作特性可参考表3。
工作机的工作特性可参考表4。
表4工作机工作特性示例注;1)额定转矩=最大切削、压制、冲击转矩。
2)额定转矩=最大启动转矩。
3)额定转矩=长时工作的最大轧制转矩。
4)用电流控制力矩限制器。
5)由于轧制带材经常断裂,可提高K A至2.0。
7.3动载系数K A动载系数K V是考虑大、小齿轮啮合振动而产生的内部附加动载荷影响的系数。
动载系数K V定义为齿轮副啮合中最大作用力与纯由外加载荷所产生的相应作用力的比值。
影响动载系数的因素有:a.齿轮精度(周节极限偏差);b.大、小齿轮的回转质量(转动惯量);c.轮齿刚度;d.考虑使用系数K A后的切向力;e.齿面接触状误解;f.轴及轴承的刚度;g.润滑情误解;h.系统阻尼特性。
齿宽系数,复合齿形系数

通过对比分析可知,yfs值与z值大小成反比;且随着z值增大,yfs值变小的速率较小。由于此参数数据离散性大,故采用yfs=4.45~4.00。
2.3.3齿轮齿宽b
当选用1t0741—42齿轮系列时,b=24 mm
当选用1t0741—41齿轮系列时,b=32 mm
组合机床通用多轴箱齿轮齿数z的范围为16~70,一般优选范围为18~50,具体对应数值为:
z=18,yfs=4.45
z=20,yfs=4.37
z=25,yfs=4.20
z=30,yfs=4.12
z=35,yfs=4.07
z=40,yfs=4.03
z=45,yfs=4.01
载荷系数k
钻扩镗铰类通用主轴箱齿轮载荷系数:
k=kakpntkvkβkα=1.1×1×1.05×1.2×1.15=1.5939
攻螺纹类多轴箱齿轮的载荷系数:
k=kakpntkvkβkα=1.25×1×1.05×1.2×
1.15=1.81125
2.3.2复合齿形系数yfs
2.3.4许用弯曲应力σfp
组合机床多轴箱齿轮所用材料为45钢,技术要求为齿部高频淬火g54,精度7级。参考有关资料,结合生产实际,分别取值如下:
一般齿轮(单向受力)σfp=1.4σflim=476mpa
中间齿轮(双向受力)σfp=σflim=340mpa
齿宽系数
一般齿宽系数在0.4以内,大于0.4就意义不大了
分两种
ቤተ መጻሕፍቲ ባይዱ
第一种:
根据大齿轮齿宽b= Φd*d1计算得出,应加以圆整,作为大齿轮的齿宽。
两齿轮齿宽要求:b1=b2+(5~10)mm。
齿轮对基本参数

齿轮对基本参数****************************法面模数:3齿数:小齿轮=16;大齿轮=69压力角:0.3491螺旋角:0.2619变位系数:小齿轮=0.1;大齿轮=-0.1齿宽:小齿轮=50;大齿轮=36端面分度圆压力角:0.3604端面节圆压力角(即啮合角):0.3604基圆螺旋角:0.2457齿顶圆直径:小齿轮=56.2942;大齿轮=219.7061基圆直径:小齿轮=46.5023;大齿轮=200.5410中心矩:132.000113960836齿数比:4.3125当量齿数:小齿轮=17.6067;大齿轮=75.9289****************************设计参数****************************机构工作级别:M5机构类型:起升机构或非平衡变幅机构机构载荷状态:L2-中(机构经常承受中等载荷,较少承受最大载荷)齿轮啮合类型:外啮合齿轮精度等级:6级允许齿厚的磨损量占原齿厚的百分比:10%试验齿轮齿面接触疲劳极限应力:小齿轮=1350N/mm2;大齿轮=895N/mm2 试验齿轮齿根弯曲疲劳极限应力:小齿轮=325N/mm2;大齿轮=330N/mm2 ****************************计算载荷****************************电动机额定力矩传到计算零件的力矩:303.8980N.m小齿轮转速:155转/min----------------------------小齿轮疲劳计算基本载荷:347.0515N.m小齿轮工作最大扭矩:390.2050N.m----------------------------分度圆上基本切向力:13967.4969N----------------------------循环次数系数:小齿轮=1.0000;大齿轮=0.8208载荷系数:小齿轮=0.8100;大齿轮=0.8100等效切向力:小齿轮=11313.6725N;大齿轮=9286.7739N----------------------------齿轮的动载系数:1.0021齿向载荷分布系数:小齿轮=1.3555;大齿轮=1.4322齿面接触强度用的齿间载荷分配系数:1.0500对于齿面接触疲劳强度计算的计算切向力:小齿轮=16135.7975;大齿轮=13995.1343N----------------------------轮齿弯曲强度用的齿间载荷分配系数:1.0500对于轮齿弯曲疲劳强度计算的计算切向力:小齿轮=16135.7975;大齿轮=13995.1343N ----------------------------分度圆上最大切向力:15704.2609N对于齿面接触静强度计算的最大计算切向力:小齿轮=22351.1439;大齿轮=23617.0211N对于轮齿弯曲静强度计算的最大计算切向力:小齿轮=22351.1439;大齿轮=23617.0211N ****************************齿面接触强度计算参数****************************节点区域系数:2.4246弹性系数:189.8000重合度系数:0.8035螺旋角系数:0.9828节圆处的计算接触应力:小齿轮=1211.2739N/mm2;大齿轮=1128.0691N/mm2----------------------------工作硬化系数:1.0000许用接触耐久性应力:小齿轮=1350.0000N/mm2;大齿轮=895.0000N/mm2齿面接触耐久性安全系数:小齿轮=1.1145;大齿轮=0.7934----------------------------节圆处的最大计算接触应力:小齿轮=1425.5978N/mm2;大齿轮=1465.4119N/mm2齿面接触静强度安全系数:小齿轮=1.5152;大齿轮=0.9772****************************齿根弯曲强度计算参数****************************齿形系数:小齿轮=2.8251;大齿轮=2.2819应力修正系数:小齿轮=1.5634;大齿轮=1.7126重合度系数:0.7327螺旋角系数:0.8764磨损系数:1.2500计算的齿根弯曲应力:小齿轮=529.6723N/mm2;大齿轮=406.4848N/mm2----------------------------试验齿轮的应力修正系数:2.0000尺寸系数:小齿轮=1.0000;大齿轮=1.0000许用弯曲疲劳应力:小齿轮=650.0000N/mm2;大齿轮=660.0000N/mm2轮齿弯曲疲劳强度的安全系数:小齿轮=1.2272;大齿轮=1.6237----------------------------齿根弯曲最大计算应力:小齿轮=733.6968N/mm2;大齿轮=685.9498N/mm2轮齿弯曲静强度的安全系数:小齿轮=2.2148;大齿轮=2.4054********************************************************************************总体评价********************************************************************************-------齿面接触计算(疲劳强度安全系数应该大于等于1.0~1.25,静强度安全系数应该大于等于1。
载荷系数

动载荷系数Kv
动载荷系数Kv
动载荷系数Kv
简化公式
动载荷系数Kv
影响动载荷系数Kv的因素: 齿轮的制造精度和圆周速度(影响最大)→齿轮圆周速度↑,制造精
度↓,传动时产生的附加动载荷↑ 齿轮啮合刚度及其变化(双对齿啮合过度到单对齿啮合或相反) 轴及轴承的刚度 齿轮传动系统的阻尼特性 齿轮的接触及润滑情况
误与弹性变形,齿距误差有关
齿间载荷分配系数kα
直齿轮齿间载荷分配计算
齿间载荷分配系数kα
弯曲强度齿间载荷分配系数KFA及实际双齿承载条件
当按总载荷W作用到单对齿啮合区外界点来计算 齿根应力时,其齿顶等效载荷为WYE,YE为弯曲强度重 合度系数。在双对齿啮合时如顶点最大载荷WA大于 WYE,则齿根应力的计算载荷应改取为WA。故KFA的 定义应为,由于双对齿啮合时载荷分配不均而导致的 齿顶最大载荷WA可能大于单对齿啮合区外侧点总载 荷的齿顶等效载荷WYE的程度。
KHβ和KFβ的计算式及其数值
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿向载荷分布系数Kβ
齿间载荷分配系数kα 是考虑齿间载荷分布的不均匀所产生影响的系数。与齿距
动载荷系数Kv
减小附加动载的方法: 限制最大圆周速度 提高精度 齿顶修缘
为了减小动载荷,对于重要的齿轮可采用齿顶修缘,即对齿顶的一小 部分渐开线齿廓适量修削。(分度圆压力角α=20°的渐开线修正成 α>20°的渐开线)→减小基圆齿距误差
齿轮的载荷系数解析

本书中介绍的齿轮传动计算方法只适用于一般精度及低速齿轮传动,故不 需作精确计算的直齿轮和β≤30°的斜齿圆柱齿轮的传动的Kα值可查下表。
1.对于硬齿面和软齿面相啮合小齿轮精度等不同时的 齿轮副,ka取其平均值,若大,则按精度等级较低 的取值。
2.对修形齿轮kFa=kHa=1
3.若kFa>eg/(eaYe),则取kFa=eg/(eaYe) 4.ea={1.88-3.2(1/z11/z2)}cosb,+用于外啮合,-用于 内啮合。
齿轮制造及装配的误差,轮齿受载后产生的
弹性变形,将使啮合轮齿的法向齿距Pb1与 Pb2不相等(见下图),因而轮齿就不能正 确啮合传动,齿轮传动瞬时传动比就不是定 值,就会产生角加速度,于是引起动载荷或
冲击。
•影响因数
主要因素有:基圆齿距(基节)偏差、齿形误差、圆周速 度、大小齿轮的质量、轮齿的啮合刚度及其在啮合过程中的 变化、载荷、轴及轴承的刚度、齿轮系统的阻尼特性等。 其中:齿轮的制造精度和圆周速度对动载荷系数影响最大, 精度越低,基圆齿距误差和齿形误差就越大。 为了减小动载荷,对于重要的齿轮可采用齿顶修缘,即对齿 顶一小部分渐开线齿廓适量修削。注意,若修缘量过大,不 仅重合度会减小,动载荷也不一定就相对减少。
改善齿向载荷分布状态的措施:
•1)适当提高零件的制造和安装精度; •2)增大轴、轴承及其支座的刚度,合理布置齿轮在轴上
的位置(尽可能采用对称支承,避免悬臂支承形式);
•3)将一对齿轮中的一个齿轮做成鼓形齿; •4)轮齿的螺旋角修形; •5)齿轮最好布置在远离转矩输入端的位置。
4.齿间载荷分配系数Kα
Kα是考虑同时啮合的各对轮齿间载荷分配不均的影响系数。 在齿面接触强度计算中记为 KH ,在轮齿弯曲强度计算中记为 KF
齿轮的载荷系数

•
Ft——分度圆上的圆周力,N
•
b ——齿宽,mm
•KHβ计算的简化公式(表4-5)
对于一般圆柱齿轮传动的齿面接触疲劳强度计算用的 由计算公式可知,在A、B、C、b、
齿向载荷分布系数KHβ 值d可1的根值据确齿定轮的在情轴况上下布,置悬形臂式支、承的 KHβ最大,对称支承最小。
齿轮的精度等级、齿宽b及齿宽系数φd (=b/d)从表 查取。
本书中介绍的齿轮传动计算方法只适用于一般精度及低速齿轮传动,故不 需作精确计算的直齿轮和β≤30°的斜齿圆柱齿轮的传动的Kα值可查下表。
1.对于硬齿面和软齿面相啮合小齿轮精度等不同时的 齿轮副,ka取其平均值,若大,则按精度等级较低 的取值。
2.对修形齿轮kFa=kHa=1 3.若kFa>eg/(eaYe),则取kFa=eg/(eaYe) 4.ea={1.88-3.2(1/z11/z2)}cosb,+用于外啮合,-用于
2 当外部机械与齿轮装置之间挠性联接时,通常KA值可适当减小
动载系数KV
• Kv 是考虑齿轮在啮合过程中因其制造精度和运转速度而引起的内
部附加动载荷影响的系数。
• 对于直齿轮传动,由双对齿啮合过渡到单对齿啮合,或是由单对齿
啮合过渡到双对齿啮合的期间,啮合齿对的刚度变化,也要起动载荷。
齿轮制造及装配的误差,轮齿受载后产生的 弹性变形,将使啮合轮齿的法向齿距Pb1与 Pb2不相等(见下图),因而轮齿就不能正 确啮合传动,齿轮传动瞬时传动比就不是定 值,就会产生角加速度,于是引起动载荷或 冲击。
定义:齿向载荷分布系数Kβ是考虑沿齿宽方向载荷分布不 均匀对齿轮强度影响的系数。
Kβ的实质是一单位齿宽上的最大载荷Wmax作为设计依据, 从而避免因载荷集中而导致轮齿的强度破坏。
行星齿轮均载系数

行星齿轮均载系数
行星齿轮均载系数是指在一定的使用寿命内,行星齿轮传动系统所能
承受的平均载荷大小。
这个参数对于确定传动系统的设计参数和材料
选择非常重要。
行星齿轮是一种常见的微型传动装置,其中具有凸轮面的行星轮围绕
太阳轮旋转,驱动外圆齿轮旋转。
行星齿轮传动具有高承载能力、高
精度和高效率等特点,因此广泛应用于机械制造、航空航天等领域。
由于行星齿轮传动中存在很多因素可能导致传动系统失效,因此在进
行设计和选材时需考虑载荷和寿命等因素。
而行星齿轮均载系数能在
一定程度上反映出传动系统承载能力和使用寿命,因而成为了传动系
统设计和选择时常用的重要参数。
综合来看,行星齿轮均载系数影响因素主要包括行星齿轮的材料、热
处理、精度等方面。
行星轮的材料需要具有高韧性和强度,才能保证
在高载荷下不发生断裂现象;同时,必须进行严格的热处理,以增强
行星轮的抗疲劳性能和减少摩擦损失。
此外,为保证齿轮传动的稳定性,必须确保行星齿轮准确配合,同时提高齿轮加工精度。
在实际应用中,确定行星齿轮均载系数需要进行大量实验和模拟计算。
通过模拟计算得到的数据和实验数据相结合,可以使计算结果更加准确。
对行星齿轮传动进行精细的设计和选材工作,可以最大程度地发挥其性能,延长传动系统使用寿命。
总之,行星齿轮均载系数是行星齿轮传动系统设计和选材时一个非常重要的参数。
通过精细的设计和选材,可以最大程度地发挥行星齿轮传动的性能,提高其使用寿命。
因此,在进行行星齿轮传动系统设计和选材时,必须充分考虑行星齿轮均载系数。
齿轮传动的载荷系数

设计计算中采用计算载荷,它与公称载荷的关系为:
Fca =K Fn
式中:
K--载荷系数,在齿轮计算中,K=KA Kv Kβ Kα
1.工作情况系数:KA
KA 是考虑啮合外部因素引起的动力过载的影响系数,这种过载取决于原动机,工作机的特性,质量和联轴器类型等的运行状态。
2.动载荷系数:Kv
Kv 考虑大、小齿轮啮合振动产生的内部因素引起动载荷的影响。
引起动载荷的因素
①齿轮的制造误差(基节和齿形误差)和安装误差
②轮齿受载后产生弹性变形
③啮合齿对的刚度变化
④大、小齿轮的质量(转动惯量)
3.齿间载荷分配系数Kα:
啮合区内齿间载荷分配,可表查
4.齿向载荷分布系数Kβ:
扭矩引起载荷分布显示
(end)。
齿轮的载荷系数

动载系数KV
• Kv 是考虑齿轮在啮合过程中因其制造精度和运转速度而引起的内
部附加动载荷影响的系数。
• 对于直齿轮传动,由双对齿啮合过渡到单对齿啮合,或是由单对齿
啮合过渡到双对齿啮合的期间,啮合齿对的刚度变化,也要起动载荷。
齿轮制造及装配的误差,轮齿受载后产生的 弹性变形,将使啮合轮齿的法向齿距Pb1与 Pb2不相等(见下图),因而轮齿就不能正 确啮合传动,齿轮传动瞬时传动比就不是定 值,就会产生角加速度,于是引起动载荷或 冲击。
•影响因数
主要因素有:基圆齿距(基节)偏差、齿形误差、圆周速 度、大小齿轮的质量、轮齿的啮合刚度及其在啮合过程中的 变化、载荷、轴及轴承的刚度、齿轮系统的阻尼特性等。
其中:齿轮的制造精度和圆周速度对动载荷系数影响最大, 精度越低,基圆齿距误差和齿形误差就越大。
为了减小动载荷,对于重要的齿轮可采用齿顶修缘,即对齿 顶一小部分渐开线齿廓适量修削。注意,若修缘量过大,不 仅重合度会减小,动载荷也不一定就相对减少。
用于一般精度及低速齿轮传动,故不 需作精确计算的直齿轮和β≤30°的斜齿圆柱齿轮的传动的Kα值可查下表。
1.对于硬齿面和软齿面相啮合小齿轮精度等不同时的 齿轮副,ka取其平均值,若大,则按精度等级较低 的取值。
2.对修形齿轮kFa=kHa=1 3.若kFa>eg/(eaYe),则取kFa=eg/(eaYe) 4.ea={1.88-3.2(1/z11/z2)}cosb,+用于外啮合,-用于
• 一、影响齿面接触强度的系数 K H
• K H 是单位齿宽上的最大载荷与平均载荷之比Hβ =Wmax/Wav
•
式中 Wmax——单位齿宽上的最大载荷,N/mm
齿向载荷分配系数kfβ

齿向载荷分配系数kfβ1.引言1.1 概述齿向载荷分配系数kfβ是一种用于评估齿轮系统中齿向载荷分布均匀性的重要参数。
对于大型机械设备和重要的传动装置而言,确保齿轮的齿向载荷分配均匀是至关重要的。
齿轮系统在运行过程中,由于工作负荷的不均匀分布,会导致部分齿轮齿向载荷过大,可能引发疲劳断裂甚至损坏。
为了减少这种不均匀分布带来的潜在风险,需要准确评估齿轮间的载荷分配情况。
齿向载荷分配系数kfβ的计算是基于齿轮系统的设计参数和工作条件进行的。
通过对齿轮参数的分析和计算,可以得到一个区间内的齿向载荷分配系数值。
这个系数的数值越接近1,表示齿轮的齿向载荷分配越均匀,系统的可靠性和使用寿命也会更高。
齿向载荷分配系数kfβ的确定对于齿轮系统的设计和分析具有重要的参考价值。
通过合理选择齿轮参数和调整传动装置的工作条件,可以提高齿向载荷分布的均匀性,减小不均匀分布所带来的风险。
本文将介绍齿向载荷分配系数kfβ的定义和计算方法,并探讨其在齿轮系统设计和分析中的意义与应用。
通过深入研究和理解齿向载荷分配系数kfβ,将有助于优化齿轮传动装置的设计,提高其工作效能和可靠性。
1.2 文章结构文章结构部分的内容可以从整体上介绍文章的组织结构,包括各个章节的主要内容和框架,以帮助读者清晰了解文章的脉络和内容安排。
【文章结构】本文按照以下章节结构进行组织:1. 引言:在本部分中,将对本文的主要内容进行概述,介绍齿向载荷分配系数kfβ的背景和意义,并概括本文的结构和目的。
2. 正文:本部分将详细阐述齿向载荷分配系数kfβ的定义和计算方法。
首先,将介绍齿向载荷分配系数kfβ的定义,包括其含义和相关理论基础。
其次,将详细介绍齿向载荷分配系数kfβ的计算方法,包括计算公式、计算步骤以及相关参数的确定方法。
3. 结论:在本部分中,将总结齿向载荷分配系数kfβ的意义和应用。
首先,将阐述齿向载荷分配系数kfβ的意义,包括对齿轮传动性能的影响和评价。
齿轮传动的计算载荷

恰好相切;受载后,轴产生弯曲变形(图<轮齿所受的载荷分布不均>),轴上的齿轮也就随之偏斜,这就使作用在齿面的载荷沿接触线分布不均匀(图<轮齿所受的载荷分布不均>)。
图<轮齿所受的载荷分布不均>当然,轴的扭转变形,轴承、支座的变形以及制造,装配的误差也是使齿面上载荷分布不均的因素。
计算轮齿强度时,为了计及齿面上载荷沿接触线分布不均的现象,通常以系数Kβ来表示齿面上分布不均的程度对轮齿强度的影响。
为了改善载荷沿接触线分布不均的程度,可以采用增大轴、轴承及支座的刚度,对称的配置轴承,以及适当的限制轮齿的宽度等措施。
同时应尽可能避免齿轮作悬臂布置(即两个支承皆在齿轮的一边)。
对高速、重载(如航空发动机)的齿轮传动应更加重视。
除上述一般措施外,也可把一个齿轮的轮齿做成鼓形(右图)。
当轴产生弯曲变形而导致齿轮偏斜时,鼓形齿齿面上载=1.11+0.18+0.15×=1.11+0.18(1+0.6)+0.15× =1.11+0.18(1+6.7)+0.15× =1.12+0.18+0.23×=1.12+0.18(1+0.6)+0.23× =1.12+0.18(1+6.7)+0.23× =1.15+0.18+0.31×=1.15+0.18(1+0.6)+0.31× =1.15+0.18(1+6.7)+0.31×=1.05+0.26+0.10×=1.05+0.26(1+0.6) +0.10×=1.05+0.26(1+6.7) +0.10×=0.99+0.31+0.12×=0.99+0.31(1+0.6) +0.12×=0.99+0.31(1+6.7) +0.12×=1.05+0.26+0.16×=1.05+0.26(1+0.6) +0.16×=1.05+0.26(1+6.7) +0.16×=1.0+0.31+0.19×=1.0+0.31(1+0.6) +0.19×=1.0+0.31(1+6.7) +0.19×。
齿轮齿面接触疲劳强度计算公式

齿轮齿面接触疲劳强度计算公式
1.齿轮疲劳强度校核公式为:Kf*S*Yf*Zv*Yδ*YN/(b*Sw)
2.其中,Kf为载荷系数,S为应力集中系数,Yf为综合载荷系数,Zv为载荷比系数,Yδ为动载荷系数,YN为可靠性系数,b为齿轮有效宽度,Sw为齿轮材料疲劳极限应力。
3.齿轮疲劳强度校核公式是根据齿轮锥齿直歯轮的疲劳强度理论推导出来的,用于计算一个齿轮在疲劳破坏前所能承受的最大载荷。
4.齿轮作为机械传动装置中的重要部分,其强度的计算和校核非常重要。
在齿轮的设计和制造中,需要根据负荷、速度、传动比等因素进行疲劳校核,以保证齿轮的安全可靠性。
齿轮的载荷系数分解

齿轮制造及装配的误差,轮齿受载后产生的
弹性变形,将使啮合轮齿的法向齿距Pb1与 Pb2不相等(见下图),因而轮齿就不能正 确啮合传动,齿轮传动瞬时传动比就不是定 值,就会产生角加速度,于是引起动载荷或
冲击。
•影响因数
主要因素有:基圆齿距(基节)偏差、齿形误差、圆周速 度、大小齿轮的质量、轮齿的啮合刚度及其在啮合过程中的 变化、载荷、轴及轴承的刚度、齿轮系统的阻尼特性等。 其中:齿轮的制造精度和圆周速度对动载荷系数影响最大, 精度越低,基圆齿距误差和齿形误差就越大。 为了减小动载荷,对于重要的齿轮可采用齿顶修缘,即对齿 顶一小部分渐开线齿廓适量修削。注意,若修缘量过大,不 仅重合度会减小,动载荷也不一定就相对减少。
定义:齿向载荷分布系数Kβ是考虑沿齿宽方向载荷分布不 均匀对齿轮强度影响的系数。 Kβ的实质是一单位齿宽上的最大载荷Wmax作为设计依据, 从而避免因载荷集中而导致轮齿的强度破坏。
• K 可分为:影响齿面接触强度的系数 KH
影响齿根弯曲强度的系数
KF
• 影响齿向载荷分布系数的因素主要有: • 1.齿轮和箱体的制造和安装误差; • 2.齿轮、轴、支承座和箱体的刚度; • 3.轴承间隙及变形,磨合效果,热膨胀和热变形; • 4.齿宽及齿面硬度(P90); • 5.齿轮布置形式。
改善齿向载荷分布状态的措施:
•1)适当提高零件的制造和安装精度; •2)增大轴、轴承及其支座的刚度,合理布置齿轮在轴上
的位置(尽可能采用对称支承,避免悬臂支承形式);
•3)将一对齿轮中的一个齿轮做成鼓形齿; •4)轮齿的螺旋角修形; •5)齿轮最好布置在远离转矩输入端的位置。
4.齿间载荷分配系数Kα
定义式 KF =Mmax/Mav
接触强度计算的齿向载荷分布系数表

《接触强度计算的齿向载荷分布系数表》在齿轮设计和分析中,接触强度计算是一个非常重要的步骤,它用于评估齿轮在工作条件下的耐用性和可靠性。
而在进行接触强度计算时,齿向载荷分布系数表是一个必不可少的工具,它可以帮助工程师们更准确地计算齿轮的接触强度,从而确保其在使用过程中不会出现疲劳断裂和过载等问题。
齿向载荷分布系数表是根据实验和理论分析得出的一些数据,在实际的工程设计中,它们能够帮助工程师们更快速地选择合适的齿轮参数,并且提供便于计算的载荷分布系数,从而准确地预测齿轮的接触强度。
在接触强度计算中,载荷分布系数表主要用于确定齿轮的载荷分布系数,而这个系数又是接触强度计算中的一个重要参数。
齿向载荷分布系数表可以根据不同的齿轮类型和工作条件,给出相应的载荷分布系数,工程师们可以根据实际情况选择合适的系数值,从而得到更准确的接触强度计算结果。
这个齿向载荷分布系数表不仅包含了常见的齿轮类型,如直齿轮、斜齿轮、蜗杆等,还考虑了不同的工作条件和应力分布情况,如动载荷、静载荷、韧性载荷等,这些都能够帮助工程师们更好地进行接触强度计算,并且在设计中考虑到更多的因素。
通过使用齿向载荷分布系数表,工程师们能够更好地进行接触强度计算,并且能够根据实际情况进行调整,得到更准确可靠的结果。
这能够有效提高齿轮的设计质量和可靠性,避免在使用过程中出现过载和疲劳断裂等问题,从而延长齿轮的使用寿命。
总结回顾:齿向载荷分布系数表在接触强度计算中起着非常重要的作用,它能够帮助工程师们更准确地评估齿轮的接触强度,避免在使用过程中出现疲劳断裂和过载等问题。
工程师们在进行接触强度计算时,应该根据实际情况选择合适的载荷分布系数,从而得到更可靠的结果。
个人观点和理解:齿向载荷分布系数表是齿轮设计和分析中一个非常实用的工具,它能够帮助工程师们更准确地进行接触强度计算,从而确保齿轮在工作条件下的可靠性和耐用性。
在实际的工程设计中,我们需要充分利用齿向载荷分布系数表,根据不同的工作条件和应力情况选择合适的系数值,从而得到更准确的接触强度计算结果,为齿轮的设计和使用提供更可靠的保障。
直齿锥齿轮的切向力及载荷系数

直齿锥齿轮的切向力及载荷系数.doc本文由豆豆相传批量上传(关于豆豆相传,请访问: | [名称]直齿锥齿轮的切向力及载荷系数.doc [大小]114176 [时间]2010-2-2 13:03:14 [编辑]2009-8-9 7:16:30豆豆相传直齿锥齿轮的切向力及载荷系数基础科学牛档搜索()直齿锥齿轮的切向力及载荷系数序号名称代号/单位计算公式和说明1 小轮转矩 T/Nm 见直齿锥齿轮强度校核的原始参数(2) 12 参考点切向力 F/N F=2 000T/d mtmt1m13 参考点切线速度υ/(m/s)υ=dn/19 098 mtmtm114 使用系数 K A动载荷系数K v*5 有效齿宽 b/mm b=bb eee6 F/(N/mm) F=FK/be KbKbmtAF100时,C=1 KbF7 齿轮啮合刚度修正系数之一 C FF<100时,C=F/100 KbFKb*b时,C=1 eb8 齿轮啮合刚度修正系数之二 C b**b<时,C=b/ ebe9 轮齿的啮合刚度 c/[N/(mmμm)] c=20CC γγFb10 单对齿刚度c′/[N/(mmμm)]c′=14CC Fb11 诱导质量 m/(kg/mm) redx12 临界转速 n/(r/min) E113 临界转速比 N N=n/n 1E114 A p根据齿轮精等级由A和C值查得 PP15 C p16 齿距极限偏差 f/μm pt调质钢,y=160f/σαptHlim灰铸铁,y= αpt17 轮齿跑合量 y/μm α渗碳淬火钢和氮化钢,y= αpt两种不同材料,y=(y+y)/2 αα1α218 有效齿距偏差 f/μm f=f-y peffpeffptα19 B B=bfc′/(FK) pppeffmtA20 C C= v1v1N时的C和C 2时,C= v1v2vαv21<ε21 C v2ε>2时,C=(ε) vαv2vα22 N时的C C 1<ε2时,C= v3v3vαv3ε>2时,C=(ε) vαv3vα1<ε2时,C= vαv423 <N时的C C v4v4ε>2时,C=()/(ε) vαv4vαvα24 C C= v5v52时,C= vαv61<ε25 C v6ε>2时,C=(ε) vαv6vαN时的C、C和C v5v6v7时,C= vαv71<ε26 <ε时,C=[π(ε-2)]+ v7vαv7vαε>时,C= vαv7N时,K=N[B(C+C)+C]+1 vpv1v2v3<N时,K=B(C+C)+C+1 vpv1v2v427 动载系数 K vN时,K=Bp(C+C)+C vv5v6v7齿向载荷分布系数K、K以及Z和Y HβFβLsε28 装配系数 K 根据装配条件和接触区检验条件,按装配系数K选取 HβbeHβ be*b>时,K= eHβΗβ be29 接触强度计算的齿向载荷分布系数 K Hβ**b时,K=b eHβHβ bee30 齿线曲率系数 K K=1 F0F031 弯曲强度计算的齿向载荷分布系数 K K=K/K FβFβHβF032 接触强度计算的载荷分配系数 Z Z=1 LSLS33 重合度系数 Y Y=+εεεvα齿间载荷分配系数K和K HαFα34 F/N F=FKKK mtHmtHmtAvHβ35 接触强度计算的齿间载荷分配系数 K Hα36 弯曲强度计算的齿间载荷分配系数 K K=K FαFαHα37 K Hαmax38 K K=1/Y FαmaxFαε当K<1时,取K=1 HαHα 39 K Hα当K>K时,取K=KHαHαmaxHαHαmax当K<1时,取K=1 FαFα 40 K Fα当K>K时,取K=K FαFαmaxFαFαmax 本文系牛档搜索()根据用户的指令自动搜索的结果,文中内涉及到的资料均来自互联网,用于学习交流经验,作品其着作权归原作者所有。
齿轮强度计算载荷系数

齿轮强度计算载荷系数齿轮是机械传动中常用的零件,用于传递和改变力和运动的方向。
在齿轮设计中,强度是一个重要的考虑因素。
齿轮强度的计算涉及到载荷系数的应用。
本文将详细介绍齿轮强度计算中载荷系数的概念、计算方法以及其在齿轮设计中的应用。
一、载荷系数的概念载荷系数是用来衡量齿轮所承受载荷的大小和性质的参数。
它是根据齿轮工作条件和使用要求来确定的。
载荷系数包括动载荷系数、静载荷系数和冲击载荷系数等。
1. 动载荷系数:动载荷系数是用来计算齿轮传递动力时的载荷大小的参数。
它与齿轮传递的功率、转速、传动比等因素有关。
动载荷系数的计算方法一般根据齿轮的标准或经验公式来确定。
2. 静载荷系数:静载荷系数是用来计算齿轮在静止状态下所承受的载荷大小的参数。
它与齿轮的材料、齿轮的几何形状等因素有关。
静载荷系数的计算方法一般考虑齿轮的强度和刚度等因素。
3. 冲击载荷系数:冲击载荷系数是用来计算齿轮在冲击载荷下所承受的载荷大小的参数。
它与齿轮传递的冲击力、冲击时间等因素有关。
冲击载荷系数的计算方法一般根据齿轮的工作条件和使用要求来确定。
二、载荷系数的计算方法载荷系数的计算方法一般根据齿轮的工作条件和使用要求来确定。
具体的计算方法可以通过齿轮的标准或经验公式来确定。
以下是一些常用的计算方法:1. 动载荷系数的计算方法:动载荷系数可以通过齿轮的标准或经验公式来计算。
一般来说,动载荷系数与齿轮的传动功率、转速、传动比等因素有关。
在计算动载荷系数时,需要考虑齿轮的工作条件和使用要求,并根据相关标准或经验公式进行计算。
2. 静载荷系数的计算方法:静载荷系数可以通过齿轮的材料、齿轮的几何形状等因素来计算。
一般来说,静载荷系数与齿轮的材料强度、齿轮的几何形状等因素有关。
在计算静载荷系数时,需要考虑齿轮的强度和刚度等因素,并根据相关标准或经验公式进行计算。
3. 冲击载荷系数的计算方法:冲击载荷系数可以通过齿轮的工作条件和使用要求来计算。
一般来说,冲击载荷系数与齿轮的冲击力、冲击时间等因素有关。
齿轮传动的算载荷

齿轮传动的计算载荷为了便于分析计算,通常取沿齿面接触线单位长度上所受的载荷进行计算。
沿齿面接触线单位长度上的平均载荷p(单位为N/mm)为式中:Fn--作用于齿面接触线上的法向载荷,N;L --沿齿面的接触线长,mm。
法向载荷Fn为公称载荷,在实际传动中,由于原动机及工作机性能的影响,以及齿轮的制造误差,特别是基节误差和齿形误差的影响,会使法向载荷增大。
此外,在同时啮合的齿对间,载荷的分配并不是均匀的,即使在一对齿上,载荷也不可能沿接触线均匀分布。
因此在计算齿轮传动强度时,应按接触线单位长度上的最大载荷,即计算载荷pca(单位为N/mm)进行计算。
即式中K为载荷系数。
计算齿轮强度用的载荷系数K,包括使用系数KA,动载系数Kv,齿间载荷分配系数Kα及齿向载荷分布系数Kβ,即KA--使用系数的啮合传动,瞬时传动比就不是定值,从动齿轮在运转中就会产生角加速度,于是引起了动载荷或冲击。
对于直齿轮传动,轮齿在啮合过程中,不论是由双对齿啮合过渡到单对齿啮合,或是由单对齿啮合过渡到双对齿啮合的期间,由于啮合齿对的刚度变化,也要引起动载荷。
为了计及动载荷的影响,引入了动载系数Kv。
齿轮的制造精度及圆周速度对轮齿啮合过程中产生动载荷的大小影响很大。
提高制造精度,减小齿轮直径以降低圆周速度,均可减小动载荷。
为了减小动载荷,可将轮齿进行齿顶修缘,即把齿顶的小部分齿廓曲线(分度圆压力角α=20°的渐开线)修正成α>20°的渐开线。
如图1所示,因Pb2>Pb1,则后一对轮齿在未进入啮合区时就开始接触,从而产生动载荷。
为此将从动轮2进行齿顶修缘,图中从动轮2的虚线齿廓即为修缘后的齿廓,实线齿廓则为未经修缘的齿廓。
由图明显地看出,修缘后的轮齿齿顶处的法节P'b2Pb1时,对修缘了的轮齿,在开始啮合阶段(如图1),相啮合的轮齿的法节差就小一些,啮合时产生的动载荷也就小一些。
图1又如图2主动轮齿修缘动画演示所示,若Pb1>Pb2,则在后一对齿已进入啮合区时,其主动齿齿根与从动齿齿顶还未啮合。
khβ和kfβ——齿向载荷分布系数

khβ和kfβ——齿向载荷分布系数螺旋线载荷分布系数K Hβ是考虑沿齿宽方向载荷分布不均匀对齿面接触应力影响的系数式中w max——单位齿宽最大载荷,N/mm;w m——单位齿宽平均载荷,N/mm;F m——分度圆上平均计算切向力,N影响齿向载荷分布的主要因素有:a.齿轮副的接触精度它主要取决于齿轮加工误差、箱体镗孔偏差、轴承的间隙和误差、大小轮轴的平行度、跑合情况等;b.轮齿啮合刚度、齿轮的尺寸结构及支承形式及轮缘、轴、箱体及机座的刚度;c.轮齿、轴、轴承的变形,热膨胀和热变形(这对高速宽齿轮尤其重要);d.切向、轴向载荷及轴上的附加载荷(例如带或链传动);e.设计中有无元件变形补偿措施(例如齿向修形)由于影响因素众多,确切的载荷分布系数应通过实际的精密测量和全面分析已知的各影响因素的量值综合确定。
如果通过测量和检查能确切掌握轮齿的接触情况,并作相应地修形,经螺旋线修形补偿的高精度齿轮副,在给定的运行条件下,其螺旋线载荷接近均匀分布,K Hβ接近于1。
在无法实现时,可按下述两种方法之一确定①一般方法按基本假定和适用范围计算K Hβ。
基本假定和适用范围:a.沿齿宽将轮齿视为具有啮合刚度cγ的弹性体,载荷和变形都呈线性分布;b.轴齿轮的扭转变形按载荷沿齿宽均布计算,弯曲变形按载荷集中作用于齿宽中点计算,没有其他额外的附加载荷;c.箱体、轴承、大齿轮及其轴的刚度足够大,其变形可忽略;d.等直径轴或阶梯轴,d sh为与实际轴产生同样弯曲变形量的当量轴径;e.轴和小齿轮的材料都为钢;小齿轮轴可以是实心轴或空心轴(其内径应<0.5d sh),齿轮的结构支承形式见图1,偏心距s/l≤0.3K Hβ的计算公式见表1,当K Hβ>1.5时,通常应采取措施降低K Hβ值。
