二人有限零和对策
《管理科学》名词解释

《管理科学》名词解释1、管理就是管理者运用各种资源达成某既定目标的过程。
2、管理科学:是一门应用多学科与多领域理论、方法、技术和知识的综合性交叉学科,其目的是研究人类利用有限资源实现组织目标的管理活动方面的动态、复杂和创新的社会行为及其规律。
3、管理科学的基本特征:(1)以管理决策为基点;(2)以科学方法论为依据;(3)以系统观点为指导;(4)以数学模型为主要工具。
4、图解法只能用于两个变量的情况,并得到两个重要结论:(1)线性规划的约束集合是凸多面体;(2)线性规划若有最优解,则最优解一定能在凸多面体的角点(定点)上达到。
5、基本解:假设B为线性规划问题的基,对约束系数矩阵A目标函数系数响亮C,决策向量X进行分块处理,则有:A=(B,N),C=(CB,CN),X=[XB,XN]T,其中,N表示非基矩阵,XB表示基变量所构成的子向量,XN表示非基变量所构成的子向量,CN为非基变量所对应的目标函数所构成的子向量,由AX =b得到:AX=(B,N) [XB,XN]T=B XB +N XN=b,由此式解出XB,并令非基变量的取值等于零,得到X =[B-1b,0]T,则称X为基B 下的基本解。
6、线性整数规划:限制部分决策变量或全部决策变量只能取整数的线性规划。
7、非线性规划:目标或约束中含有非线性函数的优化问题成为非线性规划。
8、梯度:若f(X)在X0的领域内有连续一阶偏导数,则称f(X)在点X0对n个变元的偏导数组成的向量为f(X)在X0的梯度,记为▽f(X0)9、海赛阵:若f(X)在X0的领域内有连续二阶偏导数,则称f(X)在点X0对n个变元两两组合的二阶偏导数组成的矩阵为f(X)在X0的海赛阵,记为H(X0)10、多目标规划解法的基本思想:利用一个复合函数将多目标问题转化为单目标问题求解。
11、图与网络具有的两个基本要素:一是被研究的对象,通常用点来表示;二是所研究对象之间的某种特定关系,通常用点与点之间的连线表示12、边:两点之间不带箭头的联线由点及边构成的图称之为无向图13、弧:两点之间带箭头的联线由点及弧构成的图称之为有向图14、网络:在有向图D=(V,A)中,Vs为起点,Vt为终点,而对每一弧(Vi,Vj)∈A赋以量cij>0称为弧的容量,则称这样的有向图为一个网络,记为D=(V,A,C)15、树:一个无圈的连通图16、Dijkstra方法是求解最短路问题的一种有效方法17、网络图的组成要素:箭线、结点和线路18、确定型决策:这类决策问题只可能出现一种确定的自然状态,每个行动方案在这唯一的自然状态下的结局是可以计算出来的19、风险型决策:这类决策问题在决策过程中可以出现多种自然状态,每一个行动方案在不同自然状态下有不同的结局,且能预先估计出各个自然状态出现的概率20、完全不确定型决策;这类决策问题在决策过程中可以出现多种自然状态,但在这类决策问题中,不能预先估计出各个自然状态出现的概率,所以称之为完全不确定型决策21、决策树:是一种由结点和分支构成的由左向右横向展开的树状图形22、贝叶斯决策分三步走:先验分析、预验分析、后验分析23、效用值是风险下损益值在决策者心目中的满意程度的衡量尺度24、一般来讲,库存量不足会造成缺货损失,而库存量过大又会造成物质积压,库存费用增大,流动资金占用过大25、补充就是储存系统的输入26、状态:过程各阶段所处的“位置”称为状态27、某阶段初装台决定后,从这状态向下一阶段哪个状态演变的选择称为决策28、前一阶段的状态和决策决定了下一阶段的状态,它们之间的关系称为状态转移29、由阶段k=1至阶段k=n的全过程中,由每个阶段所选择的决策构成一决策序列,称之为一个策略30、层次分析法(简称AHP)是由美国匹兹堡大学教授T.L.Saaty在20世纪70年代中期提出的,它的基本思想是把一个复杂的问题分解为各个组成因素,并将这些因素按支配关系分组,从而形成一个有序的递阶层次结构。
矩阵对策

max aij 对局中人 II,求 min j i
若 max min aij min max aij a i
i j j i
*
j*
策略 i , j 为I,II 的最优策略
这一对策 的值为 V a i
j
几个术语
局势 对策的解
最优纯策略
对策的值 鞍点 e. g. 2 (续)求解取暖购煤问题
两人零和对策
对抗对策(antagonistic game)
矩阵对策(matrix game)
二.实际问题中的矩阵对策模型
e. g. 1 扩大销售模型
公司I,公司II 的同一产品竞争市场份额,各有三种办 法扩大销售额(由于市场需求一定,一家扩大,意味 另一家缩减),三种方法比如:①改进包装;②广告; ③降价.公司I 的三种策略表示为 1 , 2 , 3 ,公司II 的三种策略为 1 , 2 , 3 ,在不同策略下销售量增长百 分比不同.下表中表示公司I 的增长率,而公司II 的即 为相反数
e. g. 6 (续)求最优策略与值
作业
P206,
Ex 6. 3:1,2
1=急转 2 =不转
1
给急转弯者以1 分,不转弯者以5 分 局中人II 局中人I 局 =急转 1 中 人 2=不转 II
3 5
1 =急转 2=不转
1 0
0
II 的支付矩阵
此对策中,若两者都想得5 分,则发生惨祸, 全部玩完.实际上两人最好的做法是同时停车 或转弯,各得3 分. Remark 此例已不是 2 人有限零和对策问题(因为在 每个对局中,双方支付的代数和不为零), 称为双矩阵对策.
e. g. 2 取暖购煤问题 某公司在秋末需决定冬季取暖用煤问题.根据气温 情况,用煤量和煤价均不同,可用下表表示: 正常气温 较冷气温 较暖气温 需求量15 吨 需求量20 吨 需求量10 吨 200元/吨 250元/吨 150元/吨
运筹学12-2对策论

3.矩阵对策的混合策略(续)
-- 优超原则:当局中人甲方的策略t被其它 策略所优超时,可在其赢得矩阵A中划去第t 行(同理,当局中人乙方的策略t被其它策 略所优超时,可在矩阵A中划去第t列)。 如此得到阶数较小的赢得矩阵A’,其对
应的矩阵对策
G’= { S1,S2,A’}与 G ={ S1,S2,A } 等价,即解相同。
17
再讨论“齐王赛马”
• “齐王赛马”的赢得矩阵A有 max min aij=-1 min max aij=3
i j j i
故需求混合策略,由于A中有非正元素, 可选k=2,令矩阵中每一元素加上k得到新的 正矩阵A’:
5 3 3 1 3 3 3 5 1 3 3 3 3 3 5 3 3 1 3 3 3 5 1 3 1 3 3 3 5 3 3 1 3 3 3 5
19
再讨论“齐王赛马”(续)
• 求乙方(田忌)最优策略的线性规划模型:
min Y1+Y2 +Y3 +Y4 +Y5 +Y6 s.t. 5Y1+3Y2 +3Y3 +3Y4 + Y5 +3Y6 1 3Y1+5Y2 +3Y3 +3Y4 +3Y5 + Y6 1 3Y1+ Y2 +5Y3 +3Y4 +3Y5 +3Y6 1 Y1+3Y2 +3Y3 +5Y4 +3Y5 +3Y6 1 3Y1+3Y2 +3Y3 + Y4 +5Y5 +3Y6 1 3Y1+3Y2 + Y3 +3Y4 +3Y5 +5Y6 1 Y1,Y2,Y3,Y4,Y5,Y6 0 可得两组解:(1/9,0,0,1/9,1/9,0)T, (1/18,1/18,1/18,1/18,1/18,1/18)T ,V’=3 于是,Y’=(1/3,0,0,1/3,1/3,0)T, Y’=(1/6,1/6,1/6,1/6,1/6,1/6)T V = V’-2 = 1 即田忌的最优混合策略值是输1千金
矩阵对策问题及其解法

矩阵对策问题及其解法背景对策论研究具有竞争性质的现象。
有权决定⾃⾝⾏为的对策参加者称为局中⼈,所有局中⼈构成集合I,在⼀局对策中可供剧中⼈选择的⼀个实际可⾏的完整的⾏动⽅案成为策略,对于任意剧中⼈i∈I,都有⾃⼰的策略集S i。
⼀局对策中由各剧中⼈选定的策略构成的策略组称为局势s=(s1,...,s n),⽽全体局势集合S=S1×...×S n。
局势决定了对策的结果,对局势s∈S,局中⼈i可以得到收益H i(s),也称为局中⼈i的赢得函数。
矩阵对策即⼆⼈有限零和对策,是⼀类较为简单的对策模型。
矩阵对策基础我们假设,局中⼈ I 有纯策略α1,...,αm,局中⼈ II 有纯策略β1,...,βn,⼆者各选择⼀个纯策略则构成m×n个纯局势 (αi,βj),将 (αi,βj)下 I 的赢得值记为a i,j,设矩阵A=[a i,j],称为 I 的赢得矩阵或 II 的⽀付矩阵。
局中⼈ II 的赢得矩阵就是 −A T。
最优纯策略若纯局势 (a i∗,b j∗) 满⾜max i minj a i,j=minjmaxi a i,j=a i∗,j∗则称为矩阵对策 {S1,S2;A} 的最优纯策略。
显然,最有纯策略在赢得矩阵中对应的元素⼀定满⾜,其是所在⾏的最⼩元素,也是所在列的最⼤元素,即矩阵的鞍点。
混合策略当纯策略不存在时,我们希望给出⼀个选取不同策略的概率分布。
我们记 I,II 的概率分布向量分别为x,y,所有概率分布向量构成的集合为S1,S2,则局中⼈ I 的赢得函数为E(x,y)=x T Ay。
纯策略是混合策略的特例。
若混合局势 (x∗,y∗) 满⾜max x miny E(x,y)=minymaxx E(x,y)=E(x∗,y∗)则称为矩阵对策 {S1,S2;A} 的最优混合策略。
同样,混合策略 (x∗,y∗) 是最有混合策略的充要条件也是 (x∗,y∗) 是函数E(x,y) 的鞍点。
两人有限零和博弈例题

两人有限零和博弈例题摘要:1.引言2.两人有限零和博弈的定义3.例题讲解3.1 题目背景3.2 博弈过程分析3.3 博弈结果及启示4.总结正文:在博弈论中,两人有限零和博弈是一种特殊的博弈模型,它指的是两个参与者在一定规则下进行的互动,其结果只有两种可能:赢或输,而且赢与输的和为零。
这种博弈模型广泛应用于经济学、社会学、政治学等多个领域。
接下来,我们将通过一个具体的例题来讲解两人有限零和博弈的原理及应用。
例题讲解:假设甲、乙两人进行一场扑克牌游戏,游戏规则如下:1.每人手中有5 张牌,且每张牌的点数分别为1 至5;2.游戏开始时,甲、乙两人分别随机抽取一张牌;3.甲、乙两人轮流进行出牌,每次出牌后,对手可以选择接受或拒绝;4.若对手接受,则游戏结束,双方点数之和为本次出牌的点数之和;5.若对手拒绝,则轮到对手出牌;6.游戏结束时,点数之和最大的一方获胜。
在这个例子中,我们可以分析甲、乙两人的策略。
为了获胜,甲、乙两人应该尽量使自己的点数之和最大化。
假设甲先出牌,且甲手中有1、2、3、4、5 五张牌,乙手中有a、b、c、d、e 五张牌,且a≤b≤c≤d≤e。
那么,甲应该如何出牌才能最大化获胜的概率呢?我们可以列出如下的出牌策略:1.如果乙手中有1、2、3、4、5 五张牌,那么甲应该选择最大的牌5;2.如果乙手中有1、2、3、4 四张牌,那么甲应该选择最大的牌4;3.如果乙手中有1、2、3 三张牌,那么甲应该选择最大的牌3;4.如果乙手中有1、2 两张牌,那么甲应该选择最大的牌2;5.如果乙手中有1 张牌,那么甲应该选择最大的牌1。
通过以上的策略分析,我们可以发现,甲、乙两人实际上在进行一场有限零和博弈。
甲要想获胜,就必须在保证自己利益的前提下,尽量削弱乙的竞争力。
同样,乙要想获胜,也必须在保证自己利益的前提下,尽量削弱甲的竞争力。
最终,博弈的结果将取决于甲、乙两人的策略选择。
通过这个例子,我们可以看到两人有限零和博弈的特点:参与者需要在保证自己利益的前提下,尽量削弱对手的竞争力。
精心整理的运筹学重点10.对策论
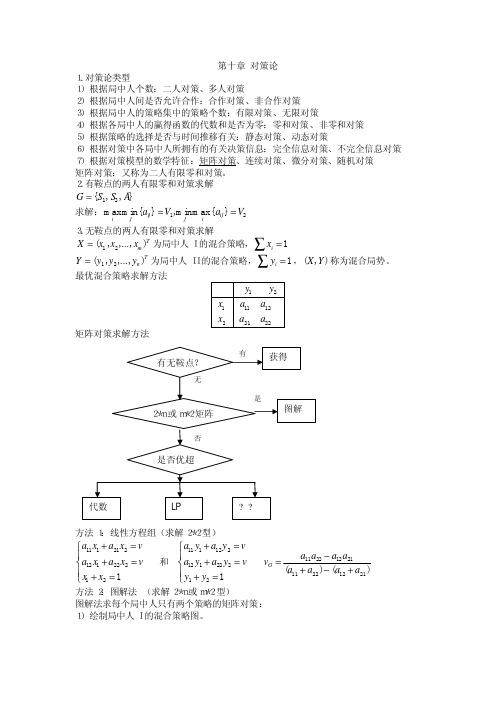
v1 = max min(3 − 2 x, 2 + 2 x) , v1 = max min(3 − 2 x, 2 + 2 x) 就是折线 ABC,它是局 0≤ x ≤1 0≤ x ≤1
中人 I 的最小赢得线,B 就是折线 ABC 的最高点,所以 B 点所对应的值就是混合策略意 义下的最大最小值。
i j j i
3.无鞍点的两人有限零和对策求解 X = ( x1 , x2 ,..., xm )T 为局中人 I 的混合策略,
Y = ( y1 , y 2 ,..., yn )
T
∑ x = 1 为局中人 II 的混合策略, ∑ y = 1 , ( X , Y ) 称为混合局势。
i i
最优混合策略求解方法 y1 y2
第十章 对策论 1.对策论类型 1)根据局中人个数:二人对策、多人对策 2)根据局中人间是否允许合作:合作对策、非合作对策 3)根据局中人的策略集中的策略个数:有限对策、无限对策 4)根据各局中人的赢得函数的代数和是否为零:零和对策、非零和对策 5)根据策略的选择是否与时间推移有关:静态对策、动态对策 6)根据对策中各局中人所拥有的有关决策信息:完全信息对策、不完全信息对策 7)根据对策模型的数学特征:矩阵对策、连续对策、微分对策、随机对策 矩阵对策:又称为二人有限零和对策。 2.有鞍点的两人有限零和对策求解 G = {S1, S2 , A} 求解: maxmin{aij } = V1,minmax{aij } = V2
x1 a11 x2 a21
矩阵对策求解方法
有
a12 a22
有无鞍点?
无 是
获得
2*n 或 m*2 矩阵
否
图解
运筹学对策论全解

赢 A
B
石头
剪子
布
石头 0 1 -1
剪子 -1 0 1
布
1 -1
0
分析:无确定最优解,可用“混合策略”求解。
4.齐王赛马
战国时期,齐国国王有一天提出要与大将军田忌赛马。 田忌答应后,双方约定: 1)每人从上中下三个等级中各出一匹马,共出三匹; 2) 一共比赛三次,每一次比赛各出一匹马; 3) 每匹被选中的马都得参加比赛,而且只能参加一次; 4) 每次比赛后输者要付给胜者一千金。
例:囚犯困境中,每个囚犯均有2个策略:
{坦白,抵赖}
(3)局势
坦白 抵赖
坦白 抵赖 -9,-9 0,-10 -10,0 -1,-1
当每个局中人从各自策略集合中选择一策略而组 成的策略组成为一个局势,用 (si , d j )来表示。
(4)赢得(支付)
局中人采用某局势时的收益值。
例:当局中人甲选择策略si ,局中人乙选策略 dj 时,局中人甲的赢得值可用 R甲(si , d j )表示。
九十年代以来博弈理论在金融、管理和经济领域中 得到广泛应用
• 九十年代以来对策理论在金融、管理和经济领域 中得到广泛应用
• 博弈论和诺贝尔经济奖
1994:非合作博弈:纳什(Nash)、泽尔腾(Selten) 、海萨尼 (Harsanyi) 1996:不对称信息激励理论:莫里斯(Mirrlees)和维克瑞(Vickrey) 2001:不完全信息市场博弈:阿克罗夫(Akerlof)(商品市场)、斯潘 塞(Spence)(教育市场)、斯蒂格里兹(Stiglitze)(保险市场) 2005: 授予罗伯特·奥曼与托马斯·谢林,以表彰他们通过博弈理论的分析 增强世人对合作与冲突的理解。 2007年,授予赫维茨(Leonid Hurwicz)、马斯金(Eric S. Maskin)以及 迈尔森(Roger B. Myerson)。三者的研究为机制设计理论奠定了基础。 2012年,授予罗斯(Alvin E. Roth)与沙普利(Lloyd S. Shapley)。他 们创建“稳定分配”的理论,并进行“市场设计”的实践。
数学建模---对策论模型

纯局势(i*,j*)为对策在纯策略下的解(亦称均衡局势)。
i*和j*分别称为局中人Ⅰ和Ⅱ的最优纯策略。
3.方法步骤: 上例求解过程可简单的表述如下:
7 1 8
A 3
2
4
16 4 3
其步骤是:
3 0
5
第一步:分别确定A各行中的最小值,并在该数字上加圈表示;
第二步:分别确定A各列中的最大值,并在该数字上加框表示;
=8xy-6y-x+8
= 8( x
3 )( 4
y
1 8
)
7
1 4
这就是说,局中人 I 分别以概率 X * (3 , 1) 选用1,2 时,至
44
少赢得 7
1 4
,同理,局中人Ⅱ分别以概率Y *
(1 8
,
7) 8
选用策略1,2,
至多损失 7 1 。但当 X * (3 , 1) 或Y * (1 , 7) 时,则会受到更大的
3.赢得函数(支付函数)
(1)局势:对策中,每一局中人所选定策略形成的策略组
合称一个局势。设局中人1从自己的策略集S1={1,2 …,m}中 选定策略i,局中人2从自己的策略集S2={1, 2 …, n}选定策 略j,则(i, j)就构成两人对策中的一个局势。
在n个对策中,设si表示第i局中人的一个策略,则n个局中 人的策略组合形成的局势为S=(s1,s2,…sn)。
aij
8
2
max i
a
i
*
j
2
3
3
V1
max i
min j
aij
2 ,V2
min j
max i
aij
2 ,V1
V2
矩阵对策的基本理论

A
a21
a22
a2n
am1 am2 amn
(12-3)
为局中人Ⅰ的赢得 矩阵。由于对策为零和的,故局中人 Ⅱ的赢得矩阵为-A。
当局中人Ⅰ、Ⅱ的策略集 S1, S2 及局中人Ⅰ的赢得矩阵 A 确定后,一个矩阵对策就给定
了。因此将矩阵对策表示为 G S1,S2;A.
矩阵对策的最优纯策略
x E m
x
x , x ,, x
12
m
T
,
x i
0, i
1,,
m,
m
x i
i 1
1
S 2
y
E
n
y
y , y ,, y
12
n
T,
y j
0,
j
1,
n,
n
j 1
y j
1
S 和S 1
2
分别称为局中人Ⅰ和Ⅱ的混合策略集;
x
S
1
和y
S
2
分别称为局中人Ⅰ和Ⅱ
的混合策略;当
x
S 1
和y
S
2
其中, T G1
和T G 2
分别为局中人 I 和 II 的策略集。
运筹学
使自己的赢得尽可能的小,理性的选择就应该是从各自可能出现的最不利的情形中争取尽可
能好的结果。
两人有限零和对策的新解法初探

两人有限零和对策 的新解法 初探
李 前进 ” 李 明 ” 夏 志刚 ’
00 4) 5 0 3
( 家 庄 铁 道 学 院 经 济 管 理 分 院 ” 校 园 规 划 与 设备 管 理 处 石 家 庄 石 ’
【 摘要 】 出 了一种 两人 有限 零和对 策新 的解 法—— “ 大 不 利 法” 该 方 法可将 混 合 策略 提 避 ,
望值 达到 最大 ( 小 ) , 中人选 择 各种纯 策 略 的概 率分 布 。 最 时 局 在局 中人 双方 互相 无 法 了解 对 方选 择某 种纯
策略 的概 率 时 , 合 策略 的解 直接 指 导 局 中人选 择 自己的纯 策略 的 意义 不是 很 大 , 就是 说 , 中人最 终 混 也 局 应选 择哪 一个纯 策 略 , 很难根 据混 合 策略 的解 做 出 明确的决 定 。 , 针对 上述 解法 存在 的不 足 , 出一种 较 简单 的新解 法 —— “ 提 避大 不 利法 ” 对 有鞍 点和 无 鞍点 的两 人有 , 限零 和 对策 统 一求 解 , 可将 混 合 策略 纯化 , 就是 寻 求无 鞍 点 的两 人有 限 零 和对 策 问题 的纯 策略 解 , 并 也 从
( ) 出赢 得矩 阵 A。 1写 ‘
() 2 在赢 得 矩 阵 A 中寻 找 最 大 的 元 素 , 用方 框 标 出 , 在 该 元 素 所 在 的 列 上 方 标 记① 来表 示 划 去 该 再 列 ; 后在剩 下 的 各列 中寻 找 最大 的 元 素并 用方 框 标 出 , 在该 元 素 所 在的 列 上方 标记 ② 表 示 划去 该 列 ; 然 再 依次 进行 , 到剩 下唯 一 的一 列元 素 。 直
维普资讯
第1卷 第3 5 期
1两人零和对策举例-PPT精品文档

8
数字a(=50),是甲台各节目收视率保守估计(35,40
,50,45)中的最大值。a表示在所有可能的选择中,
甲台所能得到保证的收视率中的最大值。a=50所对应的 节目C,也是甲台最稳妥的选择。表中的最后一行是同 一列数字中的最大的值。例如该行的第三个数字是50, 它是45、40、50、45四个数字中的最大值。这个数字对 应乙台播放节目2时的情况,说明当乙台播放节目2时, 只要甲台应对得当(此时甲应该播放节目C),甲台所
3/2/2019
1
§1 两人零和对策举例
3/2/2019
2
例1 某地区有两家电视台,在一天的同一个黄金时间
,每家各有两套节目可供选择播出。经调查,两家电视台各 种节目搭配时甲台节目收视率如下表: 表1 甲台节目收视率(%) 乙台 甲台 节目A 节目B
节目1 70 55
节目2 40 45
表中是甲台节目的收视率,乙台节目的收视率可以由以下的 公式得到:
他们之间的竞争呢?
由表中可见,如果甲台期望得到70%的收视率而选 播节目A,则乙台会播放节目2,使甲台只能得到40%的 收视率。如果甲台选播节目B,则不管乙台播放什么节 目,甲台最少可得到45%的收视率。
3/2/2019 4
两者相比,甲台必然播放节目B,乙台播放节目2。由此 推知,甲台的收视率将为45%,乙台的收视率将为55%。 现在转到从乙台的立场来考虑问题。先把上面的表转 换成乙台节目收视率的表: 表2 乙台节目收视率(%) 乙台 甲台 节目A 节目B 节目1 30 45 节目2 60 55
乙台收视率=100%—甲台收视率
3/2/2019 3
这里假设了该地区的居民只看这两家电视台的甲台。设 想两家电视台事先都知道这张表,即他们都知道彼此选 播节目后各自的收视率。为分析方便起见,我们暂时假 设他们都可以随时调整播放的节目。我们要分析这两家 电视台会播放什么节目,即他们会采取什么对策来应付
两人有限零和博弈例题

两人有限零和博弈例题
摘要:
1.零和博弈的定义
2.两人有限零和博弈的概念
3.两人有限零和博弈的例题
4.解决两人有限零和博弈的方法
正文:
【1】零和博弈的定义
零和博弈,是指在博弈过程中,参与者的收益总和为零的一种博弈。
也就是说,在一个零和博弈中,一个参与者的收益总是与另一个参与者的损失相等。
这种博弈中,没有参与者可以从中获得超过另一个参与者的损失的收益。
【2】两人有限零和博弈的概念
两人有限零和博弈,是指只有两个参与者,且每个参与者都有有限个策略可以选择的零和博弈。
在这个博弈中,每个参与者都知道对方的所有策略和可能的结果,并且每个参与者的目标是最大化自己的收益。
【3】两人有限零和博弈的例题
例如,一个游戏中,参与者A 可以选择“石头”、“剪刀”或“布”,参与者B 也可以选择“石头”、“剪刀”或“布”。
他们的收益是由他们选择的策略决定的。
如果A 选择“石头”,B 选择“剪刀”,那么A 的收益是1,B 的收益是-1;如果A 选择“石头”,B 选择“布”,那么A 的收益是-1,B 的收益是1。
这个游戏就是一个两人有限零和博弈。
【4】解决两人有限零和博弈的方法
对于两人有限零和博弈,一种解决方法是使用博弈论中的“最小最大”策略。
这个策略是,每个参与者都选择他们认为对方最可能选择的策略,然后选择一个可以最大化自己收益的策略。
第三章-对策论

纳什简介
1994年诺贝尔经济学奖获得者, 纳什在普林斯顿读博士时刚刚20岁出 头,他的一篇关于非合作对策的博士 论文和其他两篇相关文章确立了他博 奕论大师的地位。到上世纪50年代末, 他已是闻名世界的大牌科学家了。
然而,正当他的事业如日中天的时候,天妒英才,他得了 严重的精神分裂症。多亏前妻艾莉西亚的爱心呵护和普林 斯顿大学诸多朋友和同事无私的帮助才没有使他流落街头, 并最终把他推上诺贝尔经济学奖宝座(1994年获奖)。
一、纯策略与混合策略 二、纯策略对策 三、混合策略对策
一、纯策略与混合策略
纯策略是指确定的选择某策略;而混合策略 则指以某一概率分布选择各策略。
§2 二人有限零和对策
一、纯策略与混合策略 二、纯策略对策
引例 纯策略分析 纯策略对策模型的解 优超原理
三、混合策略对策
二、纯策略对策
1. 引例
例 设一对策 G S, D, A,其中 S s1, s2 , s3,
{坦白,抵赖}
(3)局势
坦白 抵赖
坦白 抵赖 -9,-9 0,-10 -10,0 -1,-1
当每个局中人从各自策略集合中选择一策略而组 成的策略组成为一个局势,用 (si , d j )来表示。
(4)赢得(支付)
局中人采用某局势时的收益值。
例:当局中人甲选择策略si ,局中人乙选策略 dj 时,局中人甲的赢得值可用 R甲(si , d j )表示。
D d1, d2 , d3 ,其赢得矩阵为:
d1 d2 d3
A
s1 s2
3 6
1 0
2 - 3
s3 - 5 - 1 4
前提: 对策双方均理智
结论: 最不利中选最有利
问:双方局中人采用何策略最佳。
习题2-1解答

《习题2-1解答》第 1 页 共 1 页 习题2-1解答
1. 二人零和对策问题:两儿童玩石头—剪子—布的游戏,每人的出法只能在{石头,剪子,布}中选择一种,当他们各选定一种出法(亦称策略)时,就确定了一个“局势”。
也就决定了各自的输赢,若规定胜者得1分,负者得1-分,平手各得零分,则对于各种可能的局势(每一局势得分之和为零即零和),试用矩阵表示他们的输赢状况。
解: B 策略→
A 石头 策 剪子 略 布 ↓
2. 有6名选手参加乒乓球比赛,成绩如下:选手1胜2,4,5,6,负于3;选手2胜4,5,6,负于1,3;选手3胜1,2,4,负于5,6;选手4胜5,6,负于1,2,3;选手5胜3,6,负于1,2,4;若胜一场得1分,负一场得零分,试用矩阵表示输赢状况,并排序。
解: 1 2 3 4 5 6
1
2
3
4
5
6 3. 能源利用系统表示为加权有向图(如图所示),试用矩阵表示之。
解: C F J P Q R U
C F J P Q
R U
⎪⎪⎪⎭
⎫ ⎝⎛---011101110⎪⎪⎪⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛001001010011000001111110011101⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---05.02.10008.13.0000000
0003.00005.1000000000100020005.100
02
00010。
第10章 第2节 矩阵对策的基本原理

v 2 min max E(x, y) * *
yS2 xS1
20
设
max min E(x, y) min E(x , y) E(x , y ) * * *
xS1 yS2 yS2 * * * min max E(x, y) max E(x, y ) E(x , y ) * * * yS2 xS1 xS1 * * *
实际中出现的更多情形是v1< v2,根据定义1, 对策不存在纯策略意义下的解。例如:赢得 矩阵为
3 A 5
6 4
16
v1 max min aij 4,
i j
i 2
*
v 2 min max aij 5,
j i
j 1
*
v 2 5 4 v1
想法:是否可以给出一个选取不同策略的 概率分布?
a12 a22 amቤተ መጻሕፍቲ ባይዱ2
a1n a2 n amn
2
为局中人I的赢得矩阵(或局中人II的支付矩阵)。由 于假定对策为零和的,故局中人II的赢得矩阵就是 -A。通常,将一个矩阵对策记成 G={I,II;S1,S2;A} 或 G={S1,S2;A}
例:齐王赛马
赢得矩阵为:
3 1 1 1 1 1 1 3 1 1 1 1 1 1 3 1 1 1 A 1 1 1 3 1 1 1 1 1 1 3 1 1 1 1 1 1 3
5
当矩阵对策模型给定后,各局中人面临的问题便是 如何选取对自己最有利的纯策略,以谋取最大的赢 得(或最少损失)。
1
S1 1 , 2 ,, m
S2 1 , 2 ,, n
运筹学第十二章二人有限非零和对策

解
y1
0 y1 1
1
图示
1 2
0 x1 1 y1 0 0 x1 1
0
1
x1
y1
1
0
1
x1
y1
3
4
y1 1
1
0 x1 1
0
1
x1
y1 1, 0 x1 1 0 y1 1, x1 0
y1
1
0
1
x1
y1
5
B1 0 B2 0 B1 0 B2 0 B1 0 B2 0 B1 0 B2 0 B1 0 B2 0
0
1
x1
6 7
8 9
x1 0,
y1
1
A2 A1
0
1
x1
y1
1
A2 A1
0
1
y1
1
x1
x1 1, 0 y1 1
0
y1
1
x1
x1 0, 0 y1 1
1
0
1
x1
条件序号
条件
B1 0 B2 0 B1 0 B2 0 B1 0 B2 0 B1 0 B2 0
丈夫的解: 4 x1 0, 0 y1 5 4 x1 1, y1 1 5 4 0 x1 1, y1 5 妻子的解: 1 y1 0, 0 x1 5 1 0 y1 1, x1 5 1 y1 1, x1 1 5
y1
4 5
y1
1 1
4 5 1 5
0 y1 1, x1 0 y1 0, 0 x1 1
B 0 x1 2 B B2 1 0 y1 1, x1 B1 B2 y1 1 y1 1, B1 B2 x1 1 y1 0, B1 B 0 y1 1, x1 2 B1B y1 1, 0 x1 2 B1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
j
i
aij
只有ai* j*
min j
max i
aij
max i
min j
aij
即(i* , j* )是鞍点
证毕
例1
-2 2 -2 7 2
4
3
8
5
3
8 -6 2 -1 6
838 7
例2
0 2 2 2
5
4
3
3
2 3 4 4
54 2
VG 3
(i* , j* ) (2 , 2 )
性质5:G1 (S1, S2 , A1), G2 (S1, S2 , A2 ), A1 (aij ), A2 (kaij ) 则:G1,G2同解,并且VG2 kVG1
三、基本定理与LP解法
定理2:
G在混合策略下有解
( X *,Y *) E( X *,Y *) max min E( X ,Y ) min max E( X ,Y )
分析*式:
E(X ,Y*) E(X *,Y*) E(X *,Y) E( X *,Y *) X *T AY *
a11
(x1* L
L
xm*
)
M
O
a1n M
y1*
M
am1 L amn yn*
分析左式:
E( X ,Y *) X T AY * (x1 L
L
xm
)
A1 M
二、性质
AiY V
性质1:
V
VG*
V
X
T
Aj
V
m
n
i1
xi
j 1
yj
1
性质2:松紧定理
X *T (V AY *) 0 (V X *T A)Y * 0
其中
V V M
V
例4:猜手游戏
0 1 1
A
1
0
1
1 1 0
该对策问题无纯策略最优, 在混合策略下求解:
解:
由性质1
得1分,平得0分,输得 -1分, 剪子 -1 0 1 则 A的赢得可用右表来表示。 布 1 -1 0
2 . 对策论的产生
1944年,纽曼与曼彻斯特发表了题为《对策论和经 济行为》。二次大战前后,由于军事需要,抽象成数学 模型。
50年代是对策论发展的鼎盛时期,纳什和夏普利等 提出了讨价还价模型和合作对策的“核”的概念。同时 ,非合作对策也开始创立。纳什于1950和1951年发表了 两篇关于非合作对策的文章,图克于1950年定义了“囚 徒困境”问题。
2阶的简单情形,记A=
a c
b d
则
X * ( d - c , a - b )Y *=( d - b , a - c ),
a-b-cd a-b-cd
a-b-cd a-b-cd
V *= ad - bc a-b-cd
例6:
3 1 2
设:A= 2
1
2
,
求解G
*
(S*, D*, A)。
1 3 1
60年代,泽尔腾(1965)引入动态分析,提出“精 练纳什均衡”概念。海萨尼(1967-1968)则把不完全信 息引入对策论的研究。
二 、对策问题的组成
1.局中人(参加者):一局对策的参加者。
2.策略:局中人在一局对策中对付对手的一个完整的方案。 策略集:局中人在一局对策中所有策略的全体。记为S (分为有限和无限)问:田忌和齐王的S=?
G的解,i*与
分别是
j*
,的最优纯策略,ai*
j*
称为G的值,记为VG 。
2.
鞍点:若局势(
i*,
)对应的
j*
ai*
j*=mai x
min j
aij= mjin
max i
aij
则称(
i*,
)为鞍点。
j*
分析上例中的a23,它就满足ai3 a23 a2 j
定理1: G在纯策略中有解(i* , j* )(i* , j* )是鞍点
4. 对于一个混合局势(X, Y), 用E(X, Y) XTAY 表示局中人的收益期望值。
5. 用G* (S1*,S*2 ,E)表示G (S1,S2 ,A)的混合扩充。
6.混合扩充的解与值
G*的值VG* E( X *,Y *)满足 : E(X ,Y*) E(X *,Y*) E(X *,Y) *式 G*的解( X *,Y *)也称G在混合策略意义下的解.
第十一章 二人有限零和对策
二人有限零和对策是对策论(Game Theory)最基本的内容。
Game Theory也可译为博弈论,是研 究决策主体的行为发生直接相互作用时的 决策以及这种决策的均衡问题的学科。
1994年诺贝尔经济学奖授给了三位博 弈论专家:纳什、泽尔腾、海萨尼。博弈 论已经成为当代经济学的基石。
进一步:
x1* A1Y *
M 中必有每个AiY* VG*
xm* AmY *
因为若有某个Ai0Y* VG*,则出i0 ,即取X=(0L 1L 0),
此时Vi0 VG* 矛盾。
i0
而且若有某 i0,使Ai0Y* <VG*,则必有X i0=0。否则, 可能得到比VG* 更小的损失,矛盾。
对右半式也可作类似的分析,可得 VG* X *T Aj
3. 局势:在一局对策中,每个局中人都选定一策略后的各 策略总和。
如在二人对策中,设 S1 1,L ,m, S2 1,L , n,
则局势为(i, j), i 1,L , m, j 1,L , n
4. 支付:局势给定后,局中人的得失(是局势的函数)。 分为非 零零 和和 :: 各各 局局 中中 人人 的的 得得 失失 之之 和和 为0非0
AY XT
A
V V
可假设X,Y的所有分量均 为非零,则左式等号成立
y2 y3 V
- x2 x3 V
y1 y3 V
y1
y2
V
且
x1
x3
V
x1 x2 V
yi 1
xi 1
解得 X * Y * (1 1 1), V 0 333
定义:
若A中第i, k行有aij akj , j 1L n 称i优超于k 。 记i f k 若A中第j,l列有aij ail ,i 1L m 称 j优超于l 。 记 j f l
min
j
max i
aij
2
max i
min j
aij
2
鞍点不存在,
即在纯策略意义下无解
例3
6 5 1 4
8 5 0 2
6 5 5
2
-1
-1
7 5 5
6 2 0
85 7 5
VG 5
(i* , j* ) (1, 2 ), (1, 4 ), (3, 2), (3, 4)
鞍点不唯一,但值唯一。
例3直观地证明了最优解的两个性质:
第二节 矩阵对策的最优纯策略
一、矩阵对策
设二人有限零和对策问题的局中人为,
策略集为S1 {1,2,L L ,m},S2 {1,2,L L ,n}
L 1
n
1 a11 K a1n
M 则支付可以用矩阵A=
M
O
M 表示,mam1 NhomakorabeaL
amn
其中aij为的得(也是的失),的得即为-aij。
故又称二人有限零和对策为矩阵对策,记为G (S1,S2 ,A)
证明 :
记
min j
ai*
j
min j
max i
aij
max i
min j
aij
max i
aij*
min j
ai*
j
ai*
j*
,
max i
aij*
ai* j*
故 aij* a , a i* j* i* j* ai* j i 1,L , m j 1,L , n
aij* ai* j* ai* j
先应用优超原理化简A
3
2
1
1 1 3
2 2
2
1
f
1
2
1
1 2 3 f 1 1
3 1
3
2 aij 1 1
0
4
3
0
A'
现先求解G' (S1' , S2' , A' )
即(i* , j* )是G的解
Q aij*
ai* j*
ai*
i
j
1,L
,m
j 1,L , n
max i
aij*
ai* j*
min j
ai*
j
min j
max i
aij
max i
aij*
ai* j*
min j
ai*
j
max i
min j
aij
但对于任意A,有 max min
i
j
aij
min max
第一节 基本概念
一、对策现象与对策论
1. 对策现象
①下棋:围棋源于我国殷代。
②齐王赛马:齐王与大将田忌赛马,各自的马都分为三
等,但齐王的同等马均强于田忌。孙膑给田忌出主意,
用下----上,上----中,中----下,
结果田忌胜出。
赢 A
B
石头
剪子
布
③猜手:小孩A与B猜手,若规定赢 石头 0 1 -1
1 无差别性. (i1 , j1 ), (i2 , j2 )是G的两个解,
则a a i1 j1
i2 j2
2 可交换性. (i1 , j1 ), (i2 , j2 )是G的两个解,
则(i1 , j2 ), (i2 , j1 )也是G的解。
