高数上第六章-弧长
2.7《弧长》课件(共18张PPT)
高数课件第六章定积分的应用:第二节定积分的几何应用

y
c
b O
x
bx
x
x x 1 sh dx ch dx c c b x xb s 2 ch dx 2c sh 0 c c 0 x b 1 x 2c sh ( c ch ) c sh c c c c
2
e e ch x 2 x x e e sh x 2 (ch x) sh x
Hale Waihona Puke 2 (t ) 2 (t ) d t
因此所求弧长
s
2 (t ) 2 (t ) d t
(3) 曲线弧由极坐标方程给出:
令 x r ( ) cos , y r ( ) sin , 则得
dx [r ( ) cos r ( ) sin ]d dy [r ( ) sin r ( ) cos ]d
2
选 x 为积分变量 (1) x [2, 0], dA1 ( x 3 6 x x 2 )dx 于是所求面积 A A1 A2
特别注意:
各积分区间 A ( x 3 6 x x 2 )dx 0 (x x 6 x)dx 上被积函数的 2 253 形式不同. . 12
0
3
2
3
x2 1 练习:1.求曲线 y , y 与直线 x 3 2 1 x 2
x 3 所围成的图形的面积。
2.求曲线 xy 1 与直线
x y 0 y 2
x y 2
P1
2
所围成的图形的面积。 2014考研题
提示:1
P2
y
1
32 1 0 2 1 1 3 x 1 x 1 1 s 2[ ( )d x ( ( 3 3 2) ) d x ] 2 0 1 x 1 3 2 2 1 x2
弧长PPT教学课件

A
B
C
例题.如图,三角形ABC的三条边长都 是27毫米。分别以A、B、C三点为圆心,27 毫米为半径画弧.
2)
A
B
C
例题.如图,三角形ABC的三条边长都 是27毫米。分别以A、B、C三点为圆心,27 毫米为半径画弧.
A
B
C
思考
下列图形中圆心角AOB各是几度?所对的弧是圆周长
张
弓站 似 一 棵
松
北第
腿
少 林武 当
功
一
部 3 32 5 56 34 32 1 - 2. 3 5.6. 1.7. 6. - - - ..
不摇 坐 如
钟走 路一 阵
太极 八卦 分掌
连 环风
. 56 17 6 - - -
中 华有 神 功
6.
1
.. 56
.
17
6 ---
.
6 . 1 56 45
3 ---
猎人合唱是德国作曲家韦伯的著名歌剧 《自由射手》第三幕里的一段选曲。这部 歌剧创作于1820年。故事取材于德国和捷 克斯洛伐克广为流传的、一个名叫《黑猎 人》的民间传说。它描写年轻的猎人马克 斯与守林人的女儿阿格泰相爱,并战胜重 重困难,最后结为夫妻的故事。
威尔第
(1813-1901)
意大利作曲家。作有29部歌剧,代表作 《博尼法乔伯爵奥贝尔托》《纳布科》 《弄臣》《茶花女》《游吟诗人》《假 面舞会》《命运的力量》《阿依达》 《奥塞四罗幕》歌和剧《《福茶斯花塔女夫》》的等剧歌本剧由,意至大利作家皮 今阿仍维在根舞据台小上仲久马演同不名衰悲。剧小说改编。1853年3月首 演于威尼斯。歌剧讲述了女主人公薇奥莱塔与青 年阿尔弗来德的爱情悲剧故事。
弧长公式高中数学

弧长公式高中数学
弧长公式是高中数学中用于计算圆或圆弧长度的重要公式。
具体来说,弧长公式有两种形式:
1. 弧长公式:L=n×π×r/180,其中n是圆心角度数,r是半径,L是圆心角弧长。
这个公式是基于角度制来计算的。
2. 弧长公式:L=α×r,其中α是圆心角度数(以弧度为单位),r是半径,L是圆心角弧长。
这个公式是基于弧度制来计算的。
需要注意的是,角度制和弧度制是两种不同的角度计量单位。
在角度制中,一个完整的圆被定义为360度;而在弧度制中,一个完整的圆被定义为2π弧度。
在实际应用中,需要根据具体情况选择合适的弧长公式来计算圆或圆弧的长度。
弧长和扇形面积课件

VS
详细描述
通过观察扇形的形状,我们可以将其分解 为三角形和其他基本图形,然后通过测量 各部分的长度来计算面积。这种方法需要 一定的几何知识,但对于一些简单的情况 非常有效。
04
弧长和扇形面积的应用
在几何图形中的应用
弧长和扇形面积是几何学中重要的概念,广泛应用于各种几何图形的研究和计算。
在圆形、椭圆、抛物线等图形中,弧长和扇形面积的计算对于确定图形的形状、大 小以及解决相关问题具有重要意义。
THANKS FOR WATCHING
感谢您的观看
扇形面积的单位
扇形面积的单位是面积单位,常用的单位有平方米、平方 厘米、平方千米等。
弧长和扇形面积的关联知识
弧长和扇形面积的关系
在同一个圆或等半径的圆中,如果圆 心角增大,则对应的弧长和扇形面积 都会增大。这是因为弧长和扇形面积 都与圆心角的大小有关。
弧长和扇形面积的应用
在实际生活中,弧长和扇形面积的应 用非常广泛,例如在几何学、工程学 、天文学等领域都有应用。
利用微积分计算弧长
总结词
通过微积分的方法,我们可以对弧长进行精确的计算,适用于复杂曲线的弧长计 算。
详细描述
微积分提供了一种积分的方法来计算曲线的长度。对于弧长,可以通过对曲线函 数进行积分来得到。具体来说,弧长 = ∫(sqrt(1 + (y')^2)) dx,其中 y' 是曲线 在 x 处的导数。
弧长和扇形面积课件
目录
• 弧长和扇形面积的基本概念 • 弧长的计算方法 • 扇形面积的计算方法 • 弧长和扇形面积的应用 • 弧长和扇形面积的扩展知识
01
弧长和扇形面积的基本 概念
弧长的定义
弧长是圆弧上任意两点间的长度,它 是圆的一部分。
弧长计算公式课件

不同形状的弧长计算公式
01
圆弧
$s = r theta$
02
椭圆弧
$s = a theta$
03
抛物线弧
$s = frac{1}{2} p theta$
04
双曲线弧
$s = e theta$
弧长计算公式的近似方法
泰勒级数展开
将弧长表示为角度的幂级数,适 用于小角度计算。
数值积分
利用数值积分方法,将弧长计算 转化为积分运算,适用于任意角度。
目录
CONTENTS
• 弧长计算公式的基本概念 • 弧长计算公式的推导过程 • 弧长计算公式的应用 • 弧长计算公式的变种和推广 • 弧长计算公式的实际案例分析
01
弧长计算公式的基本概 念
弧长的定义
01
弧长是圆弧的长度,表示圆周上 任意两点之间的距离。
02
弧长可以通过圆心角和半径来计 算,公式为:弧长 = 圆心角 /360° × 2πr。
桥梁和建筑结构设计
自动化生产线设计
弧长计算公式在桥梁和建筑结构设计 中用于计算曲线形结构的长度,以确 保结构的稳定性和安全性。
在自动化生产线设计中,弧长计算公 式用于优化机器人的运动轨迹,提高 生产效率。
管道设计
在管道设计中,弧长计算公式用于计 算管道的长度,以确保流体在管道中 的流动效率。
04
弧长计算公式的变种和 推广
详细描述
在电路设计中,电线的弧长是影响电路性能 的重要因素之一。使用弧长计算公式,工程 师可以精确地计算出电线的弧长,从而选择 合适的电线长度和弯曲程度,确保电路的正 常运行和稳定性。同时,电线的弧长也会影 响到电路的信号传输质量和能耗,因此精确 的弧长计算对于电路设计来说是非常重要的。
6[1].2弧长大学数学高数一
![6[1].2弧长大学数学高数一](https://img.taocdn.com/s3/m/a298ac4afe4733687e21aa89.png)
=a∫
= a∫
0
2π
[1 − cos t ]2 + [sint ]2 dt
2 − 2 cos t dt = 2 a ∫0
2π
0
t sin dt 2
t 2π = 4a ( − cos ) = 8a 2 0
5
曲线是极坐标方 例3 (曲线是极坐标方 曲线是 时求弧长) 程时求弧长 求心脏线
r = a (1 + cos θ )的全长。 的全长。
x a
−
x a
)由 x = −a 至
s=
−a
∫ ds = ∫
a
a
′ ) 2 dx 1+ (y
2
−a
=
−a
∫
ae 2 a
x a
−e
x − a
) dx
2
=
−a
∫
1 ⋅ (e + e 4
x a
−
x a
) dx
2
1 = 2
−a
∫ (e
x a
a
x a
+e
−
−
x a
x x − a a 求悬链线 y = (e + e a ) 2
y
ds
dx
dy
由x = − a 至 x = a 一段弧长 .
−a
o
a
x
1
直角系下 解 在直角系下,用微元法可得弧微元
ds = (dx ) 2 + (dy ) 2
dy 2 = 1 + ( ) dx = 1 + ( y′ )2 dx
a 于是悬链线 y = ( e + e 2 x = a 的一段弧长为 :
《参数函数弧长公式》课件

参数函数弧长公 式的应用实例
参数函数弧长公式的应用步骤
确定参数函数:首 先需要确定参数函 数的形式,例如 y=弧长L
验证结果:将计算 结果与实际结果进 行比较,验证公式 的正确性
应用实例:给出具 体的应用实例,如 计算圆弧的弧长等
参数函数弧长公式的应用实例解析
实例一:求曲线y=sin(x)在区间[0, π]上的弧长 实例二:求曲线y=cos(x)在区间[0, π]上的弧长 实例三:求曲线y=sin(x)在区间[0, 2π]上的弧长 实例四:求曲线y=cos(x)在区间[0, 2π]上的弧长
参数函数弧长公 式的注意事项
参数函数弧长公式的适用范围
展望
未来研究方向和热点问题
公式在工程实践中的应用案 例
参数函数弧长公式的应用前 景
公式在数学教育中的重要性 和挑战
感谢观看
汇报人:PPT
《参数函数弧 长公式》PPT 课件
PPT,a click to unlimited possibilities
汇报人:PPT
添加目录标 题
参数函数弧 长公式概述
参数函数弧 长公式的应 用实例
参数函数弧 长公式的注 意事项
参数函数弧 长公式的推 导过程
总结与展望
添加章节标题
参数函数弧长公 式概述
参数函数弧长公式的定义
参数函数弧长公 式是描述参数函 数在区间[a, b] 上的弧长的公式
公式形式:L = ∫[a, b] sqrt(1 + (dy/dx)^2) dx
其中,L表示弧 长,y表示参数 函数,x表示自 变量
公式中的sqrt 表示平方根, dy/dx表示导数
参数函数弧长公式的应用场景
物理领域:计算 曲线的长度、面 积等
大一高数课件第六章 6-4-1

a
3
0
3 sin d a . 3 2
2
五、小结
平面曲线弧长的概念
弧微分的概念 直角坐标系下
求弧长的公式 参数方程情形下 极坐标系下
思考题
闭区间[a , b] 上的连续曲线 y f ( x ) 是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
的面积;
2 2 2
s a 0
1 2 d 1 2 ln 1 2 a 1 2 2
2
2 0
例6
解
r 3a sin cos a sin cos , 3 3 3 3 3
s r 2 ( ) r 2 ( )d
一、填空题: 1、曲线 y ln x 上相应于 3 x 8 的一段弧长为 ____________; 2、渐 伸 线 x a (cos t t sin t ) , y a (sin t t cos t ) 上相应于 t 从 0 变到 的一段弧长为______; r 1 自 3 至 4 一 段 弧 长 为 3、曲 线 4 3 ____________ .
设曲线弧为 y f ( x )
( a x b) ,
o a
b
x
其中 f (x )在[a , b]上有一阶连续导数
取积分变量为 x ,在[a , b]上 任取小区间[ x, x dx],
以对应小切线段的长代替小 弧段的长, 小切线段的长
y
dy
(dx )2 (dy )2 1 y 2 dx
弧长 s
r 2 ( ) r 2 ( )d .
高数-对弧长的曲线积分讲解

质量m。如图11-1所示。
L
A
o
x
图11-1
2. 曲线形构件的质量(2)
(1) 分割: 在L上取点M1, M2, …, Mn-1 , 把L分 成n小段, 记第i小段的长度为 si
(2)近似:
m ( , )s
i
i
i
i
n
n
(3) 求和:
m
m i
(
i
,
i
)
s i
i 1
(x, y) L 。
A L f (x, y)ds
x
L
y
6. 对弧长的曲线积分的计算(1)
定理1 设 f (x, y)在曲线 L上连续, L的参数方程为
x (t),
y
(t
),
( t )
其中 (t), (t) 在[, ]上具有一阶连续导数, 且 2(t)
谢 谢!
i 1
y B
M n1
Mi
(i
,i )
M
i
si
1
L
M2
M1 A
o
图11-1
x
n
(4)
取极限:m
lim 0
i 1
( i
, i
)s i
,其中 max{s1,s2,
, sn}
3. 对弧长的曲线积分的定义(1)
定义:设L为 xoy 面内的一条光滑曲线弧,函数 f (x, y) 在 L 上有界。在
思考
(1) L能否为空间曲线?
(2) 定义的条件能否适当减弱?
(3) 可积条件?
高等数学 第6章 第四节 平面曲线的弧长

A M0
O
n
⌒
M i1 M i 的极限存在,则称此极限为曲线弧 AB 的弧长,
i 1
⌒
并称此曲线弧 AB是可求长的。
定理:
光滑曲线弧(即弧上任意点具有一阶连续导数)是可求长的。
•
M n1
• •
B Mn
x
1
二.直角坐标情形
y
设曲线弧由
y f (x)
y f ( x) (a x b)
给出, 其中f(x)在[a,b]上 上具有一阶连续导数,现在来 计算这曲线弧的长度。
(3) 极坐标
s r 2 ( ) r'2 ( )d
思考题: 一根弹簧按等速螺线 r =a 盘绕,共计10 圈,已知每圈的间隔为 10mm,求弹簧的全长。
AB
10
解: 考察第1、2两圈的间隔,如图 A、B两点的坐标分别为:
(2 ,2a), (4 ,4a)
所以AB 4a 2a 2a 10 解得: a 5
弹簧共10圈, 由0增加到20
s 20 r( )2 r'( )2 d a 20 1 2 d
0
0
查表 5 1 2
1 2 ln(
20
1 2 ) 0 3144.2(mm )
11
于是所求弧长为
s
'2 t '2 t dt
5
例3 计算摆线
x
y
a(
a(1
sin ) cos )
的一拱
y
2a
y y(x)
(0 2 ) 的长度。
2a
O
a
解:
∵
x' a(1 cos )
y' a sin
高数-对弧长的曲线积分

o z
x
B
M n1
弧 上对弧长的曲线积分为
n
f
(
x,
y,
z)ds
lim
0
i 1
f
(i
,i
,
i
)
si
.
(i ,i , i ) Mi
0 M2
si
M i 1
y
A M1
x
(6) 函数f ( x, y)在闭曲线 L上对弧长的
曲线积分记为 L f ( x, y)ds. 三、第一类曲线积分的性质
( y0 Y )
L f ( x, y)ds f [(t), (t)] (t)2 (t)2d t
公式的其它几种情形
( 3 ) 若 f ( x, y) 1, 则有
n
L
f ( x, y)ds
lim
0
i 1
f
(
i
,i
)
si
n
lim
0
si
i 1
s
(曲线弧 L 的长度)
即曲线弧 L 的长度 Lds
可看作
x
y
t,
(t),
( x0 t X ),
f ( x, y) f [x, ( x)],
d s (t)2 (t)2d t 1 (t)2d t 1 ( x)2d x
所以有
L f ( x, y)ds xX0 f [ x, ( x)] 1 2( x)dx.
( x0 X )
L f ( x, y)ds f [(t), (t)] (t)2 (t)2d t
解
(3)将 表
示成参数方程
x
a cos
华师大版弧长和扇形的面积课件

THANKS
感谢观看
实例二:计算扇形的面积
总结词
掌握扇形面积的计算方法
详细描述
本实例将介绍如何使用华师大版ppt课件来计算扇形的面积。首先,需要确定扇形的半径和圆心角的大小,然后 根据公式计算面积。公式为:扇形面积 = (圆心角/360° × 圆的面积) - (三角形面积)。在ppt中,将通过图形和公 式相结合的方式,详细解释计算过程。
实例三:计算组合图形的面积
总结词
掌握计算组合图形面积的方法
详细描述
本实例将介绍如何使用华师大版ppt课件来计算组合 图形的面积。组合图形可以由多个基本图形组成,如 三角形、矩形、圆等。首先,需要将组合图形分解为 基本图形,然后分别计算各基本图形的面积,最后将 各基本图形的面积相加得到组合图形的总面积。在 ppt中,将通过具体实例演示如何进行分解、计算和 组合,以帮助学生掌握计算组合图形面积的方法。
在学习过程中,我遇到了一些困难,如理解圆心角与弧长和扇形面积的关系,但在老师的讲 解和自己的思考下,我逐渐克服了这些困难。
通过本节课的学习,我意识到数学在实际生活中的应用价值,弧长和扇形面积的计算在日常 生活和工作中有着广泛的应用。
下节课预告与预习
下节课我们将学习圆的周长和面积的 计算方法,掌握圆的基本性质和应用 。
计算弧长的公式为:s = θ/360° × 2πr,其中 θ 是圆心角,r 是圆的半 径。
弧长是圆周长的一部分,其大小取决 于圆心角的大小。在同一个圆或等圆 中,弧长与圆心角的大小成正比。
扇形的定义
扇形是由一个圆心角及其所对的 弧长所围成的图形。
高数第六章答案
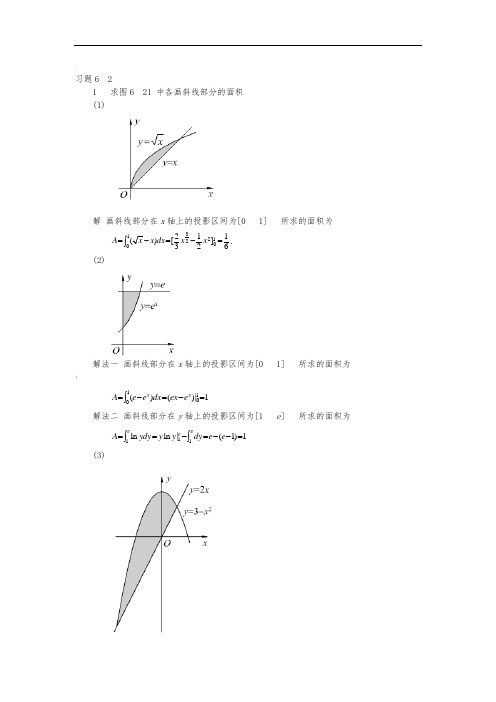
.习题621 求图621 中各画斜线部分的面积 (1)解 画斜线部分在x 轴上的投影区间为[0 1] 所求的面积为61]2132[)(1022310=-=-=⎰x x dx x x A . (2)解法一 画斜线部分在x 轴上的投影区间为[0 1] 所求的面积为 (1|)()(1010=-=-=⎰x x e ex dx e e A解法二 画斜线部分在y 轴上的投影区间为[1 e ] 所求的面积为1)1(|ln ln 111=--=-==⎰⎰e e dy y y ydy A ee e(3)解 画斜线部分在x 轴上的投影区间为[3 1] 所求的面积为332]2)3[(132=--=⎰-dx x x A(4)》解 画斜线部分在x 轴上的投影区间为[1 3] 所求的面积为332|)313()32(3132312=-+=-+=--⎰x x x dx x x A2. 求由下列各曲线所围成的图形的面积(1) 221x y =与x 2y28(两部分都要计算)解388282)218(220220*********--=--=--=⎰⎰⎰⎰dx x dx x dx x dx x x A34238cos 16402+=-=⎰ππtdt346)22(122-=-=ππS A—(2)xy 1=与直线yx 及x 2解所求的面积为 ⎰-=-=212ln 23)1(dx x x A(3) y e xy ex与直线x 1解所求的面积为⎰-+=-=-1021)(ee dx e e A x x\(4)y =ln x , y 轴与直线y =ln a , y =ln b (b >a >0). 解所求的面积为a b e dy e A ba y ba y -===⎰ln ln ln ln 3 求抛物线y x 24x 3及其在点(0 3)和(3 0)处的切线所围成的图形的面积解y 2 x 4~过点(0, 3)处的切线的斜率为4 切线方程为y 4(x 3) 过点(3, 0)处的切线的斜率为2 切线方程为y 2x 6 两切线的交点为)3 ,23( 所求的面积为49]34(62[)]34(34[23023232=-+--+-+-+---=⎰⎰dx x x x x x x A4 求抛物线y 2=2px 及其在点),2(p p 处的法线所围成的图形的面积解2y y 2p在点),2(p p处1),2(=='p p y p y 法线的斜率k 1$法线的方程为)2(px p y --=- 即y p x -=23求得法线与抛物线的两个交点为),2(p p 和)3,29(p p -法线与抛物线所围成的图形的面积为 233232316)612123()223(p y p y y p dy p y y p A p p pp =--=--=--⎰5 求由下列各曲线所围成的图形的面积(1)2a cos解所求的面积为 》⎰⎰==-2022222cos 4)cos 2(21πππθθθθd a d a A a 2(2)x a cos 3t , y a sin 3t ;解所求的面积为 ⎰⎰⎰===2042202330sin cos 34)cos ()sin (44ππtdt t a t a d t a ydx A a2206204283]sin sin [12a tdt tdt a πππ=-=⎰⎰。
微积分弧长公式

微积分弧长公式微积分弧长公式,也称微分弧长公式,是在高等数学中,表示曲线上线段长度的一种数学公式。
由德国数学家威廉布哈里发现并完成,于17是其出名的作品内容之一,它为理解曲线概念,特别是计算曲线上某点的位置和连续性,提供了非常重要的依据。
通常,当我们所讨论的曲线是由某一关系式定义的二维曲线时,需要用到微积分弧长公式,其方程式如下:弧长公式:L =_{a}^{b}[1 + (f(x))^2]dx其中,L表示曲线上某段线段的长度,a和b分别表示线段两端点的横坐标,f(x)示函数 f(x)导数。
由于古希腊数学家赫拉克利特和欧几里得对数学提出的有限次微分与微积分原理可以很好的推广到几何的概念上,微积分弧长公式也经推广到三维空间中,其方程式如下:弧长公式:L =_{a}^{b}[1 + (f(x))^2 + (f(x))^2]dx其中,f(x) f(x)别表示函数 f(x)一阶和二阶导数。
微积分弧长公式已经成为数学研究和教学中最重要的基础公式之一,在微积分教学中经常使用,有助于清晰的表示曲线的特征,从而表示形式化和让学生能够理解。
由微积分弧长公式可以推出一些其它的公式,如牛顿二次曲线的弧长公式、椭圆的弧长公式和双曲线的弧长公式。
牛顿二次曲线的弧长公式可以用来计算圆弧的长度,如:L = 2√[R^2 - (R - x)^2]其中,L示圆弧长度,R示圆半径,x示圆弧上的点的横坐标。
此外,微积分弧长公式也可以用来计算曲线的内接圆半径,如: r =[1 + (f(x))^2]其中,r示曲线上点的内接圆半径,f(x)示函数 f(x)导数。
微积分弧长公式直接影响到各种学科上的计算,它在科学计算、机械工程、地理学等方面都起着很重要的作用。
例如,在地球物理学中,它可用来描述地球表面特征,从而评估地形地貌演变等。
此外,微积分弧长公式也可以用来计算机器人工作空间中路径曲线的弧长,以确定机器人的行驶范围和行驶路径的安全性。
总之,微积分弧长公式为高数学家们 (特别是曲线几何学家)供了重要的理解曲线的依据,帮助人们更清楚的描述曲线的概念,从而让人们更好的掌握和使用曲线知识,为很多科学计算提供了有效的方法,并对实际应用有着重要的意义。
高数弧长ds的三种公式推导

高数弧长ds的三种公式推导
在高等数学中,弧长是指曲线的一部分的长度。
以下是高数弧长的三种公式推导:
1. 直角坐标系下的弧长公式:
设曲线为函数y=f(x),曲线上两点A(x₁,y₁)和B(x₂,y₂)的弧长ds为两点之间的距离,即√((x₂-x₁)²+(y₂-y₁)²)。
由于y=f(x),则y₂=f(x₂)和y₁=f(x₁)。
将这些代入距离公式,得到弧长公式为:ds=√((dx)²+(dy)²)=√(1+(dy/dx)²)dx。
2. 参数方程下的弧长公式:
设曲线的参数方程为x=x(t),y=y(t),参数t的范围为[a,b]。
曲线上两点A和B的弧长ds为两点之间的距离,即√((x(t)₂-
x(t)₁)²+(y(t)₂-y(t)₁)²)。
将参数方程代入距离公式,并利用导数的链式法则,得到弧长公式为:ds=√((dx/dt)²+(dy/dt)²)dt。
3. 极坐标系下的弧长公式:
设曲线的极坐标方程为r=r(θ),θ的范围为[α,β]。
曲线上两点A和B的弧长ds为两点之间的距离,即√((r(θ)₂-r(θ)₁)²+(r(θ)₃-r(θ)₂)²)。
将极坐标方程代入距离公式,并利用极坐标导数的公式,得到弧长公式为:ds=√(r²+(dr/dθ)²)dθ。
这些是高数中常见的弧长公式推导,可以根据不同的曲线形式和坐标系选择适合的公式进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ds (dx)2 (dy)2 [ 2(t ) 2(t )](dt )2
2(t ) 2(t )dt
弧长 s 2(t) 2(t)dt.
例3
求摆线
x y
a a1
sin cos
的一拱0
2
的长度。
解 x a1 cos y asin
s 2 x2 y2 d 0
2
2 (
x 1)3 被抛物线y 2
x
3
3
截得的一段弧的长度 .
三、计算星形线 x a cos3 t ,y a sin3 t 的全长 .
四、求心形线r a ( 1 cos )的全长.
五、证明:曲线 y sin x (0 x 2) 的弧长等于椭圆
x 2 2 y 2 2 的周长.
六、在 摆线 x a ( t sin t ), y a ( 1 cos t ) 上求 分 摆 线第一拱成1 : 3 的点的坐标.
弧长元素 ds 1 y2dx 弧长 s b 1 y2dx. a
例1
计算曲线
y
2
x
3 2
上相应于
x 从a 到b 的一
3
段弧的长度.
解
y
1
x2,
ds
1
(
x
1 2
)2
dx
1 xdx,
所求弧长为
a
b
s
b
1
xdx
2
[(1
3
b)2
(1
3
a)2 ].
a
3
x
例2. 求连续曲线段 y
cos t dt 的弧长.
解 r a,
s
r 2( ) r2( )d
2
2
0
a2 2 a2d a 0
2 1d
a 2 1 42 ln( 2 1 42 ) . 2
例6 求心形线r a1 cos a 0的全长。
解 由对称性
s2
r 2 ( ) r2 ( )d
0
2 2a 1 cos d 0
练习题答案
一、1、1 1 ln 3 ;2、a 2 ;
22
2
二、
8
[(
5
)
3 2
1].
92
三、6a .
四、8a .
六、(( 2 3)a, 3 a) . 3 22
3、 5 ln 3 . 12 2
i 1
曲线弧AB 的弧长.
二、直角坐标情形
设曲线弧为 y f ( x) y (a x b),其中 f ( x)
在[a, b]上有一阶连续导数
取积分变量为x ,在[a,b]
dy
上任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长
小切线段的长 (dx)2 (dy)2 1 y2dx
2
解:
cos x 0,
2
x
2
s 2 1 y2 d x 2 2 1 ( cos x )2 d x
2
0
2 2
0
2 cos x d x 2 2
2
2sin
x 2
2
0
4
三、参数方程情形
曲线弧为
x y
(t) ,
(t)
( t )
其中 (t ), (t )在[ , ]上具有连续导数.
四、极坐标情形
曲线弧为 r r( ) ( )
其中 ( )在[ , ]上具有连续导数.
x y
r( r(
)cos )sin
( )
ds (dx)2 (dy)2 r 2( ) r2( )d ,
弧长 s r 2( ) r2( )d .
例 5 求阿基米德螺线r a (a 0)上相应于 从0到2的弧长.
一、平面曲线弧长的概念
设 A、B 是曲线弧上的两 y
个端点,在弧上插入分点
A M0 , M1, Mi ,
M2 M1
M n1 B Mn
, Mn1, Mn B
A M0
o
x
并依次连接相邻分点得一内接折线,当分点的数目
无限增加且每个小弧段都缩向一点时,
n
此折线的长 | M i1M i |的极限存在,则称此极限为
4a cos d 8a. 02
五、小结
平面曲线弧长的概念
弧微分的概念
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
思考题
闭区间[a, b] 上的连续曲线 y f ( x)
是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
练习题
一、填空题:
1、曲线 y ln x 上相应于 3 x 8 的一段弧长为
2a
si
n
d
0
2
8a.
2
2
2
例 4 求星形线 x 3 y 3 a 3 (a 0)的全长.
解 星形线的参数方程为
x a cos3 t
y
a
sin
3
t
(0 t 2)
y
a
o
ax
根据对称性 s 4s1
4 2 0
x2 y2dt
4 2 3a sin t cos tdt 0
6a.
____________;
2、渐 伸 线 x a(cos t t sin t ) , y a(sin t t cos t)
上相应于 t 从 0 变到 的一段弧长为______;
3、曲 线 r 1 自 3 至 4 一 段 弧 长 为
4
3
____________ .
二、计算半立方抛物线 y 2
