计算题典型题总结
宏观经济学计算题总结

1.经济模型为C =20+0.75(Y -T );I =380;G =400;T =0.20Y ;Y =C +I +G (1)计算边际消费倾向(2)计算均衡收入水平(3)在均衡收入水平下,政府预算盈余为多少?(4)若G 从400增加到410,计算政府支出乘数,并解释它不等于MPC-11的原因(MPC 为边际消费倾向)。
(1)因为C =200+0.75(Y -T),所以边际消费倾向=0.75(2)Y =C +I +G =20+0.75(Y -T )+380+400=20+0.75⨯0.8Y +380+400 解得:Y =2000 (3)预算盈余为T -G =0.2⨯2000-400=0 (4)政府支出乘数5.2)20.01(75.011)1(11=--=--=t b k ggk 之所以不等于MPC-11,是因为当税收为收入的函数时,收入中要有一定比例作为税收上缴给政府,因而可支配收入减少了。
均衡时Y =C +I +G =a +b(1-t)Y +I +G 所以,MPCt b k g -≠--=11)1(11.假定边际消费倾向为0.9,所得税为收入的三分之一,政府决定增加支出以使国民生产总值增加750美元,增幅开支增加多少?这对财政赤字有何影响?)1(11t b k g --=所以)]1(1[t b Y k YG g --∆=∆=∆ 得300)]3/1(9.01[750=-⨯=∆G预算赤字的变动即政府开支变动减去税收的变动。
政府开支上升300美元,因国民生产总值增加750美元同时边际税率为1/3,即税收增加250美元,所以预算赤字上升50美元。
2.假设某经济的消费函数为C =100+0.8d Y (其中d Y 为个人可支配收入);投资I =100,政府购买支出G =200,政府转移支付TR =62.5(单位均为10亿美元),税率t =0.25。
问:(1)均衡国民收入是多少?(2)投资乘数和政府税收乘数分别是多少?(3)当政府将一笔支出用在政府购买上,对国民收入的影响是否和将这一笔支出用在政府转移支付上对国民收入的影响一样?为什么?(1)根据题意可得 Y =C +I +G =100+0.8⨯(Y -0.25Y +62.5)+100+200 =450+0.6Y 得Y =1125(2)投资乘数5.275.08.011)1(11=⨯-=--=t b k i (3) 税收乘数5.175.08.01)25.01(8.0)1(1)1(-=⨯--⨯-=----=t b t b k T(4)不一样。
50道经典典型计算题解析

50道典型计算题解析1.【基准法】93+96+97+95+89+90+94+87+95+92原式=(90+3)+(90+6)+(90+7)+(90+5)+(90-1)+90+(90+4)+(90-3)+(90+5)+(90+2)=90×10+(3+6+7+5-1+4-3+5+2)=900+28=9282.【位值原理】(123456+234561+345612+456123+561234+612345)÷3【分析】仔细观察我们可以发现1、2、3、4、5、6分别在个、十、百、千、万、十万,六个数位上各出现过一次,所以原式=[(1+2+3+4+5+6)×111111]÷3=21×111111÷3=7×111111=7777773.【巧妙分组】2005+2004-2003-2002+2001+2000-1999-1998+1997+1996-……-7-6+5+4-3-2+1【分析】将后四项每四项分为一组,每组的计算结果都是0,后2004项的计算结果都是0,剩下第一项,结果是2005。
原式=123420012002200320042005+--+--+=20054.【拆分取整】2999+999×999【分析】计算时9、99、999类的数字时可以将其看成10-1、100-1、1000-1或者拆出1和其凑整计算,故原式=2000+999+999×999=2000+999×(1+999)=2000+999000=10010005.【乘法凑整】333333×333333【分析】将333333拆成3×111111,3×3=9,999999看成1000000-1。
原式=3×111111×3×111111=999999×111111=(1000000-1)×111111=111111000000-111111=1111108888896.【乘法分配律逆用】2005×2004-2004×2003+2003×2002-2002×2001+……+3×2-2×1原式=(2005-2003)×2004+(2003-2001)×2002+……+(3-2)×2=2×(2004+2002+2000+ (2)=2×2×(1002+1001+1000+ (1)=2×2×(1002+1)×1002÷2=20100127.【乘法分配律逆用】80×1995-3990+1995×22【分析】把3990分解为1995×2,这样80×1995、2×1995、22×1995中都有相同的乘数,可以利用乘法分配律进行巧算。
高中化学计算题学霸总结(含答案)

高中化学计算题学霸总结(含答案)高中化学计算题学霸总结(含答案)阳光老师:祝你学业有成一、计算题(本大题共30小题,共240.0分)1.把铁、铝混合物溶于盐酸中,反应后盐酸的浓度变为,溶液体积变化忽略不计。
求反应中消耗HCl的物质的量和该混合物中铝、铁的物质的量。
答案】消耗HCl的物质的量:设Al、Fe的物质的量分别为x、y。
2Al + 6HCl → 2AlCl3 + 3H2↑Fe + 2HCl → FeCl2 + H2↑根据反应方程式,消耗HCl的物质的量为2x + y。
该混合物中铝、铁的物质的量:根据题意,铝、铁混合物中铝、铁的质量比为2:3,设铝、铁的质量分别为m1、m2,则有:m1/m2 = 2/3m1 + m2 = 100g解得m1 = 40g,m2 = 60g铝、铁的相对原子质量分别为27和56,所以它们的物质的量分别为x = 1.48mol,y = 1.07mol。
解析】本题考查物质的量的计算,难度不大,解题的关键是对物质的量公式的熟练应用。
2.在由Na2CO3和NaHCO3组成的混合物中加入足量盐酸充分反应后,收集CO2的质量分数。
不考虑溶解,试计算原混合物中Na2CO3的质量分数。
答案】原混合物中Na2CO3的质量分数为。
设Na2CO3的物质的量为x,NaHCO3的物质的量为y。
Na2CO3 + 2HCl → 2NaCl + CO2↑ + H2ONaHCO3 + HCl → NaCl + CO2↑ + H2O根据反应方程式,CO2的物质的量为x + y。
CO2的质量分数为:答:原混合物中Na2CO3的质量分数为。
解析】本题考查质量分数的计算,掌握物质的性质和质量分数的计算方法是解答该题的关键,试题较容易。
3.计算质量比为51:32:34的C6H5OH、CH3OH、C2H5OH,其物质的量之比为______,它们所含氢原子数之比为______,所含质子数之比为______。
有含为,则C6H5OH 的摩尔质量为______,R的相对原子质量为______。
计算方法习题集及答案(总结版)

雅克比法:
3 10 12 5
3 (k ) 2 (k ) x1( k +1) = − 5 x2 − 5 x3 −
,x
( k +1) 2
(k ) 1 (k ) =1 4 x1 − 2 x 3 + 5
18 i
,x
( k +1) 3 −4
(k ) 3 =−1 + 10 x (2 k ) + 5 x1
取初始向量 x
(2) x (3) x
3
= 1+ x2 =
,对应迭代公式 x 对应迭代公式 x
0
k +1
= 3 1 + x k2 ;
2
1 , x −1
k
+1 =
1 xk − 1
。
0
判断以上三种迭代公式在 x 解: (1) ϕ ( x) = 1 + x1
2
= 1 .5
的收敛性,选一种收敛公式求出 x
2 x3
−
2 3
= 1 .5
5
习题 3
1.
设有方程组
5 x1 + 2 x 2 + x3 = −12 − x1 + 4 x 2 + 2 x3 = 20 2 x − 3x + 10 x = 3 2 3 1
( k +1) (k )
∞
(1)
考察用 Jacobi 法,Gauss-Seidal 法解此方程组的收敛性; −x (2) 用 Jacobi 法及 Gauss-Seidal 法解方程组,要求当 x
1.
x
k +1 k k
'
<1
公式收敛
西方经济学计算题总结

1。
已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P.(1)求均衡价格P e和均衡数量Q e,并作出几何图形.(1)Q d=50-5P Q s=-10+5PQ d=Q s,有50-5P=-10+5PP e=6Q e=50-5×6=202. 已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2=30元,该消费者的效用函数为U=3X1X错误!,该消费者每年购买这两种商品的数量应各是多少?每年从中获得的总效用是多少?解答:根据消费者的效用最大化的均衡条件错误!=错误!整理得X2=错误!X1(1)预算约束条件20X1+30X2=540,得20X1+30·错误!X1=540解得X错误!=9X错误!=12因此,该消费者每年购买这两种商品的数量应该为X1=9,X2=12将以上最优的商品组合代入效用函数,得U*=3X错误!(X错误!)2=3×9×122=3 8883。
已知生产函数Q=f(L,K)=2KL-0.5L2-0.5K2,假定厂商目前处于短期生产,且K=10。
(1)写出在短期生产中该厂商关于劳动的总产量TP L函数、劳动的平均产量AP L函数和劳动的边际产量MP L函数。
(2)分别计算当劳动的总产量TP L、劳动的平均产量AP L和劳动的边际产量MP L各自达到最大值时的厂商的劳动投入量。
(3)什么时候AP L=MP L?它的值又是多少?解答:(1)由生产函数Q=2KL-0。
5L2-0。
5K2,且K=10,可得短期生产函数为Q=20L-0。
5L2-0.5×102=20L-0.5L2-50TP L=20L-0.5L2-50AP L=错误!=20-0。
5L-错误!MP L=错误!=20-L(2)关于总产量的最大值:令错误!=0,即错误!=20-L=0解得L=20所以,当劳动投入量L=20时,劳动的总产量TPL达到极大值.关于平均产量的最大值:令错误! =0,即错误! =-0.5+50L -2=0解得 L =10(已舍去负值)所以,当劳动投入量L =10时,劳动的平均产量AP L 达到极大值。
2024工程经济计算题总结

2024工程经济计算题总结一、工程经济计算题类型工程经济计算题有好多类型呢,就像资金时间价值计算。
这部分啊,有单利和复利的计算。
单利计算很直白,就像你存钱,本金乘以利率乘以时间就得到利息啦。
比如说你存100块,年利率5%,存3年,单利利息就是100×0.05×3 = 15块。
复利就不一样啦,它是利滚利的,今年的本金加上利息作为下一年的本金来计算利息,那计算起来就稍微复杂点,但也挺有趣的。
还有就是投资回收期的计算。
这个就好比你投资一个小生意,要算多久能把本钱赚回来。
有静态投资回收期和动态投资回收期。
静态的不考虑资金时间价值,就简单地把每年的净收益累加,直到等于初始投资的时候,那个时间就是静态投资回收期。
动态的呢,就要把每年的净收益折现之后再累加,这个就需要用到折现系数啦,计算起来要多费点心思。
二、关于成本计算成本计算在工程经济里也是个大头。
比如说总成本费用的计算,它包括了固定成本和可变成本。
固定成本就是那些不管你生产多少产品都不会变的成本,像厂房租金之类的。
可变成本就是随着产量变化而变化的成本,像原材料啊。
总成本费用的计算式就是固定成本加上可变成本乘以产量。
还有经营成本的计算,经营成本等于总成本费用减去折旧减去摊销减去利息支出。
这折旧和摊销的计算又有不同的方法,像直线折旧法,就是把固定资产的价值平均分摊到每个使用年限里。
三、经济效益评价指标计算这里面有净现值(NPV)的计算。
NPV就是把项目寿命期内各年的净现金流量按照一定的折现率折现到初始点的现值之和。
如果NPV大于0呢,说明这个项目在经济上是可行的,就像你找到了一个能赚钱的好项目。
内部收益率(IRR)的计算就有点麻烦啦,它是使得项目净现值为0的折现率。
要通过试错法或者使用专门的软件工具来计算。
还有投资利润率、投资利税率等指标的计算,这些指标可以从不同的角度来评价项目的经济效益。
四、设备更新计算设备更新的时候也有很多计算要做。
欧姆定律计算题(典型整理版)

欧姆定律典型题
一、串联电路
3.在如图所示的电路中,电源电压为6伏且不变。
电阻R1的阻值为10欧,滑动变阻器R2上标有“20Ω 2A”字样,两电表均为常用电表。
闭合电键S,电流表示数为0.2安。
求:(1)电压表的示数;(2)电阻R2连入电路的阻值;(3)若移动滑动变阻器滑片P到某一位置时,发现电压
表和电流表中有一个已达满刻度,此时电压表和电流表的示数。
二、并联电路
1、两个灯泡并联在电路中,电源电压为12伏特,总电阻为7.5欧姆,灯泡L1的电阻为10欧姆,求:
1)泡L2的电阻
2)灯泡L1和L2中通过的电流
3)干路电流
2、如图2所示电路,当K断开时电压表的示数为6伏, 电流表的示数为1A; K闭合时,电流表的读数为1.5安, 求:⑴灯泡L1的电阻⑵灯泡L2的电阻
3.阻值为10欧的用电器,正常工作时的电流为0.3安,现要把它接入到电流为0.8安的电路中,应怎样连接一个多大的电阻?。
计算分析题总结专题答案
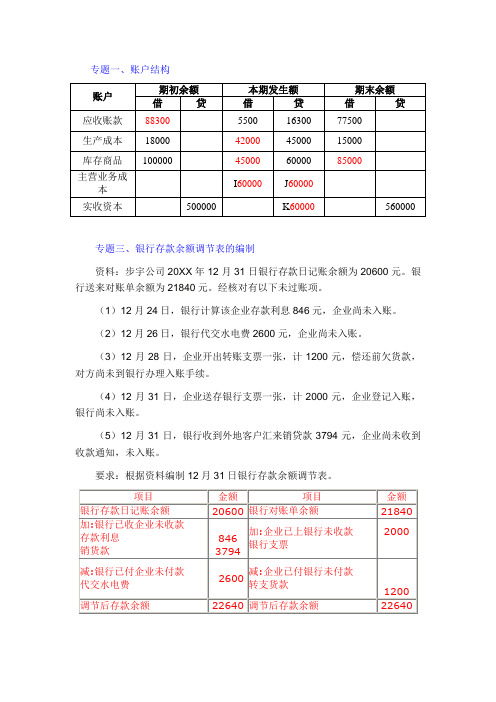
专题一、账户结构专题三、银行存款余额调节表的编制资料:步宇公司20XX年12月31日银行存款日记账余额为20600元。
银行送来对账单余额为21840元。
经核对有以下未过账项。
(1)12月24日,银行计算该企业存款利息846元,企业尚未入账。
(2)12月26日,银行代交水电费2600元,企业尚未入账。
(3)12月28日,企业开出转账支票一张,计1200元,偿还前欠货款,对方尚未到银行办理入账手续。
(4)12月31日,企业送存银行支票一张,计2000元,企业登记入账,银行尚未入账。
(5)12月31日,银行收到外地客户汇来销贷款3794元,企业尚未收到收款通知,未入账。
要求:根据资料编制12月31日银行存款余额调节表。
专题三、成本计算资料:步宇公司8月份发生以下生产经营业务。
(1)5日,生产领用各种材料185000元,其中:甲产品耗用材料98800元(A材料10000千克,C材料9700千克),乙产品耗用材料64000元(B 材料10000千克,C材料3500千克),车间一般耗用15200元(B材料2000千克,C材料1300千克),总部管理部门领用7000元(B材料1400千克)。
借生产成本—甲产品98800—乙产品64000制造费用15200管理费用7000贷原材料185000(2)25日,分配结转本月职工工资52000元,其中制造甲产品生产工人工资15000元,乙产品工人工资20000元,车间管理人员工资7000元,总部管理人员工资10000元借生产成本—甲产品15000—乙产品20000制造费用7000管理费用10000贷原材料52000(3)按工资的14%计提本月福利费。
借生产成本—甲产品2100—乙产品2800制造费用980管理费用1400贷原材料7280(4)26日,计提本月固定资产折旧22500元,其中生产车间应提15000元,总部管理部门应提7500元。
借制造费用15000管理费用7500贷累计折旧22500(5)27日,摊销应由本月负担的修理费2000元,其中生产车间1600元,总部管理部门400元。
计量经济学计算题总结

第一题:iii tii i t u x x x yu x x x y ˆˆˆˆˆˆ2211022110+++++=+++++=ββββββββ)ˆ(ˆi i i SE t ββ=ii i t SE ββˆ)ˆ(= )/()1/(k n RSS k ESS F --= 其中:n 为样本容量(样本个数),K 为模型系数个数。
显著性检验(t 、F 检验)的步骤: 1.假设:t 检验假设为:0H :0=i β;0:1≠i H β;F 检验假设为:0:3210====i H ββββ ;11:βH 、i ββ 2中有一个不为0 2计算统计量:t 检验计算t ,公式为:)ˆ(ˆi ii SE t ββ=;F 检验计算F ,公式为:)/()1/(k n RSS k ESS F --=3.检验:t 检验:若)(2m t t i α>,拒绝0H 假设,反之)(2m t t i α<,接受0H 假设,若拒绝0H 假设则结论为i x 对Y 有显著影响,若接受0H 假设,结论则为i x 对Y 没有显著影响。
注意:1.若题中给出多个)(2m t α,取m=n -k 的值,其中n 为样本容量(样本个数),K 为模型系数个数。
2.若题中只给出一个)(2m t α,则直接去)(2m t α的值。
3.若题中没有给出)(2m t α的值,则默认)(2m t α值为3F 检验:若αF F >,拒绝0H 假设,若αF F <,接受0H 假设,若拒绝0H 假设则结论为2x 、i x x 3中至少有一个对Y 有显著影响,若接受0H 假设,结论则为2x 、i x x 3对Y 都没有显著影响。
回归分析中,可以认为t 检验是对每个参数对Y 显著性进行检验,F 检验则是对整个模型的显著性检验。
若无特殊说明,显著性检验只需做t 检验即可,若说对某一解释变量系数iβ(1≥i )进行显著性检验,即是进行t 检验。
参数i β的经济学含义:无指数(函数类似:ii t u x x x y ++++=+i22110ββββ ):其它条件不变的情况下,ix增加1个单位,Y 平均变动i β个单位(变动为增加还是减少,取决于i β的符号,注意红色的“平均”二字不可少,做题时,自动把Y 和i x 换成其所代表的的含义)有指数(函数类似:i i i u x x x y +++++=ln ln ln ln 22110ββββ ):其它条件不变的情况下,i x 增加1%,Y 平均变动i β(把i β变成百分数形式,变动为增加还是减少,取决于i β的符号,注意红色的“平均”二字不可少,做题时,自动把Y 和i x 换成其所代表的的含义)亦可解释为Y 的i x 的弹性系数为i β第二题:平方和公式:TSS RSS ESS =+(带入上表中即:c b a =+)↓ ↓ ↓自由度公式:TSS RSS ESS f d f d f d ...=+(带入上表中即:z y x =+)平方和均值:fd SS MSS .=(带入上表中即:x a =α;yb=β)TSSESS R =2 k n n R n TSS k n RSSR ----=---=1)1(1)1()(1222R :可决系数,又叫综合判定系数、拟合优度,含义:通过模型可以解释原始数据Y 变动的)%100(2⨯R2R : 修正的可决系数,又叫修正后的拟合优度,含义:考虑自由度的影响,通过模型可以解释原始数据Y 变动的)%100(2⨯R第三题:回归分析结果报告(题中有时候又用:模型估计式)的模板:i ii t u x x x y ˆˆˆˆˆˆ22110+++++=ββββ SE :t :=2R =F =DW数据统计表中的重要英文含义:Dependent Variable :Y Variable :X(C 为常数项) Coefficient :i β Std.Error :)(i SE βT -Statistic :i t (t 检验中的t 值) Prob:P 值 R -squared :2R Adjusted R -square :2RF -Statistic :F (F 检验中的F 值) Durbin -Wastson stat :DW (DW 检验中的DW 值)第四题:第二问:t X 4与期望的符号不一致,因为根据经济学理论,竞争店面数量应该和销售额负相关,而模型中为正相关。
初二生物细胞分裂选择计算题总结

初二生物细胞分裂选择计算题总结
细胞分裂是细胞生命周期中重要的过程之一。
根据题目要求进行计算时,我们需要掌握相关的知识和技巧。
以下是初二生物细胞分裂选择计算题的总结:
1. 分裂时相判断
题目中常常会涉及到细胞分裂的不同时相,包括有丝分裂和无丝分裂。
我们需要根据题目给出的描述或条件来判断所处的分裂时相。
- 若题目描述细胞核消失,染色体可见,细胞质分裂等特征,则为有丝分裂。
- 若题目描述无核分裂,细胞质分裂,染色体未可见等特征,则为无丝分裂。
2. 计算基因组数目
在有丝分裂过程中,问题常常涉及到染色体的变化和基因组数目的计算。
一些常见的计算方式包括:
- 单倍体细胞染色体数目 × ploidy(倍性) = 基因组数目
- 基因组数目 ÷ ploidy = 单倍体细胞染色体数目
3. 计算细胞分裂经历的阶段数
题目中有时要求计算细胞分裂经历的阶段数,常在有丝分裂中出现。
我们需要注意以下几点:
- 有丝分裂经历包括间期、前期、中期和后期四个阶段。
- 从一个细胞周期的分裂阶段到下一个细胞周期的同一分裂阶段,称为一次孢子分裂。
4. 核型记号
在解答某些题目时,我们需要根据生物细胞的核型,使用特定的核型记号。
一些常见的核型记号包括:
- 2n:表示单倍体细胞的染色体数目。
- 2n = 4:表示单倍体细胞的染色体数目为4。
以上是初二生物细胞分裂选择计算题的一些总结,希望能对你的学习和理解有所帮助。
一级建造师案例计算题—成本工期题总结
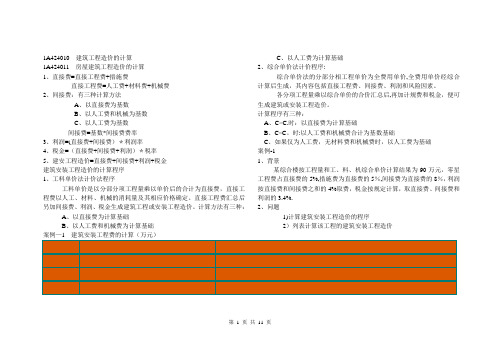
1A424010 建筑工程造价的计算1A424011 房屋建筑工程造价的计算1、直接费=直接工程费+措施费直接工程费=人工费+材料费+机械费2、间接费:有三种计算方法A、以直接费为基数B、以人工费和机械为基数C、以人工费为基数间接费=基数*间接费费率3、利润=(直接费+间接费)*利润率4、税金=(直接费+间接费+利润)*税率5、建安工程造价=直接费+间接费+利润+税金建筑安装工程造价的计算程序1、工料单价法计价法程序工料单价是以分部分项工程量乘以单价后的合计为直接费,直接工程费以人工、材料、机械的消耗量及其相应价格确定。
直接工程费汇总后另加间接费、利润、税金生成建筑工程或安装工程造价。
计算方法有三种:A、以直接费为计算基础B、以人工费和机械费为计算基础C、以人工费为计算基础2、综合单价法计价程序:综合单价法的分部分相工程单价为全费用单价,全费用单价经综合计算后生成,其内容包括直接工程费、间接费、利润和风险因素。
各分项工程量乘以综合单价的合价汇总后,再加计规费和税金,便可生成建筑或安装工程造价。
计算程序有三种:A、C>C.时:以直接费为计算基础B、C<C。
时:以人工费和机械费合计为基数基础C、如果仅为人工费,无材料费和机械费时,以人工费为基础案例-11、背景某综合楼按工程量和工、料、机综合单价计算结果为90万元,零星工程费占直接费的5%,措施费为直接费的5%,间接费为直接费的8%,利润按直接费和间接费之和的4%取费,税金按规定计算,取直接费、间接费和利润的3.4%.2、问题1)计算建筑安装工程造价的程序2)列表计算该工程的建筑安装工程造价案例—1 建筑安装工程费的计算(万元)第 1 页共11 页1A424012 装饰装修工程造价的计算一、计价方法:多采用综合单价法。
内容包括直接工程费、间接费、利润和税金二、计价基础:多采用定额人工费为计算基础计算各种费用三、措施项目费用:多根据现场实际发生情况计取1A424013 建筑工程成本的计算施工成本是指施工项目在施工的全过程中所发生的全部费用支出的总和,包括直接成本和间接成本。
机械基础计算题总结

1、梁的受力及尺寸如图所示,其中q、a均已知,求梁的支座反力。
解:先以BD为研究对象,画受力图,列平衡方程:∑F =0=0∑MAF A+F B- Fc- qa=02a•F B + qa•a/2- 3qa•a=0解得:F B=5qa/4F A=11qa/42、图示由杆AC和杆CD构成的组合梁通过中间铰链C连接。
已知均布载荷q=10kN/m,力偶M=40 kN•m。
试求支座A、B、D的约束力。
解:先以CD为研究对象,画受力图,列平衡方程:∑F =0=0∑MCF D- Fc- 2q=04F D- M- 2q×1=0解得:F D=15KN以AD为研究对象,画受力图,列平衡方程:F D+ F A +F B-4q=04F D- M- 4F A -2F B =0F B = 40 KNF A= -15 KN3、图示空气泵的操纵杆右端所受力为8.5kN ,截面Ⅰ-Ⅰ和Ⅱ-Ⅱ均为高宽比h/b=3的矩形,材料的许用应力[σ]= 50MPa ,试确定两截面的尺寸。
解∑M O =0 F=8.5×0.72=16.1 KNM 1 =8.5×(0.72-0.08)=5.44 KN •m M 2 =16.1×(0.38-0.08)=4.83 KN •m∵[]M W σ≥∴11[]M W σ≥=65.441050⨯=1.088×105mm 3h/b=3 b 1h 12/6=3b 3/6≥1.088×105 得:b 1≥41.7 mm ,h 1≥125.1 mm622 4.8310[]50M W σ⨯≥= 得:b 2≥40.1 mm ,h 1≥120.3 mm4、图示轮系中,各齿轮齿数为Z 1=20,Z 2=40,Z 2′=20,Z 3=30,Z 3′=20,Z 4=40。
试求传动比i 14(判断方向),并问:如果变更的符号,可采取什么措施? 解12341441233(1)403040(1)2020206m n Z Z Z i n Z Z Z ==-∙∙''=-⨯⨯=-如果变更传动比符号,可采取齿轮3´和齿轮4内啮合或加一个中间齿轮的办法。
初中化学计算题知识点总结

初中化学计算题专题一根据化学式的计算 (一)有关化学式的计算1、求相对分子质量,相对分子质量是指化学式中各原子的相对原子质量的总和。
在计算的过程中应留意化学式前面的数字(系数)与相对分子质量及元素符号右下角的数字与相对原子质量之间的关系是“相乘”不是“相加”;若计算结晶水合物的相对分子质量时,化学式中间的“·”与结晶水的相对分子质量之间是“相加”不是“相乘”。
例 计算5CuSO4·5H2O 的相对分子质量总和。
5CuSO4·5H2O=5×[64+32+16×4+5×(1×2+16)] =5×[160+5×18] =12502、求化合物中各元素的质量比:以合物A m B n 为例。
A 、B 元素的质量比nm⨯⨯的相对原子质量的相对原子质量B A 。
例,计算氧化铁中铁元素和氧元素的质量比。
氧化物的化学式:Fe2O3,则 Fe ∶O=56×2∶16×3=112∶48=7∶33、求化合物中某元素的质量分数:化合物中任一元素的质量分数可以用下式计算:某元素的质量分数=%100⨯化合物的总质量该元素的质量。
另:混合物中某物质的质量分数=%100⨯混合物的质量某物质的质量(二)确定化学式的计算1、根据化合物中各元素的质量比求化学式将各元素的质量分别除以其相对原子质量,得到的商之比即为相应的原子个数之比,继而确定其化学式。
例,某硫的氧化物中S 、O 元素的质量比为2:3,该硫的氧化物的化学式为 解析:S 、O 原子个数比为=163322:1:3,所以化学式为SO 3 2、根据化合物中某元素的质量分数求化学式已知某化合物中某元素的质量分数和相对分子质量,可确定该化合物中各原子个数之比,进而确定其化学式。
例,某铁的氧化物中ω(Fe )=70%,则设其化学式为解析:可设该氧化物化学式为FexOy 。
则ω(Fe )=%100y 16x 56x56⨯⨯=70%,解得x:y=2:3则其化学式为Fe2O3根据化合价确定化学式例,曾用作麻醉剂的“笑气”,是一种氮的氧化物,其中氮元素的化合价为+1,则“笑气”的化学式是( )A .N2O5B . NO2C . NO D.N2O根据质量守恒定律确定化学式,反响前后元素的种类,原子数目不变。
计算题典型题总结

1、已知效用函数为U=log a X + log a Y,预算约束为P x*x+P y*y=M。
求:(1)消费者均衡条件;(2)X与Y的需求函数;(3)X与Y的需求的点价格弹性。
2、某消费者的效用函数和预算约束分别为 U=X2/3Y 和 3X+4Y=100,而另一消费者的效用函数为U=X6Y4++lnY,预算约束也是3X+4Y=100。
求:(1)他们各自的最优商品购买数量;(2)最优商品购买量是否相同这与两条无差异曲线不能相交矛盾吗3、某消费者效用函数为 U= ,第一期和第二期的收入分别为 Y1=100 美2元和Y2=180 美元,利率为r,求:(1)第一期和第二期的最优消费;(2)当利率 r 分别取何值时该消费者在第一期将储蓄、贷款或既不储蓄也不贷款(3)当利率r 变化时,对第一期和第二期的消费有什么影响4、已知某厂商的生产函数为 Q=L3/8K5/8,又设 P L=3 元,P K=5 元。
(1)求产量Q=10 时的最低成本支出和使用的 L 与K 的数量;(2)求总成本为160 元时厂商均衡的Q、L 与K 的值。
5、一厂商用资本K 和劳动L 生产x 产品,在短期中资本是固定的,劳动是可变的。
短期生产函数是x=-L3+24L2+240L,x 是每周产量,L 是雇佣劳动量(人),每人每周工作 40 小时,工资每小时为 12 美元。
(1)计算该厂商在生产的第一、二和三阶段上 L 的数值;(2)厂商在短期中生产的话,其产品最低价格为多少;(3)如该厂商每周纯利润要达到 1096 美元,需雇佣 16 个工人,试求该厂商固定成本是多少6、公司正在考虑建造一个工厂。
现有两个方案,方案 A 的短期生产函数为2 2TC A=80+2Q A+,方案B 的短期生产成本函数为TC B=50+Q B。
(1)如果市场需求量仅有8 单位产量的产品,厂商应选哪个方案;(2)如果选择A,市场需求量至少为多少(3)如果公司已经采用两个方案分别建造一个工厂,且市场对其产品的需求量相当大,公司是否必须使用这两个工厂如果计划产量为22 个单位,厂商应如何在两个工厂之间分配产量以使总成本最低7、假设某完全竞争行业有 100 个相同的厂商,每个厂商的成本函数为S TC=+q+10,成本用美元计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.2 1、已知效用函数为 U =log a X + log a Y ,预算约束为 P x*x +P y*y =M 。
求:(1)消费者均衡条件;(2)X 与 Y 的需求函数;(3)X 与 Y 的需求的点价格弹性。
2、某消费者的效用函数和预算约束分别为 U=X 2/3Y 和 3X+4Y=100,而另一消费者的效用函数为 U=X 6Y 4+1.5lnX+lnY ,预算约束也是 3X+4Y=100。
求:(1) 他们各自的最优商品购买数量;(2)最优商品购买量是否相同?这与两条无 差异曲线不能相交矛盾吗?3、某消费者效用函数为 U=C 10.4C 0.6 ,第一期和第二期的收入分别为 Y 1=100 美元和 Y 2=180 美元,利率为 r ,求:(1)第一期和第二期的最优消费;(2)当 利率 r 分别取何值时该消费者在第一期将储蓄、贷款或既不储蓄也不贷款?(3)当利率 r 变化时,对第一期和第二期的消费有什么影响?4、已知某厂商的生产函数为 Q=L 3/8K 5/8,又设 P L =3 元,P K =5 元。
(1)求产量Q=10 时的最低成本支出和使用的 L 与 K 的数量;(2)求总成本为 160 元时 厂商均衡的 Q 、L 与 K 的值。
5、一厂商用资本 K 和劳动 L 生产 x 产品,在短期中资本是固定的,劳动是可变的。
短期生产函数是 x=-L 3+24L 2+240L ,x 是每周产量,L 是雇佣劳动量(人), 每人每周工作 40 小时,工资每小时为 12 美元。
(1)计算该厂商在生产的第一、二和三阶段上 L 的数值;(2)厂商在短期中生产的话,其产品最低价格 为多少;(3)如该厂商每周纯利润要达到 1096 美元,需雇佣 16 个工人,试 求该厂商固定成本是多少?6、公司正在考虑建造一个工厂。
现有两个方案,方案 A 的短期生产函数为2 2 TC A =80+2Q A +0.5Q A ,方案 B 的短期生产成本函数为 TC B =50+Q B 。
(1)如 果市场需求量仅有 8 单位产量的产品,厂商应选哪个方案;(2)如果选择 A , 市场需求量至少为多少?(3)如果公司已经采用两个方案分别建造一个工厂, 且市场对其产品的需求量相当大,公司是否必须使用这两个工厂?如果计划 产量为 22 个单位,厂商应如何在两个工厂之间分配产量以使总成本最低?7、假设某完全竞争行业有 100 个 相 同 的 厂 商 , 每 个 厂 商 的 成 本 函 数 为S TC=0.1q 2+q+10,成本用美元计算。
(1)求市场供给函数;(2)假设市场需求函数为Q D=4000-400P,求市场的均衡价格和产量;(3)假定对每单位产品征收0.9 美元的税,新的市场均衡价格和产量又为多少?厂商和消费者的税收负担各为多少?(4)假定社会福利为消费者剩余CS、生产者剩余CP 和政府税收的总和,试问每单位产品征税0.9 美元之后社会福利变化多少?并作草图表示。
8、一个成本不变行业中完全竞争厂商有下列长期成本函数:LTC=q3-50q2+750q。
q 是厂商每天产量,单位是吨,成本用美元计。
厂商产品的市场需求函数是Q=2000-4P。
这里,Q 是该行业每天销售量,P 是每吨产品价格。
(1)求导该行业长期供给曲线;(2)该行业长期均衡时有多少家厂商?(3)如果课征产品价格20%的营业税,则新的长期均衡时该行业有多少厂商?(4)营业税如废止,而代之以每吨50 美元的消费税,该行业在这种情况下达到长期均衡时有多少家厂商?(5)如果所有税收都废除,行业达到(2)的均衡状态,政府再给每吨产品S 美元的津贴,结果该行业中厂商增加 3 个,试问政府给每吨产品津贴多少?9、完全竞争的成本固定不变行业包含许多厂商,每个厂商的长期总成本函数为:LTC=0.1q3-1.2q2+11.1q ,q 是每个厂商的年产量。
又知市场需求函数为Q=6000-200P,Q 是该行业的年销售量。
(1)计算厂商长期平均成本为最小的产量和销售价格;(2)该行业的长期均衡产量是否为4500?(3)长期均衡状态下该行业的厂商家数;(4)假如政府决定用公开拍卖营业许可证600 张的办法把该行业竞争人数减少到600 个,即市场销售量为Q=600q。
问:① 在新的市场均衡条件下,每家厂商的产量和销售价格为若干?②假如营业许可证是免费领到的,每家厂商的利润为若干?③若领到许可证的厂商的利润为零,每张营业许可证的竞争性均衡价格为若干?10、某垄断者的短期成本函数为STC=0.1Q3-6Q2+140Q+3000,成本用美元计算,Q 为每月产量,为使唤利润极大,他每月生产40 吨,由此赚得的利润为1000 美元。
(1)计算满足上述条件的边际收益,销售价格和总收益;(2)若需求曲线为一条向右下个倾斜直线,计算需求曲线均衡点的点弹性系数之值;(3)假设需求曲线为直线P=a-bQ,从需求曲线推导出MR 曲线,并据此推导出需求方程;(4)若固定成本为3000,价格为90,该厂商能否继续生产?如要停止生产,价格至少要降到多少以下?(5)假设政府对每一单位产品征收一定税款,由此导致利润极大化的产量由原来的40 吨减为39 吨,请根据给定的需求状况和成本状况计算出产量为39 吨的MR 和MC,然后算出每单位产品的纳税额。
11、设垄断者的产品的需求曲线为P=16-Q,P 以美元计,求:(1)垄断者出售8 单位产品的总收益为多少?(2)如果垄断者实行一级价格歧视,垄断者的收益为多少?他掠夺的消费者剩余为多少?(3)如果垄断者实行二级价格歧视,对前 4 个单位的商品定价为12 美元,对后 4 个单位的商品定价为8 美元。
垄断者掠夺的消费者剩余为多少?12、某垄断者的一片工厂所生产的产品在两个分割的市场出售,产品的成本函数和两个市场的需求函数分别为:TC=Q2+10Q,Q1=32-0.4P1,Q2=18-0.1P2。
(1)假设两个市场能实行差别价格,求解利润极大化时两个市场的售价和销售量分别是P1=60,Q1=8;P2=110,Q2=7。
利润为875(提示:找出两个市场的MR 相同时的Q=Q1+Q2).(2)假如两个市场只能索取相同的价格,求解利润极大化时的售价、销售量和利润(提示:找出当两个市场的价格相同时总销售量之需求函数)。
13、某垄断厂商将建立唯一一个工厂,为两个空间上隔离的市场提供服务。
在这两个市场上,垄断厂商可以采取两种价格,不必担心市场之间的竞争和返销,两个市场相距40 英里,中间有条公路相连。
垄断厂商可以把工厂设在任意一个市场上,或者沿公路的某一点。
设 a 和(40-a)分别为从市场 1 和市场2 到工厂距离。
垄断厂商的需求函数和生产函数不受其厂址选择的影响,市场1 的需求函数为P1=100-2Q1;市场2 的需求函数为P2=120-3Q2;垄断厂商的生产成本函数为TC1=80 (Q1+Q2 )-(Q1+Q2 )2 ,运输成本函数为TC2=0.4aQ1+0.5(40-a)Q2。
试确定Q1、Q2、P1、P2 和a 的最优值。
14、垄断竞争市场中一厂商的长期总成本函数为LTC=0.001q3-0.425q2+85q,这里,LTC 是长期总成本,用美元表示,q 是月产量,不存在进入障碍,产量由该市场的整个产品集团调整。
如果产品集团中所有厂商按同样比例调整它们价格,出售产品的实际需求曲线为q=300-2.5p,这里q 是厂商月产量,p 是产品单价。
(1)计算厂商长期均衡产量和价格;(2)计算厂商主观需求曲线上长期均衡点的弹性;(3)若厂商主观需求曲线是线性的,导出厂商长期均衡时的主观需求曲线。
15、假设:(1)只有A、B 两个寡头垄断厂商出售同质且生产成本为零的产品;(2)市场对该产品的需求函数为Q d=240-10p,p 以美元计;(3)厂商A 先进入市场,随之B 进入。
各厂商确定产量时认为另一厂商会保持产量不变。
试求:(1)均衡时各厂商的产量和价格为多少?(2)与完全竞争和完全垄断相比,该产量和价格如何?(3)各厂商取得利润若干?该利润与完全竞争和完全垄断时相比情况如何?(4)如果再有一厂商进入该行业,则行业均衡产量和价格会发生什么变化?如有更多一厂商进入,情况又会怎样?16、某公司面对以下两段需求曲线,p=25-0.25Q(当产量为0—20 时),p=35-0.75Q(当产量超过20 时),公司总成本函数为:TC1=200+5Q+0.255Q2。
(1)说明该公司所属行业的市场结构是什么类型?(2)公司的最优价格和产量是多少?这是利润(亏损)多大?(3 )如果成本函数改为TC2=200+8Q+0.25Q2,最优价格和产量是多少?17、有一位车主要决定是否为其价值20000 美元的汽车安装1950 美元的防盗装置。
安装该装置后会使汽车被盗的概率从0.25 下降到0.15.(1)若效用函数V(W)=lnW,该车主的初始财富为100000 美元,他是否要安装这种防盗装置呢?(2)如果市场上有汽车防盗险可购买,这种全额保险的价格是5200 美元,即5000 美元(20000*0.25)加上200 美元的保险公司行政费用。
保险公司对车主是否安装防盗装置不加任何的监督。
那么车主会购买保险吗?同时还会安装防盗装置吗?(3)如果保险公司愿意花费10 美元来确定车主是否安装了防盗装置,并且只愿意为安装了防盗装置的车主提供全额保险,保险费是3210 美元,即3000 美元(20000*0.15)加上200 美元的保险公司行政费用和10 美元的监督费用,那么车主会购买这种保险吗?18、某人打算作一次环球旅行,计划花费10000 元,旅行给他带来的效用由U(Y)=lnY 给出,其中Y 为旅行花费,在旅行中他有25%的可能性会遗失1000 元。
(1)如果市场上有价格为250 元的保险可购买,此人愿不愿意购买这种保险呢?(2)此人为购买保险愿意支付的最高保费是多少?(3)如果此人购买保险以后变得大意,遗失1000 元的概率从25%上升到30%,这种情况下保费应该是多少?19、设某厂商只把劳动作为可变要素,其生产函数为Q=-0.01L3+L2+36L,Q 为厂商每天产量,L 为工人的日劳动小时数。
所有市场均为完全竞争的,单位产品价格为0.10 美元,小时工资率为 4.8 美元。
试求当厂商利润极大时,(1)厂商每天将投入多少劳动小时?(2)如果厂商每天支付的固定成本为50 美元,厂商每天生产的纯利润为多少?20、考虑一由两种商品和固定要素供给组成的经济。
假设以商品空间定义的社会福利函数为W=(q1+2)q2,隐含的生产函数为q1+2q2-10=0。
试求社会福利函数达最大时q1、q2 之值。
