3机械振动练习与答案
第3章 多自由度机械振动系统 作业答案

⎤ ⎡ x1 ⎤ ⎡ p1 ( t ) ⎤ ⎢x ⎥ = ⎢ p t ⎥ − k3 ⎥ ⎥ ⎢ 2 ⎥ ⎢ 2 ( )⎥ k3 + k 4 ⎥ ⎦⎢ ⎣ x3 ⎥ ⎦ ⎢ ⎣ p3 ( t ) ⎥ ⎦ 0
d ∂T ∂T ∂U ∂D ( )− + + = Qi i ∂qi ∂qi ∂q i dt ∂q
2、拉格朗日法:
1 1 2 12 + m2 x 2 T = m1 x 2 2
U=
1 2 1 1 2 ⎤ k1 x1 + k2 (2 x2 − x1 ) 2 = ⎡ (k1 + k2 ) x12 + 4k2 x1 x2 + 4k2 x2 ⎣ ⎦ 2 2 2
Dr. Rong Guo
School of automotive studies, tongji university
⎡ k1r 2 K =⎢ 2 ⎣ − k1r
⎡3 2 ⎢ 2 Mr ⎢ ⎢ 0 ⎢ ⎣ 0
⎤ ⎥ ( k1 + k2 ) r 2 ⎦ − k1r 2
− k1r 2 ⎤ ⎡θ1 ⎤ ⎡0 ⎤ ⎥⎢ ⎥ = ⎢ ⎥ θ 2 ⎦ ⎣0 ⎦ ( k1 + k2 ) r 2 ⎦ ⎣
⎤ ⎤ ⎡ k1r 2 ⎥ ⎡θ ⎥ ⎢ 1 ⎥ + ⎢ 3 −k r 2 θ Mr 2 ⎥ ⎣ 2 ⎦ ⎣ 1 ⎥ ⎦ 2
x1 2l + k1 x1 2l + m2 x2l = 0 ⎧m1 ⎨ ⎩m2 x2l + k2 ( 2 x2 − x1 ) 2l = 0 x1 + m2 x2l + 2k1 x1 = 0 ⎧2m1 ⎨ x2 − 2k2 x1 + 4k2 x2 = 0 ⎩ m2 ⎡ 2m1 ⎢ 0 ⎣ m2 ⎤ ⎡ x1 ⎤ ⎡ 2k1 ⎢ ⎥ + ⎢ −2 k m2 ⎥ x 2 ⎦⎣ 2⎦ ⎣ 0 ⎤ ⎡ x1 ⎤ ⎡0 ⎤ ⎢ x ⎥ = ⎢0 ⎥ 4k 2 ⎥ ⎦⎣ 2⎦ ⎣ ⎦
机械振动答案

机械振动答案(1)选择题1解析:选D.如图所示,设质点在A 、B 之间振动,O 点是它的平衡位置,并设向右为正.在质点由O 向A 运动过程中其位移为负值;而质点向左运动,速度也为负值.质点在通过平衡位置时,位移为零,回复力为零,加速度为零,但速度最大.振子通过平衡位置时,速度方向可正可负,由F =-kx 知,x 相同时F 相同,再由F =ma 知,a 相同,但振子在该点的速度方向可能向左也可能向右.2.解析:选B.据简谐运动的特点可知,振动的物体在平衡位置时速度最大,振动物体的位移为零,此时对应题图中的t 2时刻,B 对.3.解析:选BD.质点做简谐运动时加速度方向与回复力方向相同,与位移方向相反,总是指向平衡位置;位移增加时速度与位移方向相同,位移减小时速度与位移方向相反.4解析:选C.因为弹簧振子固有周期和频率与振幅大小无关,只由系统本身决定,所以f 1∶f 2=1∶1,选C.5解析:选B.对于阻尼振动来说,机械能不断转化为内能,但总能量是守恒的.6.解析:选B.因质点通过A 、B 两点时速度相同,说明A 、B 两点关于平衡位置对称,由时间的对称性可知,质点由B 到最大位移,与由A 到最大位移时间相等;即t 1=0.5 s ,则T2=t AB +2t 1=2 s ,即T =4 s ,由过程的对称性可知:质点在这2 s 内通过的路程恰为2 A ,即2A =12 cm ,A =6 cm ,故B 正确.7.解析:选A.两球释放后到槽最低点前的运动为简谐运动且为单摆模型.其周期T =2πR g,两球周期相同,从释放到最低点O 的时间t =T4相同,所以相遇在O 点,选项A 正确.8.解析:选C.从t =0时经过t =3π2L g 时间,这段时间为34T ,经过34T 摆球具有最大速度,说明此时摆球在平衡位置,在给出的四个图象中,经过34T 具有负向最大速度的只有C 图,选项C 正确.9.解析:选CD.单摆做简谐运动的周期T =2πlg,与摆球的质量无关,因此两单摆周期相同.碰后经过12T 都将回到最低点再次发生碰撞,下一次碰撞一定发生在平衡位置,不可能在平衡位置左侧或右侧.故C 、D 正确.10.解析:选D.通过调整发生器发出的声波就能使酒杯碎掉,是利用共振的原理,因此操作人员一定是将声波发生器发出的声波频率调到500 Hz ,故D 选项正确. 二、填空题(本题共2小题,每小题8分,共16分.把答案填在题中横线上)11答案:(1)B (2)摆长的测量、漏斗重心的变化、液体痕迹偏粗、阻力变化……12答案:(1)ABC (2)①98.50 ②B ③4π2k计算题13.(10分)解析:由题意知弹簧振子的周期T =0.5 s ,振幅A =4×10-2m. (1)a max =kx max m =kA m=40 m/s 2. (2)3 s 为6个周期,所以总路程为s =6×4×4×10-2m =0.96 m.答案:(1)40 m/s 2(2)0.96 m14.(10分)解析:设单摆的摆长为L ,地球的质量为M ,则据万有引力定律可得地面的重力加速度和高山上的重力加速度分别为:g =G M R 2,g h =G M R +h2据单摆的周期公式可知T 0=2πLg ,T =2πL g h由以上各式可求得h =(T T 0-1)R . 答案:(T T 0-1)R15.(12分解析:球A 运动的周期T A =2πl g, 球B 运动的周期T B =2π l /4g =πl g. 则该振动系统的周期T =12T A +12T B =12(T A +T B )=3π2l g. 在每个周期T 内两球会发生两次碰撞,球A 从最大位移处由静止开始释放后,经6T =9πlg,发生12次碰 撞,且第12次碰撞后A 球又回到最大位置处所用时间为t ′=T A /4. 所以从释放A 到发生第12次碰撞所用时间为t =6T -t ′=9πl g -2T 2l g =17π2lg. 答案:17π2l g16.(12分解析:在力F 作用下,玻璃板向上加速,图示OC 间曲线所反映出的是振动的音叉振动位移随时间变化的规律,其中直线OC 代表音叉振动1.5个周期内玻璃板运动的位移,而OA 、AB 、BC 间对应的时间均为0.5个周期,即t =T 2=12f=0.1 s .故可利用匀加速直线运动的规律——连续相等时间内的位移差等于恒量来求加速度.设板竖直向上的加速度为a ,则有:s BA -s AO =aT 2①s CB -s BA =aT 2,其中T =152 s =0.1 s ②由牛顿第二定律得F -mg =ma ③ 解①②③可求得F =24 N. 答案:24 N机械振动(2)机械振动(3)1【解析】 如图所示,图线中a 、b 两处,物体处于同一位置,位移为负值,加速度一定相同,但速度方向分别为负、正,A 错误,C 正确.物体的位移增大时,动能减少,势能增加,D 错误.单摆摆球在最低点时,处于平衡位置,回复力为零,但合外力不为零,B 错误.【答案】 C2【解析】 质量是惯性大小的量度,脱水桶转动过程中质量近似不变,惯性不变,脱水桶的转动频率与转速成正比,随着转动变慢,脱水桶的转动频率减小,因此,t 时刻的转动频率不是最大的,在t 时刻脱水桶的转动频率与机身的固有频率相等发生共振,故C 项正确.【答案】 C3【解析】 摆球从A 运动到B 的过程中绳拉力不为零,时间也不为零,故冲量不为零,所以选项A 错;由动能定理知选项B 对;摆球运动到B 时重力的瞬时功率是mg v cos90°=0,所以选项C 错;摆球从A 运动到B 的过程中,用时T /4,所以重力的平均功率为P =m v 2/2T /4=2m v 2T ,所以选项D 错.【答案】 B4【解析】 由振动图象可看出,在(T 2-Δt )和(T2+Δt )两时刻,振子的速度相同,加速度大小相等方向相反,相对平衡位置的位移大小相等方向相反,振动的能量相同,正确选项是D.【答案】 D5【解析】 据受迫振动发生共振的条件可知甲的振幅较大,因为甲的固有频率接近驱动力的频率.做受迫振动物体的频率等于驱动力的频率,所以B 选项正确.【答案】 B6【解析】 由题意知,在细线未断之前两个弹簧所受到的弹力是相等的,所以当细线断开后,甲、乙两个物体做简谐运动时的振幅是相等的,A 、B 错;两物体在平衡位置时的速度最大,此时的动能等于弹簧刚释放时的弹性势能,所以甲、乙两个物体的最大动能是相等的,则质量大的速度小,所以C 正确,D 错误.【答案】 C题号 1 2 3 4 5 6 7 8 9 10答案 ACBADACBDACADD(T 2-T 1)R/T 17【答案】 C8【解析】 根据题意,由能量守恒可知12kx 2=mg (h +x ),其中k 为弹簧劲度系数,h 为物块下落处距O 点的高度,x 为弹簧压缩量.当x =x 0时,物块速度为0,则kx 0-mg =ma ,a =kx 0-mg m =kx 0m -g =2mg (h +x 0)mx 0-g =2g (h +x 0)x 0-g >g ,故正确答案为D.【答案】 D9【解析】 由题中条件可得单摆的周期为T =0.30.2s =1.5s ,由周期公式T =2πlg可得l=0.56m.【答案】 A10【解析】 当摆球释放后,动能增大,势能减小,当运动至B 点时动能最大,势能最小,然后继续摆动,动能减小,势能增大,到达C 点后动能为零,势能最大,整个过程中摆球只有重力做功,摆球的机械能守恒,综上可知只有D 项正确.【答案】 D机械振动(4)1解析:选A.周期与振幅无关,故A 正确.2解析:选C.由单摆周期公式T =2π lg知周期只与l 、g 有关,与m 和v 无关,周期不变频率不变.又因为没改变质量前,设单摆最低点与最高点高度差为h ,最低点速度为v ,mgh =12m v 2.质量改变后:4mgh ′=12·4m ·(v 2)2,可知h ′≠h ,振幅改变.故选C.3解析:选D.此摆为复合摆,周期等于摆长为L 的半个周期与摆长为L2的半个周期之和,故D 正确.4解析:选B.由简谐运动的对称性可知,t Ob =0.1 s ,t bc =0.1 s ,故T4=0.2 s ,解得T =0.8s ,f =1T=1.25 Hz ,选项B 正确.5解析:选D.当单摆A 振动起来后,单摆B 、C 做受迫振动,做受迫振动的物体的周期(或频率)等于驱动力的周期(或频率),选项A 错误而D 正确;当物体的固有频率等于驱动力的频率时,发生共振现象,选项C 正确而B 错误.6解析:选BD.速度越来越大,说明振子正在向平衡位置运动,位移变小,A 错B 对;速度与位移反向,C 错D 对.7解析:选AD.P 、N 两点表示摆球的位移大小相等,所以重力势能相等,A 对;P 点的速度大,所以动能大,故B 、C 错D 对.8解析:选BD.受迫振动的频率总等于驱动力的频率,D 正确;驱动力频率越接近固有频率,受迫振动的振幅越大,B 正确.9解析:选B.读图可知,该简谐运动的周期为4 s ,频率为0.25 Hz ,在10 s 内质点经过的路程是2.5×4A =20 cm.第4 s 末的速度最大.在t =1 s 和t =3 s 两时刻,质点位移大小相等、方向相反.。
机械振动、机械波练习题(答案)

机械振动、机械波练习题(参考答案)3. 【答案】B【解析】由单摆周期公式知,T 1=2πL 1g =0.6π s ,T 2=2π L 2g =π s ,摆球从左到右的时间为t =T 1+T 24=0.4π s 。
4. 【答案】 BD5. 【答案】A6. 【答案】AC9. 【答案】AB10.【答案】C11.【答案】A【解析】 由题意得知,该波的周期为T=4s ,则波长λ=vT=1×4m=4mA 、ac 间距离等于一个波长,则波由a 传到c 的时间为4s ,c 起振方向向上,则在4秒<t <5秒这段时间内,c 点从平衡位置向上运动,加速度逐渐增大.故A 正确.B 、由于周期为4s ,所以在4秒<t <5秒这段时间内,质点a 从平衡位置向上运动,速度逐渐减小.故B 错误.C 、ad 间距离等于3/4 波长,则波由a 传到d 的时间为3s ,d 起振方向向上,则在4秒<t <5秒这段时间内,d 点从波峰向平衡位置运动,即向下运动.故C 错误.D 、af 间距离等于1.25个波长,波传到f 点需要5s 时间,所以在4秒<t <5秒这段时间内,f 还没有振动.故D 错误.12.【答案】ABE【解析】两列波相遇后不改变波的性质,所以振幅不变,振幅仍然为2cm ,A 正确;由图知波长λ=0.4m ,由v =λT 得,波的周期为T =λv =1s ,两质点传到M 的时间为34T ,当t =1s 时刻,两波的波谷恰好传到质点M ,所以位移为-4cm ,B 正确,C 错误;质点不随波迁移,只在各自的平衡位置附近振动,所以质点P 、Q 都不会运动到M 点,C 错误;由波的传播方向根据波形平移法可判断出质点的振动方向:两列简谐横波分别沿x 轴正方向和负方向传播,则质点P 、Q 均沿y 轴负方向运动,故E 正确。
13.【答案】AB【解析】图示时质点a 处是波峰与波谷相遇,两列波引起的位移正负叠加的结果是总位移为零,A 正确,质点b 是波峰与波峰相遇,c 点是波谷与波谷相遇,振动都增强,振幅最大,振幅是一列波振幅的两倍,振动最强 ,B 正确。
(完整版)机械振动试题(参考答案)
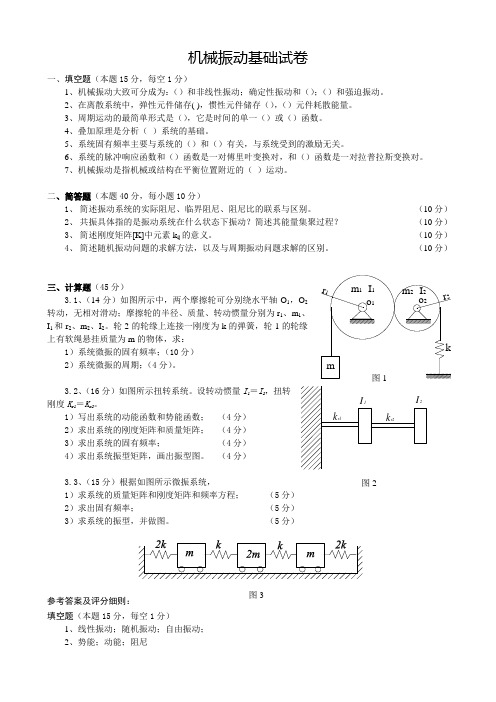
机械振动基础试卷一、填空题(本题15分,每空1分)1、机械振动大致可分成为:()和非线性振动;确定性振动和();()和强迫振动。
2、在离散系统中,弹性元件储存( ),惯性元件储存(),()元件耗散能量。
3、周期运动的最简单形式是(),它是时间的单一()或()函数。
4、叠加原理是分析( )系统的基础。
5、系统固有频率主要与系统的()和()有关,与系统受到的激励无关。
6、系统的脉冲响应函数和()函数是一对傅里叶变换对,和()函数是一对拉普拉斯变换对。
7、机械振动是指机械或结构在平衡位置附近的( )运动。
二、简答题(本题40分,每小题10分)1、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
(10分)2、 共振具体指的是振动系统在什么状态下振动?简述其能量集聚过程? (10分)3、 简述刚度矩阵[K]中元素k ij 的意义。
(10分)4、 简述随机振动问题的求解方法,以及与周期振动问题求解的区别。
(10分)三、计算题(45分) 3.1、(14分)如图所示中,两个摩擦轮可分别绕水平轴O 1,转动,无相对滑动;摩擦轮的半径、质量、转动惯量分别为r 1、m I 1和r 2、m 2、I 2。
轮2的轮缘上连接一刚度为k 的弹簧,轮1上有软绳悬挂质量为m 的物体,求: 1)系统微振的固有频率;(10分)2)系统微振的周期;(4分)。
3.2、(16分)如图所示扭转系统。
设转动惯量I 1=I 2,扭转刚度K r1=K r2。
1)写出系统的动能函数和势能函数; (4分) 2)求出系统的刚度矩阵和质量矩阵; (4分)3)求出系统的固有频率; (4分)4)求出系统振型矩阵,画出振型图。
(4分)3.3、(15分)根据如图所示微振系统, 1)求系统的质量矩阵和刚度矩阵和频率方程; (5分)2)求出固有频率; (5分)3)求系统的振型,并做图。
(5分)参考答案及评分细则:填空题(本题15分,每空1分)1、线性振动;随机振动;自由振动;2、势能;动能;阻尼图2图33、简谐运动;正弦;余弦4、线性5、刚度;质量6、频响函数;传递函数7、往复弹性简答题(本题40分,每小题10分)5、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
机械振动习题及答案完整版.docx

1.1试举出振动设计'系统识别和环境预测的实例。
1.2如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3设有两个刚度分别为心,心的线性弹簧如图T-1.3所示,试证明:1)它们并联时的总刚度k eq为:k eq = k x+ k22)它们串联时的总刚度匕满足:丿-畔+ 土keq & k2解:1)对系统施加力P,则两个弹簧的变形相同为X,但受力不同,分别为: P x = k x x<由力的平衡有:P = ^ + P,=(k1+k2)xp故等效刚度为:k eq^- = k1+k2x2)对系统施加力P,则两个弹簧的变形为:P%i=r 111,弹簧的总变形为:x = x}+x2= P(——I ---- )故等效刚度为:k =—Xk x k2k,2+ k、1 1=—l-------k、k21.4求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为心, 解:对系统施加扭矩T,则两轴的转角为:VTrx系统的总转角为:0 = G + g = Hy- + T-)褊k,i故等效刚度为:犒=二+二1.5两只减振器的粘性阻尼系数分别为q, C2,试计算总粘性阻尼系数"在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P,则两个减振器的速度同为厂受力分别为:P{ - c x x<P2=C2X由力的平衡有:P=£ + E =(q+C2)Xp故等效刚度为:c eq=- = c]+c2X2)对系统施加力P,则两个减振器的速度为:p 1 1故等效刚度为:c eq=- = - + -1.6 一简谐运动,振幅为0. 5cm,周期为0.15s,求最大速度和加速度。
解:简谐运动的a>n= — = /5),振幅为5x10 3m ;= 5x10-cos(^_ 2/r即:—5x10'丽fsin(丽血/s)*610=(話讥。
高考物理《机械振动和机械波》真题练习含答案

高考物理《机械振动和机械波》真题练习含答案1.[2023·新课标卷]船上的人和水下的潜水员都能听见轮船的鸣笛声.声波在空气中和在水中传播时的()A.波速和波长均不同B.频率和波速均不同C.波长和周期均不同D.周期和频率均不同答案:A解析:声波的周期和频率由振源决定,故声波在空气中和在水中传播的周期和频率均相同,但声波在空气和水中传播的波速不同,根据波速与波长关系v=λf可知,波长也不同,故A正确,B、C、D错误.故选A.2.[2024·浙江1月]如图1所示,质量相等的小球和点光源,分别用相同的弹簧竖直悬挂于同一水平杆上,间距为l,竖直悬挂的观测屏与小球水平间距为2l,小球和光源做小振幅运动时,在观测屏上可观测小球影子的运动.以竖直向上为正方向,小球和光源的振动图像如图2所示,则()A.t1时刻小球向上运动B.t2时刻光源的加速度向上C.t2时刻小球与影子相位差为πD.t3时刻影子的位移为5A答案:D解析:以竖直向上为正方向,根据图2可知,t1时刻,小球位于平衡位置,随后位移为负值,且位移增大,可知,t1时刻小球向下运动,A错误;t2时刻,光源的位移为正值,光源振动图像为正弦式,表明其做简谐运动,根据F回=-kx=ma可知,其加速度方向与位移方向相反,位移方向向上,则加速度方向向下,B错误;根据图2可知,小球与光源的振动步调总是相反,由于影子是光源发出的光被小球遮挡后,在屏上留下的阴影,可知,影子与小球的振动步调总是相同,即t2时刻小球与影子相位差为0,C错误;根据图2可知,t3时刻,光源位于最低点,小球位于最高点,根据光沿直线传播,光源能够在屏上留下影子的位置也处于最高点,影子位于正向最大位移处,根据几何关系有ll+2l =A+AA+x影子,解得x影子=5A,即t3时刻影子的位移为5A,D正确.3.[2024·吉林卷]某同学自制双缝干涉实验装置:在纸板上割出一条窄缝,于窄缝中央沿缝方向固定一根拉直的头发丝形成双缝,将该纸板与墙面平行放置,如图所示.用绿色激光照双缝,能够在墙面上观察到干涉条纹.下列做法可以使相邻两条亮条纹中央间距变小的是()A.换用更粗的头发丝B.换用红色激光照射双缝C.增大纸板与墙面的距离D.减小光源与纸板的距离答案:A解析:由于干涉条纹间距Δx=ldλ可知,换用更粗的头发丝,双缝间距d变大,则相邻两条亮条纹中央间距Δx变小,故A正确;换用红色激光照双缝,波长变长,则相邻两条亮条纹中央间距Δx变大,故B错误;增大纸板与墙面的距离l,则相邻两条亮条纹中央间距Δx 变大,故C错误;减小光源与纸板的距离,不会影响相邻两条亮条纹中央间距Δx,故D错误.故选A.4.[2024·浙江1月](多选)在如图所示的直角坐标系中,xOz平面为介质Ⅰ和Ⅱ的分界面(z轴垂直纸面向外).在介质Ⅰ中的P(0,4λ)处有一点波源,产生波长为λ、速度为v的波.波传到介质Ⅱ中,其速度为2v.图示时刻介质Ⅱ中仅有一个波峰,与x轴和y轴分别交于R 和S点,此时波源也恰好位于波峰.M为O、R连线的中点,入射波与反射波在O点相干加强,则()A .介质Ⅱ中波的频率为2v λB. S 点的坐标为(0,-2 λ)C .入射波与反射波在M 点相干减弱D. 折射角α的正弦值sin α=352 答案:BD解析:波从一种介质到另一种介质,频率不变,故介质Ⅱ中波的频率为f =v λ,A 错误;在介质Ⅱ中波长为λ′=2v f=2 λ,由于图示时刻介质Ⅱ中仅有一个波峰,与x 轴和y 轴分别交于R 和S 点,故S 点的坐标为(0,-2 λ),B 正确;由于S 为波峰,且波传到介质Ⅱ中,其速度为2 v .图示时刻介质Ⅱ中仅有一个波峰,与x 轴和y 轴分别交于R 和S 点,则R 也为波峰,故P 到R 比P 到O 多一个波峰,则PR =5λ,则OR =3λ,由于||MO -PM≠2n ·λ2 或(2n +1)λ2 (n =0,1,2,…),故M 点不是减弱点,C 错误;根据n =λ′λ=2 ,则n =sin αOR PR,解得sin α=352 ,D 正确. 5.[2021·天津卷]一列沿x 轴正方向传播的简谐横波,传播速度v =10 m/s ,t =0时位于坐标原点的质点从平衡位置沿y 轴正方向运动,下列图形中哪个是t =0.6 s 时的波形( )答案:B解析:由图中可以看出该波的波长为λ=4 m ,根据v =λT可知该列波的周期为T =0.4 s ,又因为t=0时位于坐标原点的质点从平衡位置沿y轴正方向运动,当t=0.6 s时经历了1.5 T,所以此时位于坐标原点的质点从平衡位置沿y轴负方向运动,结合图像可知B正确.6.[2023·湖南卷]如图(a),在均匀介质中有A、B、C和D四点,其中A、B、C三点位于同一直线上,AC=BC=4 m,DC=3 m,DC垂直AB.t=0时,位于A、B、C处的三个完全相同的横波波源同时开始振动,振动图像均如图(b)所示,振动方向与平面ABD垂直,已知波长为4 m.下列说法正确的是()A.这三列波的波速均为2 m/sB.t=2 s时,D处的质点开始振动C.t=4.5 s时,D处的质点向y轴负方向运动D.t=6 s时,D处的质点与平衡位置的距离是6 cm答案:C解析:由图(b)的振动图像可知,振动的周期为4 s,故三列波的波速为v=λT=4 m4 s=1m/s,A错误;由图(a)可知,D处距离波源C最近的距离为3 m,故开始振动后波源C处的横波传播到D处所需的时间为t C=DC v=3 m1 m/s=3 s故t=2 s时,D处的质点还未开始振动,B错误;由几何关系可知AD=BD=5 m,波源A、B产生的横波传播到D处所需的时间为t AB=ADv=5 m1 m/s=5 s故t=4.5 s时,仅波源C处的横波传播到D处,此时D处的质点振动时间为t1=t-t C =1.5 s由振动图像可知此时D处的质点向y轴负方向运动,C正确;t=6 s时,波源C处的横波传播到D处后振动时间为t2=t-t C=3 s由振动图像可知此时D处为波源C处传播横波的波谷;t=6 s时,波源A、B处的横波传播到D处后振动时间为t3=t-t AB=1 s由振动图像可知此时D处为波源A、B处传播横波的波峰.根据波的叠加原理可知此时D处质点的位移为y=2A-A=2 cm故t=6 s时,D处的质点与平衡位置的距离是2 cm,D错误.故选C.。
大学物理(第四版)课后习题及答案 机械振动

大学物理(第四版)课后习题及答案机械振动13 机械振动解答13-1 有一弹簧振子,振幅A=2.0×10-2m,周期T=1.0s,初相ϕ=3π/4。
试写出它的运动方程,并做出x--t图、v--t 图和a--t图。
13-1分析弹簧振子的振动是简谐运动。
振幅A、初相ϕ、角频率ω是简谐运动方程x=Acos(ωt+ϕ)的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A、ϕ已知外,ω可通过关系式ω=2π确定。
振子运动的速度T和加速度的计算仍与质点运动学中的计算方法相同。
解因ω=2π,则运动方程 T⎛2πt⎛x=Acos(ωt+ϕ)=Acos t+ϕ⎛⎛T⎛根据题中给出的数据得x=(2.0⨯10-2m)cos[(2πs-1)t+0.75π]振子的速度和加速度分别为v=dx/dt=-(4π⨯10-2m⋅s-1)sin[(2πs-1)t+0.75π] a=d2x/dt2=-(8π2⨯10-2m⋅s-1)cos[(2πs-1)t+0.75πx-t、v-t及a-t图如图13-l所示π⎛⎛13-2 若简谐运动方程为x=(0.01m)cos⎛(20πs-1)t+⎛,求:(1)振幅、频率、角频率、周期和4⎛⎛初相;(2)t=2s 时的位移、速度和加速度。
13-2分析可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式x=Acos(ωt+ϕ)作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t值后,即可求得结果。
解(l)将x=(0.10m)cos[(20πs-1)t+0.25π]与x=Acos(ωt+ϕ)比较后可得:振幅A= 0.10 m,角频率ω=20πs-1,初相ϕ=0.25π,则周期T=2π/ω=0.1s,频率ν=1/T=10Hz。
(2)t= 2s时的位移、速度、加速度分别为x=(0.10m)cos(40π+0.25π)=7.07⨯10-2m v=dx/dt=-(2πm⋅s-1)sin(40π+0.25π)a=d2x/dt2=-(40π2m⋅s-2)cos(40π+0.25π)13-3 设地球是一个半径为R的均匀球体,密度ρ5.5×103kg•m。
大学机械振动考试题目及答案

大学机械振动考试题目及答案一、选择题(每题2分,共10分)1. 在简谐振动中,振幅与振动的能量关系是()。
A. 无关B. 成正比C. 成反比D. 振幅越大,能量越小答案:B2. 下列哪个不是机械振动系统的自由度?()。
A. 转动B. 平动C. 振动D. 形变答案:C3. 一个单自由度系统在受到初始条件激励后,其振动形式是()。
A. 简谐振动B. 阻尼振动C. 受迫振动D. 自由振动答案:D4. 在阻尼振动中,如果阻尼系数增加,振动的振幅将()。
A. 增加B. 不变C. 减小D. 先增加后减小答案:C5. 对于一个二自由度振动系统,其振动模态数量是()。
A. 1B. 2C. 3D. 4答案:B二、填空题(每题2分,共10分)6. 一个物体做自由振动时,其频率称为______。
答案:固有频率7. 当外力的频率与系统的固有频率相等时,系统发生的振动称为______。
答案:共振8. 阻尼力与速度成正比的阻尼称为______阻尼。
答案:线性9. 振动系统的动态响应可以通过______分析法求解。
答案:傅里叶10. 在转子动力学中,临界转速是指转子发生______振动的转速。
答案:自激三、简答题(每题5分,共20分)11. 简述什么是简谐振动,并说明其运动方程的形式。
答案:简谐振动是一种周期性的振动,其加速度与位移成正比,且方向相反。
在数学上,简谐振动的运动方程可以表示为:x(t) = A * cos(ωt + φ)其中,A 是振幅,ω 是角频率,t 是时间,φ 是初相位。
12. 解释什么是阻尼振动,并说明其特点。
答案:阻尼振动是指在振动系统中存在能量耗散,导致振幅随时间逐渐减小的振动。
其特点包括振幅逐渐衰减,振动频率可能会随着振幅的减小而发生变化,且阻尼力通常与振动速度成正比。
13. 描述什么是受迫振动,并给出其稳态响应的条件。
答案:受迫振动是指系统在周期性外力作用下的振动。
当外力的频率接近系统的固有频率时,系统将发生共振,此时振幅会显著增大。
机械振动现象练习题(含答案)

机械振动现象练习题(含答案)1. 一个弹簧常数为3000 N/m, 质量为0.2 kg的物体,在弹簧下端受到一个向下的力2 sin(10t) N,其中t为时间(秒)。
求物体的振动方程。
根据牛顿第二定律,可以得到物体的振动方程为:m * x'' + k * x = F(t)其中,m是物体的质量,x是物体的位移,x''是位移对时间的二阶导数,k是弹簧的常数,F(t)是作用在物体上的外力。
根据题目中给出的数据,代入上述公式,我们可以得到:0.2 * x'' + 3000 * x = 2 sin(10t)这就是物体的振动方程。
2. 一个质点在受到一个力F(t) = 0.1 cos(3t) N的作用下进行振动,已知质点的质量为0.5 kg。
求质点的角频率和振动周期。
根据振动方程的形式,我们可以知道物体的振动频率和周期与力的形式有关。
在这个题目中,我们可以看出力的形式为cos(3t),它是一个正弦函数。
如果将cos(3t)函数展开,我们可以得到下面的表达式:F(t) = a cos(wt)其中,a是振幅,w是角频率。
根据题目中给出的数据,我们可以得到:a = 0.1 N,w = 3 rad/s由于振动的频率与角频率之间是有关联的,振动的周期T可以表示为:T = 2π/w代入上述数据,我们可以得到:T = 2π/3 s这就是质点的振动周期。
3. 一个质点质量为0.3 kg,在一竖直方向上的弹簧中振动,弹簧的劲度系数为2000 N/m。
当质点受到一个外力F(t) = 0.5 cos(5t) N时,求质点的振动方程。
根据题目中给出的数据,我们可以得到:m = 0.3 kg,k = 2000 N/m,F(t) = 0.5 cos(5t)代入振动方程的一般形式,我们可以得到:0.3 * x'' + 2000 * x = 0.5 cos(5t)这就是质点的振动方程。
高中物理机械振动练习题(含答案)
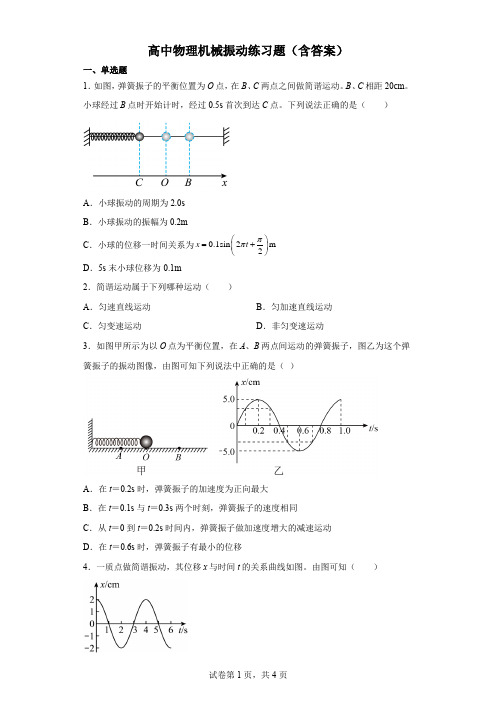
高中物理机械振动练习题(含答案)一、单选题1.如图,弹簧振子的平衡位置为O 点,在B 、C 两点之间做简谐运动。
B 、C 相距20cm 。
小球经过B 点时开始计时,经过0.5s 首次到达C 点。
下列说法正确的是( )A .小球振动的周期为2.0sB .小球振动的振幅为0.2mC .小球的位移一时间关系为0.1sin 2m 2x t ππ⎛⎫=+ ⎪⎝⎭D .5s 末小球位移为-0.1m2.简谐运动属于下列哪种运动( ) A .匀速直线运动 B .匀加速直线运动 C .匀变速运动D .非匀变速运动3.如图甲所示为以O 点为平衡位置,在A 、B 两点间运动的弹簧振子,图乙为这个弹簧振子的振动图像,由图可知下列说法中正确的是( )A .在t =0.2s 时,弹簧振子的加速度为正向最大B .在t =0.1s 与t =0.3s 两个时刻,弹簧振子的速度相同C .从t =0到t =0.2s 时间内,弹簧振子做加速度增大的减速运动D .在t =0.6s 时,弹簧振子有最小的位移4.一质点做简谐振动,其位移x 与时间t 的关系曲线如图。
由图可知( )A.质点振动的频率是4HzB.质点振动的振幅是4cmC.在t=3s时,质点的速度为最大D.在t=4s时,质点所受的回复力为零5.做简谐运动的物体,回复力和位移的关系图是()A.B.C.D.6.当一弹簧振子在竖直方向上做简谐运动时,下列说法中正确的是()A.振子在振动过程中,速度相同时,弹簧的长度一定相等B.振子从最低点向平衡位置运动过程中,弹簧弹力始终做负功C.振子在运动过程中的回复力由弹簧的弹力提供D.振子在运动过程中,系统的机械能守恒7.为使简谐运动单摆的周期变长,可采取以下哪种方法()A.振幅适当加大B.摆长适当加长C.摆球质量增大D.将单摆从上海移到北京8.做简谐振动的物体经过与平衡位置对称的两个位置时,可能相同物理量是()A.位移B.速度C.加速度D.回复力二、多选题9.弹簧振子在光滑水平面上做简谐振动,把小钢球从平衡位置向左拉一段距离,放手让其运动,从小钢球第一次通过平衡位置时开始计时,其振动图像如图所示,下列说法正确的是()A .在t 0时刻弹簧的形变量为4 cmB .钢球振动半个周期,回复力做功为零C .钢球振动一个周期,通过的路程等于10 cmD .钢球振动方程为y =5sin πt cm10.如图所示,摆长为1m 的单摆做小角度的摆动,振动过程的最大位移为6cm ,不计空气阻力,重力加速度22πm/s g =,从摆球向右通过最低点开始计时,则从 1.0s t =到2.0s t =的过程中( )A .摆球的重力势能先减小后增大B .摆球的动能先减小后增大C .摆球振动的回复力先减小后增大D .摆球的切向加速度先增大后减小11.弹簧振子做机械振动,若从平衡位置O 开始计时,经过0.3 s 时,振子第一次经过P 点,又经过了0.2 s ,振子第二次经过P 点,则到该振子第三次经过P 点可能还需要多长时间( ) A .13sB .1.0 sC .0.4 sD .1.4 s第II 卷(非选择题)请点击修改第II 卷的文字说明三、解答题12.如图甲所示,轻弹簧上端固定,下端系一质量为m =0.1kg 的小球,小球静止时弹簧伸长量为10cm。
机械振动试题及答案

机械振动试题及答案⼀、填空题1、机械振动按不同情况进⾏分类⼤致可分成(线性振动)和⾮线性振动;确定性振动和(随机振动);(⾃由振动)和强迫振动,连续振动和离散系统。
2、(弹性元件)元件、(惯性元件)元件、(阻尼元件)元件是离散振动系统的三个最基本元素。
3、在振动系统中,弹性元件存储(势能)、惯性元件存储(动能)、(阻尼元件)元件耗散能量。
4、系统固有频率主要与系统的(质量)和(刚度)有关,与系统受到的激励⽆关。
5、研究随机振动的⽅法是(数理统计),⼯程上常见的随机过程的数字特征有:(均值)(⽅差)(⾃相关函数)和(互相关函数)。
6、周期运动的最简单形式是(简谐运动),它是时间的单⼀(正弦)或(余弦)函数。
7、单⾃由度系统⽆阻尼⾃由振动的频率只与(质量)和(刚度)有关,与系统受到的激励⽆关。
8、简谐激励下单⾃由度系统的响应由(瞬态响应)和(稳态响应)组成。
9、⼯程上分析随机振动⽤(数学统计)⽅法,描述随机过程的最基本的数字特征包括均值、⽅差、(⾃相关函数)和(互相关函数)。
10、机械振动是指机械或结构在(静平衡)附近的(弹性往复)运动。
11、单位脉冲⼒激励下,系统的脉冲响应函数和系统的(频响函数)函数是⼀对傅⾥叶变换对,和系统的(传递函数)函数是⼀对拉普拉斯变换对。
12、叠加原理是分析(线性振动系统)和(振动性质)的基础。
⼆、简答题1、什么是机械振动?振动发⽣的内在原因是什么?外在原因是什么?答:机械振动是指机械或结构在它的静平衡位置附近的往复弹性运动。
振动发⽣的内在原因是机械或结构具有在振动时储存动能和势能,⽽且释放动能和势能并能使动能和势能相互转换的能⼒。
外在原因是由于外界对系统的激励或者作⽤。
2、机械振动系统的固有频率与哪些因素有关?关系如何?答:机械振动系统的固有频率与系统的质量矩阵、刚度矩阵和阻尼有关。
质量越⼤,固有频率越低;刚度越⼤,固有频率越⾼;阻尼越⼤,固有频率越低。
3、从能量、运动、共振等⾓度简述阻尼对单⾃由度系统振动的影响。
机械振动 课后习题和答案 第三章 习题和答案

3.1 如图所示扭转系统。
设12122;t t I I k k ==1.写出系统的刚度矩阵和质量矩阵;2.写出系统的频率方程并求出固有频率和振型,画出振型图。
解:1)以静平衡位置为原点,设12,I I 的转角12,θθ为广义坐标,画出12,I I 隔离体,根据牛顿第二定律得到运动微分方程:111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩ ,即:1112122222122()00t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩所以:[][]12212220,0t t t t t k k k I M K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为:[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭………… (a)或者采用能量法:系统的动能和势能分别为θθ=+2211221122T E I I θθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k求偏导也可以得到[][],M K由于12122;t t I I k k ==,所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为: 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭,代入(a )可得:[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程:22121211222()0t t t t k I k k k I ωωω--==--即:224222121()240t t I k I k ωωω=-+=解得:21,222ω==所以:1ω=2ω= ………… (c)将(c )代入(b )可得:112121211122(22220(22t t t t t t k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦解得:11212u u =-;12222u u =令21u ,得到系统的振型为:-0.70710.70713.2 求图所示系统的固有频率和振型。
物理机械振动考试题及答案

物理机械振动考试题及答案一、单项选择题(每题3分,共30分)1. 简谐运动的振动周期与振幅无关,与以下哪个因素有关?A. 质量B. 弹簧常数C. 初始位移D. 初始速度答案:B2. 阻尼振动中,振幅逐渐减小的原因是:A. 摩擦力B. 重力C. 弹力D. 空气阻力答案:A3. 以下哪个量描述了简谐运动的振动快慢?A. 振幅B. 周期C. 频率D. 相位答案:C4. 两个简谐运动的合成,以下哪个条件可以产生拍现象?A. 频率相同B. 频率不同C. 振幅相同D. 相位相反答案:B5. 以下哪个量是矢量?A. 位移B. 速度C. 加速度D. 以上都是答案:D6. 单摆的周期与以下哪个因素无关?A. 摆长B. 摆球质量C. 重力加速度D. 摆角答案:B7. 以下哪个量描述了简谐运动的能量?A. 振幅C. 频率D. 相位答案:A8. 以下哪个因素会影响单摆的周期?A. 摆长B. 摆球质量C. 摆角D. 重力加速度答案:A9. 阻尼振动中,振幅减小到原来的1/e时,经过的时间为:A. 1/2TB. TC. 2T答案:C10. 以下哪个现象不是简谐运动?A. 弹簧振子B. 单摆C. 弹簧振子的振幅逐渐减小D. 单摆的振幅逐渐减小答案:C二、填空题(每题4分,共20分)11. 简谐运动的周期公式为:T = 2π√(____/k),其中m为质量,k为弹簧常数。
答案:m12. 单摆的周期公式为:T = 2π√(L/g),其中L为摆长,g为重力加速度。
答案:L13. 阻尼振动的振幅公式为:A(t) = A0 * e^(-γt),其中A0为初始振幅,γ为阻尼系数,t为时间。
答案:A014. 简谐运动的频率公式为:f = 1/T,其中T为周期。
答案:1/T15. 简谐运动的相位公式为:φ = ωt + φ0,其中ω为角频率,t 为时间,φ0为初始相位。
答案:ωt + φ0三、计算题(每题10分,共50分)16. 一个质量为2kg的物体,通过弹簧连接在墙上,弹簧的弹簧常数为100N/m。
机械振动习题及答案【最新】

第一章概述1.一简谐振动,振幅为0.20cm,周期为0.15s,求最大速度和加速度。
解:• 1Xrnax = w * X x =2*^*/* = 2 * * A = 8.31cm/ s11 Id A / IDdA1Xnm = w2 * X niax= (2 * ” * /)2 * X niax = (2 * 7F * —)2 * A = 350.56c〃? / s22.一加速度计指示结构谐振在80HZ时具有最大加速度50g,求振动的振幅o(g=10m/s2)解:Xmax =心工皿=(2*4*/)f皿X nux =Xmax/(2*/r*/)2 =(50*10)/(2*3.14* 80)2 = 1.98〃〃〃3.一简谐振动,频率为10Hz,最大速度为4.57m/s,求谐振动的振幅、周期、最大加速度。
解:乂皿=Xnux/(2*^*/) = 4.57 / (2*3.14*10)= 72.77mm7 = —= —= 0.15f 10Xmax = W * Xmax = 2 * * Xmax =2*3.14*10*4.57 = 287.00/?/ / s'4.机械振动按激励输入类型分为哪几类?按自由度分为哪几类?答:按激励输入类型分为自由振动、强迫振动、自激振动按自由度分为单自由度系统、多自由度系统、连续系统振动5.什么是线性振动?什么是非线性振动?其中哪种振动满足叠加原理?答:描述系统的方程为线性微分方程的为线性振动系统,如I()0 + m S a0 = O描述系统的方程为非线性微分方程的为非线性振动系统+ 〃?即sin。
= 0线性系统满足线性叠加原理6.清画出同一方向的两个运动:X]Q) = 2sin(4/〃),x2(f) = 4sin(4^r)合成的的振动波形7.请画出互相垂直的两个运动:%。
)= 2sin(4^r), x2(t) = 2sin(4/zV)合成的结果。
如果是珀。
)=2sin(4^r+ ^/2),x2(t) = 2sin(4/z?)第二章单自由度系统一物体作简谐振动,当它通过距平衡位置为0.05m, 0.1m处时的速度分别为0.2姑和0.08】桃。
(完整版)机械振动知识点及习题练习+单元练习(含答案)

1、简谐运动的概念①简谐运动的定义:____________________________________________________________。
②简谐运动的物体的位移x、回复力F、加速度a、速度v、动能E K、势能E P的变化规律:A.在研究简谐运动时位移的起点都必须在处。
B.在平衡位置:位移最、回复力最、加速度最;速度最、动能最。
C.在离开平衡位置最远时:_________________________________________。
D.振动中:注意以上各量的矢量性和对称性。
③简谐运动机械能守恒,但机械能守恒的振动不一定时简谐运动。
④注意:A.回复力是效果力。
B.物体运动到平衡位置不一定处于平衡状态(如单摆,最低点有向心力)。
C.简谐运动定义式F=-K x中的K不一定是弹簧的劲度系数,是振动系数(如双弹簧)。
1.A关于回复力,下列说法正确的是( )A.回复力一定是物体受到的合外力B.回复力只能是弹簧的弹力提供C.回复力是根据力的作用效果命名的D.回复力总是指向平衡位置答案:CD2.A下列的运动属于简谐运动的是( )A.活塞在气缸中的往复运动B.拍皮球时,皮球的上下往复运动C.音叉叉股的振动D.小球在左右对称的两个斜面上来回滚动答案:C3.A一质点做简谐运动,当位移为正的最大值时,质点的( )A.速度为正的最大值,加速度为零B.速度为负的最大值,加速度为零C.速度为零,加速度为正的最大值D.速度为零,加速度为负的最大值答案:D4.A关于简谐运动的位移、加速度和速度的关系,正确的说法是( )A.位移减小时,加速度增大,速度增大B.位移方向总和加速度方向相反,和速度方向相同C.物体的速度增大时,加速度一定减小D.物体向平衡位置运动时,速度方向和位移方向相同答案:C6.B关于简谐运动中的平衡位置,下列说法正确的是( )A.平衡位置就是物体所受合外力为零的位置B.平衡位置就是加速度为零的位置C.平衡位置就是回复力为零的位置D.平衡位置就是受力平衡的位置答案:C7.B一平台沿竖直方向做简谐运动,一物体置于平台上随台一起运动,当振动平台处于什么位置时,物体对台面的压力最大( )A.振动平台在最高位置时B.振动平台向下振动经过平衡位置时C.振动平台在最低位置时D.振动平台向上运动经过平衡位置时答案:C8.B简谐运动是下列哪一种运动( )A.匀速直线运动B.匀加速运动C.匀变速运动D.变加速运动答案:D9.B做简谐运动的物体每次经过同一位置时,一定相同的物理量是( )A.速度B.位移C.回复力D.加速度答案:BCD10.B 对于弹簧振子,其回复力和位移的关系,在下图中正确的是()答案:C11.C 对简谐运动的回复力F=-kx 的理解,正确的是()A.k 只表示弹簧的劲度系数B.式中负号表示回复力总是负值C.位移x 是相对平衡位置的位移D.回复力只随位移变化,不随时间变化答案:C12.C 弹簧振子的质量是0.2kg,在水平方向做简谐运动,当它运动到平衡位置左侧x 1=2cm 的位置时,受到的回复力大小F 1=4N,则当它运动到平衡位置右侧x 2=4cm 的位置时,它的加速度是()A.20m/s 2,方向向左 B20m/s 2,方向向右C.40m/s 2,方向向左 D.40m/s 2,方向向右答案:C二、计算题(共16分)13.C 试证明:用轻弹簧悬挂一个振子,让它在竖直方向振动起来,在弹性限度内,振子是做简谐运动.(如图)答案:设振子的平衡位置为O,令向下为正方向,此时弹簧的形变为x 0,根据胡克定律及平衡条件有mg-kx 0=0.当振子向下偏离平衡位置x 时,有F=mg-k(x+x 0) 整理可得F=-kx(紧扣简谐运动特征及对称性)故重物的振动满足简谐运动的条件 2、总体上描述简谐运动的物理量①振幅A :_ _称为振幅。
机械振动试题(含答案)

机械振动试题(含答案)一、机械振动 选择题1.如图所示为某物体系统做受迫振动的振幅A 随驱动力频率f 的变化关系图,则下列说法正确的是A .物体系统的固有频率为f 0B .当驱动力频率为f 0时,物体系统会发生共振现象C .物体系统振动的频率由驱动力频率和物体系统的固有频率共同决定D .驱动力频率越大,物体系统的振幅越大2.如图所示,弹簧的一端固定,另一端与质量为2m 的物体B 相连,质量为1m 的物体A 放在B 上,212m m =.A 、B 两物体一起在光滑水平面上的N 、N '之间做简谐运动,运动过程中A 、B 之间无相对运动,O 是平衡位置.已知当两物体运动到N '时,弹簧的弹性势能为p E ,则它们由N '运动到O 的过程中,摩擦力对A 所做的功等于( )A .p EB .12p EC .13p E D .14p E 3.如图1所示,轻弹簧上端固定,下端悬吊一个钢球,把钢球从平衡位置向下拉下一段距离A ,由静止释放。
以钢球的平衡位置为坐标原点,竖直向上为正方向建立x 轴,当钢球在振动过程中某一次经过平衡位置时开始计时,钢球运动的位移—时间图像如图2所示。
已知钢球振动过程中弹簧始终处于拉伸状态,则( )A .1t 时刻钢球处于超重状态B .2t 时刻钢球的速度方向向上C .12~t t 时间内钢球的动能逐渐增大D .12~t t 时间内钢球的机械能逐渐减小4.在“用单摆测定重力加速度”的实验中,用力传感器测得摆线的拉力大小F随时间t变化的图象如图所示,已知单摆的摆长为l,则重力加速度g为( )A.224ltπB.22ltπC.2249ltπD.224ltπ5.如图所示的弹簧振子在A、B之间做简谐运动,O为平衡位置,则下列说法不正确的是()A.振子的位移增大的过程中,弹力做负功B.振子的速度增大的过程中,弹力做正功C.振子的加速度增大的过程中,弹力做正功D.振子从O点出发到再次回到O点的过程中,弹力做的总功为零6.公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板.一段时间内货物在竖直方向的振动可视为简谐运动,周期为T.取竖直向上为正方向,以t=0时刻作为计时起点,其振动图像如图所示,则A.t=14T时,货物对车厢底板的压力最大B.t=12T时,货物对车厢底板的压力最小C.t=34T时,货物对车厢底板的压力最大D.t=34T时,货物对车厢底板的压力最小7.如图所示,固定的光滑圆弧形轨道半径R=0.2m,B是轨道的最低点,在轨道上的A点(弧AB所对的圆心角小于10°)和轨道的圆心O处各有一可视为质点的静止小球,若将它们同时由静止开始释放,则()A.两小球同时到达B点B.A点释放的小球先到达B点C.O点释放的小球先到达B点D.不能确定8.一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动.可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm,周期为3.0 s.当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10 cm时,游客能舒服地登船.在一个周期内,游客能舒服登船的时间是( )A.0.5 s B.0.75 s C.1.0 s D.1.5 s9.在科学研究中,科学家常将未知现象同已知现象进行比较,找出其共同点,进一步推测未知现象的特性和规律.法国物理学家库仑在研究异种电荷的吸引力问题时,曾将扭秤的振动周期与电荷间距离的关系类比单摆的振动周期与摆球到地心距离的关系.已知单摆摆长为l,引力常量为G,地球质量为M,摆球到地心的距离为r,则单摆振动周期T与距离r的关系式为()A.T=2πr GMlB.T=2πrlGMC.T=2πGMr lD.T=2πlrGM10.如图(甲)所示,小球在内壁光滑的固定半圆形轨道最低点附近做小角度振动,其振动图象如图(乙)所示,以下说法正确的是()A.t1时刻小球速度为零,轨道对它的支持力最小B.t2时刻小球速度最大,轨道对它的支持力最小C.t3时刻小球速度为零,轨道对它的支持力最大D.t4时刻小球速度为零,轨道对它的支持力最大11.如图所示,在水平地面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,现将一个质量也为m的物体C从A的正上方一定高度处由静止释放,C和A相碰后立即粘在一起,之后在竖直方向做简谐运动。
机械振动试题(含答案)

机械振动试题(含答案)一、机械振动选择题1.悬挂在竖直方向上的弹簧振子,周期T=2s,从最低点位置向上运动时刻开始计时,在一个周期内的振动图象如图所示,关于这个图象,下列哪些说法是正确的是()A.t=1.25s时,振子的加速度为正,速度也为正B.t=1.7s时,振子的加速度为负,速度也为负C.t=1.0s时,振子的速度为零,加速度为负的最大值D.t=1.5s时,振子的速度为零,加速度为负的最大值2.如图所示的单摆,摆球a向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b发生碰撞,并粘在一起,且摆动平面不便.已知碰撞前a球摆动的最高点与最低点的高度差为h,摆动的周期为T,a球质量是b球质量的5倍,碰撞前a球在最低点的速度是b球速度的一半.则碰撞后A 5 6 TB 6 5 TC.摆球最高点与最低点的高度差为0.3hD.摆球最高点与最低点的高度差为0.25h3.用图甲所示的装置可以测量物体做匀加速直线运动的加速度,用装有墨水的小漏斗和细线做成单摆,水平纸带中央的虚线在单摆平衡位置的正下方。
物体带动纸带一起向左运动时,让单摆小幅度前后摆动,于是在纸带上留下如图所示的径迹。
图乙为某次实验中获得的纸带的俯视图,径迹与中央虚线的交点分别为A、B、C、D,用刻度尺测出A、B间的距离为x1;C、D间的距离为x2。
已知单摆的摆长为L,重力加速度为g,则此次实验中测得的物体的加速度为()A .212()x x gL π-B .212()2x x gL π-C .212()4x x gLπ-D .212()8x x gLπ-4.如图所示是扬声器纸盆中心做简谐运动的振动图象,下列判断正确的是A .t =2×10-3s 时刻纸盆中心的速度最大B .t =3×10-3s 时刻纸盆中心的加速度最大C .在0〜l×10-3s 之间纸盆中心的速度方向与加速度方向相同D .纸盆中心做简谐运动的方程为x =1.5×10-4cos50πt (m )5.如图1所示,轻弹簧上端固定,下端悬吊一个钢球,把钢球从平衡位置向下拉下一段距离A ,由静止释放。
大学物理机械振动习题含答案

t (s )v (m.s -1)12m v m vo1.3题图题图 第三章 机械振动一、选择题1.质点作简谐振动,距平衡位置2。
0cm 时,加速度a=4.0cm 2/s ,则该质点从一端运动到另一端的时间为(一端运动到另一端的时间为( C )A:1.2s B: 2.4s C:2.2s D:4.4s 解:解:s T t T xax a 2.2422,2222,22===\=====p pw pw w2.一个弹簧振子振幅为2210m -´,当0t =时振子在21.010m x -=´处,且向正方向运动,则振子的振动方程是:[ A ] A :2210cos()m3x t p w -=´-;B :2210cos()m 6x t pw -=´-;C :2210cos()m 3xt pw -=´+ ;D :2210cos()m 6x t pw -=´+;解:由旋转矢量可以得出振动的出现初相为:3p-3.用余弦函数描述一简谐振动,若其速度与时间(v —t )关系曲线如图示,则振动的初相位为:[ A ] A :6p ;B :3p ;C :2p ;D :23p ;E :56p解:振动速度为:max 0sin()v v t w j =-+0t =时,01sin2j =,所以06p j =或056p j = 由知1.3图,0t =时,速度的大小是在增加,由旋转矢量图知,旋转矢量在第一象限内,对应质点的运动是由正最大位移向平衡位置运动,速度是逐渐增加的,旋转矢量在第二象限内,对应质点的运动是由平衡位置向负最大位移运动,速度是逐渐减小的,所以只有06pj =是符合条件的。
符合条件的。
4.某人欲测钟摆摆长,将钟摆摆锤上移1毫米,测得此钟每分快0。
1秒,则此钟摆的摆长为(长为( B )A:15cm B:30cm C:45cm D:60cm 解:单摆周期解:单摆周期 ,2glT p=两侧分别对T ,和l 求导,有:求导,有:cm m m T dT dl l l dl T dT 3060)1.0(2121,21=-´-==\= 1.2题图题图xyoxy二、填空题1.有一放置在水平面上的弹簧振子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三次 机 械 振 动练习班 级 ___________________姓 名 ___________________班内序号 ___________________一.选择题1.一质点做简谐振动,如振动方程为: ) cos(ϕω+=t A x ,周期为T ,则当 2/ T t =时,质点的速度为: [ ]A .ϕωsin A -B .ϕωsin AC .ϕωcos A -D .ϕωcos A2.图示为一单摆装置,把小球从平衡位置 b ,拉开一小角度 0θ至 a 点, 在 0 =t 时刻松手让其摆动,摆动规律用余弦函数表示,则在 c a →的摆动中, 下列哪个说法是正确的? [ ]A .a 处动能最小,相位为0θ;B .b 处动能最大,相位为2/π;C .c 处动能为零,相位为0θ-;D .c b a ..三处能量相同,相位依次减少。
3.如简谐振动在 0 =t 时, 0 ,0 <>v x ,则表示该简谐振动的旋转矢量图 应该是: []4.质点沿X 轴作简谐振动,振动方程为) 2( cos 104 2ππ+⨯=-t x (SI),从0=t时刻起,到质点位置为cm x 2-=处、且向X 轴正方向运动的最短时间间隔为: A .s /21 B .s /41 C .s /61 D .s /81 [ ]5.质点作简谐振动,运动速度与时间 )( 1-⋅s m v [ ] 的曲线如图所示,若质点的运动规律用余v 弦函数描述,则其初相位是: v 5.0 A .6/π B .6/5πC .6/π-D .6/5π- )二.填空题1. 简谐振动的三个基本特征量为___________、___________ 和 ___________; 它们分别取决于 _______________ 、______________ 和 ______________ 。
2. 两个同频率、同方向简谐振动的合振动为__________________,合振动的 振幅取决于_____________________________________ ,两个相互垂直的同频率的 简谐振动,其合振动的运动轨迹一般为 ______________________ ,若两分振动的频率为简单整数比...,则合成运动的轨迹为 _______________________ 。
3.一弹簧振子作简谐振动,振幅为A ,周期为T ,其运动方程用余弦函数表 示,若 0 =t 时;(1)振子在正的最大位移处,则初相位为_____________;(2)振子在平衡位置向负方向运动,则初相位为_____________;(3)振子在位移为 A 5.0 处,且向正方向运动,则初相位为_____________。
4. 物块悬挂在弹簧下方作简谐振动,如物块在受力平衡位置时,弹簧的长度 比原来长l ∆,则系统的周期 =T _________;当这物块的位移等于振幅的一半时, 其动能是总能量的__________(以物块的受力平衡位置为各种势能的零势能点)。
5. 一质量为 m 的物体,上端与两根倔强系数分别为 1k 和 2k 的轻弹簧相连,如下图所示,则当物体被拉离平衡位置而释放时,物体将作简谐振动,其圆频率 =ω_______________ 、周期 =T _______________ 。
6. 设作简谐振动物体的 ~t x 曲线如图所示,则其初相位=0 ϕ__________ ; 位移的绝对值达最大值的时刻为: t =_________________ ;速度为最大值的时刻 为: t =________________ ;弹性势能为最大值的时刻为: t =_______________ ; 动能为最大值的时刻为: t =_________________。
第5题图 第6题图7. 两个相同的弹簧各悬挂一物体 a 和 b ,其质量之比为: 2:1: =b a m m 。
如果它们在竖直方向作简谐振动,其振幅之比为: 2:1: =b a A A ,则两周期之比 =b a T T : _________ ,振动能量之比=b a E E : _________ 。
8. 一谐振子的加速度最大值 2 48 -⋅=s cm a m ,振幅 3 cm A =。
若取速度具有正的最大值的时刻为0 =t ,则该振动的振动方程=x ____________________。
9. 有两个同方向、同频率的简谐振动,合振动的振幅为 2.0 m A =,相位与第 一振动的相位差61πϕϕ=- 。
如第一振动的振幅为)( 103 1 m A =,则第二振动的 振幅=2 A __________,第一、二振动的相位差=-2 1 ϕϕ__________。
三.计算题1. 质量为 25.0 kg 的物体,在弹簧的弹性恢复力下沿 X 轴作简谐振动,弹簧 的恢复系数为 61 1 -⋅m N 。
(1)求振动的周期和圆频率;(2)如振幅为cm 02 , 0=t 时位移cm x 100 =,且物体沿 X 轴负方向运动,求初速度 0 v 及初相位 0 ϕ;(3)写出该振动的振动方程 ;(4)求 2/ π=t 秒时弹簧对物体的作用力。
2.如下图所示,一根恢复系数 / 288.2 m N k =的轻质弹簧的一端连接一质 量 10222kg m -⨯=的滑块,放在光滑水平桌面上;弹簧的另一端固定。
今把弹簧压缩 22cm 后放手、任其自由振动,以放手时刻为计时起点。
求:(1)滑块的振动方程;(2) 48/ π=t 秒时,滑块的位移、速度、加速度和受到的作用力;(3)从起始位置运动到弹簧伸长为 2cm 处所需的最短时间;此时振动系统的动能、势能和总能量。
3.在一平板上放一质量为 2 kg 的物体,平板在竖直方向作简谐振动, 如振动的周期为 5.0 =T 秒,振幅为 5 cm A =。
求:(1)物体对平板的最大压力;(2)平板以多大的振幅振动时,物体开始离开平板?4. 某质点同时参与两个同振动方向、同频率的简谐振动,振动规律为(SI ):) 4 3 ( cos 4.0 1 π+=t x )4 3 ( cos 3.0 2 π-=t x 求:(1) 合振动的表达式;(2) 若另有一个同振动方向、同频率的简谐振动 ) 3 ( cos 5.0 3 3 ϕ+=t x ,当 3 ϕ为多少时, 1 x 、 2 x 和 3 x 三个振动的合振动振幅最大?当 3 ϕ为多少时,上述合振动的振幅最小?第三次 机械振动答案一、选择题:1. B 2. B 3. C 4. A 5. D二、填空题:1. 振幅、角频率、初相位;振动的能量、振动系统本身固有的特性、 初始时刻的选择。
2. 简谐振动,分振动各自的振幅及分振动的相位差,椭圆,稳定的曲线 (李萨如图形)。
3. (1) 0; (2)2 π; (3)3 π-。
4. 2g l ∆π ,4 3 。
5. )( 2121k k m k k +⋅⋅=ω、 )1 1( 221k k m T +⋅=π。
6. π 5.0-, )12(s n +, 4s n , )12(s n +,),2,1,0(2 =n s n7. 1 : 2,1 : 4 。
8. ()m t 5.04cos 03.0π- 。
9. m 1.0,π5.0-。
三、计算题:1. (1) 1 8-⋅=s rad ω, s T 785.04 ≈=π; (2) 3 0 πϕ= ,)( 386.1 38.0 3sin 20.08 sin 10 0 -⋅-≈-=⨯-=⋅-=s m A v πϕω; (3) )( ) 38 ( cos 20.0m t x π+=。
(4) )( 6.1 3cos 20.016 N x k F -=⨯-=-=π , 沿 X 轴负方向。
2. (1) 可以解得: m A 21022 ,-⨯==πϕ, 1 12-⋅==s rad m k ω振动方程为: ()m t x 12 cos 10222π+⨯=-。
(2) )( 02.0 10)cos ( 2221 m x -=⨯-=-π )( 0.244sin 102212121 --⋅=⋅⨯⨯=s m v π,)( 2.882-⋅=s m a , )( 10146.888.21022221 N F --⨯≈⨯⨯=,方向水平向右; (3) )( 1745.0182 s t ≈=π;总能量 J A k E 442102917.1610252.11 1--⨯≈⨯== , 势能 J E x k E p 42100729.442 1-⨯===, 动能 J E E E P k 4 102188.12-⨯=-= 。
3. 以竖直向下为X 轴正向,以平板处于正最大位移时为 0 =t ,则振动方程为 4cos t A x π=(1) 对物体:ma N mg =+ ,物体对板的压力: t ma mg N N4cos 6.16.19' 2ππ+=-=-= )( 39.356.16.19' 2max N N ≈+=∴π (2)0=N 时脱离,14c o s -=t π时压力最小,此时0162=-mA mg π,cm g A 206.6162≈=∴π4..(1))( 1419.0''48'78142857.0 71 3.04.0 3.00.4 rad tg arc tg arc tg arc ≈︒≈≈=+-=ϕ ( 或: 4 3 4 tg arc -=πϕ , 或:43 4 πϕ-=tg arc ) m A 5.0= , m tg arc t x )71 3( cos 5.0 += ; (2) 当3x 与x 同相时, 合振幅最大, 即:71 3 tg arc ==ϕϕ ; 当3x 与x 反相时, 合振幅最小, 即:ππϕϕ 7 1 3 -=-=tg arc 。
