动态规划问题常见解法

动态规划求最短路径的两种方法

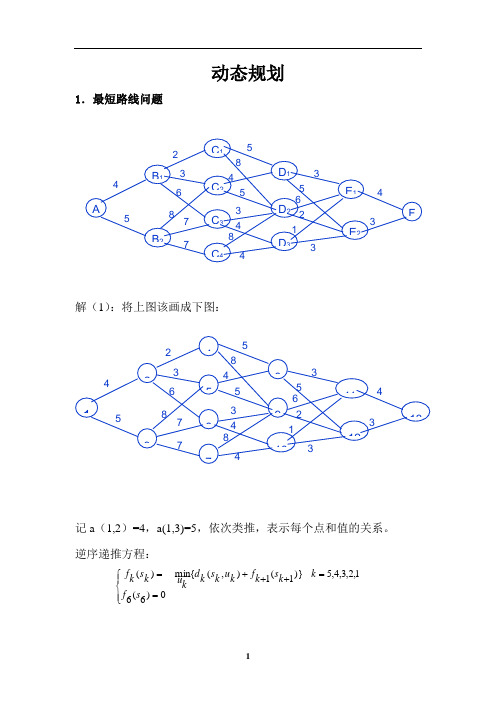
动态规划1．最短路线问题解（1）：将上图该画成下图：记a （1,2）=4，a(1,3)=5，依次类推，表示每个点和值的关系。

逆序递推方程：⎪⎩⎪⎨⎧==+++=0)6(61,2,3,4,5)}1(1),({min )(s f k k s k f k u k s k d k uk s k fAB 1B 2C 1 C 2C 3 C 4D 1D 2 D 3E 1 E 2F4523 6 8 7 75845348435 6 2 314 31234 5 6 789 101112134523 6 8 7 7584534 8435 6 2 314 3如图各状态：逆序递推，找出上一个状态到下一阶段的最小路径值。

例如，当K=4时，状态它们到F 点需经过中途点E ，需一一分析从E 到 F 的最短路：先说从D1到F 的最短路有两种选择：经过 E1, E2, 比较最短。

这说明由 D1 到F 的最短距离为7，其路径为AB 1B 2C 1 C 2C 3 C 4D 1 D 2 D 3E 1 E 2F4523 6 87 75845348435 62 31 4 3第1阶段第2阶段第3阶段第4阶段第5阶段状态 1状态 2状态3状态 4状态 5状态 6)}(),(),(),(m in{)(252141511414E f E D d E f E D d D f ++=.7}35,43min{=++=.11F E D →→},,{3214D D D S =a=[0,4,5,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf 4,0,inf,2,3,6,inf,inf,inf,inf,inf,inf,inf 5,inf,0,inf,8,7,7,inf,inf,inf,inf,inf,inf inf,2,inf,0,inf,inf,inf,5,8,inf,inf,inf,inf inf,3,8,inf,0,inf,inf,4,5,inf,inf,inf,inf inf,6,7,inf,inf,0,inf,inf,3,4,inf,inf,inf inf,inf,7,inf,inf,inf,0,inf,8,4,inf,inf,inf inf,inf,5,4,inf,inf,inf,0,inf,inf,3,5,inf inf,inf,inf,8,5,3,8,inf,0,inf,6,2,inf inf,inf,inf,inf,inf,4,4,inf,inf,0,1,3,inf inf,inf,inf,inf,inf,inf,inf,3,6,1,0,inf,4 inf,inf,inf,inf,inf,inf,inf,5,2,3,inf,0,3 inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,4,3,0]; s8=min(a(8,11)+a(11,13),a(8,12)+a(12,13)); s9=min(a(9,11)+a(11,13),a(9,12)+a(12,13)); s10=min(a(10,11)+a(11,13),a(10,12)+a(12,13)); s4=min(a(4,8)+s8,a(4,9)+s9); s5=min(a(5,8)+s8,a(5,9)+s9); s6=min(a(6,9)+s9,a(6,10)+s10); s7=min(a(7,9)+s9,a(7,10)+s10); s2=[a(2,4)+s4,a(2,5)+s5,a(2,6)+s6]; s2=min(s2);s3=[a(3,5)+s5,a(3,6)+s6,a(3,7)+s7]; s3=min(s3);s1=min(a(1,2)+s2,a(1,3)+s3)运行结果为：s8 = 7 s9 = 5 s10 = 5 s4 = 12 s5 = 10 s6 = 8 s7 = 9 s2 =13s3 = 15 s1 = 17结果分析：s 表示每个点到终点的最短距离，那么最短路程为17。

动态规划-例题众多-详细讲解

步骤2：状态转移方程：
步骤3：以自底向上的方法来计算最优解
12
程序的实现
BuyTicks(T, R)
1 n ← length[T]
2 f[0] ← 0
3 f[1] ← T[1]
4 for i ← 2 to n do
5
f[i] ← f[i-2]+R[i-1]
6
if f[i] > f[i-1]+T[i] then
n 0 1 2 3 4 5 6 7 8 9 10 F(n) 1 1 2 3 5 8 13 21 34 55 89
2
递归 vs 动态规划
递归版本:
F(n)
1 if n=0 or n=1 then
2
return 1
3 else
4
return F(n-1) + F(n-2)
太慢!
动态规划:
F(n)
1 A[0] = A[1] ← 1
这里是某支股票的价格清单：日期 1 2 3 4 5 6 7 8 9 10 11 12 价格 68 69 54 64 68 64 70 67 78 62 98 87 最优秀的投资者可以购买最多4次股票，可行方案中的一种是：日期 2 5 6 10 价格 69 68 64 62 输入第1行: N (1 <= N <= 5000)，股票发行天数第2行: N个数，是每天的股票价格。输出输出文件仅一行包含两个数:最大购买次数和拥有最大购买次数的方案数(<=231) 当二种方案“看起来一样”时（就是说它们构成的价格队列一样的时候）,这2种方案被认为是相同的。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

公共解的三种解法

公共解的三种解法
#### 1. 动态规划
使用动态规划的方法，可以把求解最大公共子序列问题转换为求解最长公共子序列问题。

动态规划的思路是：令dp[i][j]表示字符串A[0..i]和字符串B[0..j]的最长公共子序列的长度，则有状态转移方程：
```
dp[i][j] =
0 (i == 0 || j == 0)
dp[i-1][j-1] + 1 (A[i] == B[j])
max(dp[i-1][j], dp[i][j-1]) (A[i] != B[j])
```
最终结果为dp[n][m]，其中n为字符串A的长度，m为字符串B的长度。

#### 2. 递归
递归的思路是：令lcs(i, j)表示字符串A[0..i]和字符串B[0..j]的最长公共子序列的长度，则
有状态转移方程：
```
lcs(i, j) =
0 (i == 0 || j == 0)
lcs(i-1, j-1) + 1 (A[i] == B[j])
max(lcs(i-1, j), lcs(i, j-1)) (A[i] != B[j])
```
最终结果为lcs(n, m)，其中n为字符串A的长度，m为字符串B的长度。

#### 3. 滑动窗口
滑动窗口的思路是：定义两个指针i和j，分别指向字符串A和字符串B的开头，比较A[i]
和B[j]的值，如果相等，则将i和j同时向后移动，否则只有一个指针向后移动，直到两个
指针都到达字符串末尾。

最终结果为i和j指针移动的次数，即为最长公共子序列的长度。

动态规划经典——最长公共子序列问题（LCS）和最长公共子串问题

动态规划经典——最长公共⼦序列问题（LCS）和最长公共⼦串问题⼀.最长公共⼦序列问题(LCS问题)给定两个字符串A和B，长度分别为m和n，要求找出它们最长的公共⼦序列，并返回其长度。

例如： A = "Hel lo W o rld" B = "loo p"则A与B的最长公共⼦序列为 "loo",返回的长度为3。

此处只给出动态规划的解法：定义⼦问题dp[i][j]为字符串A的第⼀个字符到第 i 个字符串和字符串B 的第⼀个字符到第 j 个字符的最长公共⼦序列，如A为“app”,B为“apple”，dp[2][3]表⽰ “ap” 和 “app” 的最长公共字串。

注意到代码中 dp 的⼤⼩为 (n + 1) x (m + 1) ，这多出来的⼀⾏和⼀列是第 0 ⾏和第 0 列，初始化为 0，表⽰空字符串和另⼀字符串的⼦串的最长公共⼦序列，例如dp[0][3]表⽰ "" 和“app” 的最长公共⼦串。

当我们要求dp[i][j]，我们要先判断A的第i个元素B的第j个元素是否相同即判断A[i - 1]和 B[j -1]是否相同，如果相同它就是dp[i-1][j-1]+ 1，相当于在两个字符串都去掉⼀个字符时的最长公共⼦序列再加 1；否则最长公共⼦序列取dp[i][j - 1] 和dp[i - 1][j]中⼤者。

所以整个问题的初始状态为：dp[i][0]=0,dp[0][j]=0相应的状态转移⽅程为：dp[i][j]=max{dp[i−1][j],dp[i][j−1]},A[i−1]!=B[j−1] dp[i−1][j−1]+1,A[i−1]==B[j−1]代码的实现如下：class LCS{public:int findLCS(string A, int n, string B, int m){if(n == 0 || m == 0)//特殊输⼊return 0;int dp[n + 1][m + 1];//定义状态数组for(int i = 0 ; i <= n; i++)//初始状态dp[i][0] = 0;for(int i = 0; i <= m; i++)dp[0][i] = 0;for(int i = 1; i <= n; i++)for(int j = 1; j<= m; j++){if(A[i - 1] == B[j - 1])//判断A的第i个字符和B的第j个字符是否相同dp[i][j] = dp[i -1][j - 1] + 1;elsedp[i][j] = max(dp[i - 1][j],dp[i][j - 1]);}return dp[n][m];//最终的返回结果就是dp[n][m]}};该算法的时间复杂度为O(n*m)，空间复杂度为O(n*m)。

动态规划习题详解

动态规划动态规划是运筹学的一个分支，它是解决多阶段决策过程最优化问题的一种方法。

该方法是由美国数学家贝尔曼(R．Bellman)等人在本世纪50年代初提出的。

他们针对多阶段决策问题的特点，提出了解决这类问题的“最优化原理”，并成功地解决了生产管理、工程技术等方面的许多实际问题，从而建立了运筹学的一个新分支——动态规划。

他的名著《动态规划》于1957年出版，该书是动态规划的第一本著作。

动态规划是现代企业管理中的一种重要决策方法，在工程技术、经济管理、工农业生产及军事及其它部们都有广泛的应用，并且获得了显著的效果。

动态规划可用于解决最优路径问题、资源分配问题、生产计划与库存问题、投资分配问题、装载问题、设备更新与维修问题、排序问题及生产过程的最优控制等。

由于它所具有独特的解题思路，在处理某些优化问题时，常常比线性规划或非线性规划方法更有效。

第一节动态规划的基本方法多阶段决策的实际问题很多，下面通过具体例子，说明什么是动态规划模型及其求解方法。

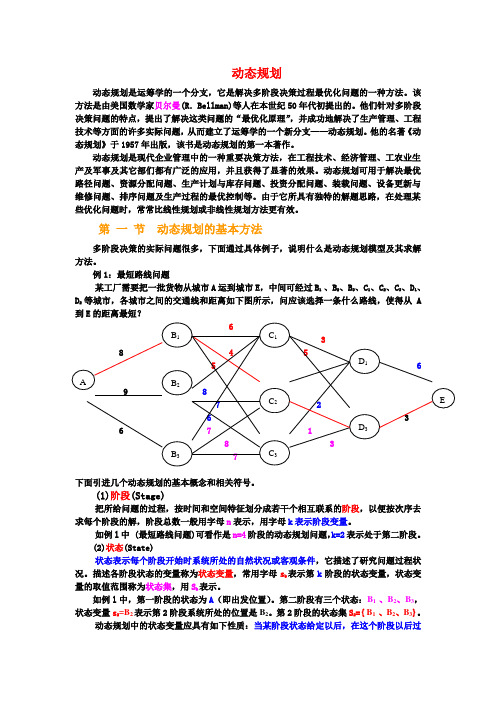
例1：最短路线问题某工厂需要把一批货物从城市A运到城市E，中间可经过B1 、B2、B3、C1、C2、C3、D1、D2等城市，各城市之间的交通线和距离如下图所示，问应该选择一条什么路线，使得从A到E的距离最短？下面引进几个动态规划的基本概念和相关符号。

(1)阶段(Stage)把所给问题的过程，按时间和空间特征划分成若干个相互联系的阶段，以便按次序去求每个阶段的解，阶段总数一般用字母n表示，用字母k表示阶段变量。

如例l中 (最短路线问题)可看作是n=4阶段的动态规划问题，k=2表示处于第二阶段。

(2)状态(State)状态表示每个阶段开始时系统所处的自然状况或客观条件，它描述了研究问题过程状况。

描述各阶段状态的变量称为状态变量，常用字母sk表示第k阶段的状态变量，状态变量的取值范围称为状态集，用Sk表示。

如例l中，第一阶段的状态为A（即出发位置）。

第二阶段有三个状态：B1 、B2、B3，状态变量s2=B2表示第2阶段系统所处的位置是B2。

动态规划算法的常见实例

动态规划算法的常见实例动态规划算法是一种将复杂问题分解为简单子问题来解决的算法，它可被应用于多个领域中，如经济学、生物学、计算机科学等。

在本文中，我们将详细讨论动态规划算法的常见实例。

一、最长公共子序列问题最长公共子序列（LCS）问题是一个经典的计算机科学问题，它要求在两个字符串中找到最长的相同连续子序列。

例如，对于字符串“ABCD”和“ACDF”，最长公共子序列为“ACD”。

使用动态规划方法来解决LCS问题。

首先定义一个m行n列的二维矩阵，其中m和n分别表示两个字符串的长度。

然后，使用以下递推关系：1. 如果一个字符串的长度为0，LCS为0。

2. 如果两个字符不相同，则LCS为它们的前一个字符集合和它们的后一个字符集合的最大值。

3. 如果两个字符相同，则LCS为它们的前一个字符集合和它们的后一个字符集合所组成的子序列中的最大值加1。

最后，矩阵右下角的值就是LCS的长度。

二、背包问题背包问题（Knapsack problem）是一个经典的组合优化问题，被广泛应用于计算机科学和其他领域。

在一个决策者必须决定是否将某些物品放入背包中的场景中，背包问题就发挥了作用。

具体来说，我们要解决的问题是：对于一个固定容量的背包，有一些物品，它们的重量和价值都不同，如何在不超过背包容量的前提下，使所装载物品的总价值最大化。

一种解决方案是使用动态规划方法。

定义一个二维数组，其行表示物品，列表示背包大小。

然后，使用以下递推关系：1. 如果所考虑的物品重量大于背包容量，则不选此物品。

2. 否则，在选取该物品和不选该物品两种情况中选择最优解作为最终结果。

最后，矩阵中右下角的值就是最大的总价值。

三、矩阵链乘法矩阵链乘法是一种计算矩阵乘积的优化算法。

它使用动态规划算法来确定矩阵乘积的最小值。

对于一个长度为n的矩阵链，我们可以定义一个n×n 的矩阵M，其中第i行第j列的元素Mi，j表示第i个矩阵与第j个矩阵相乘的最小次数。

(完整版)动态规划问题常见解法

(完整版)动态规划问题常见解法动态规划问题常见解法一、背包问题1. 0/1背包问题0/1背包问题是动态规划中的经典问题，解决的是在背包容量固定的情况下，如何选择物品放入背包，使得总价值最大化。

常见的解法有两种：记忆化搜索和动态规划。

记忆化搜索是一种自顶向下的解法，通过保存子问题的解来避免重复计算，提高效率。

动态规划是一种自底向上的解法，通过填表格的方式记录每个子问题的解，最终得到整个问题的最优解。

2. 完全背包问题完全背包问题是在背包容量固定的情况下，如何选择物品放入背包，使得总价值最大化，且每种物品可以选择任意个。

常见的解法有两种：记忆化搜索和动态规划。

记忆化搜索和动态规划的思路和0/1背包问题相似，只是在状态转移方程上有所不同。

二、最长公共子序列问题最长公共子序列问题是指给定两个序列，求它们之间最长的公共子序列的长度。

常见的解法有两种：递归和动态规划。

递归的思路是通过分别考虑两个序列末尾元素是否相等来进一步缩小问题规模，直至问题规模减小到边界情况。

动态规划的思路是通过填表格的方式记录每个子问题的解，最终得到整个问题的最优解。

三、最短路径问题最短路径问题是指在加权有向图或无向图中，求解从一个顶点到另一个顶点的最短路径的问题。

常见的解法有两种：Dijkstra算法和Bellman-Ford算法。

Dijkstra算法是通过维护一个距离表，不断选择距离最短的顶点来更新距离表，直至找到目标顶点。

Bellman-Ford算法是通过进行多次松弛操作，逐步缩小问题规模，直至找到目标顶点或发现负权环。

总结：动态规划是一种解决最优化问题的常见方法，它通过分组子问题、定义状态、确定状态转移方程和填表格的方式，来得到整个问题的最优解。

在解决动态规划问题时，可以采用记忆化搜索或者动态规划的策略，具体选择哪种方法可以根据问题的特点和优化的需要来决定。

动态规划讲解大全(含例题及答案)

基本模型
多阶段决策过程的最优化问题。在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。当然，各个阶段决策的选取不是任意确定的，它依赖于当前面临的状态，又影响以后的发展，当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线，如图所示：（看词条图）这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题就称为多阶段决策问题。
在前面的例子中，第一个阶段就是点 A，而第二个阶段就是点 A 到点 B，第三个阶段是点 B 到点 C，而第四个阶段是点 C 到点 D。
状态：状态表示每个阶段开始面临的自然状况或客观条件，它不以人们的主观意志为转移，也称为不可控因素。在上面的例子中状态就是某阶段的出发位置，它既是该阶段某路的起点，同时又是前一阶段某支路的终点。
fout.close(); return 0; }
USACO 2.3 Longest Prefix
题目如下：在生物学中，一些生物的结构是用包含其要素的大写字母序列来表示的。生物学家对于把长的序列分解成较短的（称之为元素的）序列很感兴趣。如果一个集合 P 中的元素可以通过串联（允许重复；串联，相当于 Pascal 中的 “+” 运算符）组成一个序列 S ，那么我们认为序列 S 可以分解为 P 中的元素。并不是所有的元素都必须出现。举个例子，序列 ABABACABAAB 可以分解为下面集合中的元素： {A, AB, BA, CA, BBC} 序列 S 的前面 K 个字符称作 S 中长度为 K 的前缀。设计一个程序，输入一个元素集合以及一个大写字母序列，计算这个序列最长的前缀的长度。 PROGRAM NAME: prefix INPUT FORMAT 输入数据的开头包括 1..200 个元素（长度为 1..10 ）组成的集合，用连续的以空格分开的字符串表示。字母全部是大写，数据可能不止一行。元素集合结束的标志是一个只包含一个 “.” 的行。集合中的元素没有重复。接着是大写字母序列 S ，长度为 1..200,000 ，用一行或者多行的字符串来表示，每行不超过 76 个字符。换行符并不是序列 S 的一部分。 SAMPLE INPUT (file prefix.in) A AB BA CA BBC . ABABACABAABC OUTPUT FORMAT 只有一行，输出一个整数，表示 S 能够分解成 P 中元素的最长前缀的长度。 SAMPLE OUTPUT (file prefix.out) 11 示例程序如下： #include <stdio.h>

动态规划_多阶段决策问题的求解方法

动态规划_多阶段决策问题的求解方法1.构造状态网络; :一:解决多阶段决策最优化的过程为动态规划方法在程序设计中，有一类活动的过程，由于它的特殊性，可将过程2.根据状态转移关系和状态转移方程建立最优值的分成若干个互相联系的阶段，在它的每一阶段都需要做出决策，从而3.按阶段的先后次序计算每个状态的最优值。

使整个过程达到最好的活动效果。

因此各个阶段决策的选取不能任逆向思维法是指从问题目标状态出发倒推回初始意确定，它依赖于当前面临的状态，又影响以后的发展。

当各个阶段态的思维方法。

动态规划的逆向思维法的要点可归纳为以决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条 1.分析最优值的结构，刻画其结构特征; 活动路线。

这种把一个问题看作是一个前后关联具有链状结构的多 2.递归地定义最优值; 阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。

3.按自底向上或自顶向下记忆化的方式计算最优在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列如果原问题可以分解成几个本质相同、规模较小的就是在变化的状态中产生出来的，故有"动态"的含义，我们称这种就会联想到从逆向思维的角度寻求问题的解决。

一般解决多阶段决策最优化的过程为动态规划方法。

策问题多采用动态规划逆向思维方法解决。

二、举:二:动态规划最优化原理 pascal 语例说明本文以信息学奥赛用语言——最优化原理是动态规划的基础。

任何一个问题，如果失去了这言为编程个最优化原理的支持，就不可能用动态规划方法计算。

这个“最优化说明，其他编程语言编写方法相同，语句类似。

原理”如果用数学化一点的语言来描述的话，就是:假设为了解决某 :一:问题描述一优化问题，需要依次作出 n 个决策 D1，D2，，Dn，如若这个决策设有 N 个不相同的整数组成的数列，记为: 序列是最优的，对于任何一个整数 k，1 < k < n，不论前面 k 个决策是怎样的，以后的最优决策只取决于由前面决策所确定的当前状态，即 ()且 ?? a1 a2 an aiajij以后的决策 Dk+1，Dk+2，，Dn 也是最优的。

动态规划问题常见解法

动态规划问题常见解法动态规划（Dynamic Programming）是一种常用的算法思想，用于解决一类具有重叠子问题性质和最优子结构性质的问题。

动态规划通常通过将问题划分为若干个子问题，并分别求解子问题的最优解，从而得到原问题的最优解。

以下是动态规划问题常见的解法：1. 斐波那契数列斐波那契数列是动态规划问题中的经典案例。

它的递推关系式为 F(n) = F(n-1) + F(n-2)，其中 F(0) = 0，F(1) = 1。

可以使用动态规划的思想来解决斐波那契数列问题，通过保存已经计算过的子问题的结果，避免重复计算。

2. 背包问题背包问题是一个经典的优化问题，可以使用动态规划的方法进行求解。

背包问题包括 0/1 背包问题和完全背包问题。

0/1 背包问题中每个物品要么被选中放入背包，要么不选。

完全背包问题中每个物品可以被选中多次放入背包。

通过定义状态转移方程和使用动态规划的思想，可以高效地求解背包问题。

3. 最长递增子序列最长递增子序列是一个常见的子序列问题，可以使用动态规划的方法进行求解。

最长递增子序列指的是在一个序列中，找到一个最长的子序列，使得子序列中的元素按照顺序递增。

通过定义状态转移方程和使用动态规划的思想，可以有效地求解最长递增子序列问题。

4. 最长公共子序列最长公共子序列是一个经典的字符串问题，可以使用动态规划的方法进行求解。

给定两个字符串，找到它们之间最长的公共子序列。

通过定义状态转移方程和使用动态规划的思想，可以高效地求解最长公共子序列问题。

5. 矩阵链乘法矩阵链乘法是一个求解最优括号化问题的经典案例，可以使用动态规划的方法进行求解。

给定多个矩阵的大小，需要找到一个最优的计算顺序，使得计算乘积的次数最少。

通过定义状态转移方程和使用动态规划的思想，可以高效地求解矩阵链乘法问题。

以上是动态规划问题的常见解法，通过使用动态规划的思想和方法，可以解决这些问题，并求得最优解。

动态优化问题常见解法

动态优化问题常见解法动态优化问题是计算机科学中的一个重要领域，它涉及到在给定约束条件下，寻找最优解的问题。

在解决动态优化问题时，常用的几种解法包括贪心法、动态规划法和分治法。

贪心法贪心法是一种简单而常用的动态优化问题解法。

它的基本思想是在每一步都选择当前状态下最优的解，希望通过每一步的最优选择达到全局最优解。

贪心法通常适用于一些较为简单、局部最优即能得到全局最优的情况。

然而，贪心法并不适用于所有动态优化问题，特别是那些需要考虑长远后果的问题。

在使用贪心法解决问题时，需要仔细分析问题的特性以确定贪心策略的适用性。

动态规划法动态规划法是一种比较常用且灵活的动态优化问题解法。

它通过建立一个状态转移方程来逐步求解问题。

具体而言，动态规划法将原问题分解为子问题，然后利用已解决的子问题的解来求解更大规模的问题。

动态规划法通常需要建立一个动态规划表格或数组来存储子问题的解，以便在求解大问题时可以利用已经求解过的子问题的解。

动态规划法的关键在于确定子问题的解以及状态转移方程的定义。

分治法分治法是一种将问题分割为更小的子问题并分别解决的解法。

它的基本思想是将原问题划分为多个相互独立且结构相似的子问题，然后递归地解决这些子问题。

最后，将子问题的解合并得到原问题的解。

分治法通常适用于一些较为复杂的问题，能够有效地解决大规模问题。

然而，分治法并不是适用于所有动态优化问题，具体问题需要根据其特性来确定是否适用分治法进行求解。

总结在解决动态优化问题时，贪心法、动态规划法和分治法是常见的解法。

贪心法适用于一些较为简单且局部最优即为全局最优的问题。

动态规划法通过求解子问题来逐步求解大问题，适用于各类动态优化问题。

分治法通过将问题划分为子问题并递归求解，适用于复杂的大规模问题。

在选择合适的解法时，需要充分考虑问题的特性和约束条件。

每种解法都有其优缺点，在实际应用中需要仔细分析问题的性质以确定最合适的解法。

(完整word版)TSP问题的动态规划解法

TSP问题的动态规划解法第十七组：3103038028 郑少斌3103038029 王瑞锋3103038035 江飞鸿3103038043 韩鑫3103055004 唐万强1．TSP问题简介旅行商问题（Traveling Salesman Problem,简称TSP, 亦称为货单郎问题）可以描述为：对于N 个城市，它们之间的距离已知，有一旅行商要从某一城市走遍所有的城市，且每一城市只能经过一次，最后回到出发的城市，问如何选择路线可使他走过的路径最短。

这是一个典型的组合优化问题。

它有很强的现实意义，可以应用于交通运输，物资调配，旅游线路设置。

对于了解某个国家地理分布也有一定的现实意义。

这个问题的解法有很多种，在这里我们尝试使用最优控制中的动态规划的相关知识来进行求解。

2．TSP问题分析对于这个问题，我们首先想到的是应用穷举法进行解答，但是这个方法时间和空间的复杂度很高。

从表面上看，TSP 问题很简单，其实则不然。

对于N 个城市的TSP,存在的可能路径为（N-1）!/2条，当N较大时，其数量是惊人的。

计算每条路经都需求出N 个距离之和，这样各种路径及其距离之和的计算量正比与N!/2.用搜索法要求就规模大的TSP是不现实的。

例如使用1GFLOPs 次的计算机搜索TSP 所需的时间如下表所示城市数7152050100200加法量 3105.2⨯ 11105.6⨯ 18102.1⨯ 64105.1⨯ 157105⨯ 37410搜索时间s 5105.2-⨯1.8h350yy 48105⨯ y 14210y 35810由上可知，对于这个问题采用穷举法进行解答是不现实的，这就要求我们采用其他的方法进行解答。

3．其他求解TSP 问题的方法*贪心法a. 所谓贪心法，就是在组合算法中，将每一步都取局部最优的求解方法。

b. 下表表示用贪心法求解TSP 的过程。

先将各城市间的距离用行列式形式表示，主对角线上用∞表示。

(完整word版)TSP问题的动态规划解法

TSP问题的动态规划解法第十七组：3103038028 郑少斌3103038029 王瑞锋3103038035 江飞鸿3103038043 韩鑫3103055004 唐万强1．TSP问题简介旅行商问题（Traveling Salesman Problem,简称TSP, 亦称为货单郎问题）可以描述为：对于N 个城市，它们之间的距离已知，有一旅行商要从某一城市走遍所有的城市，且每一城市只能经过一次，最后回到出发的城市，问如何选择路线可使他走过的路径最短。

这是一个典型的组合优化问题。

它有很强的现实意义，可以应用于交通运输，物资调配，旅游线路设置。

对于了解某个国家地理分布也有一定的现实意义。

这个问题的解法有很多种，在这里我们尝试使用最优控制中的动态规划的相关知识来进行求解。

2．TSP问题分析对于这个问题，我们首先想到的是应用穷举法进行解答，但是这个方法时间和空间的复杂度很高。

从表面上看，TSP 问题很简单，其实则不然。

对于N 个城市的TSP,存在的可能路径为（N-1）!/2条，当N较大时，其数量是惊人的。

计算每条路经都需求出N 个距离之和，这样各种路径及其距离之和的计算量正比与N!/2.用搜索法要求就规模大的TSP是不现实的。

例如使用1GFLOPs 次的计算机搜索TSP 所需的时间如下表所示城市数7152050100200加法量 3105.2⨯ 11105.6⨯ 18102.1⨯ 64105.1⨯ 157105⨯ 37410搜索时间s 5105.2-⨯1.8h350yy 48105⨯ y 14210y 35810由上可知，对于这个问题采用穷举法进行解答是不现实的，这就要求我们采用其他的方法进行解答。

3．其他求解TSP 问题的方法*贪心法a. 所谓贪心法，就是在组合算法中，将每一步都取局部最优的求解方法。

b. 下表表示用贪心法求解TSP 的过程。

先将各城市间的距离用行列式形式表示，主对角线上用∞表示。

分组背包问题常见解法

分组背包问题常见解法
常见的解法包括动态规划和状态压缩。

动态规划解法：
1. 定义`dp[i][j]`表示前i个物品选择j个分组所能获得的最大价值。

2. 初始化`dp`数组为0。

3. 设置状态转移方程为`dp[i][j] = max(dp[i-1][j], dp[i-1][j-group[i].size] + value[i])`，其中`group[i].size`表示第i个物品所属的分组包含的物品数量，`value[i]`表示第i个物品的价值。

4. 依次考虑物品和分组，更新`dp`数组。

5. 最终结果为`dp[n][m]`，其中n表示物品的个数，m表示分组的个数。

状态压缩解法：
1. 定义一个一维数组`dp`表示前i个物品选择j个分组所能获得的最大价值。

2. 初始化`dp`数组为0。

3. 设置状态转移方程为`dp[j] = max(dp[j], dp[j-group[i].size] + value[i])`，其中`group[i].size`表示第i个物品所属的分组包含的物品数量，`value[i]`表示第i个物品的价值。

4. 依次考虑物品和分组，更新`dp`数组。

5. 最终结果为`dp[m]`，其中m表示分组的个数。

动态规划动态转移方程大全

1. 资源问题1-----机器分配问题F[I,j]:=max(f[i-1,k]+w[i,j-k])2. 资源问题2------01背包问题F[I,j]:=max(f[i-1,j-v]+w,f[i-1,j]);3. 线性动态规划1-----朴素最长非降子序列F:=max{f[j]+1}4. 剖分问题1-----石子合并F[i,j]:=min(f[i,k]+f[k+1,j]+sum[i,j]);5. 剖分问题2-----多边形剖分F[I,j]:=min(f[i,k]+f[k,j]+a[k]*a[j]*a);6. 剖分问题3------乘积最大f[i,j]:=max(f[k,j-1]*mult[k,i]);7. 资源问题3-----系统可靠性(完全背包)F[i,j]:=max{f[i-1,j-c*k]*P[I,x]}8. 贪心的动态规划1-----快餐问题F[i,j,k]:=max{f[i-1,j',k']+(T-(j-j')*p1-(k-k')*p2) div p3}9. 贪心的动态规划2-----过河f=min{{f(i-k)} (not stone){f(i-k)}+1} (stone); +贪心压缩状态10. 剖分问题4-----多边形-讨论的动态规划F[i,j]:=max{正正f[I,k]*f[k+1,j];负负g[I,k]*f[k+1,j];正负g[I,k]*f[k+1,j];负正f[I,k]*g[k+1,j];} g为min11. 树型动态规划1-----加分二叉树(从两侧到根结点模型)F[I,j]:=max{f[I,k-1]*f[k+1,j]+c[k]}12. 树型动态规划2-----选课(多叉树转二叉树,自顶向下模型)F[I,j]表示以i为根节点选j门功课得到的最大学分f[i,j]:=max{f[t.l,k]+f[t.r,j-k-1]+c}13. 计数问题1-----砝码称重f[f[0]+1]=f[j]+k*w[j];(1<=i<=n; 1<=j<=f[0]; 1<=k<=a;)14. 递推天地1------核电站问题f[-1]:=1; f[0]:=1;f:=2*f[i-1]-f[i-1-m]15. 递推天地2------数的划分f[i,j]:=f[i-j,j]+f[i-1,j-1];16. 最大子矩阵1-----一最大01子矩阵f[i,j]:=min(f[i-1,j],v[i,j-1],v[i-1,j-1])+1;ans:=maxvalue(f);17. 判定性问题1-----能否被4整除g[1,0]:=true; g[1,1]:=false; g[1,2]:=false; g[1,3]:=false;g[i,j]:=g[i-1,k] and ((k+a[i,p]) mod 4 = j)18. 判定性问题2-----能否被k整除f[I,j±n mod k]:=f[i-1,j]; -k<=j<=k; 1<=i<=n20. 线型动态规划2-----方块消除游戏f[i,i-1,0]:=0f[i,j,k]:=max{f[i,j-1,0]+sqr(len(j)+k),f[i,p,k+len[j]]+f[p+1,j-1,0]}ans:=f[1,m,0]21. 线型动态规划3-----最长公共子串，LCS问题f[i,j]={0(i=0)&(j=0);f[i-1,j-1]+1 (i>0,j>0,x=y[j]);max{f[i,j-1]+f[i-1,j]}} (i>0,j>0,x<>y[j]);22. 最大子矩阵2-----最大带权01子矩阵O(n^2*m)枚举行的起始，压缩进数列，求最大字段和，遇0则清零23. 资源问题4-----装箱问题(判定性01背包)f[j]:=(f[j] or f[j-v]);24. 数字三角形1-----朴素の数字三角形f[i,j]:=max(f[i+1,j]+a[I,j],f[i+1,j+1]+a[i,j]);25. 数字三角形2-----晴天小猪历险记之Hill同一阶段上暴力动态规划if[i,j]:=min(f[i,j-1],f[I,j+1],f[i-1,j],f[i-1,j-1])+a[i,j]26. 双向动态规划1数字三角形3-----小胖办证f[i,j]:=max(f[i-1,j]+a[i,j],f[i,j-1]+a[i,j],f[i,j+1]+a[i,j])27. 数字三角形4-----过河卒//边界初始化f[i,j]:=f[i-1,j]+f[i,j-1];28. 数字三角形5-----朴素的打砖块f[i,j,k]:=max(f[i-1,j-k,p]+sum[i,k],f[i,j,k]);29. 数字三角形6-----优化的打砖块f[I,j,k]:=max{g[i-1,j-k,k-1]+sum[I,k]}30. 线性动态规划3-----打鼹鼠’f:=f[j]+1;(abs(x-x[j])+abs(y-y[j])<=t-t[j])31. 树形动态规划3-----贪吃的九头龙32. 状态压缩动态规划1-----炮兵阵地Max(f[Q*(r+1)+k],g[j]+num[k])If (map and plan[k]=0) and((plan[P] or plan[q]) and plan[k]=0)33. 递推天地3-----情书抄写员f:=f[i-1]+k*f[i-2]34. 递推天地4-----错位排列f:=(i-1)(f[i-2]+f[i-1]);f[n]:=n*f[n-1]+(-1)^(n-2);35. 递推天地5-----直线分平面最大区域数f[n]:=f[n-1]+n:=n*(n+1) div 2 + 1;36. 递推天地6-----折线分平面最大区域数f[n]:=(n-1)(2*n-1)+2*n;37. 递推天地7-----封闭曲线分平面最大区域数f[n]:=f[n-1]+2*(n-1):=sqr(n)-n+2;38 递推天地8-----凸多边形分三角形方法数f[n]:=C(2*n-2,n-1) div n;对于k边形f[k]:=C(2*k-4,k-2) div (k-1); //(k>=3)39 递推天地9-----Catalan数列一般形式1,1,2,5,14,42,132f[n]:=C(2k,k) div (k+1);40 递推天地10-----彩灯布置排列组合中的环形染色问题f[n]:=f[n-1]*(m-2)+f[n-2]*(m-1); (f[1]:=m; f[2]:=m(m-1);41 线性动态规划4-----找数线性扫描sum:=f+g[j];(if sum=Aim then getout; if sum<Aim then inc(i) else inc(j);)42 线性动态规划5-----隐形的翅膀min:=min{abs(w/w[j]-gold)};if w/w[j]<gold then inc(i) else inc(j);43 剖分问题5-----最大奖励f:=max(f,f[j]+(sum[j]-sum)*i-t44 最短路1-----Floydf[i,j]:=max(f[i,j],f[i,k]+f[k,j]);ans[q[i,j,k]]:=ans[q[i,j,k]]+s[i,q[i,j,k]]*s[q[i,j,k],j]/s[i,j];45 剖分问题6-----小H的小屋F[l,m,n]:=f[l-x,m-1,n-k]+S(x,k);46 计数问题2-----陨石的秘密（排列组合中的计数问题）Ans[l1,l2,l3,D]:=f[l1+1,l2,l3,D+1]-f[l1+1,l2,l3,D];F[l1,l2,l3,D]:=Sigma(f[o,p,q,d-1]*f[l1-o,l2-p,l3-q,d]);47 线性动态规划------合唱队形两次F:=max{f[j]+1}＋枚举中央结点48 资源问题------明明的预算方案：加花的动态规划f[i,j]:=max(f[i,j],f[l,j-v-v[fb]-v[fa]]+v*p+v[fb]*p[fb]+v[fa]*p[fa]);49 资源问题-----化工场装箱员50 树形动态规划-----聚会的快乐f[i,2]:=max(f[i,0],f[i,1]);f[i,1]:=sigma(f[t^.son,0]);f[i,0]:=sigma(f[t^.son,3]);51 树形动态规划-----皇宫看守f[i,2]:=max(f[i,0],f[i,1]);f[i,1]:=sigma(f[t^.son,0]);f[i,0]:=sigma(f[t^.son,3]);52 递推天地-----盒子与球f[i,1]:=1;f[i,j]:=j*(f[i-1,j-1]+f[i-1,j]);53 双重动态规划-----有限的基因序列f:=min{f[j]+1}g[c,i,j]:=(g[a,i,j] and g[b,i,j]) or (g[c,i,j])54 最大子矩阵问题-----居住空间f[i,j,k]:=min(min(min(f[i-1,j,k],f[i,j-1,k]),min(f[i,j,k-1],f[i-1,j-1,k])),min(min(f[i-1,j,k-1],f[i,j-1,k-1]),f[i-1,j-1,k-1]))+1;55 线性动态规划------日程安排f:=max{f[j]}+P[I]; (e[j]<s)56 递推天地------组合数C[I,j]:=C[i-1,j]+C[I-1,j-1]C[I,0]:=157 树形动态规划-----有向树k中值问题F[I,r,k]:=max{max{f[l,I,j]+f[r,I,k-j-1]},f[f[l,r,j]+f[r,r,k-j]+w[I,r]]}58 树形动态规划-----CTSC 2001选课F[I,j]:=w(if i∈P)+f[l,k]+f[r,m-k](0≤k≤m)(if l<>0)59 线性动态规划-----多重历史f[i,j]:=sigma{f[i-k,j-1]}(if checked)60 背包问题(+-1背包问题+回溯)-----CEOI1998 Substractf[i,j]:=f[i-1,j-a] or f[i-1,j+a]61 线性动态规划(字符串)-----NOI 2000 古城之谜f[i,1,1]:=min{f[i+length(s),2,1],f[i+length(s),1,1]+1}f[i,1,2]:=min{f[i+length(s),1,2]+words[s],f[i+length(s),1,2]+w ords[s]}62 线性动态规划-----最少单词个数f[i,j]:=max{f[I,j],f[u-1,j-1]+l}63 线型动态规划-----APIO2007 数据备份状态压缩＋剪掉每个阶段j前j*2个状态和j*2+200后的状态贪心动态规划f:=min(g[i-2]+s,f[i-1]);64 树形动态规划-----APIO2007 风铃f:=f[l]+f[r]+{1 (if c[l]<c[r])}g:=1(d[l]<>d[r]) 0(d[l]=d[r])g[l]=g[r]=1 then Halt;65 地图动态规划-----NOI 2005 adv19910F[t,i,j]:=max{f[t-1,i-dx[d[[t]],j-dy[d[k]]]+1],f[t-1,i,j];66 地图动态规划-----优化的NOI 2005 adv19910F[k,i,j]:=max{f[k-1,i,p]+1} j-b[k]<=p<=j;67 目标动态规划-----CEOI98 subtraF[I,j]:=f[I-1,j+a] or f[i-1,j-a]68 目标动态规划----- Vijos 1037搭建双塔问题F[value,delta]:=g[value+a,delta+a] or g[value,delta-a]69 树形动态规划-----有线电视网f[i,p]:=max(f[i,p],f[i,p-q]+f[j,q]-map[i,j])leaves>=p>=l, 1<=q<=p;70 地图动态规划-----vijos某题F[I,j]:=min(f[i-1,j-1],f[I,j-1],f[i-1,j]);71 最大子矩阵问题-----最大字段和问题f:=max(f[i-1]+b,b); f[1]:=b[1]72 最大子矩阵问题-----最大子立方体问题枚举一组边i的起始，压缩进矩阵B[I,j]+=a[x,I,j]枚举另外一组边的其实，做最大子矩阵73 括号序列-----线型动态规划f[I,j]:=min(f[I,j],f[i+1,j-1](ss[j]=”()”or(”[]”)),f[I+1,j+1]+1 (s[j]=”(”or”[” ] , f[I,j-1]+1(s[j]=”)”or”]” )74 棋盘切割-----线型动态规划f[k,x1,y1,x2,y2]=min{min{f[k-1,x1,y1,a,y2]+s[a+1,y1,x2,y2],f[k-1,a+1,y1,x2,y2]+s[x1,y1,a,y2]min{}}75 概率动态规划-----聪聪和可可(NOI2005)x:=p[p[i,j],j]f[I,j]:=(f[x,b[j,k]]+f[x,j])/(l[j]+1)+1f[I,i]=0f[x,j]=176 概率动态规划-----血缘关系F[A, B]=(f[A0, B]+P[A1, B])/2f[I,i]=1f[I,j]=0(I,j无相同基因)77 线性动态规划-----决斗F[I,j]=(f[I,j] and f[k,j]) and (e[I,k] or e[j,k]),i<k<j78 线性动态规划-----舞蹈家F[x,y,k]=min(f[a[k],y,k+1]+w[x,a[k]],f[x,a[k],k+1]+w[y,a[k]])79 线性动态规划-----积木游戏F[I,a,b,k]=max(f[I,a+1,b,k],f[i+1,a+1,a+1,k’],f[I,a+1,a+1,k’])80 树形动态规划（双次记录）-----NOI2003 逃学的小孩朴素的话枚举节点i和离其最远的两个节点j,k O(n^2)每个节点记录最大的两个值，并记录这最大值分别是从哪个相邻节点传过来的。

动态规划例1-求解下列整数规划的最优解

例1 求解下列整数规划得最优解:()123123max 45634510..01,2,3,j j Z x x x x x x s t x j x =++++⎧⎪⎨=⎪⎩≤≥为整数.解（1）建立动态规划模型:阶段变量: 将给每一个变量赋值瞧成一个阶段, 划分为3个阶段, 且阶段变量k=1,2,3. 设状态变量表示从第阶段到第3阶段约束右端最大值, 则设决策变量k x 表示第k 阶段赋给变量k x 得值(1,2,3)k =、状态转移方程: 阶段指标: 基本方程；()(){}()3113,2,1044()max ,()0.s k k k k k k k k k k x a f s u s x f s f s ++⎡⎤=⎢⎥⎢⎥⎣⎦⎧=+⎪⎨⎪=⎩≤≤ 其中1233,4, 5.a a a === 用逆序法求解: 当3k =时，()(){}{}33333443330055max 6max 6,ssx x f s x f s x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=+=≤≤≤而表示不超过得最大整数。

因此, 当时, ；当时, 可取0或1；当时, 可取0, 1, 2,由此确定现将有关数据列入表4.1中当时, 有()(){}(){}22222332322220044max 5max 54,ssx x f s xf s xf s x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=+=+-≤≤≤≤而。

所以当时, ；当时, ；当时。

由此确定。

现将有关数据列入表4.2中、当时,有()(){}(){}11111221211110033max 4max 43,ssx x f s x f s x f s x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=+=+-≤≤≤≤例5 用动态规划方法解下列非线性规划问题⎩⎨⎧=≥≤++⋅⋅=3,2,1 0 max 3213221i x c x x x x x x z i 解: 解决这一类静态规划问题, 需要人为地赋予时间概念, 从而将该问题转化为多阶段决策过程。

12个动态规划算法举例

动态规划是一种用于解决最优化问题的算法。

它通常用于找到最小或最大值。

这里列举了12 个常见的动态规划算法，并给出了每个算法的举例：
1 最长公共子序列（LCS）算法：用于比较两个序列，找出它们之
间的最长公共子序列。

2 最小编辑距离算法：用于比较两个字符串，找出将一个字符串变
为另一个字符串所需的最少编辑操作次数。

3 背包问题算法：用于在限制给定的总体积的情况下选择最优的物
品组合。

4 最短路径算法：用于求解有向图或路径的最短路径。

5 最小生成树算法：用于求解图的最小生成树。

6 线性规划算法：用于求解线性规划问题。

7 矩阵链乘法算法：用于计算矩阵链乘法的最优计算次序。

8 单源最短路径算法：用于求解有向图的单源最短路径问题。

9 拓扑排序算法：用于对有向无环图（DAG）进行拓扑排序。

10图形相似性算法：用两个图形进行对齐，并通过比较它们之间的差异来评估它们的相似程度。

11 11 区间动态规划算法：用于解决区间动态规划问题，例如
最小编辑代价问题。

12 分数背包问题算法：用于在限制给定的总价值的情况下选择
最优的物品组合。

13这些算法的具体细节及实现方式可以通过搜索或者学习相
关的资料来了解。

动态规划应用动态规划解决问题的思路与技巧

动态规划应用动态规划解决问题的思路与技巧动态规划应用 - 动态规划解决问题的思路与技巧动态规划（Dynamic Programming）是一种常见的算法思想，用于解决一些具有重叠子问题和最优子结构性质的问题。

通过将大问题划分为小问题，并将小问题的解存储起来以避免重复计算，可以在一定程度上优化问题的求解过程。

本文将介绍动态规划的应用，并提供一些思路与技巧。

一、动态规划的基本思路动态规划问题通常可以由以下步骤解决：1. 定义状态：将问题划分成若干子问题，并确定每个子问题需要记录的状态。

2. 定义状态转移方程：通过分析子问题之间的关系，建立状态转移方程，以表达子问题的最优解与更小规模子问题的关系。

3. 初始化边界条件：确定最小规模子问题的解，并初始化状态转移方程中需要用到的边界条件。

4. 递推求解：按照状态转移方程的定义，从较小规模的子问题开始逐步推导出较大规模的问题的解。

5. 求解目标问题：根据最终推导出的状态，得到原始问题的最优解。

二、动态规划的技巧与优化1. 滚动数组：为了降低空间复杂度，可以使用滚动数组来存储状态。

滚动数组只记录当前状态与之前一部分状态相关的信息，避免了存储所有状态的需求。

2. 状态压缩：对于某些问题，可以将状态压缩成一个整数，从而大幅减小状态的数量。

例如，当问题中涉及到某些特定的组合或排列时，可以使用二进制位来表示状态。

3. 前缀和与差分数组：对于某些问题，可以通过计算前缀和或差分数组，将问题转化为求解累加或差对应数组中的某个区间的值的问题，从而简化计算过程。

4. 贪心思想：有些动态规划问题可以结合贪心思想，在每个阶段选择局部最优解，然后得到全局最优解。

5. 双重循环与多重循环：在实际解决问题时，可以使用双重循环或多重循环来遍历状态空间，求解问题的最优解。

三、动态规划的实际应用动态规划广泛应用于各个领域，包括但不限于以下几个方面：1. 最短路径问题：例如，求解两点之间的最短路径、最小生成树等。

动态规划解决旅行商问题附代码x

void getJ(int jlist[], int c, int n)// 根据 2 进制 j 和 j 中 1 的个数找下一个 j {
int i = n-1,j; int tmp = 1 , result = 0; while(!jlist[i])i--;// 最高位的 1 的位置 j = i-1; while(jlist[j])j--;// 找最高位 1 之下的最高 0 if(!jlist[n-1])// 若最高位不为 1 {
邻接矩阵 :
node
0
1
2
3
0
5
3
2
1
5
7
9
2
3
7
12
3
2
9
12
动态填表 : 表中元素代表第 i 个节点经过 V 集合中的点最后到个值 ,取其中最小的一个 .
0 点的最短值 .如果有多
------------word 文档可编辑 -------------
i\Vj 0 1
2
3
1,2(取 min) 1,3(取 min) 2,3(取 min) 1,2,3( 取 min)
int nextj = 0;// 下一个 j int c=0;// 计数 j 的二进制有几个 1 int jlist[20]={0};// 存放 j 的二进制数组 int i=0; int tmp = 1; while(j) {
if(j%2) {
c++; jlist[i++]=1; }else { jlist[i++]=0; } j/=2; } getJ(jlist,c,N-1);// 处理 jlist
d[2][{1}]=24}
这样一共循环 (2^(N-1)-1)*(N-1) 次,就把时间复杂度缩小到 O(N*2 N )的级别 . 核心伪代码如下 :