公务员招聘模型

合集下载

公务员招聘模型

公务员招聘模型摘要在公务员招聘中，为了给招聘领导小组提出一种最优化的录用分配方案，本文本着公平、公正原则提出了一个符合题目要求的部门分配方案。

其中包括了不考虑应聘人员意愿和考虑应聘人员意愿两种情况的模型。

1 .招聘一个公务员，我们要考虑招聘人员的意愿或不考虑招聘人员的意愿。

而决定聘选一个公务员我们需要考虑到他的综合成绩，即:总成绩=笔试成绩系数×60%+面试成绩系数×40%），在其范围中来择优。

除此外我们还应该考虑到专家对应聘者特长的等级评分和用人部门的基本情况和对公务员的期望要求。

2 .模型一我们不考虑招聘人员自己的意愿，也就是不考虑各个用人单位的基本情况及工作类别，从而择优按需录取并且分配到各个部门。

3 .模型二是在模型一的基础上，我们考虑招聘人员自己的意愿从而是模型更加完善。

4 .我们从特殊的情况推广到一般的情况（即N个应聘人员M个招聘单位）。

5 .最后对模型做了评价及检验一、问题的重述我国公务员制度已实施多年，目前, 我国招聘公务员的程序一般分三步进行：公开考试（笔试）、面试考核、择优录取。

现有某市直属单位因工作需要，拟向社会公开招聘8名公务员，具体的招聘办法和程序如下：（一）公开考试：凡是年龄不超过30周岁，大学专科以上学历，身体健康者均可报名参加考试，考试科目有：综合基础知识、专业知识和“行政职业能力测验”三个部分，每科满分为100分。

根据考试总分的高低排序按1:2的比例（共16人）选择进入第二阶段的面试考核。

（二）面试考核：面试考核主要考核应聘人员的知识面、理解能力、应变能力、表达能力等综合素质。

按照一定的标准，面试专家组对每个应聘人员的各个方面都给出一个等级评分，从高到低分成A/B/C/D四个等级，具体结果见附录表１所示。

（三）由招聘领导小组综合专家组的意见、笔初试成绩以及各用人部门需求确定录用名单,并分配到各用人部门。

该单位拟将录用的8名公务员安排到所属的7个部门，并且要求每个部门至少安排一名公务员。

数学建模公务员招聘程序

数学建模公务员招聘程序数学建模是当前社会发展的一个重要领域，在各个行业中都有广泛的应用，其中也包括公务员招聘程序。

数学建模在公务员招聘中主要包括招聘考试的试题设计、成绩评估等方面。

本文将结合实际案例，探讨数学建模在公务员招聘程序中的作用。

一、试题设计公务员招聘中，试题设计是关键环节。

试题不仅要与应聘岗位紧密相关，而且要考察应聘者的智力、解决问题的能力和应变能力。

数学建模通过对具体问题的建模和求解，可以获得较好的试题设计。

通过将具体问题建模为数学模型，再根据模型求解，可以使试题更加具有针对性和实用性。

实际中，数学建模可以在各种招聘科目中应用：例如，公共基础知识、组织管理能力、综合应用能力等，都可以通过数学建模来体现。

这些试题具有很好的实用性、针对性和普遍性。

二、成绩评估公务员招聘中，成绩评估也是重要环节。

在应聘者众多的情况下，如何客观评估应聘者的能力，就显得尤为重要。

而数学建模可以通过数学或统计方法来对考生的答卷进行评估和分析，从而得出较为客观的评价。

例如，在某次公务员考试中，面试环节占了30%的总分。

为了评估面试成绩，可以根据被面试者的表现对面试得分进行评估。

具体方法如下：先对面试过程中涉及的问题进行建模，分别给出不同的权重值，并通过专家讨论的方式对权重值进一步修正，再根据考察者的表现，依次赋予不同权重的得分，得出最终成绩。

三、建立推荐模型公务员招聘中，除了考察面试等环节外，还需要建立推荐模型，根据应聘者的各项条件，分析哪些人员更适合该岗位。

建立这个模型的过程同样需要运用到数学建模的方法。

具体方法如下：1. 根据开设岗位的特点，制定不同的推荐模型。

2. 根据应聘者提交的履历，结合岗位基本要求，综合考察应聘者的学历水平、专业背景、个人能力等因素。

3. 将考察结果与招聘要求之间的匹配程度进行计算和评估，选出最合适的人选。

数学建模在公务员招聘程序中的应用显然十分重要，无论是试题设计、成绩评估还是人员选取，都需要运用到数学建模的方法，以保证招聘程序的公正科学，为公务员队伍建设提供有力保障。

基于胜任力模型的公务员选拔过程研究

基于胜任力模型的公务员选拔过程研究作者：安廷婷来源：《行政事业资产与财务》2016年第10期摘要：加强我国公务员的队伍建设，需从源头着手，重视公务员选拔，保证选拔的公平、公正。

本文从胜任力模型的研究现状出发，结合实际，找出胜任力模型在我国公务员选拔过程中存在的问题。

通过借鉴国外在此研究中的优势，提出公共部门思路转变、完善公务员胜任力模型体系以及加强考核内容科学性等建议。

争取实现胜任力模型在公务员选拔中的良好运用，保证公务员选拔的公平、公正，最大限度的实现人才选拔。

关键词：公务员；胜任力模型：公务员选拔我国公务员的选拔制度始于1994年，国家公务员考试从2003年12.5万人审核通过，5475人录用，到2016年国考有199.8万人报名，139.46万人通过资格审查，录用27817人，十多年来国家公务员考试报名人数猛增12倍。

公务员选拔过程花费大量人力、物力、财力，从选拔的第一个流程颁布公告开始，公共部门与应试者都需经历漫长的资料审核、笔试、面试以及最终录用的过程。

国家人事部早在2000年即明确提出公务员的管理与建设必须强调能力建设，“研究提出不同层次公务员的能力素质标准，积极推进全方位全员培训”，并且强调要研究和制定各级、各类型公务员的能力素质标准，为能力建设提供科学的依据，健全科学培训质量的评估体系，实现公务员培训方式的现代化。

但是，具体操作时却不尽如人意，选拔流程中存在笔试内容不科学，面试不专业等问题，影响了公务员选拔的公平性以及有效性。

因此，如何促进公务员选拔过程的科学性，实现公平选拔是现阶段公共部门面临的重要问题。

一、我国公务员及其选拔制度发展公务员是指依照法律履行公共职务，被正式纳入国家行政编制，并由国家财政负担其工资和福利的人员。

我国政务类公务员由人民代表大会选举或其常务委员会任命的各级政府人员，业务类公务员则指中央以及地方政府中除去政务类的公务员以外其他的公务员。

公务员的选拔即公务员的考试录取与任用。

全国数学建模竞赛论文示范公务员招聘

全国数学建模竞赛范题公务员招聘的优化模型摘要：本文研究了公务员录用分配的优化问题。

以现有标准为参考，采用层次分析法和Saaty等人提出的1—9尺度来量化面试中的等级，给出不同的权重，计算出每个应聘人员的量化分数，用来衡量应聘人员能力的高低，以此为基础进行择优录取。

要做到“公平、公正、自愿，择优”原则，就需要有一个合理的录取分配方法，我们运用不断增加因素的方法，逐层深入，依次建立了三个模型，得出最优的模型。

在模型1中，按分数择优录取，然后对人员进行随机分配。

在模型2中，考虑到部门之间存在优劣区分，我们把应聘人员填报的志愿看成是对不同部门优劣评价的“调查”，用统计学的知识来计算出各部门的优劣排名，把高分的人员分配到好部门。

得到分配方案为：部门1-7分别录用人员12、3；2；1；9；4；8；5。

在模型3中，考虑到各工作类别对人员各种能力的不同要求，对不同类别重新调整四种能力的权重，并在四个不同类别中分别对人员进行排名，以此来设计一种择优录取的算法，利用计算机编程实现对人员的录取分配。

得到分配方案为：部门1-7分别录用人员12；1；2、4；9；6；8；5。

如果再考虑志愿因素，则按第一志愿优先的原则，利用模型1，2，3进行求解，得出最优分配方案：部门1-7分别录用人员9；8；1；12；2、6；4；11。

我们定义了一个优越度（即所有人员所得分数与部门基本分之差的和）用来衡量人员分配方案的优劣，优越度越大，该模型的人员分配方案就越优。

用这种方法，我们对模型2和模型3的结果进行检验，其结果分别是149.9245和159.2942。

而对于模型1由于具有随机性，对其进行100次计算机随机模拟检验，其平均值为128.69。

由此得出模型3的分配方法是最优的。

针对模型的结果，对招聘单位提出了四点改进的建议。

一问题的重述目前, 我国招聘公务员的程序一般分三步进行：公开考试（笔试）、面试考核、择优录取。

现有某市直属单位因工作需要，拟向社会公开招聘8名公务员，具体的招聘办法和程序如下：（一）公开考试：凡符合条件的人均可参加，根据考试总分的高低排序按1:2的比例（共16人）选择进入第二阶段的面试考核。

公务员招聘的一种优化录用方案

1
引言在本问题中，面试专家对笔试成绩最高的 16 个应聘人员的知识面、对问题的理解能力、应变能力、表达
能力四个方面进行了考核，并给出了等级评分，评分标准有 A、 B、C、D 四个等级；用人部门对聘用公务员在上述四个方面的具体期望以等级评分的形式也做出了要求，同时用人部门也公布了本单位的基本情况，包括福利待遇、工作条件、劳动强度、晋升机会和学习深造机会．每一位应聘人员可以申报两个适合自己的工作类别志愿，便于用人部门挑选．问题的目的是，在上述 16 个公务员中选出 8 人，并将他们分配到 4 类不同性质共 7 个部门中去，要求每个部门至少安排 1 名公务员．传统的复合决策模式进行人员录用决策，首先要根据工作要求对应聘人员进行职业性质测试，得出应聘人员的测验成绩（如 D 题中对应聘者的特长等级打分），然后对基本合格人选进行与工作相互匹配的动态分析．首先，从个人的角度分析，由人去选适当的工作，即将得分最高的那项工作安排给相应得高分者；但可能会带来一个问题，即出现多人同时在某项工作上得分最高．其次，从工作的角度分析，由工作选人，即按每一工作测试最高分者来担任此工作，但也会产生一个人同时被几个工作选中的问题．如何采用更好的录用决策，使得用人部门能得到最合适的人选，同时应聘者能在被录用的工作部门充分发挥自己工作能力，这就需要建立一个新的数学模型，使得工作和应聘者的能力最佳匹配，实现用人部门和应聘者的共赢，从而能够快速解决在决策中出现的如前所述的问题。 2 两空间向量夹角最小模型在线性空间中，两个非零向量 ai 和 b j 的夹角按如下定义：
小，表明其中一个向量在另一个向量上的投影越大，即两个向量更接近．我们将每个应聘人员四种能力的等级转化为数据，由这四个数据构成人员的能力向量；同时根据每个用人部门对应聘人员四种能力的期望等级赋予四种能力不同的权重参数，并以此参数建立用人部门的权重向

IE案例分析(三)

具体要求
地点商品
电器服装食品家具计算机
1
120 80 150 90 220
2
300 350 160 200 260
3
260 300 180 －
案例五：指派问题
具体要求这是一个求最大值、人数与任务数不相等以及不可接受的配置的一个综合指派问题。
案例六：公务员招聘与指派
表１：笔试成绩，专家面试评分及个人志愿
应聘人员笔试成绩申报类别志愿专家组对应聘者特长的等级评分知识面理解能力应变能力表达能力
人员1
人员2 人员3 人员4 人员5 人员6 人员7
290
288 288 285 283 283 280
（2）（3）
（3）（1）（1）（2）（4）（3）（3）（2）（3）（4）（4）（1）
330 200
260
220 160
40
420 150
120
240 420
0
0 0
运用匈牙利算法求最优解
案例五：指派问题

用WinQSB软件求解时不必对效率矩阵进行人工转换，系统会自动转换。（1）启动程序。点击开始→程序 →WinQSB→Network Modeling。（2）建立新问题。选择Assignment problem、 Maximization，输入标题、人数（目标数）为5及任务数（配置数）为4。
案例六：公务员招聘与指派
具体要求该单位拟将录用的8名公务员安排到所属的7个部门，并且要求每个部门至少安排一名公务员。这7个部门按工作性质可分为四类：(1)行政管理、 (2)技术管理、(3)行政执法、(4)公共事业。
案例六：公务员招聘与指派

公务员招聘的优化模型

公务员招聘的优化模型队员：张大伟王震钱晓东完成日期：2011-8-9公务员招聘的优化模型摘要：本文主要利用模糊数学理论，建立了公务员招聘的优化模型，解决了我国目前公务员招聘中存在的实际问题。

在模型Ⅰ中，对问题一（即在不考虑应聘者的志愿的情况下），按“择优按需”原则，（“择优”就是综合考虑所有应聘者的初试和复试的成绩来选优；“按需”就是根据用人部门的需求，即各用人部门对应聘人员的要求和评价来选择录用），得出了录用分配方案。

在模型Ⅱ中，对问题二（即在双方都是相互了解的前提下为双方）做出选择方案。

每一个部门对所需人才都有一个期望要求，即可以认为每一个部门对要聘用的公务员都有一个实际的“满意度”：同样的，每一个应聘人员根据自己意愿对各部门也都有一个“满意度”，由此来选取使双方“满意度”最大的录用分配方案。

在两个模型建立的过程中，反复利用了偏大型柯西隶属分布函数，多次将各种不同的等级进行量化处理，最终得到人员的录用方案，实现了模型的建立，并且将其进行了推广。

关键字：公务员招聘；模糊优化；数学模型；偏大型柯西隶属分布；满意度一．问题重述我国公务员制度已实施了多年，1993年10月1日颁布施行的《国家公务员暂行条例》规定：“国家行政机关录用担任主任科员以下的非领导的国家公务员，采用公开考试、严格考核的办法，按照德才兼备的标准择优录用”。

目前，我国招聘公务员的程序一般分三步进行：公开考试（笔试）、面试考核、择优录取。

针对公开考试后，根据考试总分从高到低排序按1:2的比例选择进入第二阶段的面试考核，面试考核是由专家对应聘人员的各个方面都给出一个等级评分，根据这个等级的评分，结合笔试成绩，首先不考虑应聘人员本身的申报志愿,建立一个择优录用方案，其次，考虑应聘人员本身申报类别志愿，为招聘领导小组设计一个分配方案。

再次，进行一般情况的检验，最后，对公务员招聘过程提出改进的建议。

二．模型假设根据建立模型的需要，作出如下假设：（1）招聘对应聘者特长的四个能力方面所占比重相等。

公务员招聘.数学建模论文正稿

对公务员招聘问题的思考（2004年高教社杯获得者）编者按：该文用层次分析法确定了各招聘人员对各部门的权重，将笔试成绩和面试权重综合，融合各类工作的要求，分别给出四类工作的综合成绩权重，以总权重和为目标，建立了整数规划模型。

报告论述清楚，逻辑较为严谨。

摘要：本文利用层次分析法和0-1型整数规划建立了一个公务员招聘的数学模型，并结合实际提出了通用可行的算法。

首先利用层次分析法确定了招聘人员面试成绩对用人部门的权重，再把笔试成绩转化为相应的权重，然后将笔试成绩和面试成绩对用人部门的权重结合起来，建立了权重计算模型。

再把应聘人员的志愿转化为用人单位对应聘人员的权重，建立了双向选择的权重计算模型。

然后确定最优方案模型，被选人员对用人单位的权重之和最大时的人员选取即为所求，从而建立了应聘人员最优选取的0-1整数规划模型，制定出最优的分配方案，并对一般情况即N个应聘人员M个用人单位时，对模型做了推广。

最后利用MATLAB和LINGO编程对上述模型和算法进行了实践求解。

针对实际本文还充分考虑了多种情况下各种因素对人员招聘的影响，较完满地解决了公务员招聘问题，并检验了模型的合理性，文章分析了模型的优缺点和改进方向，同时提出了一些实用性建议。

关键词：公务员招聘；层次分析法；0-1整数规划一、问题的重述（略）二、模型的假设与符号说明1．模型的假设（1）笔试和面试的成绩客观准确地反映了各个应聘人员的真实能力。

（2）各个工作享有对应聘人员相同的支配度，不存在某个工作优先录取的情况（3）对于所有部门而言均分为四个工作种类，每个工作种类对于能力的要求不变。

（4）应聘人员的录取与分配只与我们所求出的权重有关。

（5）每个人员只能被一个单位录取，一个单位至少录取一个人。

2．符号说明r ：笔试成绩对面试成绩的比例系数ij q ：第i 个人对第j 个工作类别的综合权重Q ：方案中各个应聘人员对各个工作类别的权重矩阵1Q ：应聘人员服从调配时各应聘人员对各个工作类别的权重矩阵2Q ：应聘人员不服从调配时各应聘人员对各个工作类别的权重矩阵4N B ⨯：各应聘者对于工作类别(1)的四种能力的得分矩阵1N C ⨯：各应聘者对于工作类别(1)的权重矩阵1N D ⨯：各应聘者对于工作类别(2)的权重矩阵1N E ⨯：各应聘者对于工作类别(3)的权重矩阵1N F ⨯：各应聘者对于工作类别(4)的权重矩阵4N G ⨯：所有人员的面试成绩对于四项工作的权重矩阵M ：单位数i M ：工作类别(i )包括的用人单位数N ：应聘人数S ：应聘人员对各个部门的申报矩阵X ：人员分配矩阵A ：成对比较矩阵三、问题的分析题目要求根据用人部门的实际需要，建立最优的人员分配方案。

(招聘面试)招聘模型

（招聘面试）招聘模型公务员招聘摘要本文针对某市直属单位因工作需要向社会公开招聘8名公务员的事项，根据题目中给定的用人单位的招聘指标，及各应聘人员于成绩、志愿、能力等方面的情况。

建立数学模型以解决招聘领导小组对应聘人员的录取及分配等问题。

本文对公务员招聘问题采用模糊综合评判决策和图论中二部图匹配的方法进行研究。

首先根据笔试成绩和面试成绩得出每个应聘人员的综合成绩，择优选出8个人员。

然后对这8个人员进行合理分配，得到如下俩个模型：模型Ⅰ：于不考虑应聘人员意愿的情况下，采用模糊综合评判决策的方法进行求解由以下公式：得到人员的模糊综合评判矩阵，再引入权重概念，由表2中得到壹个模糊综合要求矩阵，令，从矩阵R中可见出每个应聘人员对于各部门的有益值。

最后引入各部门对高能力人员的急需程度，能够得到问题壹所需要的合理方案，用表格表示如下：模型Ⅱ：考虑到应聘人员的意愿，采用图论中二部图匹配的方法，画出二部图，于图形中对人员和部门进行合理的匹配，问题二所需的优化合理方案，如下表：然后根据问题（3）将之上俩个模型壹般化，且对该招聘过程提出壹定的建议。

最后我们仍对结果检验，验证了模型的稳定性和实用性，指出了模型的优缺点，且将模型加以推广。

一、问题重述某市直属单位按1993年10月1日颁布施行的《国家公务员暂行条例》的有关规定，来招聘8名公务员。

今通过公开考试，从笔试成绩优秀的人员中录取了16名进行面试。

然后专家组于面试过程中分别从知识面、理解能力、应变能力、表达能力这四个方面给各应聘人员评定等级（按A、B、C、D四个等级进行评定），见表1，招聘领导小组就根据专家组的意见、笔试成绩及用人单位需要，见表2，来确定录用名单，且将录用的8个人按壹定的要求合理分配到各部门中去，而且每个部门至少要分到1名应聘者，同时，应聘人员也可根据自己的意愿，于四种不同类别的工作中选择二种不同类别的工作。

根据这些情况，要求我们解决以下四个问题：（1）如果不考虑应聘人员的意愿，择优按需录用，试帮助招聘领导小组设计壹种录用分配方案；（2）于考虑应聘人员意愿和用人部门的希望要求的情况下，请你帮助招聘小组设计壹种分配方案;（3）你的方法对于壹般情况，即N个应聘人员M个用人单位时，是否可行？（4）你对上述招聘公务员过程认为仍有哪些地方值得改进，给出你的建议。

雨量预报评价、公务员选拔数学模型

、、全国竞赛论文（二）时间：年月日教学目的：学习全国竞赛论文写作重点及难点：论文写作教学内容及步骤（时间分配）一、雨量预报方法评价的数学模型（40分）二、公务员招聘优化模型（50分）雨量预报方法评价的数学模型【摘要】本模型用概率统计原理和方法对于题中所给宠大数据进行科学处理和计算,思路清晰、模型简洁、结果可靠。

并且借助于计算机编程快速搜索和运算，快速简便，便于操作使用。

评价雨量预报方法优劣的关键是要测算预测雨量和实际雨量的误差有多大。

但本题中给出91个实测点和2491个预测点，而且实测点分布不均，不一定在预测点上。

这样在同一时间段内的预测和实测位置的降雨量比较起来很困难，需找到与实测位置相对应的预测位置。

对于实测点A i (i=1,2…2491) 搜索与 A 1附近的预测站B j (j=1,2…2491)1. 按题中所给经纬度表，把地球经纬交线得一个单位格近似看作矩形，计算对角线长 r=2. 以A i 为中心r j 为半径作圆iA R ，搜索进入到该圆域内预测站B j 设，rJi B A =|A i B j |，若 r j ≤r 则B j 在圆iA R 内，否则不在。

不妨设B j1 , B j2 ,B j3 在圆iA R 内3. 计算与 A i 对应的预测站点雨量1)、设若得到与A i 相比较实测点为n 个：B j1 ,B j2 ,．．． B jn ，预测雨量b j1 , b j2 ,．．．b jn ；离 A i 越近的预测点对A i 影响越大，权值越大。

故 B jk 权值 P B1=12||(||||...||)i jn i j i j i j n r A B nr A B A B A B --+++，其中12...1j j j nB B B p p p +++=2）、与 A i 对应的预测站加权雨量 1212...ijjn jnA jB j B j B b b p b p b p =+++4．计算A i 点雨量a i 与对应预测站加权雨量iA b 绝对误差： ie=|a i -b A1|(i=1,2…2491)5．对于每个A i （i=1,2,…,91）都计算41天中每一天四个段内绝对误差e i计算实测站与预测站绝对误差的平均值f n=()41491111191441k j ik j i e ===⨯⨯∑∑∑,其中 j 表示第j 个时段，k 表示第k 天，i 表示第i 个实测点和准确等级百分比,n （n ＝1,2）表示用第n 种方法预测雨量6 . 统计计算误差分布，即准确程度的概率（见页表4）对于问题2 从公众感受角度对雨量预测方法评价，把雨分成6段并分别赋值，（见页表3），把雨量(实际和预测雨量)与所分的雨段对照，属于哪段，就赋什么值。

2022国家公务员考试行测技巧：削弱加强论证模型之求异论证

2022国家公务员考试行测技巧：削弱加强论证模型之求异论证2022国家公务员笔试备考已开始，为了帮助大家提早备考，山东中公国家公务员考试网特整理了国考行测备考资料，包含：常识判断、言语理解与表达、数量关系、判断推理、资料分析、行测技巧，希望可以帮助大家顺利备考。

下面为大家分享：2022国家公务员考试行测技巧：削弱加强论证模型之求异论证。

国家公务员招考信息 | 阅读资料 | 考试题库2022国家公务员考试行测技巧：削弱加强论证模型之求异论证削弱加强是行测判断推理考试中的重点和难点，其中在国考、省考、事业单位的考试中均占较大比重，其实有些削弱加强的题目，它们有着特殊的论证方式，有其典型的削弱和加强的角度，如果在做题时我们能够识别，那么将会帮助我们提升做题的速度和准确率，接下来中公教育就带大家来学习一下削弱加强题目论证模型中的求异论证。

理论回顾1、我们来了解一下，什么是求异论证。

例:两块田地：甲田：小麦黑土地磷化肥亩产700斤乙田：小麦黑土地不施肥亩产400斤推测：磷化肥是产量高的原因。

上述题目当中，有两块土地，它们都有共同的属性，即都种植了小麦、都是黑土地。

其中有两个属性不同：施肥状况不同，并且亩产不同，那么结论认为正是因为施肥使甲地亩产较高。

这就是一道典型的求异论证。

这种题目一般是对比实验，通过控制变量的方式找到结果不同的原因。

那么如何削弱加强呢?2、求异论证如何削弱加强我们之前学过，对于一道普通的削弱加强我们可以从论证、结论、论据的角度进行削弱，这些角度我们不再着重强调，我们主要来认识一下，求异论证的模型有什么典型的削弱加强的方式。

其中，削弱就是证明题干没有控制好变量，也就是找两个实验对象本质的不同点，那就证明是另有他因，从而削弱题干的结论。

简单概括就是找不同而加强就相反，我们可以找更多相同的属性证明实验控制好了变量，即找相同。

公务员网络类面试题及答案

公务员网络类面试题及答案在当下数字化时代，网络已经成为人们生活中不可或缺的一部分。

公务员招聘中，网络类面试题被广泛采用，以测量考生对网络知识和技能的掌握程度。

本文将为大家提供一些常见的公务员网络类面试题及答案，希望对大家备考有所帮助。

一、网络基础知识1. 什么是IP地址，有多少种IP地址？答案：IP地址是Internet Protocol Address的缩写，用于唯一标识连接到互联网的设备。

IP地址分为IPv4和IPv6两种，其中IPv4地址总数为2^32，约42亿个；IPv6地址总数为2^128，数量极其庞大。

2. 什么是DNS，它的作用是什么？答案：DNS是Domain Name System的缩写，它负责将域名转换为对应的IP地址。

它的作用是解析域名和IP地址之间的关联，使得人们可以通过域名访问互联网，而不需要记忆复杂的IP地址。

3. OSI模型有哪些层次，各层次的作用是什么？答案：OSI模型包括物理层、数据链路层、网络层、传输层、会话层、表示层和应用层。

各层次的作用如下：- 物理层：负责传输比特流，包括电器、电缆和物理连接介质等。

- 数据链路层：负责将数据划分为数据帧，并进行差错检测。

- 网络层：负责对数据进行逻辑寻址和路由选择。

- 传输层：负责提供端到端的可靠数据传输，包括分段和流量控制等。

- 会话层：负责建立、管理和终止会话。

- 表示层：负责数据格式转换、数据加密和数据压缩等。

- 应用层：为用户提供网络应用服务，如电子邮件、文件传输协议等。

二、网络安全1. 请简要说明网络安全的重要性。

答案：网络安全是指保护计算机网络和网络资源不受未经授权的访问、使用、更改和破坏的能力。

网络安全的重要性体现在以下几个方面：（1）保护个人隐私和信息安全；（2）保障国家安全和国家重要信息的保密性；（3）维护经济安全和商业秘密；（4）防止网络犯罪和网络攻击等。

2. 请列举几种常见的网络攻击手段。

答案：常见的网络攻击手段包括但不限于：（1）计算机病毒和蠕虫：通过传播病毒和蠕虫程序感染其他计算机系统。

基于公务员招聘问题的数学模型处理法

Ａｂｓｒｃ：ＡｎａｙｉＨｉｒｒｈｙｒｃｓ（ｔａｔｌｔｃｅａｃＰｏｅｓＡＨＰ）ｉｕｓｄｏｃｍｐｒｓｎｎａｌｉｂｓｄｎｈｅｓｅｆｒｏａｉｏａｄｎａｙｓｓａｅｏｔ
ｒｃｕｔｅｔｆｕｌｓｒａｔ．ＡＨＰｅｕｔｉａａｉｆｃｉｎａｋｆｔｃｎｉａｅｏｔａｔＯｅｒｉｍｎｏｐｂｉｅｖｎｓｃｒｓｌｓｎｓｔｓａｔｏｒｎｏｈｅａｄｄｔｓｎｈｅＤｒｆ
ｔｅｅｒｔｎｄｐｒｍｅｔａｅｌｓｒｎｏｈｅａｔｎｓｎｈｅｙｓｏｅａｄｄｔｓ０一ｈｒｃｕｉｇｅａｔｎｓｓｗｌｉａａａｋｆｔｅｄｐｒｍｅｔｉｔｅｅｆｔｃｎｉａｅ．＿ｈ
意义．
关键词：公务员招聘；层次分析法；０整数规划 —１
ቤተ መጻሕፍቲ ባይዱ
中图分类号：Ｏ１１４４．
文献标志码：Ａ
文章编号：１０ — ４５２１）４０４ — ３０８５７（０００ — ０４０
ＭａｈｅａｉａｏｅｓｇｄｆｒＲｅｒｔｅｔｏｔｍｔｃｌＭｄｌＤｅｉｎｅｏｃｕｉｍｎｆＰｕｂｌｃＳｅｖａｓｉｒｎｔ
ＣＨＥＮＷｅ－ｈｎ阿ｉｚｏｇ。Ｃｈｎｎｎａｇ— ａ
（ｐｒｍｅｔｏａｉｄｃｔｎＳｚｏｃｔｏａｉｅｓｔＤｅａｔｎｆＢｓＥｕａｉ，ｕｈｕＶｏａｉｎｌＵｎｖｒｉｃｏｙ，Ｓｚｏ１１４，Ｃｉａｕｈｕ２５０ｈｎ）

公务员录取模型

公务员录取模型摘要简述了我国目前招收公务员的状况，形势。

随着我国人事制度改革的逐步深入，为满足社会对高素质人才的需求，现各政府部门和机关都对公务员的录取工作进行了改革，即改革以往不能招聘到合理人才的做法。

同时加大了面试成绩在公务员录取中的比重。

一般是根据笔试的成绩，将达到数线的报考人员从高分到低分排序，按1:2的比例选择进入面试名单。

面试一般采用由专家组面试考核的办法，主要面试考核报考人员的专业知识面、思维的创造性、灵活的应变能力、文字和口头的表达能力和等综合素质。

针对几种问题提出了一些解决方法和改进方法，使招聘部门和各报考人员有最好的互动。

充分考虑了报考人员的意愿和基本状况，以及招聘部门对报考人员各方面素质的要求，对双方在一定方式下进行各中排序，择优录取。

使各部门都能在现实情况下最大限度的招聘到自己需要的人员。

关键词：报考人员，部门，总成绩，部门总数，排序。

The public official pass in examinations modelAbstractSummarizes our country at present to recruit official's condition, the situation. Is gradually thorough along with our country personnel system reform, for satisfies the society to the high quality talented person's demand, presently various government department and the institution all have carried on the reform to official's enrollment, namely the reform formerly could not advertise for to the reasonable talented person's procedure. Simultaneously enlarged has interviewed the result in the official enrollment proportion. Generally is according to the result which examines by writing, achieved several register for the personnel from the high score to the low score arrangement, enters according to 1:2 scale factoring interviews the name list. Interviews generally uses by the expert group interviews the inspection means, mainly interviews the inspection to register for personnel's specialized aspect of knowledge, the thought creativity, the nimble strain capacity, the writing and the oral expression ability and so on the comprehensive quality.Oposed in view of several kind of questions some solutions and the improvement method, cause the employment advertise department and respectively registers for the personnel to have the best interaction. Fully had considered registers for personnel's wish and the basic condition, And invite the section to request register for examination first personnel everyone character, carries on to both sides under the certain way each center arranges, chooses the best applicants. Enables various departments all in the realistic situation needs the maximum limit employment advertise the personnel which to oneself.Keywords: Registers for the personnel, the department, Total score,the department total, the arrangement.第一章：前言1.1背景[4]随着我国人事制度改革的逐步深入，为满足社会对高素质人才的需求，现各政府部门和机关都对公务员的录取工作进行了改革，即改善了以往不能招聘到合理人才的做法。

公务员招聘问题的模型分析

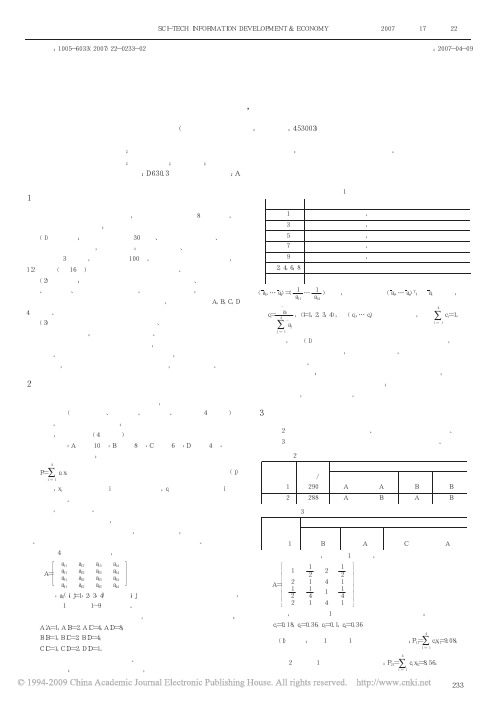
１问题的提出现有某市直属单位因工作需要，拟向社会公开招聘８名公务员，具体的招聘办法和程序如下：（１）公开考试：凡是年龄不超过３０周岁、大学专科以上学历、身体健康者均可报名参加考试，考试科目有：综合基础知识、专业知识和行政职业能力测验３个部分，每科满分为１００分。

根据考试总分的高低排序，按１∶２的比例（共１６人）选择进入第二阶段的面试考核。

（２）面试考核：面试考核主要考核应聘人员的知识面、对问题的理解能力、应变能力、表达能力等综合素质。

按照一定的标准，面试专家组对每个应聘人员的各个方面都给出一个等级评分，从高到低分成Ａ，Ｂ，Ｃ，Ｄ４个等级。

（３）由招聘领导小组综合专家组的意见、笔初试成绩以及各用人部门需求确定录用名单，并分配到各用人部门。

由于在面试考核中采取的是等级平分，对决策者来说是一个较为模糊的概念。

如何用数学模型的方法给出定量分析，以克服主观臆断所造成的片面性，使决策者较全面地作出明智的决策，是本文的主题。

２模型的建立根据每个部门对公务员特长的希望要求，并结合专家组对应聘者特长的等级评分（包括知识面、理解能力、应变能力、表达能力４个方面）和笔试成绩，设计了如下录用方案：首先，把应聘人员（４个方面）的等级评分与各部门对公务员的希望要求共同量化：Ａ表示１０分，Ｂ表示８分，Ｃ表示６分，Ｄ表示４分。

则应聘者在某部门的得分为：Ｐ＝４ｉ＝１!ｃｉｘｉ（１）式中，ｘｉ表示应聘者第ｉ项素质的量化值，ｃｉ表示该部门对第ｉ项素质要求的权数。

其次，权数的确定。

运用科学的方法确定每个部门对公务员各项素质要求的权数是至关重要的，因为这些权数的赋值反映了每个部门对公务员各项素质要求的不同侧重要求，一旦确定下来，往往可维持一段时间。

在这里我们运用层次分析法来解决各权数的取值问题。

把这４项因素两两比较，从而得到判断矩阵Ａ＝ａ１１ａ１２ａ１３ａ１４ａ２１ａ２２ａ２３ａ２４ａ３１ａ３２ａ３３ａ３４ａ４１ａ４２ａ４３ａ４４"#其中，ａｉｊ（ｉ，ｊ＝１，２，３，４）表示第ｉ，ｊ个因素相对于各部门的重要程度，其取值按表１所示的１～９标度确定。

公务员招聘择优按需录用模型

公务员招聘择优按需录用模型第23卷第2期2006年5月江苏教育学院(自然科学版)JournalofJiangsuInstituteofEducation(NaturalSciences)V o1.23No.2May,2006公务员招聘择优按需录用模型宋然兵(淮安信息职业技术学院基础部,江苏淮安223001)摘要本文建立择优系数矩阵及择优函数,把公务员录用问题转化为分配问题.有利于在计算机上实现.为招聘工作提供了较好的依据.关键词择优系数矩阵;择优函数;录用模型目前,我国招聘公务员的程序一般分三步进行:公开考试(笔试),面试考核,择优录取.公开考试阶段根据考试总分的高低排序按l2的比例(Ⅳ人)选择进入第二阶段的面试考核.面试考核主要考核应聘人员的各方面能力.按照一定的标准,面试专家组对每个应聘人员的各个方面都给出一个等级评分,从高到低分成A/B/C/D四个等级,由招聘领导小组综合专家组的意见,笔初试成绩以及各用人部门需求确定录用名单,并分配到各用人部门.表1面试人员的笔试成绩和面试考核成绩表2用人部门对公务员的期望要求应聘笔试申报类别志愿人员成绩能力1能力2能力K人员1a1(2)(3)AAB人员2a2(3)(1)BBC人员3(1)(2)DAA人员Ⅳnn(3)(2)BAD1分析和假设用人工作各部门对公务员特长的希望达到的要求部门类别能力1能力2能力部门1(1)BA部门2(2)BC部门肼(3)CBA要从Ⅳ名面试人员中选名公务员安排到所属的个部门,假定每个部门录用一名应聘人员.若部门,录用2名应聘人员,那末将该部门分成部门,.和部门,2.再虚拟Ⅳ一个部门,使面试人员数和部门数相等.依据面试人员的笔试成绩和能力等级计算出择优系数,再建立择优函数.能力等级的数量化方法,应聘者的某一能力的等级刚好达到部门要求的记为60,超过部门能力等级要求的按等级相应记为70,80或9o,不能达到部门能力等级要求的按等级相应记为5O,4o或30,(如用人能力等级要求是ABBB,而应聘人员的能力是AADC,就记为60,70,4O,50),然后将其相加,取平均值.符号说明r1(1)={:'…1'表示部门,录用人员-『;…0'表示部门,没录用人员J=.LU.(2)c表示部门,录用人员的择优系数,(3)"为择优函数,(4)如果部门2录用2人,则增加一个部门,并对应聘人员的能力的要求与部门2相同.虚拟部门对应聘人员的四方面的能力的要求都为A.2模型的建立和求解择优系数的计算方法,cd=为笔试成绩P+部门录用人员的能力评分q.虚拟部门对人员的择优系数均为0.即.=0(i>M)其数据构成择优系数矩阵C-——141---——模型建立如下maxu=∑∑c.』【∑=1例(2004高教杯全国大学生数学建模竞赛D题)当N=16,M=8时, 择优系数如下l616maxu=∑∑cqx~ii=1J=116r∑=1.￡Jl∑16:?表33028.825.328.527.326.32728282524.827.724.525.526.426.33l29.826.829.528.327.32829292625.828.725.526.527.427.3 3129.826.829.528.327.32829292625.828.725.526.527.427.3 3129.826.829.528.327.32829292625.828.725.526.527.427.33】29.826.829.528.327.32829292625.828.725.526.527.427.3 3129.826.829.528.327.32829292625.828.725.526.527.427.3 3129.826.829.528.327.32829292625.828.725.526.527.427.3 3129.826.829.528.327.32829292625.828.725.526.527.427.3运算结果如表4表4\123456789101112l3141516部门11部门2l部门31部门41部门51部门61部门71部门81该用人方案是:部门1录用人员12;部门2录用人员4;部门3录用人员1;部门4录用人员6;部门5录用人员9;部门6录用人员11;部门7录用人员7;部门8(即部门2)录用人员2. ADealModelofGood?ChoiceforTakingonOfficiaISONGRanhing(HuaianInformation&TechnologyCollege,Huaian,Jiangsu,223001,China) AbstractThispaperfoundchoicegoodcoefficientmatrixandchoicegoodfunction.Takeonof ficialquestioneonver[ofdealquestion.Itisadvantageous realizationOilcomputer.ThisisfromwallintakeO/1officia1. Keywordschoicegoodcoefficientmatrix,choicegoodfunction,takeonmodel(责任编辑胡明)一142一,,●,●,●●nnl2CC.C●●●●●●●●●●●●一,,.........................一/。

公务员招聘的优化模型

维普资讯
第２２卷第５期
２００６年１０月
大学数学
Ｃ（ＩＩＥＧＥＡＴＨＥＭＡＴＩ）ＭＣＳ
Ｖｏ．２，ｏ５１２Ｎ．
Ｏｃ．２０ｔ０６
公务员招聘的优化模型
饶从军，王成，李军。
该方案越理想．
２１２折衷型模糊决策的基本步骤．．
１）指标数据的处理
通过引入三角形模糊数，所有的定性定量指标统一化成三角形模糊数．把定义记Ｆ（为尺上的全体模糊集，Ｍ ∈Ｆ（．果Ｍ的隶属度函数Ｍ表示为尺）设尺）如
精确数，由三角形模糊数的定义，ｎ表示成三角形模糊数的形式为则
的极小值构成．后采用加权欧氏距离的测度工具来计算各备选对象与模糊正理想和模糊负理想之间然
的距离．在此基础上，再计算各备选对象属于模糊正理想的隶属度，方案优选的原则是：属度越大，其隶
源的优化配置问题，而给出了一种科学有效的公务员招聘的方法从［键词］公务员招聘；角形模糊数；衷型模糊决策；１整数规划；学模型关三折Ｏ数
：图分类号］Ｃ３．中９１１
湖北武汉４０６）３０３（．冈师范学院数学系，北黄州４８０；２１黄湖３００．武汉理工大学理学院，

matlab数学建模30个案例分析

案例4：基于微分方程的最优捕鱼策略
为了保护人类赖以生存的自然环境，可再生资源（如渔业、林业资源）的开发必须适度，一种合理、简化的策略是，在实现可持续收获的前提下，追求最大产量或最佳效益。考虑对某种鱼的最优捕鱼策略：假设这种鱼分4个年龄组：称1龄鱼，…,4龄组,各年龄组每条鱼的平均重量分别为5.07，11.55，17.86，22.99（克）各年龄组鱼的自然死亡率均为0.8（1/年）这种鱼为季节性集中产卵繁殖,平均每条4龄鱼的产卵量为1.109× 个，3龄鱼的产卵量为这个数的一半，2龄鱼和1龄鱼不产卵产卵和孵化期为每年的最后4个月,卵孵化并成活为1龄鱼，成活率（1龄鱼条数与产卵总量n之比）为1.22 × /1.22× +n）
案例12：基于主成分分析的长江水质的评价和预测模型
运用主成分分析法对长江流域主要城市水质检测报告进行分析，选取主成分，并把主成分得分按方差贡献率加权求和，得出每个地区的污染综合评价指数，进而可以计算每个月长江流域的污染综合评价指数。
第三部分优化问题
案例13：基于线性规划求解飞行管理模型
第二部分评价问题
案例7：基于层次分析法的高考志愿选择策略
一年一度的高考结束后，许多考生面临估分后填写志愿的决策过程。这个决策关系重大，请你建立一个数学模型，帮考生考虑到各种决策因素使之能轻松应对这一重大决策。成都丙、重庆丁四所大学。
现有某市直属单位因工作需要，拟向社会公开招聘8名公务员。该单位拟将录用的8名公务员安排到所属的7个部门，并且要求每个部门至少安排一名公务员。这7个部门按工作性质可分为四类：(1)行政管理、 (2)技术管理、(3)行政执法、(4)公共事业。
招聘领导小组在确定录用名单的过程中，本着公平、公开的原则，同时考虑录用人员的合理分配和使用，有利于发挥个人的特长和能力。招聘领导小组将7个用人单位的基本情况（包括福利待遇、工作条件、劳动强度、晋升机会和学习深造机会等）和四类工作对聘用公务员的具体条件的希望达到的要求都向所有应聘人员公布。每一位参加面试人员都可以申报两个自己的工作类别志愿。

公务员招聘的模糊决策模型

第22卷第4期大　学　数　学Vol.22,№.4 2006年8月COLL EGE MA T H EMA TICS Aug.2006公务员招聘的模糊决策模型姚玉平(揭阳职业技术学院,广东揭阳522000) [摘　要]运用模糊数学理论与多目标决策模糊优化方法,在不考虑应聘人员的意愿及在考虑应聘人员意愿和用人部门的希望要求的情况下,择优按需录用.分别建立相应的模型.其结果令人满意,具有较强的可靠性和适用性.[关键词]隶属度最优化;择优向量;期望值;模糊优化函数[中图分类号]O141 [文献标识码]B [文章编号]167221454(2006)04200262051　引言我国公务员制度已实施多年.目前,我国招聘公务员程序一般分为三步进行:公开考试(笔试)、面试考核、择优录用.公务员的招聘,通常都采用定量考核与定性评价相结合的方法,在专家组的定性评价中,带有一定的模糊性,往往使得评价值趋于均化,分辨率不高.公务员招聘及岗位录用对被招聘人员能力要求均具有很强的模糊性,涉及很多因素,如果方法运用不当,就会出现很大的偏差,因而失去公平性.在文献[4]中,运用了层次分析法,而层次分析法在构造成对比较矩阵时,就具有较强的主观性,而各种权重的构造亦带有主观性,当被聘人数、录用部门较多时,整个过程比较复杂.在文献[5]中,利用贴近度及模糊聚类方法,在计算贴近度时利用的是欧氏距离,很难区分应聘者实际能力与部门要求能力的差异,且实现起来比较复杂,有一定的操作难度.文献[6]运用二分图匹配的方法,权重的计算不合理.本文运用模糊多目标决策方法,使得结果客观,标准可靠,识别清晰,是一种比较实用的公务员招聘模糊数学模型.2　问题分析现有某市直属单位因工作需要,拟向社会公开招聘8名公务员,凡年龄不超过30周岁,大学专科以上学历,身体健康均可报名参加笔试.根据笔试成绩的高低选择进入第二阶段的面试考核.每个应聘人员经过面试,由招聘领导小组对其知识面、理解能力、应变能力、表达能力等进行等级评分.招聘领导小组综合专家的意见、笔试成绩、各部门需求及应聘人员的意愿择优按需录用分配到以下各用人部门: (1)行政管理、(2)技术管理、(3)行政执法、(4)公共事业.问:若不考虑应聘人员的意愿,如何设计方案使得应聘人员录用分配最优?若考虑应聘人员的意愿和用人部门的需求,则该如何设计方案?若n 个应聘人员m个用人单位时,上述方案是否可行?给出在此招聘公务员过程中需要改进的地方及建议.我们的工作是利用所给数据(应聘人员的笔试成绩)、专家对应聘人员面试考核的评价,通过分析、计算得到一种尽量公平且让人满意的录用方案,并推广到一般情况.实践中可分两种情况考虑:(1)在不考虑应聘人员的意愿的情况下,择优按需录用;(2)在考虑应聘人员意愿和用人部门的希望要求的情况下,择优按需录用.　[收稿日期]2005204220一般公务员招聘都采取定量考核(应聘人笔试)与定性评价(面试评价)相结合的方法,但由于在面试考核过程中,采用专家评价(给出A/B/C/D 四个等级),这样就带有模糊性,即分辨率不高.因此,在最后录用过程中,无法对所有应聘人员进行客观地综合比较,这样对招聘的公正、公平就会产生一些影响.我们在本文的模型中,针对其模糊性,分别将面试成绩和用人单位对公务员的期望量化,运用模糊数学理论、多目标决策模糊优化的方法进行研究.合理假设:11所有应聘人员均符合参加公开考试的要求;21男、女不限,专业不限;31专家组评价公平、公正.符号说明:X =(x ij )m ×n :应聘人员特征向量矩阵;R =(r ij )m ×n :隶属度矩阵;B =(b ij )t ×t :部门要求量化矩阵;w i =(w ij ):个人意愿向量;U =(u 1,u 2,…,u m ):应聘人员优势权重向量;w i ′=(w ′ij ):部门对公务员的期望向量;z i =w i +w i ′:应聘人员意愿与用人部门期望的综合期望向量.3　模型的建立与求解311　不考虑应聘人员的意愿,择优按需录用31111　现将16个人看成待决策优化的对象,构成备择对象集{A 1,A 2,…,A 16},将笔试成绩、知识面、理解能力、应变能力、表达能力看成五个评价因素,构成评价指标集:{B 1,B 2,B 3,B 4,B 5}.将笔试成绩与面试成绩(A/B/C/D 四个等级)分别用0～1之间的数字予以量化:290～1,288～019,285～018,283～017,280～016,278～015,277～014,275～013,274～012,273～011;A ～1,B ～0175,C ～0150,D ～0125.笔试成绩与面试成绩见表1.表1　招聘公务员笔试成绩,专家面试评分及个人志愿应聘人员笔试成绩申报类别志愿专家组对应聘者特长的等级评分知识面理解能力应变能力表达能力人员1290(2)(3)A A B B 人员2288(3)(1)A B A C 人员3288(1)(2)B A D C 人员4285(4)(3)A B B B 人员5283(3)(2)B A B C 人员6283(3)(4)B D A B 人员7280(4)(1)A B C B 人员8280(2)(4)B A A C 人员9280(1)(3)B B A B 人员10280(3)(1)D B A C 人员11278(4)(1)D C B A 人员12277(3)(4)A B C A 人员13275(2)(1)B C D A 人员14275(1)(3)D B A B 人员15274(1)(4)A B C B 人员16273(4)(1)BABC72第4期姚玉平:公务员招聘的模糊决策模型由表1可得应聘人员特征向量矩阵X=(x ij)16×5:其中x ij为第i个人第j个评价因素的特征值, i=1,2,…,16;j=1,2,3,4,5.X=1101100110001750175 0191100017511000150 0190175110001250150 0181100017501750175 0170175110001750150 0170175012511000175 0161100017501500175 0160175110011000150 0160175017511000175 0160125017511000150 0150125015001751100 0141100017501501100 0130175015001251100 0130125017511000175 0121100017501500175 011017511000175015031112　建立隶属度矩阵R=(r ij)16×5因为在择优录用过程中,对于每个评价指标应该遵循“越大越优”的原则.因此,第i个应聘人员满足第j个评价指标的隶属度为:r ij=x ij/x max,其中x max=max{x ij|i=1,2,…,16,j=1,2,…,5},由特征向量矩阵又可知,x max=1,所以隶属度矩阵R=X.31113　构造系统的优向量F和次向量S F=(f1,f2,f3,f4,f5)T=(r11∨r21∨…∨r16,1,r12∨r22∨…∨r16,2,…,r15∨r25∨…∨r16,5)T;(1) S=(s1,s2,s3,s4,s5)T=(r11∧r21∧…∧r16,1,r12∧r22∧…∧r16,2,…,r15∧r25∧…∧r16,5)T;(2)式中“∨”和“∧”分别为“取大”、“取小”运算符,由此得:F=(1,1,1,1,1)T,　S=(011,0125,0125,0125,0125)T.31114　构造择优向量U=(u1,u2,u3,u4,…,u16)利用最小二乘方准则构造目标函数,并令其导数为零,求得(过程略)系统的模糊优化函数为[2]:u i=11+∑5j=1(w j|r ij-f j|)p∑5j=1(w j|r ij-s j|)p2p,　i=1,2,…,16.(3)其中w j为评价指标的权重,p为距离系数,p=1为海明距离,p=2为欧氏距离,两种距离计算所得结论通常是一致的.根据招聘的要求及调查结果,得评价指标的权重:w==(0128,0116,0116,0116,0124),将R,F,S和w代入(3)式,并令p=2,经由Maple软件得:U=(u1,u2,u3,…,u16)=(01980,01920,01717,01904,01774,01717,01761,01800,01824,01518,01746,01379,01448, 01482,01379);根据隶属度最优化原理,由择优向量U由高到低排序可得,U=(01980,01920,01904,01824,01800,01774,01761,01746,01717,01717,01518,01482,01448, 01379,01379)82大　学　数　学第22卷=(u 1,u 2,u 4,u 9,u 8,u 5,u 7,u 12,u 3,u 6,u 10,u 11,u 15,u 14,u 13,u 16).31115　择优按需录用各用人部门对公务员的期望要求不同,有些部门要求较高,有些部门要求较低.用人部门对公务员的期望要求,见表2.表2　用人部门的基本情况及对公务员的期望要求用人部门工作类别各用人部门的基本情况各部门对公务员特长的希望达到的要求福利待遇工作条件劳动强度晋升机会深造机会知识面理解能力应变能力表达能力部门1(1)优优中多少B A C A 部门2(2)中优大多少部门3(2)中优中少多A B B C 部门4(3)优差大多多部门5(3)优中中中中C C A A 部门6(4)中中中中多部门7(4)优中大少多CBBA 我们希望综合素质较高的人录用在要求较高的部门,做到量才录用,按需录用.首先把部门要求量化,四类工作的要求向量为b 1=(0175,1,0150,1);b 2=(1,0175,0175,0150);b 3=(0150,0150,1,1);b 4=(0150,0175,0175,1).优向量f =(1,1,1,1),次向量s =(0150,0150,0150,0150),根据各部门的要求得评价指标的权重:w =(0123,0123,0123,0131),由公式(3),将R =(r ij )换成B =(b 1,b 2,b 3,b 4)T=(b ij )可得u 1=0178,u 2=0142,u 3=0157,u 4=0157,根据隶属度最优化原理,由择优向量U 从高到低排序可得四类工作的权重向量U =(0178,0157,0157,0142)=(u 1,u 3,u 4,u 2).因此一类工作的要求最高,三、四类工作次之.所以我们录用的8名公务员分别为1,2,4,9,8,5,7,12.具体分配案为:1,2到行政管理部门;4,9到行政执法部门;8,5到公共事业部门;7,12到技术管理部门.312　考虑应聘人员意愿和用人部门的希望要求31211　根据211的结果,首先确定已录用的8人.下面考虑应聘人员意愿,已录用的8人对四类工作的意愿向量分别为:w 1=(0,1,015,0);w 2=(015,0,1,0);w 4=(0,0,015,1);w 5=(0,015,1,0);w 7=(015,0,0,1);w 8=(0,1,0,015);w 9=(1,0,015,0);w 12=(0,0,1,015);其中1,015分别表示个人对申报的第一,第二志愿部门的期望值,对未申报部门的期望值视为0.31212　下面考虑用人部门对所需人才的期望要求四类工作对已录用的8个人的期望向量分别为w ′1=(0,015,015,0);w ′1=(0,0,0125,0);w ′4=(0,0,0125,0125);w ′5=(0,0,0,0);w ′7=(-0125,0,0,0);w ′8=(0,0125,0,0125);w ′9=(0,0,0125,0);w ′12=(0,0,0125,0125).其中w ′i =(w i 1,w i 2,w i 3,w i 4),若第i 个人未申报第j 个部门,则令w ij =0;若第i 个人申报了第j 个部门,则令w ij 为向量(a i -b j )的各个分量的代数和,i =1,2,4,5,7,8,9,12;j =1,2,3,4,a i =(a i 1,a i 2,a i 3,a i 4)表示第i 个人面试考核的得分向量,b j =(b j 1,b j 2,b j 3,b j 4)表示第j 个部门对公务员的期望向量.31213　综合考虑应聘人员意愿和用人部门的希望要求,确定分配方案令综合期望值为:z i =w i +w ′i ,i =1,2,4,5,7,8,9,12.92第4期姚玉平:公务员招聘的模糊决策模型03大　学　数　学第22卷z1=(0,115,1,0);z2=(015,0,1125,0);z4=(0,0,017,112);z5=(0,015,1,0);z7=(0125,0,0,1);z8=(0,112,0,112);z9=(1,0,017,0);z12=(0,0,112,017).比较所有向量的各个分量值,分量z ij:i=1,2,4,5,7,8,9,12,j=1,2,3,4,表示第i个人关于第j 类工作的综合期望值.已录用的8人中申报第一类工作的只有人员2,人员7,人员9,而他们的综合期望值分别为015,0125,1,显然综合期望值越大越优.因此分配到行政管理工作部门的是人员9和人员2,到技术管理工作部门的是人员1和人员8,到行政执法工作部门的是人员5和人员12,到公共事业工作部门的是人员4和人员7.4　结束语311的模型,由于运用了多目标决策模糊优化方法,可以对所有应聘人员进行综合排序,因此,分辨率较高,且因此所得录用结果公平、公正,比较令人满意.312的模型既考虑本人意愿,又考虑到用人部门的要求,其分配结果令双方满意.无论是311的模型还是312的模型,都很容易推广到n个应聘人员m个用人单位的情况.招聘公务员过程中,还应该考虑到以下因素:(i)学历水平的高低.上述公务员招聘所要求的学历只是大学专科以上,没有考虑应聘人员的学历水平,如本科、研究生、博士等情况,应该在招聘录取的过程中给予适当的区别,其综合素质也相应随之变化,则择优的机率更精确些.(ii)专业特点.特别是技术专业的岗位更要注重专业特点,应对不同的工作类型所要求的专业做出一定的限制,做到“因技择岗”.(iii)申报类别意愿.可适当增多申报类别意愿,即每个应聘人员都可以申报2个以上类别意愿.若第一、第二意愿达不到,可能其他意愿刚好达到,让错失人才的机率微小些.(iv)在面试考核过程中,专家组对应聘者的评价应给予量化,避免模糊性.[参　考　文　献][1]　贺仲雄.模糊数学及其应用[M].天津:天津科技出版社,1983.[2]　陈守煜.多目标决策模糊集理论模型[J].系统工程的理论与实践,1992,12(1):7-13.[3]　徐辉,等.企业发展的多目标决策模糊优化模型[J].数学的实践与认识,2003,21(10):41-43.[4]　魏然,等.对公务员招聘问题的思考[J].工程数学学报,2004,21(7):137-141.[5]　贺翔,等.公务员招聘方案的优化设计[J].工程数学学报,2004,21(7):142-146.[6]　王兵,等.公务员招聘数学模型及应用[J].枣庄学院学报,2005,22(2):19-24.Mode for R ecruiting Civil ServantsYA O Yu2pi ng(Jieyang Vocational,Guangdong Jieyang522000,China)Abstract:Without thinking wish of applicant or thinking wish of applicant and request of employing work unit,select for employment on the basis of ones qualifications as required,the mathematical model is set up respectively by f uzzy mathematical theory and multi2goal decision2making f uzzy optimization.Asatisfactory result is got,with very strong reliability and adaplability.K ey w ords:optimized degree of membership;superior vector;expectation value;f uzzy optimization function。

公务员招聘模型