中职数学区间ppt课件
合集下载
中职生数学基础模块上册课件《区间的概念》

气象预报:利用区间分析法预 测天气变化趋势
提出进一步探索的问题
01
区间的概念ห้องสมุดไป่ตู้实际生活中 的应用有哪些?
02
区间的性质和运算法则在 实际问题中有哪些应用?
03
区间的概念与其他数学概 念之间的关系是什么?
04
如何利用区间的概念解决 实际问题?
区间的表示方法
01
区间表示法:使用两个数来表示一个区间,如 [a, b]表示a到b的区间
02
区间的端点:区间的两个端点,如[a, b]中的a 和b
03
区间的包含关系:一个区间可以包含另一个区 间,如[a, b]包含[c, d]
04
区间的并集:两个或多个区间的并集,如[a, b]和[c, d]的并集为[a, d]
区间在几何中的应用:长 度、面积、体积等
区间在实际问题中的应用: 优化问题、不等式问题等
PART 6
总结与拓展
总结区间的基本概念与性质
区间的定义:区间是数轴上
01 的一段连续的点集,表示为
一个闭区间或开区间。
02
区间的性质:区间具有连续 性、有界性、可数性等性质。
04
区间的运算:区间可以进行 并集、交集、补集等运算。
区间的表示方 法:用两个端 点表示,如[a, b]
03
区间的性质: 包含所有介于 两个端点之间 的实数
04
区间的应用: 求解不等式、 函数图像、极 限等数学问题
区间与函数的关系
函数的定义域 和值域都是区
间
区间是函数的 图像
区间是函数的 单调性、周期 性等性质的基
础
区间是函数的 极限、连续性 等性质的基础
05
区间的交集:两个或多个区间的交集,如[a, b]和[c, d]的交集为[max(a, c), min(b, d)]
2024年度-中职教育数学《区间》课件

[a, b]表示闭区间。
11
03
函数在区间上性质研究
12
函数单调性判断方法
定义法
根据函数单调性的定义,通过比 较函数在区间内任意两点的函数
值大小来判断函数的单调性。
导数法
利用导数符号判断函数的单调性 。若在某区间内函数的导数大于 0,则函数在此区间内单调增加 ;若导数小于0,则函数在此区
间内单调减少。
分类
根据区间端点的开闭情况,区间 可分为开区间、闭区间、半开半 闭区间等。
4
区间表示方法
01
02
03
不等式表示法
使用不等式表示变量的取 值范围,例如$a < x < b$表示开区间$(a, b)$。
集合表示法
使用集合论中的区间表示 法,例如${ x | a < x < b }$表示开区间$(a, b)$。
影响。
19
05
典型例题分析与解答技巧分享
20
典型例题选取与展示
例题1
01
求函数$f(x) = x^2 - 4x + 3$在区间$[0, 5]$上的最大值和最小
值。
例题2
02
判断函数$f(x) = frac{1}{x}$在区间$(0, +infty)$上的单调性。
例题3
03
求不等式$2x - 1 < 5$在区间$[2, 4]$上的解集。
图像法
通过观察函数图像来判断函数的奇偶性。若函数图像关于原点对称,则函数为 奇函数;若图像关于y轴对称,则函数为偶函数。
14
函数周期性判断方法
定义法
根据函数周期性的定义,通过比较函数在不同周期点的函数值来判断函数的周期 性。若存在正数T,使得对于定义域内的任意x,都有f(x+T)=f(x),则函数为周期 函数,T为函数的周期。
11
03
函数在区间上性质研究
12
函数单调性判断方法
定义法
根据函数单调性的定义,通过比 较函数在区间内任意两点的函数
值大小来判断函数的单调性。
导数法
利用导数符号判断函数的单调性 。若在某区间内函数的导数大于 0,则函数在此区间内单调增加 ;若导数小于0,则函数在此区
间内单调减少。
分类
根据区间端点的开闭情况,区间 可分为开区间、闭区间、半开半 闭区间等。
4
区间表示方法
01
02
03
不等式表示法
使用不等式表示变量的取 值范围,例如$a < x < b$表示开区间$(a, b)$。
集合表示法
使用集合论中的区间表示 法,例如${ x | a < x < b }$表示开区间$(a, b)$。
影响。
19
05
典型例题分析与解答技巧分享
20
典型例题选取与展示
例题1
01
求函数$f(x) = x^2 - 4x + 3$在区间$[0, 5]$上的最大值和最小
值。
例题2
02
判断函数$f(x) = frac{1}{x}$在区间$(0, +infty)$上的单调性。
例题3
03
求不等式$2x - 1 < 5$在区间$[2, 4]$上的解集。
图像法
通过观察函数图像来判断函数的奇偶性。若函数图像关于原点对称,则函数为 奇函数;若图像关于y轴对称,则函数为偶函数。
14
函数周期性判断方法
定义法
根据函数周期性的定义,通过比较函数在不同周期点的函数值来判断函数的周期 性。若存在正数T,使得对于定义域内的任意x,都有f(x+T)=f(x),则函数为周期 函数,T为函数的周期。
区间的概念ppt课件

7
习
8
例题及训练
例2、用区间表示不等式 3x>2+4x 的解集,并 在数轴上表示出来。
例3、设R为全集,集合A={x -5<x<6}, B={x x≥3,或x≤-3} ,用区间表示A∩B.
9
练习
10
2.区间的概念
1
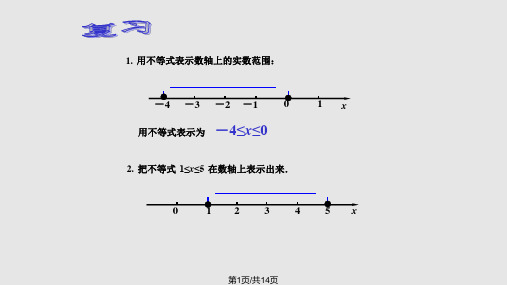
复习
我们知道: 用描述法表示一个数集时可以用不等式表示
如:{x -3<x<5} 也可以在数轴上表示出来:
x
-3
0
5
也可以用区间表示:(-3,5)
2
区间表示法
①开区间(a,b):表示数集{x a<x<b}
a
b
不包含a、b
②闭区间 [a,b] :表示数集{x a≤x≤b}
a
b
包含a,b
3
区间表示法
③左开右闭区间(a,b] :表示数集{x a<x≤b}
a
b 不包含a
④右开左闭区间 [a,b):表示数集{x a≤x<b}
a
b 不包含b
4
区间表示法
⑤左开右无界区间(a,+∞)表示数集{x x>a}
a
不包含a
⑥左闭右无界区间 [a,+∞)表示数集{x x≥a}
a
包含a
5
区间表示法
⑦左无界右开区间(-∞,a)表示数集合{x x<a}
a
不包含a
⑧左无界右闭区间(-∞,a]表示数集{x x≤a}
a
包含a
实数集R可以用区间(-∞,+∞)表示
6
例题及训练
例1、把下列集合用区间表示出来,指出它是什 么区间。
⑴ {x -3<x<1}
⑵ {x -3≤x≤1}
区间的概念职高PPT课件
闭区间
a
bx
a<x<b
{x| a<x<b} (a,b)
开区间
a
bx
a<x≤b
{x| a<x≤b} (a,b]
左半开区间
a
bx
a≤x<b
{x| a≤x<b} [a,b)
右半开区间
其中 a,b 叫做区间的端点.
第3页/共14页
ห้องสมุดไป่ตู้
例 用区间记法表示下列不等式的解集: (1)9≤x≤10 ; (2) -2<x≤0.4 .
(a,+∞)
ax x<a {x| x < a} (-∞,a)
对于实数集 R,也可用区间(- ∞ ,+∞) 表示 .
第8页/共14页
设a,b为任意实数,且a<b,则各种区间如下
第9页/共14页
用区间记法表示下列不等式的解集,
并在数轴上表示这些区间:
(1)-2≤x≤3; (2) -3<x≤4;
(3)-2≤x<3; (4)-3<x<4;
解:(1)[9,10] ;
(2)(-2,0.4 ] .
例 用集合的性质描述法表示下列区间:
(1)(-4,0);
(2)(-8 ,7].
解:(1){ x | -4<x<0}; (2){ x | -8<x≤7}.
第4页/共14页
例1、已知集合A=(-1,4),B=[0,5],求 A∪B , A∩B
-1
0
(5) x>3;
(6) x≤4.
(7)-2≤x≤3且x≠1; (8)-3<x<4且x≠0
第10页/共14页
例 2 已知集合 A (,2) ,集合 B (,4] ,
求A B,A B.
例3 设全 R , 集 A 集 0 ,为 3 , 合B 集 2 , 合 ,求
a
bx
a<x<b
{x| a<x<b} (a,b)
开区间
a
bx
a<x≤b
{x| a<x≤b} (a,b]
左半开区间
a
bx
a≤x<b
{x| a≤x<b} [a,b)
右半开区间
其中 a,b 叫做区间的端点.
第3页/共14页
ห้องสมุดไป่ตู้
例 用区间记法表示下列不等式的解集: (1)9≤x≤10 ; (2) -2<x≤0.4 .
(a,+∞)
ax x<a {x| x < a} (-∞,a)
对于实数集 R,也可用区间(- ∞ ,+∞) 表示 .
第8页/共14页
设a,b为任意实数,且a<b,则各种区间如下
第9页/共14页
用区间记法表示下列不等式的解集,
并在数轴上表示这些区间:
(1)-2≤x≤3; (2) -3<x≤4;
(3)-2≤x<3; (4)-3<x<4;
解:(1)[9,10] ;
(2)(-2,0.4 ] .
例 用集合的性质描述法表示下列区间:
(1)(-4,0);
(2)(-8 ,7].
解:(1){ x | -4<x<0}; (2){ x | -8<x≤7}.
第4页/共14页
例1、已知集合A=(-1,4),B=[0,5],求 A∪B , A∩B
-1
0
(5) x>3;
(6) x≤4.
(7)-2≤x≤3且x≠1; (8)-3<x<4且x≠0
第10页/共14页
例 2 已知集合 A (,2) ,集合 B (,4] ,
求A B,A B.
例3 设全 R , 集 A 集 0 ,为 3 , 合B 集 2 , 合 ,求
中职数学基础模块上册《区间的概念》ppt课件

作业:
P25习题1.2A组:5,6,7,8.
高一年级
第一章 1.2.1
数学
函数的概念
课题: 区间的概念
问题提出
1.什么叫函数?用什么符号表示函数?
2. 什么是函数的定义域?值域? 3.函数 f ( x) 1 x 的定义域怎样表示?
知识探究(一)
思考1:设a,b是两个实数,且a<b,介于这两个 数之间的实数x用不等式表示有哪几种可能情况?
a x b, a x b, a x b, a x b
思考2:满足上述每个不等式的实数x的集合可看 成一个区间,为了区分,它们分别叫什么名称? 思考3:如果把满足不等式的实数x的集合用符号 [a,b)表示,那么满足其它三个不等式的实数x 的集合可分别用什么符号表示?
上述知识内容总结成下表:
思考2:满足不等式 x a , x a , x a , x a 的实数x的集合也可以看成区间,那么这些集合 如何用区间符号表示?
[a,+∞),(a,+∞), (-∞,a],(-∞,a). 思考3:将实数集R看成一个大区间,怎样用区间 表示实数集R? (-∞,+∞)
思考4:一次函数y=kx+b(k≠0),二次函数
k y=ax2+bx+c(a≠0),反比例函数 y ( k 0) x
的定义域、值域分别是什么?怎样用区间表示?
理论迁移
例1 将下列集合用区间表示出来:
(1){ x | 2 x 1 0}; (2){ x | x 4, 或 1 x 2}
..
例2 已知 f ( x 1) x 2 x ,求函数 f ( x ) 的解析式.
定义 名称 符号 [ a, b ]
《区间的概念》中职数学基础模块上册2.2ppt课件1【语文版】

•
关键是,出错了你就知道上课时应该重点听哪里,注意力自然就能集中了。
•
4、即便上课时不理解也不要放弃
•
有些同学觉得老师讲的听不懂,就干脆不再听讲,按照自己的方法去学习。其实这样做真的很傻,因为不听讲就非常容易和同学们的学习进度脱节,这就会直接导致考试时成绩下降。原因是,老师讲的内容不一定都在教材中体现,有相当一部分重点内容
集合:v | 200 v 350
数轴:位于 200 与 350 之间的一段不包括端点的线段 还有其他简便方法吗?
2.2 区间
动脑思考 探索新知
由数轴上两点间的一切实数所组成的集合叫做区间. 其中,这两个点;4}
(2,4)
右半开区间
集合{x|2≤x<4}
难读到老师的表情。认真听讲不单纯是指听老师说的话,把握老师的表情和语调之类的小细节也是很有必要的。说话比平时更用力,或者表情严肃地强调的那个部分几乎百分之百地会出现在考试中。但是如果坐在后面,那种重要的提示就全都错过了。
•
与此相反,如果坐在前面,首先心情就很不同,自己比别人靠前的感觉让你听课时的态度变得更积极。与老师眼神交会的机会增多,感觉就好像是老师在做一对一个人辅导。
•
低着头,心情就放松了,但那种放松对学习一点好处也没有,之所以会放松,就是因为觉得即便是自己开小差,老师也不知道。如果你往前看,不时地和老师眼神交会一下,注意力必然会集中起来。和老师眼神交汇的那种紧张感会让你注意力集中,并充
实地听完整堂课。
•
3、课前预习
•
课前预习新课内容,找出不理解的地方标记下来。预习后尝试做课后练习题,不要怕出错,因为老师还没有讲,出错也是正常的。
“ ”与“ ”都是符号,而不是一个确切的数.
最新中职数学区间课件幻灯片

数轴表示
a
b
x
a
b
x
在实数集R中,有没有 最大的数和最小的数?
实数集R 用区间表示为( -∞,+∞ ) -∞ 读作: 负无穷大 +∞ 读作: 正无穷大
填 表:
解集表示 区间表示
{x|x≥a} [a,+ ∞)
{x|x > a} (a,+ ∞)
{x|x≤b} {x|x<b}
( -∞,b] (-∞,b)
1、不等式(组)的解集 2、不等式(组)的解集的表示方法
(1)集合描述法 (2)区间:闭区间
开区间 半开半闭区间 实数集R
不自主运动
概述
▪ 不自主运动或称异常运动,为随意肌的某一 部分、一块肌肉或某些肌群出现不自主收缩。 是指患者意识清楚而不能自行控制的骨骼肌 动作。临床上常见的有肌束颤动、肌纤维颤 搐、痉挛、抽搐、肌阵挛、震颤、舞蹈样动 作、手足徐动和扭转痉挛等。一般睡眠时停 止,情绪激动时增强,以往认为是锥体外系 病变所致。
临床表现
5. 舞蹈样运动:是一种无目的,没有预兆的无规 律、不对称、幅度不等的快速的不自主运动。 头面部舞蹈运动表现为皱额、瞬目、咧嘴、 舌不自主伸缩、摇头晃脑等转瞬即逝的怪异 活动。常影响说话,在肢体表现为无一定方 向的大幅度运动,患者常难以维持一定的姿 势。
临床表现
6. 手足徐动症:又称指划运动。以肌强直和手足缓缓 的强直性伸屈性运动为特点,可发生于上肢、下肢、 面部和头颅。通常以上肢远端和面部最明显。患者 的手指常出现不规则的“蠕动样”徐动性运动,掌 指关节过度伸展,诸指扭转,可呈“佛手”样的特 殊姿势。参与徐动性动作的肌肉张力增高。下肢受 累时,行走发生困难,诸趾扭转,拇趾自发性背屈。 患者呈现各种奇形怪状的不自主动作。舌头时而伸 出,时而缩回。头部向左右两侧扭来扭去,有时咽 肌受累而发生吞咽和构音困难。这些不自主动作于 安静时减轻,睡眠时完全停止,精神紧张或随意动 作时加重,但感觉正常,智力可有减退
区间ppt课件

区间端点处理不当
在处理区间端点时,需要注意开闭区间的区别,否则可能导致结 果不准确。
混淆不同类型区间概念
1 2 3
混淆开闭区间 开区间和闭区间在数学上有明确的定义,但解题 者容易混淆二者概念,导致解题错误。
误解区间表示方法 在数学中,区间可以用不同的方式表示,如不等 式、集合等。解题者需要熟悉各种表示方法,避 免误解。
不等式求解与证明
01
02
03
04
区间分析法
将不等式中的变量限制在某个 区间内,通过分析函数在该区
间内的性质来求解不等式。
放缩法
通过适当的放缩,将复杂的不 等式转化为简单的不等式进行
求解。
构造函数法
构造适当的函数,利用函数的 性质来证明不等式。
数学归纳法
对于某些与自然数有关的不等 式,可以利用数学归纳法进行
些变化对函数性质的影响。
谢谢聆听
利用图像求解值域
对于难以直接求解的函数,可以通过绘制函数图像来观察其值域范 围。
多变量不等式处理方法
分离变量法
将多变量不等式中的各个变量分离开来,分别求解每个变量的取 值范围,再综合得出解集。
利用基本不等式性质
利用均值不等式、柯西不等式等基本不等式性质来简化多变量不等 式,降低求解难度。
转化为单变量不等式
B
C
区间乘法
区间乘法稍微复杂一些,需要考虑区间内元 素的符号。如果两个区间内的元素同号,则 它们的积为正;如果异号,则积为负。具体 的积的范围可以通过比较区间端点的大小来 确定。
区间除法
区间除法与乘法类似,只是将乘法运算改为 除法运算。需要注意的是,除数不能为0, 因此在进行区间除法时需要排除这种情况。
经济预测中置信区间计算
在处理区间端点时,需要注意开闭区间的区别,否则可能导致结 果不准确。
混淆不同类型区间概念
1 2 3
混淆开闭区间 开区间和闭区间在数学上有明确的定义,但解题 者容易混淆二者概念,导致解题错误。
误解区间表示方法 在数学中,区间可以用不同的方式表示,如不等 式、集合等。解题者需要熟悉各种表示方法,避 免误解。
不等式求解与证明
01
02
03
04
区间分析法
将不等式中的变量限制在某个 区间内,通过分析函数在该区
间内的性质来求解不等式。
放缩法
通过适当的放缩,将复杂的不 等式转化为简单的不等式进行
求解。
构造函数法
构造适当的函数,利用函数的 性质来证明不等式。
数学归纳法
对于某些与自然数有关的不等 式,可以利用数学归纳法进行
些变化对函数性质的影响。
谢谢聆听
利用图像求解值域
对于难以直接求解的函数,可以通过绘制函数图像来观察其值域范 围。
多变量不等式处理方法
分离变量法
将多变量不等式中的各个变量分离开来,分别求解每个变量的取 值范围,再综合得出解集。
利用基本不等式性质
利用均值不等式、柯西不等式等基本不等式性质来简化多变量不等 式,降低求解难度。
转化为单变量不等式
B
C
区间乘法
区间乘法稍微复杂一些,需要考虑区间内元 素的符号。如果两个区间内的元素同号,则 它们的积为正;如果异号,则积为负。具体 的积的范围可以通过比较区间端点的大小来 确定。
区间除法
区间除法与乘法类似,只是将乘法运算改为 除法运算。需要注意的是,除数不能为0, 因此在进行区间除法时需要排除这种情况。
经济预测中置信区间计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(6)x-2>0
x-3≤0
{x| 2<x≤3 }
3
闭区间:实数集的子集 { x | a ≤ x ≤ b }叫 做以 a , b 为端点的闭区间,记作[a,b]
数轴表示
a
b
x
4
开区间:实数集的子集 { x | a < x < b } 叫做以 a , b 为端点的开区间,记作(a,b)
数轴表示
a
b
x
不等式(组) 的解集与区间
1
(1)x-3≥0 x-3>0
(2)x-2≤0 x-2<0
{x| x≥3 } {x| x>3 } {x| x≤2 } {x| x<2 }
2
(3)x-2≥0 x-3≤0
{x| 2≤x≤3 }
(4)x-2>0 x-3<0
{x| 2<x<3 }
(5)x-2≥0 x-3<0
{x| 2≤x<3 }
所以原不等式组的解集是:
{x|x≥-1}∩{x|16
练习:解不等式组 2(x 1) 5 x (1) 5x 3 3x 1 (2)
17
1、不等式(组)的解集 2、不等式(组)的解集的表示方法
(1)集合描述法 (2)区间:闭区间
开区间 半开半闭区间 实数集R
18
5
闭区间 开区间
a
b
x
a
b
x
6
半开半闭区间:实数集的子集{x|a≤x<b} 或 {x| a < x ≤ b}叫做以a,b为端点的半开半 闭区间,记作:[a,b),(a,b]
数轴表示
a
b
x
a
b
x
7
在实数集R中,有没有 最大的数和最小的数?
实数集R 用区间表示为( -∞,+∞ ) -∞ 读作: 负无穷大 +∞ 读作: 正无穷大
x
13
用区间表示下列数集,并在数 轴上表示出来:
1、{x|-3<x ≤ 4}
2、 {x|x ≥ 2}
3、 {x|x < 0}
14
讨论:
{x|x≤-1或x≥2}用区间如何表示?
解:用区间表示为
(- ∞ ,-1]∪[2,+∞)
15
{ 例题:解不等式组 7 +3x ≤ 9+5x (1) 6 + x > 4x – 3 (2) 解:原不等式组的(1)(2)的解集分别为 {x|x≥-1},{x|x<3}
8
填 表:
解集表示 区间表示
{x|x≥a} [a,+ ∞)
{x|x > a} (a,+ ∞)
{x|x≤b} {x|x<b}
( -∞,b] (-∞,b)
数轴表示
a
x
a
x
bx
bx
9
例题:用区间表示下列数集,并在数轴上表示
(1){x|-1<x<3} 解:{x|-1<x<3}表示为(-1,3)数轴表示
-1 0
3
x
10
(2){x|-2≤x<2} 解:{x|-2≤x<2}表示为[-2,2) 数轴表示
-2 -1 0 1 2
x
11
(3){x|x>-1} 解: {x|x>-1}表示为(-1,+∞), 数轴表示
-2 -1 0 1
x
12
(4){x|x≤3}
解: {x|x≤3}表示为(- ∞ ,3], 数轴表示
01 2 3
