中职数学基础模块上册《实数指数幂及其运算法则》ppt精品课件
合集下载
中职教育-数学(基础模块)上册课件:第4章 指数函数与对数函数.ppt

图4-6
接下来,我们再用描点法作出函数y log 1 x 和y log 1 x
的图像.
2
3
对数函数的定义域为(0,+∞),在定义域内取若干个x 值,分别求出对应的y值,然后列表,如表4-8、表4-9所示.
表4-8
x
… 1/4 1/2 1
2
4
…
y
…
2
1
0 -1 -2 …
表4-9
x
… 1/9 1/3 1
3
9
…
y
…
2
1
0 -1 -2 …
以表中的x值为横坐标,对应的y值为纵坐标,在直角坐标
系中依次描出相应的点(x,y),然后用光滑的曲线依次连接
这些点,即可得到函数y log 1 x 和 y log 1 x 的图像,如图4-7
所示.
2
3
图4-7
一般地,对数函数 y loga x (a 0 且 a 1)具有下列性质:
第4章 指数函数与对数函数
4.1 • 实数指数幂 4.2 • 指数函数 4.3 • 对数 4.4 • 对数函数
内容简介:本章完成了由正整数指数幂到实数指数幂 及其运算的逐步推广过程,介绍了指数函数的概念、图像和 性质,引入了对数概念及运算法则,并在此基础上介绍了对 数函数的概念、图像和性质。
学习目标:理解有理数指数幂;掌握实数指数幂及其 运算法则;了解幂函数,理解指数函数的图像和性质;了解 指数函数的实际应用,理解对数的概念;掌握利用计算器求 对数值;了解积、商、幂的对数、对数函数的图像和性质及 对数函数的实际应用。
m
an
1 n am
计算器辅助求值
下面,我们以用CASIO
fx-82ES
接下来,我们再用描点法作出函数y log 1 x 和y log 1 x
的图像.
2
3
对数函数的定义域为(0,+∞),在定义域内取若干个x 值,分别求出对应的y值,然后列表,如表4-8、表4-9所示.
表4-8
x
… 1/4 1/2 1
2
4
…
y
…
2
1
0 -1 -2 …
表4-9
x
… 1/9 1/3 1
3
9
…
y
…
2
1
0 -1 -2 …
以表中的x值为横坐标,对应的y值为纵坐标,在直角坐标
系中依次描出相应的点(x,y),然后用光滑的曲线依次连接
这些点,即可得到函数y log 1 x 和 y log 1 x 的图像,如图4-7
所示.
2
3
图4-7
一般地,对数函数 y loga x (a 0 且 a 1)具有下列性质:
第4章 指数函数与对数函数
4.1 • 实数指数幂 4.2 • 指数函数 4.3 • 对数 4.4 • 对数函数
内容简介:本章完成了由正整数指数幂到实数指数幂 及其运算的逐步推广过程,介绍了指数函数的概念、图像和 性质,引入了对数概念及运算法则,并在此基础上介绍了对 数函数的概念、图像和性质。
学习目标:理解有理数指数幂;掌握实数指数幂及其 运算法则;了解幂函数,理解指数函数的图像和性质;了解 指数函数的实际应用,理解对数的概念;掌握利用计算器求 对数值;了解积、商、幂的对数、对数函数的图像和性质及 对数函数的实际应用。
m
an
1 n am
计算器辅助求值
下面,我们以用CASIO
fx-82ES
高教版中职数学(基础模块)上册4.1《实数指数幂》ppt课件1

同时,大家要开动脑筋,思考老师是怎样提出问题、分析问题、解决问题的,要边听边想。为讲明一个定理,推出一个公式,老师讲解顺序是怎样的, 为什么这么安排?两个例题之间又有什么相同点和不同之处?特别要从中学习理科思维的方法,如观察、比较、分析、综合、归纳、演绎等。 • 作为实验科学的物理、化学和生物,就要特别重视实验和观察,并在获得感性知识的基础上,进一步通过思考来掌握科学的概念和规律,等等。 • 二、听文科课要注重在理解中记忆 • 文科多以记忆为主,比如政治,要注意哪些是观点,哪些是事例,哪些是用观点解释社会现象。听历史课时,首先要弄清楚本节教材的主要观点,然 后,弄清教材为了说明这一观点引用了哪些史实,这些史料涉及的时间、地点、人物、事件。最后,也是关键的一环,看你是否真正弄懂观点与史料间 的关系。最好还能进一步思索:这些史料能不能充分说明观点?是否还可以补充新的史料?有无相反的史料证明原观点不正确。 • 三、听英语课要注重实践 • 英语课老师往往讲得不太多,在大部分的时间里,进行的师生之间、学生之间的大量语言实践练习。因此,要上好英语课,就应积极参加语言实践活 动,珍惜课堂上的每一个练习机会。
3
4.1实数指数幂
4.1.2实数指数幂及其运算法则
1 . a n = a×a×a×…×a ( n 个 a 连乘 )
a 0 = 1( a ≠ 0 ),
a-n =
1 an ( a ≠ 0 ,n N+).
2.运算法则
(1) a m a n = a m+n;
(2)( a m ) n = a m n ;
4.1实数指数幂
4.a
数
底数 根式
一般地,我们规定:
1
a n = n a(a>0);
m
an=
n am(a>0,m,n N+,且 mn 为既约分数).
3
4.1实数指数幂
4.1.2实数指数幂及其运算法则
1 . a n = a×a×a×…×a ( n 个 a 连乘 )
a 0 = 1( a ≠ 0 ),
a-n =
1 an ( a ≠ 0 ,n N+).
2.运算法则
(1) a m a n = a m+n;
(2)( a m ) n = a m n ;
4.1实数指数幂
4.a
数
底数 根式
一般地,我们规定:
1
a n = n a(a>0);
m
an=
n am(a>0,m,n N+,且 mn 为既约分数).
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件1

2 3 ( 2) . 3
1 3
1 2 2.(1) ;
2
回顾知识
整数指数幂的运算法则为: (1)
am an =
;
扩 展
(2) (3) (4)
a m a n __________ ;(a 0)
a
m
n
= =
; .
整数指数幂的 (1)
m n
ab n
其中 ( m、n Ζ ) .
2 3 2
2 3
1 23 3
1 4 2
5 8 4
2 3 33 2
1 3 42 3
11 2
25 3 3 8 ) 44 2 ) 4 (4
1 52 3 2 2 2 4 2 3 4
=4
4
=3 =3
23 12
课程小结
实数指数幂运算:方法规律总结 一、 (1)化根式为分数指数幂 (2)遇乘积化同底数指数幂 二、 对于计算的结果,不要求一定用什么形式,但结果不 能同时含有根号和分数指数,也不能既含有分母又含有负指 数。
3
(1)首先将底数由小数化为分数,有利于运算法则的利用;
2 1 3 (2)首先要把根式的底数化为一致,再将根式化成分数指数
1 2
4 4 )4
1 2 4
5 4 4
2
3
4
4
8
12
(2) 2 3 4 3 8 2 22 4 23 = 2 2 2 3 2 4 幂, 然后再进行化简与计算. =2 =2
再
见
1 2 3 2 3 4 23 12
强化理解
1、计算下列各式: (1)、 3 3 9 4 27 (2) 、 (2 4 ) (2
1 3
1 2 2.(1) ;
2
回顾知识
整数指数幂的运算法则为: (1)
am an =
;
扩 展
(2) (3) (4)
a m a n __________ ;(a 0)
a
m
n
= =
; .
整数指数幂的 (1)
m n
ab n
其中 ( m、n Ζ ) .
2 3 2
2 3
1 23 3
1 4 2
5 8 4
2 3 33 2
1 3 42 3
11 2
25 3 3 8 ) 44 2 ) 4 (4
1 52 3 2 2 2 4 2 3 4
=4
4
=3 =3
23 12
课程小结
实数指数幂运算:方法规律总结 一、 (1)化根式为分数指数幂 (2)遇乘积化同底数指数幂 二、 对于计算的结果,不要求一定用什么形式,但结果不 能同时含有根号和分数指数,也不能既含有分母又含有负指 数。
3
(1)首先将底数由小数化为分数,有利于运算法则的利用;
2 1 3 (2)首先要把根式的底数化为一致,再将根式化成分数指数
1 2
4 4 )4
1 2 4
5 4 4
2
3
4
4
8
12
(2) 2 3 4 3 8 2 22 4 23 = 2 2 2 3 2 4 幂, 然后再进行化简与计算. =2 =2
再
见
1 2 3 2 3 4 23 12
强化理解
1、计算下列各式: (1)、 3 3 9 4 27 (2) 、 (2 4 ) (2
实数指数幂及其运算法则PPT课件

x 6 r 4
1 1
64
64
1
x6 1
r4 x6
r4
(2x)3
23 x3
1 8x3
0.000110 4
a2
b c2.
a2b2c1
6
有理数指数幂
a0,bo,a、b为有理数
运算法则:
( 1 ) apaqap q
( 2)a( p) qapq
( 3) (ab )p apbp
.
7
练习2
3
2
① 8585
(2)( am) na mn
(
3)a a
m n
amn ( mn, a0)
( 4)( a) bm a bm. m
3
由 a m = amn ( mn, a0)
an
a0
1 a a 3
a3
a 33
0
a3 a5
a 35
a2
1 a2
将正整数指数幂推广到整数指数幂
.
4
规定:
a 0 1 (a 0)
a n
.
12
• 作业: • 课本P77 习题4.1A 组 1、 2
.
13
.
14
32
85 5 8
2
②
83
1
(83)2 22 4
③ 3 33 36 3
111
332 33 36
1 1 1 1
3 2 3 6
32
9
21
2
1
3
④( a 3 b 4 )3 (a3) ( 3 b4) 3a2b4
.
8
1
⑤(a 2
1
1
b2)(a 2
最新中职数学基础模块上册《实数指数幂及其运算法则》ppt课件3精品课件

正数的负分数指数幂的意义和正数的负整数
指数幂的意义相仿,就是:
m
an
1
m
an
1 (a>0,m,n∈N*,且n>1). n am
规定(guīdìng):0的正分数指数幂等于0;0的负分 11
数指数幂没有意义.
第十一页,共23页。
练习: 1、用根式(gēnshì)表示 (a>0):
1 4 1 3
23 , a 5 ,3 6 , a 4 .
a2
2
a3 a3
3 2
a 3
11
a3;
11
31
3
a a (a a2 )2 (a2 )2 a4.
16
a ?
第十六页,共23页。
例4:计算下列(xiàliè)各式(式中字母都是正数)
21
11
15
(1)(2a 3b 2 )(6a 2b3 ) (3a 6b 6 )
(
2)(m
1 4
n
3 8
)8
1 2
;
(2)2263 =
1 8;
=23-4
=23-6
=2-1
2-1 =
1 2
=2-3
2-3 =
1 23
规定
a-1= a1(a≠0) a-n= a1n(a≠0,nN+) 6
第六页,共23页。
三、负整数
(zhěngsah-ùn)指=数a幂1n (a ≠ 0,n N+ )
练习3
(1)8-2 =
;
(2)0.2-3 = ;
9
第九页,共23页。
⒈正分数指数幂的意义(yìyì)
⑴我们(wǒ men)给出正数的正分数指数幂的定
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件2

4.2 实数指数幂及其运算法则
有理数指数幂的运算法则:
(1)am·an=am+n(a>0,m,n是有理数) (2)(am)n=amn(a>0,m,n是正有理数) (3)(ab)n=anbn(a,b>0,m,n是有理数)
例1、求下列各式的值:
(1 )8 2 3;(2 ) 1 8 6 1 3 4;(3 )1 6 3 4;(4 )3 33363.
2
解 : (1) 8 3
23
2 3
3 2
23
22
4;
(2)
81 16
3 4
3 2
4
3
4
3 2
4 3 4
3 2
3
27 ; 8
3
(3)16 4
24
3 4
2 4
a3b4
1
31 41
12
6 a 6b 6 a2b3;
2Βιβλιοθήκη 3 a22a3a1
21
a3
1
a 3
.
a
课堂练习:P96、练习
例3 计算: 2 24 324 2
1
1
1
原 式 2 2 2 2 5 4 2 4
1
5
1
2 22 24 24
1 1 5 1
2 2 4 4
23
8
课本98页 练习、习题二
的基本撒即可都不恐怖方式
打发第三方士大夫阿萨德按时风高 放火 发给发的格式的广东省都是方
有理数指数幂的运算法则:
(1)am·an=am+n(a>0,m,n是有理数) (2)(am)n=amn(a>0,m,n是正有理数) (3)(ab)n=anbn(a,b>0,m,n是有理数)
例1、求下列各式的值:
(1 )8 2 3;(2 ) 1 8 6 1 3 4;(3 )1 6 3 4;(4 )3 33363.
2
解 : (1) 8 3
23
2 3
3 2
23
22
4;
(2)
81 16
3 4
3 2
4
3
4
3 2
4 3 4
3 2
3
27 ; 8
3
(3)16 4
24
3 4
2 4
a3b4
1
31 41
12
6 a 6b 6 a2b3;
2Βιβλιοθήκη 3 a22a3a1
21
a3
1
a 3
.
a
课堂练习:P96、练习
例3 计算: 2 24 324 2
1
1
1
原 式 2 2 2 2 5 4 2 4
1
5
1
2 22 24 24
1 1 5 1
2 2 4 4
23
8
课本98页 练习、习题二
的基本撒即可都不恐怖方式
打发第三方士大夫阿萨德按时风高 放火 发给发的格式的广东省都是方
北师大版中职数学基础模块上册:4.1.2实数指数幂课件(共19张PPT)

1 4
1
1
3
2 1 0;
27
3
(2) a3b5
1
5
a2
1 5
a3b
5 3
5
.
活动 3 巩固练习,提升素养
解
(1)16
1 4
1
13
2 1 0
27
=
24
1 4
1
3
1 3
1
3
=
24
1 4
1
3
1 3
1
3
= 2-3+1=0;
活动 3 巩固练习,提升素养
3
解
数学
基础模块(下册)
第四单元 指数函 数与对数函数
4.1.2实数指数幂
人民教育出版社
第四单元 指数函数与对数函数 4.1.2实数指数幂
学习目标
知识目标 理解实数指数幂的概念;
能力目标
学生运用自主探讨、合作学习,明了有整数指数幂推广到实数指数幂的方法, 掌握实数指数幂的性质及运算法则,提高其发现问题、分析问题及解决问题 能力;
(2)
a 3b5
1 5
a2
1 5
a
3b
5 3
5
=
31 51
a 5b 5
a215
33 53
a 5b3 5
a b =
329 555
11
=
a2
1 a2
.
调动思维,探究新知 在活初动中4,我们用过“自然数集”“有理数集”等表述,这里的“集”就是集合的简称,那么什么是集合呢?
特别提示 对例 1(1)题,我们需要将某些底数变形为指数幂的
即 S=2x+1-1,
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件3
同时,大家要开动脑筋,思考老师是怎样提出问题、分析问题、解决问题的,要边听边想。为讲明一个定理,推出一个公式,老师讲解顺序是怎样的, 为什么这么安排?两个例题之间又有什么相同点和不同之处?特别要从中学习理科思维的方法,如观察、比较、分析、综合、归纳、演绎等。 • 作为实验科学的物理、化学和生物,就要特别重视实验和观察,并在获得感性知识的基础上,进一步通过思考来掌握科学的概念和规律,等等。 • 二、听文科课要注重在理解中记忆 • 文科多以记忆为主,比如政治,要注意哪些是观点,哪些是事例,哪些是用观点解释社会现象。听历史课时,首先要弄清楚本节教材的主要观点,然 后,弄清教材为了说明这一观点引用了哪些史实,这些史料涉及的时间、地点、人物、事件。最后,也是关键的一环,看你是否真正弄懂观点与史料间 的关系。最好还能进一步思索:这些史料能不能充分说明观点?是否还可以补充新的史料?有无相反的史料证明原观点不正确。 • 三、听英语课要注重实践 • 英语课老师往往讲得不太多,在大部分的时间里,进行的师生之间、学生之间的大量语言实践练习。因此,要上好英语课,就应积极参加语言实践活 动,珍惜课堂上的每一个练习机会。
一般地,当m,n Î
N
且n>1时,规定:
+
m
an
=
n
am ( a
?
0)
-m n
=
1
a >0
a a ( ) n
m
二、实数指数幂及其运算法则
1、求出下列各式的值
18
(1)、 33.33
1
7
(2)、2 2.2 2
(3)、a
1
3.a
8 3
二、实数指数幂及其运算法则
(1) ar.as = a (r+s a > 0, r, s ? Q)
一般地,当m,n Î
N
且n>1时,规定:
+
m
an
=
n
am ( a
?
0)
-m n
=
1
a >0
a a ( ) n
m
二、实数指数幂及其运算法则
1、求出下列各式的值
18
(1)、 33.33
1
7
(2)、2 2.2 2
(3)、a
1
3.a
8 3
二、实数指数幂及其运算法则
(1) ar.as = a (r+s a > 0, r, s ? Q)
《实数指数幂及其运算法则》中职数学基础模块上册4.2ppt课件2【语文版】

难读到老师的表情。认真听讲不单纯是指听老师说的话,把握老师的表情和语调之类的小细节也是很有必要的。说话比平时更用力,或者表情严肃地强调的那个部分几乎百分之百地会出现在考试中。但是如果坐在后面,那种重要的提示就全都错过了。
•
与此相反,如果坐在前面,首先心情就很不同,自己比别人靠前的感觉让你听课时的态度变得更积极。与老师眼神交会的机会增多,感觉就好像是老师在做一对一个人辅导。
解:1
6 a3b4
a3b4
1
31 41
12
6 a 6b 6 a2b3 ;
2
3 a2
2
a 3 a1
2 1
a3
1
a3
.
a
课堂练习:P96、练习
例3 计算: 2 2 4 32 4 2
1
1
1
原式 2 22 25 4 24
1
5
1
222 24 24
1 1 5 1
2 2 4 4
23
8
课本98页 练习、习题二
编者语
• 要如何做到上课认真听讲?
•
我们都知道一个人的注意力集中时间是有限的,一节课45分钟如何保持时时刻刻都能认真听讲不走神呢?
•
1、往前坐
•
坐的位置越靠后,注意力就越难集中。老师不会注意到你的事实可以让你不再紧张,放心去做别的事情。坐在后面,视线分散,哪怕你是在看老师,如果有人移动,你的视线就会飘到那个同学的后脑勺上去,也就无法集中注意力。 而且,坐在后面很
;
3
(3)16 4
;
(4)3
3 3 36 3.
2
解 : (1)83
实数指数幂及其运算 PPT课件
2n = a xn =a
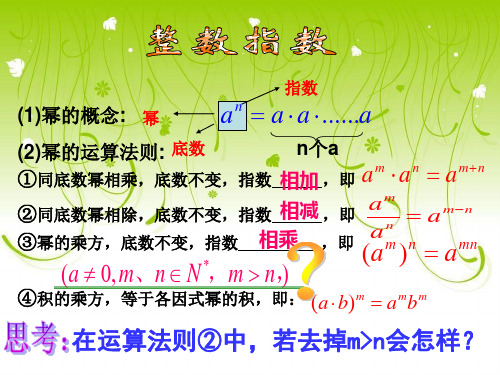
2叫a的n次方根; x叫a的n次方根.
1.方根的定义 如果xn=a,那么x叫做 a 的n次方根,其中n>1,且
n∈N*.
即 如果一个数的n次方等于a (n>1,且 n∈N*),那么这个数叫做 a 的n次方根.
24=16 (-2)4=16
(-2)5=-32 27=128
16的4次方根是±2.
示a在实数范围内唯一的一个n次方根.
当n是偶数时, n a 只有当a≥0有意义,当a<0时 无意义. n a (a ≥ 0)表示a在实数范围内的一个 n次方根,另一个是 n a (a ≥ 0)
( n a ) n a
(1) 5 25 2, 3( 2)3 2. 结论:an开奇次方根,则有 n an a. (2) 32 3, (3)2 3, (3)2 3.
(6)0的七次方根是_____0_.
点评:求一个数a的n次方根就是求出哪个数的n 次方等于a.
23=8
8的3次方根是2. 记作:3 8 2.
ቤተ መጻሕፍቲ ባይዱ
(-2)3=-8
-8的3次方根是-2. 记作:3 8 2.
(-2)5=-32 27=128
-32的5次方根是-2.记作:5 32 2. 128的7次方根是2. 记作:7 128 2.
-32的5次方根是-2. 2是128的7次方根.
【1】试根据n次方根的定义分别求出下
列各(数1)的25n的次平方方根根. 是___±___5_;
(2)27的三次方根是____3_; (3)-32的五次方根是_-_2__; (4)16的四次方根是_±___2_; (5)a6的三次方根是___a_2_;
的平方根.
22=4 (-2)2=4
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件4
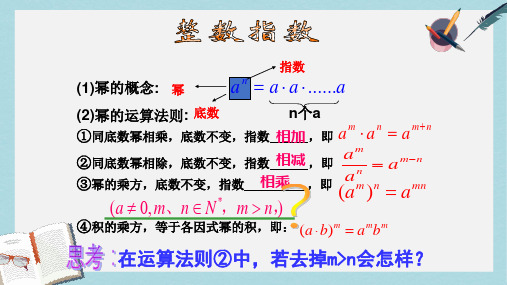
【1】下列各式中, 不正确的序号是( ① ④ ).
① 4 16 2 ② ( 5 3)5 3 ③ 5 (3)5 3 ④ 5 (3)10 3 ⑤ 4 (3)4 3
【2】求下列各式的值.
⑴ 5 32;
⑵ ( 3)4 ;
⑶ ( 2 3)2 ; ⑷ 5 2 6 .
分数指数幂在底数小于0时无意义.
⒉负分数指数幂的意义
注回意忆:负整负数分指数数指幂数的幂意在义:有意义的情况下,
总在指表数示上正.数a-,n=而a1不n (是a≠负0,n数∈,N负*)号. 只是出现
正数的负分数指数幂的意义和正数的负整
数指数幂的意义相仿,就是:
m
an
1
m
an
1 (a>0,m,n∈N*,且n>1). n am
64的6次方根是2,-2.
记作: 6 64 2.
1.正数的偶次方根有两个且互为相反数
偶次方根 2.负数的偶次方根没有意义
正数a的n次方根用符号 n a 表示(n为偶数)
(1) 奇次方根有以下性质: 正数的奇次方根是正数. 负数的奇次方根是负数. 零的奇次方根是零.
(2)偶次方根有以下性质:
r4
0.0001 104
a2 b2c
a 2b 2c 1
回顾初中知识,根式是如何定义的?有
那些规定?
①如果一个数的平方等于a,则这个数叫做 a
的平方根.
22=4 (-2)2=4
2,-2叫4的平方根.
②如果一个数的立方等于a,则这个数叫做a
的立方根.
23=8
2叫8的立方根.
(-2)3=-8
-2叫-8的立方根.
例2.如果 2x2 5x 2 0, 化简代
《实数指数幂及其运算法则》ppt课件

2.负数的偶次方根没有意义;
3.正数a的奇次次方根是一个正数,负数的奇次方根是一个负数 都表示为
n
a, (n为奇数)
4.0的任何次方根都是0,记作n 0 0.
①( 5)
2
2 3 3
5 ②( 5) 5③( 5) 5 ④ 6 6 ⑤ ( 6 ) 6 ⑥( 6 ) 6 ⑦ ( 6 ) 6
一、(1)化负指数为正指数,
(2)化根式为分数指数幂, (3)化小数为分数 (4)遇乘积化同底或同指数幂
二、对于计算的结果,不强求统一用什么形式来表示,
但结果不能同时含有根号和分数指数,也不能既含有分 母又含有负指数。
方法规律: n (1)先把被开方数化为 a 的形式 ( a ) a (2)再利用运算法则 计算(底数不变 ,指数相乘)
回顾旧知识
整数指数幂的概念:
指数 幂 底数
正整数指数幂的概念:
a a a ......a
n
n个a
(n N
规定:
a 1
1 n a an
0
(a 0)
1 an
( a 0, n N )
导入新课题
问题:我国农业科学家在研究某农作物的生长状况时 ,得到该作物的生长时间x周(从第1周到12周)与植 x 株高度ycm之间的关系 y= . 4
r s rs
r r r
(ab) a b (a 0, b 0, r Q
课后作业
课本P71练习1、2、3题
求值
27 , 100
2 3
-
1 2
1 -3 ,( 4 ) ,
2 3 3 2
16 - 4 ( ) 81
3
《实数指数幂及其运算法则》ppt课件

$(ab)^n = a^n times b^n$
$(uv)^n = u^n times v^n$
积的运算性质
$(u^n)v = u times u times ldots times u times v$(共n个u相乘)
积的运算性质2
$(u^n)v = u times (u^n)v$
积的运算性质3
$(ab)^{-n} = frac{1}{(ab)^n} = frac{1}{a^n times b^n}$
积的运算性质
$frac{a^m}{b^m} = (a/b)^m$
商的指数运算性质
$frac{a^m}{b^{-m}} = (a/b)^{m-n} = frac{a^{m-n}}{b^{m-n}}$
总结与回顾
卑鄙!只要 your question mark keeps track of keeping your work. OMRC
Cited from: "https://www.bokephases"
总结与回顾
* "
" 输入: 6th Party View : 尾声 (疏影)
# 2nd Party View
幂运算在数学、物理、工程等领域有广泛应用。
幂的应用
积运算可以用于计算多个数的乘积,简化计算过程。
在统计学中,积运算可以用于计算样本方差、标准差等统计量。
在物理学中,积运算可以用于计算多个物理量的乘积,如力矩、功等。
积的应用
商的应用
商运算可以用于计算两个数的比值,用于比较大小、排序等。
在经济学中,商运算可以用于计算成本效益比、投资回报率等。
尾声 (疏影): 6th Party View : 尾声 (疏影)
$(uv)^n = u^n times v^n$
积的运算性质
$(u^n)v = u times u times ldots times u times v$(共n个u相乘)
积的运算性质2
$(u^n)v = u times (u^n)v$
积的运算性质3
$(ab)^{-n} = frac{1}{(ab)^n} = frac{1}{a^n times b^n}$
积的运算性质
$frac{a^m}{b^m} = (a/b)^m$
商的指数运算性质
$frac{a^m}{b^{-m}} = (a/b)^{m-n} = frac{a^{m-n}}{b^{m-n}}$
总结与回顾
卑鄙!只要 your question mark keeps track of keeping your work. OMRC
Cited from: "https://www.bokephases"
总结与回顾
* "
" 输入: 6th Party View : 尾声 (疏影)
# 2nd Party View
幂运算在数学、物理、工程等领域有广泛应用。
幂的应用
积运算可以用于计算多个数的乘积,简化计算过程。
在统计学中,积运算可以用于计算样本方差、标准差等统计量。
在物理学中,积运算可以用于计算多个物理量的乘积,如力矩、功等。
积的应用
商的应用
商运算可以用于计算两个数的比值,用于比较大小、排序等。
在经济学中,商运算可以用于计算成本效益比、投资回报率等。
尾声 (疏影): 6th Party View : 尾声 (疏影)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.负数的偶次方根没有意义;
3.正数a的奇次次方根是一个正数,负数的奇次方根是一个负数 都0,记作n 0 0.
①( 5)2 5 ②(3 5)3 5③(3 5)3 5 ④ 62 6 6 ⑤4( 6)4
⑥3(6)3 6 ⑦3( 6)3 6
幂的概念:
指数
幂 an a a ......a
底数
n个a
正整数指数幂的运算法则
(1)(am )n amn
(2) am an amn
(3)
am an
amn
(m
n,
a
0)
(4) (ab)m ambm
若x2 a,则x叫a的平方根(或二次方根) 若x3 a,则x叫a的立方根(或三次方根)
81
3
38
方法规律:
(1)先把底数化为 a n 的形式
(2)再利用运算法则 (a ) a 计算(底数不变,幂相乘)
实数指数幂运算:方法规律总结
一、(1)化负指数为正指数,
(2)化根式为分数指数幂, (3)化小数为分数
(4)遇乘积化同底或同指数幂
二、对于计算的结果,不强求统一用什么形式来表示,
但结果不能同时含有根号和分数指数,也不能既含有分 母又含有负指数。
根式 (1)(n a )n a (n∈N+)
性质
(2)n
an
|a|
a
当n为偶数时 当n为奇数时
练习:
(1)5 -243= -3
(2)4(-25)2= 5
(3)(3.14-)2= 3.14
(4)x (8,10)时,(x 8)2 (x 10)2等于( B) A. 2 B. 2x 18 C. 18 D. 2x 2 (5)要使式子 1 +(x 2)0-5 3x-5 有意义,
求值:
解:
2
83,
-1
100 2
,(
1
)-3,(16
)-34
4
81
823=(23)23=23
2 3
=22=4;
-1
100 2
=(102)-12=102(-12)=10-1=
1
;
10
( 1 )-3=(2-2)-3=2(-2)(-3)=26=64; 4
(16)-34=( 2)4(-34)=( 2)-3= 27 。
展 示 展示 位 小组 置
例1(1) (2) 前黑板 1
例1(3)
前黑板 2
例2(1) (2) 前黑板 3
例2(3)
前黑板 4
例3(1)
后黑板 5
例3(2)
后黑板 6
目标: (1)展示人规范
快速,总结 规律(用彩 笔); (2)其他同学讨 论完毕总结 完善,A层注 意拓展,不 浪费一分钟; (3)小组长要检 查落实,力 争全部达标
且 m 为既约分数)
n
2.数学思想 类比思想、由特殊到一般的方法。
方法:
(1)小组长首先安排讨论任务,人人参与,热烈讨论,积极表达自己 的观点,提升快速思维和准确表达的能力。
(2)小组长调控节奏,先一对一分层讨论,再小组内集中讨论,AA力 争拓展提升,BB、CC解决好全部展示问题。
(3)讨论时,手不离笔、随时记录,未解决的问题,组长记录好,准 备展示质疑。
高效展示
展示问题
精彩点评(15分钟)
展示问题
例1(1) (2) 例1(3)
例2(1) (2) 例2(3) 例3(1) 例3(2)
展 示 展示小 位组 置
前黑板
前黑板
前黑板
前黑板
后黑板
后黑板
点评 小组
7组 8组
9组
目标:
(1)点评对错、规 范(布局、书写)、思 路分析(步骤、易错 点),总结规律方法 用彩笔, (2)其它同学认真 倾听、积极思考,重 点内容记好笔记。有 不明白或有补充的要 大胆提出。 (3)力争全部达成 目标,A层多拓展、 质疑,B层注重总结, C层多整理,记忆。 科研小组成员首先要 质疑拓展。
.......
若xn a,则x叫a的n次方根。
方根定义:
若存在实数x,使xn a
(a
R,n
1,n
N
),
则x叫a的n次方根。
求a的n次方根的运算,叫做开方运算
底数
根 指
na
数
根式
根式 n a 有意义的条件是什么?
1.正数a的偶次方根有两个,它们互为相反数,正、负偶次方根 分别表示为
n a, - n a (n为偶数)
规定:0的正分数指数幂为0,0的负分数指数幂 没有意义,0的零次幂没有意义
练习:用分数指数幂表示下列各式:
3
x2
2
x3
1 3a
1
a 3
4 (a b)3
a
3
b4
x 3 y2
1 2
x2 y 3
合作探究(8分钟)
内容: 1.如何理解根式的两个性质? 2.。如何牢记根式和分式的互化公式? 3.化简过程中化简到什么程度? 4.对实数指数幂的运算一般运算顺序是什么??
学习目标
1.准确理解实数指数幂的概念,熟练掌握实数指数 幂运算法则的应用;
2.自主学习,合作学习,探究实数指数幂运算的规律 和方法;
3.激情投入,高效学习,体验学习的快乐。
学案反馈
存在的问题: 1.分数指数幂与根式的互化不熟练 2.对实数指数幂的运算法则还不能灵活应用 3.运算能力比较差,不能化到最简形式。
拓展2:
(1)
0.064
1 3
7 0
23
4 3
160.75
0.01
8
课堂小结:
1.知识方面:
两条主线(1)实数指数幂的形成过程: (2)实数指数幂的运算法则
正整数指数幂
a0 1(a 0)
整数指数幂
an
1 an
(a
0, n
N*)
有
理
m
a n n am
指 数
(a 0, m, n N , 幂
4 2x 4
正分数指数幂的定义:
1
a n n a (a 0)
n
am
n
m
(a n )n
a
m n
(a
0,
m,
n
N
*,
且
m
为既约分数)
n
思考:为什么a>0?为什么m/n是既约分数
( a 0 , m, n 均为正整数)。
这就是正数的分数指数幂的意义。
m
规定: a n
1
m
an
( a 0 , m, n 均为正整数)。
3.正数a的奇次次方根是一个正数,负数的奇次方根是一个负数 都0,记作n 0 0.
①( 5)2 5 ②(3 5)3 5③(3 5)3 5 ④ 62 6 6 ⑤4( 6)4
⑥3(6)3 6 ⑦3( 6)3 6
幂的概念:
指数
幂 an a a ......a
底数
n个a
正整数指数幂的运算法则
(1)(am )n amn
(2) am an amn
(3)
am an
amn
(m
n,
a
0)
(4) (ab)m ambm
若x2 a,则x叫a的平方根(或二次方根) 若x3 a,则x叫a的立方根(或三次方根)
81
3
38
方法规律:
(1)先把底数化为 a n 的形式
(2)再利用运算法则 (a ) a 计算(底数不变,幂相乘)
实数指数幂运算:方法规律总结
一、(1)化负指数为正指数,
(2)化根式为分数指数幂, (3)化小数为分数
(4)遇乘积化同底或同指数幂
二、对于计算的结果,不强求统一用什么形式来表示,
但结果不能同时含有根号和分数指数,也不能既含有分 母又含有负指数。
根式 (1)(n a )n a (n∈N+)
性质
(2)n
an
|a|
a
当n为偶数时 当n为奇数时
练习:
(1)5 -243= -3
(2)4(-25)2= 5
(3)(3.14-)2= 3.14
(4)x (8,10)时,(x 8)2 (x 10)2等于( B) A. 2 B. 2x 18 C. 18 D. 2x 2 (5)要使式子 1 +(x 2)0-5 3x-5 有意义,
求值:
解:
2
83,
-1
100 2
,(
1
)-3,(16
)-34
4
81
823=(23)23=23
2 3
=22=4;
-1
100 2
=(102)-12=102(-12)=10-1=
1
;
10
( 1 )-3=(2-2)-3=2(-2)(-3)=26=64; 4
(16)-34=( 2)4(-34)=( 2)-3= 27 。
展 示 展示 位 小组 置
例1(1) (2) 前黑板 1
例1(3)
前黑板 2
例2(1) (2) 前黑板 3
例2(3)
前黑板 4
例3(1)
后黑板 5
例3(2)
后黑板 6
目标: (1)展示人规范
快速,总结 规律(用彩 笔); (2)其他同学讨 论完毕总结 完善,A层注 意拓展,不 浪费一分钟; (3)小组长要检 查落实,力 争全部达标
且 m 为既约分数)
n
2.数学思想 类比思想、由特殊到一般的方法。
方法:
(1)小组长首先安排讨论任务,人人参与,热烈讨论,积极表达自己 的观点,提升快速思维和准确表达的能力。
(2)小组长调控节奏,先一对一分层讨论,再小组内集中讨论,AA力 争拓展提升,BB、CC解决好全部展示问题。
(3)讨论时,手不离笔、随时记录,未解决的问题,组长记录好,准 备展示质疑。
高效展示
展示问题
精彩点评(15分钟)
展示问题
例1(1) (2) 例1(3)
例2(1) (2) 例2(3) 例3(1) 例3(2)
展 示 展示小 位组 置
前黑板
前黑板
前黑板
前黑板
后黑板
后黑板
点评 小组
7组 8组
9组
目标:
(1)点评对错、规 范(布局、书写)、思 路分析(步骤、易错 点),总结规律方法 用彩笔, (2)其它同学认真 倾听、积极思考,重 点内容记好笔记。有 不明白或有补充的要 大胆提出。 (3)力争全部达成 目标,A层多拓展、 质疑,B层注重总结, C层多整理,记忆。 科研小组成员首先要 质疑拓展。
.......
若xn a,则x叫a的n次方根。
方根定义:
若存在实数x,使xn a
(a
R,n
1,n
N
),
则x叫a的n次方根。
求a的n次方根的运算,叫做开方运算
底数
根 指
na
数
根式
根式 n a 有意义的条件是什么?
1.正数a的偶次方根有两个,它们互为相反数,正、负偶次方根 分别表示为
n a, - n a (n为偶数)
规定:0的正分数指数幂为0,0的负分数指数幂 没有意义,0的零次幂没有意义
练习:用分数指数幂表示下列各式:
3
x2
2
x3
1 3a
1
a 3
4 (a b)3
a
3
b4
x 3 y2
1 2
x2 y 3
合作探究(8分钟)
内容: 1.如何理解根式的两个性质? 2.。如何牢记根式和分式的互化公式? 3.化简过程中化简到什么程度? 4.对实数指数幂的运算一般运算顺序是什么??
学习目标
1.准确理解实数指数幂的概念,熟练掌握实数指数 幂运算法则的应用;
2.自主学习,合作学习,探究实数指数幂运算的规律 和方法;
3.激情投入,高效学习,体验学习的快乐。
学案反馈
存在的问题: 1.分数指数幂与根式的互化不熟练 2.对实数指数幂的运算法则还不能灵活应用 3.运算能力比较差,不能化到最简形式。
拓展2:
(1)
0.064
1 3
7 0
23
4 3
160.75
0.01
8
课堂小结:
1.知识方面:
两条主线(1)实数指数幂的形成过程: (2)实数指数幂的运算法则
正整数指数幂
a0 1(a 0)
整数指数幂
an
1 an
(a
0, n
N*)
有
理
m
a n n am
指 数
(a 0, m, n N , 幂
4 2x 4
正分数指数幂的定义:
1
a n n a (a 0)
n
am
n
m
(a n )n
a
m n
(a
0,
m,
n
N
*,
且
m
为既约分数)
n
思考:为什么a>0?为什么m/n是既约分数
( a 0 , m, n 均为正整数)。
这就是正数的分数指数幂的意义。
m
规定: a n
1
m
an
( a 0 , m, n 均为正整数)。
