对数函数及性质 说课课件
合集下载
《对数函数的图象与性质》优质课比赛课件[](共25张PPT)
](https://img.taocdn.com/s3/m/b80f5fdf4128915f804d2b160b4e767f5acf8002.png)
如果把这个指数式转换成对数式的形式应为
如果把x和y的位置互换,那么这个函数应为
x=log2y
y = log2x
(一)对数函数的定义
★ 函数 y = log a x (a>0,a≠1)叫做对数函
数. 其中x是自变量,定义域是(0,+∞)
为什么函数的 定义域是(0,+∞)?
想一想?
(二)作y=log2x和y=logx图象
注意:若底数不确定,那就要对底数进行分类讨论 即0<a<1 和 a > 1
你能口答吗?
变一变还能口答吗?
l o g 1 0 6 < l o g 1 0 8 log10 m< log10 n 则 m < n
l o g 0 .5 6 > l o g 0 .5 8 log0.5 m> log0.5 n 则 m < n
l o g 2 0 . 6 > l o g 2 0 . 8
log2 m > log2 n 则 m < n
3
3
3
3
l o g 1 .5 6 < l o g 1 .5 8
log1.5 m < log1.5 n 则 m < n
教学总结
•对数函数的定义 •对数函数图象作法 对数函数性质
想一想?
的图像如图,则 所下 示列式子中正(确 C )的
y ylogb x A .0 a b 1 c d
yloga x B .0 b a 1 d c
x
O
C .0 d c 1 b a
ylogd x
ylogc x D .0 a b 1 d c
y y=2x y=x
图(像二㈠ )在作(y1=,l0o)g点2x右和边y=的logx图象 定∴ y义=域log是2( x0在,+(∞0),+∞)
《对数函数及其性质》课件

THANK YOU
对数函数的定义域和值域
理解对数函数的定义域和值域,并能够判断特定函数的定义域和值 域。
对数函数的单调性
理解对数函数的单调性,并能够判断特定函数的单调性。
进阶题目
01
02
03
复合对数函数
理解复合对数函数,并能 够求解复合对数函数的值 。
对数函数的图像
理解对数函数的图像,并 能够根据图像判断函数的 性质。
分析对数函数的值域和定义域。对于自然对数函数y=log(x) ,其值域为R;对于以a为底的对数函数y=log(x),其定义域 为(0, +∞)。对于复合对数函数y=log(u),其值域和定义域取 决于u的取值范围。
03
对数函数的应用
实际应用场景
金融计算
在复利、折旧等计算中 ,对数函数有广泛应用
。
《对数函数及其性质》ppt课件
• 对数函数的定义与性质 • 对数函数的图像与性质 • 对数函数的应用 • 对数函数与其他知识点的联系 • 习题与练习
01
对数函数的定义与性质
定义与表示
总结词
对数函数是一种特殊的函数,其 定义域为正实数集,值域为全体 实数集。常用对数函数以10为底 ,自然对数函数以e为底。
么以a为底N的对数等于b。
对数函数和指数函数在解决实际 问题中经常一起出现,例如在计 算复利、解决声学和光学问题时
。
对数函数与三角函数的联系
对数函数和三角函数在形式上有些相似,特别是在自然对数函数和正弦函数中。
在复数域中,对数函数和三角函数有更密切的联系,它们都可以用来表示复数的幂 。
在解决一些物理问题时,例如波动和振动问题,可能需要同时使用对数函数和三角 函数。
对数函数及其性质课件ppt

统计学
决策理论
在决策理论中,对数函数用于构建效 用函数,以评估不同选项的风险和收 益。
在统计学中,对数函数用于描述概率 分布,如泊松分布和二项分布。
05 练习与思考
基础练习题
01
02
03
04
基础练习题1
请计算以2为底9的对数。
基础练习题2
请计算以3为底8的对数。
基础练习题3
请计算以10为底7的对数奇函数也不是偶 函数。
周期性
• 无周期性:对数函数没有周期性,因为其图像不会重复出 现。
03 对数函数的运算性质
换底公式
总结词
换底公式是用来转换对数的底数的公 式,它对于解决对数问题非常有用。
详细描述
换底公式是log_b(a) = log_c(a) / log_c(b),其中a、b、c是正实数,且b 和c都不等于1。通过换底公式,我们可 以将对数函数转换为任意底数的对数函 数,从而简化计算过程。
图像绘制
对数函数的图像通常在直角坐标系 中绘制,随着底数$a$的取值不同, 图像的形状和位置也会有所变化。
单调性
单调递增
当底数$a > 1$时,对数函数是单调递增的,即随着$x$的增 大,$y$的值也增大。
单调递减
当$0 < a < 1$时,对数函数是单调递减的,即随着$x$的增 大,$y$的值减小。
对数函数的乘法性质
总结词
对数函数的乘法性质是指当两个对数 函数相乘时,其结果的对数等于两个 对数函数分别取对数后的积。
详细描述
对数函数的乘法性质公式为log_b(m) * log_b(n) = log_b(m * n),其中m 和n是正实数。这个性质在对数运算 中也非常有用,因为它可以简化对数 的计算过程。
对数函数的图像与性质(公开课》省公开课获奖课件说课比赛一等奖课件
比较两个同底对数值旳大小时:
1.观察底数是不小于1还是不不小于1( a>1时为增函
小数
2.比较真数值旳大小;
结
0<a<1时为减函数)
3.根据单调性得出成果。
练习3
变一变还能口答吗?
lg 6 < lg 8 log10 m< log10 n 则 m < n
log0.5 6 < log0.5 4 log0.5 m> log0.5 n 则 m < n
提醒:分别将 y=2x 和y=log2x
y=0.5x 和y= log0.5x 旳图象画在一种坐标内 ,观察图象旳特点!
(书面作业)
•P82--- 5
例3 比较下列各组中两个值旳大小: ⑴.log 67 , log 7 6 ; ⑵.log 3π , log 2 0.8 .
解: ⑴ ∵ log67>log66=1
(一)对数函数旳定义
★ 函数 y = log a x (a>0,且a≠1)叫做对数函数.
其中x是自变量,定义域是(0,+∞)
对数函数解析式有哪些构造特征? ①底数:不小于0且不等于1旳常数 ②真数: 单个自变量x
③系数: log a x 旳系数为1
想一想?
练习1
下列函数中,哪些是对数函数?
① y loga x2; ② y log2 x 1; ③ y 2 log8 x;
解2:考察函数y=log 0.3 x , ∵a=0.3< 1, ∴函数在区间(0,+∞)上是减函数; ∵1.8<2.7 ∴ log 0.3 1.8> log 0.3 2.7
• 例2:比较下列各组中,两个值旳大小: • (1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7
《对数函数的图象和性质》说课稿课件

(3) 比较大小 loga3与 loga5 (a>0,且 a≠1)
பைடு நூலகம்
4、研究当a在(1,+∞)中 变化,观察对数函数图象有 何变化?
•由学生自主研究,小组讨论,得出 结论,并做以下练习:
例2 比较以下各组数的大小:
(1)log23与log33 (2)log50.3与log70.3
5、研究当a在(0,1)中变化时, 观察对数函数图象有何变化?
对数函数的图象和性质
(说课稿)
一、教材分析
1、教材所处地位及作用 本节是在指数函数学习之后,利用
指数函数与对数函数之间的关系,得到 对数函数的图象,并研究对数函数的性 质的一节课。它对学生加深理解对数函 数的概念和性质,并灵活运用性质解题 大有帮助。在研究的过程中发现有很多 重要的数学思想和方法在此得到体现。
(二)正课
1、链接到:
2、让学生画出对数函数的图象, 通过图象研究对数函数的性质。
(1)、定义域; (2)、值域; (3)、单调性; (4)、何时函数值为正值,何时函数值 为负值。
这是0<a<1时的图象
这是a>1时的图象
3、例题巩固
例1 比较两数的大 小 (1)log23与log25
(2) log0.23与log0.25
2、教学目标
(1)正确画出对数函数的图象; (2)由对数函数的图象得到对数函 数的性质; (3)灵活运用对数函数的性质来解 题。
3、教学重点、难点及关键
本节的重点是由指数函数与对数 函数之间的关系,得到对数函数的 图象和性质,利用对数函数的性质 来解题。关键是学会探索、发现规 律。
4、学法指导分析
系吗?
(三)练习: 课本练习1、2、3。
对数函数及性质说课课件完美版PPT

设计意图:通过问题的解决,可以及时检验与稳固学生对定义的理解 以及对数函数性质的简单应用情况,学生的认知也得以升华。
归纳总结
〔1〕归纳总结 ①对数函数及简单复合函数的图象:根本变换;
②探究性质应用:定义域、值域、单调性;
③重视函数定义域,对数函数真数大于零;
④数形结合、分类讨论、化归数学思想。
设计意图:让学生自主归纳,将本节课的知识有机的串联起来,以便有一个 系统全面的认识.培养了学生概括能力,语言表达能力,还能让学生对本节 课的知识做以简单回忆,方法以总结。
能力目标
1.通过对底数a的讨 论,使学生对分类讨 论的思想有进一步的 认识;体会数形结合 的数学思想; 2.通过例题.习题的 解决,使学生领会化 归思想在解决问题中 的作用.
情感目标
学生在参与中感受 数学,探索数学, 提高学习数学的兴 趣,增强学好数学 的自信心.
三.课堂结构设计
1、以学生活动为主体; 2、以培养学生能力为中心; 3、以提高课堂教学质量为目标.
(1).ylog2 x2 (2)ylog1(4x)
(1)log0.31.8和 log32.7
(2)loga3.4和 loga8.5
2
例3 已知函数 f(x)=loga(2-ax),函数 f(x)在[0,1]上是关于 x
的减函数,求 a 的取值范围_____.
例4.函数 y lo g 2(x 2 2 x 5 )的 值 域 。
稳固提高
lg 6
题组练习1:求以下函数的定义域:
1、 ylo5(g 1x)
2、y 1 log2 x
3、y
1
log7(13x)
题组练习2: 求函数单调区间:
1 .函 数 y lo g 1 (2 x 2 3 x 1 ) 的 递 减 区 间 为 ( )
对数函数PPT课件

04 对数函数与其他函数的比 较
与指数函数的比较
指数函数和对数函数是互为反函数, 它们的图像关于直线y=x对称。
当a>1时,指数函数和对数函数都是 增函数,但它们的增长速度不同,对 数函数的增长速度更慢。
指数函数y=a^x(a>0且a≠1)的图 像总是经过点(0,1),而对数函数 y=log_a x(a>0且a≠1)的图像则 总是经过点(1,0)。
对数函数和三角函数的应用领域也不同。对数函数主要用于解决与对数运算相关的问题,如 对数的换底公式、对数的运算性质等;而三角函数则主要用于解决与三角形的边角关系、周 期性等问题相关的问题。
05 对数函数的学习方法与技 巧
学习方法
1 2 3
理解对数函数的定义
首先需要理解对数函数的基本定义,包括对数函 数的定义域、值域以及其变化规律。
对数函数ppt课件
目录
• 对数函数的定义与性质 • 对数函数的运算性质 • 对数函数的应用 • 对数函数与其他函数的比较 • 对数函数的学习方法与技巧
01 对数函数的定义与性质
定义
自然对数
以e为底的对数,记作lnx,其中e是自然对数的底数,约等于 2.71828。
常用对数
以10为底的对数,记作lgx。
当0<a<1时,指数函数和对数函数都 是减函数,但它们的下降速度也不同, 对数函数的下降速度更快。
与幂函数的比较
幂函数y=x^n(n为实数)的图像在 第一象限和第三象限都存在,而对数 函数y=log_a x(a>0且a≠1)的图像 只存在于第一象限。
幂函数的增长速度与指数和对数函数 不同,当n>0时,幂函数的增长速度 比对数函数更快;当n<0时,幂函数 的增长速度比对数函数更慢。
新人教A版必修一对数函数的概念对数函数图像和性质课件(22张)
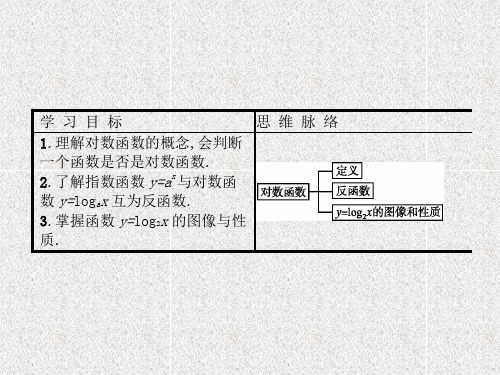
;
(2)下列函数中,是对数函数的是
.(填序号)
①y=log4x;②y=log2(3x);③y=logx2;④y=log3(x-1);⑤y=log2x2;
1
⑥y= 2 log3x.
探究一
探究二
探究三
易错辨析
解析:(1)设 f(x)=logax(a>0,且 a≠1),
1
依题意有 loga4=-1,故 a=4,
探究三
易错辨析
对于含有偶次根式中被开方式为对数式时,要注意被开方的代数
式为非负,还要顾及对数式中本身的真数大于0这一隐含信息,错解
中显然忘记了真数大于0这一隐含条件.
1
2
3
4
5
6
1.下列函数中,是对数函数的是(
A.y=log2x-1
B.y=logx3x
C.y= log 1 x
D.y=3log5x
2
探究一
探究二
探究三
易错辨析
变式训练2函数f(x)=3x(0<x≤2)的反函数的定义域为(
A.(0,+∞)
B.(1,9]
C.(0,1)
D.[9,+∞)
解析:∵ 0<x≤2,∴1<3x≤9,
即函数f(x)的值域为(1,9].
故函数f(x)的反函数的定义域为(1,9].
答案:B
)
探究一
探究二
探究三
易错辨析
C.
2
D.x2
解析:由题意,知 f(x)=logax.∵f(x)的图像过点(√,a),
1
∴a=loga√.∴a=2.∴f(x)=log 1 x.故选 B.
2
答案:B
函数y=logax(a>0,且a≠1)的反函数是y=ax(a>0,且a≠1);函数
(2)下列函数中,是对数函数的是
.(填序号)
①y=log4x;②y=log2(3x);③y=logx2;④y=log3(x-1);⑤y=log2x2;
1
⑥y= 2 log3x.
探究一
探究二
探究三
易错辨析
解析:(1)设 f(x)=logax(a>0,且 a≠1),
1
依题意有 loga4=-1,故 a=4,
探究三
易错辨析
对于含有偶次根式中被开方式为对数式时,要注意被开方的代数
式为非负,还要顾及对数式中本身的真数大于0这一隐含信息,错解
中显然忘记了真数大于0这一隐含条件.
1
2
3
4
5
6
1.下列函数中,是对数函数的是(
A.y=log2x-1
B.y=logx3x
C.y= log 1 x
D.y=3log5x
2
探究一
探究二
探究三
易错辨析
变式训练2函数f(x)=3x(0<x≤2)的反函数的定义域为(
A.(0,+∞)
B.(1,9]
C.(0,1)
D.[9,+∞)
解析:∵ 0<x≤2,∴1<3x≤9,
即函数f(x)的值域为(1,9].
故函数f(x)的反函数的定义域为(1,9].
答案:B
)
探究一
探究二
探究三
易错辨析
C.
2
D.x2
解析:由题意,知 f(x)=logax.∵f(x)的图像过点(√,a),
1
∴a=loga√.∴a=2.∴f(x)=log 1 x.故选 B.
2
答案:B
函数y=logax(a>0,且a≠1)的反函数是y=ax(a>0,且a≠1);函数
课件10:2.2.2 对数函数及其性质 第一课时

x≠1,
∴x>23且 x≠1.
故原函数的定义域为xx>23且x≠1 .
1.求下列函数的定义域:
(1)y= lg2-x;
(2)y=log331x-2.
解:(1)由题意,得 lg(2-x)≥0,即 2-x≥1,所以 x≤1,
则 y= lg2-x的定义域为{x|x≤1}.
(2)由l3oxg-332x>-0,2≠0, 得33xx- >22,≠1, 解得 x>23且 x≠1. 所以 y=log331x-2的定义域为xx>23且x≠1 .
题型二 对数函数的图象 【例2】 已知a>0且a≠1,函数y=ax与y=loga(-x)的图象 可能是下图中的( )
思路点拨:利用对数函数的图象与性质求解.
解析:首先,曲线y=ax只可能在上半平面,y=loga(-x) 只可能在左半平面,从而排除A,D.
其次,从单调性着眼,y=ax与y=loga(-x)的增减性正好 相反,又可排除C.∴应选B.
2.2 对数函数
2.2.2 对数函数及其性质
第1课时 对数函数的图ห้องสมุดไป่ตู้及性质
自学导引
1.对数函数的定义:一般地,我们把函数y=logax(a>0且 a≠1)叫做__对__数__函__数___,其中x是自变量,函数的定义域是(0, +∞).
2.对数函数的图象与性质:
定义
y=logax(a>0,且 a≠1)
2.对数函数单调性等重要性质要借助图象来理解与掌握. 3.掌握对数函数不但要清楚对数函数自身的图象和性质, 还要结合指数函数的图象和性质来对比掌握.
本节内容结束 更多精彩内容请登录:
因为 0<x<3,所以 3x(3-x)=-3x-322+247∈0,247,
∴x>23且 x≠1.
故原函数的定义域为xx>23且x≠1 .
1.求下列函数的定义域:
(1)y= lg2-x;
(2)y=log331x-2.
解:(1)由题意,得 lg(2-x)≥0,即 2-x≥1,所以 x≤1,
则 y= lg2-x的定义域为{x|x≤1}.
(2)由l3oxg-332x>-0,2≠0, 得33xx- >22,≠1, 解得 x>23且 x≠1. 所以 y=log331x-2的定义域为xx>23且x≠1 .
题型二 对数函数的图象 【例2】 已知a>0且a≠1,函数y=ax与y=loga(-x)的图象 可能是下图中的( )
思路点拨:利用对数函数的图象与性质求解.
解析:首先,曲线y=ax只可能在上半平面,y=loga(-x) 只可能在左半平面,从而排除A,D.
其次,从单调性着眼,y=ax与y=loga(-x)的增减性正好 相反,又可排除C.∴应选B.
2.2 对数函数
2.2.2 对数函数及其性质
第1课时 对数函数的图ห้องสมุดไป่ตู้及性质
自学导引
1.对数函数的定义:一般地,我们把函数y=logax(a>0且 a≠1)叫做__对__数__函__数___,其中x是自变量,函数的定义域是(0, +∞).
2.对数函数的图象与性质:
定义
y=logax(a>0,且 a≠1)
2.对数函数单调性等重要性质要借助图象来理解与掌握. 3.掌握对数函数不但要清楚对数函数自身的图象和性质, 还要结合指数函数的图象和性质来对比掌握.
本节内容结束 更多精彩内容请登录:
因为 0<x<3,所以 3x(3-x)=-3x-322+247∈0,247,
对数函数及其性质ppt

符号
常用对数函数记作f(x) = lgₐx,以10 为底;自然对数函数记作f(x) = lnₐx, 以e为底。源自对数函数的性质定义域
对数函数的定义域为(0, +∞),这是因为对数函数的底数必须大于0且不等于1。
值域
对数函数的值域为R,即所有实数。
单调性
当a > 1时,对数函数是增函数;当0 < a < 1时,对数函数是减函数。
对数函数的除法性质
总结词
对数函数的除法性质是指当两个对数相除时,其结果等于将被除数的底数取倒数后再取对数。
详细描述
对数函数的除法性质可以表示为log_b(m) / log_b(n) = log_b(1/n) / log_b(1/m) = log_b(m/n),其中 m和n是正实数,且n不等于1。这个性质在对数运算中也非常重要,因为它简化了多个对数项的除法运算。
对数函数,我们可以更好地理解放射性物质在环境中的行为和影响。
THANKS
感谢观看
对数函数及其性质
• 对数函数的定义与性质 • 对数函数的运算性质 • 对数函数的应用 • 对数函数与其他函数的比较 • 对数函数在实际问题中的应用案例
01
对数函数的定义与性质
定义与符号
定义
对数函数是指数函数的反函数,记作 f(x) = logₐx (a > 0, a ≠ 1),其定义 域为(0, +∞)。
对数运算法则
对数函数具有对数运算法则,包括换底公式、对数乘法公式、对数除法公式等。
对数函数的图象
01
图像形状
对数函数的图像通常为单调递增或递减的曲线,随着x的增大而无限接
近y轴。
02
图像特点
对数函数的图像具有垂直渐近线,即x=1和x=0。此外,当a>1时,图
常用对数函数记作f(x) = lgₐx,以10 为底;自然对数函数记作f(x) = lnₐx, 以e为底。源自对数函数的性质定义域
对数函数的定义域为(0, +∞),这是因为对数函数的底数必须大于0且不等于1。
值域
对数函数的值域为R,即所有实数。
单调性
当a > 1时,对数函数是增函数;当0 < a < 1时,对数函数是减函数。
对数函数的除法性质
总结词
对数函数的除法性质是指当两个对数相除时,其结果等于将被除数的底数取倒数后再取对数。
详细描述
对数函数的除法性质可以表示为log_b(m) / log_b(n) = log_b(1/n) / log_b(1/m) = log_b(m/n),其中 m和n是正实数,且n不等于1。这个性质在对数运算中也非常重要,因为它简化了多个对数项的除法运算。
对数函数,我们可以更好地理解放射性物质在环境中的行为和影响。
THANKS
感谢观看
对数函数及其性质
• 对数函数的定义与性质 • 对数函数的运算性质 • 对数函数的应用 • 对数函数与其他函数的比较 • 对数函数在实际问题中的应用案例
01
对数函数的定义与性质
定义与符号
定义
对数函数是指数函数的反函数,记作 f(x) = logₐx (a > 0, a ≠ 1),其定义 域为(0, +∞)。
对数运算法则
对数函数具有对数运算法则,包括换底公式、对数乘法公式、对数除法公式等。
对数函数的图象
01
图像形状
对数函数的图像通常为单调递增或递减的曲线,随着x的增大而无限接
近y轴。
02
图像特点
对数函数的图像具有垂直渐近线,即x=1和x=0。此外,当a>1时,图
4.4.2对数函数的图象和性质课件(人教版)

7.40)之间的稳定状态。体内酸、碱产生过多或不足,引起血
液pH值改变,此状态称为酸碱失衡。维持基本的生命活动主要
取决于体内精细的酸碱平衡或内环境稳定,即使是微小的失衡
,也可能在很大程度上影响机体的代谢和重要器官的功能.
课堂小结
图象
对数函数的
图象及性质
定义域
值域
性质
பைடு நூலகம்
(0, +∞)
过定点(1,0),即 = 1时, = 0
酸碱度与溶液中氢离子的浓度之间的变化关系;
解 (1)根据对数的运算性质,有
= − lg
+
= lg
+ −1
= lg
1
+
,
所以,在(0, +∞)上,随着 + 的增大, 减小.
因此,溶液中氢离子的浓度越大,溶液的酸性就越强.
例题精讲
例4 (2)已知纯净水中氢离子的浓度为 + = 10−7 摩尔/升,
减函数
增函数
课后作业
1.完成习题4.4
2.探究互为反函数的两个函数图象间的关系.
谢谢
知识像一艘船让它载着我们驶向理想的
……
分析
第一步,列表
0.5
−1
第二步,描点
1
2
2.58
3
3.58
4
新知讲授
探究 用描点法画出函数 = 2 的图象.
分析续
第三步,连线
新知讲授
探究
画出函数 = 1 的图象,并与函数 = 2 的图
2
象进行比较,它们有什么关系?能否利用函数 = 2 的图
象,画出函数 = 1 的图象?
液pH值改变,此状态称为酸碱失衡。维持基本的生命活动主要
取决于体内精细的酸碱平衡或内环境稳定,即使是微小的失衡
,也可能在很大程度上影响机体的代谢和重要器官的功能.
课堂小结
图象
对数函数的
图象及性质
定义域
值域
性质
பைடு நூலகம்
(0, +∞)
过定点(1,0),即 = 1时, = 0
酸碱度与溶液中氢离子的浓度之间的变化关系;
解 (1)根据对数的运算性质,有
= − lg
+
= lg
+ −1
= lg
1
+
,
所以,在(0, +∞)上,随着 + 的增大, 减小.
因此,溶液中氢离子的浓度越大,溶液的酸性就越强.
例题精讲
例4 (2)已知纯净水中氢离子的浓度为 + = 10−7 摩尔/升,
减函数
增函数
课后作业
1.完成习题4.4
2.探究互为反函数的两个函数图象间的关系.
谢谢
知识像一艘船让它载着我们驶向理想的
……
分析
第一步,列表
0.5
−1
第二步,描点
1
2
2.58
3
3.58
4
新知讲授
探究 用描点法画出函数 = 2 的图象.
分析续
第三步,连线
新知讲授
探究
画出函数 = 1 的图象,并与函数 = 2 的图
2
象进行比较,它们有什么关系?能否利用函数 = 2 的图
象,画出函数 = 1 的图象?
对数函数及其性质 课件

2.填空:
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自
变量,函数的定义域是(0,+∞).
3.判断一个函数是不是对数函数的依据是什么?
提示:对数函数的定义与指数函数类似,只有满足①函数解析式
右边的系数为1;②底数为大于0且不等于1的常数;③真数仅有自变
量x这三个条件,才是对数函数.如:y=2logax;y=loga(4-x);y=logax2都
的图象如图所示.
(3)从(2)的图中可以发现:y=lg x 与 y=log 1 x,y=log5x 与
10
y=log 1 x,y=log2x 与 y=log 1 x 的图象分别关于 x 轴对称.
5
2
5
10
探究三利用对数函数的性质比较大小
例3 比较下列各组中两个值的大小:
(1)log31.9,log32;
点(3,-6).
答案:(1)A (2)D (3)(3,-6)
三、反函数
1.函数y=log2x与y=2x的定义域和值域之间有什么关系?其图象之
间是什么关系?
提示:函数y=log2x与y=2x的定义域和值域之间是互换的,两者的
图象关于直线y=x对称.
2.填空:
对数函数y=logax(a>0且a≠1)和指数函数y=ax(a>0且a≠1)互为反
同理可得函数y=log0.2(x2-2x+2)在(-∞,1]上是增函数.
故函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1],单调减区间为
[1,+∞).
以f(1.9)<f(2),即log31.9<log32.
(2)(中间量法)因为log23>log21=0,log0.32<log0.31=0,所以
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自
变量,函数的定义域是(0,+∞).
3.判断一个函数是不是对数函数的依据是什么?
提示:对数函数的定义与指数函数类似,只有满足①函数解析式
右边的系数为1;②底数为大于0且不等于1的常数;③真数仅有自变
量x这三个条件,才是对数函数.如:y=2logax;y=loga(4-x);y=logax2都
的图象如图所示.
(3)从(2)的图中可以发现:y=lg x 与 y=log 1 x,y=log5x 与
10
y=log 1 x,y=log2x 与 y=log 1 x 的图象分别关于 x 轴对称.
5
2
5
10
探究三利用对数函数的性质比较大小
例3 比较下列各组中两个值的大小:
(1)log31.9,log32;
点(3,-6).
答案:(1)A (2)D (3)(3,-6)
三、反函数
1.函数y=log2x与y=2x的定义域和值域之间有什么关系?其图象之
间是什么关系?
提示:函数y=log2x与y=2x的定义域和值域之间是互换的,两者的
图象关于直线y=x对称.
2.填空:
对数函数y=logax(a>0且a≠1)和指数函数y=ax(a>0且a≠1)互为反
同理可得函数y=log0.2(x2-2x+2)在(-∞,1]上是增函数.
故函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1],单调减区间为
[1,+∞).
以f(1.9)<f(2),即log31.9<log32.
(2)(中间量法)因为log23>log21=0,log0.32<log0.31=0,所以
对数函数的性质与应用课件

函数的除法性质
总结词
对数函数的除法性质是指当两个对数函数相 除时,其对应的对数值也相除。
详细描述
设函数$f(x) = log_a(x)$和$g(x) = log_a(x)$,若$f(x) / g(x) = log_a(x) / log_a(x) = log_a(frac{1}{x})$,则对数函数 的除法性质成立。
对数在数学中有着广泛的应用,例如 在求解复合函数、反函数、幂函数等 问题时,对数函数可以提供一种简便 的解决方法。
在几何学中,对数函数可以用于研究 几何图形的面积、体积等方面的问题 。
在数学分析中,对数函数可以用于研 究函数的单调性、奇偶性、周期性等 性质,以及求解函数的极限、导数和 积分等。
对数在物理中的应用
图像的平移与伸缩
要点一
总结词
对数函数图像的平移和伸缩规律是重要的数学性质。
要点二
详细描述
对数函数图像的平移规律包括向上或向下平移,伸缩规律 则包括横向和纵向的拉伸或压缩。这些变换规律可以通过 代数表达式来描述,并应用于解决实际问题。
图像的对称性分析
总结词
对数函数图像的对称性分析有助于理解函数的性质。
在金融领域中,对数函数还可以用于评估投资组合的风险 和回报率,以及制定投资策略和资产配置方案等。
04
对数函数与其他函数的关 系
对数函数与指数函数的关系
互为反函数
对数函数和指数函数是一对互为反函 数的函数,即如果有一个对数函数f(x) = log(a)(x),那么它的反函数就是指 数函数f^(-1)(x) = a^x。
性质关系
对数函数和幂函数之间有一些重要的性质关 系,例如对数函数的换底公式和幂函数的乘 法法则等。这些性质关系在对数函数和幂函
高一对数函数及其性质(优质课)课件

指数函数和对数函数的性质互补 ,即当一个函数的某个性质成立 时,另一个函数的相应性质必然
不成立。
02
对数函数的图像与性质
对数函数的图像
总结词
对数函数的图像是学习对数函数的基础,通过图像可以直观地理解对数函数的 性质和特点。
详细描述
对数函数的图像通常在平面直角坐标系中绘制,以实数轴为底边,以真数为横 坐标,以对数为纵坐标。常见的对数函数包括自然对数函数和以10为底的对数 函数等。
高一对数函数及其性质(优质课)课 件
• 对数函数的定义与性质 • 对数函数的图像与性质 • 对数函数的应用 • 对数函数与其他函数的关系 • 习题与解析
01
对数函数的定义与性质
对数函数的定义
常用对数
以10为底的对数, 记作lgx。
对数定义域
真数必须大于0,即 x>0。
自然对数
以e为底的对数,记 作lnx。
知的。
地震的里氏震级
地震的震级也是使用对数函数来测 量的,因为地震的能量是以指数方 式增长的。
测量声谱和色谱
在声音和颜色的分析中,对数函数 被用来测量频谱和色谱,以帮助我 们更好地理解和分析声音和颜色的 组成。
对数在科学计算中的应用
放射性衰变
放射性衰变是一个指数过程,而对数 函数在处理指数函数时非常有用,因 此它在计算放射性衰变时被广泛应用 。
对数函数的单调性
总结词
对数函数的单调性是指函数值随自变量变化的趋势,通过研究单调性可以更好地 理解对数函数的性质。
详细描述
对数函数在其定义域内通常是单调的,即随着自变量的增加,函数值也相应增加 。对于以10为底的对数函数,当底数大于1时,函数是增函数;当底数小于1时, 函数是减函数。
对数函数及其性质说课课件-高一上学期数学人教A版必修1

从本节核心来看,本节课的主
要内容始终是围绕着对数函数
性质展开的.
教 学 分 析
一、教学内容分析
教学难点:探索对数函数性质
突出重点的方法:类比指数函数的研究过程,交流、
共同确认研究对数函数的内容和方法,设计具体的操
作方案,并进行具体实践操作,从中体会获得对数函
数性质的方法,进一步积累研究经验.
教 学 分 析
答问题时,应该集中精神仔细听学生的表达。
LOGO
力提升.因此,本节课设计时,就先设计梳理指数函数的研究
过程的环节,之后经历从实际情景中抽象出对数函数研究思路和方法,
并设计具体的操作方案后,给予学生充分的时间,独立思考、
六、教学反思
交流分享,教师及时点评,这样设计不仅可以明确对数函数的
研究内容和方法,还能在这一过程中发展学生的具体操作能力
性质
表示
应用
定义域、值域、单调性、
奇偶性、定点
设计意图:通过指数与对数关系的回顾,获得指数
研究方法: 借助图象和解析式研究函数性质
与对数关系的再次巩固;引导学生回顾指数函数的研
观察图
究过程,梳理研究具体函数的思路和方法.
画具体函数
象共同
归纳性质
具体操作:
图象
特点
一、创设情景,引入新课
1
2.碳14的衰减规律:( 1 ) 5730 0.9998
斗鸡图
设计意图:通过指数与对数关系的回顾,获得指数
P=0.8385
t=1456
与对数关系的再次巩固;引导学生回顾指数函数的研
公元550年北周
究过程,梳理研究具体函数的思路和方法.
良渚古玉器
P=0.5267
对数函数及其性质 说课稿课件

y loga x的图象与y log 1 x的图象之间的关系吗?
a
设计意图:让学生观察这两个函数的特点,另辟
新径画出图象.目的在于培养学生从多方面思考
问题的能力.
底数的变化规律
..........
探索研究:
在同一坐标系中画出下列对数函数的图象;
(1)y log 2 x
y
(2)y log 1 x
人民教育出版社A版高中数学必修1第二章第二节第二小节
2.2.2 对数函数及其性质
教材分析 教学方法及手段
教学过程 板书设计 教学评价
教材分析
教学方法及手段
教学过程 板书设计 教学评价
1.教材地位、作用
《对数函数及其性质》一课是高中数学人教A版必修一 的第2课时第2节内容,它是高中阶段我们所要研究的重要的 基本初等函数之一.本节内容是在学生已经学过指数函数、 对数基础上引入的,因此既是对上述知识的拓展和延伸,也 是对函数这一重要数学思想的进一步认识与理解.本节课的 学习使学生的知识体系更加完整、系统,同时它也为学生今 后进一步学习对数方程、对数不等式等内容起到了一个铺垫 作用。
y log3 x
(3) y
log
2 3
x
y log2 x
(4)y log1 x . . . . . . . . . . .
3
o
x
y log 1 x
2
y log 1 x
3
Y
b>a>1>d>c>0
Y=logax
Y=logbx
O1
X
y logc X
规律:在第一象限内,底数越Y=logdx
大,图像按顺时针方向旋转。
对数函数说课课件

教学过程 导入新课 合作探究 分享成果 整合应用 小结作业
小结
教学过程 导入新课 合作探究 分享成果 整合应用 小结作业
作业
课后作业: (1)数学作业本 (2)预习提纲:
① 同底数的两对数如何比较大小? ② 不同底数的两对数如何比较大小?
教学课件放在教师的个人博客上,学生在家可 以直接下载继续使用和探究,在探究中出现的
教学过程 导入新课 合作探究 分享成果 整合应用 小结作业
知识整合
变式训练:
引导学生运用对 数函数图像研究
(1)如果y log2 x的值域是数学y问题y 0 ,
求x的取值;
(2)如果y log2 x的值域是 y y 1 ,
求x的取值;
借助几何画板,
(3)如果y loga x的值域作是出函y数图y 像 ,0 ,
§2.2.2 对数函数及其性质
第一课时
人民教育出版社普通高中课程标准实验教科书
数学必修1
高一年级
教
学
教
ቤተ መጻሕፍቲ ባይዱ
分
学
教
析
目
学
教
标
重
学
教
点
过
学
程
反
思
教学分析 教学目标 教学重点 教学过程 教学反思
教材的地位和作用
对数函数是函数中又一类重要的基本初等函数, 它是在学习了对数以及指数函数的基础上引入 的.是对数和函数知识的拓展与延伸,也是对函数 这一重要数学思想的进一步认识与理解.对数函 数的概念,图象与性质的学习使学生的知识体系 更加完整,系统.同时它又是解决有关自然科学领 域中实际问题的重要工具,是学生今后学习对数 方程,对数不等式的基础.
2、信息技术的使用,让本节数学概念课不再枯燥乏味,课 堂变得生动,学生学得主动.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设计意图:通过题组训练不仅培养了学生的独立意识,而且更加有效的突破了 本节课的难点,教师对学生出现的问题也有了一个深刻的认识.
六.教学评价分析
1.关注学生在整个探究过程中的表现,包括学生的投入程度, 思维水平的发展,具体体现在:
①在对数函数图象的变换过程中学生的思维发展过程,学生的概括问 题的能力; ②在对数函数性质的探究过程中,学生分析和解决问题的能力;
(1). y log2 x2 (2) y log 1 (4 x)
2
(1) log0.3 1.8和log3 2.7
(2)loga 3 .4和log a 8.5
例3 已知函数 f(x)=loga(2-ax),函数 f(x)在[0,1]上是关于 x
的减函数,求 a 的取值范围_____.
2 y log ( x 2x 5)的值域。 例4.函数 2
2.函数y log2 ( x2 5x 6)的单调增区间为 ( )
2
(1)若f(x)的定义域为R,求实数a的取值范围; (2)若f(x)的值域为R,求实数a的取值范围; (3)若函数f(x)在[-1,+∞)内有意义,求实数a的值; (4)若函数f(x)的定义域为(-∞,1)∪(3,+∞),求实数a的值.
理 解 概 念
1.复习对数函数的概念;
2.复习对数函数的图象和性质
3.练一练,判断下列哪些是对数 函数:
(1)、y 5 log2 x 5
(2)、y log2 x
2.让学生对对数函数的定 义有更深刻的理解.
(3)、y 2 log2 x
温故知新
1.画出下列三组函数的图象:
画 出 图 象
第一组: 第二组: 第三组:
利用几何画板演示作图,展示图象动态变化过程.
五.教学过程设计
复 习 性 质
6 分 钟
基 本 方 法
基 本 训 练
难 点 突 破
重 点 题 型
14 分 钟
应巩 用固 知提 识高
10 分 钟
归 纳 总 结
布 置 作 业
8 分 钟
2 分 钟
复习巩固
教学内容 设计意图
1.对数函数的一般形式, 注意真数大于零,底数取 值.
情感目标
学生在参与中感受
论的思想有进一步的
认识;体会数形结合 的数学思想;
数学,探索数学,
提高学习数学的兴 趣,增强学好数学
2.会求和对数函数
有关的函数的定义 域、值域、单调性、 图象有关问题;
2.通过例题.习题的
解决,使学生领会化 归思想在解决问题中 的作用.
的自信心.
三.课堂结构设计
1、以学生活动为主体; 2、以培养学生能力为中心; 3、以提高课堂教学质量为目标.
设计意图:通过问题的解决,可以及时检验与巩固学生对定义的理解 以及对数函数性质的简单应用情况,学生的认知也得以升华。
归纳总结
(1)归纳总结 ①对数函数及简单复合函数的图象:基本变换;
②探究性质应用:定义域、值域、单调性;
③重视函数定义域,对数函数真数大于零;
④数形结合、分类讨论、化归数学思想。
设计意图:让学生自主归纳,将本节课的知识有机的串联起来,以便有一个 系统全面的认识.培养了学生概括能力,语言表达能力,还能让学生对本节 课的知识做以简单回顾,方法以总结。
对数函数图象及其性质
一 二 三 四 五
背景分析
教学目标设计 课堂结构设计 教学媒体设计 教学过程设计 教学评价分析
六
一.背景分析
1.地位和作用
已学过对 数函数及 性质
深化对数 函数图象 和性质应 用
解决函数 综合问题
一.背景分析
2.学情分析 2.
学生对对数函 数及复合函数 一定的函数基础 定义域、值域 已有知识 、单调性、图 与技能 象应用不熟练
三.课堂结构设计
复 习 性 质
6 分 钟
基 本 方 法
基 本 训 练
难 点 突 破
重 点 题 型
14 分 钟
应巩 用固 知提 识高
10 分 钟
归 纳 总 结
布 置 作 业
8 分 钟
2 分 钟
四.教学媒体设计
媒体类型 媒体内容要点
回顾复习本节课要用到的知识 基本知识练习 课件 反馈知识 重点、难点练习 应用练习反馈内容
2.在练习中检测学生对定义的理解及对数函数性质的综合 应用情况.
设计意图:通过以上教学评价,学生的学习激情更加高涨, 老师也可以根据学生的反映情况随时调控教学.
板书设计
§2.2.2对数函数图象及其 性质应用
1.对数函数的定义
PPT 展 示 区
2.对数函数的性质
3.例题讲解
设计意图:好的板书可以让学生更加清晰准确的把握知识的要点 .
教学作用
提供事实,建立经验 创设情境,引发动机 设难置疑,引起思辨 提供事实,建立经验 展示事例,开阔视野
几何画板文件
板书
对数函数的图象随着底数a变化 而变化的过程
本节课重要概念.例题.结论
展示事例,开阔视野; 欣赏审美,陶冶情操.
提供事实,建立经验
四.教学媒体设计
利用多媒体课件展示公式概念.例题.习题和练习;
y log2 x 和 y log2 ( x)
y log3 x 和 y log ( x 1) 3
y log 1 x
2
和 y log 1 x
2
2.各组中两函数图象有什么关系? 3.总结基本函数图象变换。
设计意图:比较函数图像,熟悉变换过程。 Nhomakorabea 基本训练
例1.求下列函数的定义域和单调区间: 例2.比较下列数值的大小:
lg 6
巩固提高
2、y 1 log2 x 3、y 1 log7 (1 3 x )
题组练习1:求下列函数的定义域:
1、y log5 (1 x)
4、y log3 x
题组练习2: 求函数单调区间:
2
1.函数y log 1 (2 x2 3x 1)的递减区间为( )
2 题组练习3:对于函数f x log 1 ( x 2ax 3), 解答下列问题 :
布置作业
(2)布置作业
①必做作业:练习题第7题、8题和第9题. ②选做作业:指数函数和对数函数之间有怎样 的关系呢?试做练习题第10题。
设计意图:体现作业的巩固性和发展性原则.
需巩固提高
一.背景分析
教 学 重 点 及 难 点
教学重点
理解对数函数的定义,掌握对数函数图象和性质.
教学难点
利用对数函数的图象和性质解决有关 定义域、最值、单调性、图象等问题 .
二. 教学目标设计
知识目标
1.理解对数函数
的定义,掌握对数 函数的图象和性质;
能力目标
1.通过对底数a的讨 论,使学生对分类讨
六.教学评价分析
1.关注学生在整个探究过程中的表现,包括学生的投入程度, 思维水平的发展,具体体现在:
①在对数函数图象的变换过程中学生的思维发展过程,学生的概括问 题的能力; ②在对数函数性质的探究过程中,学生分析和解决问题的能力;
(1). y log2 x2 (2) y log 1 (4 x)
2
(1) log0.3 1.8和log3 2.7
(2)loga 3 .4和log a 8.5
例3 已知函数 f(x)=loga(2-ax),函数 f(x)在[0,1]上是关于 x
的减函数,求 a 的取值范围_____.
2 y log ( x 2x 5)的值域。 例4.函数 2
2.函数y log2 ( x2 5x 6)的单调增区间为 ( )
2
(1)若f(x)的定义域为R,求实数a的取值范围; (2)若f(x)的值域为R,求实数a的取值范围; (3)若函数f(x)在[-1,+∞)内有意义,求实数a的值; (4)若函数f(x)的定义域为(-∞,1)∪(3,+∞),求实数a的值.
理 解 概 念
1.复习对数函数的概念;
2.复习对数函数的图象和性质
3.练一练,判断下列哪些是对数 函数:
(1)、y 5 log2 x 5
(2)、y log2 x
2.让学生对对数函数的定 义有更深刻的理解.
(3)、y 2 log2 x
温故知新
1.画出下列三组函数的图象:
画 出 图 象
第一组: 第二组: 第三组:
利用几何画板演示作图,展示图象动态变化过程.
五.教学过程设计
复 习 性 质
6 分 钟
基 本 方 法
基 本 训 练
难 点 突 破
重 点 题 型
14 分 钟
应巩 用固 知提 识高
10 分 钟
归 纳 总 结
布 置 作 业
8 分 钟
2 分 钟
复习巩固
教学内容 设计意图
1.对数函数的一般形式, 注意真数大于零,底数取 值.
情感目标
学生在参与中感受
论的思想有进一步的
认识;体会数形结合 的数学思想;
数学,探索数学,
提高学习数学的兴 趣,增强学好数学
2.会求和对数函数
有关的函数的定义 域、值域、单调性、 图象有关问题;
2.通过例题.习题的
解决,使学生领会化 归思想在解决问题中 的作用.
的自信心.
三.课堂结构设计
1、以学生活动为主体; 2、以培养学生能力为中心; 3、以提高课堂教学质量为目标.
设计意图:通过问题的解决,可以及时检验与巩固学生对定义的理解 以及对数函数性质的简单应用情况,学生的认知也得以升华。
归纳总结
(1)归纳总结 ①对数函数及简单复合函数的图象:基本变换;
②探究性质应用:定义域、值域、单调性;
③重视函数定义域,对数函数真数大于零;
④数形结合、分类讨论、化归数学思想。
设计意图:让学生自主归纳,将本节课的知识有机的串联起来,以便有一个 系统全面的认识.培养了学生概括能力,语言表达能力,还能让学生对本节 课的知识做以简单回顾,方法以总结。
对数函数图象及其性质
一 二 三 四 五
背景分析
教学目标设计 课堂结构设计 教学媒体设计 教学过程设计 教学评价分析
六
一.背景分析
1.地位和作用
已学过对 数函数及 性质
深化对数 函数图象 和性质应 用
解决函数 综合问题
一.背景分析
2.学情分析 2.
学生对对数函 数及复合函数 一定的函数基础 定义域、值域 已有知识 、单调性、图 与技能 象应用不熟练
三.课堂结构设计
复 习 性 质
6 分 钟
基 本 方 法
基 本 训 练
难 点 突 破
重 点 题 型
14 分 钟
应巩 用固 知提 识高
10 分 钟
归 纳 总 结
布 置 作 业
8 分 钟
2 分 钟
四.教学媒体设计
媒体类型 媒体内容要点
回顾复习本节课要用到的知识 基本知识练习 课件 反馈知识 重点、难点练习 应用练习反馈内容
2.在练习中检测学生对定义的理解及对数函数性质的综合 应用情况.
设计意图:通过以上教学评价,学生的学习激情更加高涨, 老师也可以根据学生的反映情况随时调控教学.
板书设计
§2.2.2对数函数图象及其 性质应用
1.对数函数的定义
PPT 展 示 区
2.对数函数的性质
3.例题讲解
设计意图:好的板书可以让学生更加清晰准确的把握知识的要点 .
教学作用
提供事实,建立经验 创设情境,引发动机 设难置疑,引起思辨 提供事实,建立经验 展示事例,开阔视野
几何画板文件
板书
对数函数的图象随着底数a变化 而变化的过程
本节课重要概念.例题.结论
展示事例,开阔视野; 欣赏审美,陶冶情操.
提供事实,建立经验
四.教学媒体设计
利用多媒体课件展示公式概念.例题.习题和练习;
y log2 x 和 y log2 ( x)
y log3 x 和 y log ( x 1) 3
y log 1 x
2
和 y log 1 x
2
2.各组中两函数图象有什么关系? 3.总结基本函数图象变换。
设计意图:比较函数图像,熟悉变换过程。 Nhomakorabea 基本训练
例1.求下列函数的定义域和单调区间: 例2.比较下列数值的大小:
lg 6
巩固提高
2、y 1 log2 x 3、y 1 log7 (1 3 x )
题组练习1:求下列函数的定义域:
1、y log5 (1 x)
4、y log3 x
题组练习2: 求函数单调区间:
2
1.函数y log 1 (2 x2 3x 1)的递减区间为( )
2 题组练习3:对于函数f x log 1 ( x 2ax 3), 解答下列问题 :
布置作业
(2)布置作业
①必做作业:练习题第7题、8题和第9题. ②选做作业:指数函数和对数函数之间有怎样 的关系呢?试做练习题第10题。
设计意图:体现作业的巩固性和发展性原则.
需巩固提高
一.背景分析
教 学 重 点 及 难 点
教学重点
理解对数函数的定义,掌握对数函数图象和性质.
教学难点
利用对数函数的图象和性质解决有关 定义域、最值、单调性、图象等问题 .
二. 教学目标设计
知识目标
1.理解对数函数
的定义,掌握对数 函数的图象和性质;
能力目标
1.通过对底数a的讨 论,使学生对分类讨
