离散线性时不变系统分析
系统的时域分析 线性时不变系统的描述及特点 连续时间LTI系统的响应

y x (t ) K1e 2t K 2 e 3t
y(0)=yx(0)=K1+K2=1 y' (0)= y'x(0)= 2K13K2 =3
解得 K1= 6,K2= 5
y x (t ) 6e 2t 5e 3t , t 0
18
[例] 已知某线性时不变系统的动态方程式为: y" (t)+4y ' (t) +4y (t) = 2f ' (t )+3f(t), t>0 系统的初始状态为y(0) = 2,y'(0) = 1, 求系统的零输入响应yx(t)。 解: 系统的特征方程为 系统的特征根为
2t
Be
4t
1 y (0) A B 1 3 解得 A=5/2,B= 11/6 1 y ' (0) 2 A 4 B 2 3
5 2t 11 4t 1 t y(t ) e e e , t 0 2 6 3
12
1 t e 3
系统的几个概念:
9
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et u(t), 求系统的完全响应y(t)。
解:
(1) 求齐次方程y''(t)+6y'(t)+8y(t) = 0的齐次解yh(t)
11
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
第五章线性时不变系统的变换分析

相位失真:线性相移 一种轻微的失真 产生序列上的移位 延迟失真 (不产生波形上的变形) 近似理想滤波器设计:线性相位响应 理想模型 例:具有线性相位的理想低通滤波器
具有线性相位的理想频率选择性滤波器: 分隔输入信号频带(频率选择) 非因果 输出延迟nd 群延迟(group delay): 相位特性线性程度的一种度量 定义: 含义:对窄带输入x[n]=s[n]cos(ω0n) s[n] 为包络,ω0载波频率 即X(ejω)仅在ω= ω0附近为非零 系统的相位效果(在ω= ω0附近): 即系统的输出: 包络的延迟 相位特性导数的负值
表示H(z)的全部零点在单位圆内。 当且仅当H(z)的零点和极点都在单位圆内时。 稳定因果系统 稳定因果逆系统 定义为:最小相位系统(minimum-phase systems)
5.2.3 有理系统函数的单位脉冲响应 H(z)作z反变换(部分分式法) h[n] 一阶极点的有理系统函数:
若系统因果,可得:
例子:衰减和群延迟的效果
5.2 用线性常系数差分方程表征系统的系统函数
理想频率选择性滤波器 (近似、逼近)一类频率选择性滤波器 考虑由线性常系数差分方程表示的一类系统:
a
k 0
N
k
y[n k ] bk x[n k ]
k 0
M
对于初始松弛(initial rest)的辅助条件因果、线性、时不变 z变换 (分析、描述) 线性常系数差分方程(表示系统)的性质、特征 方程两边z变换 N M k k a z Y ( z ) b z k k X ( z)
j 1
极点:z = 0 零点:z = rejӨ 频率响应: ( z
e j )
e re H (e ) j e
离散时间系统的时域特性分析实验报告

信号、系统与信号处理实验报告实验一、离散时间系统的时域特性分析姓名:学号:班级:专业:一.实验目的线性时不变(LTI)离散时间系统在时域中可以通过常系数线性差分方程来描述,冲激响应列可以刻画时域特性。
本次实验通过使用MATLAB函数研究离散时间系统的时域特性,以加深对离散时间系统的差分方程、冲激响应和系统的线性和时不变性的理解。
二.基本原理一个离散时间系统是将输入序列变换成输出序列的一种运算。
离散时间系统中最重要、最常用的是“线性时不变系统”。
1.线性系统满足叠加原理的系统称为线性系统,即若某一输入是由N个信号的加权和组成的,则输出就是系统对这几个信号中每一个输入的响应的加权和。
即那么当且仅当系统同时满足和时,系统是线性的。
在证明一个系统是线性系统时,必须证明此系统同时满足可加性和比例性,而且信号以及任何比例系数都可以是复数。
2.时不变系统系统的运算关系在整个运算过程中不随时间(也即序列的先后)而变化,这种系统称为时不变系统(或称移不变系统)。
若输入的输出为,则将输入序列移动任意位后,其输出序列除了跟着位移外,数值应该保持不变,即则满足以上关系的系统称为时不变系统。
3.常系数线性差分方程线性时不变离散系统的输入、输出关系可用以下常系数线性差分方程描述:当输入为单位冲激序列时,输出即为系统的单位冲激响应。
当时,是有限长度的,称系统为有限长单位冲激响应(FIR)系统;反之,则称系统为无限长单位冲激响应(IIR)系统。
三.实验内容及实验结果1.实验内容考虑如下差分方程描述的两个离散时间系统:系统1:系统2:输入:(1)编程求上述两个系统的输出,并画出系统的输入与输出波形。
(2)编程求上述两个系统的冲激响应序列,并画出波形。
(3)若系统的初始状态为零,判断系统2是否为时不变的?是否为线性的?2.实验结果(1)编程求上述两个系统的输出和冲激响应序列,并画出系统的输入、输出与冲激响应波形。
clf;n=0:300;x=cos((20*pi*n)/256)+cos((200*pi*n)/256);num1=[0.5 0.27 0.77];den1=[1];num2=[0.45 0.5 0.45];den2=[1 -0.53 0.46];y1=filter(num1,den1,x);y2=filter(num2,den2,x);subplot(3,1,1);stem(n,x);xlabel('时间信号');ylabel('信号幅度');title('输入信号');subplot(3,1,2);stem(y1);xlabel('时间信号n');ylabel('信号幅度');title('输出信号');subplot(3,1,3);stem(y2);xlabel('时间序号n ');ylabel('信号幅度');title('冲激响应序列');(2)N=40;num1=[0.5 0.27 0.77];den1=[1];num2=[0.45 0.5 0.45];den2=[1 -0.53 0.46];y1=impz(num1,den1,N);y2=impz(num2,den2,N);subplot(2,1,1);stem(y1);xlabel('时间信号n ');ylabel('信号幅度');title('³冲激响应');subplot(2,1,2);stem(y2);xlabel('时间信号n ');ylabel('信号幅度');title('³冲激响应');1.应用叠加原理验证系统2是否为线性系统:clear allclcn = 0 : 1 : 299;x1 = cos(20 * pi * n / 256);x2 = cos(200 * pi * n / 256);x = x1 + x2;num = [0.45 0.5 0.45];den = [1 -0.53 0.46];y1 = filter(num, den, x1);y2 = filter(num, den, x2);y= filter(num, den, x);yt = y1 + y2;figuresubplot(2, 1, 1);stem(n, y, 'g');xlabel('时间信号n');ylabel('信号幅度');axis([0 100 -2 2]);grid;subplot(2, 1, 2);stem(n, yt, 'r');xlabel('时间信号n');ylabel('信号幅度');axis([0 100 -2 2]);grid;2.应用时延差值来判断系统2是否为时不变系统。
随机序列通过离散线性系统分析_-两种分析方法
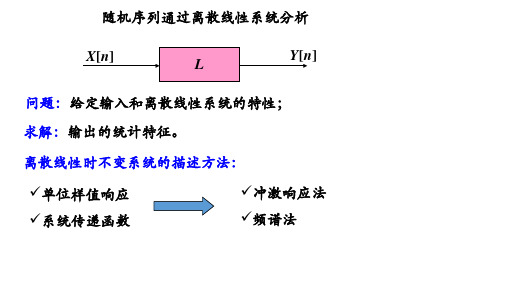
问题:给定输入和离散线性系统的特性;求解:输出的统计特征。
✓冲激响应法✓频谱法]离散线性时不变系统的描述方法:✓单位样值响应✓系统传递函数⏹冲激响应法⏹频谱法⏹常用时间序列模型][][][][][]k Y n h k X n k h n X n +∞=−∞=−=∗∑系统输出:均值:[]([])([()])[][]Y X m n E Y n E L X n h n m n ===∗X m []Y n[,][][][,]121212Y X R n n h n h n R n n =∗∗[,]([][])[][,]1212212XY X R n n E X n Y n h n R n n ==∗相关函数:][][][][][]k Y n h k X n k h n X n +∞=−∞=−=∗∑系统输出:[][][]XY X R m h m R m =−∗[][][][]Y X R m h m h m R m =−∗∗[]()0Y X X k m m h k m H +∞=−∞=∑若X [n ]平稳:则输出平稳,而且输入输出联合平稳2. 频谱法若X [n ]平稳:2()()()|()|()Y XY X G H G H G ωωωωω==*()()()XY X G H G ωωω=1()()()XY X G z H z G z −=1()()()()()()Y XY X G z H z G z H z H z G z −==若用z 变换表示:则输出平稳,而且输入输出联合平稳只适用于平稳随机序列的分析例1:一个平稳随机序列X[n]的自相关函数为,线性系统的单位样值响应是, 求输出Y(n)的自相关函数及功率谱密度。
2[]m σδ[],nh n r =0,||1n r ≥<[][][][]Y X R m h m h m R m =−∗∗2[][]h m h m =−∗σ222201mm k k r r r r ∞==−∑σσ[解]20k m kk r r ∞+=⋅∑σ当m ≧0时,例1:一个平稳随机序列X[n]的自相关函数为,线性系统的单位样值响应是, 求输出Y(n)的自相关函数及功率谱密度。
信号分析与处理第5章 离散时间线性时不变系统的分析

yzs (n) 3yzs (n 1) 2 yzs (n 2) x(n)
对于因果系统,有 yzs (i) 0 i 0 ,因此,
y(i) yzi (i)
i0
y(i) yzi (i) yzs (i) i 0
求 N 阶差分方程,需用到 N 个初始条件。求零输
入响应的 N 个初始条件为 yzi (i) i 1,2, , N ;求零状态
响应的 N 个初始条件为 yzs (i) i 0,1, , N -1 ;求全响应的 N
5.3 离散时间线性时不变系统的 Z 域分析
5.3.1 Z 变换解差分方程 5.3.2 系统函数 5.3.3 由系统函数的零极点分布确定时域特性 5.3.4 系统的因果性和稳定性
5.4 离散时间线性时不变系统的频域分析
5.4.1 系统的频率特性 5.4.2 离时间信号通过系统的频域分析 5.4.3 理想低通数字滤波器
yzi (n) Czi1 (1)n Czi2 (2)n
n 0
代入初始条件
yzi
(1)
y(1)
0,
yzi
(2)
y(2)
1 2
,有
yzi (1)
Czi1
1 2 Czi2
0
yzi (2)
Czi1
1 4
Czi
2
1 2
解得 Czi1 1, Czi2 2。故系统的零输入响应为
个初始条件为 y(i) i 0,1, , N -1。
2、离散时间线性时不变系统响应的迭代求解
差分方程可用迭代法求解。差分方程可改写为
离散系统的时域分析法

第五章离散系统的时域分析法目录5.1 引言5.2 离散时间信号5.3 离散系统的数学模型-差分方程 5.4 线性常系数差分方程的求解5.5 单位样值响应5.6 卷积和§5.1引言连续时间信号、连续时间系统连续时间信号:f(t)是连续变化的t的函数,除若干不连续点之外对于任意时间值都可以给出确定的函数值。
函数的波形都是具有平滑曲线的形状,一般也称模拟信号。
模拟信号抽样信号量化信号连续时间系统:系统的输入、输出都是连续的时间信号。
离散时间信号、离散时间系统离散时间信号:时间变量是离散的,函数只在某些规定的时刻有确定的值,在其他时间没有定义。
离散时间系统:系统的输入、输出都是离散的时间信号。
如数字计算机。
o k t ()k t f 2t 1−t 1t 3t 2−t 离散信号可以由模拟信号抽样而得,也可以由实际系统生成。
量化幅值量化——幅值只能分级变化。
采样过程就是对模拟信号的时间取离散的量化值过程——得到离散信号。
数字信号:离散信号在各离散点的幅值被量化的信号。
ot ()t f T T 2T 31.32.45.19.0o T T 2T 3()t f q t3421离散时间系统的优点•便于实现大规模集成,从而在重量和体积方面显示其优越性;•容易作到精度高,模拟元件精度低,而数字系统的精度取决于位数;•可靠性好;•存储器的合理运用使系统具有灵活的功能;•易消除噪声干扰;•数字系统容易利用可编程技术,借助于软件控制,大大改善了系统的灵活性和通用性;•易处理速率很低的信号。
离散时间系统的困难和缺点高速时实现困难,设备复杂,成本高,通信系统由模拟转化为数字要牺牲带宽。
应用前景由于数字系统的优点,使许多模拟系统逐步被淘汰,被数字(更多是模/数混合)系统所代替;人们提出了“数字地球”、“数字化世界”、“数字化生存”等概念,数字化技术逐步渗透到人类工作与生活的每个角落。
数字信号处理技术正在使人类生产和生活质量提高到前所未有的新境界。
第2章 线性时不变系统

0 t
2.4 LTI系统的性质
举例:累加系统(accumulator)
y[n]
k
x[k ]
n
它是LTI系统,其单位脉冲响应为
h[n] u[n]
h[n] k [n] Memory h[n] 0, n 0 Causal
2.4 LTI系统的性质
从以上推导得出以下结论: DT LTI 系统的单位阶跃响应是其单位脉冲响应的求和函数; DT LTI 系统的单位脉冲响应是其单位阶跃响应的一次差分 同理,对于CT LTI 系统: 单位阶跃响应是其单位冲激响应的积分函数
s(t ) h( )d
t
单位冲激响应是其单位阶跃响应的一阶导数
2.7小结
2.1概述
(1)线性与时不变性(Linearity and Time-Invariance): 很多物理过程都具有这两个性质 这些物理过程能用LTI系统表征 可以对LTI系统进行详细的分析:
能够将LTI系统的输入用一组基本信号的线性组合表示 根据该系统对基本信号的响应,利用叠加性质求得整个系统的输出
2.4 LTI系统的性质
离散时间LTI系统用 卷积和表示
连续时间LTI系统用 卷积积分表示
LTI系统的特性可以 完全由其单位冲激响 应决定
2.4 LTI系统的性质
卷积的交换律性质 The Commutative Property of Convolution
2.4 LTI系统的性质
卷积的三个代数性质:交换律、结合律、分配律 Three algebraic properties of convolution
第二章 线性时不变系统

9
例5 y[n] 6,5,24,13,22,10,n 0,1,2,3,4,5 h[n] 3,1,4,2 n 0,1,2,3
y[n] x[n]h[n] 求 x[n]
2 t 5t2 x(t)
x[n] x[k] [n k] 离散的信号分解成脉冲
k
信号的 线性组合的形式
把任意一个序列表示成一串移位的单位脉冲序列 [n k]
的线性组合,而这个线性组合式中的权因子就是 x[k]
4
二. 离散时间线性时不变系统卷积和表示
[n] h[n]
[n k] h[n k]
时不变
x[k] [n k] x[k]h[n k] 齐次性
11
二. 连续时间线性时不变系统的卷积积分表示
(t) h (t)
(t k)
x(k) (t k)
x(k) (t k)
k
h (t k)
时不变
x(k
)h
(t
k
)
齐次性
x(k)h (t k) 可加性
k
xˆ(t)
yˆ (t )
y(t) x( )h(t )d x(t) h(t)
12
卷积的计算
(1)由定义计算卷积积分
例:设某一线性时不变系统的输入为x(t),其单位冲
激响应为h(t) x(t) eatu(t) , a 0 h(t) u(t)
试求 x(t) h(t)
x(t) h(t) ea u( )u(t )d
t ea d ,
0
t0
0,
t0
1 1 eat u(t) a
1
如何分析判断系统是否为稳定系统、因果系统、线性系统?

如何分析判断系统是否为稳定系统、因果系统、线性
系统?
如何判断一个系统是否为线性系统,时不变系统以及稳定系统?
先线性运算再经过系统=先经过系统再线性运算是线性系统;
先时移再经过系统=先经过系统再时移为时不变系统;
时间趋于无穷大时系统值有界则为稳定的系统,或者对连续系统S 域变换,离散系统Z域变换,H(s)极点均在左半平面则稳定,H(z)极点均在单位圆内部则稳定;
一般的常微分差分方程都是LTI,输入输出有关于t的尺度变换则时变,微分差分方程的系数为关于时间t的函数也时变。
怎幺判断出系统是因果系统还是非因果系统的?。
6.离散时间信号与系统的时域分析

0, n 1 1 z ( n) x ( n) y ( n) , n 1 2 1 n 1 ( 2 )( n 1)( 2 ) , n 0
6 线性时不变离散系统的时域分析
5. 累加 设某一序列为x(n),则x(n)的累加序列 y(n)定义为
y ( n)
k
x(k ) x(n) * u(n)
n
根据上述性质可以推得以下结论:
f (n n1 ) * (n n2 ) f (n n1 n2 )
6 线性时不变离散系统的时域分析
例 已知 x1 (n) (n) 3 (n 1) 2 (n 2) x2 (n) u(n) u(n 3) 试求信号 x (n) ,它满足 x(n) x1 (n) x2 (n) 解:可利用上面讲述的性质求解。
1 1/ 2 1/4 -2 -1 0 1 1/8 ... 2
n
x(-n) 1 1/2 1/8 1/4 ... -2 -1 0
1
2
n
6 线性时不变离散系统的时域分析
3.序列的加减 两序列的加、减是指同序号(n)的序列值逐项对 应相加得一新序列。
6 线性时不变离散系统的时域分析
例:
x(n) 1 1/2 1/4 -2 -1 0 y(n) 2 1 1/4 1/2 1 2 n …
6 线性时不变离散系统的时域分析
2.单位阶跃序列
u(n)
1, u ( n) 0,
n0 n0
u(n)
...
-1 0 1 2 3 n
(n) u (n) u (n) u (n 1)
m 0
u (n) (n m) (n) (n 1) (n 2)
信号处理与系统分析 第2章线性时不变系统

从波形的角度来观察离散时间信号,它可以 看成是由许多加权了的单位冲激信号组合 而成的
x[n] x[1] [n 1] x[0] [n] x[2] [n 2]
对于任意的离散时间信号:
累加序号 自变量
加权值 移位的冲激信号
x[n]
k
x[k ] [n k ]
n
卷积公式是无穷多项求和,而我们实际遇到的常 常是有限长度序列,特别是在计算机离线处理的场 合,因为计算机不可能处理无穷多的信息。 在进行有限长度的序列的卷积时候,长度为N和M 的2个序列作卷积时,反转序列从左到右进入重叠 直至移出重叠,只有存在重叠项时,卷积和才可能 非零。 卷积序列的长度为M+N-1。
求解系统响应的卷积方法是系统分析的重要工具。
单位冲激响应h[n]完全描述了线性时不变系统的变换 规律。不同的系统输入,都在h[n]的作用下产生相应的 响应,因此,给定了一个LTI系统的单位冲激响应h[n]就 等于给定了该系统。
从计算某一个特定点的角度来看
yy [n [n 0]
k k
第2章 线性时不变系统
线性时不变(简称LTI,Linear, Time-invariant)系统
为什么引入LTI ?
如果不对系统的性质加以限制,那么分析 一个系统将是十分困难的。 给系统加上线性和时不变性的限制,那么 系统的分析将变得十分简便。 LTI系统的分析还为非线性系统的分析方法 提供了思路。例如,线性时不变系统可以 用冲激响应来表达,非线性系统可以用 Volterra级数来表达。
上式应该理解为许多以为n自变量的函数的相 加,而不是数值相加。
许多移了位的冲激信号的加权和,构成了x[n] 。
特别地,我们有
数字信号处理讲义线性时不变系统的变换分析

第5章线性时不变系统的变换分析[教学目的]1.了解LTI 系统频率响应的概念;2.掌握线性常系数差分方程所表征系数的系统函数的方法;3.掌握有理系统频率响应分析方法4.理解线性相位系统、广义线性相位系统与因果广义线性相位系统的概念,几类线性相位系统。
[教学重点与难点]重点:1.线性常系数差分方程所表征系数的系统函数的方法;2.有理系统频率响应分析方法;3.几类线性相位系统。
难点:1. 有理系统频率响应分析方法几类线性相位系统5.1 LTI 系统的频率响应前面已经讨论过,在时域中,一个线性时不变系统完全可以由它的单位脉冲响应h (n )来表示。
对于一个给定的输入x (n ),其输出y (n )为对等式两端取Z 变换,得则 (5-1)两边做离散傅立叶变换有:|Y (e j ω)|=|H (e j ω)|·|X (e j ω)| (5-2)|Y (e j ω)|=|H (e j ω)|·|X (e j ω)|arg [Y (e j ω)]=arg [H (e j ω)]+arg [X (e j ω)]|H (e j ω)| 幅度响应 : 增益/幅频特性调整输入信号各频率分量的相对强度(幅度)关系Arg[H (e j ω)] 频率响应的相位响应 : 相移/相频特性调整输入信号各频率分量的相对位置(相位)关系H (e j ω) 调整输入信号各频率分量的相对大小(幅度)及位置(相∑∞-∞=-=*=m m n h m x n h n x n y )()()()()()()()(z X z H z Y =)()()(z X z Y z H =位)关系5.1.1理想低通滤波器的选择性5.1.2相位失真与延时线性相位 : 不会改变信号的相对位置,时延相同线性相位的效应 : 时延 非线性相位:改变信号的相对位置时延不相同⎩⎨⎧≤<≤=πωωωωω||,0||,1)(c c j H n n n h c F πωsin ][=−→←()()|()|j H j H j H j eωωω=0 : ()near Phase H j t ωω=-0()H j t ωω≠-5.2 用线性常系数差分方程所表征系统的系统函数一个线性时不变系统也可以用常系数线性差分方程来表示,其N 阶常系数线性差分方程的一般形式为若系统起始状态为零,这样就可以直接对上式两端取Z 变换,利用Z 变换的线性特性和移位特性可得这样就得到系统函数为(5-3)由此看出系统函数分子、分母多项式的系数分别就是差分方程的系数。
信号与系统PPT 第六章 离散时域分析

例:求z(n)=x(n)·y(n)
解:
z(0)=x(0)·y(0) z(1)=x(1)·y(1) z(2)=x(2)·y(2)
…
例:当 m =3时
例:
5、序列的差分运算:一个序列与一个移位序列之差。
一阶前向差分: x[n] x[n 1] x[n] 一阶后向差分: x[n] x[n] x[n 1]
[n]
1
0
t
t
u(t) ( )d ------ 积分关系
u[n]
1
...
-2 -1 0 1 2 3 n
-2 -1 0 1 2 3 n
[n] u[n]u[n 1] ------ 差分关系
u[n] [n][n 1][n 2] [n m] ------ 求和关系 m0
(3)矩形序列
x(m)和h(m)如图所示
x(m) 3/2
1 1/2
0123
m
h(m) 1
01 2
m
h(0-m) 1 n=0反褶
-2 -1 0
m
h(-1-m) 1 n=-1左移
-3 -2 -1 0
m
反褶 .以m=0为对称轴, 折叠h(m) 得到h(0-m)
可见, 当n<1时,x(m)与 h(n-m)无交叠,相乘处 处为 零,即y(n)=0,n<1
若有两个序列 x1n和x2 n,定义和式
x1k x2n k
k
为x1n和x2 n的卷积和,记作1n x2 n
(2)计算方法: 离散线性卷积的计算:图解法、解析法,对位相乘法
•图解法
卷积和的图解过程:换元 反褶 平移 相乘 取和
h[-m]、 h[n-m]、x[m] h[n-m]、 x[m]h[n m] m
实验四线性时不变离散时间系统的频域分析

实验四线性时不变离散时间系统的频域分析一、引言离散时间系统是指输入和输出都以离散的时间点进行采样的系统。
频域分析是通过将时域信号转换到频域来研究系统的特性和性能的一种方法。
实验四旨在通过频域分析方法研究线性时不变离散时间系统的特性。
二、理论分析线性时不变离散时间系统的输入输出关系可以表示为:y[n]=H(e^(jω))*x[n]其中,H(e^(jω))表示系统的频率响应,是输入和输出的傅里叶变换之比。
线性时不变离散时间系统的频率响应可以通过离散傅里叶变换(DFT)来求得。
DFT是时域序列经过离散采样后进行离散傅里叶变换得到频域表示的方法。
DFT的定义如下:X(k) = Σ[x(n)e^(-j2πkn/N)]其中,x(n)为时域序列,X(k)为频域序列,N为采样点数。
通过DFT可以将时域序列转换为频域序列,从而得到系统的频谱特性,包括幅度和相位。
三、实验步骤1.准备实验设备和软件:计算机、MATLAB软件。
2.设置实验输入信号:生成离散时间序列x[n]。
3.进行离散傅里叶变换:使用MATLAB软件进行离散傅里叶变换,得到频域序列X(k)。
4.计算幅度谱和相位谱:根据频域序列X(k)计算幅度谱和相位谱。
5.绘制频谱图:根据幅度谱和相位谱绘制频谱图。
6.分析系统特性:根据频谱图分析系统的频率响应特性。
四、实验注意事项1.在进行离散傅里叶变换时,注意采样点数N的选择,一般应满足N>2L,其中L为时域信号的长度。
2.在绘制频谱图时,注意选择适当的频率范围,以便观察频域特性。
五、实验结果分析实验通过离散傅里叶变换将时域信号转换为频域信号,得到了系统的频谱特性。
根据频谱图可以分析系统的频率响应,包括系统的幅度响应和相位响应。
六、实验总结通过实验四的实验,我们学习了线性时不变离散时间系统的频域分析方法。
通过离散傅里叶变换,我们可以将时域序列转换为频域序列,从而得到系统的频谱特性。
通过分析频谱图,我们可以了解系统的幅度响应和相位响应,进一步了解系统的特性和性能。
离散系统的时域分析实验报告

实验2 离散系统的时域分析一、实验目的1、熟悉并掌握离散系统的差分方程表示法;2、加深对冲激响应和卷积分析方法的理解。
二、实验原理在时域中,离散时间系统对输入信号或者延迟信号进行运算处理,生成具有所需特性的输出信号,具体框图如下:其输入、输出关系可用以下差分方程描述:输入信号分解为冲激信号,记系统单位冲激响应,则系统响应为如下的卷积计算式:当时,h[n]是有限长度的(),称系统为FIR系统;反之,称系统为IIR系统。
三、实验内容1、用MATLAB求系统响应1)卷积的实现线性移不变系统可由它的单位脉冲响应来表征。
若已知了单位脉冲响应和系统激励就可通过卷积运算来求取系统响应,即程序:x=input(‘Type in the input sequence=’); %输入xh=input(‘Type in the impulse response sequence=’); %输入hy=conv(x,h); % 对x,h进行卷积N=length(y)-1; %求出N的值n=0:1:N; %n从0开始,间隔为1的取值取到N为止disp(‘output sequence=’); disp(y); %输出ystem(n,y); %画出n为横轴,y为纵轴的离散图xlabel(‘Time index n’); ylable(‘Amplitude’); % 规定x轴y 轴的标签输入为:x=[-2 0 1 -1 3]h=[1 2 0 -1]图形:2)单位脉冲响应的求取线性时不变因果系统可用MATLAB的函数filter来仿真y=filter(b,a,x);其中,x和y是长度相等的两个矢量。
矢量x表示激励,矢量a,b 表示系统函数形式滤波器的分子和分母系数,得到的响应为矢量y。
例如计算以下系统的单位脉冲响应y(n)+0.7y(n-1)-0.45y(y-2)-0.6y(y-3)=0.8x(n)-0.44x(n-1)+0.36x(n-2)+0.02x(n-3)程序:N=input(‘Desired impuse response length=’);b=input(‘Type in the vector b=’);a=input(‘Type in the vector a=’);x=[1 zeros(1,N-1)];y=filter(b,a,x);k=0:1:N-1;stem(k,y);xlabel(’Time index n’); ylable(‘Amplitude’);输入:N=41b=[0.8 -0.44 0.36 0.02]a=[1 0.7 -0.45 -0.6]图形:2、以下程序中分别使用conv和filter函数计算h和x的卷积y和y1,运行程序,并分析y和y1是否有差别,为什么要使用x[n]补零后的x1来产生y1;具体分析当h[n]有i个值,x[n]有j个值,使用filter完成卷积功能,需要如何补零?程序:clf;h = [3 2 1 -2 1 0 -4 0 3]; %impulse responsex = [1 -2 3 -4 3 2 1]; %input sequencey = conv(h,x);n = 0:14;subplot(2,1,1);stem(n,y);xlabel('Time index n'); ylabel('Amplitude');title('Output Obtained by Convolution'); grid;x1 = [x zeros(1,8)];y1 = filter(h,1,x1);subplot(2,1,2);stem(n,y1);xlabel('Time index n'); ylabel('Amplitude');title('Output Generated by Filtering'); grid;图形:因为在y=filter(b,a,x)中,利用给定矢量a和b对x中的数据进行滤波,结果放入y矢量中,y与x长度要相等,所以要使用x[n]补零后的x1来产生y1。
信号与系统matlab实验线性时不变系统的时域分析(最新整理)

答案
1. x n hn u n u n 4 ;
nx=0:9;x=ones(1,length(nx)); nh=0:4;h=ones(1,length(nh)); y=conv(x,h); % 下限=下限1+下限2 ny_min=min(nx)+min(nh); % 上限=上限1+上限2 ny_max=max(nx)+max(nh); ny=ny_min:ny_max; subplot(3,1,1);stem(nx,x); xlabel('n');ylabel('x(n)');axis([ny_min ny_max 0 max(x)]); subplot(3,1,2);stem(nh,h); xlabel('n');ylabel('h(n)');axis([ny_min ny_max 0 max(h)]); subplot(3,1,3);stem(ny,y); xlabel('n');ylabel('x(n)*h(n)');axis([ny_min ny_max 0 max(y)]);
到连续卷积的数值近似,具体算法如下:
y=conv(x,h)*dt
% dt 为近似矩形脉冲的宽度即抽样间隔
例 2-2:采用不同的抽样间隔 值,用分段常数函数近似 x t u t u t 1 与
h t sin t u t u t π 的 卷 积 , 并 与 卷 积 的 解 析 表 达 式
x(t)
h(t)
1 0.5
0 0 0.5 1 1.5 2 2.5 3 3.5 t
1 0.5
0 0 0.5 1 1.5 2 2.5 3 3.5 t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六 离散线性时不变系统分析
一、 实验目的
1. 掌握离散LSI 系统的单位序列响应、单位阶跃响应和任意激励下响应的MATLAB 求解方法。
2. 掌握离散LSI 系统的频域分析方法;
3. 掌握离散LSI 系统的复频域分析方法;
4. 掌握离散LSI 系统的零极点分布与系统特性的关系。
二、实验原理及方法
1. 离散LSI 系统的时域分析
描述一个N 阶线性时不变离散时间系统的数学模型是线性常系统差分方程,N 阶LSI 离散系统的差分方程一般形式为
)
()(0
0i n x b k n y a M
i i N k k -=-∑∑== (6.1) 也可用系统函数来表示
12001212120()()()()()1M i M i i M N N
k N k
k b z b b z b z b z Y z b z H z X z a z a z a z a z a z ----=----=++++====++++∑∑ (6.2) 系统函数()H z 反映了系统响应和激励间的关系。
一旦上式中k a ,i b 的数据确定了,系统的性质也就确定了。
特别注意0a 必须进行归一化处理,即01a =。
对于复杂信号激励下的线性系统,可以将激励信号在时域中分解为单位序列或单位阶跃序列的线性叠加,把这些单元激励信号分别加于系统求其响应,然后把这些响应叠加,即可得到复杂信号作用于系统的零状态响应。
因此,求解系统的单位序列响应和单位阶跃响应尤为重要。
由图6-1可以看出一个离散LSI 系统响应与激励的关系。
图6-1 离散LSI 系统响应与激励的关系
(1) 单位序列响应(单位响应)
单位响应()h n 是指离散LSI 系统在单位序列()n δ激励下的零状态响应,因此()h n 满足线性常系数差分方程(6.1)及零初始状态,即
00()()N M
k i
k i a h n k b n i δ==-=-∑∑, (1)(2)0h h -=-== (6.3)
按照定义,它也可表示为
()()()h n h n n δ=* (6.4)
对于离散LSI 系统,若其输入信号为()x n ,单位响应为()h n ,则其零状态响应()zs y n 为
()()*()zs
y n x n h n = (6.5)
可见,()h n 能够刻画和表征系统的固有特性,与何种激励无关。
一旦知道了系统的单位响应()h n ,就可求得系统对任何输入信号()x n 所产生的零状态响应()zs
y n 。
MATLAB 提供了专门用于求连续系统冲激响应的函数impz(),其调用格式有
[h,n]=impz(b,a)
求解离散系统的单位响应,其中012[,,,,]M b b b b b =,12[1,,,,]N a a a a =,[0,1,2,]n '=;
[h,n]=impz(b,a,N)
求解离散系统的单位响应,采样点数由N 确定,[0,1,2,,N-1]n '=; impz(b,a) :在当前窗口,用stem(n,h)绘出图形。
(2)单位阶跃响应
单位阶跃响应()s n 是指离散LTI 系统在单位阶跃序列()u n 激励下的零状态响应,它可以表示为
()()()()n
m s n u n h n h m =-∞=*=
∑ (6.6)
上式表明,离散LSI 系统的单位阶跃响应是单位响应的累加和,系统的单位阶跃响应和系统的单位响应之间有着确定的关系,因此,单位阶跃响应也能完全刻画和表征一个LSI 系统。
MATLAB 提供了专门用于求离散系统单位阶跃响应的函数stepz( ),其调用格式有
[s,n]=stepz(b,a) :求解离散系统的单位阶跃响应,其中012[,,,,]M b b b b b =,
12[1,,,,]N a a a a =,[0,1,2,]n '=;
[s,n]=stepz(b,a,N) :求解离散系统的单位阶跃响应,采样点数由N 确定,[0,1,2,,N-1]n '=;
stepz(b,a) :在当前窗口,用stem(n,s)绘出图形。
(3) 任意激励下的零状态响应
已经知道,离散LSI 系统可用常系数线性差分方程(6.1)式来描述,Matlab 提供的函数dlsim( )能对上述差分方程描述的离散LSI 系统的响应进行仿真,该函数不仅能绘制指定时间范围内的系统响应波形图,而且还能求出系统响应的数值解。
其调用格式有
dlsim(b,a, x) :求解输入序列为x 的零状态响应
需要特别强调的是,Matlab 总是把由分子和分母多项式表示的任何系统都当作是因果系统。
所以,利用impz (b,a),stepz(b,a),d lsim(b,a,x)函数求得的响应总是因果信号。
同时,卷积和也是LSI 系统求解零状态响应的重要工具之一。
假设系统的输入信号为()x n ,单位响应为()h n ,则系统的零状态响应()zs y n 可由(6.5)式求解。
Matlab 提供了专门用于求离散系统卷积和的函数conv( ),其调用格式有
y=conv(x,h) :求解序列x ,h 的卷积和,若序列x 的长度为n1,序列h 的长度为n2,卷积和y 的长度为n1+n2-1。
这一点需要特别注意,否则,作图时容易造成横纵坐标长度不匹配。
(4)带初始状态的任意激励下的全响应
任意激励下的离散LSI 系统的全响应为零输入响应和零状态响应之和,表示为
()()()zi zs y n y n y n =+ (6.7)
在理论学习的过程中,同学们对低阶差分方程的求解已颇为头痛,高阶差分方程直接求解几乎不可能。
Matlab 提供了用于求离散系统全响应的函数filter( ),其调用格式有
y=filter( b,a,x) :求解零状态响应;
y=filter( b,a,x,zi) :求解初始条件为zi 的系统的全响应,zi 向量的长度为max(length(a),length(b))-1,返回值为系统的全响应。
z = filtic(b,a,y,x):将初始状态转换为初始条件,其中[(1),(2),(x x x x x m =----,[(1),(2),(3),,()]y y y y y n =----;
z = filtic(b,a,y):将初始状态转换为初始条件,其中0x =,[(1),(2),(3),,()]y y y y y n =----。
2 离散LSI 系统的复频域(Z 域)分析
(1)利用Z 变换解差分方程
在前面图6-1中表示了离散系统的响应与激励的关系,由图可知,系统的响应既可以用时域的方法求解,也可以用Z 域的方法求解。
当已知系统输入序列的Z 变换()X z ,系统函数()H z 时,系统响应序列的Z 变换可由()()()Y z X z H z =求出。
Matlab 提供了用于求序列Z 变换和Z 反变换的函数,其调用格式有
X=ztrans(x):求无限长序列x 的Z 变换,返回Z 变换的表达式,注意这里x ,X 都是符号表达式;
x=iztrans(X):求X (z )的Z 反变换x(n),返回Z 反变换的表达式,注意这里x ,X 都是符号表达式;
[r,p,c]=residuez(b,a):把b(z)/a(z)展开成部分分式;
[b,a]=residuez(r,p,c):根据部分分式的r 、p 、c 数组,返回有理多项式。
(2)系统的零极点分布与系统因果性和稳定性的关系
因果系统的单位响应)(n h 一定满足当0<n 时,)(n h =0,那么其系统函数)(z H 的收敛域一定包含∞点,即∞点不是极点,极点分布在某个圆的圆内,收敛域是圆外区域。
系统稳定要求 ∞
<∑∞
-∞=n n h |)(| ,对照z 变换定义,系统稳定要求收敛域包含单位圆。
如果系统因果且稳定,收敛域包含∞点和单位圆,那么收敛域可表示为:
10,||<<∞≤<r z r (6.8)
MATLAB 提供了用于求系统零极点的函数,其调用格式有
roots():利用多项式求根函数来确定系统函数的零极点位置;
roots(a):求极点位置,a 为系统函数)(z H 分母多项式所构成的系数向量;
roots(b):求零点位置,b 为系统函数)(z H 分子多项式所构成的系数向量;
zplane(b,a):绘制由行向量b 和a 构成的系统函数的零极点分布图;
zplane(z,p):绘制由列向量z 确定的零点、列向量p 确定的极点构成的零极点分布图。
(3)系统的零极点分布与系统频率响应的关系
将式(6.2)因式分解,得到
∏∏=-=---=N k k M
m
m z d z c A z H 1111)
1()
1()( (6.9) 式中,00a b A =,m c 是)(z H 的零点,k d 是其极点。
A 参数影响频率响应的幅度大小,
影响系统特性的是零点m c 和极点k
d 的分布。
下面采用几何方法研究系统零极点分布对系统频率特性的影响。
将式(6.9)的分子、分母同乘以M N z +,得到:。
