123相反数
1.2.3 相反数 课件(共12张PPT)人教版七年级上册

解:
A52
5
B2
0
这两个点表示的数分别是 5 和 5 .
22
课堂小结
回顾本节课所学内容,请回答以下问题: (1) 什么是相反数? (2) 在数轴上,互为相反数的两个数所表示的点有什 么 特点?
相反数
只有符号不同的 两个数互为相反数
与原点距离相等
-2 与 +2
-2 -1 0 1 2
数
数形结合
形
课后任务
例题精讲
例
1
(1)分别写出-7
和
4 3
的相反数;
(2)a 的相反数是 2.4,写出 a 的值.
4
4
解:(1)-7
的相反数是
7, 3
的相反数是 3
,
(2)因为 2.4 与-2.4 互为相反数,
所以 a 的值是-2.4.
例 2 在数轴上,如果点 A,B 分别表示互为相反的数分别是多少?
-a
a
-3 -2 -1 0 1 2 3
11 像 3 和-3, 2 和- 2 这样只有符号不同的两个数, 互为相反数. 0 的相反数是 0.
这里的“互为”如何理解呢? 这就是说,3 的相反数是-3,-3 的相反数是 3,3 与 -3 互为相反数.
11 像 3 和-3, 2 和- 2 这样只有符号不同的两个数, 互为相反数. 0 的相反数是 0.
1 2
的点有几个
?这些点分
别表示什么数? 这两个数之间有什么关系?
1 1 22
-5 -4 -3 -2 -1 0 1 2 3 4 5
数轴上与原点的距离是
1 2
的点有两个,这两个点所表
示的数是+ 1 和 - 1 . 这两个数只有符号不同.
七年级上册123相反数教学设计与反思

1.2.3相反数教学内容:七年级上册第9页—10页教学目标:1.知识与技能:借助数轴理解相反数的概念,会求一个数的相反数,会用相反数的定义进行化简。
2.过程与方法:培养学生分类讨论和数形结合的思想,提高观察、归纳与概括的能力。
3.情感态度价值观:培养学生初步感受数学文化的教育价值,认识对立统一的规律。
教学重点、难点:重点:了解相反数的意义。
难点:多重符号的化简。
教学过程:一、创设情境,导入新课师生互动:师要求二个学生在讲为课桌前背靠背站好(分左右),听教师口令“向前2步走”。
师:规定向右为正(正号可以省略),向右走2步,向左走2步各记作什么?生:向右走2步记作2步;向左走2步记作-2步。
师:规定两个同学未走时的点为原点,用上一节课学的数轴将上述问题情境中的2和-2表示出来。
生:画数轴,在数轴上标出表示2和-2的点。
师:展示下图并问:从数轴上观察,这两位同学各走的距离都是2步,但方向相反,可用2和-2表示,这两个数具有哪些意义?生1:2和-2这两个数具有相反意义。
师:回答很好。
还这其他说法吗?生2:2和-2的数字相同(都是2),但性质符号不同。
生3:2和-2这两个数表示距原点都是两个单位(距离相等)。
师:在代数中,把具有上述特点的两个数称为互为相反数,今天我们就来学习相反数的概念。
师板书课题:1.2.3相反数二、启发思考,学习新课1.互为相反数的概念的引出师:板书画一数轴,请学生观察、讨论并回答:⑴在数轴上分别与1,-3,5到原点距离相等的点是哪些?⑵在数轴上与原点距离都为1,3,5的点有几个?⑶利用数轴说出与原点距离相等的点的两个数的位置特征和符号特征。
生:利用已画出数轴,先描点,然后观察、讨论上述问题。
师:巡视学生学习情况并及时对个别学生进行辅导。
师:抽学生回答上述两个问题。
生1:在数轴上与1,-3 ,5到原点距离相等的点分别是-1,3,-5。
师板书并在数轴上标出到原点与1,-3 ,5距离相等的点。
人教版七年级数学上册《1.2.3相反数》教案

举例:强调+3的相反数是-3,-3的相反数是+3;讲解0的相反数仍然是0,这是重点知识,需要学生深刻理解。
2.教学难点
-理解负数的相反数:对于负数的相反数理解可能会有困难,如-(-3)的理解,需要学生理解负号的去括号法则。
-相反数的运算:在相反数的加减运算中,学生可能会混淆运算规则,如不知道如何处理两个相反数相加或相减的情况。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“相反数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考,如“相反数在解决什么类型的问题时特别有用?”
学生小组讨论的部分,总体来说进行得不错。学生们能够围绕相反数的实际应用提出自己的见解,但在分享成果时,我发现有些小组的表达不够清晰,逻辑性有待提高。在未来的教学中,我需要更多地关注学生表达能力的培养,让他们学会如何条理清晰地表达自己的思考。
总的来说,今天的课堂让我看到了学生的进步,但也发现了不少需要改进的地方。在接下来的教学中,我会根据今天的教学反思,调整教学方法,尽量让每个学生都能更好地理解和掌握相反数的概念和运算。同时,我也会继续关注学生的学习反馈,及时调整教学策略,以提高教学效果。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了相反数的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对相反数的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
123相反数

象这样只有符号不同的两个数叫做 互为相反数 (opposite number)
互为相反数.即 是 如9 和- 9 互为相反数 即 9是- 9 的相反数. 是 的相反数. 的相反数 - 9是9 的相反数 再如2的相反数是 的相反数是- - 的相 再如 的相反数是-2,-2的相 反数是2; 的相反数是 的相反数是- - 反数是 ;5的相反数是-5,-5 的相反数是5. 的相反数是
1、填一填: 、填一填:
动手操作
右面是一个正方体纸盒的展图请 、-2、- 把-10、7、10、- 、- 、2 、 、 、- 、-7、 分别填入六个正方形, 分别填入六个正方形,使得按虚 线折成正方体后, 线折成正方体后,相对面上的两 上数互为相反数。 上数互为相反数。 2.图是一多面体展开图,每个面上都标注了字母 2.图是一多面体展开图,每个面上都标注了字母,请 图是一多面体展开图 每个面上都标注了字母,请 将+6,-3,+(-6),-(-3),5.5,-5.5这些数分别填 这些数分别填 入六个面,使多面体折叠后 相对面上两数互为相反 入六个面 使多面体折叠后,相对面上两数互为相反 使多面体折叠后 数. -3
化简下列各数: 例2 化简下列各数 (1) -(+10); (2) +(-0.15) ; (3) +(+3) (4) -(-20)
解 (1)-(+10)=-10 (2)+(-0.15)=-0.15 (3)+(+3)=+3 = 3 (4)-(-20)=20
课堂练习: 课堂练习
1. 填 : 空 (1)2.5的 反 是 ; 相 数 (2) 是 -100的 反 ; 相 数 1 (3) 5 是 的 反 ; 相 数 (4) 的 反 是 相 数 -1.1; 5 (5)8.2和 互 相 数 为 反 .
123相反数(新)
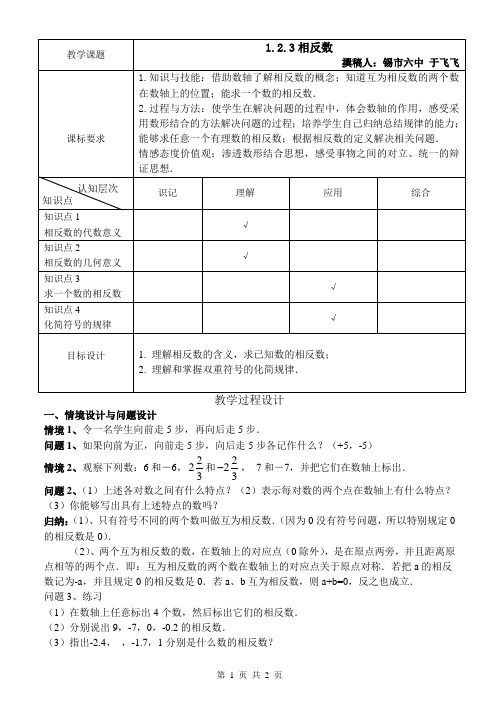
一、情境设计与问题设计情境1、令一名学生向前走5步,再向后走5步.问题1、如果向前为正,向前走5步,向后走5步各记作什么?(+5,-5)情境2、观察下列数:6和-6,223和223,7和-7,并把它们在数轴上标出.问题2、(1)上述各对数之间有什么特点?(2)表示每对数的两个点在数轴上有什么特点?(3)你能够写出具有上述特点的数吗?归纳:(1)、只有符号不同的两个数叫做互为相反数.(因为0没有符号问题,所以特别规定0的相反数是0).(2)、两个互为相反数的数,在数轴上的对应点(0除外),是在原点两旁,并且距离原点相等的两个点.即:互为相反数的两个数在数轴上的对应点关于原点对称.若把a的相反数记为-a,并且规定0的相反数是0.若a、b互为相反数,则a+b=0,反之也成立.问题3、练习(1)在数轴上任意标出4个数,然后标出它们的相反数.(2)分别说出9,-7,0,-0.2的相反数.(3)指出-2.4,,-1.7,1分别是什么数的相反数?(4)猜想一下:如果字母a 表示一个有理数,那么它的相反数是什么? 归纳:一般的,数a 和-a 互为相反数,特别的,0的相反数是0 问题4、 巩固练习:(口答) 1.()4+-是 的相反数; 2.⎪⎭⎫⎝⎛+-51是 的相反数; 3.()1.7--是 的相反数; 4.()100--是 的相反数. 习题精选例1、说出下面式子的意义: ()5+-、()7--、0-、()[]2---(求+5的相反数、求-7的相反数、求0的相反数、求-2相反数的相反数)归纳:求一个数的相反数的方法就是在这个数前面添加一个“-”号,新的数就是原数的相反数.例2、化简:(1)()[]3--- (2)(){}5+--+⎡⎤⎣⎦; 解:(1)()[]3---=-3 (2)(){}5+--+⎡⎤⎣⎦=5归纳:化简最终结果的符号问题与其前面“-”的个数有关,若有奇数个“-”,则最后结果为“-”,若有偶数个“-”,则最后结果为“+”,它与“+”的个数无关. 二、习题设计 1.(落实知识点1)判断题:(1)-3是相反数( ) (2)-7和7是相反数( )(3)-a 的相反数是a ,它们互为相反数( ) (4)符号不同的两个数互为相反数( ) (5)一个数总比它的相反数大( )2.(落实知识点2)已知有理数m 、-3、n 在数轴上的位置如图所示,请将m 、-3、n 的相反数在数轴上表示出来,并将这六个数用“<”连接起来.3.(落实知识点2)数轴上表示互为相反数的两个点之间的距离为26.8,则这两个数是 . 4.(落实知识点3)-(-8)的相反数是 , +(-6)是 的相反数,a-b 的相反数是 , 的相反数a -1. 5.(落实知识点4)化简:(1)()[]3--- (2)(){}5+--+⎡⎤⎣⎦;。
123相反数

1.2.3 相反数一、教学目标:知识与技能(1)借助数轴了解相反数的概念,知道两个互为相反数的位置关系。
(2)给出一个数,能求出它的相反数。
过程与方法借助数轴,通过观察特例,总结出相反数的概念。
从数和形两个侧面理解相反数。
情感态度与价值观鼓励学生积极进行归纳、比较交流等活动。
二、教学重点:相反数的概念及其表示方法,理解相反数的代数定义和几何定义的一致性。
三、教学难点:负数的相反数的表示方法。
四、课时安排:1课时五、课堂类型:新课六、教学方法:活动探究法七、教具学具:多媒体八、教学过程:(一)复习引入在数轴上,画出表示①6,-6,②2.5,-2.5,③314,314-各数的点。
(二)新课新授请同学们观察后回答: 1.上述中6和-6;2.5和-2.5,314,314-每对数有什么特点? 2.每对数在数轴上所表示的点有什么特点?3.再观察课本第8页的图1.2-1中点D 和点B ,它们的位置关系如何?•它们各表示的数有什么特点?概括:(1)每一对数,只有符号不同。
(2)在数轴上表示每一对数的两个点分别在原点的两边,•并且离开原点的距离相等。
(3)点D 和点B 分别位于原点的两边,且与原点的距离相等,它们分别表示-3•和3。
思考:数轴上与原点的距离是2的点有几个?这些点表示的数是什么?•与原点的距离是5的点呢?归纳:一般地,设a 是一个正数,数轴上与原点的距离是a 的点有两个,它们分别在原点左右,表示-a 和a ,那么称这两个点关于原点对称,如下图:像这样只有符号不同的两个数叫做互为相反数,例如6和-6,2.5和-2.5,-2-a a都是互为相反数,也就是说6的相反数是-6,-2.5的相反数是2.5。
一般地,a 和-a 互为相反数,特别地,0的相反数仍是0。
问:数轴上表示相反数的两个点和原点有什么关系?注意相反数与倒数的区别,若两个数只有符号不同,那么这两个数叫做互为相反数;若两个数的乘积等于1,则这两个数叫互为倒数。
§123相反数

数学学科教案
§.1.2.3 相反数(第3 课时)
教学任务分析
教学流程安排
活动流程图活动内容和目的
活动1 通过数轴导入
活动2 动手操作
活动3 理解相反数概念活动4 相反数的分析
活动5 巩固相反数概念活动 6 相反数概念的延
伸
活动7 巩固练习使学生能够对数与形加深理解
渗透理论联系实际的思考问题的方法。
使学生对于相反数有更深的理解。
加深学生对于相反数的认识。
通过练习,使学生掌握相反数。
进一步抽象,使学生理解化简的意义。
使学生进一步巩固相反数的概念。
课前准备
教具学具补充材料投影仪课件资料,图片
教学过程设计
是()
A一个数的相反数一定是负数;
B一个数的相反数的相反数一定是正数;
C一个数的相反数一定有倒数;
D一个数的倒数一定有相反数。
3.总结:
这节课我们学会了哪些知识?你能向大家说一说吗?
4.作业:
教科书第18页第3题,学生用书同步练习。
教师与学生共同总
结,达到共同理解。
教师布置作业,学生记
录作业。
加强学生的口语
表达能力,发展学生的
个性特长。
对所学加以巩固,
灵活运用理解。
123 相反数(解析版)

1.2.3相反数相反数的概念题型一:找一个数的相反数【例题1】(2021·内蒙古赤峰市·中考真题)-2021的相反数是( ) A .2021 B .-2021C .12021D .12021-【答案】A【分析】根据相反数的定义判断即可. 【详解】解:-2021的相反数是2021, 故选:A .【点睛】本题考查了相反数的概念,解题关键是明确相反数的定义,准确求解. 变式训练【变式1-1】(2021·云南红河哈尼族彝族自治州·九年级一模)若一个数的相反数是7-,则这个数为___________. 【答案】7【分析】根据相反数的定义即可直接解答. 【详解】∵7的相反数是-7, ∵这个数为7.故答案为:7.【点睛】本题考查相反数.理解相反数的定义是解答本题的关键.知识点管理 归类探究 互为相反数意义:只有符号不同的两个数叫做相反数。
相反数意义:把其中一个数叫做另一个的相反数。
正数的相反数是负数,负数的相反数就是正数。
0的相反数是0,也就是0的相反数是它本身。
【变式1-2】(2021·山东青岛市·九年级二模)12021-的倒数的相反数是( ) A .2021- B .12021C .2021D .12021-【答案】C【分析】利用倒数和相反数的定义分析得出答案.乘积为1的两个数互为倒数;只是符号不同的两个数叫做互为相反数。
规定0的相反数为0. 【详解】∵12021-的倒数是2021-, 又∵2021-的相反数是2021, ∵12021-的倒数的相反数是2021 . 故选:C .【点睛】本题主要考查了倒数和相反数,正确把握倒数和相反数的定义是解题的关键.【变式1-3】(2021·全国七年级专题练习)画出数轴,把下列各数及它们的相反数表示在数轴上,并将这些数按从小到大的顺序用“<”连接.2,0,-12,-3. 【答案】数轴见解析,113202322-<-<-<<<< 【分析】先求出各数的相反数,再在数轴上表示出来,根据数轴上的位置,用“<”连接即可. 【详解】解:2的相反数是-2,0的相反数是0,-12的相反数是12,-3的相反数是3,在数轴是表示如图所示,用“<”连接如下:113202322-<-<-<<<<.【点睛】本题考查了相反数的意义和在数轴上表示数以及有理数的大小,解题关键是准确求出各数的相反数,在正确的在数轴上表示出来,利用数轴比较大小. 题型二:判定两个数是否互为相反数【例题2】(2021·深圳市南山区华侨城中学九年级二模)下列各组数中互为相反数的是( ) A .-4 和14B .14和 4 C .-4 和-14D .4 和-4【答案】D【分析】根据相反数的概念进行判断即可.【详解】解:4的相反数是-4, ∵互为相反数的是4与4-, 故选:D .【点睛】本题考查相反数的概念,掌握只有符号不同的两个数叫做互为相反数是解题关键. 变式训练【变式2-1】(2021·江苏苏州市·九年级专题练习)-1是1的( ) A .倒数 B .相反数C .绝对值D .相反数的绝对值【答案】B【分析】根据相反数的定义判断即可. 【详解】解:-1是1的相反数, 故选:B .【点睛】本题考查了相反数的定义,解题关键是理解相反数的定义,准确进行判断.【变式2-2】(2020·四川省自贡市贡井区成佳中学校七年级月考)下列各对数中,互为相反数的是( ) A .()5+-与5- B .()5++与5-C .()5--与5D .5与()5++【答案】B【分析】依据相反数的概念求值,并要注意符号的变化.相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0.【详解】解:A 、+(-5)=-5,选项不符合; B 、+(+5)=5,5与-5互为相反数,选项符合; C 、-(-5)=5,选项不符合; D 、+(+5)=5,选项不符合. 故选:B .【点睛】此题主要考查相反数的概念及定义.相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0.【变式2-3】(2021·河南三门峡市·七年级期末)在0和0,34和34-,13和3这三对数中,互为相反数的有( ) A .3对 B .2对C .1对D .0对【答案】B【分析】只有符号不同的两个数叫做互为相反数. 【详解】互为相反数的是: 0和0,34和-34,共有2对, 故选: B.【点睛】本题考查了相反数的定义,是基础题,熟记概念是解题的关键.相反数的性质题型三:相反数的性质【例题3】(2020·山东七年级月考)若34a +与26b -互为相反数,则46b a +的值为________________. 【答案】4【分析】根据相反数的定义求解即可.【详解】解:由题意可得出,34(26)0a b ++-=, ∵322a b +=∵46224b a +=⨯=. 故答案为:4.【点睛】本题考查的知识点是相反数的定义以及求代数式的值,利用已知条件得出322a b +=是解此题的关键. 变式训练【变式3-1】(2020·南通市东方中学七年级月考)若a -5和-7互为相反数,则a 的值为______. 【答案】12【分析】根据一个数的相反数就是在这个数前面添上“-”号,求解即可. 【详解】解:由题意,得 a -5+(-7)=0, 解得a=12, 故答案为:12.【点睛】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.【变式3-2】(2020·泰州市姜堰区励才实验学校七年级月考)已知2a -与6-互为相反数,求21a -的值. 【答案】15相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.【分析】根据互为相反数的两个数的和为0,可求得a 的值,然后代入到21a -可得答案. 【详解】∵2a -与6-互为相反数, ∵()260a -+-=, ∵8a =,2128115a ∴-=⨯-=.【点睛】本题主要考查了互为相反数的两个数的特点:互为相反数的两个数的和为0是解决本题的关键; 【变式3-3】(2020·南昌市心远中学七年级期中)若2m +的相反数是3,那么m -=_____. 【答案】5【分析】根据相反数的概念求解即可. 【详解】解:∵ 2m +的相反数是3, ∵m+2+3=0 ∵m=﹣5,∵﹣m=5. 故答案为:5.【点睛】本题考查相反数的定义,解答本题需要熟练掌握相反数的概念.多重符合化简题型四:多重符合化简【例题4】(2020·临沂第十七中学七年级月考)化简下列各数:(1)1-(-)2=________________; (2)-(+3.5)=_____________; (3)+(-4)=_______________;【答案】12-3.5 -4【分析】根据多重符号的化简规律进行化简即可. 【详解】解:11-(-)=22,-(+3.5)=-3.5,+(-4)=-4; 故答案为:12,-3.5,-4 【点睛】本题考查符号的化简.化简符号的规律是:非0数的正负与前边的正号的个数无关,而与负号的个数有关,当有奇数个负号时,值是负数,当有偶数个负号时,值是正数.一个正数的前面有偶数个“-”时,可以化简为这个数字本身。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在一个数的前面加“+”或“-”,结果 的符号与前面“-”的个数有关:
①若有奇数个“-”,则最后结果为 “-”;
②若有偶数个“-”,则最后结果为“+”; ③它与“+”的个数无关 .
1.相反数的理解
相反数的代数意义:只有符号不同的两个数;
相反数的几何意义:在数轴上的原点两侧,且到原
点的距离相等的两个数互为相反数.
负数
0
正数
已知有理数m、-3、n在数轴上的位置如 图所示,请将m、-3、n的相反数在数轴上 表示出来,并将这六个数用“<”连接起来.
-3m0 n1. 解:如图,-3<-n<m<-m<n<3.
-n
-m
-3
m0 n3
观察下列数,并把它们在数轴上标出:
6和-6,2 2 和 2 2,7和-7, 5 和 5 .
3
3
77
(1)上述各对数之间有什么特点?
每一对数只有符号不同。
(2)表示每对数的两个点在数轴上有什么特点?
表示每对数的两点关于原点对称,分别位 于原点的两边且到原点的距离相等。
(3)你能够写出具有上述特点的数么?
代数式+(-5)的意义__-_5_的_相__反_数_____;
课堂检测
(4)若 a 是负数,则-a 是 正 数; 若 - a 是负数,则 a 是 正 数.
(5)数轴上表示互为相反数的两个点之间的距离为 26.8,则这两个数是 13.4和-13.4 .
(6)回答下列问题: (1)什么数的相反数大于本身? (2)什么数的相反数等于本身? (3)什么数的相反数小于本身?
堂 检
D、π与3.14
测
(2)下列说法不正确的是(D)
A.与原点距离相等的两个点所表示的数一定互为相反数
B.在一个数的前面添上“-”号,就得到它的相反数
C.任何一个有理数都有相反数
D.符号不同的两个数互为相反数
(3) 填空:①若-x=-5,则x=__5__;若- x=3,则x=_-_3_.
② 若2x+1是-9的相反数,则x=_4___. ③ 代数式-(+5)的意义__5__的__相__反__数_________;
2.利用相反数化简数的符号
在一个数的前面加“+”或“-”,结果的符号与 前面“-”的个数有关:
若有奇数个“-”,则最后结果为“-”; 若有偶数个“-”,则最后结果为“+”; 它与“+”的个数无关 .
(1)下面两个数是互为相反数的是( C ) 课
A、- 1与0.2 2
C、-2.25与2
1 4
B、1 与-0.333 3
如:-10和10,9和-9,-1.5和1.5,……
观察这两个数,有什么相同和不同?
符号不同
2.5 2.5
数字相同
定义:
1.相反数:只有符号不同的两个数叫做互为
相反数.
2.特别规定: 0的相反数是0.
3.表示相反数的两个点分别位于原点的两边
且到原点的距离相等。
或“位于原点两边且到原点的距离相等的
练习
请同学们说说下面几个式子的意义:
5 7
0
2
求+5的相反数 求-7的相反数 求0的相反数 求-2相反数的相反数
练习
1. -(+4)是 的相反数;
2.
1 5
是
的相反数;
3. 7.1 是 的相反数;
4. 100 是 的相反数.
练习 化简下列各符号
1. 3 ;
2. 5 ; 3. 6 (. 共n个负号)
例2 化简下列各数: (1)-(+10); (2)+(-0.15); (3)+(+3); (4)-(-20).
我们通常把在一个数前面添上“-”号,表示这个数的 相反数. 例如 -(-4)=4, -(+5.5)=-5.5,- 0 = 0.
同样,在一个数前面添上“+”号,表示这个数本身.
例如 +(-4)=-4,+(+12)=12,+ 0 = 0.
两个点所表示的数是相反数”
• 一般地,a的相反数是 -a
.
-a的相反数是 a
.
判断:
(1)-2是-(-2)的相反数 (2)-3和+3都是相反数 (3)-3是3的相反数 (4)-3与+3互为相反数 (5)+3是-3的相反数 (6)一个数的相反数不可能是它本身
例 1 分别写出下列各数的相反数 : 5,-7,- 3 1 ,+11.2 a-1 a+b 2
