(新课标)201X中考数学复习第三章函数及其图像第11节第1课时反比例函数的图象和性质及应用(正文)
中考数学考点专题复习课件反比例函数的图象和性质

解:(1)过点 D 作 x 轴的垂线,垂足为 F,∵点 D 的坐标为(4,3),∴OF
=4,DF=3,∴OD=5,∴AD=5,∴点 A 坐标为(4,8),∴k=xy=4×8
=32,∴k=32 (2)将菱形 ABCD 沿 x 轴正方向平移,使得点 D 落在函数 y=3x2(x>0)的
图象 D′点处,过点 D′做 x 轴的垂线,垂足为 F′.∵DF=3,∴D′F′=3,∴ 点 D′的纵坐标为 3,∵点 D′在 y=3x2的图象上,∴3=3x2,解得:x=332,即 OF′=332,∴FF′=332-4=230,∴菱形 ABCD 平移的距离为230
3.(2015·苏州)若点 A(a,b)在反比例函数 y=2x的图象上,则代数式 ab
-4 的值为( B)
A.0 B.-2 C.2 D.-6
4.(2015·牡丹江)在同一直角坐标系中,函数 y=-xa与 y=ax+1(a≠0)
的图象可能是( B )
,A)
,B)
,C)
,D)
5.(2015·青岛)如图,正比例函数 y1=k1x 的图象与反 比例函数 y2=kx2的图象相交于 A,B 两点,其中点 A 的横坐标为 2,当
①ACMN =||kk12||; ②阴影部分面积是12(k1+k2); ③当∠AOC=90°时,|k1|=|k2|; ④若 OABC 是菱形,则两双曲线既关于 x 轴对称,也关于 y 轴对称.
其中正确的是①__④__.(把所有正确的结论的序号都填上)
(3)(2015·宿迁)如图,在平面直角坐标系中,已知点 A(8,1),B(0,-3), 反比例函数 y=kx(x>0)的图象经过点 A,动直线 x=t(0<t<8)与反比例函数 的图象交于点 M,与直线 AB 交于点 N.
人教版九下中考知识点梳理第11讲 反比例函数
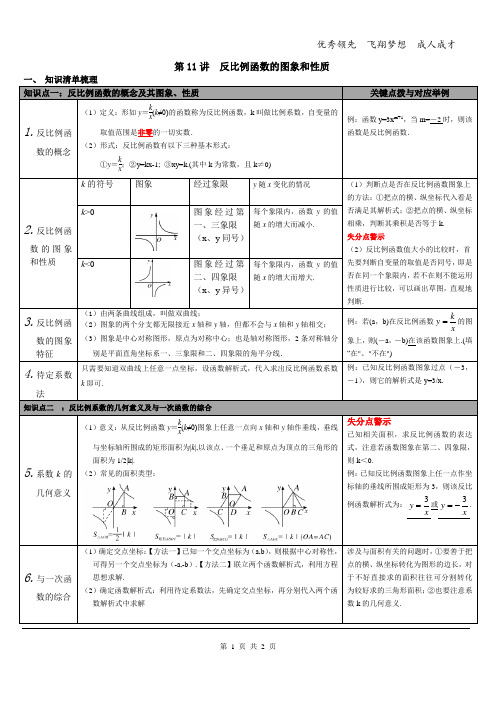
第11讲反比例函数的图象和性质知识点一:反比例函数的概念及其图象、性质关键点拨与对应举例1.反比例函数的概念(1)定义:形如y=kx(k≠0)的函数称为反比例函数,k叫做比例系数,自变量的取值范围是非零的一切实数.(2)形式:反比例函数有以下三种基本形式:①y=kx;②y=kx-1; ③xy=k.(其中k为常数,且k≠0)例:函数y=3x m+1,当m=-2时,则该函数是反比例函数.2.反比例函数的图象和性质k的符号图象经过象限y随x变化的情况(1)判断点是否在反比例函数图象上的方法:①把点的横、纵坐标代入看是否满足其解析式;②把点的横、纵坐标相乘,判断其乘积是否等于k.失分点警示(2)反比例函数值大小的比较时,首先要判断自变量的取值是否同号,即是否在同一个象限内,若不在则不能运用性质进行比较,可以画出草图,直观地判断.k>0 图象经过第一、三象限(x、y同号)每个象限内,函数y的值随x的增大而减小.k<0 图象经过第二、四象限(x、y异号)每个象限内,函数y的值随x的增大而增大.3.反比例函数的图象特征(1)由两条曲线组成,叫做双曲线;(2)图象的两个分支都无限接近x轴和y轴,但都不会与x轴和y轴相交;(3)图象是中心对称图形,原点为对称中心;也是轴对称图形,2条对称轴分别是平面直角坐标系一、三象限和二、四象限的角平分线.例:若(a,b)在反比例函数kyx=的图象上,则(-a,-b)在该函数图象上.(填“在"、"不在")4.待定系数法只需要知道双曲线上任意一点坐标,设函数解析式,代入求出反比例函数系数k即可.例:已知反比例函数图象过点(-3,-1),则它的解析式是y=3/x.知识点二:反比例系数的几何意义及与一次函数的综合5.系数k的几何意义(1)意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|.(2)常见的面积类型:失分点警示已知相关面积,求反比例函数的表达式,注意若函数图象在第二、四象限,则k<0.例:已知反比例函数图象上任一点作坐标轴的垂线所围成矩形为3,则该反比例函数解析式为:3yx=或3yx=-.6.与一次函数的综合(1)确定交点坐标:【方法一】已知一个交点坐标为(a,b),则根据中心对称性,可得另一个交点坐标为(-a,-b).【方法二】联立两个函数解析式,利用方程思想求解.(2)确定函数解析式:利用待定系数法,先确定交点坐标,再分别代入两个函数解析式中求解涉及与面积有关的问题时,①要善于把点的横、纵坐标转化为图形的边长,对于不好直接求的面积往往可分割转化为较好求的三角形面积;②也要注意系数k的几何意义.(3)在同一坐标系中判断函数图象:充分利用函数图象与各字母系数的关系,可采用假设法,分k>0和k<0两种情况讨论,看哪个选项符合要求即可.也可逐一选项判断、排除.(4)比较函数值的大小:主要通过观察图象,图象在上方的值大,图象在下方的值小,结合交点坐标,确定出解集的范围. 例:如图所示,三个阴影部分的面积按从小到大的顺序排列为:S△AOC=S△OPE >S△BOD.知识点三:反比例函数的实际应用7.一般步骤(1题意找出自变量与因变量之间的乘积关系;(2设出函数表达式;(3)依题意求解函数表达式;(4)根据反比例函数的表达式或性质解决相关问题.。
【人教版】九年级数学下册中考知识点梳理:第11讲 反比例函数
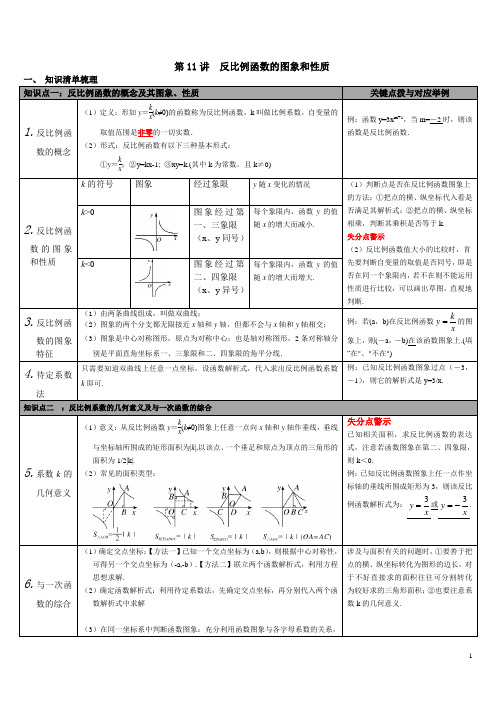
第11讲反比例函数的图象和性质知识点一:反比例函数的概念及其图象、性质关键点拨与对应举例1.反比例函数的概念(1)定义:形如y=kx(k≠0)的函数称为反比例函数,k叫做比例系数,自变量的取值范围是非零的一切实数.(2)形式:反比例函数有以下三种基本形式:①y=kx;②y=kx-1; ③xy=k.(其中k为常数,且k≠0)例:函数y=3x m+1,当m=-2时,则该函数是反比例函数.2.反比例函数的图象和性质k的符号图象经过象限y随x变化的情况(1)判断点是否在反比例函数图象上的方法:①把点的横、纵坐标代入看是否满足其解析式;②把点的横、纵坐标相乘,判断其乘积是否等于k.失分点警示(2)反比例函数值大小的比较时,首先要判断自变量的取值是否同号,即是否在同一个象限内,若不在则不能运用性质进行比较,可以画出草图,直观地判断.k>0 图象经过第一、三象限(x、y同号)每个象限内,函数y的值随x的增大而减小.k<0 图象经过第二、四象限(x、y异号)每个象限内,函数y的值随x的增大而增大.3.反比例函数的图象特征(1)由两条曲线组成,叫做双曲线;(2)图象的两个分支都无限接近x轴和y轴,但都不会与x轴和y轴相交;(3)图象是中心对称图形,原点为对称中心;也是轴对称图形,2条对称轴分别是平面直角坐标系一、三象限和二、四象限的角平分线.例:若(a,b)在反比例函数kyx=的图象上,则(-a,-b)在该函数图象上.(填“在"、"不在")4.待定系数法只需要知道双曲线上任意一点坐标,设函数解析式,代入求出反比例函数系数k即可.例:已知反比例函数图象过点(-3,-1),则它的解析式是y=3/x.知识点二:反比例系数的几何意义及与一次函数的综合5.系数k的几何意义(1)意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|.(2)常见的面积类型:失分点警示已知相关面积,求反比例函数的表达式,注意若函数图象在第二、四象限,则k<0.例:已知反比例函数图象上任一点作坐标轴的垂线所围成矩形为3,则该反比例函数解析式为:3yx=或3yx=-.6.与一次函数的综合(1)确定交点坐标:【方法一】已知一个交点坐标为(a,b),则根据中心对称性,可得另一个交点坐标为(-a,-b).【方法二】联立两个函数解析式,利用方程思想求解.(2)确定函数解析式:利用待定系数法,先确定交点坐标,再分别代入两个函数解析式中求解(3)在同一坐标系中判断函数图象:充分利用函数图象与各字母系数的关系,涉及与面积有关的问题时,①要善于把点的横、纵坐标转化为图形的边长,对于不好直接求的面积往往可分割转化为较好求的三角形面积;②也要注意系数k的几何意义.可采用假设法,分k>0和k<0两种情况讨论,看哪个选项符合要求即可.也可逐一选项判断、排除.(4)比较函数值的大小:主要通过观察图象,图象在上方的值大,图象在下方的值小,结合交点坐标,确定出解集的范围. 例:如图所示,三个阴影部分的面积按从小到大的顺序排列为:S△AOC=S△OPE >S△BOD.知识点三:反比例函数的实际应用7.一般步骤(1题意找出自变量与因变量之间的乘积关系;(2设出函数表达式;(3)依题意求解函数表达式;(4)根据反比例函数的表达式或性质解决相关问题.。
反比例函数的图像和性质ppt课件

7、若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 y = - 1 0 0 的图象上,则(
xቤተ መጻሕፍቲ ባይዱ
B
)
A、y1>y2>y3 C、y3>y1>y2
B、y2>y1>y3 D、y3>y2>y1
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
已知点A(2,y1), B(5,y2)C是(反-3比,y例3)函是数y 象上的两点.请比较y1,y2的,y大3的小大.小.
4 x
图
y
⑴代入求值
y1 A B
-3 y2 O2 5
C y3
⑵利用增减性
⑶根据图象判断
x
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
1、反比例函数y= - 5 的图象大致是( D )
y
x
y
A:
o
x
B:
o
x
y
C:
o
x
D:
y
o x
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
2、我校食堂有5吨煤,用y表示可以用的天数
,用x表示每天的烧煤量,则y关于x的函数的
10
1、这几个函数图象有 8 什么共同点?
2、函数图象分别位于 6 哪几个象限?
4
3、y随的x变化有怎
初三反比例函数ppt课件

从函数形式上,我们可以将反比例函 数表示为y=k/x,其中k为常数,且 k≠0。这表明函数的输出y与输入x成 反比关系。
反比例函数的表达形式基本源自式y=k/x,其中k为常数,且k≠0。
变形形式
当k>0时,函数图像位于第一、三象限,y随x的增大而减小;当k<0时,函数图 像位于第二、四象限,y随x的增大而增大。
交点与函数图像的关系
01
当两个函数有交点时,交点的横 纵坐标分别对应两个函数在某一 点处的函数值。
02
通过交点,可以观察两个函数在 某一点处的相互关系及其变化趋 势。
利用交点解决实际问题
路程问题
01
在两个物体以不同速度相对运动的问题中,交点的横坐标表示
相遇的时间,纵坐标表示相遇的地点。
工程问题
02
满足奇偶性定义
由于反比例函数满足奇函数的定义 ,即$f( - x) = - f(x)$,因此它是奇 函数。
反比例函数的凹凸性
二阶导数判定
通过求二阶导数判断函数的凹凸 性。如果二阶导数大于0,则函 数是凹函数;如果二阶导数小于 0,则函数是凸函数。对于反比 例函数,可以通过求导再求二阶
导数来判断凹凸性。
在工程进度问题中,交点的横坐标表示完成工程所需的总时间
,纵坐标表示完成工程量。
经济问题
03
在投入产出问题中,交点的横坐标表示投资额,纵坐标表示产
值。
06
CATALOGUE
复习与巩固
反比例函数的概念与性质复习
总结词:掌握基础
详细描述:通过图表和实例,复习反 比例函数的概念和性质,包括定义、 表达式、图像等。
凹函数
通过计算二阶导数发现,反比例 函数是凹函数。这意味着函数图
(江西专用)2019中考数学总复习 第一部分 教材同步复习 第三章 函数 第11讲 反比例函数课件

0)作 x 轴的垂线 l1 和 l2,探究直线 l1,直线 l2 与双曲线 y=3x的关系,下列结论中错 误的是( D )
A.两直线中总有一条与双曲线相交 B.当 m=1 时,两直线与双曲线的交点到原点的距离相等 C.当-2<m<0 时,两直线与双曲线的交点在 y 轴两侧 D.当两直线与双曲线都有交点时,这两交点的最短距离是 2
∴△DBM∽△PDM,∴DBMM=DPMM . ∵OA=4,AD⊥x 轴,∴设 D 的坐标是(4,y)(y>0),∴3-4 y= 7+y 4, 解得 y=1,y=-5(舍去), 即 D 点的坐标是(4,1),
把 D 点坐标代入 y=kx得 k=4,即反比例函数的解析式是 y=4x.
16
命题点2 反比例函数与一次函数的图象与性质(5年4考)
8
4.如图,点 A 在反比例函数 y=kx(x>0)的图象上,AB⊥x 轴于点 B,△AOB 的面积为 5,则 k=___1_0____.
9
知识点三 反比例函数解析式的确定 1.待定系数法 (1)设解析式为 y=kx(k≠0); (2)找出反比例函数图象上的一点 P(a,b); (3)将 P(a,b)代入解析式得 k=ab; (4)确定反比例函数的解析式 y=axb. 2.利用 k 的几何意义求解:当已知面积时,可考虑用 k 的几何意义.由面积得 |k|值,再结合图象所在象限判断 k 的正负,从而得出 k 值,代入解析式即可.
的弯曲程度都与k有关;(3)反比例函数图象的增减性必须强调在每一
个分支上,不能认为在整个自变量取值范围内增大(或减小).
5
1.下列函数中,表示 y 是 x 的反比例函数的是( B )
初三反比例函数ppt课件ppt课件

反比例函数是具有极限的函数,当x趋 近于无穷大或无穷小时,y的值趋近于 0。
反比例函数的图像是关于原点对称的 。
02CHBiblioteka PTER反比例函数的应用生活中的反比例现象
总结词
生活中常见的反比例现象
详细描述
在日常生活中,许多现象可以用反比例函数来描述。例如,当两个量之间的比例保持恒定时,其中一个量增加, 另一个量会相应减少,形成反比例关系。这种现象在很多场合都可以观察到,如物体的质量和体积、电路中的电 流和电阻等。
提高练习题解析
总结词
提升解题能力
详细描述
提高练习题相对于基础练习题难度有所增加,题目设计更加灵活,需要学生具备一定的数学思维和解 题技巧。这些题目通常涉及到反比例函数与其他数学知识的综合运用,如与一次函数、二次函数等知 识的结合。
竞赛练习题解析
总结词
挑战高难度
详细描述
竞赛练习题是针对数学竞赛和数学特长生设计的题目,难度较大,题目设计更加复杂和 综合。这些题目不仅要求学生掌握反比例函数的知识,还需要具备较高的数学素养和解 题能力。通过解答这些题目,学生可以挑战自己的数学思维和解题能力,提升数学学习
对未来学习的展望
学生可以在反比例函数的基础上,进一 步学习其他类型的函数,如幂函数、对 数函数等,以拓展数学知识的广度和深
度。
学生可以尝试将反比例函数与其他学科 的知识点进行结合,例如与物理中的电 流、电压等概念进行联系,加深对相关
概念的理解。
学生可以通过参加数学竞赛、科研项目 等活动,进一步提高自己的数学素养和 解决问题的能力,为未来的学习和职业
总结词
掌握实际应用题的解题技巧是提高解 题效率的关键。
详细描述
在解决反比例函数实际应用题时,需 要将问题转化为数学模型,并运用适 当的解题技巧,如排除法、比较法等 ,以简化问题并快速找到答案。
【人教版】精选九年级数学下册:全册中考知识点梳理-第11讲 反比例函数
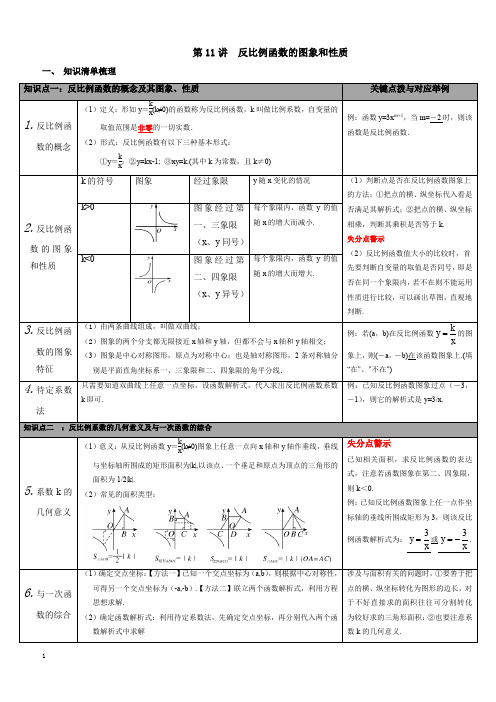
(1)意义:从反比例函数y= (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|.
(2)常见的面积类型:
失分点警示
已知相关面积,求反比例函数的表达式,注意若函数图象在第二、四象限,则k<0.
例:已知反比例函数图象上任一点作坐标轴的垂线所围成矩形为3,则该反比例函数解析式为: 或 .
第11讲反比例函数的图象和性质
一、知识清单梳理
知识点一:反比例函数的概念及其图象、性质
关键点拨与对应举例
1.反比例函数的概念
(1)定义:形如y= (k≠0)的函数称为反比例函数,k叫做比例系数,自变量的取值范围是非零的一切实数.
(2)形式:反比例函数有以下三种基本形式:
①y= ;②y=kx-1;③xy=k.(其中k为常数,且k≠0)
(4)比较函数值的大小:主要通过观察图象,图象在上方的值大,图象在下方的值小,结合交点坐标,确定出解集的范围.
涉及与面积有关的问题时,①要善于把点的横、纵坐标转化为图形的边长,对于不好直接求的面积往往可分割转化为较好求的三角形面积;②也要注意系数k的几何意义.
例:如图所示,三个阴影部分的面积按从小到大的顺序排列为:S△AOC=S△OPE>S△BOD.
例:若(a,b)在反比例函数 的图象上,则(-a,-b)在该函数图象上.(填“在"、"不在")
4.待定系数法
只需要知道双曲线上任意一点坐标,设函数解析式,代入求出反比例函数系数k即可.
例:已知反比例函数图象过点(-3,-1),则它的解析式是y=3/x.
知识点二:反比例系数的几何意义及与一次函数的综合
