展开与折叠(正方体的展开图).pptx
合集下载
立体图形的展开与折叠 ppt课件

立体图形的展开与折叠
6
第一类,中间四连方,两侧各一 个,共六种。
“141”型 立体图形的展开与折叠
7
第二类,中间三连方,两侧各有 一、二个,共三种。
“231”型 立体图形的展开与折叠
8
第三类,中间二连方,两侧各有二 个,只有一种。 “222”型
第四类,两排各三个,只有一种。
“33”型 立体图形的展开与折叠
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
4
注意事项
把正方体展成一个平面, 是指正方体中的6个面展成平 面图形,所得到的6个正方形中, 每一个至少有一条边和其它正 方形的某条边相连。
立体图形的展开与折叠
5
议一议: 怎样把所得到的 正方体表面展开图进行 分类?
面内部都标注了字母,请根据要求填空:
1)如果D面在左面,那么F面在
;
2)如果B面在后面,从左面看是D面,
那么上面是
。
D
E
DE
A
B
AB
C
C
F
F 立体图形的展开与折叠
19
2、“坚”在下面,“就”在后面, 胜利在哪里?
坚
持就是
胜
利
立体图形的展开与折叠
17
2、如下图是一个正方体的展开图,图中 已标出三个面在正方体中的位置,F: 前面;R:右面;D:下面。试判定另外 三个面A、B、C在正方体中的位置。
a
A
b
c
d
BCD
f
r
FR
立体图形的展开与折叠
18
3、如下图是一个正方体的展开图,每个
9
将相对的两个面涂上相同的颜色,正方 体的平面展开图共有以下11种:
《展开与折叠》PPT课件_OK

38
把下面的正三角形沿虚线折叠后的几何 体是什么?
39
将下图中五角星状的图形沿虚线折叠,得 到一个几何体,你在生活中见过和这个几 何体形状类似的物体吗?
40
考考你 如图,上面的图形分别是下面哪个立体图 形展开的形状?把它们用线连起来。
41
下图是一些立体图形的展开图, 用它们能围成怎样的立体图形?
123
4
5
67
8
9 10
22
挑战自己
如图所示的纸板上有10个无阴影的 正方形,从中选出一个,与图中5个有 阴影的正方形一起折一个正方体的包 装盒,有多少种不同的选法。
123
4
5
67
8
9 10
23
右图需再添上一个面,折叠后才能围成 一个正方体,下面是四位同学补画的情 况(图中阴影部分),其中正确的是 (B )
白 黄红
乙
绿 兰黄
丙
31
提示:找到相邻面的颜色,利用排 除法,就可以得出相对面的颜色了
红黄蓝绿黑白 红 黄 蓝 绿 黑 白
32
红黄蓝绿黑白 红 黄 蓝 绿 黑 白
33
练习:有一正方体木块,它的六个面分别标 上数字1——6,下图是这个正方体木块从不 同面所观察到的数字情况。请问数字1和5对 面的数字各是多少?
1 25
4
1 2
6 41
提示:方法仍然是找出所有相邻面的颜色
34
想一想、折一折 1、以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
(5)
(6)
35
2、哪种几何体的表面能展开成下面的图形? 先想一想,再折一折。
36
观察思考:
观察圆柱形纸筒展开的侧面是一个什么图形
把下面的正三角形沿虚线折叠后的几何 体是什么?
39
将下图中五角星状的图形沿虚线折叠,得 到一个几何体,你在生活中见过和这个几 何体形状类似的物体吗?
40
考考你 如图,上面的图形分别是下面哪个立体图 形展开的形状?把它们用线连起来。
41
下图是一些立体图形的展开图, 用它们能围成怎样的立体图形?
123
4
5
67
8
9 10
22
挑战自己
如图所示的纸板上有10个无阴影的 正方形,从中选出一个,与图中5个有 阴影的正方形一起折一个正方体的包 装盒,有多少种不同的选法。
123
4
5
67
8
9 10
23
右图需再添上一个面,折叠后才能围成 一个正方体,下面是四位同学补画的情 况(图中阴影部分),其中正确的是 (B )
白 黄红
乙
绿 兰黄
丙
31
提示:找到相邻面的颜色,利用排 除法,就可以得出相对面的颜色了
红黄蓝绿黑白 红 黄 蓝 绿 黑 白
32
红黄蓝绿黑白 红 黄 蓝 绿 黑 白
33
练习:有一正方体木块,它的六个面分别标 上数字1——6,下图是这个正方体木块从不 同面所观察到的数字情况。请问数字1和5对 面的数字各是多少?
1 25
4
1 2
6 41
提示:方法仍然是找出所有相邻面的颜色
34
想一想、折一折 1、以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
(5)
(6)
35
2、哪种几何体的表面能展开成下面的图形? 先想一想,再折一折。
36
观察思考:
观察圆柱形纸筒展开的侧面是一个什么图形
正方体的展开与折叠.ppt

•
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2020/11/102020/11/102020/11/102020/11/10
谢谢观看
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
3、下面是正方体的表面展开图,每个面内 都标注了数字。数字6所对的数字是几?
1 2 345
6
(1)
12 34 5 6
(2)
123 4 56
12 34 56
(3)
(4)
探究3组对面
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/11/102020/11/10Tuesday, November 10, 2020
第三类、两两三行排有序,恰似登天上云梯,仅
一种。(记忆口诀:2 2 2)
第四类、三个三个排两行,中间一“日” 放光芒,
仅一种。(记忆口诀:3 3 )
快乐练习 1、下列的哪个图形能折叠成正方体?
× 图1
× 图2ቤተ መጻሕፍቲ ባይዱ
121正方体的展开与折叠PPT课件

第四类:两排各三个,只有一种(33).
新知探究
正方体展开图”口诀”
中间四个面,上下各一面 中间三个面,一二隔河见 中间两个面,楼梯天天见 中间没有面,三三连一线
新知探究
1.把一个正方体的表面沿某些棱剪开,展成一 个平面图形,你能得到下面这些平面图形吗?
能
2.下面哪一个图形经过折叠可以得到正方体?
第一章 丰富的图形世界
展开与折叠
第1课时
课件
学习目标
1.通过动手操作,使学生能将一个正方体的表面沿某些棱剪开,展 开成一个平面图形; 2.会判断一个平面图形是不是正方体的表面展开图. 重点:将一个正方体的表面沿某些棱展开,展成平面图形;表面展 开图的辨认. 难点:鼓励学生尽可能多地将一个正方体展成平面图形,并用语言 描述其过程.
问题:你能将得到的平面图形分类吗? 你是按什么规律来分类的?
小组活动:分组讨论,得出分类. 用自己的语言表示其分类规律
新知探究
第一类:中间四个面,两侧各一个, 共六种(141).
新知探究
第二类:中间三个面,两侧各有一、 二个面,共三种(231).
新知探究
第三类:中间两个面,两侧各有两 个面,只有一种(222).
141型 6种 231型 3种 222型 1种
33型 1种
展
折
开
叠
立体图形
2、不同的展开图可以折叠成同一个立体图形
课堂小测
1.下列平面图形中不能围成正方体的是 (A )
课堂小测
2. 如图是一个正方体纸盒的展开图,每
个面内都标注了数字,则面2在展开前
所对的面
新课引入
在生活中,我们经常见到正方体形状的物体.
将正方体完全展开 后形状是怎样的?
新知探究
正方体展开图”口诀”
中间四个面,上下各一面 中间三个面,一二隔河见 中间两个面,楼梯天天见 中间没有面,三三连一线
新知探究
1.把一个正方体的表面沿某些棱剪开,展成一 个平面图形,你能得到下面这些平面图形吗?
能
2.下面哪一个图形经过折叠可以得到正方体?
第一章 丰富的图形世界
展开与折叠
第1课时
课件
学习目标
1.通过动手操作,使学生能将一个正方体的表面沿某些棱剪开,展 开成一个平面图形; 2.会判断一个平面图形是不是正方体的表面展开图. 重点:将一个正方体的表面沿某些棱展开,展成平面图形;表面展 开图的辨认. 难点:鼓励学生尽可能多地将一个正方体展成平面图形,并用语言 描述其过程.
问题:你能将得到的平面图形分类吗? 你是按什么规律来分类的?
小组活动:分组讨论,得出分类. 用自己的语言表示其分类规律
新知探究
第一类:中间四个面,两侧各一个, 共六种(141).
新知探究
第二类:中间三个面,两侧各有一、 二个面,共三种(231).
新知探究
第三类:中间两个面,两侧各有两 个面,只有一种(222).
141型 6种 231型 3种 222型 1种
33型 1种
展
折
开
叠
立体图形
2、不同的展开图可以折叠成同一个立体图形
课堂小测
1.下列平面图形中不能围成正方体的是 (A )
课堂小测
2. 如图是一个正方体纸盒的展开图,每
个面内都标注了数字,则面2在展开前
所对的面
新课引入
在生活中,我们经常见到正方体形状的物体.
将正方体完全展开 后形状是怎样的?
1-2展开与折叠共23张PPT
小结:
(1)正方体的展开图是平面图形; (2)正方体的展开图,因展开方式
的不同而不同,共有11种。
是不是所有的立体图形 展开后,都是平面图形?
球体的展开图是不是平面图形?
考考你
1、如果“你”在前面,那么什么在后面?
了! 太棒 你们
KEY: 棒
2、“坚”在下,“就”在后,“胜”、“利” 在哪里?
小结
1、立体图形是由平面图形组成的。 2、能根据展开图判断立体图形。 3、能判断平面图形是否为立体图形的展开图。
1、下面是一多面体的展开图,平面图形的旁 边都标注了字母,请根据要求回答问题:
(1)如果A面在多面体的底部,哪一面会在上面?
(2)如果面F在前面,面B在左面,哪一面会在 上面?
(3)如果面C在右面,面D在后面,哪一面会在 上面?
坚
持就是
胜
利
思考:
(1)如果将它的侧面展开,会变成什么样的图形? (2)如果将它的表面展开,会变成什么样的图形?
圆锥
扇形பைடு நூலகம்
看一看,想一想
如图,上面的图形分别是下面哪个立体图 形展开的形状?把它们用线连起来。
想一想、折一折
以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
想一想: 下面几个图形是一些常见几何 体的展开图,你能正确说出这些几何 体的名字么?
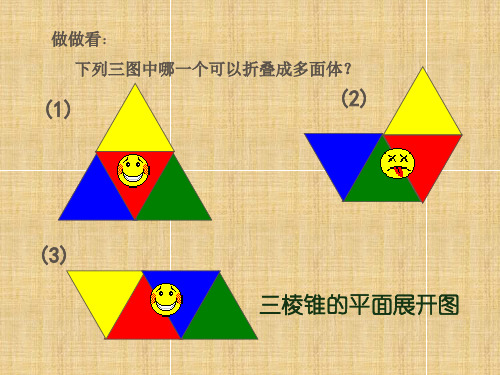
做做看:
下列三图中哪一个可以折叠成多面体?
(1)
(2)
(3) 三棱锥的平面展开图
正方体 四棱锥
长方体 三棱柱
练习:
下列图形中是什么多面体的展开图? (1)
长方体
(2)
五棱锥
(3)
三棱柱
《展开与折叠》课件

通过复杂的折叠机构设计,实现自行车的可折叠性,便于携带和存储。
折叠式自行车
通过简单的折叠机构设计,实现家具的可折叠性,节省空间并方便搬运。
折叠式家具
THANKS
感谢您的观看
折纸艺术是一种以纸张为主要材料的艺术形式,通过折叠、剪切、拼贴等技巧创造出各种形态的作品。在折纸艺术中,展开与折叠是基本的技巧之一,通过不同的折叠方式可以形成各种不同的形态和图案。折纸艺术的应用范围广泛,可以用于装饰、礼品、玩具等方面。
详细描述
通过简单的折叠技巧,将一张纸折叠成千纸鹤的形态,具有观赏和装饰价值。
千纸鹤
通过复杂的折叠技巧,将一张纸折叠成各种有趣的玩具,如战斗机、动物等。
折纸玩具
总结词
探讨产品设计中的展开与折叠原理,分析其在现代产品设计中的应用和价值。
要点一
要点二
详细描述
在产品设计中,展开与折叠是一种常见的结构形式。通过巧妙的设计,可以让产品在展开时呈现完整的功能和形态,而在折叠状态下则便于携带和存储。这种结构形式广泛应用于各种产品领域,如家居用品、办公用品、电子产品等。产品设计中的展开与折叠需要考虑材料、结构、工艺等方面的因素,以确保产品的实用性和美观性。
展开与折叠在日常生活中有着广泛的应用,如纸盒的制作、包装、折纸艺术等。
展开的基本形式
线性展开是一种常见的展开方式,其特点是展开后的形状或结构呈直线或线段排列。定义实例 Nhomakorabea特点
例如,纸盒的拆开、拉链的拉开等都属于线性展开。
线性展开具有简单、直观的特点,便于理解和操作。
03
02
01
旋转展开是指展开后的形状或结构围绕某一点进行旋转,形成圆周或类似圆周的排列。
根据内容选择
1-2展开与折叠共23张PPT

做做看:
下列三图中哪一个可以折叠成多面体?
(1)
(2)
(3) 三棱锥的平面展开图
正方体 四棱锥
长方体 三棱柱
练习:
下列图形中是什么多面体的展开图? (1)
长方体
(2)
五棱锥
(3)
三棱柱
将一个正方体的表面沿某 些棱剪开,展成一个平面 图形.你能得到哪些图形?
想一想:
下列的图形都是正方体的展开图吗?
坚
持就是
胜
利
思考:
(1)如果将它的侧面展开,会变成什么样的图形? (2)如果将它的表面展开,会变成什么样的图形?
圆锥
扇形
看一看,想一想
如图,上面的图形分别是下面哪个立体图 形展开的形状?把它们用线连起来。
想一想、折一折
以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
想一想: 下面几个图形是一些常见几何 体的展开图,你能正确说出这些几何 体的名字么?
下面六个正方形连在一起的图形,经折 叠后能围成正方体的图形有哪几个?
A
B
C
D
E
F
G
有一个正方体,在它的各个面上分别涂了
白、红、黄、兰、绿、黑六种颜色。甲、乙、 丙三位同学从三个不同的角度去观察此正方体, 结果如下图,问这个正方体各个面的对面的颜 色是什么?
黑 红兰
甲
白 黄红
乙
绿 兰黄 丙
小结:
(1)正方体的展开图是平面图形; (2)正方体的展开图,因展开方式
的不同而不同,共有11种。
是不是所有的立体图形 展开后,都是平面图形?
球体的展开图是不是平面图形?
考考你
1、如果“你”在前面,那么什么在后面?
下列三图中哪一个可以折叠成多面体?
(1)
(2)
(3) 三棱锥的平面展开图
正方体 四棱锥
长方体 三棱柱
练习:
下列图形中是什么多面体的展开图? (1)
长方体
(2)
五棱锥
(3)
三棱柱
将一个正方体的表面沿某 些棱剪开,展成一个平面 图形.你能得到哪些图形?
想一想:
下列的图形都是正方体的展开图吗?
坚
持就是
胜
利
思考:
(1)如果将它的侧面展开,会变成什么样的图形? (2)如果将它的表面展开,会变成什么样的图形?
圆锥
扇形
看一看,想一想
如图,上面的图形分别是下面哪个立体图 形展开的形状?把它们用线连起来。
想一想、折一折
以下哪些图形经过折叠可以围成一个棱柱?
⑴
⑵
⑶
⑷
想一想: 下面几个图形是一些常见几何 体的展开图,你能正确说出这些几何 体的名字么?
下面六个正方形连在一起的图形,经折 叠后能围成正方体的图形有哪几个?
A
B
C
D
E
F
G
有一个正方体,在它的各个面上分别涂了
白、红、黄、兰、绿、黑六种颜色。甲、乙、 丙三位同学从三个不同的角度去观察此正方体, 结果如下图,问这个正方体各个面的对面的颜 色是什么?
黑 红兰
甲
白 黄红
乙
绿 兰黄 丙
小结:
(1)正方体的展开图是平面图形; (2)正方体的展开图,因展开方式
的不同而不同,共有11种。
是不是所有的立体图形 展开后,都是平面图形?
球体的展开图是不是平面图形?
考考你
1、如果“你”在前面,那么什么在后面?
