计算方法上机实验题1~6
(完整版)数值计算方法上机实习题答案

(完整版)数值计算⽅法上机实习题答案1.设?+=105dx xx I nn ,(1)由递推公式nI I n n 151+-=-,从0I 的⼏个近似值出发,计算20I ;解:易得:0I =ln6-ln5=0.1823, 程序为:I=0.182; for n=1:20I=(-5)*I+1/n; end I输出结果为:20I = -3.0666e+010 (2)粗糙估计20I ,⽤nI I n n 515111+-=--,计算0I ;因为 0095.056 0079.01020201020≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2120=+=I 程序为:I=0.0087; for n=1:20I=(-1/5)*I+1/(5*n); end I0I = 0.0083(3)分析结果的可靠性及产⽣此现象的原因(重点分析原因)。
⾸先分析两种递推式的误差;设第⼀递推式中开始时的误差为000I I E '-=,递推过程的舍⼊误差不计。
并记nn n I I E '-=,则有01)5(5E E E n n n -==-=-Λ。
因为=20E 20020)5(I E >>-,所此递推式不可靠。
⽽在第⼆种递推式中n n E E E )51(5110-==-=Λ,误差在缩⼩,所以此递推式是可靠的。
出现以上运⾏结果的主要原因是在构造递推式过程中,考虑误差是否得到控制,即算法是否数值稳定。
2.求⽅程0210=-+x e x的近似根,要求41105-+?<-k k x x ,并⽐较计算量。
(1)在[0,1]上⽤⼆分法;程序:a=0;b=1.0;while abs(b-a)>5*1e-4 c=(b+a)/2;if exp(c)+10*c-2>0 b=c; else a=c; end end c结果:c =0.0903(2)取初值00=x ,并⽤迭代1021x k e x -=+;程序:x=0; a=1;while abs(x-a)>5*1e-4 a=x;x=(2-exp(x))/10; end x结果:x =0.0905(3)加速迭代的结果;程序:x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;y=exp(x)+10*x-2; z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x); b=x; end x结果:x =0.0995(4)取初值00=x ,并⽤⽜顿迭代法;程序:x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x; end x结果: x =0.0905(5)分析绝对误差。
《计算方法》上机实验试题

《计算方法》上机实验试题
1. (25分)计算积分
dx x x I n n ⎰
+=105, n=0,1,2,…,20 若用下列两种算法 (A) n I I n n 151+
-=- (B) ⎪⎭
⎫ ⎝⎛-=-n n I n I 1511 试依据积分I n 的性质及数值结果说明何种算法更合理。
2. (25分)求解方程f(x)=0有如下牛顿迭代公式
)()(111---'-
=n n n n x f x f x x , n ≥1,x 0给定 (1) 编制上述算法的通用程序,并以ε<--1n n x x (ε为预定精度)作为终止迭
代的准则。
(2)
利用上述算法求解方程 0cos :)(=-=x x x f
这里给定x 0=π/4,且预定精度ε=10-10。
3. (25分) 已知)3()(x x e x e x f -=,
(1)
利用插值节点x 0=1.00,x 1=1.02,x 2=1.04,x 3=1.06,构造三次Lagrange 插值公式,由此计算f(1.03)的近似值,并给出其实际误差; (2) 利用插值节点x 0=1,x 1=1.05构造三次Hermite 插值公式,由此计算f(1.03)的近
似值,并给出其实际误差。
4. (25分) 利用Romberg 算法计算积分
⎰
+4802cos 1dx x
精确到10
-4
总体要求:打印各题的程序代码及数值结果。
《数值计算方法》试题集及答案(1-6)#优选.

《计算方法》期中复习试题一、填空题:1、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用辛普生(辛卜生)公式计算求得⎰≈31_________)(dx x f ,用三点式求得≈')1(f 。
答案:2.367,0.252、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L3、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;4、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );答案)(1)(1n n n n n x f x f x x x '---=+5、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );6、计算方法主要研究( 截断 )误差和( 舍入 )误差;7、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n a b );8、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 ); 11、 两点式高斯型求积公式⎰1d )(xx f ≈(⎰++-≈1)]3213()3213([21d )(f f x x f ),代数精度为( 5 );12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5,1 ,进行两步后根的所在区间为 0.5,0.75 。
数值计算方法上机实习题考证

数值计算⽅法上机实习题考证--------------------------------------------------- 此⽂档包含我们计算⽅法的经典算法包含(数值计算⽅法上机实习题)1.设?+=105dx xx I nn ,(1)由递推公式n I I n n 151+-=-,从0I 的⼏个近似值出发,计算20I ;(2)粗糙估计20I ,⽤nI I n n 51511+-=-,计算0I ;(3)分析结果的可靠性及产⽣此现象的原因(重点分析原因)。
(1) 解答:n=0,0.1823)05ln()15ln()5(51515101010=+-+=++=+=+=x d xdx x dx x x I nn这⾥可以⽤for 循环,while 循环,根据个⼈喜好与习惯:for 循环程序: While 循环程序: I=0.1823; I=0.1823; for n=1:20 i=1;I=(-5)*I+1/n; while i<21 End I=(-5)*I+1/i; I i=i+1; fprintf('I20=%f',I) end I = -2.0558e+009 >> II20=-2055816073.851284>> I = -2.0558e+009 (2) 粗略估计I 20: Mathcad 计算结果: for 循环程序: While 循环程序: >> I=0.007998; I=0.007998; >> for n=1:20 n=1;I=(-0.2)*I+1/(5*n); while n<21End I=(-0.2)*I+1/(5*n); >> I n=n+1; I =0.0083 end >> II =0.0083(3) 算法误差分析:计算在递推过程中传递截断误差和舍⼊误差第⼀种算法:(从1——>20)1x x 205x +d 7.998103-?=*000e I I =-*115(5)5()555n n n n n n n n n n e I I I I I I e e e n n------=-=-+--+=-===误差放⼤了5n倍,算法稳定性很不好;第⼆种算法:(从20——>1)*n n ne I I =-***111111111()()555555n n n n n n nn e I I I I I I e n n ---=-=-+--+=-=0111...()55n ne e e ===误差在逐步缩⼩,算法趋近稳定,收敛。
计算方法上机实验

1. 用二分法解非线性方程:3()10200f x x x =+-=在(1,2)内的根,410ε-=输出格式:(k 从0开始)k k a k bk x ()k f xDivided times k =Root x =2. 用迭代法解非线性方程:()10x f x e x -=-+=410ε-=迭代函数:()1x x e ϕ-=+输出格式:(k 从0开始)k k xIterative times k =Root x =3. 有牛顿法解非线性方程:32()34560f x x x x =-+-+=在1.0附近的实根510ε-=输出格式:(k 从0开始)k k xIterative times k =Root x =1. 用弦割法求方程:32()390f x x x x =--+=在区间[-2,-1]内的一个实根近似值k x ,使5()10k f x -≤。
输出格式:(k 从0开始)k k x ()k f xIterative times k =Root x =2. 用艾特肯算法求方程:32()4100f x x x =--=在区间[1,2]内的近似值,取0 1.5x =,()g x ,精确到5110k k x x -+-≤输出格式:(k 从0开始)k k x k y k zIterative times k =Root x =1. 用高斯顺序消元法求解下面的线性方程组Ax b =:123123123242650422x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩输出方式:消元后的增广矩阵为:方程组的解为:x[1] =x[2] =x[3] =2. 用高斯列主元消元法求解下面的线性代数方程组Ax b =12341234123412340.40960.12340.36780.29430.40430.22460.38720.40150.11290.15500.36450.19200.37810.06430.42400.17840.40020.27860.39270.2557x x x x x x x x x x x x x x x x +++=⎧⎪+++=⎪⎨+++=⎪⎪+++=-⎩ 输出方式:消元后的增广矩阵为:方程组的解为:x[1] =x[2] =x[3] =1. 用杜利特尔三角分解法解线性方程组:AX =b123123123243421132411x x x x x x x x x --=⎧⎪+-=⎨⎪-+=⎩输出方式:分解后的三角阵L 为:分解后的三角阵U 为:方程组的解为:x[1] =x[2] =x[3] =2. 用追赶法解线性方程组:AX =b123421001131020141300154x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 输出方式:分解后的三角阵L 为:分解后的三角阵U 为:方程组的解为:x[1] =x[2] =x[3] =x[4] =1. 用雅可比迭代法解线性方程组:AX =b,精度要求16||||10k k X X --∞-≤12321143421132411x x x --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦输入方式:Input n=Input Matrix element of A:Input bInput vector x0:输出方式:k [1]x [2]x ⋅⋅⋅ []x nJacobi ? times!Output Solution:[1]x = ,[2]x = ,⋅⋅⋅,[]x n =2. 用高斯-赛德尔迭代法解线性方程组:AX =b ,精度要求16||||10k k X X --∞-≤12321143421132411x x x --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦输入输出方式与雅可比迭代法相同从函数表出发,用下列方法计算f(0.15)、f(0.31)及f(0.47)的近似值:(1)、分段线性插值。
数值计算方法上机实验考试答案

数值计算方法上机实验考试答案1. 小型火箭初始质量为900千克,其中包括600千克燃料。
火箭竖直向上发射时燃料以15千克/秒的速率燃烧掉,由此产生30000牛顿的恒定推力。
当燃料用尽时引擎关闭。
设火箭上升的整个过程中,空气阻力与速度平方成正比,比例系数为0.4(千克/米)。
重力加速度取9.8米/秒2.A. 建立火箭升空过程的数学模型(微分方程);B. 求引擎关闭瞬间火箭的高度、速度、加速度,及火箭到达最高点的时间和高度。
解:A . 建立模型:)(t x ——t 时刻的火箭高度;T =30000(牛顿)——火箭推力,当时间t >40秒时,T=0; m t m 150-=——火箭飞行过程中的质量,t >40秒时,300=m 千克0m =900(千克)——火箭初始质量; 1m =600(千克)——燃料质量;c =15(千克/秒)——燃料的燃烧速率; k =0.4(千克/米)——空气阻力系数; g =9.8(米/秒2)——重力加速度由能量守恒定律,可得到火箭飞行过程的方程:mg T t x k t x m -+'-=''2)]([)(这是一个初值问题,初始条件为 0)0(,0)0(='=x x设)(),(21t x x t x x '==,则问题化为求下列微分方程组的初值问题:⎪⎩⎪⎨⎧--+--='='g t m T x t m k x x x 151******** 0)0(,0)0(21==x xB . 关闭引擎时4015/600==t (秒),所求的是此时火箭的高度)40(1x ;速度)40(2x ;加速度)40()40(21x x '''或,及火箭到最高点的时间m t 和高度)(1m t x 。
具体的Matlab 程序如下: 首先建立微分方程的的m 文件:function y=huojian(t,x)k=0.4;g=9.8;m0=900;T=30000;m=m0-15*t;if t>40T=0;m=300;endy=[x(2),-(k/m)*x(2)^2+T/m-g]';主程序:%feixing.mk=0.4;g=9.8;m0=900;T=30000;x0=[0,0];ts=0:1:55;[t,x]=ode23('huojian',ts,x0);[t,x(:,1)]%------a=[t,x];x40=a(41,2) %燃料用尽时的高度v40=a(41,3) %燃料用尽时的速度a40=-(k/300)*v40^2+T/300-g %燃料用尽时的加速度%-------xmax=max(x(:,1)) %火箭到达最高点的高度subplot(2,1,1),plot(t,x(:,1)),title('altitude') subplot(2,1,2),plot(t,x(:,2)),title('speed')运行结果为:1.0e+003 *0 00.0010 0.01180.0020 0.04750.0030 0.10670.0040 0.18890.0050 0.29270.0060 0.41680.0070 0.55920.0080 0.71800.0090 0.89140.0100 1.07700.0380 7.80510.0390 8.06310.0400 8.32240.0410 8.54000.0420 8.70040.0430 8.82420.0440 8.92180.0450 8.99940.0460 9.06070.0470 9.10830.0480 9.14370.0490 9.16810.0500 9.18220.0510 9.18640.0520 9.18070.0530 9.16510.0540 9.13900.0550 9.1018x40 =8322.4v40 = 254.1728a40 = 4.0616xmax =9186.4关闭引擎时4015/600==t (秒),此时火箭的高度h=)40(1x =8322.4米,速度v=)40(2x =254.1728米/秒,加速度为a=)40(1x ''= 4.0616米/秒2,火箭到最高点的时间m t =51秒,高度)(1m t x =9186.4米。
计算方法上机题目

计算⽅法上机题⽬⽬录1.计算⽅法A 上机作业 (1)上机练习⽬的 (1)上机练习任务 (1)计算⽅法A 上机题⽬ (1)程序设计要求 (1)上机报告要求 (1)2.QR 分解法求解线性⽅程组 (2)计算原理 (2)程序框图 (7)计算实习 (8)Matlab代码 (8)3.共轭梯度法求解线性⽅程组 (10)计算原理 (10)程序框图 (11)计算实习 (12)Matlab代码 (12)4.三次样条插值 (14)计算原理 (14)程序框图 (16)计算实习 (17)Matlab代码 (17)5.四阶龙格-库塔法求解常微分⽅程的初值问题 (21)计算原理 (21)程序框图 (22)计算实习 (23)Matlab代码 (23)1.计算⽅法A 上机作业上机练习⽬的复习和巩固数值计算⽅法的基本数学模型,全⾯掌握运⽤计算机进⾏数值计算的具体过程及相关问题。
利⽤计算机语⾔独⽴编写、调试数值计算⽅法程序,培养学⽣利⽤计算机和所学理论知识分析解决实际问题的能⼒。
上机练习任务利⽤计算机语⾔编写并调试⼀系列数值⽅法计算通⽤程序,并能正确计算给定题⽬,掌握调试技能。
掌握⽂件使⽤编程技能,如⽂件的各类操作,数据格式设计、通⽤程序运⾏过程中⽂件输⼊输出运⾏⽅式设计等。
写出上机练习报告。
计算⽅法A 上机题⽬1. QR 分解⽅法求解线性⽅程组。
(第⼆章)2. 共轭梯度法求解线性⽅程组。
(第三章)3. 三次样条插值(第四章)4. 四阶龙格-库塔法求解常微分⽅程的初值问题程序设计要求1. 程序要求是通⽤的,在程序设计时要充分考虑哪些变量应该可变的。
2. 程序要求调试通过。
上机报告要求报告内容包括:●每种⽅法的算法原理及程序框图。
●程序使⽤说明。
●算例计算结果。
2. QR 分解法求解线性⽅程组计算原理当nx R∈是任意给定的⾮零向量,nv R∈是任意给定的单位向量,则存在初等反射阵2THI u u=-,使得H xvσ=,其中σ为常数,当取单位向量2x v ux vσσ-=-时,由u 确定的矩阵H 必定满⾜H xvσ=,所以在计算过程中取u 的值为上述值。
计算方法上机实习题大作业(实验报告)

计算方法实验报告班级: 学号: 姓名: 成绩:1 舍入误差及稳定性一、实验目的(1)通过上机编程,复习巩固以前所学程序设计语言及上机操作指令;(2)通过上机计算,了解舍入误差所引起的数值不稳定性二、实验内容1、用两种不同的顺序计算1000021n n -=∑,分析其误差的变化 2、已知连分数()101223//(.../)n n a f b b a b a a b =++++,利用下面的算法计算f : 11,i n n i i i a d b d b d ++==+ (1,2,...,0)i n n =-- 0f d = 写一程序,读入011,,,...,,,...,,n n n b b b a a 计算并打印f3、给出一个有效的算法和一个无效的算法计算积分1041nn x y dx x =+⎰ (0,1,...,10)n = 4、设2211N N j S j ==-∑,已知其精确值为1311221N N ⎛⎫-- ⎪+⎝⎭(1)编制按从大到小的顺序计算N S 的程序(2)编制按从小到大的顺序计算N S 的程序(3)按两种顺序分别计算10001000030000,,,S S S 并指出有效位数三、实验步骤、程序设计、实验结果及分析1、用两种不同的顺序计算1000021n n -=∑,分析其误差的变化 (1)实验步骤:分别从1~10000和从10000~1两种顺序进行计算,应包含的头文件有stdio.h 和math.h(2)程序设计:a.顺序计算#include<stdio.h>#include<math.h>void main(){double sum=0;int n=1;while(1){sum=sum+(1/pow(n,2)); if(n%1000==0)printf("sun[%d]=%-30f",n,sum);if(n>=10000)break;n++;}printf("sum[%d]=%f\n",n,sum); }b.逆序计算#include<stdio.h>#include<math.h>void main(){double sum=0;int n=10000;while(1){sum=sum+(1/pow(n,2));if(n%1000==0)printf("sum[%d]=%-30f",n,sum);if(n<=1)break;n--;}printf("sum[%d]=%f\n",n,sum);}(3)实验结果及分析:程序运行结果:a.顺序计算b.逆序计算结果分析:两种不同顺序计算结果是一样的,顺序计算误差从一开始就很小,而逆序计算误差最开始十分大,后来结果正确。
计算方法上机实习题

数值计算方法上机实习题1. 设⎰+=105dx xx I nn , (1) 由递推公式nI I n n 151+-=-,从0=0.1822I , 0=0.1823I 出发,计算20I ; (2) 20=0I ,20=10000I , 用nI I n n 51511+-=-,计算0I ;(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
解:(1)程序如下: clear all clc I=0.1822; %题中的已知数据 for n=1:20; I=(-5)*I+1/n; %由递推公式所得 end fprintf('I20=%f\n',I) M=0.1823; %与I 的计算结果形成对比for i=1:20; M=(-5)*M+1/i; %由递推公式所得 end fprintf('M20=%f\n',M) 输出结果为: I20=-11592559237.912731 M20=-2055816073.851284 (2)程序如下: clear all clc I=0; %赋予I20的初始值 for n=0:19; I=(-1/5)*I+1/(5*(20-n)); %有递推公式得 end fprintf('I0=%f\n',I)M=10000; for i=0:19; M=(-1/5)*M+1/(5*(20-i));%有递推公式得 end fprintf('M0=%f\n',M) 输出结果为: I0=0.182322 M0=0.182322(3)由输出结果可看出第一种算法为不稳定算法,第二中算法为稳定算法。
由于误差*000***21111120115(5)5()555nn n n n n n n n n e I I e I I I I I I e e e n n------=-=-=-+--+=-===第一种算法为正向迭代算法,每计算一步误差增长5倍,虽然所给的初始值很接近,随着n 的增大,误差也越来越大。
计算方法上机实习作业
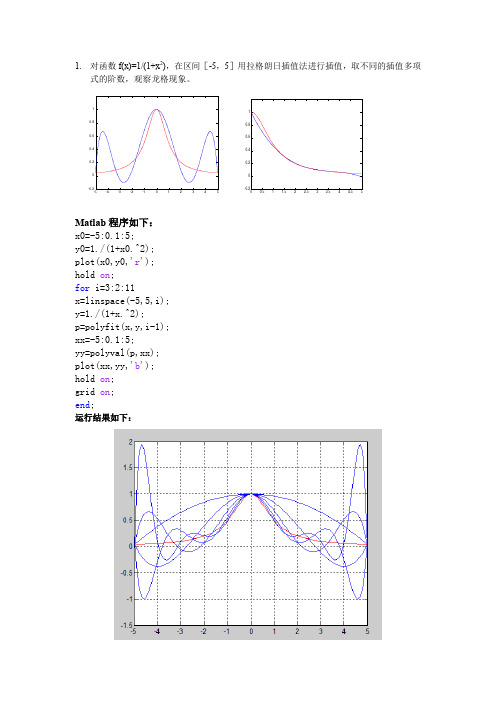
如图所示,在两端出现龙格现象,并且阶数越高龙格现象越明显。 若在区间[0,5]进行插值,是否还存在龙格现象?
Matlab 程序如下: x0=0:0.1:5; y0=1./(1+x0.^2); plot(x0,y0,'r'); hold on; for i=3:2:11 x=linspace(-0,5,i); y=1./(1+x.^2); p=polyfit(x,y,i-1); xx=0:0.1:5; yy=polyval(p,xx); plot(xx,yy,'b'); hold on; grid on; end;
0
1
2
3
4
Matlab 程序如下: clear;clc; x=0:0.1:2.5; y=sin(x); y1=x; y2=x-x.^3/6; y3=x-x.^3/6+x.^5/120; plot(x,y,'b',x,y1,'g',x,y2,'r',x,y3,'k')
输出结果如图:
1.500000000000000 1.414213562374690 1.414213562373095
1.416666666666667 1.414213562373095
2.000000000000000 1.732050810014727 1.732050807568877
1.750000000000000 1.732050807568877
x 2 n 1 ,编写程序实 ( 2n 1)! k 1 现如下功能:对 n=1,2,3,绘制出区间[0,2.5 ]上的近似函数的图形以及 sin x 本身的图
4.由正弦函数的 Tylor 展开式取前 n 项,得 sin x ( 1) n1
计算方法上机题

1. 计算100000211k S k==∑,要求误差小于610-,给出实现算法。
算法组织:利用绝对值的递增相加可以减小误差 具体算法:%% 公式求和 %% S = 0; k = 100000;%%利用for 循环对公式进行求和 for n = 1: 100000 S = S+1/(k*k); k = k-1; end%%精确到小数点后6位,以保证误差范围 vpa(S,7)运行程序后,得到的结果是1.644924,精确到了小数点后6位。
2. 编写实现对N 阶非奇矩阵A 进行LU 分解的程序。
算法组织:(1) 根据定理可知若N 阶矩阵的各阶顺序主子式行列式不为零,则存在唯一的单位下三角矩阵L 和上三角矩阵U ,满足A=LU ,因此首先需要判断A 中的元素a kk (k=0,1,2…,n )不为零。
(2) 根据如下的式子计算L 和U 中的元素121231(,,...,1,0,0...0)000j j jj ij i i i ii u u u a l l l l -⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭11(,1,2,3,)i ij ik kj ij k a l u u j i i n -==+≥=∑1(,1,2,3,)j ij ik kj k a l u j i i n ==<=∑当i=1时,得到u 1j =a 1j (j=1,2,3,…,n),而当j=1时,得l i1= a i1/u 11,由此可以计算出L 的第一列元素和U 的第一行元素。
然后可以依据下式计算L 和U 中的其他元素。
11(,1,2,3,)i ij ij it tj t u a l u j i i i i n -==-=+++∑111()(1,2,3,)i ki ki it tj t ii l a l u k i i i n u -==-=+++∑具体算法:[n,n]=size(A); %检测A 的阶数 L=eye(n); %初始化单位下三角阵L U=zeros(n,n); %初始化上三角阵Ufor i=1:nU(1,i)=A(1,i); %给上三角阵U 的第一行赋值L(i,1)=A(i,1)/U(1,1); %给单位下三角阵L 的第一列赋值 end for i=2:n for j=i:n for k=1:i-1M(k)=L(i,k)*U(k,j); endU(i,j)=A(i,j)-sum(M); %给上三角阵U 的第i 行赋值 endfor j=i+1:n for k=1:i-1M(k)=L(j,k)*U(k,i); endL(j,i)=(A(j,i)-sum(M))/U(i,i); %给单位下三角阵L 的第i 列赋值 end end%分别输出L,U 的矩阵 L U3.编写程序实现大规模方程组的列主元高斯消去法程序,并对所附的方程组进行求解。
(完整)《数值计算方法》试题集及答案(1-6) 2

《计算方法》期中复习试题一、填空题:1、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用辛普生(辛卜生)公式计算求得⎰≈31_________)(dx x f ,用三点式求得≈')1(f 。
答案:2.367,0.252、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L3、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;4、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );答案)(1)(1n n n n n x f x f x x x '---=+5、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );6、计算方法主要研究( 截断 )误差和( 舍入 )误差;7、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n ab );8、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0。
15 );11、 两点式高斯型求积公式⎰1d )(xx f ≈(⎰++-≈1)]3213()3213([21d )(f f x x f ),代数精度为( 5 );12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5,1 ,进行两步后根的所在区间为 0。
《数值计算方法》试题集及答案(1-6)-2..

《计算方法》期中复习试题一、填空题:1、已知3.1)3(,2.1)2(,0.1)1(===f f f ,则用辛普生(辛卜生)公式计算求得⎰≈31_________)(dx x f ,用三点式求得≈')1(f 。
答案:2.367,0.252、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L3、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;4、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );答案)(1)(1n n n n n x f x f x x x '---=+5、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );6、计算方法主要研究( 截断 )误差和( 舍入 )误差;7、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n a b );8、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 ); 11、 两点式高斯型求积公式⎰1d )(xx f ≈(⎰++-≈1)]3213()3213([21d )(f f x x f ),代数精度为( 5 );12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5,1 ,进行两步后根的所在区间为 0.5,0.75 。
数值计算方法上机实习题

数值计算方法上机实习题(总13页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--数值计算方法上机实习题1.设⎰+=105dx xx I nn , (1) 由递推公式nI I n n 151+-=-,从I 0=0.1824, 0=0.1823I 出发,计算20I ; (2) 20=0I ,20=10000I , 用nI I n n 515111+-=--,计算0I ;(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
答:第一个算法可得出e 0=|I 0−I 0∗| e n =|I n −I n ∗|=5n |e 0|易知第一个算法每一步计算都把误差放大了5倍,n 次计算后更是放大了5n 倍,可靠性低。
第二个算法可得出e n =|I n −I n ∗| e 0=(1)n|e n |可以看出第二个算法每一步计算就把误差缩小5倍,n 次后缩小了5n 倍,可靠性高。
2.求方程0210=-+x e x 的近似根,要求41105-+⨯<-k k x x ,并比较计算量。
(1) 在[0,1]上用二分法; (1) [0,1]上的二分法二分法子程序:function [root,n]=EFF3(f,x1,x2) %第二题(1)二分法f1=subs(f,symvar(f),x1);%函数在x=x1的值 f2=subs(f,symvar(f),x2);%x=x2 n=0;%步数er=5*10^-4;%误差 if(f1==0) root=x1; return; elseif(f2==0) root=x2; return;elseif(f1*f2>0)disp('两端点函数值乘积大于0!'); return; elsewhile(abs(x1-x2)>er)%循环 x3=(x1+x2)/2;f3=subs(f,symvar(f),x3); n=n+1; if(f3==0) root=x3; break;elseif(f1*f3>0) x1=x3; elsex2=x3; end endroot=(x1+x2)/2;%while 循环少一步需加上 end计算根与步数程序:fplot(@(x) exp(x)+10*x-2,[0,1]); grid on; syms x;f=exp(x)+10*x-2; [root,n]=EFF3(f,0,1);fprintf('root=% ,n=%d \n',root,n);计算结果显示:root= ,n=11(2) 取初值00=x ,并用迭代1021x k e x -=+;(2) 初值x 0=0迭代 迭代法子程序:function [root,n]=DDF(g,x0,err,max) (接下页) %root 根,n+1步数,g 函数,x0初值,err 误差,max 最大迭代次数 X(1)=x0; for n=2:maxX(n)=subs(g,symvar(g),X(n-1)); c=abs(X(n)-X(n-1)); root=X(n); if(c<err)计算根与步数程序:syms x;f=(2-exp(x))/10; (接下页) x0=0;err=5*10^(-4); max=100;[root,n]=DDF(f,x0,err,max); fprintf('root=% ,n=%d \n',root,n);计算结果显示: root= ,n=4(3) 加速迭代的结果;(4) 取初值00 x ,并用牛顿迭代法;(5) 分析绝对误差。
数值计算方法上机实习题答案.doc

1.设I n 1 x ndx ,0 5 x( 1)由递推公式 I n 5I n 11,从 I 0的几个近似值出发,计算I 20;n解:易得: I 0 ln6-ln5=0.1823, 程序为:I=0.182;for n=1:20I=(-5)*I+1/n;endI输出结果为: I 20= -3.0666e+010( 2)粗糙估计 I 20,用 I n 1 1I n 1 1 ,计算 I 0;5 5n0.0079 1 x 20 1 x 200.0095因为dx I 20dx 6 5所以取 I 20 1(0.0079 0.0095) 0.0087 2程序为: I=0.0087;for n=1:20I=(-1/5)*I+1/(5*n);endII 0= 0.0083( 3)分析结果的可靠性及产生此现象的原因(重点分析原因 )。
首先分析两种递推式的误差;设第一递推式中开始时的误差为E0 I 0 I 0,递推过程的舍入误差不计。
并记 E n I n I n,则有 E n 5E n 1 ( 5) n E0。
因为 E20( 5) 20 E0 I 20,所此递推式不可靠。
而在第二种递推式中E0 1E1 (1)n E n,误差在缩小,5 5所以此递推式是可靠的。
出现以上运行结果的主要原因是在构造递推式过程中,考虑误差是否得到控制,即算法是否数值稳定。
2.求方程e x10x 2 0 的近似根,要求x k 1x k 5 10 4,并比较计算量。
(1)在 [0, 1]上用二分法;程序: a=0;b=1.0;while abs(b-a)>5*1e-4c=(b+a)/2;if exp(c)+10*c-2>0b=c;else a=c;endendc结果: c =0.0903( 2)取初值x0 0,并用迭代 x k 1 2 e x ;10程序: x=0;a=1;while abs(x-a)>5*1e-4a=x;x=(2-exp(x))/10;endx结果: x =0.0905(3)加速迭代的结果;程序: x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;y=exp(x)+10*x-2;z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x);b=x;endx结果: x =0.0995( 4)取初值x00 ,并用牛顿迭代法;程序: x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x;end x 结果: x =0.0905( 5) 分析绝对误差。
数值计算方法上机实习题NEW

数值计算方法上机实习题1. 设,(1) 由递推公式,从 , 出发,计算 ; 程序如下:function I=myhs(I0,n) if n>=1I=myhs(I0,n-1)*(-5)+1/n; elseif n==0 I=I0; end命令行窗口输入: I0=0.1822;I1=myhs(I0,20); I0=0.1823;I2=myhs(I0,20);运行结果:当I0=0.1822时,I20=-1.1593e+10。
当I0=0.1823时,I20= -2.0558e+9。
(2) ,20=10000I , 用,计算0I ; 程序如下:function I=myhs2(I20,n) if (n<20)I=myhs2(I20,n+1)*(-1)/5+1/(5*(n+1)); elseif n==20 I=I20; end命令行窗口输入:I20=0;I1=myhs2(I20,20); I20=10000;I2=myhs2(I20,20);运行结果:当I 20=0时,I 0=0.182321556793955。
当I 20=10000时,I 0= 0.182321556898812。
(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
根据上式,假设I n 的真值为I*,误差为e n ,即e=I*-I n 。
综合递推式,有e n =-5*e n-1,这意味着哪怕开始只有一点点误差,只要n 足够大,按照这种计算一步误差增长5倍的方式,所得的结果总是不可信的,因此整个算法是不稳定的。
根据上式,假设I n 的真值为I*,误差为e n ,即e=I*-I n 。
综合递推式,有e n-1. =(-1/5)*e n ,按照这种计算误差会以每步缩小到1/5的方式进行,根据(2)得到的结果而言,该算法是相对稳定的。
2. 求方程0210=-+x e x 的近似根,要求41105-+⨯<-k k x x ,并比较计算量。
数值分析上机作业1-1解析

数值计算方法上机题目11、实验1. 病态问题实验目的:算法有“优”与“劣”之分,问题也有“好”和“坏”之别。
所谓坏问题就是问题本身的解对数据变化的比较敏感,反之属于好问题。
希望读者通过本实验对此有一个初步的体会。
数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。
病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。
问题提出:考虑一个高次的代数多项式∏=-=---=201)()20)...(2)(1()(k k x x x x x p (E1-1)显然该多项式的全部根为l ,2,…,20,共计20个,且每个根都是单重的(也称为简单的)。
现考虑该多项式方程的一个扰动0)(19=+xx p ε (E1-2)其中ε是一个非常小的数。
这相当于是对(E1-1)中19x 的系数作一个小的扰动。
我们希望比较(E1-1)和(E1-2)根的差别,从而分析方程(E1-1)的解对扰动的敏感性。
实验内容:为了实现方便,我们先介绍两个 Matlab 函数:“roots ”和“poly ”,输入函数u =roots (a )其中若变量a 存储1+n 维的向量,则该函数的输出u 为一个n 维的向量。
设a 的元素依次为121,...,,+n a a a ,则输出u 的各分量是多项式方程0...1121=++++-n n n n a x a x a x a的全部根,而函数b=poly(v)的输出b 是一个n +1维变量,它是以n 维变量v 的各分量为根的多项式的系数。
可见“roots ”和“Poly ”是两个互逆的运算函数.ve=zeros(1,21); ve(2)=ess;roots(poly(1:20))+ve)上述简单的Matlab 程序便得到(E1-2)的全部根,程序中的“ess ”即是(E1-2)中的ε。
实验要求:(1)选择充分小的ess ,反复进行上述实验,记录结果的变化并分析它们。
数值计算方法上机实验题

数值计算方法上机实验实验内容:1.要求:分别用复化梯形法,复化Simpson 法和 Romberg 公式计算.2.给定积分dx e x⎰31和dx x ⎰311 ,分别用下列方法计算积分值要求准确到510- ,并比较分析计算时间. 1)变步长梯形法; 2)变步长 Simpson 法; 3) Romberg 方法.算法描述:1、复合梯形法:⎰=tdt t a t V 0)()( ))()(2)((211∑-=++=n k k n b f x f a f hT输入 被积函数数据点t,a. 输出 积分值.n T复合Simpson 法:⎰=tdt t a t V 0)()( ))()(2)(4)((6101121∑∑---=++++=n k n k k k n b f x f x f a f hS输入 被积函数f(x),积分区间[a,b]和n 输出 复合Simpson 积分值n S步1 .);()(;a x b f a f S nab h n ⇐-⇐-⇐ 步2 对n k ,,2,1 =执行).(2;2);(4;2x f S S hx x x f S S h x x n n n n +⇐+⇐+⇐+⇐步3 n n S hS ⨯⇐6步4 输出n SRomberg 积分法:根据已知数据对其进行多项式拟合得出p(x);f(x)⇐p(x); 输入 被积函数f(x),积分区间端点a,b,允许误差ε 输出 Romberg 积分值n R 2 步1 .0;0;0;0));()((2;1111⇐===+⇐-⇐k R C S b f a f hT a b h 步2 反复执行步3→步9. 步3 .2;0h a x S +⇐⇐ 步4 反复执行步5→步6. 步5 ;);(h x x x f S S +⇐+⇐步6 若x ≥b,则退出本层循环. 步7 执行.6316364;1511516;3134;2212212212212C C R S S C T T S S h T T -⇐-⇐-⇐+⇐步8 执行.1;;;;;2;2121212112+⇐⇐⇐⇐⇐⇐-⇐k k R R C C S S T T hh R R e 步9 若e ≤ε且k ≥5,则退出循环. 步10 .22R R n ⇐ 步11 输出.2n R2、变步长梯形算法:功能 求积分⎰ba)(dx x f ,允许误差为ε。
上机实验六_答案(请自行校对)

上机实验六一维数组学号: 姓名:一.目的要求1.掌握一维数组的基本概念,如何定义一维数组,如何初始化一维数组。
2.掌握数组的基本操作:引用数组元素、行(列)求和,行(列)最大最小值,整个数组的输入输出等。
3.掌握与数组有关的算法,如排序、找最大最小值(或位置)等。
二.实验内容第1题、输入n(n不超过10),然后输入n个数组元素,要求将数组元素在同一个数组中按逆序重新存放并输出。
如输入51 2 3 4 5应输出5 4 3 2 1#include <stdio.h>void main(){int a[10], i, n ;printf("请输入小于10的数n:\n");scanf("%d", &n);printf("请输入%d个整数:\n", n);for (i=0; i<n; i++) //for语句里面只有一条语句,所以{}可以省scanf("%d", &a[i]);// 下面逐个打印这n个整数for (i=n-1; i>=0; i--)printf("%d ", a[i]);printf("\n", n);}第2题、输入一个数组的所有元素,再输入一个整数m,把该数组的后m个数字移到数组的前头。
比如数组元素为:1 2 3 4 5 6 7 8 9 10,m=4,应输出:7 8 9 10 1 2 3 4 5 6#include <stdio.h>void main(){int a[10], i, m, t, j ;printf("请输入10个整数:\n");for (i=0; i < 10; i++)scanf("%d", &a[i]);printf("请输入一个小于10的数m:");scanf("%d", &m);// 下面循环重复m次,每次将最后一个元素放到第一个位置for (i=0; i<m; i++) {t = a[9]; // 将数组最后一个位置腾出来;//这个循环是将每个数据元素往后挪动一位for (j=9; j>0; j--) {a[j] = a[j-1];}a[0] = t; //将最后那个元素放到第一个位置}// 下面逐个打印数组元素for (i=0; i<10; i++)printf("%d ", a[i]);printf("\n");}第3题、输入一个数组的所有元素值,将最大的元素与第一个元素交换,最小的元素与最后一个元素交换,然后输出数组所有元素。
数值计算方法上机实习题考证

---------------------------------------------------此文档包含我们计算方法的经典算法包含(数值计算方法上机实习题)1. 设⎰+=105dx x x I nn , (1) 由递推公式nI I n n 151+-=-,从0I 的几个近似值出发,计算20I ; (2) 粗糙估计20I ,用n I I n n 51511+-=-,计算0I ; (3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
(1) 解答:n=0,0.1823)05ln()15ln()5(51515101010=+-+=++=+=+=⎰⎰⎰x d x dx x dx x x I nn 这里可以用for 循环,while 循环,根据个人喜好与习惯:for 循环程序: While 循环程序:I=0.1823; I=0.1823;for n=1:20 i=1;I=(-5)*I+1/n; while i<21End I=(-5)*I+1/i;I i=i+1;fprintf('I20=%f',I) endI = -2.0558e+009 >> II20=-2055816073.851284>> I = -2.0558e+009(2) 粗略估计I 20: Mathcad 计算结果: for 循环程序: While 循环程序: >> I=0.007998; I=0.007998;>> for n=1:20 n=1;I=(-0.2)*I+1/(5*n); while n<21End I=(-0.2)*I+1/(5*n);>> I n=n+1;I =0.0083 end>> II =0.0083(3) 算法误差分析:计算在递推过程中传递截断误差和舍入误差第一种算法:(从1——>20)01x x 205x +⎛⎜⎜⎜⎠d 7.998103-⨯=*000e I I =-***21111120115(5)5()555n n n n n n n n n n e I I I I I I e e e n n------=-=-+--+=-===误差放大了5n 倍,算法稳定性很不好;第二种算法:(从20——>1)*n n ne I I =- ***111111111()()555555n n n n n n n n e I I I I I I e n n ---=-=-+--+=-=0111...()55n n e e e === 误差在逐步缩小,算法趋近稳定,收敛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一:误差传播与算法稳定性
实验目的:体会稳定性在选择算法中的地位。
实验内容:考虑一个简单的由积分定义的序列
1
0I ,0,1,10n
n x dx n a x
==+⎰
其中a 为参数,分别对0.05a =及15a =按下列两种方法计算。
方案1:用递推公式 11,1,2,,10n n I aI n n -=-+=
递推初值可由积分直接得 01
ln a I a +=
方案2:用递推公式 111
(),
,1,,1n n I I n N N a n
-=-+=-
根据估计式 当1n a n ≥
+时,11
(1)(1)(1)
n I a n a n <<+++或
当01n a n ≤<
+时,
11
(1)(1)n I a n n
<≤++ 取递推初值 当1n a n ≥
+时, 11121()2(1)(1)(1)2(1)(1)N N a I I a N a N a a N +≈+=+++++ 当01n a n ≤<
+时,111()2(1)(1)N N I I a N N
≈+++ 实验要求:列出结果,并对其稳定性进行分析比较,说明原因。
实验二:非线性方程数值解法
实验目的:探讨不同方法的计算效果和各自特点 实验内容:应用算法(1)牛顿法;(2)割线法 实验要求:
(1)用上述各种方法,分别计算下面的两个例子。
在达到精度相同的前提下,比较其迭代次数。
(I )3
1080x x +-=,取00x =;
(II) 2
2
81(0.1)sin 1.060x x x -+++=,取00x =;
(2) 取其它的初值0x ,结果如何?反复选取不同的初值,比较其结果; (3) 总结归纳你的实验结果,试说明各种方法的特点。
实验三:选主元高斯消去法----主元的选取与算法的稳定性
问题提出:Gauss 消去法是我们在线性代数中已经熟悉的。
但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss 消去法作为数值算法的稳定性呢?Gauss 消去法从理论算法到数值算法,其关键是主元的选择。
主元的选择从数学理论上看起来平凡,它却是数值分析中十分典型的问题。
实验内容:考虑线性方程组
n n n R b R A b Ax ∈∈=⨯,,
编制一个能自动选取主元的求解线性方程组的Gauss 消去过程。
实验要求:
(1)取矩阵⎥⎥
⎥
⎥⎥
⎥⎦
⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157,6816816816 b A ,则方程有解T x )1,,1,1(* =。
取n=10计算,让程序自动选取主元,结果如何?
(2)现在每步消去过程总选取按模最小或按模尽可能小的元素作为主元,观察并记录计算结果。
若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。
(3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用。
(4)将上述矩阵A 中的主元改为0.00006再重新作一次数值实验看看。
(5)选取其他你感兴趣的问题或者随机生成矩阵,重复上述实验,观察记录并分析实验结果。
实验四:线性方程组的迭代解法
实验目的:研究对比Jacobi 迭代法与G-S 迭代法。
实验内容:分别用Jacobi 迭代法与G-S 迭代法求解下列方程组。
(1)123103
19211371131235x x x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪-= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,()*
254T x =-
(2)12310.40.430.410.4 3.60.40.41 4.2x x x ⎛⎫⎛⎫⎛⎫
⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,()*
123T x =
(3)123522141311222632x x x --⎛⎫⎛⎫⎛⎫
⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭
,()*
235T x =-
(4)12331101
411811512x x x ⎛⎫⎛⎫⎛⎫
⎪⎪ ⎪
-= ⎪⎪ ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎝⎭
,()*363T x =- 取迭代初值(0)
0x
=
实验要求:
(1)编程求解,并与精确解对比;
(2)考查迭代法的收敛性,若收敛,对比两种方法的收敛速度。
实验五:插值(从以后两个实验中任选其一)
实验5.1:多项式插值的振荡现象
问题提出:考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时,)(x L n 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数
22511)(x x f +=
实验内容:考虑区间[-1,1]的一个等距划分,分点为
n i n i
x i ,,2,1,0,21 =+
-=
则拉格朗日插值多项式为
∑
=+=n
i i
j
n x l x x L 02)(2511
)(
其中的n i x l i ,,2,1,0),( =是n 次拉格朗日插值基函数。
实验要求:
(1) 选择不断增大的分点数目n=2,3….,如果所用软件能够画图则画出原函数f(x)及插值多项式函数
)(x L n 在[-1,1]上的图像,比较并分析实验结果;如果不能够画图,则列出
函数f(x)及插值多项式函数
)(x L n 在[-1,1]上部分函数值,比较并分析实验结果。
(2)选择其他的函数,例如定义在区间[-5,5]上的函数
x x g x x
x h arctan )(,1)(4
=+=
重复上述的实验看其结果如何。
(3)区间[a,b]上切比雪夫点的定义为
1,,2,1,)1(2)12(c o s 22+=⎪⎪⎭⎫
⎝⎛+--++=
n k n k a b a b x k π
以
121,,+n x x x 为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果
实验5.2:Lagrange 插值法和Newton 插值法
实验目的:掌握Lagrange 插值法和Newton 插值法
问题提出:设22
()
t x
f x e dt -
-∞
=
,已知()f x 的函数值表:
用插值法求(0.13)f 和(0.36)f 的近似值
实验内容:
(1)分别用Lagrange 插值法和Newton 插值法编程求解。
(2)求出插值多项式的系数,对比计算结果。
实验要求:
(1)分析这两种插值方法的时间复杂度;
(2)测量计算时间,并与理论分析结果对比。
为测量计算时间,可计算出很多点的函数
值;
实验六:数值积分
实验目的:练习使用基本的复化求积公式计算积分近似值 实验内容:计算下列程式右端定积分的近似值 (1)3
22
1ln 22
1
dx x =--⎰
(2)1201
41dx x π=+⎰ (3)
10
23ln 3x dx =⎰(4)22
1x e xe dx =⎰ 实验要求:
(1)若用复化梯形公式、复化Simpson 公式作计算,要求绝对误差限为,分别利用它们的余项对每种算法作出步长的事前估计。
(2) 分别用复化梯形公式、复化Simpson 公式作计算,列出实验结果。
