高三数学每周一测(抛物线)解答.许兴华

合集下载

高三数学每周一测(抛物线).许兴华

高三数学每周一测(抛物线).许兴华(附注:答案详见《百度文库》PPT 课件.许兴华)班级学号姓名一、选择题（每小题10分，共60分）1．抛物线2y ax =的焦点与双曲线2213x y -=的左焦点重合，则这条抛物线的方程是（）A ．24y x =B ．24y x =-C ．2y =-D ．28y x =- 2．抛物线2y x =-上的点到直线4380x y +-=的距离的最小值是（）A ．43B ．75C ．85D ．33．设12,,0,x x R a ∈>常数定义运算“*”：22121212()(),x x x x x x *=+--若0x ≥，则动点(P x 的轨迹是（）A ．圆B ．椭圆的一部分C ．双曲线的一部分D ．抛物线的一部分 4．过抛物线2(0)y ax a =>的焦点F 任作一直线交抛物线于P 、Q 两点，若线段PF 与FQ的长分别为p 、q ，则11p q+的值为（） A ．2aB ．12aC ．4aD ．4a 5．点M 是抛物线2y x =的动点，点N 是圆221:(1)(4)110C x y x y ++-=-+=关于直线对称曲线C 上的一点，则MN 的最小值是（）A ．12- B ．12- C ．2 D 1 6．已知抛物线21x y =+上一定点A （－1，0）和两动点P ，Q ，当PA PQ ⊥时，点Q的横坐标的取值范围是（）A ．(,3]-∞-B ．[1,)+∞C ．[－3，1]D ．(,3][1,)-∞-+∞二、填空题（每小题10分，共40分）7．设点P 是抛物线2x y =上到直线23y x =-的距离最短的点，F 是该抛物线的焦点，则PF = ．8．定点N （1，0），动点A 、B 分别在如图所示的抛物线x y 42=及椭圆22143x y +=的实线部分上运动，且AB //x 轴，则NAB l ∆的周长的取值范围是．9．对于顶点在原点的抛物线，给出下列条件：①焦点在y 轴上；②焦点在x 轴上；③抛物线上横坐标为1的点到焦点的距离等于6；④抛物线的通径的长为5；⑤由原点向过焦点的某条直线作垂线，垂足坐标为（2，1）．能使此抛物线方程为210y x =的条件是．10．椭圆22122:1(0)x y C a b a b+=>>的左准线为l ，左、右焦点分别为F 1、F 2，抛物线C 2的准线为l ，一个焦点为F 2，C 1与C 2的一个交点为P ，则12112F F PF PF PF -等于．三、解答题（共20分）11．已知抛物线C ：2y ax =，点P （1，－1）在抛物线C 上，过点P 作斜率为k 1、k 2的两条直线，分别交抛物线C 于异于点P 的两点112212(,),(,),0.A x y B x y k k +=且满足（1）求抛物线C 的焦点坐标；（2）若点M 满足BM MA = ，求点M 的轨迹方程．。

椭圆双曲线抛物线习题课.许兴华

件
| AB | (1 k )[( x1 x2) 4x1 x2]
2 2 2

1 2 ( k 1)(3 k 1 m )
2 2 2
(3 k 1)
2
2

3( k 1)(9 k 1)
2 2
(3 k 1)
2
2
3
12k
4
2 2
9k 6k 1
3
2
12 9k 1 k
兴 T 华
许
N S
E
E
V
课
Firstpage首页 upward return next last 铃
件
k1k2
16 2 y1 y2 2( y1 y2) 4 0 ( y1 2)( y2 2)
兴 T 华
许
N S
E
E
V
课
Firstpage首页 upward return next last 铃
兴 T 华
许E 许
N S
E N 兴S T 华
E
E
V 课 V
课
件 Firstpage首页 upward return next last 铃件
2a
2
2
2
2
289 17 . 消去 x2 得，－，∵a>0，∴a＝ . 2＝ 1－a 60 13
兴 T 华
许
N S
E
E
V
课
Firstpage首页 upward return next last 铃
件
兴 T 华
许
N S
E
E
V
课
Firstpage首页 upward return next last 铃

高中数学每周一测(圆锥曲线).许兴华

高中数学每周一测.圆锥曲线２０１２.１０.１２一．选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．设P 是椭圆x 225＋y 216＝1上的点，若F 1、F 2是椭圆的两个焦点，则|PF 1|＋|PF 2|等于 ( )A ．4B ．5C ．8D ．102．双曲线221102x y -=的焦距为 ( )A ．32B ．3C ．22D ． 23．设抛物线的顶点在原点，准线方程为2-=x ，则抛物线的方程是 ( )A ．x y 82-=B ．x y 82=C ．x y 42-=D ．x y 42=4．抛物线y ＝4x 2的焦点到准线的距离是 ( )A ．18B ．14C ．116D ．15．已知点M (3，0)，椭圆x24＋y 2＝1与直线y ＝k (x ＋3)交于点A 、B ，则ΔABM 的周长为( )A ．4B ．8C ．12D ．166．设椭圆x 2m 2＋y2n 2＝1(m >0，n >0)的右焦点与抛物线x y 82=的焦点相同，离心率为21，则此椭圆的方程为 ( )A ．x 212＋y 216＝1B ．x 216＋y 212＝1C ．x 248＋y 264＝1D ．x 264＋y 248＝17．已知双曲线x 22－y 22＝1的准线经过椭圆x 24＋y 2b2＝1(b ＞0)的焦点，则b ＝( )A ．3 B. 5 C. 3 D. 28．已知双曲线x 2a 2－y2b 2＝1(a >0，b >0)的两条渐近线均和圆C ：x 2＋y 2－6x ＋5＝0相切，且双曲线的右焦点为圆C 的圆心，则该双曲线的方程为 ( )A ．x 25－y 24＝1B ．x 24－y 25＝1C ．x 23－y 26＝1D ．x 26－y 23＝19．已知点P 是抛物线y 2＝－8x 上一点，设P 到此抛物线准线的距离是d 1，到直线x ＋y －10＝0的距离是d 2，则d 1＋d 2的最小值是 ( )A ． 3B ．2 3C ．6 2D ．310．已知椭圆x 216＋y 29＝1的左、右焦点分别为F 1、F 2，点P 在椭圆上．若P 、F 1、F 2是一个直角三角形的三个顶点，则点P 到x 轴的距离为 ( )A ．95B ．3C ．977D ．9411．过抛物线y 2＝2px (p >0)的焦点F 的直线l 与抛物线在第一象限的交点为A ，与抛物线的准线的交点为B ，点A 在抛物线的准线上的射影为C ，若AF →＝FB →，BA →·BC →＝48，则抛物线的方程为( )A ．y 2＝16xB ．y 2＝8xC ．y 2＝4xD ．y 2＝42x12．已知双曲线x 29－y 216＝1，其右焦点为F ，P 为其上一点，点M 满足|MF →|＝1，MF →·MP →＝0，则|MP →|的最小值为 ( )A ． 3B ．3C ．2D . 2 ∵x 0≤－3或x 0≥3，∴|MP →|2min ＝3，∴|MP →|m i n ＝ 3.二．填空题(本大题共4小题，每小题5分，共20分，把答案填在答题卷对应横线上)13．若抛物线y 2＝2px 的焦点与双曲线x 2－y 23＝1的右焦点重合，则p 的值为________．14．若点P (2,0)到双曲线x 2a 2－y2b2＝1的一条渐近线的距离为2，则该双曲线的离心率为________．15．过椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的一个顶点作圆x 2＋y 2＝b 2的两条切线，切点分别为A ，B ，若∠AOB ＝90°(O 为坐标原点)，则椭圆C 的离心率为________．16．设M 是椭圆x 24＋y 23＝1上的动点，A 1和A 2分别是椭圆的左、右顶点，则MA 1→·MA 2→的最小值等于________．三、解答题(本大题共2小题，共20分，解答应写出文字说明、证明过程或演算步骤) 17．（本小题满分12分）如图，直线l ：y ＝x ＋b 与抛物线C ：x 2＝4y 相切于点A .(1)求实数b 的值；(2)求以点A 为圆心，且与抛物线C 的准线相切的圆的方程．18．（本小题满分12分）已知椭圆C :2222by a x +=1(a ＞b ＞0)的离心率为36,短轴一个端点到右焦点的距离为3.(Ⅰ)求椭圆C 的方程; (Ⅱ)圆4322=+y x 的切线l 与椭圆C 交于A 、B 两点，求△AOB面积的最大值(O 为坐标原点).高中数学每周一测.圆锥曲线(参考答案)1．D 解析：∵a 2＝25，∴a ＝5，∴|PF 1|＋|PF 2|＝2a ＝10.2．B 解析：由双曲线方程得22210,212==∴=a b c ，于是2==c c B 3．B 解析：∵,22-=-p∴p ＝4，∴抛物线的方程x px y 822==. 4．A 解析：由y x 412=知，p ＝18，所以焦点到准线的距离为p ＝18.5．B 解析：M (3，0)是椭圆的焦点，而y ＝k (x ＋3)过椭圆的另一个焦点(－3，0)，所以ΔABM 的周长为4a ＝8.6．B 解析：抛物线y 2＝8x 的焦点F (2,0)，由条件得⎩⎪⎨⎪⎧m 2－n 2＝42m ＝12，∴⎩⎪⎨⎪⎧m 2＝16n 2＝12，7．C 解析：已知双曲线的准线方程为x ＝±a 2c ＝±22＋2＝±1，∴椭圆的焦点坐标为(±1,0)，即c ＝1. ∴b 2＝4－1＝3，∴b ＝ 3.故选C. 8．A 解析：双曲线的渐近线方程为y ＝±bax ，圆C 的圆心C (3,0)，半径r ＝2，由条件知⎩⎪⎨⎪⎧a 2＋b 2＝93b a 2＋b2＝2，∴⎩⎪⎨⎪⎧b 2＝4a 2＝5.9．C 解析：抛物线y 2＝－8x 的焦点F (－2,0)，根据抛物线的定义知，d 1＋d 2＝|PF |＋d 2，显然当由点F 向直线x ＋y －10＝0作垂线与抛物线的交点为P 时，d 1＋d 2取到最小值，即|－2＋0－10|2＝6 2. 10．D 解析：设椭圆短轴的一个端点为M .由于a ＝4，b ＝3，∴c ＝7<b .∴∠F 1MF 2<90°，∴只能∠PF 1F 2＝90°或∠PF 2F 1＝90°. 令x ＝±7得y 2＝9⎝⎛⎭⎫1－716＝9216，∴|y |＝94. 即P 到x 轴的距离为94.11．C 解析：由AF →＝FB →及|AF →|＝|AC →|知在R t △ACB 中，∠CBF ＝30°，|DF |＝p 2＋p2＝p ，∴AC ＝2p ，BC ＝23p ，BA →·BC →＝4p ·23p ·c o s 30°＝48，∴p ＝2.抛物线方程为y 2＝4x .12．A 解析：∵|MF →|＝1，F 为定点，∴点M 在以F 为圆心，1为半径的圆上，又P 在双曲线上，设P (x 0，y 0)，则x 209－y 2016＝1，∴y 20＝169x 20－16，∵MF →·MP →＝0，∴MF ⊥MP ， ∴|MP →|2＝|PF |2－|MF |2＝(x 0－5)2＋y 20－1＝(x 0－5)2＋169x 20－17＝259x 20－10x 0＋8＝259(x 0－95)2－1，13．答案：4解析：双曲线x 2－y 23＝1的右焦点为(2,0)，由题意，p2＝2，∴p ＝4.14．答案：2 解析：由于双曲线渐近线方程为bx ±ay ＝0，故点P 到直线的距离d ＝2ba 2＋b 2＝2,∴a ＝b ，即双曲线为等轴双曲线，故其离心率e ＝1＋⎝⎛⎭⎫b a 2＝ 2.15．答案：22解析：因为∠AOB ＝90°，所以∠AOF ＝45°，所以b a ＝22，所以e 2＝c 2a 2＝a 2－b 2a 2＝1－b 2a 2＝12，即e ＝22.16．答案：－1解析：设M (x 0，y 0)，则MA 1→＝(－2－x 0，－y 0)， MA 2→＝(2－x 0，－y 0)∴MA 1→·MA 2→＝x 20＋y 20－4＝x 20＋⎝⎛⎭⎫3－34x 20－4＝14x 20－1，显然当x 0＝0时，MA 1→·MA 2→取最小值为－1.17解：(1)由⎩⎪⎨⎪⎧y ＝x ＋bx 2＝4y得x 2－4x －4b ＝0(*)∵直线l 与抛物线相切, ∴△＝(－4)2－4×(－4b )＝0, ∴b ＝－1(2)由(1)知b ＝－1，方程(*)为x 2－4x ＋4＝0 解得x ＝2，代入x 2＝4y 中得，y ＝1，∴A (2,1) ∵圆A 与抛物线准线y ＝－1相切, ∴r ＝|1－(－1)|＝2. 所以圆A 的方程为(x －2)2＋(y －1)2＝4.18.解：（Ⅰ）设椭圆的半焦距为c，依题意c a a ⎧=⎪⎨⎪=⎩1b ∴=，∴所求椭圆方程为2213x y +=．（Ⅱ）设11()A x y ，，22()B x y ，．（1）当AB x ⊥轴时，AB = （2）当AB 与x 轴不垂直时，设直线AB 的方程为y kx m =+．2=，得223(1)4m k =+．把y kx m =+代入椭圆方程，整理得222(31)6330k x kmx m +++-=， 122631kmx x k -∴+=+，21223(1)31m x x k -=+． 22221(1)()AB k x x ∴=+-22222223612(1)(1)(31)31k m m k k k ⎡⎤-=+-⎢⎥++⎣⎦ 22222222212(1)(31)3(1)(91)(31)(31)k k m k k k k ++-++==++2422212121233(0)34196123696k k k k k k=+=+≠+=++⨯+++≤．当且仅当2219k k=，即3k =时等号成立．当0k =时，AB =，综上所述ma x2AB =．∴当AB 最大时，A O B △面积取最大值m a 132S A B =⨯=．。

高三数学每周一测(函数值域).许兴华

高三数学每周一测(函数值域).许兴华班别学号姓名一、选择题（每小题7分） 1．函数()4323ln 1)(22+--++-=x x x x xx f 的定义域为（） A ．),2[]4,(+∞--∞ B ．)1,0()0,4( -C ．]1,0()0,4[ -D ．)1,0()0,4[ -2．已知函数324)(,lg )(1--==+x x x g x x f ，那么函数)]([x g f 的定义域是（）A ．)2,(-∞B ．),2(+∞C ． 3(log 2, )∞+D ．)3log ,(2-∞3．函数21x x y -+=的值域是（）A ．]2,1[-B ．]1,1[-C ．]1,0[D ．]2,0[4．函数)1()1(613842->+++=x x x x y 的最小值是（）A ．1B ．23 C ．2 D ．35．若)3(log 27log )(927133x x x f ，x ⋅=≤≤则（） A ．有最小值932-，最大值—3； B ．有最小值—4，最大值12；C ．有最小值932-，无最大值； D ．无最小值，最大值12；6．设)(,1,1,)(2x g x x x x x f ⎪⎩⎪⎨⎧<≥=是二次函数，若)]([x g f 的值域是),0[+∞，则)(x g 的值域是（）A ．),1[]1,(+∞--∞B ．),0[]1,(+∞--∞C ．),0[+∞D ． ),1[+∞二、填空题（每小题7分）7．函数1cos 4sin 2++=x x y 的值域是8．函数1322+-+-=x x x x y 的值域是9．函数4cos 21sin 4-+=x x y 的值域为10．已知数列{}n a 的通项)(5920096*∈--=N n n n a n ，则数列{}n a 的前12项中，最大项和最小项分别是三、解答题（每小题15分）11．已知函数18log )(223+++=x nx mx x f 的定义域),(+∞-∞，值域为[0，2]，求实数n m ,的值。

2018高考一轮数学浙江专版练习第8章第7节抛物线含答案精品

第七节抛物线1．抛物线的概念平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．2．抛物线的标准方程与几何性质1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线．()(2)方程y ＝ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线，且其焦点坐标是⎝ ⎛⎭⎪⎫a 4，0，准线方程是x ＝－a 4.( )(3)抛物线既是中心对称图形，又是轴对称图形．( )(4)AB 为抛物线y 2＝2px (p >0)的过焦点F ⎝ ⎛⎭⎪⎫p 2，0的弦，若A (x 1，y 1)，B (x 2，y 2)，则x 1x 2＝p 24，y 1y 2＝－p 2，弦长|AB |＝x 1＋x 2＋p .( )[答案] (1)× (2)× (3)× (4)√2．(教材改编)若抛物线y ＝4x 2上的一点M 到焦点的距离为1，则点M 的纵坐标是( )A.1716 B.1516 C.78D ．0B [M 到准线的距离等于M 到焦点的距离，又准线方程为y ＝－116，设M (x ，y )，则y ＋116＝1，∴y ＝1516.] 3．抛物线y ＝14x 2的准线方程是( ) A ．y ＝－1 B ．y ＝－2 C ．x ＝－1D ．x ＝－2A [∵y ＝14x 2，∴x 2＝4y ，∴准线方程为y ＝－1.]4．(2017·衢州质检)若抛物线y 2＝2px (p >0)的准线经过双曲线x 2－y 2＝1的一个焦点，则p ＝__________.22 [抛物线的准线方程为x ＝－p2，p >0，双曲线的焦点为F 1(－2，0)，F 2(2，0)，所以－p2＝－2，p ＝2 2.]5．(2016·浙江高考)若抛物线y 2＝4x 上的点M 到焦点的距离为10，则M 到y 轴的距离是________．9 [设点M 的横坐标为x 0，则点M 到准线x ＝－1的距离为x 0＋1，由抛物线的定义知x 0＋1＝10，∴x 0＝9，∴点M 到y 轴的距离为9.]00上一点，|AF |＝54x 0，则x 0＝( )A ．1B ．2C ．4D ．8(2)已知抛物线y 2＝4x ，过焦点F 的直线与抛物线交于A ，B 两点，过A ，B 分别作y 轴的垂线，垂足分别为C ，D ，则|AC |＋|BD |的最小值为__________.【导学号：51062296】(1)A (2)2 [(1)由y 2＝x ，知2p ＝1，即p ＝12，因此焦点F ⎝ ⎛⎭⎪⎫14，0，准线l 的方程为x ＝－14.设点A (x 0，y 0)到准线l 的距离为d ，则由抛物线的定义可知d ＝|AF |. 从而x 0＋14＝54x 0，解得x 0＝1.(2)由y 2＝4x ，知p ＝2，焦点F (1,0)，准线x ＝－1. 根据抛物线的定义，|AF |＝|AC |＋1，|BF |＝|BD |＋1. 因此|AC |＋|BD |＝|AF |＋|BF |－2＝|AB |－2.所以|AC |＋|BD |取到最小值，当且仅当|AB |取得最小值，又|AB |＝2p ＝4为最小值．故|AC |＋|BD |的最小值为4－2＝2.][规律方法] 1.凡涉及抛物线上的点到焦点距离时，一般运用定义转化为到准线距离处理．如本例充分运用抛物线定义实施转化，使解答简捷、明快．2．若P (x 0，y 0)为抛物线y 2＝2px (p >0)上一点，由定义易得|PF |＝x 0＋p2；若过焦点的弦AB 的端点坐标为A (x 1，y 1)，B (x 2，y 2)，则弦长为|AB |＝x 1＋x 2＋p ，x 1＋x 2可由根与系数的关系整体求出．[变式训练1] 设P 是抛物线y 2＝4x 上的一个动点，则点P 到点A (－1,1)的距离与点P 到直线x ＝－1的距离之和的最小值为__________．5 [如图，易知抛物线的焦点为F (1,0)，准线是x ＝－1，由抛物线的定义知：点P 到直线x ＝－1的距离等于点P 到F 的距离．于是，问题转化为在抛物线上求一点P ，使点P 到点A (－1,1)的距离与点P 到F (1,0)的距离之和最小．连接AF 交抛物线于点P ，此时最小值为 |AF |＝[1－(－1)]2＋(0－1)2＝ 5.]方程是( )A ．x 2＝112y B ．x 2＝112y 或x 2＝－136y C ．x 2＝－136yD ．x 2＝12y 或x 2＝－36y(2)以抛物线C 的顶点为圆心的圆交C 于A ，B 两点，交C 的准线于D ，E 两点．已知|AB |＝42，|DE |＝25，则C 的焦点到准线的距离为( )A ．2B ．4C ．6D ．8(1)D (2)B [(1)将y ＝ax 2化为x 2＝1a y .当a >0时，准线y ＝－14a ，则3＋14a ＝6，∴a ＝112. 当a <0时，准线y ＝－14a ，则⎪⎪⎪⎪⎪⎪3＋14a ＝6，∴a ＝－136.∴抛物线方程为x 2＝12y 或x 2＝－36y .(2)设抛物线的方程为y 2＝2px (p ＞0)，圆的方程为x 2＋y 2＝r 2. ∵|AB |＝42，|DE |＝25，抛物线的准线方程为x ＝－p2，∴不妨设A ⎝ ⎛⎭⎪⎫4p ，22，D ⎝ ⎛⎭⎪⎫－p 2，5.∵点A ⎝ ⎛⎭⎪⎫4p ，22，D ⎝ ⎛⎭⎪⎫－p 2，5在圆x 2＋y 2＝r 2上，∴⎩⎪⎨⎪⎧16p2＋8＝r 2，p 24＋5＝r 2，∴16p 2＋8＝p 24＋5，∴p ＝4(负值舍去)．∴C 的焦点到准线的距离为4.][规律方法] 1.求抛物线的标准方程的方法：(1)求抛物线的标准方程常用待定系数法，因为未知数只有p ，所以只需一个条件确定p 值即可．(2)因为抛物线方程有四种标准形式，因此求抛物线方程时，需先定位，再定量．2．由抛物线的方程可以确定抛物线的开口方向、焦点位置、焦点到准线的距离；从而进一步确定抛物线的焦点坐标及准线方程．[变式训练2] (1)(2017·浙江名校联考)抛物线y 2＝2px (p >0)的焦点为F ，O 为坐标原点，M 为抛物线上一点，且|MF |＝4|OF |，△MFO 的面积为43，则抛物线的方程为 ( )A ．y 2＝6xB ．y 2＝8xC ．y 2＝16xD ．y 2＝15x2(2)若抛物线y 2＝2px 的焦点与椭圆x 29＋y 25＝1的右焦点重合，则该抛物线的准线方程为__________．(1)B (2)x ＝－2 [(1)设M (x ，y )，因为|OF |＝p2，|MF |＝4|OF |，所以|MF |＝2p ，由抛物线定义知x ＋p2＝2p ，所以x ＝32p ，所以y ＝±3p . 又△MFO 的面积为43，所以12×p2×3p ＝43，解得p ＝4(p ＝－4舍去)．所以抛物线的方程为y 2＝8x .(2)由椭圆x 29＋y 25＝1，知a ＝3，b ＝5，所以c 2＝a 2－b 2＝4，所以c ＝2. 因此椭圆的右焦点为(2,0)，又抛物线y 2＝2px 的焦点为⎝ ⎛⎭⎪⎫p 2，0.依题意，得p2＝2，于是抛物线的准线x ＝－2.]☞角度1 直线与抛物线的交点问题在直角坐标系xOy 中，直线l ：y ＝t (t ≠0)交y 轴于点M ，交抛物线C ：y 2＝2px (p >0)于点P ，M 关于点P 的对称点为N ，连接ON 并延长交C 于点H .(1)求|OH ||ON |；(2)除H 以外，直线MH 与C 是否有其他公共点？说明理由.【导学号：51062297】[解] (1)如图，由已知得M (0，t )，P ⎝ ⎛⎭⎪⎫t 22p ，t .又N 为M 关于点P 的对称点，故N ⎝ ⎛⎭⎪⎫t 2p ，t ，2分故直线ON 的方程为y ＝p t x ，将其代入y 2＝2px 整理得px 2－2t 2x ＝0,解得x 1＝0，x 2＝2t 2p .因此H ⎝ ⎛⎭⎪⎫2t 2p ，2t .所以N 为OH 的中点，即|OH ||ON |＝2.6分(2)直线MH 与C 除H 以外没有其他公共点．理由如下：直线MH 的方程为y －t ＝p 2t x ，即x ＝2tp (y －t ).9分代入y 2＝2px 得y 2－4ty ＋4t 2＝0，解得y 1＝y 2＝2t ，即直线MH 与C 只有一个公共点，所以除H 以外，直线MH 与C 没有其他公共点.15分[规律方法] 1.(1)本题求解的关键是求出点N ，H 的坐标．(2)第(2)问将直线MH 的方程与抛物线C 的方程联立，根据方程组的解的个数进行判断．2．(1)判断直线与圆锥曲线的交点个数时，可直接求解相应方程组得到交点坐标，也可利用消元后的一元二次方程的判别式来确定，需注意利用判别式的前提是二次项系数不为0.(2)解题时注意应用根与系数的关系及设而不求、整体代换的技巧．☞角度2 与抛物线弦长或中点有关的问题(2017·嘉兴模拟)已知抛物线C ：y 2＝2px (p >0)的焦点为F ，抛物线C 与直线l 1：y ＝－x 的一个交点的横坐标为8.(1)求抛物线C 的方程；(2)不过原点的直线l 2与l 1的垂直，且与抛物线交于不同的两点A ，B ，若线段AB 的中点为P ，且|OP |＝|PB |，求△F AB 的面积．[解] (1)易知直线与抛物线的交点坐标为(8，－8)，2分 ∴(－8)2＝2p ×8，∴2p ＝8，∴抛物线方程为y 2＝8x .5分(2)直线l 2与l 1垂直，故可设直线l 2：x ＝y ＋m ，A (x 1，y 1)，B (x 2，y 2)，且直线l 2与x 轴的交点为M .6分由⎩⎨⎧y 2＝8x ，x ＝y ＋m ，得y 2－8y －8m ＝0， Δ＝64＋32m >0，∴m >－2. y 1＋y 2＝8，y 1y 2＝－8m ，∴x 1x 2＝y 21y 2264＝m 2.10分由题意可知OA ⊥OB ，即x 1x 2＋y 1y 2＝m 2－8m ＝0， ∴m ＝8或m ＝0(舍)，∴直线l 2：x ＝y ＋8，M (8,0).12分故S △F AB ＝S △FMB ＋S △FMA ＝12·|FM |·|y 1－y 2| ＝3(y 1＋y 2)2－4y 1y 2＝24 5.15分[规律方法] 1.有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式．2．涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等方法．3．涉及弦的中点、斜率时，一般用“点差法”求解．[思想与方法]1．抛物线定义的实质可归结为“一动三定”：一个动点M ，一个定点F (抛物线的焦点)，一条定直线l (抛物线的准线)，一个定值1(抛物线的离心率)．2．抛物线的定义中指明了抛物线上点到焦点的距离与到准线距离的等价性，故二者可相互转化，这一转化思想在解题中有着重要作用．3．抛物线的焦点弦：设过抛物线y 2＝2px (p >0)的焦点的直线与抛物线交于A (x 1，y 1)，B (x 2，y 2)，则：(1)y 1y 2＝－p 2，x 1x 2＝p24；(2)若直线AB 的倾斜角为θ，则|AB |＝2psin 2θ＝x 1＋x 2＋p . [易错与防范]1．认真区分四种形式的标准方程．(1)区分y ＝ax 2(a ≠0)与y 2＝2px (p >0)，前者不是抛物线的标准方程． (2)求标准方程要先确定形式，必要时要进行分类讨论，标准方程有时可设为y 2＝mx 或x 2＝my (m ≠0)．2．直线与抛物线结合的问题，不要忘记验证判别式．3．抛物线的定义中易忽视“定点不在定直线上”这一条件，当定点在定直线上时，动点的轨迹是过定点且与直线垂直的直线．当直线与抛物线有一个公共点，并不表明直线与抛物线相切．课时分层训练(四十九) 抛物线A 组基础达标 (建议用时：30分钟)一、选择题1．抛物线y 2＝4x 的焦点坐标是( ) A ．(0,2) B ．(0,1) C ．(2,0)D ．(1,0)D [由y 2＝4x 知p ＝2，故抛物线的焦点坐标为(1,0)．]2．(2017·宁波二模)若动圆的圆心在抛物线y ＝112x 2上，且与直线y ＋3＝0相切，则此圆恒过定点( )A ．(0,2)B ．(0，－3)C ．(0,3)D ．(0,6)C [直线y ＋3＝0是抛物线x 2＝12y 的准线，由抛物线的定义知抛物线上的点到直线y ＝－3的距离与到焦点(0,3)的距离相等，所以此圆恒过定点(0,3)．]3．抛物线y 2＝4x 的焦点到双曲线x 2－y 23＝1的渐近线的距离是( )A.12B.32 C ．1D. 3B [由双曲线x 2－y 23＝1知其渐近线方程为y ＝±3x ，即3x ±y ＝0，又y 2＝4x 的焦点F (1,0)，∴焦点F 到直线的距离d ＝3(3)2＋(－1)2＝32.] 4．设抛物线C ：y 2＝2px (p >0)的焦点为F ，点M 在C 上，|MF |＝5.若以MF 为直径的圆过点(0,2)，则C 的方程为( ) 【导学号：51062298】A ．y 2＝4x 或y 2＝8xB ．y 2＝2x 或y 2＝8xC ．y 2＝4x 或y 2＝16xD ．y 2＝2x 或y 2＝16xC [由已知得抛物线的焦点F ⎝ ⎛⎭⎪⎫p 2，0，设点A (0,2)，点M (x 0，y 0)．则AF →＝⎝ ⎛⎭⎪⎫p 2，－2，AM →＝⎝ ⎛⎭⎪⎫y 202p ，y 0－2. 由已知得，AF →·AM →＝0，即y 20－8y 0＋16＝0，因而y 0＝4，M ⎝ ⎛⎭⎪⎫8p ，4. 由|MF |＝5，得⎝ ⎛⎭⎪⎫8p －p 22＋16＝5，又p >0，解得p ＝2或p ＝8.故C 的方程为y 2＝4x 或y 2＝16x .]5．O 为坐标原点，F 为抛物线C ：y 2＝42x 的焦点，P 为C 上一点，若|PF |＝42，则△POF 的面积为( )A ．2B ．2 2C ．2 3D ．4C [如图，设点P 的坐标为(x 0，y 0)，由|PF |＝x 0＋2＝42，得x 0＝32，代入抛物线方程得，y 20＝42×32＝24，所以|y 0|＝26，所以S △POF ＝12|OF ||y 0|＝12×2×26＝2 3.]二、填空题6．(2017·浙江五校三联)过抛物线y 2＝4x 的焦点F 作倾斜角为45°的直线交抛物线于A ，B 两点，则弦长|AB |为__________. 【导学号：51062299】8 [设A (x 1，y 1)，B (x 2，y 2)．易得抛物线的焦点是F (1,0)，所以直线AB 的方程是y ＝x －1.联立⎩⎨⎧y 2＝4x ，y ＝x －1，消去y 得x 2－6x ＋1＝0. 所以x 1＋x 2＝6，所以|AB |＝x 1＋x 2＋p ＝6＋2＝8.]7．已知点A (－2,3)在抛物线C ：y 2＝2px 的准线上，记C 的焦点为F ，则直线AF 的斜率为__________．－34 [∵点A (－2,3)在抛物线C 的准线上．∴－p 2＝－2，∴p ＝4，焦点F (2,0)．因此k AF ＝3－0－2－2＝－34.] 8．(2017·江西九校联考)抛物线y 2＝2px (p >0)的焦点为F ，其准线与双曲线y 2－x 2＝1相交于A ，B 两点，若△ABF 为等边三角形，则p ＝__________. 23 [y 2＝2px 的准线为x ＝－p 2.由于△ABF 为等边三角形．因此不妨设A ⎝ ⎛⎭⎪⎫－p 2，p 3，B ⎝⎛⎭⎪⎫－p 2，－p 3. 又点A ，B 在双曲线y 2－x 2＝1，从而p 23－p 24＝1，所以p ＝2 3.]三、解答题9．已知抛物线y 2＝2px (p >0)，过点C (－2,0)的直线l 交抛物线于A ，B 两点，坐标原点为O ，OA →·OB →＝12.(1)求抛物线的方程；(2)当以|AB |为直径的圆与y 轴相切时，求直线l 的方程. 【导学号：51062300】[解] (1)设l ：x ＝my －2，代入y 2＝2px 中，得y 2－2pmy ＋4p ＝0.2分设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝2pm ，y 1y 2＝4p ，则x 1x 2＝y 21y 224p 2＝4，因为OA →·OB →＝x 1x 2＋y 1y 2＝4＋4p ＝12，可得p ＝2，则抛物线的方程为y 2＝4x .6分(2)由(1)知y 2＝4x ，p ＝2，可知y 1＋y 2＝4m ，y 1y 2＝8.8分设AB 的中点为M ，则|AB |＝2x M ＝x 1＋x 2＝m (y 1＋y 2)－4＝4m 2－4.①又|AB |＝1＋m 2|y 1－y 2|＝(1＋m 2)(16m 2－32).②由①②得(1＋m 2)(16m 2－32)＝(4m 2－4)2，12分解得m 2＝3，m ＝±3，所以直线l 的方程为x ＋3y ＋2＝0或x －3y ＋2＝0.15分10．已知过抛物线y 2＝2px (p >0)的焦点，斜率为22的直线交抛物线于A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)两点，且|AB |＝9.(1)求该抛物线的方程；(2)O 为坐标原点，C 为抛物线上一点，若OC →＝OA →＋λOB →，求λ的值．[解] (1)由题意得直线AB 的方程为y ＝22⎝ ⎛⎭⎪⎫x －p 2，与y 2＝2px 联立，从而有4x 2－5px ＋p 2＝0，所以x 1＋x 2＝5p 4.3分由抛物线定义得|AB |＝x 1＋x 2＋p ＝5p 4＋p ＝9，所以p ＝4，从而该抛物线的方程为y 2＝8x .6分(2)由(1)得4x 2－5px ＋p 2＝0，即x 2－5x ＋4＝0，则x 1＝1，x 2＝4，于是y 1＝－22，y 2＝42，从而A (1，－22)，B (4,42).9分设C (x 3，y 3)，则OC →＝(x 3，y 3)＝(1，－22)＋λ(4,42)＝(4λ＋1,42λ－22).12分又y 23＝8x 3，所以[22(2λ－1)]2＝8(4λ＋1)，整理得(2λ－1)2＝4λ＋1，解得λ＝0或λ＝2.15分B 组能力提升(建议用时：15分钟)1．设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，则|AB |＝( ) A.303B ．6C ．12D ．7 3C [∵F 为抛物线C ：y 2＝3x 的焦点，∴F ⎝ ⎛⎭⎪⎫34，0， ∴AB 的方程为y －0＝tan 30°⎝ ⎛⎭⎪⎫x －34，即y ＝33x －34. 联立⎩⎨⎧ y 2＝3x ，y ＝33x －34，得13x 2－72x ＋316＝0，∴x 1＋x 2＝－－7213＝212，即x A ＋x B ＝212.由于|AB |＝x A ＋x B ＋p ，∴|AB |＝212＋32＝12.]2．(2017·浙江模拟训练冲刺卷一)已知点F 为抛物线x 2＝4y 的焦点，O 为坐标原点，点M 是抛物线准线上一动点，A 在抛物线上，且|AF |＝2，则|OA |＝________；|MA |＋|MO |的最小值是________． 5 13 [易知F (0,1)．设A (x ，y )，由|AF |＝2，得y ＋1＝2，∴y ＝1，代入x 2＝4y 得x ＝±2，所以A (±2,1)，则|OA |＝ 5.设B (0，－2)，因点M 在抛物线准线上，则|MO |＝|MB |，从而|MA |＋|MO |的最小值就是|MA |＋|MB |的最小值．因为A ，B 为定点则|MA |＋|MB |的最小值即为|AB |＝13，故|MA |＋|MO |的最小值是13.]3．抛物线y 2＝4x 的焦点为F ，过点F 的直线交抛物线于A ，B 两点．(1)若AF →＝2 FB →，求直线AB 的斜率；(2)设点M 在线段AB 上运动，原点O 关于点M 的对称点为C ，求四边形OACB 面积的最小值. 【导学号：51062301】[解] (1)依题意知F (1,0)，设直线AB 的方程为x ＝my ＋1.将直线AB 的方程与抛物线的方程联立，消去x 得y 2－4my －4＝0.2分设A (x 1，y 1)，B (x 2，y 2)，所以y 1＋y 2＝4m ，y 1y 2＝－4.因为AF →＝2 FB →，所以y 1＝－2y 2.联立上述三式，消去y 1，y 2得m ＝±24.所以直线AB 的斜率是±2 2.6分(2)由点C 与原点O 关于点M 对称，得M 是线段OC 的中点，从而点O 与点C 到直线AB 的距离相等，所以四边形OACB 的面积等于2S △AOB .10分因为2S △AOB ＝2×12·|OF |·|y 1－y 2|＝(y 1＋y 2)2－4y 1y 2＝41＋m 2，所以当m ＝0时，四边形OACB 的面积最小，最小值是4.15分。

2020版新一线高考理科数学一轮复习教学案：第8章第7节抛物线含答案

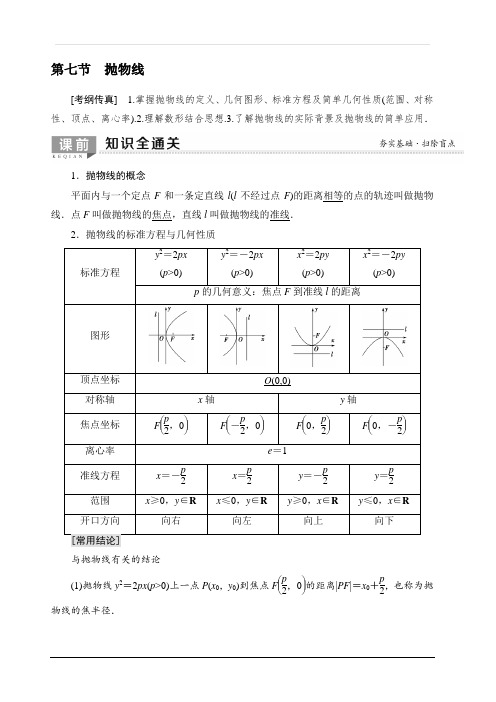
第七节抛物线[考纲传真] 1.掌握抛物线的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率).2.理解数形结合思想.3.了解抛物线的实际背景及抛物线的简单应用．1．抛物线的概念平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线．2．抛物线的标准方程与几何性质与抛物线有关的结论(1)抛物线y 2＝2px (p >0)上一点P (x 0，y 0)到焦点F ⎝ ⎛⎭⎪⎫p 2，0的距离|PF |＝x 0＋p 2，也称为抛物线的焦半径．(2)y 2＝ax (a ≠0)的焦点坐标为⎝ ⎛⎭⎪⎫a 4，0，准线方程为x ＝－a 4.(3)设AB 是过抛物线y 2＝2px (p >0)焦点F 的弦，若A (x 1，y 1)，B (x 2，y 2)，则①x 1x 2＝p 24，y 1y 2＝－p 2. ②弦长|AB |＝x 1＋x 2＋p ＝2psin 2α(α为弦AB 的倾斜角)． ③以弦AB 为直径的圆与准线相切．④通径：过焦点垂直于对称轴的弦，长等于2p ，通径是过焦点最短的弦．[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线．( )(2)方程y ＝ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线，且其焦点坐标是⎝ ⎛⎭⎪⎫a 4，0，准线方程是x ＝－a4.( )(3)抛物线既是中心对称图形，又是轴对称图形．( )(4)若直线与抛物线只有一个交点，则直线与抛物线一定相切． ( ) [答案] (1)× (2)× (3)× (4)× 2．抛物线y ＝14x 2的准线方程是( ) A ．y ＝－1 B ．y ＝－2 C ．x ＝－1D ．x ＝－2A [∵y ＝14x 2，∴x 2＝4y ，∴准线方程为y ＝－1.]3．(教材改编)若抛物线y ＝4x 2上的一点M 到焦点的距离为1，则点M 的纵坐标是( )A.1716B.1516C.78 D ．0B [M 到准线的距离等于M 到焦点的距离，又准线方程为y ＝－116，设M (x ，y )，则y ＋116＝1，∴y ＝1516.]4．(教材改编)过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1，y 1)，Q (x 2，y 2)两点，如果x1＋x2＝6，则|PQ|等于( )A．9 B．8 C．7 D．6B[抛物线y2＝4x的焦点为F(1,0)，准线方程为x＝－1.根据题意可得，|PQ|＝|PF|＋|QF|＝x 1＋1＋x2＋1＝x1＋x2＋2＝8.]5．(教材改编)已知抛物线的顶点是原点，对称轴为坐标轴，并且经过点P(－2，－4)，则该抛物线的标准方程为________．y2＝－8x或x2＝－y[设抛物线方程为y2＝2px(p≠0)或x2＝2py(p≠0)．将P(－2，－4)代入，分别得方程为y2＝－8x或x2＝－y.]抛物线的定义与应用【例1】设P|PB|＋|PF|的最小值为________．4[如图，过点B作BQ垂直准线于点Q，交抛物线于点P1，则|P1Q|＝|P1F|.则有|PB|＋|PF|≥|P1B|＋|P1Q|＝|BQ|＝4，即|PB|＋|PF|的最小值为4.][拓展探究](1)若将本例中的B点坐标改为(3,4)，试求|PB|＋|PF|的最小值．(2)若将本例中的条件改为：已知抛物线方程为y2＝4x，直线l的方程为x－y＋5＝0，在抛物线上有一动点P到y轴的距离为d1，到直线l的距离为d2，求d1＋d2的最小值．[解](1)由题意可知点B(3,4)在抛物线的外部．∵|PB|＋|PF|的最小值即为B，F两点间的距离，F(1,0)，∴|PB|＋|PF|≥|BF|＝42＋22＝25，即|PB|＋|PF|的最小值为2 5.(2)由题意知，抛物线的焦点为F(1,0)．点P到y轴的距离d1＝|PF|－1，所以d1＋d2＝d2＋|PF|－1.易知d2＋|PF|的最小值为点F到直线l的距离，故d2＋|PF|的最小值为|1＋5|12＋(－1)2＝32，所以d1＋d2的最小值为32－1.的一个动点，N(1,0)是一个定点，则|PQ|＋|PN|的最小值为( )A．3 B．4 C．5 D.2＋1(2)动圆过点(1,0)，且与直线x＝－1相切，则动圆的圆心的轨迹方程为________.(1)A(2)y2＝4x[(1)由抛物线方程y2＝4x，可得抛物线的焦点F(1,0)，又N(1,0)，所以N与F重合．过圆(x－3)2＋(y－1)2＝1的圆心M作抛物线准线的垂线MH，交圆于Q，交抛物线于P，则|PQ|＋|PN|的最小值等于|MH|－1＝3.(2)设动圆的圆心坐标为(x，y)，则圆心到点(1,0)的距离与到直线x＝－1的距离相等，根据抛物线的定义易知动圆的圆心的轨迹方程为y2＝4x.]抛物线的标准方程与几何性质【例2】是( )A．x2＝112y B．x2＝112y或x2＝－136yC．x2＝－136y D．x2＝12y或x2＝－36y(2)(2016·全国卷Ⅰ)以抛物线C的顶点为圆心的圆交C于A，B两点，交C的准线于D，E两点．已知|AB|＝42，|DE|＝25，则C的焦点到准线的距离为( ) A．2 B．4 C．6 D．8(3)如图所示，过抛物线y 2＝2px (p >0)的焦点F 的直线交抛物线于点A ，B ，交其准线l 于点C ，若|BC |＝2|BF |，且|AF |＝3，则此抛物线的方程为( )A ．y 2＝32x B ．y 2＝9x C ．y 2＝92xD ．y 2＝3x(1)D (2)B (3)D [(1)将y ＝ax 2化为x 2＝1a y .当a >0时，准线y ＝－14a ，则3＋14a ＝6，∴a ＝112.当a <0时，准线y ＝－14a ，则⎪⎪⎪⎪⎪⎪3＋14a ＝6，∴a ＝－136.∴抛物线方程为x 2＝12y 或x 2＝－36y .(2)设抛物线的方程为y 2＝2px (p ＞0)，圆的方程为x 2＋y 2＝r 2. ∵|AB |＝42，|DE |＝25，抛物线的准线方程为x ＝－p2， ∴不妨设A ⎝ ⎛⎭⎪⎫4p ，22，D ⎝ ⎛⎭⎪⎫－p 2，5.∵点A ⎝ ⎛⎭⎪⎫4p ，22，D ⎝ ⎛⎭⎪⎫－p 2，5在圆x 2＋y 2＝r 2上，∴⎩⎪⎨⎪⎧16p 2＋8＝r 2，p 24＋5＝r 2，∴16p 2＋8＝p 24＋5，∴p ＝4(负值舍去)．∴C 的焦点到准线的距离为4.(3)分别过点A ，B 作AA 1⊥l ，BB 1⊥l ，且垂足分别为A 1，B 1，由已知条件|BC |＝2|BF |，得|BC |＝2|BB 1|，所以∠BCB 1＝30°.又|AA 1|＝|AF |＝3，所以|AC |＝2|AA 1|＝6，所以|CF |＝|AC |－|AF |＝6－3＝3，所以F 为线段AC 的中点．故点F 到准线的距离为p ＝12|AA 1|＝32，故抛物线的方程为y 2＝3x .]直线与抛物线的位置关系►考法1 【例3】 (2017·全国卷Ⅰ)设A ，B 为曲线C ：y ＝x 24上两点，A 与B 的横坐标之和为4.(1)求直线AB 的斜率；(2)设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程．[解] (1)设A (x 1，y 1)，B (x 2，y 2)，则x 1≠x 2，y 1＝x 214，y 2＝x 224，x 1＋x 2＝4，于是直线AB 的斜率k ＝y 1－y 2x 1－x 2＝x 1＋x 24＝1. (2)由 y ＝x 24，得y ′＝x2.设M (x 3，y 3)，由题设知x 32＝1，解得x 3＝2，于是M (2,1)．设直线AB 的方程为y ＝x ＋m ，故线段AB 的中点为N (2,2＋m )，|MN |＝|m ＋1|. 将y ＝x ＋m 代入y ＝x 24得x 2－4x －4m ＝0.当Δ＝16(m ＋1)>0，即m >－1时，x 1,2＝2±2m ＋1. 从而|AB |＝2|x 1－x 2|＝42(m ＋1).由题设知|AB |＝2|MN |，即42(m ＋1)＝2(m ＋1)，解得m ＝7. 所以直线AB 的方程为y ＝x ＋7.►考法2 与抛物线弦长或中点有关的问题【例4】已知抛物线C ：x 2＝2py (p ＞0)，过焦点F 的直线交C 于A ，B 两点，D 是抛物线的准线l 与y 轴的交点．(1)若AB ∥l ，且△ABD 的面积为1，求抛物线的方程；(2)设M 为AB 的中点，过M 作l 的垂线，垂足为N .证明：直线AN 与抛物线相切． [解] (1)∵AB ∥l ，∴|FD |＝p ，|AB |＝2p .∴S △ABD ＝p 2，∴p ＝1，故抛物线C 的方程为x 2＝2y . (2)设直线AB 的方程为y ＝kx ＋p 2，由⎝⎛y ＝kx ＋p 2，x 2＝2py得x 2－2kpx －p 2＝0，∴x 1＋x 2＝2kp ，x 1x 2＝－p 2.其中A ⎝ ⎛⎭⎪⎫x 1，x 212p ，B ⎝ ⎛⎭⎪⎫x 2，x 222p .∴M ⎝ ⎛⎭⎪⎫kp ，k 2p ＋p 2，N ⎝ ⎛⎭⎪⎫kp ，－p 2.∴k AN ＝x 212p ＋p 2x 1－kp ＝x 212p ＋p 2x 1－x 1＋x 22＝x 21＋p 22p x 1－x 22＝x 21－x 1x 22p x 1－x 22＝x 1p .又x 2＝2py ，∴y ′＝x p .∴抛物线x 2＝2py 在点A 处的切线斜率k ＝x 1p . ∴直线AN 与抛物线相切．1的一个交点的横坐标为8.(1)求抛物线C 的方程；(2)不过原点的直线l 2与l 1垂直，且与抛物线交于不同的两点A ，B ，若线段AB 的中点为P ，且|OP |＝|PB |，求△F AB 的面积.[解] (1)易知直线与抛物线的交点坐标为(8，－8)， ∴(－8)2＝2p ×8， ∴2p ＝8，∴抛物线方程为y 2＝8x .(2)直线l 2与l 1垂直，故可设直线l 2：x ＝y ＋m ，A (x 1，y 1)，B (x 2，y 2)，且直线l 2与x 轴的交点为M .由⎩⎨⎧y 2＝8x ，x ＝y ＋m ，得y 2－8y －8m ＝0，Δ＝64＋32m >0，∴m >－2. y 1＋y 2＝8，y 1y 2＝－8m ，∴x 1x 2＝y 21y 2264＝m 2.由题意可知OA ⊥OB ，即x 1x 2＋y 1y 2＝m 2－8m ＝0， ∴m ＝8或m ＝0(舍)，∴直线l 2：x ＝y ＋8，M (8,0)．故S △F AB ＝S △FMB ＋S △FMA ＝12·|FM |·|y 1－y 2| ＝3(y 1＋y 2)2－4y 1y 2＝24 5.1．(2018·全国卷Ⅰ)设抛物线C ：y 2＝4x 的焦点为F ，过点(－2,0)且斜率为23的直线与C 交于M ，N 两点，则FM →·FN →＝( )A ．5B ．6C ．7D ．8D [法一：过点(－2,0)且斜率为23的直线的方程为y ＝23(x ＋2)，由⎩⎪⎨⎪⎧y ＝23(x ＋2)，y 2＝4x ，得x 2－5x ＋4＝0，解得x ＝1或x ＝4，所以⎩⎨⎧ x ＝1，y ＝2或⎩⎨⎧x ＝4，y ＝4，不妨设M (1,2)，N (4,4)，易知F (1,0)，所以FM →＝(0,2)，FN →＝(3,4)，所以FM →·FN →＝8.故选D.法二：过点(－2,0)且斜率为23的直线的方程为y ＝23(x ＋2)，由⎩⎪⎨⎪⎧y ＝23(x ＋2)，y 2＝4x ，得x 2－5x ＋4＝0，设M (x 1，y 1)，N (x 2，y 2)，则y 1＞0，y 2＞0，根据根与系数的关系，得x 1＋x 2＝5，x 1x 2＝4.易知F (1,0)，所以FM →＝(x 1－1，y 1)，FN →＝(x 2－1，y 2)，所以FM →·FN →＝(x 1－1)(x 2－1)＋y 1y 2＝x 1x 2－(x 1＋x 2)＋1＋4x 1x 2＝4－5＋1＋8＝8.故选D.]2．(2016·全国卷Ⅱ)设F 为抛物线C ：y 2＝4x 的焦点，曲线y ＝kx (k ＞0)与C 交于点P ，PF ⊥x 轴，则k ＝( )A.12 B ．1 C.32D ．2D [∵y 2＝4x ，∴F (1,0)．又∵曲线y ＝kx (k ＞0)与C 交于点P ，PF ⊥x 轴，∴P (1,2)．将点P (1,2)的坐标代入y ＝kx (k ＞0)得k ＝2.故选D.]3．(2018·全国卷Ⅲ)已知点M (－1,1)和抛物线C ：y 2＝4x ，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若∠AMB ＝90°，则k ＝________.2 [法一：由题意知抛物线的焦点为(1,0)，则过C 的焦点且斜率为k 的直线方程为y ＝k (x －1)(k ≠0)，由⎩⎨⎧y ＝k (x －1)，y 2＝4x 消去y 得k 2(x －1)2＝4x ，即k 2x 2－(2k 2＋4)x ＋k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1.由⎩⎨⎧y ＝k (x －1)，y 2＝4x 消去x 得y 2＝4⎝ ⎛⎭⎪⎫1k y ＋1，即y 2－4k y －4＝0，则y 1＋y 2＝4k ，y 1y 2＝－4.由∠AMB ＝90°，得MA →·MB →＝(x 1＋1，y 1－1)·(x 2＋1，y 2－1)＝x 1x 2＋x 1＋x 2＋1＋y 1y 2－(y 1＋y 2)＋1＝0，将x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1与y 1＋y 2＝4k ，y 1y 2＝－4代入，得k ＝2.法二：设抛物线的焦点为F ，A (x 1，y 1)，B (x 2，y 2)，则⎩⎨⎧y 21＝4x 1y 22＝4x 2，所以y 21－y 22＝4(x 1－x 2)，则k ＝y 1－y 2x 1－x 2＝4y 1＋y 2.取AB 的中点M ′(x 0，y 0)，分别过点A ，B 作准线x ＝－1的垂线，垂足分别为A ′，B ′，又∠AMB ＝90°，点M 在准线x ＝－1上，所以|MM ′|＝12|AB |＝12(|AF |＋|BF |)＝12(|AA ′|＋|BB ′|)．又M ′为AB 的中点，所以MM ′平行于x 轴，且y 0＝1，所以y 1＋y 2＝2，所以k ＝2.]4．(2017·全国卷Ⅱ)已知F 是抛物线C ：y 2＝8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则|FN |＝________.6 [如图，不妨设点M 位于第一象限内，抛物线C 的准线交x 轴于点A ，过点M 作准线的垂线，垂足为点B ，交y 轴于点P ，∴PM ∥OF .由题意知，F (2,0)，|FO |＝|AO |＝2. ∵点M 为FN 的中点，PM ∥OF ， ∴|MP |＝12|FO |＝1. 又|BP |＝|AO |＝2， ∴|MB |＝|MP |＋|BP |＝3.由抛物线的定义知|MF |＝|MB |＝3，故|FN |＝2|MF |＝6.]自我感悟：______________________________________________________ ________________________________________________________________ ________________________________________________________________。

高考数学一轮复习抛物线同步提升检测(含解析)

高考数学一轮复习抛物线同步提升检测（含解析）平面内，到定点与定直线的距离相等的点的轨迹叫做抛物线，下面是查字典数学网整理的抛物线同步提升检测，请考生及时练习。

一、选择题1.(2021宜春模拟)动点P到点A(0,2)的距离比它到直线l:y=-4的距离小2,那么动点P的轨迹方程为()(A)y2=4x (B)y2=8x(C)x2=4y (D)x2=8y2.假定抛物线y2=2px(p0)的焦点在圆x2+y2+2x-3=0上,那么p=()(A) (B)1 (C)2 (D) 33.抛物线y=-2x2上的一点M到焦点的距离为1,那么点M的纵坐标是()(A) (B) (C)- (D)-4.正三角形的一个顶点位于原点,另外两个顶点在抛物线y2=4x上,那么这个正三角形的边长为()(A)4 (B)8 (C)8 (D)165.抛物线y2=2px(p0),过其焦点且斜率为1的直线交抛物线于A,B两点,假定线段AB的中点的纵坐标为2,那么该抛物线的准线方程为()(A)x=1 (B)x=-1(C)x=2 (D)x=-26.直线l过抛物线y2=2px(p0)的焦点，且交抛物线于A，B 两点，交其准线于C点，|AF|=4，=3，那么p=()(A)2 (B) (C) (D)47.(2021西安模拟)假定双曲线-=1(a0)的左右焦点区分为F1,F2,线段F1F2被抛物线x=y2的焦点分红3∶2的两段,那么此双曲线的离心率为()(A) (B) (C) (D)8.(才干应战题)假定点Q(4,0)和抛物线y=x2+2上一动点P(x,y),那么y+|PQ|最小值为()(A)2+2 (B)11(C)1+2 (D)6二、填空题9.以抛物线x2=16y的焦点为圆心,且与抛物线的准线相切的圆的方程为 .10.(2021巢湖模拟)抛物线y=x2的焦点与双曲线-=1的上焦点重合,那么m=.11.(2021铜川模拟)点P是抛物线y2=4x上的动点,点P在y 轴上的射影是M,点A的坐标是(4,a),那么当|a|4时,|PA|+|PM|的最小值是.三、解答题12.圆心为P的动圆与直线y=-2相切,且与定圆x2+(y-1)2=1内切,记点P的轨迹为曲线E.(1)求曲线E的方程.(2)设斜率为2的直线与曲线E相切,求此时直线到原点的距离.13.(2021宝鸡模拟)抛物线C:y2=2px(p0)过点A(1,-2).(1)求抛物线C的方程,并求其准线方程.(2)能否存在平行于OA(O为坐标原点)的直线l,使得直线l 与抛物线C有公共点,且直线OA与l的距离等于?假定存在,求出直线l的方程;假定不存在,说明理由.14.(才干应战题)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一局部,曲线C2是以原点O为顶点,F2为焦点的抛物线的一局部,A,B是曲线C1和C2的交点且AF2F1为钝角,假定|AF1|=,|AF2|=.(1)求曲线C1和C2的方程.(2)设点C,D是曲线C2所在抛物线上的两点(如图).设直线OC的斜率为k1,直线OD的斜率为k2,且k1+k2=,证明:直线CD过定点,并求该定点的坐标.答案解析1.【解析】选D.由得,动点P到点A(0,2)的距离与它到直线l:y=-2的距离相等,依据抛物线的定义得,该轨迹为以A(0,2)为焦点,y=-2为准线的抛物线,且=2,p=4.又焦点在y轴上,启齿向上,所以所求方程为:x2=8y.2.【解析】选C.由(,0)在圆x2+y2+2x-3=0上,所以有+2-3=0, 即p2+4p-12=0,解得p=2或p=-6(舍去).3.【解析】选D.由抛物线y=-2x2得x2=-y,所以其焦点为F(0,-),设点M纵坐标为y0,由抛物线定义得-y0=1,得y0=-.【方法技巧】求解抛物线上的点到焦点的距离和到准线的距离效果的技巧抛物线上的点到焦点的距离与抛物线上的点到准线的距离经常相互转化:(1)假定求点到焦点的距离,那么可联想点到准线的距离;(2)假定求点到准线的距离,那么经常联想点到焦点的距离.解题时一定要留意.4.【解析】选B.设其中一个顶点为(x,2),∵是正三角形,=tan 30=,即=,x=12.除原点外的另外两个顶点是(12,4)与(12,-4),这个正三角形的边长为8.5.【解析】选B.方法一:设A(x1,y1),B(x2,y2),由题意知直线AB的方程为:y=x-,与y2=2px联立得:y2-2py-p2=0,y1+y2=2p,由题意知:y1+y2=4,p=2,抛物线的方程为y2=4x,其准线方程为x=-1,应选B.方法二:设A(x1,y1),B(x2,y2),由题意得y1+y2=4,=2px1,=2px2,两式相减得:kAB====1,p=2,抛物线的方程为y2=4x,其准线方程为x=-1.6.【解析】选C.过A，B区分作准线的垂线交准线于E，D.由于|AF|=4，=3，所以|AE|=4，|CB|=3|BF|，且|BF|=|BD|，设|BF|=|BD|=a，那么|BC|=3a，依据三角形的相似性可得=，即=，解得a=2，所以=，即==，所以p==，选C.7.【解析】选D.由得F1(-c,0),F2(c,0),抛物线x=y2,即y2=2bx的焦点F(,0),依题意=.即=,得:5b=2c25b2=4c2,又b2=c2-a2,25(c2-a2)=4c2,解得c=a.故双曲线的离心率为=.8.【解析】选D.抛物线y=+2的准线是y=1,焦点F(0,3).用抛物线的定义:设P到准线的距离为d,那么y+|PQ|=d+1+|PQ|=|PF|+|PQ|+1|FQ|+1=5+1=6,(当且仅当F,Q,P共线时取等号)故y+|PQ|的最小值是6.9.【解析】抛物线x2=16y的焦点为(0,4),准线方程为y=-4,故圆的圆心为(0,4),又圆与抛物线的准线相切,所以圆的半径r=4-(-4)=8,所以圆的方程为x2+(y-4)2=64.答案:x2+(y-4)2=6410.【解析】由于抛物线y=x2的规范方程为x2=16y,焦点坐标为(0,4),又由于双曲线-=1的上焦点坐标为(0,),依题意有4=,解得m=13.答案:13【误区警示】此题易出现y=x2的焦点为(0,)的错误,缘由是对抛物线的规范方程记忆不准确.11.【解析】由y2=4x得,抛物线的焦点F(1,0),准线方程为x=-1,由|a|4知点A(4,a)在抛物线的外部,要使|PA|+|PM|最小,只需|PA|+|PF|最小,这只需点A,P,F三点共线即可,此时:(|PA|+|PF|)min==,所以:|PA|+|PM|的最小值为(|PA|+|PF|)min-1=-1.答案:-112.【解析】(1)由题意,得点P到直线y=-1和点(0,1)距离相等,点P的轨迹是以点(0,1)为焦点,以直线y=-1为准线的抛物线,曲线E的方程是x2=4y.(2)设斜率为2的直线方程为y=2x+m,由消去y,得x2-8x-4m=0,由直线与曲线E相切,得=(-8)2+16m=0,得m=-8,直线方程为y=2x-8,即2x-y-8=0.原点到直线的距离为d==.13.【解析】(1)将(1,-2)代入y2=2px,得(-2)2=2p1,所以p=2.故所求的抛物线C的方程为y2=4x,其准线方程为x=-1.(2)存在.假定存在契合题意的直线l,其方程为y=-2x+t.由得y2+2y-2t=0.∵直线l与抛物线C有公共点,=4+8t0,解得t-.由直线OA与l的距离d=,可得=,解得t=1.∵-1[-,+),1[-,+).契合题意的直线l存在,其方程为2x+y-1=0.14.【解析】(1)设A(xA,yA),F1(-c,0),F2(c,0),曲线C1所在椭圆的长轴长为2a,那么2a=|AF1|+|AF2|=6.又由及圆锥曲线的定义得:(xA-c)2+=,(xA+c)2+=,xA+c=,得:(xA-c)2=.又∵AF2F1为钝角,xA-c=,故xA=,c=1,即曲线C1的方程为+=1(-3),曲线C2的方程为y2=4x(0).(2)设直线OC的方程为:y=k1x,由得(k1x)2-4x=0,即C(,),同理得:D(,),直线CD的方程为:y-=(x-),即y=x+2,当x=0时,恒有y=2,即直线CD过定点(0,2).抛物线同步提升检测和答案的全部内容就是这些，更多精彩内容请考生继续关注查字典数学网。

2012高考数学综合训练1(理).许兴华

南宁三中2012高考数学模拟试题1(理)命题人：许兴华(Steven)一、选择题（共12小题，每题5分，共60分）1．设k =︒460cos ,则)(80tan =︒ 22221)(1)(1)(1)(kk D kk C kk B kk A -±-±---2．若ω是方程01x x 2=++的根(i 是虚数单位)，则)(21011=++++ωωωω1)(2321)(0)(1)(-±-D i C B A3．设向量)37cos ,53(cos b ),67cos ,23(cos a ︒︒=︒︒= ，则)(b a =⋅21)D (23)C (21)B (23)A (--4．已知椭圆1my 5x 22=+的离心率510e =,则)(m =15或3155(D)5(C)325(B)3或(A)35．设集合}N n ,2n 7y y {B },N k ,3k 5x x {A **∈+==∈+==，则B A 中的最小元素是（）(D)58(C)23(B)16(A)136．若动点P(x,y)在方程11y 1x =++-围成的封闭图形的内部（含边界），则22y x +的最小值是（）21)(23)(23)(22)(D C B A7．曲线012=-+x y 与曲线)(0R a ax y ∈=+的交点的个数一定是( )个1)(4)(3)(2)(D C B A8．双曲线1y 4x 22=-的两个焦点为21F ,F ，点P 在双曲线上，21PF F ∆的面积是3，则)(PF PF 21=⋅3)(3)(2)(2)(D C B A --9．函数b a x x )x (f ++=是奇函数的充要条件是（）1b a )D (0b a )C (0b R a )B (0b 1a )A (=====∈==且且 10．设9)2x x a (-的展开式中3x 项的系数是49,则常数)(a =4)D (4)C (8)B (8)A (--11. 棱长为12的正四面体PABC 有内切球O,该棱锥P-ABC 的中截面为M,则点O 到平面M 的距离是（） 223)(6)(62)(3)(D C B A 12．过点P(1,1)作曲线3x y =的两条切线21,l l ,设21,l l 的夹角为θ,则)(tan =θ36)(139)(1315)(33)(D C B A 二、填空题（共4小题，每题5分，共20分）13．某仪器显示屏上有7个小孔排成一排，每个小孔可显示出0或1，若每次显示其中3个小孔，但相邻的两个孔不能同时显示，则这个显示屏共能显示出的信号总数是 .14．以长方体1111D C B A ABCD -的任意三个顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率P 为 .(用分数作答)15. 过抛物线()220x py p =>的焦点F 作倾斜角为30°的直线，与抛物线分别交于A 、B 两点(点A 在y 轴左侧)，则FBAF＝． 16．各项都是正数的等比数列}a {n 的公比1q ≠,且132a ,2a ,a 成等差数列，令)N n (b )a a a a (*n 1n 2n 1n 1n n ∈=++-+++,则=+++∞→)(lim 21n n b b b .三、解答题（共6小题，满分共70分）17．（满分10分)已知向量()())x sin(,1b ,1),x sin(a +θ-=-θ=.（1）若R x ∈时,恒有b a⊥成立,求角θ的值；（2）若θ+⋅=cos 2b a )x (f 的最大值为0,且),43(,532sin ππ-∈θ=θ,求θcos 的值.18．(满分12分)由计算机随机选出大批正整数，取其最高位数（如35为3，918为9）出现的次数构成一个分布.已知这个分布中，数字1，2，3，4，…，9出现的概率正好构成一个首项为51的等差数列.现从这批正整数中任取一个，记其最高位数为)9,,3,2,1=( ξξ. （1）求ξ的分布列；（2）求ξ的数学期望ξE ..19.(12分) 如图，在三棱锥P -ABC 中，AC =BC =2，∠ACB =90°，AP =BP =AB ，PC ⊥AC . （Ⅰ）求证：PC ⊥AB ；（Ⅱ）求二面角B-AP-C 的大小；（Ⅲ）求点C 到平面APB 的距离.20．（满分12分）已知定义在区间),0(+∞上的函数)1(ln 21)(2≥+-=m k x m x x f 在),1[+∞上是单调递增函数.(1)求)(x f 的单调区间；(2)若对]3,21[∈x ，不等式2)(k x f >恒成立，求实数k 的取值范围.21．（满分12分）以O 为原点，所在直线为x 轴，建立如图所示的直角坐标系，设OF ·FG =1，点F 的坐标为（t,0），),3[+∞∈t ，点G 的坐标为（x 0，y 0）.（1）求x 0关于t 的函数x 0=f(t)的表达式，判断函数f(t)的单调性，并用定义证明你的判断；（2）设△OFG 的面积t S 631=，若以O 为中心，Ｆ为焦点的椭圆经过点Ｇ，求当||取最小值时椭圆的方程.22．（满分12分）已知数列}{n a 满足)(5221212121*33221N n n a a a a n n ∈+=++++ ，其前n 项和为n S . (1)求数列}{n a 的通项公式； (2)记.834,1433221+<++++=+n T S S S S S S S S T n n n n 求证：OF xyG南宁三中2012高三数学答题卷1班级：姓名：座号：13、；14、；15、；16、.三.解答题(解每个大题时,请注意在“解”字前面标明题号！)。

2013高考数学模拟试题(2).许兴华

试卷第1页，总6页绝密★启用前2013年高考数学模拟试卷(2)考试范围：高中数学；考试时间：100分钟；命题人：许兴华1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题（题型注释）1．已知⎩⎨⎧≥-<+--=),0)(1(),0(2)(2x x f x a x x x f x x f y-=)(恰有3个不同的零点，则实数a 的取值范围是（）A ．[)1,-+∞B ．[)1,0-C ．[)2,-+∞D ．()0,+∞ 2．只要将函数sin 2y x =的图象（） A C3．若定义在R 上的偶函数()f x 对任意12,[0,)∈+∞x x 12()≠x x ，有A ．(3)(2)(1)<-<f f fB ．(1)(2)(3)<-<f f fC ．(1)(3)(2)<<-f f fD ．(2)(3)(1)-<<f f f4．定义在R 上的偶函数f （x ）的一个单调递增区间为（3，5），则y=f （x-1） A. 图象的对称轴为x=-1，且在（2，4）内递增 B. 图象的对称轴为x=-1，且在（2，4）内递减试卷第2页，总6页C. 图象的对称轴为x=1，且在（4，6）内递增D. 图象的对称轴为x=1，且在（4，6）内递减5．若函数)(x f 的图像在点P （1，m m 的值为( )A ．B ．6．若函数)0(c o s s i n )(≠+=ωωωx x x f 对任意实数x 都有） A ．1- B ．1 C D 7．过点P(x,y)的直线分别与x 轴和y 轴的正半轴交于A,B 两点,点Q 与点P关于y 轴对称，O 为坐标原点，若2BP PA = 且OQ AB ⋅=1，则点P 的轨迹方程是（） AC 8．已知等差数列{an}满足a2=3，n n 3S S －－=51(n>3) ，n S = 100，则n 的值为A. 8B. 9C. 10D. 119．在ΔABC 中，角A,B,C 所对的对边长分别为a 、b 、c ，sinA 、sinB 、sinC 成等比数列，且c= 2a ，则cosB 的值为10．若实数,,a b c 满足log 2log 2log 2a b c <<，则下列关系中不可能成立．．．．．的是（）A ．a b c <<B ．b a c <<C ． c b a <<D ．a c b <<11．在三棱锥P －ABC 中，PA ⊥平面ABC ，∠BAC ＝90°，D 、E 、F 分别是棱AB 、BC 、CP 的中点，AB ＝AC ＝1，PA ＝2，则直线PA 与平面DEF 所成角的正弦值为( )试卷第3页，总6页12．已知F 1、F 2＞b ＞0)的两个焦点，过F 2作椭圆的弦AB ，若△AF 1B 的周长为16 ）D试卷第4页，总6页第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题（题型注释）13．若52345012345(12),x a a x a x a x a x a x +=+++则a 3= 。

高三数学导数单元测验(文).许兴华

高三数学（导数）单元测验（文）.许兴华一. 选择题1. 函数1x 3x )x (f 23+-=是减函数的区间为 ( )A. (2,)+∞B. (,2)-∞C. (,0)-∞D. (0,2)2. 函数9x 3ax x )x (f 23-++=, 已知)x (f 在3x -=时取得极值, 则=a ( ) A. 2 B. 3 C. 4 D. 53. 在函数x 8x y 3-=的图象上, 其切线的倾斜角小于4π的点中, 坐标为整数的点的个数是 ( ) A. 3 B. 2 C. 1 D. 04. 函数1ax y 2+=的图象与直线x y =相切, 则=a ( )A. 18B. 41C. 21D. 15. 已知函数m x 21x 3)x (f 23+-=(m 为常数) 图象上点A 处的切线与直线03y x =+- 的夹角为45 , 则点A 的横坐标为 ( ) A. 0 B. 1 C. 0或61 D. 1或616. 已知: a (a x 6x 2)x (f 23+-=为常数)在]2,2[-上有最大值是3, 那么]2,2[-在上的最小值是 ( ) A. 5- B. 11- C. 29- D. 37-二. 填空题7. 曲线3x y =在点)1,1(处的切线与x 轴、直线2x =所围成的三角形的面积为 .8. 曲线1x x y 3++=在点)3,1(处的切线方程是 .9. 曲线4x 6x 3x y 23+++=的所有切线中, 斜率最小的切线的方程是 .10.函数x 6x 3x 4y 23++-=的单调递减区间为 , 极大值为 ,极小值为 .三. 解答题11. 已知函数,a x 9x 3x )x (f 23+++-= (1) 求)x (f 的单调递减区间;(2) 若)x (f 在区间]2,2[ -上的最大值为20, 求它在该区间上的最小值.12. 已知c 2bx 3x )x (f 3++=, 若函数)x (f 的一个极值点落在x 轴上, 求23c b +的值.13. 已知函数d ax bx x )x (f 23+++=的图象过点P )2,0(, 且在点M ))1(f ,1(--处的切线方程为07y x 6=+-.(1) 求函数)x (f y =的解析式; (2) 求函数)x (f y =的单调区间.14. 已知1x =是函数1nx x )1m (3mx )x (f 23+++-=的一个极值点, 其中,0m ,R n ,m <∈(1) 求m 与n 的关系式; (2) 求)x (f 的单调区间;(3) 当]1,1[x -∈时, 函数)x (f y =的图象上任意一点的切线斜率恒大于3m, 求m 的取值范围.高三数学（导数）单元测验（文）答案一.6.（提示: )a 8)2(f ,a )0(f ,a 40)2(f +-==+-=-二. 填空题7.38; 8. 1x 4y -=; 9. ;3x 3y += 10. ,),1(),21,(+∞--∞ 5 , .47- 9. (提示: 3)1x (36x 6x 3)x (f 22++=++=', 当1x -=时,)x (f '的最小值为3,所以当1x -=时, 0y =所求切线过点)0,1(-且斜率为3, 所以切线方程为.)3x 3y +=三. 解答题11. 解: (1) .9x 6x 3)x (f 2++-='令1x 0)x (f -<⇒<'或,3x > 所以函数)x (f 的单调递减区间为)1,(--∞ , ),3(∞+ .(2) 因为,a 2a 18128)2(f +=+-+=- ,a 22a 18128)2(f +=+++-=所以)2(f )2(f ->. 因为在)3,1( -上0)x (f >', 所以)x (f 在]2,1[ -上单调递增, 又由于)x (f 在]1,2[-- 上单调递减, 因此)2(f 和)1(f -分别是)x (f 在区间]2,2[ -上的最大值和最小值, 于是有2a 20a 22-=⇒=+. 故,2x 9x 3x )x (f 23-++-=因此72931)1(f -=--+=-, 即函数)x (f 在区间]2,2[ -上的最小值为7-.12. 解: b 3x 3)x (f 2+=', 设)x (f 的极值点为（)0,m , 则0)m (f ,0)m (f ='=所以 ,0b 3m 30c 20b 3m 23⎪⎩⎪⎨⎧=+=+⨯+ 所以,0c 2bm 2,0c 2bm 3bm =+=++-所以22c )bm (=, ,c )b (b 22=-所以.0c b 23=+13. 解: (1) 由)x (f 的图象经过P )2,0(,知2d =, 所以,2cx bx x )x (f 23+++=c bx 2x 3)x (f 2++='.即.6)1(f ,1)1(f =-'=-由在))1(f ,1(M --处的切线方程是07y x 6=+-, 知07)1(f 6=+---,⎩⎨⎧-=-=⇒⎩⎨⎧=+-+-=+-∴3c 3b 12c b 16c b 23 故所求的解析式是 .2x 3x 3x )x (f 23+--=(2) .3x 6x 3)x (f 2--='令,03x 6x 32=--即.01x 2x 2=--解得 .21x ,21x 21+=-= 当;0)x (f ,21x ,21x >'+>-<时或当.0)x (f ,21x 21<'+<<-时故2x 3x 3x )x (f 23+--=在)2,(--∞内是增函数, 在)21,21(+-内是减函数,在),21(+∞+内是增函数.14. 解: (1) n x )1m (6mx 3)x (f 2++-='因为1x =是函数)x (f 的一个极值点, 所以 0)1(f =', 即,0n )1m (6m 3=++-所以6m 3n +=(2) 由(1)知, 6m 3x )1m (6mx 3)x (f 2+++-=')]m21(x )[1x (m 3+--= 当0m <时, 有,m211+>当x 变化时，)x (f 与)x (f '的变化如下表:故有上表知, 当0m <时, )x (f 在)m 21,(+-∞单调递减, 在)1,m21(+单调递增, 在),1(+∞上单调递减.(3) 由已知得m 3)x (f >', 即02x )1m (2mx 2>++-又0m <所以0m 2x )1m (m 2x 2<++-, 即]1,1[x ,0m 2x )1m (m 2x 2-∈<++-……① 设,m2x )m 11(2x )x (g 2++-= 其函数开口向上, 由题意知①式恒成立,所以0m 34010m2m 2210)1(g 0)1(g <<-⇒⎪⎩⎪⎨⎧<-<+++⇒⎩⎨⎧<<-, 即m 的取值范围为)0,34(-.。

高三数学(理)综合测试题1.许兴华

530021广西南宁三中许兴华文集高考数学综合模拟测试题（理科）（1）530021广西南宁三中许兴华一、选择题（共12小题，每题5分，共60分）1．设集合{}{}34,22,A x x B x y x x A B =-≤==-+-= 则（）A ．{}0B ．{}2C ．{}112x -<≤D ．{}27x x ≤≤2．设z 为复数，2,2zz i i+-均为实数，则z =（） A ．2i -B ．12i -C ．42i -D ．22i -3．已知等比数列}{n a 的前n 项和为n S ，且321,2,4a a a 成等差数列，若11=a ，则=4S （）A ．7B ．8C ．15D ．164．一个容量为20的样本数据，分组后，组距与频数如下：(10,20],2; (20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2. 则样本在(10,50]上的频率为（）A ．120B ．14C ．12D ．7105．某班要从3名男生和3名女生中选出3人分别担任数学、物理、化学课代表，要求至少一名女生，则不同的选择方案有（） A ．54种B ．114种C ．19种D ．180种6．已知βα,表示两个不同的平面，m 为平面α内的一条直线，则""βα⊥是""β⊥m 的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7．已知随机变量ξ服从正态分布21(,),(2)2N P μσξ>=若，则必有（） A ．2μ=B ．12μ=C ．2σ=D ．2σ=8．设()f x 是定义在R 上以2为周期的偶函数，当(0,1)x ∈时，0.5()log (2)f x x =-，则函数()f x 在区间（1，2）上（） A ．是增函数，且()0f x < B ．是增函数，且()0f x > C ．是减函数，且()0f x <D ．是减函数，且()0f x >9．过椭圆2222:1(0)x y C a b a b+=>>的左顶点A 的斜率为k 的直线交椭圆C 于另一点B ，且点B 在x 轴上的射影恰好为右焦点F ，若1132k <<，则椭圆离心率e 的取值范围是（）A ．12(,)33B ．12(,)23C ．12(,)43D ．12(,)5310．偶函数42()(1)2(23)41(32),f x a x ax b x b a x a =--+--+--≤≤()y f x =则(2,(2))a f a --在点处切线的斜率为（） A ．10B ．－10C ．4D ．无法确定11．等比数列{}n a 的公比22cos 103sin110q -︒=-︒，前n 项和为53,n S S a =则（）A ．152B ．312C ．314D ．17212．若对于函数()f x 定义域内的任意一个自变量x 1，都存在唯一一个自变量x 2, 使得阶段12()()1f x f x =成立，则称()f x 为“好函数”. 以下四个函数：①()10x f x =；②1()lg ;f x x=③()sin ,(0,)f x x x π=∈；④cos ()2,(0,).x f x x π=∈ 其中为“好函数”的函数的个数为（） A ．1B ．2C ．3D ．4530021广西南宁三中许兴华文集二、填空题（每小题5分，共20分）13．6)12(xx -展开式中的常数项为 .（用数字作答）14.求值=+++-∞→)1(lim 2x x x x .15．13sin10sin80-=︒︒. （用数字作答） 16．已知半球O 的半径为R ，点A 、B 、C 都在底面⊙O 的圆周上，且AB 为⊙O 的直径，BC=2，半球面上一点D 到平面ABC 的距离为R ，又二面角D －AC －B 的平面角的余弦值为33，则该半球的表面积为 .三、解答题(共有6小题，共70分)17．（10分）已知向量1(cos ,1),(1,sin ),(0,).5a xb x x π=-+=∈ 其中（1）若45a b ⋅= ，求sin x 的值；（2）若(1tan )sin 2,1sin cos x xa b x x+⋅⊥++ 求的值.18．（12分）乒乓球爱好者小张有红色乒乓球2个，黄色乒乓球3个，白色乒乓球5个，将这10个乒乓球装在一个袋内，现从中任意取出4个，且取出的乒乓球中同色的2个编为一组，并设红色一组得5分，黄色一组得3分，白色一组得1分，用ξ表示所得分数之和. （1）求ξ共有多少种不同取值；（2）求ξ取最大值时的概率.19．（12分）已知函数k bx ax x x f +++=23)(满足：0)32()1(=-'='f f ．（1）求a 、b 的值及函数)(x f 的单调递增区间；（2）若对]2,1[-∈x ，不等式2)(k x f <恒成立，求k 的取值范围．530021广西南宁三中许兴华文集20．（12分）如图，四棱锥P —ABCD 的底面是正方形，P A ⊥底面,2,45ABCD PA PDA =∠=︒，点E 、F 分别为棱AB 、PD 的中点. （1）求证：//;AF PCE 平面（2）求二面角E PD C --的大小.21．（12分）已知点A （－1，0）、B （1，0）和动点M 满足：22,cos 3,AMB AM BM θθ∠=⋅=且动点M 的轨迹为曲线C ，过点B 的直线交曲线C 于P 、Q 两点. （1）求曲线C 的方程；（2）求APQ ∆面积的最大值.22．（12分）设数列{}n a 的各项都是正数，且对任意的33332123n nn N a a a a S *∈++++= 都有，其中n S 为数列{}n a 的前n 项和. （1）求证：22n n n a S a =-；（2）求数列{}n a 的通项公式；（3）设13(1)2(na nn n b λλ-=+-⋅为非零整数，n N *∈），试确定λ的值，使得对任意的n N *∈，都有1n n b b +>成立.高考数学综合模拟测试题（理科）（1）参考答案选择题：1-5 BCCDB 6-10 BACBC 11-12CC填空题：13.240 14.12- 15．4 16.π6一、选择题（共12小题，每题5分，共60分）1．B解析：∵{}{}{}17,2,2A x x B x x A B =-≤≤==∴= ，选B 2．C解析：设204,,4 2.20,2b a z a bi z i a b b +==⎧⎧=+∴=-⎨⎨+==-⎩⎩则即3．C解析：设数列}{n a 的公比为q,由31244a a a +=,即211144q a a q a +=,得q=2,15212144=--=S 4．D解析：在（10，50）上的频数为2+3+4+5=14，则其频率为147.2010= 5．B解析：从6个人中选出3人有2036=C 种不同的方法，其中不选女生只有1种方法，则满足题意的不同选派方案共有114)120(33=⨯-A 种.6．B解析：若α⊂m ,β⊥m ,则βα⊥;若βα⊥,则m 未必垂直于β,即""""βαβ⊥⇒⊥m ,而βα⊥得不到β⊥m . 7．A解析：数形结合，根据正态分布曲线关于直线x μ=对称可知 2.μ=530021广西南宁三中许兴华文集8．C解析：当0.5(0,1),()log (2)0x f x x ∈=-<时为增函数，由()f x 为偶函数知()(1,0)f x -在上为减函数，()0f x <；再由周期性可知，当(1,2),()0x f x ∈<时且是减函数. 9．B解析：如图，由题设有，2,,,tan ,b BFBF AF a c Rt ABF k BAF a AF ==+∴∆==在中 2211121,1,.()3223b b ac a k e e e c c a c a a -∴====-∴<-<<<++即10．C解析：偶函数的定义域关于y 轴对称，即423320,3;()(),,()265,2a a a f x f xb f x x x --+==-===--得再由得所以3()812,f x x x '=- (2)(1)4k f a f ''=-=-= 11．C解析：255231cos 2022cos 1011312,.3sin1103cos 202(1)4S q q a q q +︒--︒-=====-︒-︒- 12．C解析：对于①1212()()101,x x f x f x +==只需1220,x x x +=唯一； ②1212122111()()lglg 1,lg ,lg f x f x x x x x x =⋅==只需唯一； ③12122()()sin sin 1,f x f x x x x ==不存在；④12cos cos 12122()()21,cos cos 0,x x f x f x x x x ==+=唯一。

2022版高考数学一轮复习第八章解析几何第七讲抛物线学案(含解析)新人教版

学习资料2022版高考数学一轮复习第八章解析几何第七讲抛物线学案（含解析）新人教版班级：科目：第七讲抛物线知识梳理·双基自测错误!错误!错误!错误!知识点一抛物线的定义抛物线需要满足以下三个条件:（1)在平面内；(2)动点到定点F的距离与到定直线l的距离__相等__；(3)定点F与定直线l的关系为__点F∉l__．知识点二抛物线的标准方程与几何性质标准方程y2＝2px(p＞0)y2＝－2px（p＞0)x2＝2py(p＞0)x2＝－2py（p＞0)p的几何意义：焦点F到准线l的距离图形顶点O（0,0）对称轴y＝0 x＝0焦点F__错误!__F__错误!__F__错误!__F__错误!__ 离心率e＝__1__准线方程__x＝－错误!____x＝错误!____y＝－错误!____y＝错误!__ 范围x≥0，y∈R x≤0，y∈R y≥0，x∈R y≤0,x∈R 开口方向向右向左向上向下焦半径(其中P（x0，y0)）｜PF｜＝__x0＋错误!__｜PF｜＝__－x0＋错误!__｜PF|＝__y0＋错误!__｜PF｜＝__－y0＋p2__归错误!错误!错误!抛物线焦点弦的处理规律直线AB过抛物线y2＝2px(p＞0)的焦点F，交抛物线于A(x1，y1），B（x2，y2)两点，如图．(1)y1y2＝－p2,x1x2＝错误!．(2)｜AB|＝x1＋x2＋p，x1＋x2≥2错误!＝p,即当x1＝x2时，弦长最短为2p．（3）错误!＋错误!＝错误!．（4)弦长AB＝错误!（α为AB的倾斜角)．(5)以AB为直径的圆与准线相切．（6）焦点F对A，B在准线上射影的张角为90°．（7）A、O、D三点共线；B、O、C三点共线．错误!错误!错误!错误!题组一走出误区1．判断下列结论是否正确（请在括号中打“√”或“×”）(1）平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线．（×)(2）方程y＝ax2（a≠0）表示的曲线是焦点在x轴上的抛物线，且其焦点坐标是错误!，准线方程是x＝－错误!．(×）（3）抛物线既是中心对称图形，又是轴对称图形．（×)(4）AB为抛物线y2＝2px（p＞0）的过焦点F错误!的弦，若A(x1，y1），B（x2，y2），则x1x2＝错误!,y1y2＝－p2，弦长｜AB｜＝x1＋x2＋p．(√）（5)过抛物线的焦点与抛物线对称轴垂直的直线被抛物线截得的线段叫做抛物线的通径，那么抛物线x2＝－2ay（a＞0)的通径长为2a．(√)题组二走进教材2．(必修2P69例4)(2021·甘肃张掖诊断）过抛物线y2＝4x的焦点的直线l交抛物线于P(x1，y1),Q(x2,y2）两点，如果x1＋x2＝6，则|PQ|等于(B）A．9 B．8C．7 D．6[解析］抛物线y2＝4x的焦点为F（1，0)，准线方程为x＝－1．根据题意可得，|PQ|＝|PF|＋｜QF|＝x1＋1＋x2＋1＝x1＋x2＋2＝8．3．(2021·河南郑州名校调研）抛物线y＝－4x2上的一点M到焦点的距离为1，则点M 的纵坐标是（B)A．－错误!B．－错误!C．错误!D．错误!［解析］由抛物线的方程y＝－4x2，可得标准方程为x2＝－错误!y，则焦点坐标为F 错误!，准线方程为y＝错误!，设M（x0，y0),则由抛物线的定义可得－y0＋错误!＝1，解得y0＝－错误!．故选B．题组三走向高考4．(2019·课标全国Ⅱ)若抛物线y2＝2px(p＞0)的焦点是椭圆错误!＋错误!＝1的一个焦点，则p＝（D)A．2 B．3C．4 D．8[解析］∵抛物线y2＝2px(p＞0)的焦点坐标为错误!，∴椭圆错误!＋错误!＝1的一个焦点为错误!,∴3p－p＝错误!，∴p＝8．故选D．5．(2020·新课标Ⅰ）已知A为抛物线C：y2＝2px(p＞0）上一点，点A到C的焦点的距离为12，到y轴的距离为9，则p＝(C）A．2 B．3C．6 D．9［解析］A为抛物线C：y2＝2px（p＞0)上一点,点A到C的焦点的距离为12，到y轴的距离为9,因为抛物线上的点到焦点的距离和到准线的距离相等，故有:9＋错误!＝12⇒p＝6；故选C．考点突破·互动探究考点一抛物线的定义及应用——多维探究角度1轨迹问题例1 (1)动圆与定圆A：（x＋2）2＋y2＝1外切，且和直线x＝1相切，则动圆圆心的轨迹是（D)A．直线B．椭圆C．双曲线D．抛物线［解析］设动圆的圆心为C，则C到定圆A：(x＋2)2＋y2＝1的圆心的距离等于r＋1，而动圆的圆心到直线x＝1的距离等于r,所以动圆到直线x＝2距离为r＋1，即动圆圆心到定点（－2,0）和定直线x＝2的距离相等，根据抛物线的定义知，动圆的圆心轨迹为抛物线，所以答案为D．角度2到焦点与到定点距离之和最小问题(2)①（2021·河北保定七校联考）已知M是抛物线x2＝4y上一点，F为其焦点，C为圆(x＋1)2＋（y－2)2＝1的圆心，则｜MF｜＋|MC|的最小值为(B）A．2 B．3C．4 D．5②(2021·山西运城联考)已知抛物线C：x2＝8y的焦点为F，O为原点,点P是抛物线C的准线上的一动点,点A在抛物线C上，且｜AF｜＝4，则｜P A|＋｜PO|的最小值为(B) A．4错误!B．2错误!C．3错误!D．4错误!［解析]①设抛物线x2＝4y的准线方程为l：y＝－1，C为圆（x＋1）2＋（y－2)2＝1的圆心，所以C的坐标为(－1，2)，过M作l的垂线，垂足为E,根据抛物线的定义可知|MF|＝|ME|，所以问题求｜MF｜＋｜MC|的最小值，就转化为求｜ME|＋|MC｜的最小值，由平面几何的知识可知，当C，M，E在一条直线上时，此时CE⊥l，|ME｜＋｜MC|有最小值，最小值为｜CE｜＝2－（－1）＝3,故选B．②由抛物线的定义知｜AF|＝y A＋错误!＝y A＋2＝4，∴y A＝2，代入x2＝8y,得x A＝±4，不妨取A（4，2)，又O关于准线y＝－2的对称点为O′(0,－4），∴|P A|＋｜PO|＝｜P A｜＋｜PO′｜≥｜AO′｜＝错误!＝2错误!，当且仅当A、P、O′共线时取等号，故选B．[引申]本例(2）①中，（ⅰ)|MC｜－｜MF|的最大值为__错误!__；最小值为__－错误! __；(ⅱ）若N为⊙C上任一点,则｜MF|＋｜MN｜的最小值为__2__．角度3到准线与到定点距离之和最小问题（3）已知圆C:x2＋y2＋6x＋8y＋21＝0，抛物线y2＝8x的准线为l，设抛物线上任意一点P到直线l的距离为d，则d＋|PC|的最小值为(A）A．错误!B．7C．6 D．9［解析］由题意得圆的方程为（x＋3)2＋(y＋4)2＝4，圆心C的坐标为（－3,－4）．由抛物线定义知，当d＋｜PC｜最小时为圆心与抛物线焦点间的距离，即d＋｜PC|＝(－3－2)2＋(－4)2＝错误!．角度4到两定直线的距离之和最小问题（4）（2021·北京人大附中测试)点P在曲线y2＝4x上，过P分别作直线x＝－1及y＝x ＋3的垂线,垂足分别为G，H，则｜PG|＋｜PH|的最小值为（B)A．错误!B．2错误!C．错误!＋1 D．错误!＋2[解析］由题可知x＝－1是抛物线的准线，焦点F(1,0），由抛物线的性质可知|PG|＝|PF|,∴｜PG|＋｜PH｜＝｜PF|＋｜PH｜≤｜FH｜＝错误!＝2错误!，当且仅当H、P、F三点共线时取等号，∴｜PG|＋|PH｜的最小值为2错误!．故选B．名师点拨利用抛物线的定义可解决的常见问题（1)轨迹问题：用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是否为抛物线．（2)距离问题:涉及抛物线上的点到焦点的距离和到准线的距离问题时，注意在解题中利用两者之间的关系进行相互转化．(3）看到准线想焦点，看到焦点想准线，这是解决抛物线焦点弦有关问题的重要途径．〔变式训练1〕（1)(角度1）到定点A （0,2)的距离比到定直线l ：y ＝－1大1的动点P 的轨迹方程为__x 2＝8y __．（2）(角度1)(2021·吉林省吉林市调研)已知抛物线y 2＝4x 的焦点F ，点A (4，3)，P 为抛物线上一点,且P 不在直线AF 上,则△P AF 周长取最小值时,线段PF 的长为( B )A ．1B ．134C ．5D ．214（3)(角度2)（2021·山西大学附中模拟)已知点Q (2错误!，0）及抛物线y ＝错误!上一动点P （x ，y ），则y ＋|PQ ｜的最小值是__2__．（4）(角度3）(2021·上海虹口区二模）已知直线l 1：4x －3y ＋6＝0和直线l 2：x ＝－1,抛物线y 2＝4x 上一动点P 到直线l 1和l 2的距离之和的最小值为（ C ）A ．错误!B ．错误!C ．2D ．错误![解析] (1）由题意知P 到A 的距离等于其到直线y ＝－2的距离,故P 的轨迹是以A 为焦点,直线y ＝－2为准线的抛物线，所以其方程为x 2＝8y ．(2)求△P AF 周长的最小值,即求|P A |＋｜PF ｜的最小值，设点P 在准线上的射影为D ，根据抛物线的定义，可知｜PF ｜＝｜PD |，因此,｜P A |＋｜PF |的最小值，即｜P A |＋｜PD |的最小值．根据平面几何知识,可得当D ，P ,A 三点共线时｜P A ｜＋|PD |最小，此时P 错误!，且｜PF ｜＝错误!＋1＝错误!，故选B ．(3）抛物线y ＝x 24即x 2＝4y ，其焦点坐标为F (0,1)，准线方程为y ＝－1．因为点Q 的坐标为(2错误!,0），所以|FQ ｜＝错误!＝3．过点P 作准线的垂线PH ，交x 轴于点D ，如图所示．结合抛物线的定义，有y ＋|PQ ｜＝｜PD ｜＋|PQ |＝|PH |＋｜PQ ｜－1＝｜PF ｜＋|PQ |－1≥｜FQ ｜－1＝3－1＝2，即y ＋|PQ |的最小值是2．(4)直线l 2：x ＝－1是抛物线y 2＝4x 的准线，抛物线y 2＝4x 的焦点为F (1，0），则点P 到直线l 2:x ＝－1的距离等于PF ,过点F 作直线l 1：4x －3y ＋6＝0的垂线，和抛物线的交点就是点P ，所以点P 到直线l 1:4x －3y ＋6＝0的距离和到直线l 2:x ＝－1的距离之和的最小值就是点F (1,0)到直线l 1：4x －3y ＋6＝0的距离,所以最小值为错误!＝2，故选C ．考点二抛物线的标准方程—-自主练透例2 （1)过点P （－3,2)的抛物线的标准方程为__y 2＝－错误!x 或x 2＝错误!y __．（2)焦点在直线x －2y －4＝0上的抛物线的标准方程为__y 2＝16x 或x 2＝－8y __，准线方程为__x ＝－4或y ＝2__．（3)如图,过抛物线y 2＝2px （p ＞0)的焦点F 的直线依次交抛物线及准线于点A ，B ,C ，若｜BC |＝2｜BF ｜，且｜AF |＝3,则抛物线的方程为（ B )A ．y 2＝32xB ．y 2＝3xC ．y 2＝错误!xD ．y 2＝9x[解析] (1）设所求抛物线的方程为y 2＝－2px (p ＞0）或x 2＝2py (p ＞0)． ∵过点（－3，2),∴4＝－2p ·(－3）或9＝2p ·2． ∴p ＝23或p ＝错误!．∴所求抛物线的标准方程为y 2＝－错误!x 或x 2＝错误!y ．（2)令x ＝0，得y ＝－2，令y ＝0，得x ＝4． ∴抛物线的焦点为(4,0)或（0,－2）．当焦点为（4，0)时，p2＝4，∴p ＝8，此时抛物线方程为y 2＝16x ；当焦点为（0，－2）时，p2＝2，∴p ＝4，此时抛物线方程为x 2＝－8y ．∴所求的抛物线的标准方程为y 2＝16x 或x 2＝－8y ，对应的准线方程分别是x ＝－4，y ＝2．（3)如图,分别过点A ，B 作准线的垂线，分别交准线于点E ，D ,设｜BF ｜＝a ，则由已知得｜BC ｜＝2a ,由定义得｜BD |＝a ，故∠BCD ＝30°．在直角三角形ACE 中，∵|AE ｜＝｜AF ｜＝3，｜AC |＝3＋3a ,2｜AE ｜＝｜AC |， ∴3＋3a ＝6，从而得a ＝1．∵BD ∥FG ，∴错误!＝错误!，即错误!＝错误!，求得p ＝错误!，因此抛物线的方程为y 2＝3x ．名师点拨求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法，若焦点位置确定，因为未知数只有p ，所以只需一个条件确定p 值即可．（2）因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量．一般焦点在x 轴上的抛物线的方程可设为y 2＝ax (a ≠0)；焦点在y 轴上的抛物线的方程可设为x 2＝ay (a ≠0)．〔变式训练2〕(1）(2021·重庆沙坪坝区模拟)已知抛物线C :y 2＝2px （p ＞0)的焦点为F ，过点(p,0)且垂直于x 轴的直线与抛物线C 在第一象限内的交点为A ，若｜AF |＝1，则抛物线C 的方程为（ A )A ．y 2＝43xB ．y 2＝2xC ．y 2＝3xD ．y 2＝4x(2）（2021·安徽蚌埠一中期中)已知抛物线的顶点在原点,焦点在y 轴上，其上的点P (m ，－3）到焦点的距离为5，则抛物线方程为（ D )A ．x 2＝8yB ．x 2＝4yC ．x 2＝－4yD ．x 2＝－8y[解析］ (1）由题意知x A ＝p ,又|AF |＝x A ＋错误!＝错误!＝1，∴p ＝错误!,∴抛物线C 的方程为y 2＝43x ，故选A ．（2）由题意可知抛物线的焦点在y 轴负半轴上,故设其方程为x 2＝－2py （p ＞0），所以3＋错误!＝5,即p ＝4，所以所求抛物线方程为x 2＝－8y ，故选D ．考点三,抛物线的几何性质-—师生共研例3 (1)(2021·广西四校联考）已知抛物线y 2＝2px (p ＞0）上横坐标为4的点到此抛物线焦点的距离为9,则该抛物线的焦点到准线的距离为( C ）A ．4B ．9C ．10D ．18（2)(理）（2021·四川眉山模拟）点F 为抛物线C ：y 2＝2px （p ＞0)的焦点,过F 的直线交抛物线C 于A ，B 两点（点A 在第一象限)，过A 、B 分别作抛物线C 的准线的垂线段，垂足分别为M 、N ，若|MF |＝4，|NF |＝3，则直线AB 的斜率为（ D )A ．1B ．错误!C ．2D ．错误!（文)(2021·四川师大附中期中）已知抛物线y 2＝2px （p ＞0)，F 为抛物线的焦点，O为坐标原点A (x 1，y 1)，B （x 2,y 2)为抛物线上的两点,A ，B 的中点到抛物线准线的距离为5，△ABO 的重心为F ，则p ＝（ D ）A ．1B ．2C ．3D ．4[解析] (1)抛物线y 2＝2px 的焦点为错误!,准线方程为x ＝－错误!．由题意可得4＋错误!＝9，解得p ＝10,所以该抛物线的焦点到准线的距离为10．故选C ．(2）(理)由抛物线定义知|AM ｜＝|AF |，|BN |＝｜BF ｜， ∴∠AFM ＋∠BFM ＝360°－∠MAF －∠NBF2＝90°，∴∠MFN ＝90°，又｜MF |＝4，|NF |＝3，∴|MN |＝5，∴p ＝|KF ｜＝错误!＝错误!，又∠AFM ＝∠AMF ＝∠MFK ，∴k AB ＝tan （180°－2∠MFK ）＝－错误!＝－错误!＝错误!．故选D ．(文）错误!＋错误!＝5,错误!＝错误!， ∴10－p ＝错误!，所以p ＝4．故选D ．名师点拨在解决与抛物线的性质有关的问题时,要注意利用几何图形形象、直观的特点来解题，特别是涉及焦点、顶点、准线的问题更是如此．〔变式训练3〕(1）（2021·广东茂名五校联考)设抛物线y 2＝2px (p ＞0)的焦点为F (1，0）,过焦点的直线交抛物线于A 、B 两点，若｜AF |＝4|BF ｜，则｜AB ｜＝__错误!__．（2)(2021·湖北荆州模拟）从抛物线y2＝4x在第一象限内的一点P引抛物线准线的垂线,垂足为M，且|PM|＝9，设抛物线的焦点为F，则直线PF的斜率为(C）A．错误!B．错误!C．错误!D．错误![解析]（1）∵错误!＝1，∴p＝2，不妨设直线AB方程为x＝my＋1,A（x1,y1）,B（x2,y2），由错误!,得y2－4my－4＝0，∴y1y2＝－4,又｜AF|＝4|BF|，∴y1＝－4y2，∴y2＝－1，从而x2＝错误!，∴｜BF|＝1＋错误!＝错误!,∴|AB|＝5｜BF|＝错误!．(2）设P（x0，y0)，由抛物线y2＝4x，可知其焦点F的坐标为(1，0),故|PM|＝x0＋1＝9，解得x0＝8，故P点坐标为（8,4错误!)，所以k PF＝错误!＝错误!．故选C．考点四，直线与抛物线的综合问题——师生共研例4 (1)已知抛物线y2＝2px（p＞0)的焦点F与双曲线错误!－错误!＝1的一个焦点重合,直线y＝x－4与抛物线交于A，B两点，则|AB｜等于(B）A．28 B．32C．20 D．40(2）(2021·陕西师大附中期中)已知抛物线y2＝4x的一条弦AB恰好以P(1，1)为中点，则弦AB所在直线的方程是（B)A．y＝x－1 B．y＝2x－1C．y＝－x＋2 D．y＝－2x＋3（3)（2021·湖南五市十校联考）已知抛物线C:y2＝2px（p＞0)，直线y＝x－1与C相交所得的长为8．①求p的值；②过原点O的直线l与抛物线C交于M点，与直线x＝－1交于H点,过点H作y轴的垂线交抛物线C于N点,求证：直线MN过定点．［解析］(1)双曲线错误!－错误!＝1的焦点坐标为(±4，0)，故抛物线的焦点F的坐标为（4，0）．因此p＝8，故抛物线方程为y2＝16x，易知直线y＝x－4过抛物线的焦点．设A、B两点坐标分别为(x1，y1),（x2，y2)．由错误!可得x2－24x＋16＝0，故x1＋x2＝24．故｜AB|＝x1＋x2＋p＝24＋8＝32．故选B．(2）设A(x1，y1)，B（x2，y2)，∴y1＋y2＝2,由错误!，知k AB＝错误!＝错误!＝2，∴AB的方程为y－1＝2（x－1），即2x－y－1＝0，故选B．（3)①由错误!，消x可得y2－2py－2p＝0，∴y1＋y2＝2p，y1y2＝－2p，∴弦长为错误!·错误!＝错误!·错误!＝8,解得p＝2或p＝－4(舍去)，∴p＝2，②由①可得y2＝ 4x，设M错误!，∴直线OM的方程y＝错误!x，当x＝－1时，∴y H＝－4y0,代入抛物线方程y2＝4x，可得x N＝错误!，∴N错误!，∴直线MN的斜率k＝错误!＝错误!，直线MN的方程为y－y0＝错误!错误!，整理可得y＝错误!(x－1)，故直线MN过点(1,0）．名师点拨(1）直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要将两方程联立，消元,用到根与系数的关系．(2）有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点．若过抛物线的焦点(设焦点在x轴的正半轴上)，可直接使用公式｜AB｜＝x1＋x2＋p，若不过焦点，则必须用一般弦长公式．（3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．提醒：涉及弦的中点、斜率问题一般用“点差法”求解．〔变式训练4〕（1)(2021·甘肃诊断)直线l过抛物线y2＝2px（p＞0)的焦点，且交抛物线于A，B两点，交其准线于C点，已知|AF｜＝4，错误!＝3错误!,则p＝（C)A．2 B．错误!C．错误!D．4（2）（2021·安徽皖南八校模拟）已知抛物线C:y2＝2px(p＞0)的焦点F到直线x－y＋1＝0的距离为错误!．①求抛物线C的方程；②过点F的直线l与C交于A，B两点，交y轴于点P．若｜错误!|＝3｜错误!|,求直线l 的方程．［解析](1)过A，B分别作准线的垂线交准线于E，D两点，设|BF|＝a，根据抛物线的性质可知，｜BD|＝a，|AE|＝4，根据平行线段比例可知错误!＝错误!,即错误!＝错误!，解得a＝2，又错误!＝错误!，即错误!＝错误!，解得p＝错误!a＝错误!，故选C．（2)①由抛物线C：y2＝2px(p＞0),可得焦点F错误!，因为焦点到x－y＋1＝0的距离为错误!，即错误!＝错误!，解得p＝2，所以抛物线C的方程y2＝4x．②由①知焦点F（1，0)，设直线l：y＝k(x－1），A(x1,y1)，B（x2，y2)，联立方程组{y＝k(x－1)，y2＝4x，整理得k2x2－（2k2＋4)x＋k2＝0，所以x1＋x2＝2＋错误!,①x1x2＝1，②又由｜错误!|＝3｜错误!|，得错误!＝3错误!,可得x1＝4x2，③由②③,可得x1＝2，x2＝错误!，代入①，可得2＋错误!＝错误!，解得k＝±2错误!，所以直线l的方程为2错误!x－y－2错误!＝0或2错误!x＋y－2错误!＝0．名师讲坛·素养提升巧解抛物线的切线问题例5 (1）抛物线C 1：x 2＝2py （p ＞0)的焦点与双曲线C 2：x 23－y 2＝1的右焦点的连线交C 1于第一象限的点M ．若C 1在点M 处的切线平行于C 2的一条渐近线，则p ＝（ D ）A ．错误!B ．错误!C ．错误!D ．错误!(2）（2019·新课标Ⅲ，节选)已知曲线C ：y ＝错误!，D 为直线y ＝－错误!上的动点,过D 作C 的两条切线，切点分别为A ，B ．证明:直线AB 过定点．[解析] (1）抛物线C 1：x 2＝2py （p ＞0)的焦点坐标为错误!，双曲线错误!－y 2＝1的右焦点坐标为（2，0）,两点连线的方程为y ＝－错误!（x －2），联立错误!得2x 2＋p 2x －2p 2＝0．设点M 的横坐标为m ，易知在M 点处切线的斜率存在，则在点M 处切线的斜率为y ′错误!x ＝m ＝错误!．又双曲线错误!－y 2＝1的渐近线方程为错误!±y ＝0,其与切线平行，所以错误!＝错误!，即m ＝错误!p ,代入2x 2＋p 2x －2p 2＝0，得p ＝错误!或p ＝0(舍去)．(2）设D 错误!，A (x 1，y 1)，则x 21＝2y 1，由于y ′＝x ，∴切线DA 的斜率为x 1,故错误!＝x 1，整理得：2tx 1－2y 1＋1＝0．设B (x 2，y 2），同理可得2tx 2－2y 2＋1＝0．故直线AB 的方程为2tx －2y ＋1＝0，即y －错误!＝tx ． ∴直线AB 过定点错误!．名师点拨利用导数工具解决抛物线的切线问题，使问题变得巧妙而简单，若用判别式解决抛物线的切线问题，计算量大，易出错．注意：直线与抛物线只有一个公共点是直线与抛物线相切的必要不充分条件，过抛物线外一点与抛物线只有一个公共点的直线有0条或3条;过抛物线上一点和抛物线只有一个公共点的直线有2条．〔变式训练5〕（1)已知抛物线C :y 2＝2px （p ＞0)，过点M 错误!作C 的切线,则切线的斜率为__±1__． (2）已知抛物线x 2＝8y ，过点P （b ，4）作该抛物线的切线P A ，PB ，切点为A ,B ，若直线AB 恒过定点，则该定点为( C ）A ．（4，0)B ．(3，2)C ．（0，－4)D ．（4,1)[解析] (1)设斜率为k ,则切线为y ＝k 错误!代入y 2＝2px 中得k 2x 2＋p (k 2－2）x ＋错误!＝0．Δ＝0，即p 2（k 2－2）2－4·k 2·k 2p 24＝0．解得k 2＝1,∴k ＝±1．(2）设A ，B 的坐标为（x 1,y 1），(x 2，y 2）， ∵y ＝x 28，y ′＝错误!,∴P A ，PB 的方程y －y 1＝x 14(x －x 1），y －y 2＝错误!（x －x 2)，由y 1＝错误!，y 2＝错误!，可得y ＝错误!x －y 1，y ＝错误!x －y 2， ∵切线P A ，PB 都过点P （b,4), ∴4＝错误!×b －y 1,4＝错误!×b －y 2，故可知过A ，B 两点的直线方程为4＝错误!x －y ，当x ＝0时，y ＝－4，∴直线AB 恒过定点（0，－4）．故选C ．。

高三数学每周一测(不等式).许兴华

高三数学每周一测(不等式).许兴华班级学号姓名一、选择题（每题10分，共60分）1．若01a <<，则下列不等式中正确的是（） A ．1132(1)(1)a a ->- B ．(1)log (1)0a a -+>C ．32(1)(1)a a ->+D ．1(1)1a a +->2．若等式1cos 22x x θ+=，则实数x 为（）A ．1x x =或<0B ．10x x =->或C ．1x =±D ．11x x <->或3．已知log (5)01,11,b x a b a x -<<>>且则的取值范围是（）A ．5x >B ．6x <C ．56x <<D ．56x x <>或41x +的解集是（）A ．{}01x x <≤B ．{}0x x >C ．{}1x x >-D ．{}11x x -≤≤5．关于x 的不等式20a x b x c -+<的解集为(,3)(2,-∞--+∞ ，则不等式20c x b x a ++>的解集为（）A ．11(,)23-B ．11(,)32--C ．11(,)32-D ．11(,)326．已知不等式1()()9ax y x y++≥对任意正实数x 、y 恒成立，则正实数a 的最小值为（） A ．8 B ．6 C ．4D ．2二、填空题（每小题10分，共30分）7．不等式组02233x x x x x <⎧⎪--⎨≤⎪++⎩的解集为。

8．若关于x 的不等式12x x a -+-≥的解集为R ，则a 的范围是。

9．设0,2t a π<<是大于0的常数，1()cos 1cos a f t t t=+-的最小值是16，则a = 。

三、解答题（每小题10分，共30分）10．解不等式：22(21)log (321)1x x x -+-<．11．已知2()f x ax bx c =++的图象过点（－1，0）．问：是否存在常数a 、b 、c ，使21()(1)2x f x x ≤≤+对一切x R ∈恒成立？若存在，求出a 、b 、c ．12．已知1,1,1,1a b c abc ab c <<<->-求证:．高三数学每周一测(不等式).参考答案1．选A 特殊值法：取12a A =知正确，B 、C 、D 错。

立体几何典型题精选1.许兴华

立体几何典型题精选1.许兴华1. 设棱锥M —ABCD 的底面是正方形，且MA ＝MD ，MA ⊥AB ，如果ΔAMD 的面积为1，试求能够放入这个棱锥的最大球的半径.解析： ∵AB ⊥AD ，AB ⊥MA ，∴AB ⊥平面MAD ，由此，面MAD ⊥面AC.记E 是AD 的中点，从而ME ⊥AD.∴ME ⊥平面AC ， ME ⊥EF设球O 是与平面MAD 、AC 、平面MBC 都相切的球.不妨设O ∈平面MEF ，于是O 是ΔMEF 的内心.设球O 的半径为r ，则r ＝MF EM EF S MEF ++△2 设AD ＝EF ＝a,∵S ΔAMD ＝1.∴ME ＝a 2.MF ＝22)2(aa +, r ＝22)2(22a a a a +++≤2222+＝2-1 当且仅当a ＝a2，即a ＝2时，等号成立. ∴当AD ＝ME ＝2时，满足条件的球最大半径为2-1.2. 在正方体ABCD —A 1B 1C 1D 1中，期棱长为a.(1)求证BD ⊥截面AB 1C ；(2)求点B 到截面AB 1C 的距离；(3)求BB 1与截面AB 1C 所成的角的余弦值。

()111:DD BD AC ⊥⎫⇒⊥⎬⊥⎭证明面ABCD BDAC同理BD 1⊥AB 1.∴BD 1⊥面ACB 1. (2)AB=BC=BB 1⇒G 为△AB 1C 的中心.AC=2a AG=36323a 22=⨯∙ a ∴BG=222229396)36(a a a a a =-=-=33a (3)∠BB 1G 为所求cos ∠BB 1G=363611==a a BB GB 3. 已知Ｐ为ＡＢＣＤ所在平面外一点，Ｍ为ＰＢ的中点，求证：ＰＤ∥平面ＭＡＣ．解析：因M 为PB 的中点，连BD ∩AC 于O 后，可将PD 缩小平移到MO ，可见MO 为所求作的平行线．证明连ＡＣ交ＢＤ于Ｏ，连ＭＯ，则ＭＯ为△ＰＢＤ的中位线，∴ＰＤ∥ＭＯ，∵ＰＤ⊄平面ＭＡＣ，ＭＯ平面ＭＡＣ，∴ＰＤ∥平面ＭＡＣ．4. 如图，在正方体ＡＢＣＤ－Ａ1Ｂ1Ｃ1Ｄ1中，M ，N ，Ｅ，Ｆ分别是棱Ｂ1Ｃ1，A 1D 1，Ｄ1Ｄ，ＡＢ的中点．（１）求证：Ａ1Ｅ⊥平面ＡＢＭＮ．（２）平面直线A 1E 与MF 所成的角．解析：（１）要证A 1E ⊥平面ABMN ，只要在平面中找到两条相交直线与A 1E 都垂直，显然MN 与它垂直，这是因为MN ⊥平面A 1ADD 1，另一方面，AN 与A 1E 是否垂直，这是同一个平面中的问题，只要画出平面几何图形，用平几知识解决．（２）为（１）的应用．证明（１）∵AB ⊥平面A 1ADD 1，而Ａ1Ｅ⊂平面A 1ADD 1，∴AB ⊥Ａ1Ｅ．在平面A 1ADD 1中，A 1E ⊥AN ，∵AN ∩AB ＝A ，∴A 1E ⊥平面ABMN ．解（２）由（１）知A 1E ⊥平面ABMN ，而MF ⊂平面ABMN ，∴A 1E ⊥MF ，则A 1E 与MF 所成的角为９０°5. 如图，在正方体ＡＢＣＤ－Ａ1Ｂ1Ｃ1Ｄ1中，M 为棱C Ｃ1的中点，AC 交BD 于点O ，求证：A 1O ⊥平面MBD ．解析：要证A 1O ⊥平面MBD ，只要在平面MBD 内找到两条相交直线与A 1O 都垂直，首先想到DB ，先观察 A 1O 垂直DB 吗？方法１：发现A 1O 平分DB ，想到什么？（△A 1DB 是否为等腰三角形）∵A 1D ＝A 1B ，DO ＝OB ，∴A 1O ⊥DB ．方法２：A 1O ⊥DB 吗？即DB ⊥A 1O 吗？DB 垂直包含A 1O 的平面吗？（易见DB ⊥平面A 1ACC 1）再观察A 1O 垂直何直线？DM ？BM ？因这两条直线与A 1O 均异面，故难以直接观察，平面MDB 中还有何直线？易想到MO ，因MO 与A 1O 相交，它们在同一平面内，这是一个平几问题，可画出平几图进行观察．证明取CC 1中点M ，连结MO ，∵DB ⊥A 1A ，DB ⊥AC ，A 1A ∩AC=A ，∴DB ⊥平面A 1ACC 1，而A 1O ⊂平面A 1ACC 1，∴A 1O ⊥DB ．在矩形A 1ACC 1中，∵tan ∠AA 1O=22，tan ∠MOC=22，∴∠AA 1O=∠MOC ，则∠A 1OA ＋∠MOC ＝９０°，∴A 1O ⊥OM ，∵OM ∩DB ＝O ，∴A 1O ⊥平面MBD ．6. 点P 在线段AB 上，且AP ∶PB ＝１∶２，若A ，B 到平面α的距离分别为a ，b ，求点P 到平面α的距离．解析：（１）A ，B 在平面α的同侧时，P 平面α的距离为323132b a b a +=+；（２）A ，B 在平面α的异侧时，P 平面α的距离为32)(3132b a b a -=-+．点评一是画图时，只要画出如右上图的平面图形即可，无需画出空间图形；二是对第（２）种情形，若以平面为“水平面”，在其上方的点高度为正，在其下方的点高度为负，则第（２）种情形的结论，就是将（１）结论中的b 改为(－b)，而无需再画另一图形加以求解．7. 若两直线a 与b 异面，则过a 且与b 垂直的平面（）（Ａ）有且只有一个（Ｂ）可能存在也可能不存在（Ｃ）有无数多个（Ｄ）一定不存在（Ｂ）解析：若存在，则a ⊥b ，而由条件知，a 不一定与b 垂直．8. 在正方体ＡＢＣＤ－Ａ1Ｂ1Ｃ1Ｄ1中，若E 是A 1C 1的中点，则直线CE 垂直于（）（Ａ）AC （Ｂ）BD （Ｃ）A 1D （Ｄ）A 1D 1解析：（Ｂ）BD ⊥AC ，BD ⊥CC 1，∴BD ⊥平面A 1ACC 1，∴BD ⊥CE ．9. 定点P 不在△ABC 所在平面内，过P 作平面α，使△ABC 的三个顶点到α的距离相等，这样的平面共有（）（Ａ）１个（Ｂ）２个（Ｃ）３个（Ｄ）４个解析：D过P 作一个与AB ，AC 都平行的平面，则它符合要求；设边AB ，BC ，CA 的中点分别为E ，F ，G ，则平面PEF 符合要求；同理平面PFG ，平面PGE 符合要求10. P 为矩形ABCD 所在平面外一点，且PA ⊥平面ABCD ，P 到B ，C ，D 三点的距离分别是5，17，13，则P 到A 点的距离是（）（Ａ）１（Ｂ）２（Ｃ）3 （Ｄ）４解析：（A ）设AB ＝a ，BC ＝b ，PA ＝h ，则a 2+h 2=5, b 2+h 2=13, a 2+b 2+h 2=17,∴h=1．11. 线段AB 的两个端点A ，B 到平面α的距离分别为6cm, 9cm, P 在线段AB 上，AP ：PB ＝１：２，则P 到平面α的距离为．解析：７cm 或１cm ．分A ，B 在平面α的同侧与异侧两种情况．同侧时，P 到平面α的距离为319326⨯+⨯＝７（cm ），异侧时，P 到平面α的距离为319326⨯-⨯＝１（cm ）．12. △ABC 的三个顶点A ，B ，C 到平面α的距离分别为2cm, 3cm, 4cm ,且它们在α的同一侧，则△ABC 的重心到平面α的距离为．解析：3cm ．3543++＝3cm ． 13. Rt △ABC 中，D 是斜边AB 的中点，AC ＝６，BC ＝８，EC ⊥平面ABC ，且EC ＝１２，则ED ＝．解析：１３．AB ＝１０，∴CD ＝５，则ED ＝22125+＝１３．14. 如图，在正方体ＡＢＣＤ－Ａ1Ｂ1Ｃ1Ｄ1中，求：（１）A 1B 与平面A 1B 1CD 所成的角；（２）B 1B 在平面A 1C 1B 所成角的正切值．解析：求线面成角，一定要找准斜线在平面内的射影．（１）先找到斜足A 1，再找出B 在平面A 1B 1CD 内的射影，即从B 向平面A 1B 1CD 作垂线，一定要证明它是平面A 1B 1CD 的垂线．这里可证BC 1⊥平面A 1B 1CD ，O 为垂足，∴A 1O 为A 1B 在平面A 1B 1CD 上的射影．（２）若将平面D 1D 1BB 竖直放置在正前方，则A 1C 1横放在正前方，估计B 1B 在平面A 1C 1B 内的射影应落在O 1B 上，这是因为A 1C 1⊥平面D 1DBB 1，∴故作B 1H ⊥O 1B 交于H 时，BH 1⊥A 1C 1，即H 为B 1在平面A 1C 1B 内的射影．另在求此角大小时，只要求∠B 1BO 1即可．解析：（１）如图，连结BC 1，交B 1C 于O ，连A 1O ．∵A 1B 1⊥平面B 1BCC 1，BC 1⊂平面B 1BCC 1，∴A 1B 1⊥BC 1．又B 1C ⊥BC 1，A 1B 1∩B 1C ＝B 1，∴BC 1⊥平面A 1B 1CD ，O 为垂足，∴A 1O 为A 1B 在平面A 1B 1CD 上的射影，则∠BA 1O 为A 1B 与平面A 1B 1CD 所成的角．sin ∠BA 1O ＝211=B A BO ，∴∠BA 1O ＝３０°．（２）连结A 1C 1交B 1D 1于O 1，连BO 1，作B 1H ⊥BO 1于H ．∵A 1C 1⊥平面D 1DBB 1，∴A 1C 1⊥B 1H ．又B 1H ⊥BO 1，A 1C 1∩BO 1＝O 1，∴B 1H ⊥平面A 1C 1B ，∴∠B 1BO 1为B 1B 与平面A 1C 1B 所成的角，tan ∠B 1BO =22111=B B O B ，即B 1B 与平面A 1C 1B 所成的角的正切值为22． 15. Rt △ABC 中，∠C ＝９０°，BC ＝３６，若平面ABC 外一点P 与平面A ，B ，C 三点等距离，且P 到平面ABC 的距离为８０，M 为AC 的中点．（１）求证：PM ⊥AC ；（２）求P 到直线AC 的距离；（３）求PM 与平面ABC 所成角的正切值．解析：点P 到△ABC 的三个顶点等距离，则P 在平面ABC 内的射影为△ABC 的外心，而△ABC 为直角三角形，其外心为斜边的中点．证明（１）∵PA ＝PC ，M 是AC 中点，∴PM ⊥AC解（２）∵BC ＝３６，∴MH ＝１８，又PH ＝８０，∴PM ＝8218802222=+=+MH PH ，即P 到直线AC 的距离为８２；（３）∵PM=PB=PC ，∴P 在平面ABC 内的射线为△ABC 的外心，∵∠C=90° ∴P 在平面ABC 内的射线为AB 的中点H 。

NNSZ高二数学周测立体几何.许兴华

NNSZ 高二数学周测立体几何.许兴华(考试时间:40分钟)班别座号姓名一、选择题与填空题： (1０×１０=１００分)１、设EF 是异面直线a 、b 的公垂线，直线l ∥EF ，则l 与a 、b 交点的个数为（） A 、0 B 、1 C 、0或1 D 、0，1或22、正方体ABCD －A 1B 1C 1D 1中，AC 与B 1D 所成的角为（）A 、6πB 、4πC 、3πD 、2π３、已知P 为△ABC 所在平面α外一点，PA=PB=PC ，则P 点在平面α内的射影一定是 △ABC 的 ( )A 、内心B 、外心C 、垂心D 、重心４、直线a 与平面α所成的角为30o ，直线b 在平面α内，若直线a 与b 所成的角为ϕ，则( )A 、0º<ϕ≤30ºB 、0º<ϕ≤90ºC 、30º≤ϕ≤90ºD 、30º≤ϕ<180º ５、如右图，正方体ABCD －A 1B 1C 1D 1中，E 为A 1C 1的中点，则直线CE 垂直于 ( ) A 、直线AC B 、直线B 1D 1 C 、直线A 1D 1 D 、直线A 1A６、在正方体ABCD －A 1B 1C 1D 1中(如图)，M 、N 分别是A 1A 、 AB 上的点，若∠NMC 1=90°，则∠NMB 1 ＝ ( )A 、90°B 、60°C 、75°D 、120°７、平面α外有两点A 、B 到平面α的距离分别为8和12，则线段AB 的中点M 到平面α的距离为 ______________.８、已知E 、F 分别为棱长为2a 的正方体ABCD －A 1B 1C 1D 1的棱BB 1、B 1C 1的中点，则A 1到EF 的距离为 . ９、在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝3，AA 1＝4，则异面直线AB 1与 A 1D 所成的角的余弦值为 .１０.已知ABC ∆在平面α的同一侧，且Ａ、Ｂ、Ｃ三点到平E PDC A 面α的距离分别是)0(,,>>>c b a c b a ，则ABC ∆的重心Ｇ到平面α的距离是 . 二、解答题(２０分)11、(10分)在P 是直角梯形ABCD 所在平面外一点，PA ⊥平面ABCD ， ∠BAD ＝90°，AD ∥BC ，AB ＝BC ＝a ，AD ＝2a ， PD 与底面成30°角， BE ⊥PD 于E ，试求直线BE 与平面PAD 所成的角．１２．(10分)在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ， AC BC ⊥，2AC BC BD AE ===，M 是AB 的中点. （１）求证：CM EM ⊥；(４分)（２）求CM 与平面CDE 所成的角．(６分)E MACBDEP D CB ANNSZ 数学周测立体几何参考答案一、1.C 2.D 3.B 4.C 5.B 6.A 102.7或 a 223.83.102516.9c b a ++.二.解答题: 11、解：∵ PA ⊥平面ABCD,∴ ∠PDA 为PD 与底面所成的角，PA ⊥AB, ∵ ∠BAD ＝90°, ∴ AB ⊥AD∴ AB ⊥平面PAD. ∴ ∠BEA 为BE 与平面PAD 所成的角,∵ B E ⊥PD, ∴ AE ⊥PD, 在Rt △PAD 中，∠PDA ＝30°, AD ＝2a ∴ AE ＝a, ∠BEA ＝45°.１２.解：（1）证明：因为AC BC =，M 是AB 的中点，所以CM AB ⊥．又EA ⊥平面ABC ，所以CM EM ⊥．（2）过点M 作MH ⊥平面CDE ，垂足是H ，连结CH 交延长交ED 于点F ，连结MF ，MD ．FCM ∠是直线CM 和平面CDE 所成的角．因为MH ⊥平面CDE ，所以MH ED ⊥，又因为CM ⊥平面EDM ，所以CM ED ⊥，则ED ⊥平面CMF ，因此ED MF ⊥．设EA a =，2BD BC AC a ===，在直角梯形ABDE 中，AB =，M 是AB 的中点，所以3DE a =，EM =，MD =，得EMD △是直角三角形，其中90EMD =∠，所以.2a DEMD EM MF =⋅=EDC M A BE H在Rt CMF △中，tan 1MFFCM MC==∠，所以45FCM =∠，故CM 与平面CDE 所成的角是45．。

广东高考导与练文科数学一轮复习课时训练8.5抛物线(含答案详析)

第 5 节抛物线课时训练练题感提知能【选题明细表】知识点、方法题号抛物线的定义1、3、4、5、10抛物线的标准方程2、4、8抛物线的几何性质7、9、14直线与抛物线的关系6、11、12、15、16综合问题13A组一、选择题1.(2013 银川模拟 ) 抛物线 x2=2y 的焦点坐标为 ( C )(A)( ,0) (B)(1,0) (C)(0,)(D)(0,1)分析 : 抛物线焦点在y 轴上 ,p=1, 它的焦点坐标是 (0, ). 应选 C.2.抛物线的焦点为椭圆 + =1 的下焦点 , 极点在椭圆中心 , 则抛物线方程为( A )(A)x2=-4y(B)y2=-4x(C)x2=-4y (D)y2=-4x分析 : 由椭圆方程知 ,a 2=9,b 2=4, 焦点在 y 轴上 , 下焦点坐标为 (0,-c),此中 c== ,∴抛物线焦点坐标为 (0,-),∴抛物线方程为x2=-4 y. 应选 A.3.已知抛物线 y2=2px, 以过焦点的弦为直径的圆与抛物线准线的地点关系是( C )(A) 相离 (B) 订交(C)相切 (D) 不确立分析 : 如下图 , 设抛物线焦点弦为AB,中点为 M,准线为 l,A 1、B1分别为 A、B 在直线 l 上的射影 , 则|AA1|=|AF|,|BB 1|=|BF|,于是M到l的距离d= (|AA 1|+|BB 1|)= (|AF|+|BF|)=|AB|, 故圆与抛物线准线相切 . 应选 C.4. 已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3, 则线段 AB的中点到 y 轴的距离为 ( C )(A)(B)1 (C)(D)分析 : ∵|AF|+|BF|=x A+x B+ =3,∴x A+x B= .∴线段 AB的中点到 y 轴的距离为= .应选 C.5. 已知直线 l 1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P 到直线 l 1和直线 l 2的距离之和的最小值是( A )(A)2 (B)3 (C)(D)分析 : 如下图 , 动点 P 到 l 2 :x=-1 的距离可转变为点P 到点 F 的距离 .则 P 到直线 l 1和到直线 l 2的距离之和 |PF|+|PM'| ≥FM,即距离和的最小值为点 F 到直线 l 1的距离 d==2. 应选 A.6.(2013 洛阳高三一致考试 ) 已知 F 是抛物线 y2=4x 的焦点 , 过点 F 的直线与抛物线交于 A,B 两点 , 且|AF|=3|BF|, 则线段 AB的中点到该抛物线准线的距离为 ( B )(A)(B)(C)(D)10分析 : 设点 A(x1,y 1),B(x 2,y 2),此中 x1 >0,x 2>0,过 A,B 两点的直线方程为 x=my+1,将 x=my+1与 y2=4x 联立得 y2-4my-4=0,y1y2=-4,则由解得 x1 =3,x 2= ,故线段 AB的中点到该抛物线的准线x=-1 的距离等于+1= . 故选 B.二、填空题7.以抛物线 x2=16y 的焦点为圆心 , 且与抛物线的准线相切的圆的方程为.分析 : 抛物线的焦点为F(0,4),准线为y=-4, 则圆心为 (0,4),半径r=8.所以 , 圆的方程为 x2+(y-4) 2=64.答案 :x 2+(y-4) 2=648.(2013 清远调研 ) 已知抛物线 y2=2px(p>0) 上一点 M(1,m)(m>0) 到其焦点的距离为5, 双曲线-y 2=1 的左极点为 A, 若双曲线的一条渐近线与直线 AM平行 , 则正数 a 的值为.分析 : 由抛物线定义可得1+ =5? p=8, 将 x=1 代入抛物线方程可得M(1,4), 又 A(-a,0),由直线AM 与双曲线渐近线平行可得= , 解得a= .答案 :9.(2012 年高考北京卷 ) 在直角坐标系 xOy 中, 直线 l 过抛物线 y2=4x 的焦点 F, 且与该抛物线订交于 A,B 两点 , 此中点 A 在 x 轴上方 , 若直线 l 的倾斜角为 60° , 则△ OAF的面积为.分析 :∵抛物线y2 =4x,∴焦点 F 的坐标为(1,0).又∵直线 l 倾斜角为 60°,∴直线斜率为,∴直线方程为y=(x-1).联立方程解得或由已知得 A 的坐标为 (3,2 ),∴S△OAF= |OF| ·|y A|= ×1×2 = .答案 :10.已知点 P 是抛物线 y2=2x 上的动点 , 点 P 在 y 轴上的射影是 M,点A, 则|PA|+|PM| 的最小值是.分析 : 设点 M在抛物线的准线上的射影为M'.由已知可得抛物线的准线方程为x=- , 焦点 F 坐标为.求|PA|+|PM| 的最小值 , 可先求 |PA|+|PM'| 的最小值 .由抛物线的定义可知 ,|PM'|=|PF|,所以 |PA|+|PF|=|PA|+|PM'|,当点A、P、F在一条直线上时,|PA|+|PF| 有最小值 |AF|=5,所以 |PA|+|PM'|≥ 5,又因为 |PM'|=|PM|+ ,所以 |PA|+|PM| ≥5- = .答案 :三、解答题11.若抛物线 y=2x2上的两点 A(x 1,y 1) 、B(x 2,y 2) 对于直线 l:y=x+m 对称, 且 x1x2=- , 务实数 m的值 .解: 法一如下图,连结AB,∵A、B 两点对于直线l 对称 ,∴A B⊥l, 且 AB中点 M(x0,y 0) 在直线 l 上.可设 l AB:y=-x+n,由得 2x2+x-n=0,∴x1+x2 =- ,x 1x2=- .由 x1x2=- , 得 n=1.又 x0==- ,y0=-x 0+n= +1= ,即点M为,由点 M在直线 l 上, 得 =- +m,∴m=.法二∵A、B 两点在抛物线 y=2x2上 .∴∴y1-y 2 =2(x 1+x2)(x 1-x 2).设 AB中点 M(x0,y 0),则 x1+x2=2x0,k AB= =4x0.又 AB⊥l, ∴k AB=-1, 进而 x0=- .又点 M在 l 上,∴y0=x0 +m=m-,即 M,∴AB的方程是 y-=-,即 y=-x+m- ,代入 y=2x2,得 2x2+x-=0,∴x1x2=- =- ,∴m=.12.已知过抛物线 y2=2px(p>0) 的焦点 , 斜率为 2 的直线交抛物线于A(x 1,y 1),B(x 2,y 2)(x 1<x2) 两点 , 且|AB|=9.(1)求该抛物线的方程 ;(2)O 为坐标原点 ,C 为抛物线上一点 , 若= +λ, 求λ的值 .解:(1) 直线 AB的方程是 y=2 (x- ), 与 y2=2px 联立 ,进而有 4x2-5px+p 2=0,所以 x1 +x2= .由抛物线定义得 |AB|=x 1+x2+p=9,所以 p=4, 进而抛物线方程是y2=8x.(2) 由 p=4 知 4x2-5px+p 2=0 可化为 x2-5x+4=0,进而 x1 =1,x 2=4,y1=-2 ,y 2=4 ,进而 A(1,-2 ),B(4,4).设 =(x ,y)=(1,-2)+ λ(4,4 )33=(4 λ+1,4 λ-2),即 C(4λ +1,4 λ-2 ),所以 [2 (2 λ-1)]2=8(4 λ+1),即(2 λ-1) 2=4λ+1,解得λ =0 或λ=2.13.(2013湛江调研)已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为 4, 且位于 x 轴上方的点 ,A 到抛物线准线的距离等于5, 过A 作 AB垂直于 y 轴, 垂足为 B,OB的中点为 M.(1) 求抛物线方程 ;(2)过 M作 MN⊥FA,垂足为 N,求点 N的坐标 ;(3)以 M为圆心 ,MB为半径作☉ M,当 K(m,0) 是 x 轴上一动点时 , 议论直线 AK与☉ M的地点关系 .解:(1) 抛物线 y2=2px 的准线为 x=- ,∴4+ =5,∴p=2,∴抛物线方程为y2=4x.(2) ∵点 A的坐标是 (4,4),由题意得B(0,4),M(0,2).又∵ F(1,0),∴k FA= .∵M N⊥FA,∴k MN=- ,∴F A 的方程为 y= (x-1),MN的方程为 y-2=- x.解方程组得得∴N(, ).(3)由题意得 , ☉M的圆心是点 M(0,2), 半径为 2.当 m=4时, 直线 AK的方程为 x=4,此时 , 直线 AK与☉ M相离 ;当 m≠4 时, 直线 AK的方程为 y= (x-m),即 4x-(4-m)y-4m=0.圆心 M(0,2) 到直线 AK的距离 d=,令 d>2, 解得 m>1.∴综上所述 ,当 m>1时, 直线 AK与☉ M相离 .B组14.设 M(x0,y 0) 为抛物线 C:x 2=8y 上一点 ,F 为抛物线 C的焦点 , 以 F 为圆心、 |FM| 为半径的圆和抛物线 C的准线订交 , 则 y0的取值范围是( C)(A)(0,2) (B)[0,2] (C)(2,+∞)(D)[2,+∞)分析 : ∵x2=8y, ∴焦点 F 的坐标为 (0,2),准线方程为 y=-2.由抛物线的定义知 |MF|=y 0+2.以 F 为圆心、 |FM| 为半径的圆的标准方程为x2+(y-2) 2=(y 0+2) 2.因为以 F 为圆心、 |FM| 为半径的圆与准线订交, 又圆心 F 到准线的距离为 4,故 4<y0 +2, ∴y0>2. 应选 C.15.设抛物线 C:y 2=4x 的焦点为 F, 直线 l 过 F 且与 C 交于 A,B 两点 . 若|AF|=3|BF|,则l的方程为.分析 : 设 A(x 1,y 1),B(x 2,y 2),又 F(1,0),则 =(1-x 1,-y 1),=(x 2-1,y 2),由题意知=3 ,所以即又由 A、 B均在抛物线上知解得直线l的斜率为=±,所以直线答案 :y=l 的方程为 y=(x-1) 或 y=-(x-1)(x-1)或y=-(x-1).16.设抛物线 y2=4x 的焦点为 F, 过点 M(-1,0) 的直线在第一象限交抛物线于 A、B, 且·=0, 则直线 AB的斜率 k 等于.分析 : 焦点 F(1,0),设 A(x1 ,y 1),B(x 2,y 2),由题意可设直线AB为 y=k(x+1),代入 y2 =4x 中,得 k2(x 2+2x+1)=4x,k2x2+(2k 2-4)x+k 2=0,则 x1+x2= , x1·x2=1.又· =(1-x )(1-x2)+y y=1-(x1+x )+x x+2 ×2112212 =1-+1+4×1=0,∴k= 或 k=- ( 舍去 ).答案 :。