高二数学倍角公式和半角公式
倍角公式与半角公式复习

倍角公式与半角公式复习倍角公式和半角公式是三角函数中的重要公式之一,可以用来求解角的倍数关系和角的半数关系。
下面将详细介绍倍角公式和半角公式,并给出一些例题进行练习。
一、倍角公式倍角公式是用来计算角的倍数关系的公式,根据三角函数的性质,可以推导出如下三个倍角公式:1.正弦倍角公式sin(2θ) = 2sinθcosθ2.余弦倍角公式cos(2θ) = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ3.正切倍角公式tan(2θ) = (2tanθ)/(1 - tan²θ)二、半角公式半角公式是用来计算角的半数关系的公式,根据三角函数的性质,可以推导出如下三个半角公式:1.正弦半角公式sin(θ/2) = ±√[(1 - cosθ)/2],取决于θ的正负性。
2.余弦半角公式cos(θ/2) = ±√[(1 + cosθ)/2],取决于θ的正负性。
3.正切半角公式tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)],取决于θ的正负性。
以上公式都可以通过使用三角函数的定义,以及用倍角公式和半角公式递归求解推导得到。
接下来,我们通过一些例题进行练习。
例题1:已知sinθ = 3/5,求cos2θ。
解:根据已知,我们可以得到cosθ = √(1 - sin²θ) = √(1 -9/25) = 4/5利用余弦倍角公式,可以计算cos2θ = cos²θ - sin²θ = (4/5)² - (3/5)² = 16/25 - 9/25 = 7/25例题2:已知sin(θ/2) = 2/3,且θ ∈ [0, π/2],求sinθ。
解:根据已知,我们可以得到cos(θ/2) = ±√[(1 + cosθ)/2] =±√[(1 + (√(1 - sin²θ)))/2] = ±√[(1 + (√(1 - 4/9)))/2] =±√(5/9)。
5.5二倍角与半角的正弦余弦正切

x ∈ ( 0, π )
x π 2 cos 2 , x ∈ 0, 2 原式 = 2sin x , x ∈ π , π 2 2
练习:若 则
θ
θ 是第三象限角, 1 + sin θ = cos 2 + sin 2
象限角
二
θ
θ
2
是第
例3:
(1)用cos θ 表示 cos 3θ
cos 3θ = 4 cos θ 3cos θ
3
(2)用sin θ 表示 sin 3θ
sin 3θ = 3sin θ 4sin θ
3
例4:求 cos 20 icos 40 icos80 的值
1 8
举一反三: sin 70 isin 50 isin10
cos α icos 2α icos 4α iicos ( 2 iα )
1 cos α = sin α
练习:66页——1,2
3 例1:已知 cos α = 5 且 α
α 在第二象限,
2 ± 5 5
求 sin 的值 tan
2
2
3π 例2:若 π < θ < 2
,化简
1 1 1 1 + + cos 2θ 2 2 2 2
= sin
1 sin θ
θ
θ
2
(sin
θ
cos ) = cos 2 2 2
θ
练习:化简
1 + sin x sin 2 x π x [ tan( )] cos x 2 cos 2 ( π x ) 4 2 4 2 2sin x 1
例3:求证
1 cos θ + sin θ θ = tan 1 + cos θ + sin θ 2
高考数学中的三角函数半角公式与倍角公式

高考数学中的三角函数半角公式与倍角公式三角函数是高中数学中一个重要的概念,而其中就包括三角函数的半角和倍角公式。
这两个公式在高考数学中非常重要,在考试中经常会有相关的问题出现。
本文将详细介绍三角函数的半角公式与倍角公式。
一、三角函数的定义三角函数是以角度为自变量,以角的正弦、余弦、正切、余切、正割、余割为函数值的六种函数。
其中,正弦、余弦、正切、余切是最常用的四种三角函数,它们在数学、物理等各个领域都有着广泛的应用。
二、半角公式的定义三角函数的半角公式是指在一个角的基础上,通过一定的运算,得到一个新的角度进行求解。
具体的公式如下:sin(x/2)=[√(1+cosx)]/2cos(x/2)=[√(1+sinx)]/2tan(x/2)=[sinx]/[1+cosx]其中,x为角度值。
三、半角公式的应用半角公式常常用于解决三角函数运算中的复杂问题。
例如,在解决辨识正负号的问题时,可以使用半角公式将一个角分解成两个半角,进而得到正确的结果。
此外,半角公式还可以用于求解一些特殊角,例如,sin45°=sin(90°/2)=[√(1+cos90°)]/2=[√(1+0)]/2=1/√2。
四、倍角公式的定义三角函数的倍角公式是指将一个角度值翻倍,得到一个新的角度值进行求解。
具体的公式如下:sin 2x = 2sinxcosxcos 2x = cos²x - sin²xtan 2x = (2tanx) / (1 - tan²x)其中,x为角度值。
五、倍角公式的应用倍角公式常常用于解决一些常见的问题,例如,求两个角的正弦、余弦、正切、余切的和与差。
此外,倍角公式还可以用于化简三角函数的表达式,从而简化计算过程。
例如,为了解决sin 120°sin 240°sin 360°的问题,可以用cos²60°减去1/4的方式,化简成了(√3/2)²-1/4,从而可以快速求解出答案。
三角函数的倍角公式与半角公式

三角函数的倍角公式与半角公式在学习三角函数的过程中,倍角公式和半角公式是非常重要的推导与应用。
它们能够使我们简化复杂的三角函数运算,并且在解决问题时提供更加灵活和便捷的方法。
本文将详细介绍三角函数的倍角公式和半角公式,并探讨它们的应用。
一、三角函数的倍角公式1. 正弦函数的倍角公式对于一个角θ,正弦函数的倍角公式可以表示为:sin(2θ) = 2sinθcosθ这个公式告诉我们,当我们需要求一个角的正弦函数的两倍时,可以通过将这个角的正弦函数与余弦函数相乘得到。
这在解决一些三角函数运算较为复杂的问题时非常有用。
2. 余弦函数的倍角公式同样地,余弦函数的倍角公式可以表示为:cos(2θ) = cos²θ - sin²θ这个公式告诉我们,当我们需要求一个角的余弦函数的两倍时,可以通过将这个角的余弦函数的平方减去正弦函数的平方得到。
这个公式可以在求解一些三角函数的平方和差问题时提供便捷的方法。
3. 正切函数的倍角公式tan(2θ) = (2tanθ)/(1-tan²θ)这个公式给出了正切函数的两倍与原角度的正切函数之间的关系。
在一些复杂的三角函数问题中,这个公式能够帮助我们简化计算,得出更加精确的结果。
二、三角函数的半角公式1. 正弦函数的半角公式对于一个角θ,正弦函数的半角公式可以表示为:sin(θ/2) = √[(1 - cosθ)/2]这个公式告诉我们,当我们需要求一个角的半角的正弦函数时,可以通过将这个角的余弦函数与1的差再除以2开方得到。
这个公式在一些角的半角问题的解决中非常有用。
2. 余弦函数的半角公式余弦函数的半角公式可以表示为:cos(θ/2) = √[(1 + cosθ)/2]这个公式告诉我们,当我们需要求一个角的半角的余弦函数时,可以通过将这个角的余弦函数与1的和再除以2开方得到。
在一些复杂的三角函数问题中,这个公式能够提供简化计算的方法。
3. 正切函数的半角公式tan(θ/2) = sinθ/(1 + cosθ)这个公式给出了正切函数的半角与原角度的正弦函数和余弦函数之间的关系。
三角形倍角公式和半角公式

三角形倍角公式和半角公式大家好,今天我们来聊聊三角形倍角公式和半角公式。
这两个公式可是数学里的小宝贝哦!它们可以帮助我们解决很多三角形的问题。
不过,别看它们小小的,可是个个都是“大腕儿”呢!让我们来认识一下三角形倍角公式。
三角形倍角公式是这样的:sin2A + sin2B +sin2C = 2sin(A + B)cos(A B)。
你看,这个公式里面有三个角A、B、C,而且这三个角都是三角形的内角。
这个公式的意思是说,一个三角形的两个角的正弦值的平方之和等于另外两个角的正弦值的两倍乘以这两个角的余弦值之差。
这个公式可厉害了,它可以帮助我们求出三角形的各个角度,还可以用来判断一个三角形是不是直角三角形。
接下来,我们来说说半角公式。
半角公式是这样的:cos(A/2) = (1 tan(A/2)) / (1 + tan(A/2))。
这个公式里面只有一个角A,而且这个角也是三角形的一个内角。
这个公式的意思是说,一个三角形的一个角度的一半的余弦值等于这个角度一半的正切值减一除以这个角度一半的正切值加一。
这个公式可神奇了,它可以帮助我们求出一个三角形的一个角度的一半的余弦值,还可以用来判断一个三角形是不是等腰三角形。
那么,这两个公式有什么用呢?其实,它们在我们的日常生活中也有很多应用。
比如说,我们在装修房子的时候,需要测量墙角的角度,这时候就可以用到这两个公式了。
还有,我们在玩游戏的时候,如果要让角色沿着一个圆弧走,也可以用到这两个公式。
这两个公式可是我们生活中的小助手哦!学会了这两个公式还不够,我们还需要知道它们的逆运算。
比如说,我们知道了sin2A + sin2B + sin2C = 2sin(A + B)cos(A B),那么它的逆运算就是什么呢?没错,就是sin(A + B)cos(A B) = sin2A + sin2B + sin2C。
同样地,我们知道了cos(A/2) = (1 tan(A/2))/ (1 + tan(A/2)),那么它的逆运算就是什么呢?没错,就是tan(A/2) = (1 cos(A/2)) / (1 + cos(A/2))。
倍角公式和半角公式
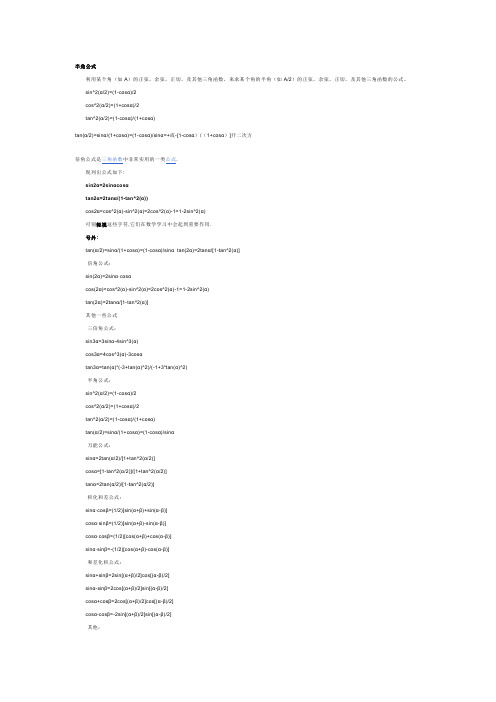
半角公式利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。
sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα=+或-[1-cosα)/(1+cosα)]开二次方倍角公式是三角函数中非常实用的一类公式.现列出公式如下:sin2α=2sinαcosαtan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)可别轻视这些字符,它们在数学学习中会起到重要作用.号外:tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα tan(2α)=2tanα/[1-tan^2(α)]·倍角公式:sin(2α)=2sinα·cosαcos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]其他一些公式·三倍角公式:sin3α=3sinα-4sin^3(α)cos3α=4cos^3(α)-3cosαtan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)·半角公式:sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式:sin4A=-4*(cosA*sinA*(2*sinA^2-1))cos4A=1+(-8*cosA^2+8*cosA^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式:sin5A=16sinA^5-20sinA^3+5sinAcos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式:sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式:sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式:sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1))cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式:sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式:sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4))cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)【本讲教育信息】一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进行简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进行求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
最新倍角公式和半角公式一资料

最新倍角公式和半角公式一资料倍角公式和半角公式是解析几何中常用的一组公式,用于求解两个角的倍角和半角。
它们在三角函数、平面几何和立体几何等应用领域都有广泛的应用。
下面将详细介绍最新的倍角公式和半角公式,并给出相关的例题和解析。
一、倍角公式倍角公式是指将一个角的角度加倍后的角的正弦、余弦、正切等三角函数与原来的角度的三角函数之间的关系。
1.正弦的倍角公式sin2θ = 2sinθcosθ通过这个公式,我们可以将一个角的正弦值表示为这个角的余弦值和正弦值的乘积的二倍。
例题1:已知角A的正弦值为1/2,求角2A的正弦值。
解析:根据倍角公式,sin2A = 2sinAcosA代入sinA = 1/2,得到sin2A = 2 × 1/2 × √3/2 = √3/2所以角2A的正弦值为√3/22.余弦的倍角公式cos2θ = cos^2θ - sin^2θ通过这个公式,我们可以将一个角的余弦值表示为这个角的余弦值和正弦值的差的平方。
解析:根据倍角公式,cos2B = cos^2B - sin^2B代入cosB = 3/5,sinB = √1 - cos^2B = √1 - 9/25 = 4/5,得到cos2B = (3/5)^2 - (4/5)^2 = 9/25 - 16/25 = -7/25所以角2B的余弦值为-7/253.正切的倍角公式tan2θ = (2tanθ)/(1 - tan^2θ)通过这个公式,我们可以将一个角的正切值表示为这个角的正切值的两倍除以1减去这个角的正切值的平方。
例题3:已知角C的正切值为2,求角2C的正切值。
解析:根据倍角公式,tan2C = (2tanC)/(1 - tan^2C)代入tanC = 2,得到tan2C = (2 × 2)/(1 - 2^2) = -8/3所以角2C的正切值为-8/3二、半角公式半角公式是指将一个角的角度减半后的角的正弦、余弦、正切等三角函数与原来的角度的三角函数之间的关系。
高中数学倍角公式半角公式

高中数学倍角公式半角公式
高中数学倍角公式
一、正弦定理
正弦定理指的是在一个三角形中,任意一边的长度与其对边的正弦值成正比:
a:b=sin A:sin B
其中a,b分别为直角边的长度,A,B分别为对边的角度。
二、余弦定理
余弦定理指的是在一个三角形中,任意一边的长度与其对边的余弦值成正比:
a:b=cos A:cos B
其中a,b分别为直角边的长度,A,B分别为对边的角度。
三、正切定理
正切定理指的是在一个三角形中,任意一边的长度与其对边的正切值成正比:
a:b=tan A:tan B
其中a,b分别为直角边的长度,A,B分别为对边的角度。
四、倍角公式
倍角公式指的是在三角形中,任意一边的长度与其倍角的正弦、余弦和正切值成正比:
a:b=2sin A:sin 2A
a:b=2cos A:cos 2A
a:b=2tan A:tan 2A
其中a,b分别为直角边的长度,A分别为对边的角度。
半角公式
一、正弦定理
正弦定理指的是在一个三角形中,任意一边的长度与其对边的正弦值成反比:
a:b=sin A:sin (A/2)
其中a,b分别为直角边的长度,A为对边的角度。
二、余弦定理
余弦定理指的是在一个三角形中,任意一边的长度与其对边的余弦值成反比:
a:b=cos A:cos (A/2)
其中a,b分别为直角边的长度,A为对边的角度。
三、正切定理
正切定理指的是在一个三角形中,任意一边的长度与其对边的正切值成反比:
a:b=tan A:tan (A/2)
其中a,b分别为直角边的长度,A为对边的角度。
三角函数倍角半角公式大全

三角函数倍角半角公式大全二倍角公式:sin2α=2sinαcosαtan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 半角公式:sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]拓展资料:倍角公式:是三角函数中非常实用的一类公式。
就是把二倍角的三角函数用本角的三角函数表示出来。
在计算中可以用来化简计算式、减少求三角函数的次数,在工程中也有广泛的运用。
半角公式:是利用某个角(如∠A)的正弦值、余弦值、正切值,及其他三角函数值,来求其半角的正弦值,余弦值,正切值,及其他三角函数值的公式。
三角函数差角公式又称三角函数的减法定理是几个角的和(差)的三角函数通过其中各个角的三角函数来表示的关系。
高数—二倍角与半角的余弦、正弦和正切教师版
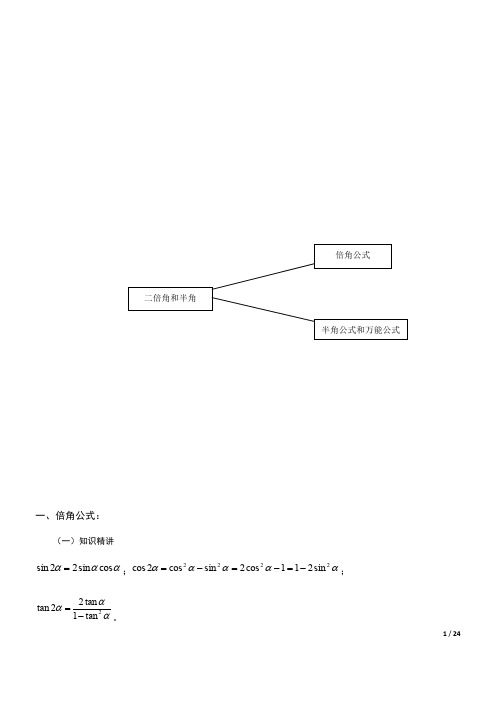
【答案】 证明:由 3sin2 1 2sin2 得 3sin2 cos 2 ……①
由 3sin 2 2sin 2 得 3sin cos sin 2 ……② , 都是锐角
①②得 sin cos 2 cos cos 2 sin sin 2 0 cos sin 2
22
2
二、半角公式和万能公式
(一)知识精讲
sin 1 cos ; cos 1 cos ; tan 1 cos
2
2
2
2
2 1 cos
( tan sin 1 cos ) 2 1 cos sin
2 tan
1 tan2
2 tan
13
5
【难度】★★
【答案】∵ 0 π ,∴ cos 1 sin2 5 .
2
13
又∵ 0 π , 0 π ,∴ 0 .若 0 π ,
2
2
2
∵ sin( ) sin ,∴ 不可能.故 π .∴ cos( ) 3 .
3 / 24
【难度】★★
【答案】 a b 1 ab
【例 8】(1)已知 sin 5 , ( , ) ,求 sin 2 , cos 2 , tan 2 的值;
13
2
(2) tan 1 , 则cos 2
;
2
(3)若 cos 48 a , 则sin 2004 的值是
0,
2
,则
sin
.
7 / 24
【难度】★★
【答案】 sin 4 2 . 9
高二数学倍角公式和半角公式

注意:
切化弦
四、课堂练习
1 1、若 sin cos 2, tan 的值 2 1 tan
C 2 在任何条件下均成立 2、公式成立条件:S 2 、
即
T2成立,则需 1 tan2 0且 tan 有意义
k
k
4
且
k (k Z ) 2
3、注意: 当 但是
2
(k Z )
tan 时,
不存在,
tan2 tan(2k ) 0
证明:左边
2
tan
2sin cos sin 2(cos sin ) 2sin cos
2 2 2
sin (2 cos 1) cos (2 cos 1) tan =右边
所以等式成立
例4、化简:
sin 50 (1 3 tan10 )
2 2 2 5 7 cos sin 4 2 4 2 2 原式 sin
cos
cos
sin
2
返回
五、归纳总结
1、二倍角公式是和角公式的特例,体现将 一般化归为特殊的基本数学思想方法。 2、二倍角公式与和角、差角公式一样,反 映的都是如何用单角的三角函数值表示 复角(和、差、倍)的三角函数值,结 合前面学习到的同角三角函数关系式和 诱导公式可以解决三角函数中有关的求 值、化简和证明问题。
三角函数的倍角和半角公式

三角函数的倍角和半角公式三角函数中的倍角和半角公式,那可是数学世界里相当有趣又实用的家伙们!咱们先来说说倍角公式。
sin2α = 2sinαcosα,cos2α = cos²α - sin²α =2cos²α - 1 = 1 - 2sin²α,tan2α = 2tanα / (1 - tan²α)。
这些公式看起来有点复杂,但只要咱们好好理解,就会发现它们其实就像咱们熟悉的好朋友。
记得我以前教过一个学生小明,他一开始对这些公式那叫一个头疼。
有一次上课,我出了一道题:已知sinα = 3/5,α是锐角,求sin2α 的值。
小明瞪着题目,一脸茫然。
我就引导他,先根据sinα 求出cosα,然后再用倍角公式。
我一步一步地带着他算,最后得出了答案。
从那以后,小明像是突然开了窍,对倍角公式不再害怕了。
再说说半角公式,sin²(α/2) = (1 - cosα) / 2 ,cos²(α/2) = (1 + cosα) / 2 ,tan(α/2) = ±√[(1 - cosα)/(1 + cosα)] 。
这些公式在解决一些复杂的三角问题时,往往能起到意想不到的效果。
就像有一次考试,有一道题是求一个角的半角的正弦值。
好多同学都被难住了,但平时认真掌握了半角公式的同学就轻松地做出来了。
其实啊,倍角和半角公式就像是数学大厦里的一块块基石,虽然它们本身可能不起眼,但组合起来就能构建出各种复杂而美妙的数学结构。
比如说在解决几何问题中,如果遇到角度之间的倍数或者半倍关系,这时候倍角和半角公式就能大显身手啦。
想象一下一个三角形,其中一个角是另一个角的两倍,我们就可以通过这些公式找到它们之间的关系,从而求出未知的角度或者边长。
在物理中,当研究波动、振动这些现象时,也常常会用到三角函数的倍角和半角公式。
比如声波的传播,电磁波的变化,都离不开这些公式的帮助。
(完整版)两倍角与半角公式与万能公式
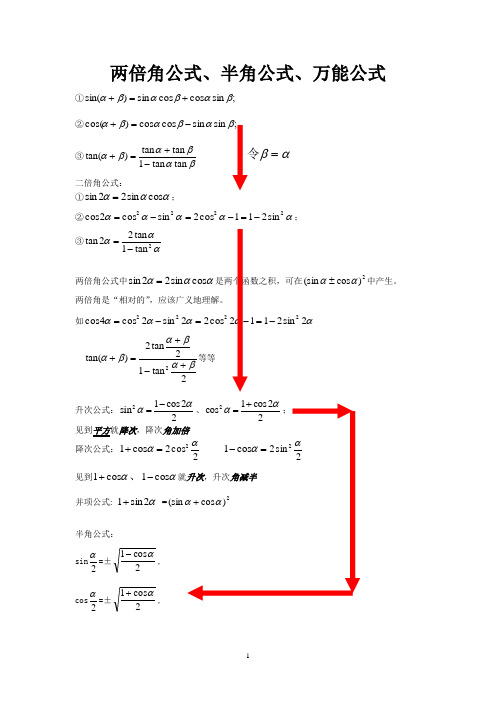
两倍角公式、半角公式、万能公式 ①;sin cos cos sin )sin(βαβαβα+=+②;sin sin cos cos )cos(βαβαβα-=+③βαβαβαtan tan 1tan tan )tan(-+=+ αβ=令 二倍角公式:①αααcos sin 22sin =;②ααααα2222sin 211cos 2sin cos 2cos -=-=-=;③ααα2tan 1tan 22tan -=两倍角公式中αααcos sin 22sin =是两个函数之积,可在2)cos (sin αα±中产生。
两倍角是“相对的”,应该广义地理解。
如ααααα2sin 2112cos 22sin 2cos 4cos 2222-=-=-= 2tan12tan2)tan(2βαβαβα+-+=+等等见到平方就见到1+并项公式sin 2α=±cos2α=±tg 2α=±ααcos 1cos 1+-=ααcos 1sin +=ααsin cos 1-. 半角公式中的正负号如何选取?依照左边2α的函数值而定。
如果给你象限角,如I ∈α,2α的终边在第几象限?公式前的±号如何选取? 如果给你区间角,如()ππα4,3∈,2α的终边在第几象限?公式前的±号如何选取? 如果给你三角比值,如⎩⎨⎧<⋅>⋅0cos tan 0cos sin αααα,2α的终边在第几象限?公式前的±号如何选取?半角的正切公式中的后两个tg 2α=ααcos 1sin +=ααsin cos 1- 前面没有正负号, 万能公式:(并非万能,仅是用2tan α可将αsin 、αcos 、αtan 都表示出来的含义) sin α=2tan 12tan22αα+,cos α=2tan 12tan 122αα+-,tan α=2tan 12tan22αα-题型一、求值问题补充问题 已知91)2cos(=-βα,32)2sin(=-βα,且24παπ<<,44πβπ<<- 求)cos(βα+的值解:考虑目标角和已知角的关系:(2βα-)—(βα-2)=2βα+再运用两倍角公式求值题型二、化简问题。
高中数学 第三章 三角恒等变换 3.2 倍角公式和半角公

3.2倍角公式和半角公式知识梳理 1.倍角公式(1)公式:sin2α=2sinαcosα;(S 2α)cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;(C 2α) tan2α=αα2tan 1tan 2-.(T 2α)(2)公式的理解①成立的条件:在公式S 2α、C 2α中,角α可以为任意角,T 2α则只有当α≠kπ+2π及α≠2πk +4π(k∈Z )时才成立. ②倍角公式不仅限于2α是α的二倍形式,其他如4α是2α的二倍、2α是4α的二倍、3α是23α的二倍等都是适用的.要熟悉多种形式的两个角的倍数关系,才能熟练地应用好二倍角公式,这是灵活运用公式的关键. ③cos2α的变形:cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α; cos 2α=22cos 1α+,sin 2α=22cos 1α-;(这两个公式称为降幂公式) 1+cos2α=2cos 2α,1-cos2α=2sin 2α.(这两个公式称为升幂公式)2.半角公式 (1)公式:sin2α=±2cos 1α-;cos2α=±2cos 1α+;tan2α=±ααcos 1cos 1+-=ααsin cos 1-=ααcos 1sin +.(2)公式的理解①关于半角正切公式:tan2α=ααsin cos 1-不带有根号,而且分母为单项式,运用起来特别方便,但要注意它与以下两个公式:tan2α=±ααcos 1cos 1+-和tan 2α=ααcos 1sin +的使用范围不完全相同,后两个公式只要α≠(2k+1)π(k∈Z ),而第一个公式除α≠(2k+1)π(k∈Z )之外,还必须有α≠2kπ(k∈Z ).当然,这三个公式可以互化,在使用时要根据题目中式子的特征灵活选用.②对于半角公式,也必须明确“半角”是相对而言,不能认为2α才是半角.如2α是4α的半角,23α是3α的半角;反之,2α、2α分别是4α、α的倍角,正是根据这个思想,才由二倍角公式得出了半角公式.知识导学(1)要学好本节,有必要复习两角和的正弦、余弦、正切公式;(2)学好本节的小窍门:在公式的选择运用上,审题是关键,找准题目的突破口,选择适当的方法,定能事半功倍;(3)选择二倍角余弦公式形式的策略: ①加余弦想余弦;②减余弦想正弦;幂升一次角减半;幂降一次角翻番. 解释如下:疑难突破1.求半角的正切值常用什么方法?剖析:难点是半角的正切值公式有三种形式,到底选择哪个来处理问题.突破的路径是靠平时经验的积累.根据经验,处理半角的正切问题有三条途径:第一种方法是用tan2α=±ααcos 1cos 1+-来处理;第二种方法是用tan2α=ααsin cos 1-来处理;第三种方法是用tan 2α=ααcos 1sin +来处理.例如:已知cosα=33,α为第四象限的角,求tan 2α的值. 解法一:(用tan2α=±ααcos 1cos 1+-来处理)∵α为第四象限的角,∴2α是第二或四象限的角. ∴tan2α<0. ∴tan 2α=-ααcos 1cos 1+-=-331331+-=-32-=-21348-=-212)26(-=262-. 解法二:(用tan2α=ααsin cos 1-来处理)∵α为第四象限的角,∴sinα<0. ∴sinα=-α2cos 1-=-311-=-36.∴tan 2α=ααsin cos 1-=36331--=262-. 解法三:(用tan2α=ααcos 1sin +来处理) ∵α为第四象限的角,∴sinα<0. ∴sinα=-α2cos 1-=-311-=-36.∴tan 2α=ααcos 1sin +=33361--=3336--=262-. 比较上述三种解法可知:在求半角的正切tan2α时,用tan 2α=±ααcos 1cos 1+-来处理,要由α所在的象限确定2α所在的象限,再用三角函数值的符号取舍根号前的双重符号;而用tan 2α=ααsin cos 1-或tan 2α=ααcos 1sin +来处理,可以避免这些问题.尤其是tan 2α=ααsin cos 1-,分母是单项式,容易计算.因此常用tan 2α=ααsin cos 1-求半角的正切值.2.为什么说1+sinα和1-sinα是完全平方的形式?剖析:疑点是对此结论总是产生质疑.其突破的方法是学会推导.要明确这个问题,先从完全平方公式来分析.(a+b)2=a 2+2ab+b 2;(a-b)2=a 2-2ab+b 2,由此看一个式子是完全平方的形式,必须有a 2+2ab+b 2或a 2-2ab+b 2的形式特点.1±sinα要具备这种形式特点,需要进行恒等变形.观察到完全平方的式子中有a 2和b 2,联想1±sinα中的1能变形为平方和的形式,即变形的方向是1=a 2+b 2,sinα=2ab.由同角三角函数基本关系式和二倍角的正弦公式得1±sinα=sin 22α+cos 22α±2sin 2αcos 2α=(sin 2α±cos 2α)2,这个结论应用很广泛.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
