圆柱和圆锥的体积ppt课件

合集下载

人教版六年级数学下册第三单元《圆柱与圆锥》课件共10个精品课件

柱的底面直径与高的比。
πd＝h d ：h ＝ 1 ：π
课堂总结
通过这节课的学习，你有什么收获?
义务教育人教版六年级下册
第3单元圆柱与圆锥 1.圆柱
第 5 课时圆柱的体积
复习导入
填空。圆柱的侧面积＝（底面周长×高）圆柱的表面积＝（侧面积＋底面积×2 ）长方体的体积＝（长×宽×高）正方体的体积＝（棱长×棱长×棱长）
底面侧面
圆柱的底面都是圆，并且大小一样。
底面圆柱的侧面是曲面。
哪个圆柱比较高？为什么？
底面 O
侧面高
底面 O 侧面高
底面 O
底面
圆柱两个底面之间的距离叫做高，圆柱有无数条高。
动手操作：如果把一张长方形的硬纸贴在木棒上，快速转
动木棒，想一想，转出来的是什么形状？
转动起来像一个圆柱。
8cm
要解决这个问题，就
是要计算什么？
10cm
杯子的容积
10cm
杯子的底面积：杯子的容积：
8cm
3.14×(8÷2)2
50.24×10
＝3.14×42
＝502.4 (cm3 )
＝3.14×16
＝502.4 (mL)
＝50.24 (cm2 )
答：因为502.4大于498，所以杯子能装下这袋牛奶。
（长方体）
（正方体）
（圆柱）
课堂总结
通过这节课的学习，你有什么收获?
义务教育人教版六年级下册
第3单元圆柱与圆锥 1.圆柱
第 2 课时圆柱的认识（2）
复习导入
圆柱由哪几部分组成？有什么特征？
上、下底面：圆侧面：曲面
探究新知

圆柱和圆锥的体积

长方体的底面积等于圆柱体的底面积长方体的高等于圆柱体的高
长方体的体积=长×宽×高圆柱的体积=底面积×高 V=Sh V=πr ² h
20厘米 25厘米
20)2＝314(cm2) (1)水桶的底面积：3.14×( 2 3 (2)水桶的容积： 314×25＝7850（cm ）
4分米 10分米
把一个棱长是6厘米的正方体木块，加工成一个最大的圆锥体，圆锥的体积是多少立方厘米？
0.8米
求各圆柱的体积。
0.5分米
求下面各圆柱的体积。
1、底面半径3cm，高5cm。 2、底面直径8m，高10m。 3、底面周长25.12dm，高2dm。
圆柱体积＝底面积
高
圆柱体积＝底面积
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝底面积
高
高
圆柱体积＝底面积圆锥体积＝底面积
高
高
1 3
圆柱与圆锥的体积之间有什么关系？
等底等高圆锥体积是圆柱体积的三分之一等底底面周长31.4米，高15米，这个玻璃罩的容积是多少立方米？（玻璃厚度忽略不计）
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
高
圆柱体积＝底面积圆锥体积＝
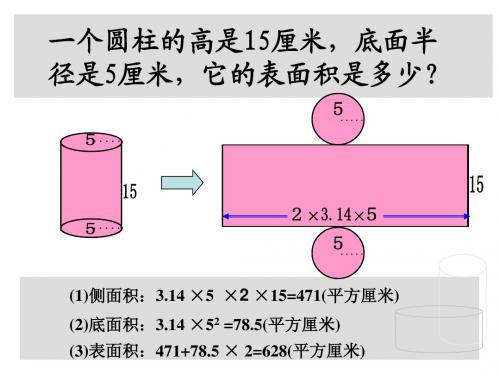
一个圆柱的高是15厘米，底面半径是5厘米，它的表面积是多少？

【课件】圆柱、圆锥、圆台的表面积与体积+课件高一下学期数学人教A版(2019)必修第二册

设圆台的上底面面积为S'，下底面面积为S
r O
1
1
2
2
2
2
V圆台 (r r r r )h ( S S S S )h
3
3
1
这和V棱台 ( S S S S )h是一致的。
3
1
因而得 V台体 = ( S S S S )h
3
【练习】如图，在直角梯形 ABCD 中，BC∥AD，∠ABC＝90°，AB＝5，
1
V锥体 Sh
3
1 2
r h
3
1
V台体 = ( S SS S )h
3
1
= h(r 2 rr r 2 )
3
2
感谢聆听
S圆柱 =πr +πr +2πrl 2πr (r l )
2
2
(1)圆柱的表面积、体积
圆柱的侧面展开图是什么？如何计算它的表面积？
r O
l
2 r
O
圆柱的侧面展开图是一个矩形，
S圆柱表面积 2r 2rl 2r (r l ).
2
V圆柱 = πr h
2
例1 将一个边长分别为4π，8π的矩形卷成一个圆柱的侧面，则
圆台的表面积为(
A．81π
)
B．100π
C．168π
D．169π
解圆台的轴截面如图所示，
设上底面半径为 r，下底面半径为 R，则它的母线长为
l＝ h2＋R－r2＝ 4r2＋3r2＝5r＝10，
所以 r＝2，R＝8。
故 S 侧＝π(R＋r)l＝π(8＋2)×10＝100π，
S 表＝S 侧＋πr2＋πR2＝100π＋4π＋64π＝168π。故选 C。

苏教版六年级下册数学《圆柱的体积》圆柱和圆锥PPT(第3课时)

教学新知
例二：计算圆柱的表面积。（单位：cm）（π取3.14）
S=2π×0.8+2π≈11.304 S=2π×0.5×3.5+2π×0.5²≈12.56
教学新知
例三：一个圆柱形油桶，底面直径是0.6米，高是1米。做这个油桶至少需要铁皮多少平方米？（得数保留两位小数）
S=2π×0.3×1+2π×0.3²≈2.45（㎡）
能想到一些什么？（2）全部浸入，水面上升9厘米，你又能想到什么？怎样
计算出这个圆钢的体积？（3）这题还可以怎样思考？
教学新知
例一：一个圆柱形水桶的容积是80立方分米，里面装了2/5的水。已知它的底面积是10平方分米，里面水的深度是多少？
【讲解】根据“水桶的容积是80立方分米”和“里面装了 2/5的水”这两个条件，我们可以求出水桶内水的体积，然后用水的体积除以水桶底面积得出水桶内水的深度。 80× =32（立方分米）……水桶内水的体积 32÷10=3.2（分米）……水桶平均剖成两片，其中一片如图所示。（单位：厘米）（1）剖面面积是多少平方厘米？（2）这片木料的表面积和体积各是多少？
（1）S1=20×12=240（cm²）（2）S2=πrh+πr²+S1=3.14×6×20+3.14×6²+240=792.84（cm²）
V=1/2S3h=1/2×3.14×6²×20=1130.4（cm³）
课后习题
7.把一根长2.4米的圆柱形状的木料锯成4段，表面积增加了 0.18平方米。
这根木料原来的体积是多少立方米？
S=0.18÷6=0.03（m²）
V=sh=0.03×2.4=0.072（m³）
8.一个圆柱高4厘米，底面半径是2厘米。如果将它的底面平均分成若干份，

圆柱圆锥圆台体积和表面积.ppt

1
1
A.4
B.2
3 C. 6
3 D. 4
[答案] D
[解析]
三棱锥B1－ABC的高h＝3，底面积S＝S△ABC＝
3 4
×12＝ 43，
则VB1－ABC＝13Sh＝13×
43×3＝
3 4.
5．若一圆柱与圆锥的高相等，且轴截面面积也相等，那
么圆柱与圆锥的体积之比为( )
A．1
1 B.2
3
3
C. 2
D.4
例题解析
命题方向多面体与旋转体的面积
【例1】圆台的上、下底面半径分别是10 cm和20 cm，它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?
命题方向多面体的体积
[例 2] 长方体相邻三个面的面积分别为 2、3、6 求它的
体积．
[解析] 设长方体的长、宽、高分别为a、b、c则有
据条件得到
1 2
πl2＝2π，解得母线长l＝2,2πr＝πl＝2π，r＝1所以
该圆锥的体积为：V圆锥＝13Sh＝13×
22－12π＝
3 3 π.
[点评] 本题主要考查空间几何体的体积公式和侧面展开图．审清题意，所求的为体积，不是其他的量，分清图形在展开前后的变化；其次，对空间几何体的体积公式要记准记牢，属于中低档题．
[解析]
三棱台ABC－A1B1C1的上、下底面积之比为4:9.连接 A1B、BC1和AC1，把棱台分为三个棱锥B－A1B1C1，C1－ ABC，A1－ABC1.则这三个棱锥体积之比为________．
[答案] 4:9:6
[解析] 如图，设三棱锥B－A1B1C1，C1－ABC，A1－ ABC1体积分别为V1、V2、V3，又设棱台的高为h，上、下底面积分别为S1、S2.依题意，得

人教版《圆柱与圆锥》(完美版)PPT课件1

解答此类题的关键是明确长方形的长（宽）或正方形的边长等于圆柱的底面周长，根据公式 C＝2πr 或C＝πd求出圆的周长，然后与长方形的长（宽）或正方形的边长进行比较即可确定答案。
规范解答：选择①和B、②和A或②和C都恰好能做成圆柱形的盒子。
1.把圆柱的侧面沿高展开，得到一个（长方形），它的长等于圆柱底面的（周长），宽等于圆柱的（高）。
思路分析：塔的顶端呈圆锥形，求塔的顶端的体积就
是求圆锥的体积。计算时先根据公式S底=π
求
出圆锥的底面积，再根据公式V
求出圆锥的体
积。
规范解答：：圆锥的底面积： 3.14×（18.84÷3.14÷2）²
＝3.14×9 ＝28.26（m²）圆锥的体积：
×28.26×6 ＝2×28.26 ＝56.52（m³）答：塔的顶端的体积是 56.52立方米。
20×2×3.14×60＋202×3.14＝8792（cm²）答：做这个水桶至少需要8792平方厘米铁皮。
例3 一根钢管，长50厘米，外圆直径是10厘米，钢管厚2cm（如下图）。铸造这样一根钢管需要钢材多少立方厘米？
思路分析：求铸造这样一根钢管需要钢材的体积，就是用大圆柱的体积减去中空的小圆柱的体积。
思路分析：瓶子正放和倒放时的容积与饮料的体积不
变，所以瓶子空余部分的容积相等。因此，饮料瓶的
容积就相当于一个高为（20＋4）cm 的圆柱形容器的
容积，可推知饮料体积占瓶子容积的
，即
480mL的
。
确定瓶中饮料的体积占瓶子容积的几分之几是解答
此题的关键。
规范解答：20＋4＝24（cm） 480× ＝400（mL）答：瓶内现有饮料400毫升。
3.一个内半径是10cm的饮料瓶里，饮料的高度为 4cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度为16cm，这个瓶子的容积是多少？

人教版数学必修第二册8.3.2圆柱、圆锥、圆台、球的表面积和体积课件

(2)半径和球心是球的关键要素，把握住这两点，计算球的表
面积或体积的相关题目也就易如反掌了．
跟踪训练
1. (1)两个球的半径相差1，表面积之差为28π，则它们的
364
体积和为________；
3
设大、小两球半径分别为R，r，则由题意可得
− =1
R＝4
42 − 4 2 = 28
r＝3
∵棱长为a，∴BE＝
3
2
3
a× ＝ a.
2
3
3
∴在Rt△ABE中，AE＝
2
−
2
3
＝
6
a.
3
设球心为O，半径为R，则(AE－R)2＋BE2＝R2，
∴R＝
6
6 2
3
a，∴S球＝4π×( a) ＝ πa2.
4
4
2
2. 设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个
球面上，则该球的表面积为( B )
∴R＝2.
4
3
∴V＝ πR3＝
32
.
3
5．有一个倒圆锥形容器，它的轴截面是一个正三角形，在容器内放一个
半径为r的铁球，并注入水，使水面与球正好相切，然后将球取出，求这
时容器中水的深度．
由题意知，圆锥的轴截面为正三角形，如图所示为圆锥的轴截面．
根据切线的性质知，当球在容器内时，水深CP为3r，水面的半径AC
3
2
12
总结提升
1.正方体的内切球
球与正方体的六个面都相切，称球为正方体的内切球，此时球的

2
半径为r1＝，过在一个平面上的四个切点作截面如图．
总结提升
2．长方体的外接球

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

圆柱与圆锥的体积
长方体的体积＝底面积 × 高底面积
长方体的体积＝底面积 ×高底面积
长方体的体积＝底面积 ×高底面积
长方体的体积＝底面积 ×高底面积
长方体的体积＝底面积 x 高底面积
长方体的体积＝底面积 x 高底面积
长方体的体积＝底面积 ×高圆柱体的体积＝底面积积＝底面积高
圆柱体积＝底面积高
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
感谢亲观看此幻灯片，此课件部分内容来源于网络，如有侵权请及时联系我们删除，谢谢配合！
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝
圆柱体积＝底面积高圆锥体积＝底面积高
圆柱体积＝底面积高
圆锥体积＝底面积
高
1 3
圆柱体积＝底面积高
圆锥体积＝底面积
高
1 3
圆锥的体积= 1 ×底面积×高 3
3.14×3²×10 =3.14×9×10 =282.6（cm²）
3.14×（8÷2）²×8 =3.14×16×8 =50.24×8 =401.92（cm²）
3.14×（4÷2）²×10
=3.14×4×10 =12.56×10 =125.6（cm²）