麦克斯韦速率分布定律共25页
合集下载
§2[1].3麦克斯韦速率分布
![§2[1].3麦克斯韦速率分布](https://img.taocdn.com/s3/m/b635b63887c24028915fc3b6.png)
∫ vdN = v=
∞
2.方均根速率: v2 方均根速率: 方均根速率
v =
2
v2dN ∫ N
=
2
v2 Nf (v)dv ∫ N
= ∫ v2 f (v)dv =
0
∞
3kT 3RT = m µ
3kT 3RT RT v = = ≈1.73 . m µ µ
3.三种速率之比: v p : v : v 2 = 1 : 1.128 : 1.224 三种速率之比: 三种速率之比 它们三者之间相差不超过 23%,而以方均根速率为最大. 而以方均根速率为最大. 而以方均根速率为最大 右图表示了麦克斯韦速率分布 中的三种速率的相对大小. 中的三种速率的相对大小. 在§1.6理想气体分子碰撞数及理想气体压强公式 理想气体分子碰撞数及理想气体压强公式 证明中曾用到近似条件 v ≅ v 2
三.用麦克斯韦速率分布律求平均值
1.平均速率: 平均速率: 平均速率 (1)定义:大量分子速率的算术平均值. 定义:大量分子速率的算术平均值. 定义
(2)计算:* 计算:* 计算
由平均速率定义: 由平均速率定义:
∑ v ∆N v =
i
i
N
得:
∞ vNf (v)dv ∫0 N = ∫0 vf (v)dv N 将麦克斯韦速率分布函数代入上式可得: 将麦克斯韦速率分布函数代入上式可得: 8kT R 8RT RT v= ∵k = ∴v = ≈1.60 . πm NA πµ µ
l A S S ω B
φ P C
由于分子的速度大小不同,分子自 由于分子的速度大小不同,分子自B 到C 所需的时 间也不同,所以并非所有通过B 盘的分子,都能通过C 间也不同,所以并非所有通过 盘的分子,都能通过 盘狭缝射到P上 设分子的速率为v 盘狭缝射到 上.设分子的速率为 ,自B 到C 所需的时 间为 t ,
大学物理第十二章气体动理论第6节 麦克斯韦气体分子速率分布律
解
m(H 2 ) m(O2 ) v p ( H 2 ) v p (O 2 )
vp (H2 ) 2 000m.s-1
2kT vp m
o
2 000
v/ ms
1
vp ( H 2 )
m( O 2 ) 32 4 v p (O 2 ) m( H 2 ) 2
vp (O2 ) 500m.s
f ( v)
dS
dN f ( v)dv dS N
v
第十二章 气体动理论
o
v v dv
概率密度
3
物理学
第五版
12-6 麦克斯韦气体分子速率分布律
f (v)dv物理意义
表示在温度为 T 的平衡状态下，速 率在 v 附近单位速率区间 的分子数占总 数的百分比 .
f (v)dv 的物理意义：
表示速率在 v v dv 区间的分 子数占总分子数的百分比.
第十二章 气体动理论
4
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
dN Nf ( v)dv 速率在 v v dv 内分子数： 速率位于 v1 v2区间的分子数： v2 N v N f (v)dv 1 速率位于 v1 v2 区间的分 f ( v)
-1
第十二章 气体动理论
17
f (v )
vp v v
2
第十二章 气体动理论
vp v 2 v
v
15
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
讨论 1 已知分子数 N ，分子质量 m ，分布函 数 f ( v) . 求 （1） 速率在 vp ~ v 间的分子 数；（2）速率在 vp ~ 间所有分子动能 之和 . 解 （ 1）
麦克斯韦气体速率分布律
麦克斯韦气体速率分布律Maxwell Velocity Distribution大家知道，由气体的温度公式可以得出气体分子的方均根速率。
例如在时，氦气。
氧气。
但我们要注意的是，方均根速率仅是运动速率的一种统计平均值，并非气体分子都以方均根速率运动。
事实上，处于平衡状态下的任何一种气体，各个分子均以不同的速率、沿各个方向运动着。
有的速率大于方均根速率，有的速率小于方均根速率，它们的速率可以取零到无穷大之间的任意值。
而且由于气体分子间的相互碰撞，每个分子的速度也在不断地改变，所以在某一时刻，对某个分子来说，其速度的大小和方向完全是偶然的。
然而就大量分子整体而言，在平衡状态下，分子的速率分布遵守一个完全确定的统计性分布规律又是必然的。
下面我们介绍麦克斯韦应用统计理论和方法导出的分子速率分布规律。
气体分子按速率分布的统计规律，最早是由麦克斯韦于1859年在概率论的基础上导出的，1877年玻耳兹曼由经典统计力学中也导出该规律。
由于技术条件的限制，测定气体分子速率分布的实验，直到本世纪二十年代才实现。
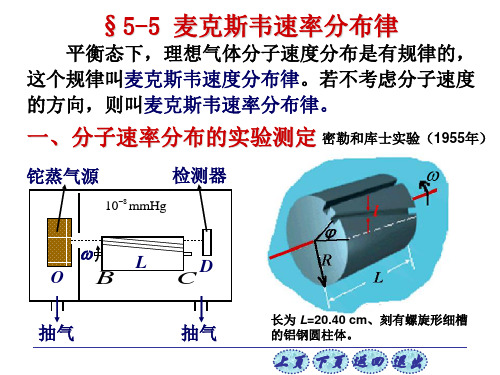
1920年斯特恩（O.Stern首先测出银蒸汽分子的速率分布；1934年我国物理学家葛正权测出铋蒸汽分子的速率分布；1955年密勒（Mlier和库士（Kusch测出钍蒸汽分子的速率分布。
斯特恩实验是历史上最早验证麦克斯韦速率分布律的实验。
限于数学上的原因和本课程的要求，我们不推导这个定律，只介绍它的一些基本内容。
*麦克斯韦（J. C. Maxwell，1831—1879）英国物理学家，经典电磁理论的奠基人，气体动理论的创始人之一。
他提出了有旋电场和位移电流概念，建立了经典电磁理论，这个理论包括电磁现象的所有基本定律，并预言了以光速传播的电磁波的存在。
1873年，他的《电磁学通论》问世，这本书凝聚着杜费、富烂克林、库仑、奥斯特、安培、法拉第……的心血，这是一本划时代巨著，它与牛顿时代的《自然哲学的数学原理》并驾齐驱，它是人类探索电磁规律的一个里程碑。
7-6麦克斯韦气体分子速率分布定律剖析.
7 – 6 麦克斯韦气体分子速率分布率
物理学教程 （第二版）
f (v)
S
o
v1 v2
dN f (v)dv dS N 速率位于v v dv 内分子数
v
dN Nf (v)dv
速率位于
v1
v2
区间的分子数
N
v2
v1
N
f
(v)dv
速率位于 v1 v2 区间的分子数占总数的百分比
第七章 气体动理论
f (v) dN Ndv
f (v)
o
v
7 – 6 麦克斯韦气体分子速率分布率
物理学教程 （第二版）
二 三种统计速率
1）最概然速率 v p
df (v) 0 dv vvp
根据分布函数求得
f (v)
f max
o
vp
v
M mNA , R NA k
vp
2kT 1.41 kT
v
N2 分子在不同温 度下的速率分布
第七章 气体动理论
f (v)
O2 H2
o vp0 vpH
v
同一温度下不同 气体的速率分布
7 – 6 麦克斯韦气体分子速率分布率
物理学教程 （第二版）
例 计算在 27 C 时，氢气和氧气分子的方均
根速率 vrms .
解 MH 0.002kg mol1
MO 0.032kg mol1
8kT
0
πm
o
v
v 1.60 kT 1.60 RT
m
M
第七章 气体动理论
7 – 6 麦克斯韦气体分子速率分布率
物理学教程 （第二版）
大学物理,气体动理论14-06 麦克斯韦气体分子速率分布律
i ~ i 1
N i
N i N
5
14.6 麦克斯韦速率分布律
第14章 气体动理论
气体分子按速率分布的统计规律最早是由麦克 斯韦于1859年在概率论的基础上导出的，1877年玻 耳兹曼由经典统计力学导出。 由于技术条件的限制，测定气体分子速率分布 的实验，直到20世纪二十年代才实现。 1920年斯特 恩首先测出银蒸汽分子的速率分布；1934年我国物 理学家葛正权测出铋蒸汽分子的速率分布；1955年 密勒和库士测出钍蒸汽分子的速率分布。 斯特恩实验是历史上最早验证麦克斯韦速率分 布律的实验。实验证实了麦克斯韦的分子按速率分 布的统计规律。
14.6 麦克斯韦速率分布律
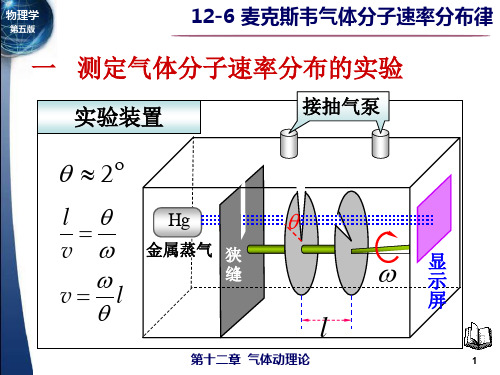
一 测定气体分子速率分布的实验
第14章 气体动理论
实验装置
接抽气泵
2
l v
Hg
金属蒸汽 狭 缝
v l
显 示 屏
8
l
14.6 麦克斯韦速率分布律
第14章 气体动理论
9
14.6 麦克斯韦速率分布律
测量原理
第14章 气体动理论
(1) 能通过细槽到达检测 器的分子所满足的条件 L v L v (2) 通过改变角速度ω的 大小，选择速率 v
28
14.6 麦克斯韦速率分布律
第14章 气体动理论
求：速率在 v1 ~ v2 之间的分子的平均速率。
(3) 通过细槽的宽度，选择不同的速率区间 L v v 2
(4) 沉积在检测器上相应的金属层厚度必定正比 相应速率下的分子数。
10
14.6 麦克斯韦速率分布律
速率区间 (m/s) 实验数据 氧分子在 273K时的 速率分布
经典：第四讲-速度分布函数-麦克斯韦速率
速率v的函数，称为速率分布函数。
f (v) dN Ndv
速率分布函数
理解分布函数的几个要点：
1.条件：一定温度（平衡态）和确定的气体系统，T和m是一定的； 2.范围：（速率v附近的）单位速率间隔，所以要除以dv；
3.数学形式：（分子数的）比例，局域分子数与总分子数之比。
8
物理意义：
速率在 v 附近，单位速率区间的分子数占总分子数
• dN/N 是 v 的函数； •当速率区间足够小时（宏观小，微观大）， dN/N还应与
区间大小成正比。
为此，规定以单位速率间隔为比较标准，即 dN ，这样，比
Ndv
值 dN
Ndv
就反映出了分布随速率v的改变而改变。为此我们规定；
7
定义：处于一定温度下的气体，分布在速率v附近的
单位速率间隔内的分子数占总分子数的百分比只是
(2) 氢气在该温度时的最概然速率和方均根速率
解 (2)
vp
2RT
M
RT 2 103
1000
m/s
RT
f(v)
(v p )H2 103
1.41 103 m/s
( v 2 )H2
3RT M
1.73103 m/s
He H2
1000
v
29
例2 有N 个粒子，其速率分布函数为
f (v )
(2) 因为速率分布曲线下的面积代表一定速率区间内 的分子与总分子数的比率，所以
v v0 的分子数与总分子数的比率为
N
N
v0a
v0
2 3v 0
2 3
N 2 N
3
因此， v>v0 的分子数为 ( 2N/3 ) f (v )
f (v) dN Ndv
速率分布函数
理解分布函数的几个要点：
1.条件：一定温度（平衡态）和确定的气体系统，T和m是一定的； 2.范围：（速率v附近的）单位速率间隔，所以要除以dv；
3.数学形式：（分子数的）比例，局域分子数与总分子数之比。
8
物理意义：
速率在 v 附近，单位速率区间的分子数占总分子数
• dN/N 是 v 的函数； •当速率区间足够小时（宏观小，微观大）， dN/N还应与
区间大小成正比。
为此，规定以单位速率间隔为比较标准，即 dN ，这样，比
Ndv
值 dN
Ndv
就反映出了分布随速率v的改变而改变。为此我们规定；
7
定义：处于一定温度下的气体，分布在速率v附近的
单位速率间隔内的分子数占总分子数的百分比只是
(2) 氢气在该温度时的最概然速率和方均根速率
解 (2)
vp
2RT
M
RT 2 103
1000
m/s
RT
f(v)
(v p )H2 103
1.41 103 m/s
( v 2 )H2
3RT M
1.73103 m/s
He H2
1000
v
29
例2 有N 个粒子，其速率分布函数为
f (v )
(2) 因为速率分布曲线下的面积代表一定速率区间内 的分子与总分子数的比率，所以
v v0 的分子数与总分子数的比率为
N
N
v0a
v0
2 3v 0
2 3
N 2 N
3
因此， v>v0 的分子数为 ( 2N/3 ) f (v )
7-(4-5)麦克斯韦速率分布
(1) 不同温度下的同种气体
f (v)
T 1
T2 > T 1
T2
v
T > T2 , orT < T2 ? 1 1
vp1 = 2RT 1
vp1 vp2
2RT2
µ
vp2 =
µ
vp1 < vp2
T < T2 1
第六章 气体动理学理论 (2) 同温度下的不同种气体
f (v)
O2 , H2 ?
1
2RT
2
v
vp1 vp2
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 出现在v附近 单位速率区间内的分子数dN 附近、 出现在 附近、单位速率区间内的分子数
说出下列各式的物理意义
第六章 气体动理学理论
(4)∫ f (v)dv= ∫
v1
v2
v2
v1
∆Nv1 →v2 dN dv = Ndv N
对于一定量的气体，在温度为 的平衡态下 的平衡态下， 对于一定量的气体，在温度为T的平衡态下，气体分子速率 占总分子数N的百分比 概率 概率)。 v1～v2区间内的分子数△N占总分子数 的百分比 (概率 。 占总分子数
(5)∫ Nf (v)dv = ∫
v1
v2
dN N = ∆Nv1→v2 N
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 v1～v2区间内的分子数△N。 。
一、分子速率分布函数
速率分布： 速率分布：各种不同速率范围内的分子数占总分子数的 百分比为多大。 百分比为多大。
伽 耳 顿 板
第六章 气体动理学理论
f (v)
T 1
T2 > T 1
T2
v
T > T2 , orT < T2 ? 1 1
vp1 = 2RT 1
vp1 vp2
2RT2
µ
vp2 =
µ
vp1 < vp2
T < T2 1
第六章 气体动理学理论 (2) 同温度下的不同种气体
f (v)
O2 , H2 ?
1
2RT
2
v
vp1 vp2
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 出现在v附近 单位速率区间内的分子数dN 附近、 出现在 附近、单位速率区间内的分子数
说出下列各式的物理意义
第六章 气体动理学理论
(4)∫ f (v)dv= ∫
v1
v2
v2
v1
∆Nv1 →v2 dN dv = Ndv N
对于一定量的气体，在温度为 的平衡态下 的平衡态下， 对于一定量的气体，在温度为T的平衡态下，气体分子速率 占总分子数N的百分比 概率 概率)。 v1～v2区间内的分子数△N占总分子数 的百分比 (概率 。 占总分子数
(5)∫ Nf (v)dv = ∫
v1
v2
dN N = ∆Nv1→v2 N
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 v1～v2区间内的分子数△N。 。
一、分子速率分布函数
速率分布： 速率分布：各种不同速率范围内的分子数占总分子数的 百分比为多大。 百分比为多大。
伽 耳 顿 板
第六章 气体动理学理论
-麦克斯韦速率分布律
0
x x x
x
太原理工大学物理系
一、 速率分布函数
o
+
把速率分成很多相等的间隔
统计出每个间隔内的分子数N
N + 间隔内分子数与分子总数N之比 N
某 处单位速率间隔内分子数与总数之比 N 1 N v
N 1 N v 只与速率v有关，只是v 的函数。
vp
取 v v 2 ，并注意到
v2
3kT m
ቤተ መጻሕፍቲ ባይዱ
3 2
2kT m
3 2
v
2 p
太原理工大学物理系
f ( v2 )
概率之比为
4
3
1
3
e2
2 vp
f (vp )dv
f (vp )
2
e
1 2
1.10
f ( v2 )dv f ( v2 ) 3
太原理工大学物理系
四、分子速率的实验测定
速率分布函数 f(v)可写为
f (v) 4 (
m
)3
2
v2e
mv2 2kT
2 kT
4
1
3
2
v2 v3p
ev2
v
2 p
4
2
v v2
v
2 p
e 3
vp
太原理工大学物理系
f (v)
4
2
v ev2
v
2 p
v
3 p
在上式中取v=vp ,得
f (vp )
4 1 e1
mol用于讨论速率分布用于计算分子的平均平动动能三种速率的使用场合地球形成之初大气中应有大量的氢氦但很多分子和he原子的方均根速率超过了地球表面的逃逸速率112kms故现今地球大气中已没有氢和氦了
麦克斯韦速率分布定律
(4) 平均速率和方均根速率.
f ( )
解：（1）求 C :
C (0 ) (0 0 ) 0 ( 0 )
0
f ( )d 1 C
6
3 0
（2） N 0 ~ 0 / 4 N
0 / 4
0
5 f ( ) d N 32
0 df ( ) （3）最可几速率 0 p d p 2
6.5 麦克斯韦速率分布定律
气体中个别分子的速度大小和方向完全是偶然的 , 但 平衡态下，气体分子的速度分布遵从一定的统计规律 — — 麦克斯韦速度分布定律. 若不考虑分子速度的方向， 这个规律就成为麦克斯韦速率分布定律.
1859年, 麦克斯韦用概率论导出了气体分子速率分布 定律，后由玻尔兹曼使用经典统计力学理论导出. 1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
f (v )
av ， (0 v v 0 ) 0 ， (v v 0 )
2
f (v )
v0 v 求： （1）常量 a 和υ0 的关系 0 （2）平均速率 v v0 （3）速率在 0 之间分子的平均速率 v 2
解： （1）由归一化条件
0
2 0
0
f ( )d 1
3 得 a 3 v0
f ( v)
T1 300K T2 1200K
f ( v)
麦克斯韦速率分布律.pptx
第3页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(1)nf (v)dv
f (v) dN , n N
Ndv
V
nf (v)dv
dN V
表示单位体积内分布在速率区间 v 内v的 dv
分子数。
第4页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度， 说明下式的物理意义：
(2)Nf (v)dv
f (v) dN Ndv
Nf (v)dv dN
表示分布在速率区间 v v 内的dv分子数。
第5页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(3)n v2 f (v)dv
v1
f (v)
dN
,n
N
Ndv
V
n v2 f (v)dv N N N
把这些量值代入，即得
W v＝ 1 v p 50
N＝
N
4
99 100
2
e
99 100
2
1 50
1.66%
第19页/共20页
f (v ) p3
T1
T2
T1 T2 T3
温度越高，速率 大的分子数越多
T3
v v v O
p1 p 2 p3
v
第15页/共20页
气体的三种统计速率
同一温度下不同种气体速率分布比较
f (v)
m1
m1 m2 m3
m2
分子质量越小，速
率大的分子数越多
。
m3
O
v
第16页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(1)nf (v)dv
f (v) dN , n N
Ndv
V
nf (v)dv
dN V
表示单位体积内分布在速率区间 v 内v的 dv
分子数。
第4页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度， 说明下式的物理意义：
(2)Nf (v)dv
f (v) dN Ndv
Nf (v)dv dN
表示分布在速率区间 v v 内的dv分子数。
第5页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(3)n v2 f (v)dv
v1
f (v)
dN
,n
N
Ndv
V
n v2 f (v)dv N N N
把这些量值代入，即得
W v＝ 1 v p 50
N＝
N
4
99 100
2
e
99 100
2
1 50
1.66%
第19页/共20页
f (v ) p3
T1
T2
T1 T2 T3
温度越高，速率 大的分子数越多
T3
v v v O
p1 p 2 p3
v
第15页/共20页
气体的三种统计速率
同一温度下不同种气体速率分布比较
f (v)
m1
m1 m2 m3
m2
分子质量越小，速
率大的分子数越多
。
m3
O
v
第16页/共20页
普通物理PPT课件4.3 麦克斯韦速率分布律
速率在v1 的百分比为
v2 区间的分子数N 占分子总数
v2 N ＝ f (v )dv v1 N
它对应于曲线下阴影部分的面积
0
f (v )dv＝1
——速率分布函数的归一化
*由麦克斯韦速率分布函数表示一些平均值
v
v
2
vdN N
2
0
0
dN v N
vf (v )dv
0
在v = vp 附近单位速率区间（v =1m· s-1）内 的分子数总数为
6.02 1023 105 0.2 0 0 1.2 1026 个
在v = 10vp 附近单位速率区间（v =1m· s-1） 内的分子数总数为
6.02 1023 105 2.0 1042 0 0 1.2 10
速率在区间的分子数占分子总数的百分比为它对应于曲线下阴影部分的面积速率分布函数的归一化432最概然速率平均速率和方均根速率最概然速率定义速率分布曲线上速率分布函数f最大值对应的速率叫做最概然速率
4.3 麦克斯韦速率分布律
4.3.1 麦克斯韦速率分布律 4.3.2 最概然速率 平均速率和方均根速率 4.3.4 例题分析
v2
k 玻耳兹曼常数 m 分子的质量 T－热力学温度
以v为横坐标，f (v)为纵坐标画出的曲线叫 做气体分子的速率分布曲线．
f (v )
dN f ( v )dv N
o
vp
v v dv
v
麦克斯韦速率分布曲线
3.麦克斯韦速率分布曲线
面积：
f(v)
意义：分布在区间v~ v+v 内的分子数的百分率 面积：
v2 区间的分子数N 占分子总数
v2 N ＝ f (v )dv v1 N
它对应于曲线下阴影部分的面积
0
f (v )dv＝1
——速率分布函数的归一化
*由麦克斯韦速率分布函数表示一些平均值
v
v
2
vdN N
2
0
0
dN v N
vf (v )dv
0
在v = vp 附近单位速率区间（v =1m· s-1）内 的分子数总数为
6.02 1023 105 0.2 0 0 1.2 1026 个
在v = 10vp 附近单位速率区间（v =1m· s-1） 内的分子数总数为
6.02 1023 105 2.0 1042 0 0 1.2 10
速率在区间的分子数占分子总数的百分比为它对应于曲线下阴影部分的面积速率分布函数的归一化432最概然速率平均速率和方均根速率最概然速率定义速率分布曲线上速率分布函数f最大值对应的速率叫做最概然速率
4.3 麦克斯韦速率分布律
4.3.1 麦克斯韦速率分布律 4.3.2 最概然速率 平均速率和方均根速率 4.3.4 例题分析
v2
k 玻耳兹曼常数 m 分子的质量 T－热力学温度
以v为横坐标，f (v)为纵坐标画出的曲线叫 做气体分子的速率分布曲线．
f (v )
dN f ( v )dv N
o
vp
v v dv
v
麦克斯韦速率分布曲线
3.麦克斯韦速率分布曲线
面积：
f(v)
意义：分布在区间v~ v+v 内的分子数的百分率 面积：
麦克斯韦速率分布律ppt课件.ppt
f (v)
dS
o v v dv
v
dN f (v)dv dS N
归一化条件
物理意义
表示在温度为 T 的平衡
状态下，速率在 v 附近单位
速率区间 的分子数占总数的 百分比。
表示速率在v v dv
区间的分子数占总分子数的 百分比 。
0N
dN N
0
f
(v)dv
1
首页
上页
下页
末页
退出
f (v)
S
o
（2） v2 f (v)dv， f (v)dv， v0 Nf (v)dv ；
v1
0
0
（3） v2 f (v)dv ， v2 Nvf (v)dv 。
0
v1
首页
上页
下页
末页
退出
【例题7–3】有一N个粒子组成的系统，其速率分 布函数如图7–9所示。（1）由v0求常量C；（2）求粒 子的平均速率。
解：（1）由归一化条
f(v)
件，有
C
1 2
Cv0
1
C 2 v0
（2）粒子的速率分布函数为 O
图7–9
4v
f
(v)
v02
4v v0
1
v v0
0 v v0
2
v0 2
v
v0
首页
上页
下页
v0 v
末页
退出
粒子的平均速率为
v 0 vf (v)dv
v0 0
/
2
v
4v v02
dv
v0 v0 / 2
dN 4π(
m
)3
2
mv 2
e 2kT
v2dv
6-(4-5) 能量均分定律 麦克斯韦速率分布率
6.74( K )
6 – 4
能量均分定律
理想气体内能
第六章气体动理论
一、统计规律的演示 一个小球落在哪里 有偶然性；少量小球 的分布每次都可能不 同；大量小球的分布 却是稳定的。
【演示】伽尔顿板
统计规律：大量偶然事件所显示的稳定的 规律 。
6 – 4
能量均分定律 理想气体内能 第六章气体动理论 下面列出了氧气分子在0OC时分子速率的分布情况
v
8 kT π m
f (v )
O2
v
2
3 kT mT 2 1200 K NhomakorabeaH2
o
v p1 v p 2
v
o
v p 0 v pH
v
N2 分子在不同温 度下的速率分布
同一温度下不同 气体的速率分布
6 – 5
麦克斯韦速率分布定律 讨论
第六章气体动理论
麦克斯韦速率分布中最概然速率 v p 的概念
下面哪种表述正确？ （A） v p 是气体分子中大部分分子所具有的速率. （B） v （C） v p 是麦克斯韦速率分布函数的最大值. （D） 速率大小与最概然速率相近的气体分子的比 率最大.
麦氏分布函数 f ( v ) 4 π (
其物理意义是：处于 温度为T的平衡气体，分子 速率出现在v附近、单位速 率区间内的分子数占总分 子数的百分率。
m 2 π kT
)
3 2
e
2 kT
v
2
f (v)
f (v )
dN Nd v
o
v
6 – 5
麦克斯韦速率分布定律
第六章气体动理论
分子速率分布与温度的关系： 1）存在最可几速率vp 。T增大，速率大的分子数增 多，最可几速率vp增大。 2）f(v)满足归一化条件： f (v )dv 1
麦克斯韦速率分布定律
υ 附近单位速率区
间的分子数
(5) nf ()d N dN dN
VN V
单位体积中速率在υ ~ υ+dυ区间的分子数
(6) 2 f ()d 1
dN N
N1 2 N
速率在υ1 ~ υ2区间的分
子数占总分子数的百分比
(7) 2 Nf ()d 1
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
(1) f () dN Nd
(2) f ( )d dN
N
υ附近单位速率区间的分子
数占总分子数的百分比
速率在υ ~ υ+dυ区间的分
子数占总分子数的百分比
(3) N f ()d N dN dN
N
速率在υ ~ υ+dυ
区间的分子数
(4) N f () N dN dN Nd d
f ()
T1
T2 T1
T2
p
2kT m
大学物理05-5麦克斯韦速率分布律
抽气
上页 下页 返回 退出
当铝钢圆柱体以给定角 速度 转动时，只有满足下 列关系式的原子才能顺利通 过细槽出口：
L t v
长为 L=20.40 cm、刻有螺旋形 细槽的铝钢圆柱体。
v L
这里的斜槽是一速率选择器。
而其它速率的原子则将沉积在槽壁上而不能通 过。改变角速度，检测器D则测出通过细槽的不 同速率的原子射线强度，于是可得原子蒸气的速率 分布，见下图。
上页 下页 返回 退出
O
v
麦克斯韦（James Clerk Maxwell 1831—1879）
•他提出了有旋电场和位移电流概念，建 立了经典电磁理论（麦克斯韦方程组）， 预言了以光速传播的电磁波的存在。
•1873年，他的《电磁学通论》问世，这 是一本划时代巨著，它与牛顿的《自然哲 学的数学原理》并驾齐驱，它是人类探索 电磁规律的一个里程碑。
将速率分成若干相等的区间，如
0 ~ 10 m/s; 10 m/s ~ 20 m/s; 20 m/s ~ 30 m/s;
上页 下页 返回 退出
设任一速率区间为： v ~ v v 设总的气体分子数为N，在该区间内的分子数为ΔN
N ——分布在速率 v附近单位速率间隔内的分子数 v N ——分布在速率 v 附近单位速率间隔内的分子数 vN 占总分子数的比率。
0
——归一化条件
O dv
v1 v2
v
上页 下页 返回 退出
三、麦克斯韦速率分布律
早在1859年，麦克斯韦应用统计概念和力学原理 导出在平衡态下气体分子速率分布函数的具体形式
m 32 f (v) 4π( ) e 2πkT
f (v )
mv2 2 kT
麦克斯韦速率分布定律
1859年, 麦克斯韦用概率论导出了气体分子速率分布 定律，后由玻尔兹曼使用经典统计力学理论导出.
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
氧气分子在 0ºC 时的分子速率分布
(m / s)
100以下
N / N (%)
1.4
100－200
8.1
200－300
16.5
300－400
21.4
400－500
20.6
500－600
15.1
600－700
9.2
700－800
4.8
800－900
2.0
二．气体分子速率分布 N /(Nv)
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
N
0 / 4 0
f ()d
5N 32
（3）最可几速率
df () d p
0p
0
2
（4）
f
( )d
0
0
2
rms
2
[
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
氧气分子在 0ºC 时的分子速率分布
(m / s)
100以下
N / N (%)
1.4
100－200
8.1
200－300
16.5
300－400
21.4
400－500
20.6
500－600
15.1
600－700
9.2
700－800
4.8
800－900
2.0
二．气体分子速率分布 N /(Nv)
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
N
0 / 4 0
f ()d
5N 32
（3）最可几速率
df () d p
0p
0
2
（4）
f
( )d
0
0
2
rms
2
[
麦克斯韦气体速率分布律
却进行得很慢。(演示）
克劳修斯指出：气体分子的速度虽然很大，但前
进中要与其他分子作频繁的碰撞，每碰一次，分
子运动方向就发生改变，所走的路程非常曲折。
一、平均自由程 和平均碰撞次数的定义
1、平均自由程 分子在连续两次碰撞之间
所经过的路程的平均值叫做平均自由程。(演示）
2、平均碰撞频率 Z 在单位时间内一个分子与其它分子碰撞的平均次 数，叫做分子的平均碰撞次数或平均碰撞频率。 3、二者关系
D l R 2
2、实验结果
•分子数在总分子数中所占 的比率与速率和速率间隔的 大小有关； •速率特别大和特别小的分 子数的比率非常小； •在某一速率附近的分子数 的比率最大； •改变气体的种类或气体的 温度时，上述分布情况有所 差别，但都具有上述特点。
二、麦克斯韦气体分子速率分布律
4-5 麦克斯韦气体速率分布律
4-6
4-7
玻尔兹曼能量分布律 等温气压公式(自学)
分子平均碰撞次数和平均自由程
4－5 麦克斯韦气体速率分布律
平衡态下，理想气体分子速度分布是有规律的， 这个规律叫麦克斯韦速度分布律。若不考虑分子速度 的方向，则叫麦克斯韦速率分布律。 气体分子按速率分布的统计规律最早是由麦克
间v1 ~ v2 内的分子数 占总分子数的比率。
—— 分布在有限速率区
5. Nf (v )dv
v1
v2
N ( v2 )
N ( v1 )
dN
间 v1 ~ v2 内的分子数。
—— 分布在 0 ～ ∞ 速率区
6.
0
f (v )dv 1
间内的分子数占总分子数的 比率。（ 归一化条件）
—— v2 的平均值。
克劳修斯指出：气体分子的速度虽然很大，但前
进中要与其他分子作频繁的碰撞，每碰一次，分
子运动方向就发生改变，所走的路程非常曲折。
一、平均自由程 和平均碰撞次数的定义
1、平均自由程 分子在连续两次碰撞之间
所经过的路程的平均值叫做平均自由程。(演示）
2、平均碰撞频率 Z 在单位时间内一个分子与其它分子碰撞的平均次 数，叫做分子的平均碰撞次数或平均碰撞频率。 3、二者关系
D l R 2
2、实验结果
•分子数在总分子数中所占 的比率与速率和速率间隔的 大小有关； •速率特别大和特别小的分 子数的比率非常小； •在某一速率附近的分子数 的比率最大； •改变气体的种类或气体的 温度时，上述分布情况有所 差别，但都具有上述特点。
二、麦克斯韦气体分子速率分布律
4-5 麦克斯韦气体速率分布律
4-6
4-7
玻尔兹曼能量分布律 等温气压公式(自学)
分子平均碰撞次数和平均自由程
4－5 麦克斯韦气体速率分布律
平衡态下，理想气体分子速度分布是有规律的， 这个规律叫麦克斯韦速度分布律。若不考虑分子速度 的方向，则叫麦克斯韦速率分布律。 气体分子按速率分布的统计规律最早是由麦克
间v1 ~ v2 内的分子数 占总分子数的比率。
—— 分布在有限速率区
5. Nf (v )dv
v1
v2
N ( v2 )
N ( v1 )
dN
间 v1 ~ v2 内的分子数。
—— 分布在 0 ～ ∞ 速率区
6.
0
f (v )dv 1
间内的分子数占总分子数的 比率。（ 归一化条件）
—— v2 的平均值。
高二物理竞赛麦克斯韦速率分布律课件
2 3
n k
微观 理论
(p, V, T)
温度公式
T
2 3
1 k
k
统计规律
能量均分定理
ki
1 2
kT
理想气体模型：
宏观 规律 1、忽略分子大小 ( 看作质点 )
2、忽略分子间的作用力，忽略重力
3、碰撞(分子之间、分子与器壁间)属完全弹性
气体状态方程 4、分子服从经典力学规律
pV M R T M mol
8
分子速率的实验测定
1、实验装置
2、实验原理
O —— 蒸汽源 S —— 分子束射出方向孔 R —— 长为 l 、刻有螺旋形细槽的铝钢滚筒 D —— 检测器，测定通过细槽的分子射线强度
当圆盘以角速度ω转动时，
每转动一周，分子射线通
过圆盘一次，由于分子的
速率不一样，分子通过圆
盘的时间不一样，只有速
率满足下式的分子才能通
提出了有旋电场和位移电流概念，建立了经典电磁理论，
预言了以光速传播的电磁波的存在。
讨论速率分布(不同温度、同温但分子质量不同)时——
用最概然速率
都含有统计的平均意义，
反映大量分子作热运动的统计规律。
例3 图为同一种气体，处于不同温度状态下的速率分布曲线，问：（1）哪一条曲线对应的温度高？（2）如果这两条曲线分别对应的
则分布在vP所在区间的分子数比率最大(而不是速率最大)。
是分布函数的一个特征值。
• vP的值：
df v
0 dv
vvp
vp
2 RT M mol
1.41 RT M mol
15
三种统计速率
1、最概然速率
vp
2 RT M mol
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
45、自己的饭量自、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬