人大版微积分第三版课件定积分应用
合集下载
高等数学(上) 第3版教学课件5-6 定积分应用举例

通常交流电器上注明的功率就是平均功率
《高等数学》
谢谢观看
于是 A f ( x)dx
b
A lim f ( x)dx a f ( x)dx.
o a x x dxb x
所求量U 符合下列条件时能用定积分
表达:
(1)U 是与一个变量 x的变化区间a, b有关
的量;
( 2 ) U 对 于 区 间 a, b具 有 可 加 性 , 就 是 说,如果把区间a, b分成许多部分区间,则
例8 计算从时刻 0 到 T 秒时间段内
自由落体运动的平均速度.
解:自由落体运动的速度为 v gt
根据定积分的物理意义及平均值公式得:
v 1 T
T 0
gtdt
g T
1 2
t2
T 0
1 2
gT
例9 计算纯电阻电路中正弦交流电 i m sin t
在一个周期上的平均功率.
解: 设电阻为 R ,则这个电路的电压为
积分变量,在 2,1 上任取一个小区间 x, x dx
则相应 于此小区间的窄条面积可用高为 x 1 1 x
xx
,宽为dx 的小矩形面积近似代替,从而得面积微元
根据微元法得
dA 1 x dx x
A 1 1 x dx
2 x
ln x 1 x2 1 3 ln 2
2 2 2
形的曲边是上半个(或下半个)椭圆
y
a b
a2 x2 ,
代入体积公式得:V
a b a a
a2 x2 dx
2b 2
a2
a a 2 x2 dx
0
2b 2
a2
a2 x
1 3
x3
a 0
4 3
《高等数学》
谢谢观看
于是 A f ( x)dx
b
A lim f ( x)dx a f ( x)dx.
o a x x dxb x
所求量U 符合下列条件时能用定积分
表达:
(1)U 是与一个变量 x的变化区间a, b有关
的量;
( 2 ) U 对 于 区 间 a, b具 有 可 加 性 , 就 是 说,如果把区间a, b分成许多部分区间,则
例8 计算从时刻 0 到 T 秒时间段内
自由落体运动的平均速度.
解:自由落体运动的速度为 v gt
根据定积分的物理意义及平均值公式得:
v 1 T
T 0
gtdt
g T
1 2
t2
T 0
1 2
gT
例9 计算纯电阻电路中正弦交流电 i m sin t
在一个周期上的平均功率.
解: 设电阻为 R ,则这个电路的电压为
积分变量,在 2,1 上任取一个小区间 x, x dx
则相应 于此小区间的窄条面积可用高为 x 1 1 x
xx
,宽为dx 的小矩形面积近似代替,从而得面积微元
根据微元法得
dA 1 x dx x
A 1 1 x dx
2 x
ln x 1 x2 1 3 ln 2
2 2 2
形的曲边是上半个(或下半个)椭圆
y
a b
a2 x2 ,
代入体积公式得:V
a b a a
a2 x2 dx
2b 2
a2
a a 2 x2 dx
0
2b 2
a2
a2 x
1 3
x3
a 0
4 3
高等数学(第三版)课件:定积分的应用

线 y f ( x,) 直线 x a, x b (a b) 与
• x 轴围成的面积是在x 轴上方和下方曲边梯形
面积的差.
• • 同样可由微元法分析
•⒉ 一般地,根据微元法由曲线 y f ( x), y g( x),
• ( f ( x) g( x)) 及直线x a, x b 所围的图形
• 面积.(右图所示)
• 解: 取 为积分变量,
•
面积微元为
d
A
1 2
(a )2
d
• 于是
A 2 1 (a )2d a 2 2
02
23
2 4 a 2 3
03
• 例5 计算双纽线 r 2 a2 cos2 (a 0)
•
所围成的平面图形的面积(下图所示)
• 解 因 r 2 0,故 的变化范围是 [ 3 , 5 ,]
• ⑴分割区间[a,b],将所求量(曲边梯形面积 A )
分为部分量(小曲边梯形面积 Ai)之和;
• ⑵确定各部分量的近似值(小矩形面积);
Ai f (i )xi
• ⑶求和得所求量的近似值(各小矩形面积之和);
n
A f (i )xi
i 1
• ⑷对和式取极限得所求量的精确值(曲边梯形面积).
n
A lim 0
• 它表示高为f ( x) 、底为 dx 的一个矩形面积.
• ⑵由定积分几何意义可知,当 f (x) 0 时,由曲
线 y f (x),直线 x a, x b (a b) 与 x 轴所围成
的曲边梯形的面积A为
A
b
f (x)dx
.
a
• ⑶当 f ( x)在区间 [a, b]上的值有正有负时,则曲
•
定积分的几何应用课件

电场中的电势
总结词
定积分可计算电场中的电势
详细描述
在静电场中,电势差与电场强度成正比。通过定积分可以计算出 某一点处的电势,即对电场强度进行积分。
公式表示
电势 = ∫E·dl
05
定积分的近似计算
方法
矩形法
总结词
矩形法是一种简单直观的定积分近似计算方法,通过将积分 区间划分为若干个小的矩形,然后求和来逼近定积分。
详细描述
辛普森法则是梯形法的一种改进,它考虑了函数在积分区间的整体变化趋势,将 积分区间分成若干个小的子区间,然后在每个子区间上应用梯形法来逼近定积分 。辛普森法则的精度比矩形法和梯形法更高,但计算量也相对较大。
THANKS
感谢您的观看
3
曲边三角形面积的近似计算
在无法直接计算定积分的情况下,可以使用近似 方法计算曲边三角形的面积,如矩形法、梯形法 等。
任意图形的面积
任意图形面积的计算
01
通过定积分计算任意图形的面积,首先需要找到图形的边界曲
线表达式,然后确定上下限,最后计算定积分。
任意图形面积的几何意义
02
任意图形面积表示的是边界曲线围成的平面区域面积。
详细描述
矩形法的基本思想是将积分区间分成若干个小的矩形,每个 矩形的宽度为小区间的宽度,高度为函数在相应小区间的平 均值。然后,将这些矩形的面积加起来,得到的就是定积分 的近似值。
梯形法
总结词
梯形法是一种基于几何直观的定积分近似计算方法,通过将积分区间划分为若干个小的梯形,然后求 和来逼近定积分。
围绕旋转轴旋转的平面图形被称为 旋转面。
旋转体的体积公式
圆柱的体积公式
V = πr²h,其中r是底面半径,h是高。
人大版微积分第三版课件第六章习题课

b a
( A).a-b (C ).a 2 -b2
dx 其中 a和b为常数,且 a b.
设f ( x)连续,则
1 ( B). a b 2 1 2 2 ( D). a b d b 2
__ , a f ( x y )dy __________
d e x x 若 f t dt =e 则f x = dx 0 ( A).x 2 ( B). x 2 (C ).e2 x
b
c
b
f ( x )dx
性质4
如果在区间[a , b] 上 f ( x ) g( x ) ,
则 f ( x )dx g( x )dx
a a
b
b
(a b)
性质5
a 1 dx a
b
b
dx b a
[a , b] 性质6 设 M 及 m 分别是函数 f ( x ) 在区间
0 i 1
n
实例2 (求变速直线运动的路程)
设某物体作直线运动,已知速度v v ( t ) 是时间 t 的一个连续函数,且v ( t ) 0 ,求 间隔[T1 , T2 ]上 物体在这段时间内所经过的路程 S.
s lim v ( i )t i
0 i 1
n
方法:分割、近似、求和、取极限.
性质1
性质2
a [ f ( x ) g( x )]dx a f ( x )dx a g( x )dx
a kf ( x )dx k a f ( x )dx
b b
b
b
b
k ( 为常数)
性质3 假设a c b
a f ( x )dx a f ( x )dx c
( A).a-b (C ).a 2 -b2
dx 其中 a和b为常数,且 a b.
设f ( x)连续,则
1 ( B). a b 2 1 2 2 ( D). a b d b 2
__ , a f ( x y )dy __________
d e x x 若 f t dt =e 则f x = dx 0 ( A).x 2 ( B). x 2 (C ).e2 x
b
c
b
f ( x )dx
性质4
如果在区间[a , b] 上 f ( x ) g( x ) ,
则 f ( x )dx g( x )dx
a a
b
b
(a b)
性质5
a 1 dx a
b
b
dx b a
[a , b] 性质6 设 M 及 m 分别是函数 f ( x ) 在区间
0 i 1
n
实例2 (求变速直线运动的路程)
设某物体作直线运动,已知速度v v ( t ) 是时间 t 的一个连续函数,且v ( t ) 0 ,求 间隔[T1 , T2 ]上 物体在这段时间内所经过的路程 S.
s lim v ( i )t i
0 i 1
n
方法:分割、近似、求和、取极限.
性质1
性质2
a [ f ( x ) g( x )]dx a f ( x )dx a g( x )dx
a kf ( x )dx k a f ( x )dx
b b
b
b
b
k ( 为常数)
性质3 假设a c b
a f ( x )dx a f ( x )dx c
人大微积分课件5-4定积分的分部积分法

常用积分公式 2
• $\int x^n\,dx=\frac{1}{n+1}x^{n+1}+C$ • $\int \frac{1}{x}\,dx=\ln|x|+C$ • $\int \ln(x)\,dx=x(\ln(x)-1)+C$
2
步骤二
进行分部积分计算,得到新的积分公式。
3
步骤三
对新的积分公式进行简化,找出可以直接计算的函数。
求解反函数的方法
对于给定的函数,通过求解其反函数,可以进一步利用分部积分法来求解积 分问题。
定积分的线性性质和换元法
线性性质 换元法
对于两个函数的定积分,可以先对其中一个进 行分部积分,再对另一个进行求导,得到相同 的积分结果。
典型的分部积分法例题
例题 1
计算定积分$\int x \cos(x)\,dx$
例题 2
计算定积分$\int e^x \sin(x)\,dx$
例题 3
计算定积分$\int x^2 \ln(x)\,dx$
常用的定积分公式
常用积分公式 1
• $\int e^x\,dx=e^x+C$ • $\int \sin(x)\,dx=-\cos(x)+C$ • $\int \cos(x)\,dx=\sin(x)+C$
通过引入新的变量替换积分变量,可以将复杂 的积分问题转化为更加简单的形式。
定积分的周期性质和复合函数积分
周期性质
对于满足一定周期条件的函数,可以通过周期 性质将定积分化简为更小的区间。
复合函数积分
通过将复合函数进行分解,可以利用分部积分 法求解更加复杂的积分问题。
分部积分法的限制条件和步骤
1 限制条件
高等数学-定积分及其应用ppt课件.ppt
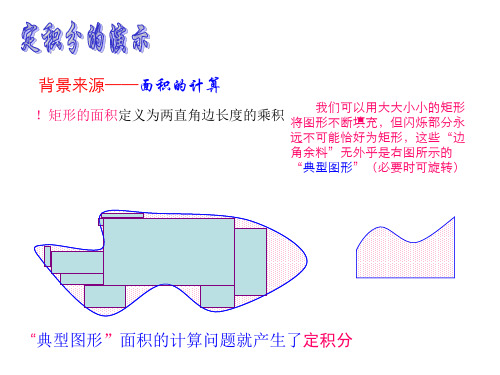
一、引例
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间 的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外 性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K,则 性质4 定积分的区间可加性 若 c 是 [ a , b ] 内的任一点,则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?
在变速直线运动中, 已知位置函数
与速度函数
之间有关系:
物体在时间间隔
内经过的路程为
这种积分与原函数的关系在一定条件下具有普遍性 .
5.3 定积分的计算
则积分上限函数
证:
则有
定理1. 若
5.3.1 牛顿 – 莱布尼兹公式
说明:
1) 定理 1 证明了连续函数的原函数是存在的.
2) 变限积分求导:
5.6.1 广义积分
引例. 曲线
和直线
及 x 轴所围成的开口曲
边梯形的面积
可记作
其含义可理解为
1 连续函数在无限区间上的积分
定义1. 设
若
存在 ,
则称此极限为 f (x) 在区间 的广义积分,
记作
这时称广义积分
收敛 ;
如果上述极限不存在,
就称广义积分
发散 .
类似地 , 若
公式, 复化求积公式等,
并有现成的数学软件可供调用.
性质1 常数因子可提到积分号外 性质2 函数代数和的积分等于它们积分的代数和。
5.2 定积分的简单性质
性质3 若在区间 [ a , b ]上 f (x)≡K,则 性质4 定积分的区间可加性 若 c 是 [ a , b ] 内的任一点,则
的面积 .
解:
例3. 汽车以每小时 36 km 的速度行驶 ,
速停车,
解: 设开始刹车时刻为
则此时刻汽车速度
刹车后汽车减速行驶 , 其速度为
当汽车停住时,
即
得
故在这段时间内汽车所走的距离为
刹车,
问从开始刹
到某处需要减
设汽车以等加速度
车到停车走了多少距离?
最新人大版微积分第三版课件8-7教学讲义ppt课件

zf(x,y)
n
Vl i0m k 1f(k,k)k
f(k,k)
(k ,k ) k
机动 目录 上页 下页 返回 结束
2. 平面薄片的质量
有一个平面薄片, 在 xoy 平面上占有区域 D , 其面密
度为(x,y) C,计算该薄片的质量 M .
若 (x,y)(常)数 ,设D 的面积为 , 则
M
若 (x,y)非常数 , 仍可用
o
x
f(x,y)df(x,y)dxdy
D
D
问题:根据二重积 几分 何的 意义
1x2 y2dxdy
D:x2y21
机动 目录 上页 下页 返回 结束
三、二重积分的性质
1 .D kf(x,y)d kD f(x ,y)d ( k 为常数)
2 .D [ f( x ,y ) g ( x ,y )d ]
人大版微积分第三版课件87
回忆定积分概念 :求曲边梯形面积步骤
1) 大化小. 在区间 [a , b] 中任意插入 n –1 个分点 a x 0 x 1 x 2 x n 1 x n b
用直线 x xi将曲边梯形分成 n 个小曲边梯形;
2) 常代变. 在第i 个窄曲边梯形上任取i[xi1,xi]
任 意 的 .
(2 )当 f(x ,y )在 闭 区 域 上 连 续 时 , 定 义 中 和 式
的 极 限 必 存 在 , 即 二 重 积 分 必 存 在 .
二重积分的几何意义 当被积函数大于零时,二重积分是柱体的体积. 当被积函数小于零时,二重积分是柱体的体积的 负值.
机动 目录 上页 下页 返回 结束
作以[xi1, xi]为底 , f (i )
y
为高的小矩形, 并以此小
《定积分的简单应用》课件讲解学习

0
[解析] v=ddxt=(bt3)′=3bt2, 媒质阻力F阻=kv2=k(3bt2)2=9kb2t4,其中k为比例常
数,k>0.
当x=0时,t=0,当x=a时,t=ab13,
ds=vdt,故阻力做的功为W阻=
t
kv2·vdt=k
t
v3dt=k
t
0
0
0
(3bt2)3dt=277k3 a7b2.
• [点评] 本题常见的错误是在计算所做的功 时,误将W阻=∫t10F阻ds写为∫t10F阻dt.
(1)P从原点出发,当t=6时,求点P离开原点 的路程和位移;
(2)P从原点出发,经过时间t后又返回原点时 的t值.
• [解析] (1)由v(t)=8t-t2≥0得0≤t≤4, • 即当0≤t≤4时,P点向x轴正方向运动, • 当t>4时,P点向x轴负方向运动. • 故t=6时,点P离开原点的路程
对于已知运动规律求做功的问题,首先确定其运动速 度,进而由 ds=vdt 来确定做功的积分式 W=t Fvdt.
0
6.已知自由落体的速率v=gt,则落体从t= 0到tA=.13gt0t20所走的路程为B(.gt20 )
C.12gt20
D.16gt20
[答案] C
[解析] 如果变速直线运动的速度为v=v(t)(v(t)≥0),
那么从时刻t=a到t=b所经过的路程是bv(t)dt, a
∴
=12gt2t00 =12g(t20-0)=12gt02.故应选C.
7.如果1N能拉长弹簧1cm,为了将弹簧拉 长6cm,所耗费的功为
()
A.0.18J
B.0.26J
C.0.12J
D.0.28J
[答案] A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线
、 ( a b )及 轴所围成的平面
图形绕 x轴旋转而成的旋转体,见图6-19,求它
的体积 Vx.
(1) 用分点 a x0 x1 x2 xn b
把区间 [a,b] 分成 n个小区间
[xi1, xi ](i 1, 2, , n)
这些小区间的长分别为 xi xi xi1(i 1, 2, , n)
定积分的应用
平面图形的面积 旋转体的体积
已知函数 求由曲线 梯形的面积 .
在区间
,
,
上连续,如何 所围成的曲边
1. 如果在 见图6-10
则由定积分
上
,
的几何意义知:
2. 如果在
上
,见图6-11,
3. 对于在
上函数
面积 可以表示为
有时取正有时取负,见图6-12,
类似地,由曲线 x ( y)( 0),直线 y c, y d 及 y
n
因此整个旋转体体积 Vx
[ f (i )]2 xi
i 1
(3) 记
x
max
1in
xi
当分点数
n , x 0
整个旋转体的体积
n
Vx
lim
x0
i 1
[
f
(i )]2 xi
b
[
f
(
x)]2dx
a
同理可得绕y轴旋转而成的旋转体的体积的计算公式为
Vy
d [( y)]2dy
c
求椭圆
分别绕 轴与 轴旋转产生的旋转体体积
4b a2 ab
a4
a2 x2 dx
例 求抛物线 y2 2x 与直线 y x 4
2
所围成的图形的面积.
解:求出抛物线与直线的交
点
,
,再画已知方
程的图形,见图6-17阴影部分.
S 4 ( y 4 y2 )dy
2
2
(
y2 2
4y
y3 ) 6
4 2
18
旋转体的体积
x 设一立体是以连续曲线 y f (x)( 0)、直
Vx 2
a
[
f
( x)]2 dx
2
0
a 0
b2 a2
(a2
x2 )dx
2
b2 a2
(a2x
1 3
x3)
a 0
4 ab2
3
Vy 2
b x2dy
0
2
b 0
a2 b2
(b2
y2 )dy
4 a2b
3
过 i (xi1 i xi )(i 1, 2, , n) 作与 x 轴垂
直的平面,将旋转体分成 n 个小旋转体.
2) 把每个小旋转体分别用底半径为 f (i ),高为xi (i 1, 2, , n)
的直圆柱来 xi (i 1, 2, , n)
轴所围成的曲边梯形面积 S (如图6-13)
d
S ( y)dy c
如果在 [a, b] 上,总有
0 g(x) f (x)
则曲线 f (x) 与 g(x) 所夹的面积 S 为
b
b
S f (x)dx g(x)dx
a
a
b
[ f (x) g(x)]dx
a
一般地,在 [a, b] 上,曲线 f (x) 与 g(x)所夹图形面积
b
S f (x) g(x)dx
a
类似地,由曲线 ( y) 与 ( y)所夹图形的面积 S
d
S ( y) ( y)dy
c
例1 求椭圆
x2 a2
y2 b2
1
的面积
因为椭圆是关于坐标轴对称的,所以整 个椭圆的面积 是第一象限内那部分的 四倍,即有
a
S 4 ydx
4
ab
0
0a
4b a a2 x2 dx a0
