八年级数学《二元一次方程组》的知识点归纳
认识二元一次方程组(知识梳理与考点分类讲解)-八年级数学上册基础知识专项突破讲与练(北师大版)

专题5.1认识二元一次方程组(知识梳理与考点分类讲解)【知识点1】二元一次方程1.定义含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.2.二元一次方程的条件(1)整式方程;(2)只含有两个未知数;3.关于x,y的两元一次方程的一般形式:ax+by=c(a≠0,b≠0).特别提醒:“所含未知数的项的次数都是1”不可理解为两个未知数的次数都是1,例如2xy+1=0不是二元一次方程.【知识点2】二元一次方程组1.定义共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.2.二元一次方程组应满足的条件:(1)两个方程都是整式方程;(2)共含有两个未知数;(3)两个方程都是一次方程;特别提醒:判断二元一次方程组时,误认为每个方程必须是二元一次方程.【知识点3】二元一次方程的解1.二元一次方程组的解适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.2.判断一对数值是不是二元一次方程的解的方法:判断一对数值是不是二元一次方程的解,只需将这对数值分别代入方程的左右两边,看其是否相等.特别提醒:二元一次方程只要给定其中的一个未知数的值,就可以相应地求出另一个未知数的值,因此二元一次方程有无数个解.二元一次方程的整数解有时只有有限个.【知识点4】二元一次方程组的解1.二元一次方程组的解二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.2.判断一对数值是不是二元一次方程组的解的方法判断一对数值是否为一个二元一次方程组的解,必须将这对数值分别带入方程组中的每一个方程进行检验,若满足没一个方程,则这对数值就是这个方程组的解,否则就不是这个方程组的解.特别提醒:方程组的解一定是方程组中每个方程的解,而方程组中某个方程的解不一定是方程组的解.【考点目录】【考点1】二元一次方程的认识;【考点2】二元一次方程组的认识【考点3】二元一次方程的解;【考点4】二元一次方程组的解【答案】0【分析】根据二元一次方程的定义:含有两个未知数,并且所含未知数的项的次数都是1的整式方程,进行求解即可解:∵方程()()33420m n m xn y --+--=是关于x y ,的二元一次方程,∴40312031m m n n +≠⎧⎪-=⎪⎨-≠⎪⎪-=⎩,∴44m n ==,,∴m n -440=-=【点拨】本题考查二元一次方程的定义,掌握二元一次方程组的定义是解题关键.二元一次方程需满足三个条件:①首先是整式方程.②方程中共含有两个未知数.③所有未知项的次数都是一次.【举一反三】【变式1】(2023上·河北张家口·八年级统考期中)下列是二元一次方程的是()A .215x -=B .21x y +=C .23x y +=D .12y x+=【答案】C【分析】本题考查了二元一次方程的定义,二元一次方程需满足三个条件:①首先是整式方程,②方程中共含有两个未知数,③所有未知项的次数都是一次,不符合上述任何一个条件的都不叫二元一次方程.解:A .215x -=,是一元一次方程,故本选项不符合题意;B .21x y +=,是二元二次方程,故本选项不符合题意;C .23x y +=,是二元一次方程,故本选项符合题意;D .12y x+=,是分式方程,故本选项不符合题意.故选:C .【变式2】(2022下·湖北荆州·七年级校考期中)若方程:223m x ++514n y -=6是关于x 、y 的二元一次方程,则n m -的平方根为.【答案】2±【分析】根据二元一次方程的定义,得各个未知数的次数为1,求得m ,n 的值,进而求解.解:由题意,得:231m +=,5141n -=,解得1m =-,3n =.∴()314n m -=--=,∴n m -的平方根2=±.故答案为:2±.【点拨】本题考查二元一次方程的定义,平方根,熟练掌握只含有两个未知数,且未知项的次数为1的整式方程是二元一次方程是解题的关键.【考点二】二元一次方程组的认识【例2】(2017下·四川宜宾·七年级校联考阶段练习)已知方程组()()2233112m x m ym x --⎧--=⎪⎨+=-⎪⎩是二元一次方程组,求m 的值.【答案】m =5解:依题意,得:|m -2|-2=1,且m -3≠0,且m +1≠0,解得:m =5.【点拨】本题考查了二元一次方程组的定义.二元一次方程组也满足三个条件:①方程组中的两个方程都是整式方程,②方程组中共含有两个未知数,③每个方程都是一次方程.【举一反三】【变式1】(2023下·河北廊坊·七年级统考期末)下列方程组中是二元一次方程组的是()A .436231x y y z -=⎧⎨-=⎩B .45342x y x =⎧⎨-=⎩C .46323xy x y =⎧⎨+=⎩D .23325y xy x ⎧+=⎪⎨⎪+=⎩【答案】B【分析】根据二元一次方程组定义判断即可.解: A.此方程组含有,,x y z 三个未知数,故不是二元一次方程组,故此选项不符合题意;B .该方程组是二元一次方程组,故此选项符合题意;C .46xy =是二元二次方程,故不是二元一次方程组,故此选项不符合题意;D .233y x+=是分式方程,故不是二元一次方程组,故此选项不符合题意;故选:B .【点拨】本题主要考查了二元一次方程的定义.一定要紧扣二元一次方程组的定义回答.【变式2】(2023下·江苏徐州·七年级统考期末)观察所给的4个方程组:①23x y =⎧⎨=⎩;②415343x y x =⎧⎨-=-⎩;③2164x y x y +=⎧⎨-=⎩;④352494x y x y +=⎧⎨+=⎩,其中,符合二元一次方程组定义的是(写出所有正确的序号).【答案】①②④【分析】含有两个未知数,且未知数的最高次数是1,这样的整式方程组是二元一次方程组,根据定义逐一判断即可.解:①23x y =⎧⎨=⎩,符合二元一次方程组定义;②415343x y x =⎧⎨-=-⎩,符合二元一次方程组定义;③2164x y x y +=⎧⎨-=⎩,未知数x 的最高次数是2,不符合二元一次方程组定义;④352494x y x y +=⎧⎨+=⎩,符合二元一次方程组定义;所以符合二元一次方程组定义的是①②④.故答案为:①②④.【点拨】本题考查的是二元一次方程组的定义,熟记定义是解本题的关键.【考点三】二元一次方程的解【例3】(2023上·河北张家口·八年级统考期中)已知24x y =⎧⎨=⎩是关于x ,y 的二元一次方程314x ay +=的一组解.(1)求a 的值(2)请用含有x 的代数式表示y .【答案】(1)2a =;(2)372y x=-【分析】(1)将二元一次方程的解24x y =⎧⎨=⎩代入314x ay +=得到关于a 的方程,解关于a 的方程即可;(2)将2a =代入314x ay +=得到3214x y +=,将x 看作已知数,y 看作未知数,解关于y 的方程即可.(1)解:将24x y =⎧⎨=⎩代入314x ay +=,得:32414a ⨯+=,解得2a =;(2)解:∵2a =,∴原方程可变为3214x y +=,∴372y x =-.【举一反三】【变式1】(2023上·陕西西安·八年级高新一中校考期中)若关于x 、y 的二元一次方程221x y a +=-的一组解为3x =,1y =,则a 的值是()A .3B .2C .1D .1-【答案】A【分析】本题考查了二元一次方程的解,解题的关键是掌握二元一次方程的定义.把3x =,1y =代入到221x y a +=-中即可求解.解:把3x =,1y =代入到221x y a +=-中得:21321a -=+⨯,216a -=,3a =,故选:A .【变式2】(2023上·全国·八年级专题练习)小方解方程组232ax by cx y +=⎧⎨-=-⎩时,因抄错了a ,解得11x y =⎧⎨=⎩,则c 的值为.【答案】1【分析】本题主要考查了二元一次方程的解,将解代入第二个方程即可解答.解:把11x y =⎧⎨=⎩代入32cx y -=-得:32c -=-,解得:1c =.故答案为:1.【考点四】二元一次方程组的解【例4】(2023上·全国·八年级专题练习)甲和乙两人同解方程组125bx y x ay +=⎧⎨+=⎩,甲因抄错了a ,解得52x y =⎧⎨=⎩,乙因抄错了b ,解得32x y =⎧⎨=⎩,求52a b -的值.【答案】1【分析】本题考查了二元一次方程组的解,将甲、乙求得的解分别代入正确的方程,求出a ,b 的值即可求解,用代入法解方程是解本题关键.解:由题意52x y =⎧⎨=⎩,是12bx y +=的解,∴5212b +=,解得2b =,又 32x y =⎧⎨=⎩是5x ay +=的解,∴325a +=,解得1a =,5251221a b ∴-=⨯-⨯=.【举一反三】【变式1】(2023上·广东深圳·八年级校联考期中)若关于x ,y 的二元一次方程组2138x ay bx y -=-⎧⎨+=⎩的解是15x y =⎧⎨=⎩,则关于m 、n 的二元一次方程组()()()()2138m n a m n b m n m n ⎧+--=-⎪⎨++-=⎪⎩的解是()A .15m n =⎧⎨=⎩B .51m n =⎧⎨=⎩C .23m n =-⎧⎨=⎩D .32m n =⎧⎨=-⎩【答案】D【分析】本题考查了二元一次方程组的解及解二元一次方程组,先将15x y =⎧⎨=⎩代入2138x ay bx y -=-⎧⎨+=⎩解得357a b ⎧=⎪⎨⎪=-⎩,再将357a b ⎧=⎪⎨⎪=-⎩代入()()()()2138m n a m n b m n m n ⎧+--=-⎪⎨++-=⎪⎩即可求解,熟练掌握二元一次方程组的解及利用加减消元法解二元一次方程组是解题的关键.解:将15x y =⎧⎨=⎩代入2138x ay bx y -=-⎧⎨+=⎩得:251158a b -=-⎧⎨+=⎩,解得:357a b ⎧=⎪⎨⎪=-⎩,()()()()3215738m n m n m n m n ⎧+--=-⎪∴⎨⎪-++-=⎩,解得:32m n =⎧⎨=-⎩,故选D .【变式2】(2023下·七年级单元测试)写出一个解为25x y =⎧⎨=-⎩的二元一次方程组:.【答案】37x y x y +=-⎧⎨-=⎩(答案不唯一)【分析】方程组的解,指的是该数值满足方程组中的每一方程.在求解时,应先围绕25x y =⎧⎨=-⎩列一组算式,如253-=-,257+=,然后用x ,y 代换,可得方程组.解:先围绕25x y =⎧⎨=-⎩列一组算式,如:253-=-,257+=,然后用x ,y 代换,可得37x y x y +=-⎧⎨-=⎩等.答案不唯一,符合题意即可.故答案为:37x y x y +=-⎧⎨-=⎩(答案不唯一).【点拨】本题考查二元一次方程组的解,此题是开放性题目,答案不唯一.掌握二元一次方程组解的意义是解题的关键.。
八年级数学二元一次方程组知识点

八年级数学二元一次方程组知识点
以下是八年级数学二元一次方程组的主要知识点:
1. 二元一次方程组的定义:由两个未知数的一次方程组成的方程组。
2. 解二元一次方程组的方法:
a. 消元法:通过变换方程组中的某一方程使得两个方程的系数相同,从而使得方程组中某个未知数的系数为零,然后解得另一个未知数,再回代求解另一个未知数。
b. 代入法:将一个方程的一个未知数用另一个未知数表示,然后代入另一个方程,得到包含一个未知数的一次方程,从而解出这个未知数,再代入另一个方程解出另一个未知数。
3. 方程组的解的情况:
a. 有唯一解:方程组有一个解,即两个方程表示的直线在某一点相交。
b. 无解:方程组的两个方程表示的直线平行,不相交。
c. 无穷多解:方程组的两个方程表示的直线重合,有无穷多个解。
4. 方程组解的判断:
a. 可以通过将解代入方程组中验证方程组是否成立,以确定解是否正确。
b. 可以通过画出方程组所表示的直线来观察直线的相交情况,以判断方程组是否有解及解的情况。
5. 方程组应用题:将实际问题转化为方程组,通过解方程组求解实际问题,如两个人同时出发,相遇时互相报告行进的时间等问题。
这些是八年级数学二元一次方程组的主要知识点,希望对你有帮助。
第五章 二元一次方程组-八年级数学上册教学课件(北师大版)

2
x
7.判断三点A(3,1),B(0,-2),C(4,2)是否在
同一条直线上.
解:设过A,B两点的直线的表达式为y=kx+b.
由题意可知,
1 = 3 +
=1
∴
−2 = 0 +
= −2
∴过A,B两点的直线的表达式为y=x-2.
∵当x=4时,y=4-2=2.
∴点C(4,2)在直线y=x-2上.
次函数的图象的关系
方程组的解是对应的两条直
线的交点坐标
两条线的交点坐标是
对应的方程组的解
做一做
x+2y=10
1.二元一次方程组
A.
C.
x=4
y=2x
的解是( C )
x=3
B.
y=3
y=6
x=2
x=4
y=4
D.
y=2
2.解下列方程组.
y=2x
(1)
(2)
x+y=12
解: (1)
4x+3y=65
x=4
设:设未知数.
列:根据等量关系,列出方程组.
解:解方程组,求出未知数.
答:检验所求出未知数是否符合题意,写出答案.
知识点五 二元一次方程组与一次函数
二元一次方程和一次
函数的图象的关系
以二元一次方程的解为坐标
的点都在对应的函数图象上.
一次函数图象上的点的坐标
都适合对应的二元一次方程.
二元一次方程组和一
(2)把这个含x的代数式代入另一个方程中,
消去y,得到一个关于x的一元一次方程;
(3)解一元一次方程,求出x的Байду номын сангаас;
北师大版八年级上册数学《求解二元一次方程组》二元一次方程组教学说课复习课件

①
观察系数
2x+5y=9
解:由①×5得
② 15x-20 =10 ③
由②×4得 8x+20 =36
③+④得 23x=46
统一系数
④
加法消元
解得 x=2
把 x=2代入①得 6-4y=2
解得
=1
∴原方程组的解是
x=2
{ y=1
回代求解
写解
最小公倍数
归纳总结
观察系数
未知数的系数相等或互为相反数
加减消元法
观察系数
4x+6x+15=65
x=2+3y
②
解:将②代入①,得2(2+3y)+5y=15
4+6y+5y=15
11y=11
10x=50
x=5
将x=5代入①,得y=15
x=5
所以方程组的解为
y=15
y=1
将y=1代入②,得x=5
x=5
所以方程组的解为
y=1
趁热打铁【1】 用代入消元法解方程组:
(3)解方程组
2x+3y=16 ①
转化 解:由①,得 x = y + 3 .③
代入 把③代入②,得 3(y+3)-8y=14.
思考:把③
代入①可以吗?
求解 解这个方程,得 y=-1.
回代 把y=-1代入③,得 x=2.
x = 2,
写解 所以这个方程组的解是 y =-1.
注意:检验方程组的解
做一做
若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、
第五章 二元一次方程组
八年级上册第五章二元一次方程组知识点整理

八年级上册---第五章---二元一次方程组-知识点整理(数学教研组)八年级上册 第五章 二元一次方程组 知识点整理一、本章知识点梳理:知识点1:二元一次方程(组)的定义 知识点2:二元一次方程组的解定义知识点3:二元一次方程组的解法 知识点4:一次函数与二元一次方程(组) 知识点5:实际问题与二元一次方程组 二、各知识点分类讲解知识点1:二元一次方程(组)的定义1、二元一次方程的概念含有两个未知数,且所含未知数的项的次数都是1的方程叫做二元一次方程注意:1、(1)方程中的元指的是未知数,即二元一次方程有且只有两个未知数.(2)含有未知数的项的次数都是1.(3)二元一次方程的左右两边都必须是等式. (三个条件完全满足的就是二元一次方程)2.含有未知数的项的系数不等于零,且两未知数的次数为1。
即若ax m +by n=c 是二元一次方程,则a ≠0,b ≠0且m=1,n=1 例1:已知(a -2)x -by |a|-1=5是关于x 、y 的二元一次方程,则a =______,b =_____.例2:下列方程为二元一次方程的有_________ ①y x =-52,②14=-x ,③2=xy ,④3=+y x ,⑤22=-y x,⑥22=-+y x xy ,⑦71=+y x⑧y x 23+,⑨1=++c b a 【巩固练习】下列方程中是二元一次方程的是( )A .3x-y 2=0B .2x +1y =1C .3x -52y=6 D .4xy=3 2、二元一次方程组的概念由两个二元一次方程所组成的方程组叫二元一次方程组 注意:①方程组中有且只有两个未知数。
②方程组中含有未知数的项的次数为1。
③方程组中每个方程均为整式方程。
例:下列方程组中,是二元一次方程组的是( ) A 、228423119 (23754624)x y x y a b x B C D x y b c y x x y +=+=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩【巩固练习】1、 已知下列方程组:(1)32x y y =⎧⎨=-⎩,(2)324x y y z +=⎧⎨-=⎩,(3)1310x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩,(4)3x y x y +=⎧⎨-=⎩, 其中属于二元一次方程组的个数为( )A .1 B. 2 C . 3 D . 4 2、 若753313=+--m n m y x 是关于x 、y 二元一次方程,则m =_________,n =_________。
北师大版八年级上册数学第22讲《应用二元一次方程组》知识点梳理

北师大版八年级上册数学第 22 讲《应用二元一次方程组》知识点梳理【学习目标】1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数问题的数学模型;2.熟练掌握用方程组解决鸡兔同笼,增收节支,里程碑上的数等实际问题.【要点梳理】要点一、常见的一些等量关系1.和差倍分问题:增长量=原有量×增长率较大量=较小量+多余量,总量=倍数×倍量.2.增收节支问题:(1)增长(递减)率公式:原来的量×(1+增长率)=后来的量;原来的量×(1-递减率)=后来的量;(2)利润公式:利润=总收入-总支出;利润=售价-成本(或进价)=成本×利润率;标价=成本(或进价)×(1+利润率)(3)银行利率公式:利息=本金×利率×期数.本息和(本利和)=本金+利息=本金+本金×利率×期数=本金×(1+利率×期数) .年利率=月利率×12.月利率=年利率×.要点诠释:增收节支问题常常借助列表分析问题中所蕴涵的数量关系,这种方法清晰明了,能够充分突出解题过程.3.行程问题:速度×时间=路程.顺水速度=静水速度+水流速度.逆水速度=静水速度-水流速度.4.数字问题:已知各数位上的数字,写出两位数,三位数等这类问题一般设间接未知数,例如:若一个两位数的个位数字为a,十位数字为b,则这个两位数可以表示为10b+a.要点二、实际问题与二元一次方程组1.列方程组解应用题的基本思想列方程组解应用题,是把“未知”转换成“已知”的重要方法,它的关键是把已知量和未知量联系起来,找出题目中的等量关系.一般来说,有几个未知量就必须列出几个方程,所列方程必须满足:①方程两边表示的是同类量:②同类量的单位要统一;③方程两边的数要相等.2.列二元一次方程组解应用题的一般步骤:设:用两个字母表示问题中的两个未知数;列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);解:解方程组,求出未知数的值;验:检验求得的值是否正确和符合实际情形;答:写出答案.要点诠释:(1)解实际应用问题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的解应该舍去;(2)“设”、“答”两步,都要写清单位名称;(3)一般来说,设几个未知数就应该列出几个方程并组成方程组.【典型例题】类型一、鸡兔同笼问题1.(2016•茂名)我国古代数学名著《孙子算经》中记载了一道题,大意是:100 匹马恰好拉了100 片瓦,已知1 匹大马能拉3 片瓦,3 匹小马能拉1 片瓦,问有多少匹大马、多少匹小马?若设大马有x 匹,小马有y 匹,那么可列方程组为()A.B.C.D.⎨ y = 2⎩ 【思路点拨】设有 x 匹大马,y 匹小马,根据 100 匹马恰好拉了 100 片瓦,已知一匹大马能拉 3 片瓦, 3 匹小马能拉 1 片瓦,列方程组即可.【答案与解析】解:设有 x 匹大马,y 匹小马,根据题意得,故选 C【总结升华】本题考查了二元一次方程的应用,利用二元一次方程组求解的应用题一般情况下题中要给出 2 个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.举一反三:【变式】根据图中所给出的信息,求出每个篮球和每个羽毛球的价格.【答案】解:设每个篮球 x 元,每个羽毛球 y 元.根据题意列方程组:⎧2x + 2 y = 44 ⎨x + 3y = 26解得⎧x = 20 ⎩ 答:每个篮球 20 元,每个羽毛球 2 元.类型二、增收节支问题2.(2015•北京)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”译文:“假设有 5 头牛、2 只羊,值金 10 两;2 头牛、5 只羊,值金 8 两.问:每头牛、每只羊各值金多少两?”设每头牛值金x 两,每只羊值金y 两,可列方程组为.【思路点拨】由实际问题抽象出二元一次方程组.根据“假设有5 头牛、2 只羊,值金10 两;2 头牛、5 只羊,值金8 两”,得到等量关系,即可列出方程组.【答案与解析】解:根据题意得:.【总结升华】考查了由实际问题抽象出二元一次方程组的能力,解决本题的关键是找到题目中所存在的等量关系.举一反三【变式】小明想开一家时尚G点专卖店,开店前他到其它专卖店调查价格.他看中了一套新款春装,成本共500 元,专卖店店员告诉他在上市时通常将上衣按50﹪的利润定价,裤子按40﹪的利润定价. 由于新年将至,节日优惠,在实际出售时,为吸引顾客,两件服装均按9 折出售,这样专卖店共获利157 元,小明觉得上衣款式好,销路会好些,想问问上衣的成本价,但店员有事走开了,你能帮助他吗?【答案】上衣成本+裤子成本=500 元上衣利润+裤子利润=157 元分析:设上衣的成本价为x元,裤子的成本价为y元:成本(元)实际售价(元)利润(元)上衣x 0.9 ⨯ (1+ 50%)x0.9 ⨯ (1+ 50%)x -x⎨35x + 26y = 15700 ...... ② ⎨ ⎩ ⎨ y = 69000 ⎩裤子y 0.9 ⨯ (1+ 40%) y 0.9 ⨯ (1+ 40%) y - y:设上衣的成本价为 x元,裤子的成本价为y元,则⎧⎪x + y = 500 ⎪⎩0.9⨯ (1+ 50%) x - x + 0.9⨯(1+ 40%) y - y = 157整理得: ⎧x + y = 500 ...... ① ⎩ ②-① ×26,得 9x=2700, ∴x =300. 把其代入①,得 y=500-300=200 ⎧x = 300 ⎨ y = 200答:上衣成本 300 元,裤子成本 200 元.3. 蔬菜种植专业户徐先生要办一个小型蔬菜加工厂,分别向银行申请了甲,乙两种贷款,共 13 万元,徐先生每年须付利息 6075 元,已知甲种贷款的年利率为 6%,乙种贷款的年利率为 3.5%,则甲, 乙两种贷款分别是多少元?【思路点拨】本题的等量关系:甲种贷款+乙种贷款=13 万元;甲种贷款的年利息+乙种贷款的年利息=6075 元.【答案与解析】解:设甲,乙两种贷款分别是 x ,y 元,根据题意得:⎧ x + y = 130000⎨6%x + 3.5% y = 6075解得: ⎧ x = 61000 ⎩ 答:甲,乙两种贷款分别是 61000 元和 69000 元. 【总结升华】利息=贷款金额×利息率.类型三、里程碑上的数(数字问题)⎨ ⎨ y = 4与原数的和是 143,求这个两位数.【思路点拨】本题中的等量关系:①个位上的数-十位上的数=5;②原数+新数=143.【答案与解析】解:设原来的两位数中,个位上的数字为 x ,十位上的数字为 y .则原数为 10y+x ,把这两个数的位置对换后,所得的新数为 10x+y ,根据题意,得:⎧x - y = 5 ⎩10 y + x +10x + y = 143 ,解方程组,得⎧x = 9 . ⎩故这个两位数为 10y+x =10×4+9=49. 答:这个两位数为 49.【总结升华】对于两位数、三位数的数字问题,关键是明确它们与各数位上的数字之间的关系:两位数=十位数字×10+个位数字;三位数=百位数字×100+十位数字×10+个位数字.【变式】(2015•黑龙江)为推进课改,王老师把班级里 40 名学生分成若干小组,每小组只能是 5 人或 6 人,则有几种分组方案() A .4 B .3 C .2 D .1 【答案】解:设 5 人一组的有 x 个,6 人一组的有 y 个,根据题意可得:5x+6y=40,当 x=1,则 y=(不合题意);当 x=2,则 y=5;当 x=3,则 y=(不合题意);当 x=4,则 y=(不合题意);当 x=5,则 y=(不合题意);当 x=6,则 y=(不合题意);当 x=7,则 y=(不合题意);当 x=8,则 y=0;所以有 2 种分组方案.故选:C .类型四、行程问题4.有一个两位数,个位上的数比十位上的数大 5,如果把这两个数的位置对换,那么所得的新数⎨ ⎩5. A 、B 两地相距 480 千米,一列慢车从 A 地开出,一列快车从 B 地开出.(1) 如果两车同时开出相向而行,那么 3 小时后相遇;如果两车同时开出同向(沿 BA 方向)而行,那么快车 12 小时可追上慢车,求快车与慢车的速度各是多少?(2) 如果慢车先开出 l 小时,两车相向而行,那么快车开出几小时可与慢车相遇?【思路点拨】这两个问题均可以利用路程、速度和时间之间的关系列方程(组)求解.(1) “同时开出相向而行”可用下图表示.“同时开出同向而行”可用下图表示.(2) 慢车先开出 1 小时,两车相向而行,仿照(1)用示意图表示出来,并用等式表示出来.【答案与解析】解:(1)设快车和慢车的速度分别为 x 千米/时和 y 千米/时.根据题意,得⎧3x + 3y = 480 , ⎩12x -12 y = 480⎧x = 100 解得 ⎨ y = 60答:快车和慢车的速度分别为 100 千米/时和 60 千米/时.(2)设快车开出 x 小时可与慢车相遇,则此时慢车开出(x+1)小时,根据题意,得 60(x+1)+100x =480.解得 x = 2 5 . 8答:快车开出2 5小时两车相遇. 8 【总结升华】比较复杂的行程问题可以通过画“线条”图帮助分析,求解时应分清相遇、追及、相向、同向等关键词.。
求解二元一次方程组(知识梳理与考点分类讲解)-八年级数学上册基础知识专项突破讲与练(北师大版)
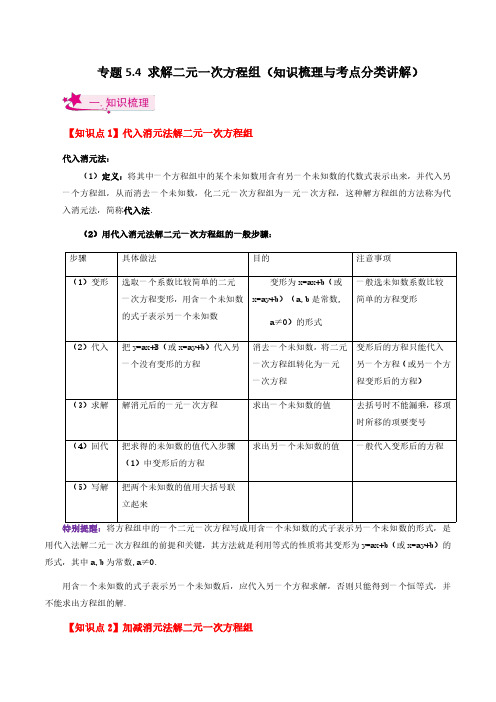
专题5.4求解二元一次方程组(知识梳理与考点分类讲解)【知识点1】代入消元法解二元一次方程组代入消元法:(1)定义:将其中一个方程组中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程组,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代入消元法,简称代入法.(2)用代入消元法解二元一次方程组的一般步骤:步骤具体做法目的注意事项(1)变形选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数变形为x=ax+b(或x=ay+b)(a,b 是常数,a≠0)的形式一般选未知数系数比较简单的方程变形(2)代入把y=ax+B(或x=ay+b)代入另一个没有变形的方程消去一个未知数,将二元一次方程组转化为一元一次方程变形后的方程只能代入另一个方程(或另一个方程变形后的方程)(3)求解解消元后的一元一次方程求出一个未知数的值去括号时不能漏乘,移项时所移的项要变号(4)回代把求得的未知数的值代入步骤(1)中变形后的方程求出另一个未知数的值一般代入变形后的方程(5)写解把两个未知数的值用大括号联立起来特别提醒:将方程组中的一个二元一次方程写成用含一个未知数的式子表示另一个未知数的形式,是用代入法解二元一次方程组的前提和关键,其方法就是利用等式的性质将其变形为y=ax+b(或x=ay+b)的形式,其中a,b 为常数,a≠0.用含一个未知数的式子表示另一个未知数后,应代入另一个方程求解,否则只能得到一个恒等式,并不能求出方程组的解.【知识点2】加减消元法解二元一次方程组1.加减消元法的定义通过将两个方程相加(减)消去其中一个未知数,将二元一次方程组转化为一元一次方程来解,这种解二元一次方程组的方法叫做加减消元法,简称加减法.2.用加减消元法解二元一次方程组的一般步骤步骤具体做法目的注意事项(1)变形根据绝对值较小的未知数(同一个未知数)的系数的最小公倍数,给方程的两边都乘适当的数.使某一个未知数在两个方程中的系数相等或互为相反数.给某个方程乘一个数时,方程两边的每一项都要和这个数相乘(2)代入两个方程中同一个未知数的系数互为相反数时,将两个方程相加;同一个未知数的系数相等时,将两个方程相减.消去一个未知数,将二元一次方程组转化为一元一次方程把两个方程相加(减)时,一定要把两个方程两边分别相加(减).(3)求解解消元后的一元一次方程求出一个未知数的值(4)回代把求得的未知数的值代入方程组中某个较简单的方程求出另一个未知数的值回代时选择系数较简单的方程(5)写解把两个未知数的值用大括号联立起来特别提醒:1.两个方程同一未知数的系数的绝对值相等或成倍数关系时,解方程组应考虑用加减消元法.2.如果同一未知数的系数的绝对值既不相等又不成倍数关系,我们应设法将一个未知数的系数的绝对值转化为相等关系.3.用加减法时,一般选择系数比较简单(同一未知数的系数的绝对值相等或成倍数关系)的未知数作为消元对象.【考点目录】【考点1】代入消元法解二元一次方程组;【考点2】加减消元法解二元一次方程组;【考点3】同解方程组;【考点4】整体思想解二元一次方程组;【考点5】求解二元一次方程组——错题复原问题;【考点6】求解二元一次方程组——参数问题;【考点7】构造二元一次方程组求解。
应用二元一次方程组——增收节支(知识梳理与考点分类讲解)-八年级数学上册基础知识专项突破讲与练

专题5.16应用二元一次方程组——增收节支(知识梳理与考点分类讲解)【知识点1】列二元一次方程组解决增收节支问题(1)增长(降低)率问题:增长(降低)率=增(减)量/基数×100%,增长(减少)后的数量=基数×【1±增长(降低)率】.(2)销售问题:销售额=售价×销量,总利润=总销售额-总成本=单件的利润×销量=(售价-进价)×销量,利润率=利润/进价×100%,打折后的价格=原价×折数÷10(3)储蓄问题:利息=本金×利率×期数.本息和=本金+利息.注意:在计算过程中要保持单位的统一.【特别提醒】1.对于增长(降低)率问题,审题时一定要看清是增长还是降低,而且要看准在哪一个量的基础上增长或降低,不要颠倒.2.在储蓄问题中注意利率要根据期数而定,期数是按月算的,利率就用月利率,期数是按年算的,利率就用年利率.【考点目录】【考点1】方案问题;【考点2】行程问题;【考点3】工程问题;【考点4】销售与利润问题.【考点一】方案问题【例1】(2022上·广东深圳·八年级校考期末)现欲将一批荔枝运往外地销售,若用2辆A型车和1辆B型车载满荔枝一次可运走10吨;1辆A型车和2辆B型车载满荔枝一次可运走11吨.现有荔枝31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题::(1)1辆A型车和1辆B型车都载满荔枝一次可分别运送多少吨?(2)请你帮该物流公司设计租车方案.【答案】(1)1辆A 型车载满荔枝一次可运送3吨,1辆B 型车载满荔枝一次可运送4吨;(2)该物流公司共有3种租车方案,方案1:租用9辆A 型车,1辆B 型车;方案2:租用5辆A 型车,4辆B 型车;方案3:租用1辆A 型车,7辆B 型车.【分析】(1)设1辆A 型车载满荔枝一次可运送x 吨,1辆B 型车载满荔枝一次可运送y 吨,由“用2辆A 型车和1辆B 型车载满荔枝一次可运走10吨;1辆A 型车和2辆B 型车载满荔枝一次可运走11吨”,列出二元一次方程组,解方程组即可得出结论;(2)由“现有荔枝31吨,计划同时租用A 型车a 辆,B 型车b 辆,一次运完,且恰好每辆车都载满荔枝”,列出二元一次方程,结合a 、b 均为非负整数,即可得出各租车方案.(1)解:设1辆A 型车载满荔枝一次可运送x 吨,1辆B 型车载满荔枝一次可运送y 吨,由题意得:210211x y x y +=⎧⎨+=⎩,解得:34x y =⎧⎨=⎩,答:1辆A 型车载满荔枝一次可运送3吨,1辆B 型车载满荔枝一次可运送4吨;(2)由题意得:3431a b +=,∴3143b a -=,又∵a 、b 均为非负整数,∴91a b =⎧⎨=⎩或54a b =⎧⎨=⎩或17a b =⎧⎨=⎩,∴该物流公司共有3种租车方案,方案1:租用9辆A 型车,1辆B 型车;方案2:租用5辆A 型车,4辆B 型车;方案3:租用1辆A 型车,7辆B 型车.【点拨】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程.【举一反三】【变式1】(2023下·黑龙江齐齐哈尔·七年级统考期末)五四青年节某校举办歌咏比赛,为鼓励本班同学们积极参加,刘老师花了48元钱买了甲、乙两种(两种都买)碳素笔作为奖品.已知甲种碳素笔每支6元,乙种碳素笔每支4元,则老师购买碳素笔的方案共有()A .4种B .3种C .2种D .1种【答案】B 【分析】本题考查了二元一次方程的应用,设刘老师购买x 本甲种碳素笔,y 本乙种碳素笔,利用总价=单价⨯数量,可得出关于x ,y 的二元一次方程,结合x ,y 均为正整数,即可得出张老师购买碳素笔的方案共有3种.解:设刘老师购买x 本甲种碳素笔,y 本乙种碳素笔,根据题意得:6448x y +=,∴3122y x =- ,x y 是正整数,∴29x y =⎧⎨=⎩或46x y =⎧⎨=⎩或63x y =⎧⎨=⎩∴刘老师购买碳素笔的方案共有3种.故选:B .【变式2】(2023下·山东烟台·七年级统考期中)五一小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为.【答案】26【分析】设1艘大船可载x 人,1艘小船可载y 人,依题意:1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.列出二元一次方程组,求出x y +的值即可.解:设1艘大船可载x 人,1艘小船可载y 人,依题意得:232246x y x y +=⎧⎨+=⎩①②,①+②得:3378x y +=,26x y ∴+=,即1艘大船与1艘小船一次共可以满载游客的人数为26,故答案为:26.【点拨】此题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.【考点二】行程问题【例2】(2023下·重庆渝中·七年级重庆市求精中学校校考期中)甲乙两地相距240千米,一辆小车和一辆摩托车分别从甲、乙两地同时出发相向而行,1小时20分两车相遇.相遇后,摩托车继续前进,小车在相遇处停留1个小时后调头按原速返回甲地,小车在返回后半小时追上了摩托车,(1)求小车和摩托车的速度.(2)求相遇后,摩托车继续行驶多少小时两车相距30千米?【答案】(1)小汽车和摩托车速度分别为135千米/小时,45千米/小时;(2)23小时或76小时或116小时或103小时【分析】(1)小车的速度为x 千米/时,摩托车的速度为y 千米/时,利用路程=速度⨯时间,结合两车速度间的关系,可得出关于x ,y 的二元一次方程组,解之即可得出小车和摩托车的速度;(2)设相遇后,摩托车继续行驶m 小时两车相距30千米,利用路程=速度⨯时间,结合两车相距30千米,可得出关于m 的一元一次方程,解之即可得出结论.(1)解:1小时20分43=小时.设小车的速度为x 千米/时,摩托车的速度为y 千米/时,根据题意得:4()240311(1)22x y x y ⎧+=⎪⎪⎨⎪=+⎪⎩,解得:13545x y =⎧⎨=⎩.答:小车的速度为135千米/时,摩托车的速度为45千米/时;(2)设相遇后,摩托车继续行驶m 小时两车相距30千米,根据题意得:4530m =或45135(1)30m m --=或135(1)4530m m --=或4524030m =-,解得:23m =或7m 6=或116m =或143m =.答:相遇后,摩托车继续行驶23小时或76小时或116小时或103小时两车相距30千米.【点拨】本题考查了一元一次方程的实际应用,解题的关键是对于(2)要用分类讨论的思想求解,注意不要漏解.【举一反三】【变式1】(2023下·贵州·七年级校联考阶段练习)甲、乙两地相距880km ,小轿车从甲地出发2h 后,大客车从乙地出发相向而行,又经过4h 两车相遇.已知小轿车比大客车每小时多行20km ,设大客车每小时行km x ,小轿车每小时行km y ,则可列方程组为()A .20,64880x y x y -=⎧⎨+=⎩B .20,64880y x y x -=⎧⎨+=⎩C .880,6420y x y x -=⎧⎨+=⎩D .20,46880y x y x -=⎧⎨+=⎩【答案】B 【分析】设大客车每小时行km x ,小轿车每小时行km y ,根据小轿车比大客车每小时多行20千米,甲车行驶2小时,两车相向行驶4小时共走了880千米,据此列方程组求解.解:设大客车每小时行km x ,小轿车每小时行km y ,由题意得:2064880y x y x -=⎧⎨+=⎩,故选:B .【点拨】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.【变式2】(2023下·云南曲靖·七年级统考期末)从甲地到乙地有一段上坡路与一段平路,如果上坡每小时走3km ,平路每小时走4km ,下坡每小时走5km ,那么从甲地到乙地需要36分钟,从乙地到甲地需要24分钟,甲地到乙地全程是多少?根据题意,老师给出的方程组为363460245460x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,则方程组中x 表示.【答案】从甲地到乙地的上坡路程【分析】设从甲地到乙地的上坡路为km x ,平路为km y ,根据保持上坡每小时走3km ,平路每小时走4km ,下坡每小时走5km ,那么从甲地到乙地用36分钟,从乙地到甲地用24分钟即可列出方程组363460245460x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,据此解答即可.解:设从甲地到乙地的上坡路为km x ,平路为km y ,依题意得363460245460x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,∴方程组中x 表示从甲地到乙地的上坡路程,故答案为:从甲地到乙地的上坡路程.【点拨】根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.【考点三】工程问题【例3】(2022下·河北石家庄·七年级校考阶段练习)现有一段长为180米的河道整治任务由A ,B 两个工程队先后接力完成.A 工程队每天整治12米,B 工程队每天整治8米,共用时20天.(1)根据题意,甲列出的方程组为20128180x y x y +=⎧⎨+=⎩,,分析甲所列的方程组,请指出未知数x ,y 表示的意义,x 表示,y 表示;(2)若设A 工程队共整治河道m 米,B 工程队共整治河道n 米,请根据题意列出二元一次方程组,并求出m ,n 的值.【答案】(1)A 工程队整治河道的天数;B 工程队整治河道的天数;(2)18020128m n m n +=⎧⎪⎨+=⎪⎩;60,120【分析】(1)根据所列的方程组,结合题意,作答即可;(2)根据有一段长为180米的河道整治任务由A ,B 两个工程队先后接力完成,得到180m n +=,根据共用时20天得到:20128m n +=,即可得出方程组,再求解即可.(1)解:由题意和所列方程组可知:x 表示A 工程队整治河道的天数,y 表示:B 工程队整治河道的天数,故答案为:A 工程队整治河道的天数;B 工程队整治河道的天数;(2)设A 工程队共整治河道m 米,B 工程队共整治河道n 米,由题意,得:18020128m n m n +=⎧⎪⎨+=⎪⎩,解得:12060m n =⎧⎨=⎩.即m ,n 的值分别为60,120.【点拨】本题考查二元一次方程组的实际应用,找准等量关系,正确的列出方程组是解题的关键.【举一反三】【变式1】(2021上·四川巴中·八年级四川省巴中中学校考期中)某污水处理厂库池里现有待处理的污水m 吨.另有从城区流入库池的待处理污水(新流入污水按每小时n 吨的定流量增加).若该厂同时开动2台机组,需30小时处理完污水;若同时开动3台机组,需15小时处理完污水.若5小时处理完污水,则需同时开动的机组数为()A .6台B .7台C .8台D .9台【答案】B【分析】设同时开动x 台机组,每台机组每小时处理a 吨污水,根据“如果同时开动2台机组要30小时刚好处理完污水,同时开动3台机组要15小时刚好处理完污水”,即可得出关于m ,n 的二元一次方程组,解之即可得出m ,n 的值(用含a 的代数式表示),再由5小时内将污水处理完毕,即可得出关于关于x 的一元一次方程,解之可得出结论.解:设同时开动x 台机组,每台机组每小时处理a 吨污水,依题意,得2303031515a m n a m n ⨯=+⎧⎨⨯=+⎩,解得:30m a n a =⎧⎨=⎩,∵5ax =30a +5a ,∴x =7.答:要同时开动7台机组.故选:B .【点拨】本题考查的是用二元一次方程组来解决实际问题,正确的理解题意是解题的关键.【变式2】(2020上·重庆万州·八年级校考期中)一水池有一个进水管和三个完全相同的出水管,现水池中有一定量的水,打开进水管(注水速度一致),若只打开一个出水管,则1小时正好能把水池中的水放完;若打开两个出水管,则20分钟正好能把水池中的水放完;问若打开三个出水管,则需要分钟恰好能把水池中的水放完.【答案】12【分析】设进水管的进水速度为x ,每一个出水管的出水速度为y ,水池中原有水量为a ,根据题意列方程组求解解:设进水管的进水速度为x ,每一个出水管的出水速度为y ,水池中原有水量为a ,由题意可得:1111233a x y a x y +⋅=⋅⎧⎪⎨+=⨯⎪⎩,解得:2x a y a =⎧⎨=⎩设打开三个出水管需要b 小时能把水池中的水放完,则3a xb b y+=⋅13325a ab y x a a ===-⨯-时=12分故答案为:12【点拨】本题考查二元一次方程组的应用,理解题意,正确列出等量关系求解是关键.【考点四】销售与利润问题【例4】(2023上·全国·八年级专题练习)为促进消费,某商家对商品进行打折促销.打折前,2件A 商品和1件B 商品的总售价为30元;1件A 商品和2件B 商品的总售价为33元.(1)求每件A 商品和每件B 商品的售价;(2)若两种商品的折扣相同,打折后,9件A 商品和8件B 商品共用了141.6元.求商家打几折出售这两种商品.【答案】(1)每件A 商品售价为9元,每件B 商品的售价为12元;(2)商家打8折出售这两种商品【分析】本题考查一元一次方程,二元一次方程组的应用.(1)设每件A 商品售价为x 元,每件B 商品的售价为y 元,根据2件A 商品和1件B 商品的总售价为30元;1件A 商品和2件B 商品的总售价为33元得解方程组求解即可;(2)设商家打m 折出售这两种商品,根据9件A 商品和8件B 商品共用了141.6元列方程求解即可.解:(1)设每件A 商品售价为x 元,每件B 商品的售价为y 元,根据题意得:230233x y x y +=⎧⎨+=⎩,解得912x y =⎧⎨=⎩,∴每件A 商品售价为9元,每件B 商品的售价为12元;(2)设商家打m 折出售这两种商品,根据题意得:99812141.61010m m ⨯⨯+⨯⨯=,解得8m =,答:商家打8折出售这两种商品.【举一反三】【变式1】(2023下·湖南益阳·七年级校考期中)五一节前夕,某超市用1680元购进A ,B 两种商品共60件,A 型商品每件24元,B 型商品每件36元,设购进A 型商品x 件,B 型商品y 件,依题意列方程组正确的是()A .3624601680x y x y +=⎧⎨+=⎩B .6024361680x y x y +=⎧⎨+=⎩C .6036241680x y x y +=⎧⎨+=⎩D .2436601680x y x y +=⎧⎨+=⎩【答案】B【分析】根据A 、B 两种商品共60件以及用1680元购进A 、B 两种商品,分别得出等式组成方程组即可.解:设购进A 型商品x 件,B 型商品y 件,根据题意,得6024361680x y x y +=⎧⎨+=⎩.故选:B【点拨】本题考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程组.【变式2】(2023下·河北秦皇岛·七年级统考期中)在当地农业技术部门的指导下,小明家种植的大棚油桃喜获丰收,去年大棚油桃的利润(利润=收入-支出)为12000元,今年大棚油桃的收入比去年增加了20%,支出减少了10%,预计今年的利润比去年多11400元,设小明家去年种植大棚油桃的收入为x 元,支出是y 元.依题意列方程组.【答案】12000(120%)(110%)1200011400x y x y -=⎧⎨+--=+⎩【分析】审题,明确等量关系,建立方程组.解:由题意知,今年收入为(120%)x +,今年支出(110%)y -,故12000(120%)(110%)1200011400x y x y -=⎧⎨+--=+⎩故答案为:12000(120%)(110%)1200011400x y x y -=⎧⎨+--=+⎩【点拨】本题考查二元一次方程组的应用,根据题意明确等量关系是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学《二元一次方程组》的知识点归纳
八年级数学《二元一次方程组》的知识点归纳
兴趣可以使人集中注意,如果要让学生感兴趣,教师就要饱含情感。
数学网编辑了八年级数学知识点:二元一次方程组,欢迎阅读!
1、二元一次方程
含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程。
2、二元一次方程的解
适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的.一个解。
3、二元一次方程组
含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组。
4二元一次方程组的解
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解。
5、二元一次方程组的解法
(1)代入(消元)法(2)加减(消元)法
6、一次函数与二元一次方程(组)的关系:
(1)一次函数与二元一次方程的关系:
直线y=kx+b上任意一点的坐标都是它所对应的二元一次方程
kx-y+b=0的解
当函数图象有交点时,说明相应的二元一次方程组有解;当函数图象(直线)平行即无交点时,说明相应的二元一次方程组无解。
