【最新】人教版八年级数学下册第十九章《 变量与函数》公开课课件.ppt
合集下载
人教版八年级数学下册《19.1.1 变量与函数》教学课件精品PPT优秀公开课4

解:(1)s = 80t
(2)y = 4x
根据以上式子你能总结出函数解析式的定义吗?
探究
知识点:函数解析式与函数值
1.函数解析式 用关于自变量的数学式子表示函数与自变 量之间的关系,是描述函数的常用方法,这种式子叫做函 数的解析式.
通常函数解析式等号右边的代数式中的变量是自000吨,每天发电用煤50吨,设发电 天数为 x,该发电厂开始发电后,储存煤量为 y 吨. 请写出 y 与 x 之间的函数解析式及自变量 x 的取值范围.
分析:运用等量关系“储存煤量=总储存煤量-用煤量”列函 数解析式.
解:每天发电用煤50吨,发电 x 天,则用煤量为 50x 吨. 发电前共储存煤1000吨,则发电 x 天后储存煤(1000-50x)吨. 因此 y 与 x之间的函数解析式为 y=-50x+1000(0≤x≤20).
拓展
1.李老师带着学生去科技馆参观,李老师的票价为 40 元,每 个学生的票价为 30 元,试写出李老师应带门票的总费用 y (元)和学生人数 x 之间的函数解析式.
解:根据题意,得 1 个学生的门票的单价是 30 元,则 x 个学生的门票总费用是 30x. 李老师应带的门票的总费用=李老师的门票费用 + 所有学 生的门票总费用,即 y = 40+30x.
2.甲乙两地相距 150 公里,张三驾驶私家车从甲地开往乙地,并且 以每小时 45 公里的速度匀速行驶,t 小时后张三距离乙地 s 公里, 请写出 s 和 t 的函数解析式,并计算 3 小时后,s 的值为多少?
分析:根据距离乙地的距离=甲乙两地之间的距离-张三已经行 驶的距离,列出函数解析式.
解:每小时行驶 45 公里,t 小时行驶了45t 公里.
人教版八年级下册数学课件:19.1.1变量和函数(共20张PPT)

时,重叠部分的面积是多少?
解 :设重叠部分面积为
y cm2,MA长为x cm
y与x之间的函数关系式为
当x=y1=时1 2,yx=21 12 1
2
2
1 答:MA=1cm时,重叠部分的面积是2 cm2
1.分别写出下列各问题中的函数关系式及自变量的取 值范围: (1).某市民用电费标准为每度0.50元,求电费
y(元)关于用电度数x的函数关系式; (2).已知等腰三角形的面积为20cm2,设它的底边长为x (cm),求底边上的高y(cm)关于x的函数关系式;
(3).在一个半径为10 cm的圆形纸片中剪去一个半径为r (cm)的同心圆,得到一个圆环.设圆环的面积为S (cm2),求S关于r的函数关系式.
2.一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的
y=10-x
对于问题1中的函数,当自变量x=3时,对应的函数y 的值y=10-3=7 ,则把7做这个函数当x=3时的函数值
例1 求下列函数中自变量x的取值范围:
(1) y=3x-1; (2) y=2x2+7;
(3) y=
1;
x2
(4) y= x 2 .
解:
(1)(2)中x取任意实数,3x-1,2x2 7
都有意义
(3)中,x≠-2时,原式有意义.
(4)中x≥2时,原式有意义.
巩固训练
1.求下列函数中自变量x的取值范围
(1)y=
5x 7 2
;(2)y=x2-x-2;
(3)y=
3 4x 8
;(4)y= x 3
答案:(1)(2)x为任意实数;
(3)x≠-2; (4)x≥-3
例2 在上面试一试的问题(3)中,当MA=1 cm
积
解 :设重叠部分面积为
y cm2,MA长为x cm
y与x之间的函数关系式为
当x=y1=时1 2,yx=21 12 1
2
2
1 答:MA=1cm时,重叠部分的面积是2 cm2
1.分别写出下列各问题中的函数关系式及自变量的取 值范围: (1).某市民用电费标准为每度0.50元,求电费
y(元)关于用电度数x的函数关系式; (2).已知等腰三角形的面积为20cm2,设它的底边长为x (cm),求底边上的高y(cm)关于x的函数关系式;
(3).在一个半径为10 cm的圆形纸片中剪去一个半径为r (cm)的同心圆,得到一个圆环.设圆环的面积为S (cm2),求S关于r的函数关系式.
2.一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的
y=10-x
对于问题1中的函数,当自变量x=3时,对应的函数y 的值y=10-3=7 ,则把7做这个函数当x=3时的函数值
例1 求下列函数中自变量x的取值范围:
(1) y=3x-1; (2) y=2x2+7;
(3) y=
1;
x2
(4) y= x 2 .
解:
(1)(2)中x取任意实数,3x-1,2x2 7
都有意义
(3)中,x≠-2时,原式有意义.
(4)中x≥2时,原式有意义.
巩固训练
1.求下列函数中自变量x的取值范围
(1)y=
5x 7 2
;(2)y=x2-x-2;
(3)y=
3 4x 8
;(4)y= x 3
答案:(1)(2)x为任意实数;
(3)x≠-2; (4)x≥-3
例2 在上面试一试的问题(3)中,当MA=1 cm
积
人教版数学八年级下册19.1.1《变量与函数》课件

在一个变化过程中,数值发 生变化的量为变量;数值始终 不变的量为常量。
闯关吧!少年!
第一关:简单!
指出下列问题中的变量和常量 1,某市的自来水价为4元/立方米。现要抽取若干户居民调查水费支出 情况,记某户月用水量为x立方米,月应交水费为y元。
变量是:月用水量为x、月应交水费为y;常量是:自来 水价为4元/立方米
2,某地手机通话费为0.2元/分钟。李明的手机通话时间为t分钟,话 费卡中的余额为m元(在这个过程中,李明没有充话费,也没有欠费 停机)。 变量:时间t、余额m;常量:通话费为0.2元/分钟
3,你有一本读物,是可以在学校合法看的,所以你每天读10页,已 经读了x天,还剩下y页未读。
变量:时间x天、读物剩余页数y;常量:每天的读书量10.
4,有10本书,我带走x本,还剩下y本。 变量:x、y;常量:10
第一关战后总结 你觉得,判断变量与常量的关键是什么?
数值变还是不变是判断变量与常 量的关键!
第二关:学校那点事儿
1,你有一本读物,是私下里跟其他同学借的,读的时候不能被 老师发现,你同学只给了你5天的时间,每天读得多少取决于自 习的多少以及课下我过来的多少,设你每天读x页,还剩余y页
(1)试分别写出长度变和不变的线段,面积变和不变的三角形。
长度不变的线段:AB、BC、CD、AD; 长度变的线段:AP、PD、PB、PC; 面积不变的三角形是:△PBC; 面积变的三角形是:△ABP、△PDC。
(2)若AP=x,BC=8,AB=4,求 S P C D 和 SPBC
SPCD
1 4(8 2
80
160
240
320 ...
请用时间t表示路程s:_s_=_8_0_t
第二关战后总结
八年级数学下册第19章一次函数19.1变量与函数19.1.1变量与函数课件(新版)新人教版

例2 下列变量间的关系是函数关系的是
.
①长方形的长与面积;②圆的面积与半径;
③y=± x ;④S= 1 ah中的S与h.
2
解析 ①因为长方形的长、宽、面积都不确定,有三个变量,所以长方
形的长与面积不是函数关系.②因为圆的面积公式为S=πr2,当半径r取一
个确定的值时,面积S就唯一确定,所以圆的面积与半径是函数关系.③当
解析 (1)根据函数的定义可知,对于底面半径的每个值,都有一个确定 的体积的值按照一定的法则与之相对应,所以自变量是底面半径,因变 量是体积. (2)体积增加了(π×102-π×12)×3=297π cm3.
2.(2018湖北咸宁咸安模拟)若函数y=
x
2
2(
x
2),
则当函数值y=8时,自
答案 B 把h=2代入T=21-6h,得T=21-6×2=9.故选B.
5.在函数y=3x+4中,当x=1时,函数值为 为10.
,当x=
时,函数值
答案 7;2
解析 当x=1时,y=3x+4=3×1+4=7.当函数值为10时,3x+4=10,解得x=2.
知识点三 自变量的取值范围
6.(2018江苏宿迁中考)函数y= 1 中,自变量x的取值范围是( )
知识点一 常量与变量 1.(2017河北唐山乐亭期中)一辆汽车以50 km/h的速度行驶,行驶的路程 s(km)与行驶的时间t(h)之间的关系式为s=50t,其中变量是 ( ) A.速度与路程 B.速度与时间 C.路程与时间 D.三者均为变量
答案 C 在s=50t中路程随时间的变化而变化,所以行驶时间是自变 量,行驶路程是因变量,速度为50 km/h,是常量.故选C.
【最新】人教版八年级数学下册第十九章《 19.1.1 变量与函数》公开课课件.ppt

(4) y的值随x的值的y=变1化0x而变化吗?
y的值随x的值的变化而变化
三、研读课文
3、你见过水中涟漪吗?圆形水波慢慢地扩大. 在这一过程中,当圆的半径分别为10 cm, 20 cm,30 cm时,圆的面积s分别为多少?s 的值随r的值的变化而变化吗?
当圆的半径为10cm时,面积为s=100πcm 2 ; 当圆的半径为20cm时,面积为s=400πcm 2 ; 当圆的半径为30cm时,面积为s=900πcm 2 .
随t 的值的变化而变化吗?
表19-1
t /h
1
2
3
4
5
s /km
60 12 180 240 30
0
0
(1)请同学们根据题意填写下表:
(2)在以上这个过程中,变化的是_时__间__t __, 不变化的量是__速__度__.
(3)试用含t的式子表示s 是_s_=_6_0_t__.
三、研读课文
2、每张电影票的售价为10元,如果第一场售出150 张票,第二场售出205张票,第三场售出310 张票, (1)第一场电影的票房收入 _____元;
长y随x的变化而变化,其中常量是_3_6___,变量是 __x_,__y_.
2、分别指出下列各式中的常量与变量.
(1)圆的面积公式S r2 ;
常量:π;变量:S、r
(2)正方形的周长 l 4a ;
常量:4;变量:l、 a (3)大米的单价为2.50元/千克,则购买的大米 的数量 x(kg)与金额y的关系为y=2.5x.
变量:t, w ; 常量:0.2 , 30
三、研读课文
(3)水中涟漪(圆形水波)不断扩大,记它的 半径为r,圆周长为C,圆周率(圆周长与直径的 比)为π.
y的值随x的值的变化而变化
三、研读课文
3、你见过水中涟漪吗?圆形水波慢慢地扩大. 在这一过程中,当圆的半径分别为10 cm, 20 cm,30 cm时,圆的面积s分别为多少?s 的值随r的值的变化而变化吗?
当圆的半径为10cm时,面积为s=100πcm 2 ; 当圆的半径为20cm时,面积为s=400πcm 2 ; 当圆的半径为30cm时,面积为s=900πcm 2 .
随t 的值的变化而变化吗?
表19-1
t /h
1
2
3
4
5
s /km
60 12 180 240 30
0
0
(1)请同学们根据题意填写下表:
(2)在以上这个过程中,变化的是_时__间__t __, 不变化的量是__速__度__.
(3)试用含t的式子表示s 是_s_=_6_0_t__.
三、研读课文
2、每张电影票的售价为10元,如果第一场售出150 张票,第二场售出205张票,第三场售出310 张票, (1)第一场电影的票房收入 _____元;
长y随x的变化而变化,其中常量是_3_6___,变量是 __x_,__y_.
2、分别指出下列各式中的常量与变量.
(1)圆的面积公式S r2 ;
常量:π;变量:S、r
(2)正方形的周长 l 4a ;
常量:4;变量:l、 a (3)大米的单价为2.50元/千克,则购买的大米 的数量 x(kg)与金额y的关系为y=2.5x.
变量:t, w ; 常量:0.2 , 30
三、研读课文
(3)水中涟漪(圆形水波)不断扩大,记它的 半径为r,圆周长为C,圆周率(圆周长与直径的 比)为π.
2021年人教版八年级数学下册第十九章《19.1.1 变量与函数(1)》公开课课件.ppt

作业:讲学稿上的相关练习。
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/92021/1/9Saturday, January 09, 2021
• 10、人的志向通常和他们的能力成正比例。2021/1/92021/1/92021/1/91/9/2021 3:34:30 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/92021/1/92021/1/9Jan-219-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/92021/1/92021/1/9Saturday, January 09, 2021 • 13、志不立,天下无可成之事。2021/1/92021/1/92021/1/92021/1/91/9/2021
在实际问题中,函数的自变量取值范围往往是有限 制的,在限制的范围内,函数才有实际意义;超出这个 范围,函数没有实际意义,我们把这种自变量可以取的 数值范围叫函数的自变量取值范围.
练一练
问题2 你能用含自变量的式子表示下列函数,并 说出自变量的取值范围吗?
(1)等腰三角形的面积为12,底边长为 x,底边上 的高为 y,y 随着 x 的变化而变化;
时间t/s 0 10 20 30 油温w/℃ 10 25 40 55
请你按下面的问题进行思考: (2)能写出w 与t 的函数解析式吗?
做一做
例2 小明想用最大刻度为100℃的温度计测量食用 油的沸点温度(远高于100℃),显然不能直接测量, 于是他想到了另一种方法,把常温10℃的食用油放在锅 内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一 次油温,共测量了4次,测得的数据如下:
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/92021/1/9Saturday, January 09, 2021
• 10、人的志向通常和他们的能力成正比例。2021/1/92021/1/92021/1/91/9/2021 3:34:30 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/92021/1/92021/1/9Jan-219-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/92021/1/92021/1/9Saturday, January 09, 2021 • 13、志不立,天下无可成之事。2021/1/92021/1/92021/1/92021/1/91/9/2021
在实际问题中,函数的自变量取值范围往往是有限 制的,在限制的范围内,函数才有实际意义;超出这个 范围,函数没有实际意义,我们把这种自变量可以取的 数值范围叫函数的自变量取值范围.
练一练
问题2 你能用含自变量的式子表示下列函数,并 说出自变量的取值范围吗?
(1)等腰三角形的面积为12,底边长为 x,底边上 的高为 y,y 随着 x 的变化而变化;
时间t/s 0 10 20 30 油温w/℃ 10 25 40 55
请你按下面的问题进行思考: (2)能写出w 与t 的函数解析式吗?
做一做
例2 小明想用最大刻度为100℃的温度计测量食用 油的沸点温度(远高于100℃),显然不能直接测量, 于是他想到了另一种方法,把常温10℃的食用油放在锅 内用煤气灶均匀地加热,开始加热后,每隔10 s 测量一 次油温,共测量了4次,测得的数据如下:
八年级数学下册 变量与函数 变量与函数课件新人教版

3 意义:学会用运动变化的观念去观察事物,从而建 立函数数学模型解决实际问题。
课后作业
作业:教科书第82~83页习题19.1 第5,10,11 题.
Thank you!
水平距离 t/cm
3.下列各曲线中不表示 y 是 x 的函数的是( 4 )
反思小结
本节课你有哪些收获?
1 函数概念: 一般地,在一个变化过程中,如果有两个变量
x 与y,并且对于 x 的每一个确定的值,y 都有唯一 确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
2 函数值:如果当x=a时y=b,那么b叫做当自变量的 值为a时的函数值。
3 (2)向一水池每分钟注水0.1 m3,注水量 y(单位: m3)
4
随注水时间 x(单位:min)的变化而变化;
交流分享、共同成长
2. 下图是一只不听话的蚂蚁在竖直的墙面上的爬行图, 请问:蚂蚁离地高度 h 是离起点的水平距离 t 的函数吗? 为什么? 离地高度 h/cm
6 5 4 3 2 1
1 2 34 5 6
19.1.1 变量与函数
第2课时 函数
万物皆变
• 学习目标
• 1.进一步体会运动变化过程中的数量变化; • 2.从典型实例中抽象概括出函数的概念,
了解 • 函数的概念.
• 学习重点: • • 概括并理解函数概念中的单值对应关系. •
设计问题、创设情景
1 什么是变量?什么是常量? 在一个变化过程中,我们称数值发生变
唯一
t s t 2.“我国人口数统计表中”,对于年份x的每一个值,人口数y都有
应,所以 是自变量, 是 的函数.
______的值与之对
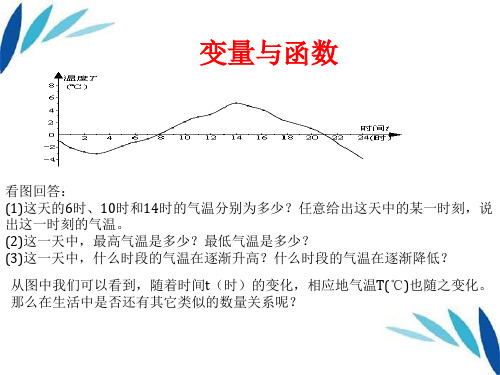
3.“某地一天的气温变化图”,对于时间t的每一个值,温度T就有____的值与之对应,所
课后作业
作业:教科书第82~83页习题19.1 第5,10,11 题.
Thank you!
水平距离 t/cm
3.下列各曲线中不表示 y 是 x 的函数的是( 4 )
反思小结
本节课你有哪些收获?
1 函数概念: 一般地,在一个变化过程中,如果有两个变量
x 与y,并且对于 x 的每一个确定的值,y 都有唯一 确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
2 函数值:如果当x=a时y=b,那么b叫做当自变量的 值为a时的函数值。
3 (2)向一水池每分钟注水0.1 m3,注水量 y(单位: m3)
4
随注水时间 x(单位:min)的变化而变化;
交流分享、共同成长
2. 下图是一只不听话的蚂蚁在竖直的墙面上的爬行图, 请问:蚂蚁离地高度 h 是离起点的水平距离 t 的函数吗? 为什么? 离地高度 h/cm
6 5 4 3 2 1
1 2 34 5 6
19.1.1 变量与函数
第2课时 函数
万物皆变
• 学习目标
• 1.进一步体会运动变化过程中的数量变化; • 2.从典型实例中抽象概括出函数的概念,
了解 • 函数的概念.
• 学习重点: • • 概括并理解函数概念中的单值对应关系. •
设计问题、创设情景
1 什么是变量?什么是常量? 在一个变化过程中,我们称数值发生变
唯一
t s t 2.“我国人口数统计表中”,对于年份x的每一个值,人口数y都有
应,所以 是自变量, 是 的函数.
______的值与之对
3.“某地一天的气温变化图”,对于时间t的每一个值,温度T就有____的值与之对应,所
人教版八年级下册数学第十九章《 19.1变量与函数》优课件(共28张PPT)

在问题三中,是否各有两个变量?同一 个问题中的变量之 间有什么联系?
问题三
在一根弹簧的下端挂重物,改变并记录重物的质量, 观察并记录弹簧长度的变化,探索它们的变化规律。如 果弹簧长原长为10cm,每1千克重物使弹簧伸长0.5cm,
怎样用含重物质量x(单位:kg)的式子表示受力后的
弹簧长度 L(单位:cm)?
八年级 数学
第十九章 一次函数
19.1.1变量与函数
解:∵花盆图案形如三角形,每边花有n个,总共有3n个, 其中重复了算3个。
∴ s 与 n 的函数关系式为: s = 3n-3
八年级 数学
第十九章 一次函数
19.1.1变量与函数 课堂练习(备用)
4、节约资源是当前最热门的话题,我市居民每月用电 不超过100度时,按0.57元/度计算;超过100度电时,其中不 超过100度部分按0.57元/度计算,超过部分按0.8元/度计算.
常量:在一个变化过程中,数值始终不变的量为常量。
请指出上面各个变化过程中的常量、变量。
八年级 数学
第十九章 一次函数
19.1 .1 变量与函数
探究:指出下列关系式中的变量与常量:
(1) y = 5x -6
6
(2) y= x
(3) y= 4x2+5x-7 (4) S = Лr2
巩固练习
• 填空:
• 1、计划购买50元的乒乓球,所能购买的总数
2.圆的周长公式C2r,这里的变量是 r和C ,常量
是 2 。
3.下列表格是王辉从4岁到10岁的体重情况
年龄(岁) 4 5 6 7 8 9
10 …
体重(千克)15.4 16.7 18.0 19.6 21.5 23.2 25.2 …
人教版数学八年级下册19.1.1变量与函数课件 (共21张PPT)

第2课时 函数
[解析] (1)中用-3x+1 表示 y,所以自变量 x 取全体实数;
2
2x-1
(2)中用x-1表示 y,所以 x-1≠0,故 x≠1;(3)中用 3+x 表
1 示 y,所以 3+x≠0 且 2x-1≥0,解得 x≥2;(4)因为 0≤y≤50,
所以 0≤x≤500.
第2课时 函数
第2课时 函数
2.已知三角形三边的长分别为 10 cm,7 cm,x cm,它的周长
为 y cm. (1)求 y 关于 x 的函数解析式;
C
(2)当 x=18 时,你能求出三角形的周长吗?为什么?
某同学的解答如下: 解:(1)y=10+7+x=17+x.
(2)能,当 x=18 时,y=17+18=35.
第2课பைடு நூலகம் 函数
探究新知
► 活动1 知识准备 甲、乙两地相距s千米,某人行驶完全程所用的时间t(时)与 他的速度v(千米/时)满足vt=s,在这个变化过程中,下列判断 中错误的是( A )
A.s是变量 B.t是变量 C.v是变量 D.s是常量
[解析] 因为两地间距离不变,所以s是常量.
第2课时 函数
课堂总结反思
[反思] 1.求函数 y= 2xx--11的自变量的取值范围. 解:由题意,得2xx--11≠≥00,,解得 x≥12且 x≠1,∴函数 y= 2xx--11的自变量的取值范围是 x≥12且 x≠1. 以上解答正确吗?若不正确,请分析错误原因,并给出正确答 案.
第2课时 函数
他的解答正确吗?为什么?如不正确,请你给出正确答案.
第2课时 函数
[答案] 不正确.理由:在实际问题中求函数解析式时,要求出 自变量的取值范围.
人教版八年级数学下册第十九章:19.1.1变量和函数 课件(共45张PPT)

数值不断 变化的量
变量
数值固定 不变的量
常量
例题
指出下列变化过程中的变量和常量:
(1)汽油的价格是7.4元/升,加油 x L,车主加油付油费 y 元; (2)小明看一本200 页的小说,看完这本小说需要t 天,平均每天 所看的页数为 n; (3)用长为40 cm 的绳子围矩形,围成的矩形一边长为 x cm,其 面积为 S cm2.
请你按下面的问题进行思考: (1)在这个测量过程中,锅中油的温度w 是加热时间t 的函数吗?
练习
小明想用最大刻度为100℃的温度计测量食用油的沸点温度(远高 于100℃),显然不能直接测量,于是他想到了另一种方法,把常 温10℃的食用油放在锅内用煤气灶均匀地加热,开始加热后,每隔 10 s 测量一次油温,共测量了4次,测得的数据如下:
这个问题中有几个变量 当?x取定一个值时,y有几个值与之对应 ?
两个 一个
观察思考 分析变化 (3)圆形水波慢慢地扩大,圆的半径为r,圆的面积为S.
这个问题中有几个变量 当?r取定一个值时,S有几个值与之对应 ?
两个 一个
观察思考 分析变化
(4)用10 m长的绳子围一个矩形,设矩形的一边长为 x,它的邻边长y.
观察思考 分析变化
补全下表:
(1)汽车以60 km/h 的速度匀速行驶,行驶的时间为t h,行 驶的路程为s km;
行驶时间 t/h
1
行驶里程s/km 60
3
3.4
4
9
……
180
204
240
540
……
这个问题中有几个变量 当?t取定一个值时,s有几个值与之对应 ?
两个 一个
观察思考 分析变化
人教版八年级数学下册 课件-19.1.1 变量和函数 (共16张PPT)

二、概括,形成概念
1、在上面四个问题的变化过程中,都有几个变 量?它们是如何变化的? 2、当其中一个变量的值确定之后另一个变量的 值确定吗?是唯一的吗?
二、概括,形成概念
1.定义:在一个变化过程中,如果有两个变量x和y,并 且对于x的每一个确定的值,y都有一个唯一确定的值与 其对应,我们就说x是自变量,y是x的函数,如果当x=a 时,y=b,那么b叫做当自变量的值为a时的函数值
(4).你能用一个式子表示这个关系吗?
一、四个问题
2、小王计划用火车运输的方式运输这批苹果。火车速
度为100千米每小时。形式路程s千米,行驶时间t小时
(1).填写下表:
时间 1
2
3
4
t
路程
(2).在这个过程中有几个变量?哪个变量主动变化?哪 个变量跟着发生改变? (3).当行驶时间确定时,行驶路程是唯一确定的吗?
2.函数的解析式:用关于自变量的数学式子表示函数与 自变量之间的对应关系。这种式子叫做函数的解析式
三、举例说明
函数是刻画变量之间对应关系的数学模型
1、你能举一个函数的例子吗?试试看! 2、和小组成员交流,判断一下,他的例子是函数吗? 3、我来举一个例子
三、举例说明
三、举例说明
科比投篮,篮球出 手后,篮球的高度 和时间是函数吗? 说说看!
四、巩固练习
1.课本74页练习题1. 2.一辆汽车油箱现有汽油50L,如果不再加油,那么油 箱中的油量y(L)随行驶里程x(km)的增加而减少, 平均耗油量为0.1L/km. (1)写出表示y与x的函数关系式. (2)指出自变量x的取值范围. (3)汽车行驶200km时,油箱中还有多少汽油?
五、当堂检测
(4).你能用一个式子表示这个关系吗?
人教版八年级下册课件 19.2 变量与函数 (共15张PPT)
变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其
对应,那么我们就说x是自变量,y是x的函数。
函数值的定义:如果当x=a时y=b,那么b叫做当自变量的值为a时
的函数值
(1) 行程问题:s=60t
t是自变量 , s是t的函数
(2) 票房收入问题 :y=10x
x是自变你与量能 函, 发 数y现 值是函 有x的数 什函数 么区别吗?
解:(1)常量是3000,-300;变量是x,y;自变量是 x;y是x的函数。
(2)常量是2;变量是x,y;自变量是x;y是x的函数。
(3)常量是π;变量是r,s;自变量是r;s是r的函数。
本节课学到哪些知识?
变量与函数
(1)在一个变化过程 中
没有发生变化的量 常量
发生变化的量
变量
(2)函数的定义:(包括y值的存在性和唯一性) 一般地,在一个变化过程中,如果有两个变量x与y, 并且对于x的每一个确定的值,y都有唯一确定的值与 其对应,那么我们就说x是自变量,y是x的函数。 (3)函数值的定义: 如果当x=a时y=b,那么b叫做当自变量的值为a时的 函数值
其中的一个变量取定一个值,另一个变量
的值也有唯一确定的对应值。
函数概念 一般地,在一个变化过程中,如果有两个变量
(假定为x和y),对于x的每一个确定的值,y都
有唯一确定的值与其对应,那么我们就说x是自变
量, y是x的函数.
一般地, 如果当x=a时,y=b,则b叫做当自变量为a时的函数值。
函数的定义:一般地,在一个变化过程中,如果有两个
函数是变量例如y=10+0.5x,y是随x的 变化而变化的量,L是m的函数,函数值 是一个变量所取的某个具体的数值.
《变量与函数》ppt完美课件

2
自变量x的取值范围 2<x≤5
《变量与函数》完美实用课件(PPT优 秀课件 )
解:时间T是自变量,水量V是T的函数 函数解析式为 V=10-0.05T
《变量与函数》完美实用课件(PPT优 秀课件 )
《变量与函数》完美实用课件(PPT优 秀课件 )
归纳
小结
1、一般地,在一个变化过程中,如果有两__个__
变量x和y,并且对于x
的
每一个确定的值
,y都有
_唯__一__确__定__的__值__与其对应,那么我们就说x
新课讲解
下列问题中哪些量是自变量?哪些量是自变量的 函数?试写出函数的解析式. (1)改变正方形的边长x,正方形的面积s随之 改变。
解:边长x是自变量 ,面积S是x的函数 函数解析式为 s=x2
(2)每分向一水池注水0.1m3,注水量y(单位: m3)随注水时间x(单位:min)的变化而变化。
解:时间x是自变量, 水量y是x的函数 函数解析式为 y=0.1x
(3) 汽车行驶200㎞时,油箱中还有多少汽油?
解:(1)y与x的函数关系式为y=_5_0_-_0_._1_x__
(2)因为x代表的实际意义为行驶路程,所以x不能
取 负数 .且行驶中的耗油量为 0.1x ,它不能超过油
箱中现有汽油量的值50,即
0.1x≤50
因此,自变量x
的取值范围是___0_≤___x__≤___5_0__
是
自变量
,y是x的 函数 。
2、如果当x=a时,y=b,那么 a 叫做当自变
量的值为 b 时的函数值.
3、用关于
自变量的式子 表示_变__量_____
之间的关系,这种式子叫做函数的解析式.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:时间x是自变量, 水量y是x的函数
函数解析式为 y=0.1x
(3)秀水村练的耕一地练面积是106㎡,这个村人
均占有耕地面积y(单位:㎡)随这个村人 数n的变化而变化。
解:人数n是自变量, 面积y是n的函数 函数解析式为 y= 106
n
(4)水池中有水10L,此后每小时漏水 0.05L,水池中的水量V(单位:L)随时间T (单位:t)的变化而变化。
• 10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 11:07:38 AM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/162020/12/162020/12/16Dec-2016-Dec-20 • 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/162020/12/162020/12/16Wednesday, December 16, 2020 • 13、志不立,天下无可成之事。2020/12/162020/12/162020/12/162020/12/1612/16/2020
解:时间T是自变量,水量V是T的函数
函数解析式为 V=10-0.05T
四、归纳小结
1、一般地,在一个变化过程中,如果有 两个变
量x和y,并且对于x的每一个确定的值 ,y都有
__唯__一__确_定__的__值__与其对应,那么我们就说x
是 自变量 ,y是x的 函数 。
2量、的如值果为当xa=a时时的,函y=数b值,. 那么
义.
三、研读课文
认真阅读课本第73至74页的 内容,完成下面练习并体验知识 点的形成过程。
s60t
三、研读课文
两变量之间的关系
知 思考 下列式子S=60t,y=10x,S=πr2, 识 C=5-x中存在几个变量?在同一个式子中 点 的变量之间有什么联系?
一
答:两个变量
归纳 每个问题中的 两个 变量互相联
答:是
归纳 一些用 图 或 表格 表达的问题中,
也能看到两个变量之间的联系.
三、研读课文
自变量和函数的概念
1、一般地,在一个变化过程中,如果有两个变量x和
知 识 点
y,并且对于x的每一个确定的值,y都有 唯一 确定
x y 的值与其对应,那么我们就说 是自变量,____
x 是
的函数.
如果当x=a时,y=b,那么b叫做当自变量的值为a时
形面积S关于x的函数解析式及自变量
x的取值范围。
解:函数解析式为S= 3(2 x)
即s=3+1.5x
2
自变量x的取值范围 2<x≤5
Thank you!
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/162020/12/16Wednesday, December 16, 2020
X
表示 X 与___Y__
之间的关系,这种式子叫做 函数 ,它是
描述函数的常用方法.
练一练:
下列问题中哪些量是自变量?哪些量是自变 量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积s随 之改变。
解:边长x是自变量 ,面积S是x的函数
函数解析式为 s=x2
(2)每分向一水池注水0.1m3,注水量y(单 位:m3)随注水时间x(单位:min)的变化 而变化。
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
系,当其中一个变量取定一个值时,另 一个变量就有唯一确定的值与其对应 。
三、研读课文
思考
(1)在心电图中,对于横坐标表示时间x的每一
个确定的值,纵坐标表示心脏部位的生物电流y
知
都有唯一确定的值与其对应吗?
识
答:有
点 (2)在我国人口数统计表中,对于每一个
一 确定的年份x,都对应着一个确定的人口数
y吗?
在(x3=)20汽0时车的行函驶数x=值20。0即时:,y 油=5箱0中-0的.汽1×油量2是00函=数_y__3=_05_0__-0.1x
答:汽车行驶200时,油箱中还有30L汽油.
三、研读课文
温馨提示:确定自变量的取值范围时
知
①要使 函数关系式 有意义.
识 点
②要符合 问题 的实际意义.
二Leabharlann 3、用关于自变量㎞ 平均耗油量为0.1L/ .
(1)写出表示y与x的函数关系式. (2)指出自变量x的取值范围.
㎞ (3) 汽车行驶200 时,油箱中还有多少汽油?
解: (1)y与x的函数关系式为y=_5_0_-__0_._1_x_ (2)因为x代表的实际意义为行驶路程,所以x不能取负数 .且 行驶中的耗油量为 0.1x,它不能超过油箱中现有汽油量的值50, 即0.1x≤50因此,自变量x的取值范围是__0_≤____x__≤___5_0__
二 的 函数值 .
2、在计算器中操作y=2x+5后填表:
x 1 2 -4 0 101 -5.2
y 7 9 -3 5 207 -5.4
显示的计算结果是输入数值的函数吗?为什么? 答:是,因为对于x的每一个确定的值,y都 有唯一确定的值与其对应。
练一练:
例1 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中 的油量y(单位:L)随行驶里程x(单位:千米)的增加而减少,
第十九章 函数 19.1.1变量与函数2
一、新课引入
购买一些铅笔,单价为0.2元/
支,总价y元随铅笔支数x变化,
指出其中的常量与变量,并用含
有x的式子表示y。
答:常量是0.2 ,变量是 x和y . 式子表示为 y=0.2x
二、学习目标
理解函数的概念,能准确识别 1 出函数关系中的自变量和函数;
确定函数中自变量的取值 2 范围,注意问题的实际意
b
叫做当自变
3、用关于自变量的式子表示 变量 之间的关
系,这种式子叫做函数的解析式.
4、学习反思:_____________________
_____________________
五、强化训练
1、在y=3x+1中,如果 x 是自变量, 那么 是yx的函数。
2、梯形的上底长2㎝,高3㎝,下底长
x㎝大于上底长但不超过5㎝。写出梯
函数解析式为 y=0.1x
(3)秀水村练的耕一地练面积是106㎡,这个村人
均占有耕地面积y(单位:㎡)随这个村人 数n的变化而变化。
解:人数n是自变量, 面积y是n的函数 函数解析式为 y= 106
n
(4)水池中有水10L,此后每小时漏水 0.05L,水池中的水量V(单位:L)随时间T (单位:t)的变化而变化。
• 10、人的志向通常和他们的能力成正比例。2020/12/162020/12/162020/12/1612/16/2020 11:07:38 AM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/162020/12/162020/12/16Dec-2016-Dec-20 • 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/162020/12/162020/12/16Wednesday, December 16, 2020 • 13、志不立,天下无可成之事。2020/12/162020/12/162020/12/162020/12/1612/16/2020
解:时间T是自变量,水量V是T的函数
函数解析式为 V=10-0.05T
四、归纳小结
1、一般地,在一个变化过程中,如果有 两个变
量x和y,并且对于x的每一个确定的值 ,y都有
__唯__一__确_定__的__值__与其对应,那么我们就说x
是 自变量 ,y是x的 函数 。
2量、的如值果为当xa=a时时的,函y=数b值,. 那么
义.
三、研读课文
认真阅读课本第73至74页的 内容,完成下面练习并体验知识 点的形成过程。
s60t
三、研读课文
两变量之间的关系
知 思考 下列式子S=60t,y=10x,S=πr2, 识 C=5-x中存在几个变量?在同一个式子中 点 的变量之间有什么联系?
一
答:两个变量
归纳 每个问题中的 两个 变量互相联
答:是
归纳 一些用 图 或 表格 表达的问题中,
也能看到两个变量之间的联系.
三、研读课文
自变量和函数的概念
1、一般地,在一个变化过程中,如果有两个变量x和
知 识 点
y,并且对于x的每一个确定的值,y都有 唯一 确定
x y 的值与其对应,那么我们就说 是自变量,____
x 是
的函数.
如果当x=a时,y=b,那么b叫做当自变量的值为a时
形面积S关于x的函数解析式及自变量
x的取值范围。
解:函数解析式为S= 3(2 x)
即s=3+1.5x
2
自变量x的取值范围 2<x≤5
Thank you!
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/162020/12/16Wednesday, December 16, 2020
X
表示 X 与___Y__
之间的关系,这种式子叫做 函数 ,它是
描述函数的常用方法.
练一练:
下列问题中哪些量是自变量?哪些量是自变 量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积s随 之改变。
解:边长x是自变量 ,面积S是x的函数
函数解析式为 s=x2
(2)每分向一水池注水0.1m3,注水量y(单 位:m3)随注水时间x(单位:min)的变化 而变化。
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
系,当其中一个变量取定一个值时,另 一个变量就有唯一确定的值与其对应 。
三、研读课文
思考
(1)在心电图中,对于横坐标表示时间x的每一
个确定的值,纵坐标表示心脏部位的生物电流y
知
都有唯一确定的值与其对应吗?
识
答:有
点 (2)在我国人口数统计表中,对于每一个
一 确定的年份x,都对应着一个确定的人口数
y吗?
在(x3=)20汽0时车的行函驶数x=值20。0即时:,y 油=5箱0中-0的.汽1×油量2是00函=数_y__3=_05_0__-0.1x
答:汽车行驶200时,油箱中还有30L汽油.
三、研读课文
温馨提示:确定自变量的取值范围时
知
①要使 函数关系式 有意义.
识 点
②要符合 问题 的实际意义.
二Leabharlann 3、用关于自变量㎞ 平均耗油量为0.1L/ .
(1)写出表示y与x的函数关系式. (2)指出自变量x的取值范围.
㎞ (3) 汽车行驶200 时,油箱中还有多少汽油?
解: (1)y与x的函数关系式为y=_5_0_-__0_._1_x_ (2)因为x代表的实际意义为行驶路程,所以x不能取负数 .且 行驶中的耗油量为 0.1x,它不能超过油箱中现有汽油量的值50, 即0.1x≤50因此,自变量x的取值范围是__0_≤____x__≤___5_0__
二 的 函数值 .
2、在计算器中操作y=2x+5后填表:
x 1 2 -4 0 101 -5.2
y 7 9 -3 5 207 -5.4
显示的计算结果是输入数值的函数吗?为什么? 答:是,因为对于x的每一个确定的值,y都 有唯一确定的值与其对应。
练一练:
例1 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中 的油量y(单位:L)随行驶里程x(单位:千米)的增加而减少,
第十九章 函数 19.1.1变量与函数2
一、新课引入
购买一些铅笔,单价为0.2元/
支,总价y元随铅笔支数x变化,
指出其中的常量与变量,并用含
有x的式子表示y。
答:常量是0.2 ,变量是 x和y . 式子表示为 y=0.2x
二、学习目标
理解函数的概念,能准确识别 1 出函数关系中的自变量和函数;
确定函数中自变量的取值 2 范围,注意问题的实际意
b
叫做当自变
3、用关于自变量的式子表示 变量 之间的关
系,这种式子叫做函数的解析式.
4、学习反思:_____________________
_____________________
五、强化训练
1、在y=3x+1中,如果 x 是自变量, 那么 是yx的函数。
2、梯形的上底长2㎝,高3㎝,下底长
x㎝大于上底长但不超过5㎝。写出梯
