估计水塔的水流量
历届美国数学建模竞赛赛题(汉语版)

历届美国数学建模竞赛赛题, 1985-2006AMCM1985问题-A 动物群体的管理AMCM1985问题-B 战购物资储备的管理AMCM1986问题-A 水道测量数据AMCM1986问题-B 应急设施的位置AMCM1987问题-A 盐的存贮AMCM1987问题-B 停车场AMCM1988问题-A 确定毒品走私船的位置AMCM1988问题-B 两辆铁路平板车的装货问题AMCM1989问题-A 蠓的分类AMCM1989问题-B 飞机排队AMCM1990问题-A 药物在脑内的分布AMCM1990问题-B 扫雪问题AMCM1991问题-A 估计水塔的水流量AMCM1992问题-A 空中交通控制雷达的功率问题AMCM1992问题-B 应急电力修复系统的修复计划AMCM1993问题-A 加速餐厅剩菜堆肥的生成AMCM1993问题-B 倒煤台的操作方案AMCM1994问题-A 住宅的保温AMCM1994问题-B 计算机网络的最短传输时间AMCM1995问题-A 单一螺旋线AMCM1995问题-B A1uacha Balaclava学院AMCM1996问题-A 噪音场中潜艇的探测AMCM1996问题-B 竞赛评判问题AMCM1997问题-A Velociraptor(疾走龙属)问题AMCM1997问题-B为取得富有成果的讨论怎样搭配与会成员AMCM1998问题-A 磁共振成像扫描仪AMCM1998问题-B 成绩给分的通胀AMCM1999问题-A 大碰撞AMCM1999问题-B “非法”聚会AMCM1999问题- C 大地污染AMCM2000问题-A空间交通管制AMCM2000问题-B: 无线电信道分配AMCM2000问题-C:大象群落的兴衰AMCM2001问题- A: 选择自行车车轮AMCM2001问题-B:逃避飓风怒吼(一场恶风…)AMCM2001问题-C我们的水系-不确定的前景AMCM2002问题-A风和喷水池AMCM2002问题-B航空公司超员订票AMCM2002问题-C蜥蜴问题AMCM2003问题-A: 特技演员AMCM2003问题-C航空行李的扫描对策AMCM2004问题-A:指纹是独一无二的吗?AMCM2004问题-B:更快的快通系统AMCM2004问题-C:安全与否?AMCM2005问题-A:.水灾计划AMCM2005问题-B:TollboothsAMCM2005问题-C:.Nonrenewable ResourcesAMCM2006问题-A:用于灌溉的自动洒水器的安置和移动调度AMCM2006问题-B:通过机场的轮椅AMCM2006问题-C:在与HIV/爱滋病的战斗中的交易AMCM85问题-A 动物群体的管理在一个资源有限,即有限的食物、空间、水等等的环境里发现天然存在的动物群体。
估计水塔的水流new

估计水塔的水流量New表1 水塔中水位原始数据>> t=[0 0.921 1.843 2.949 3.871 4.978 5.900...7.006 7.928 8.967 9.981 10.925 10.954 12.032...12.954 13.875 14.982 15.903 16.826 17.931 19.037...19.959 20.839 22.015 22.958 23.880 24.986 25.908];>> h=[9.677 9.479 9.308 9.125 8.982 8.814 8.686...8.525 8.388 8.220 0 0 10.820 10.500...10.210 9.936 9.653 9.409 9.180 8.921 8.662...8.433 8.220 0 10.820 10.591 10.354 10.180];>> D=17.4;>> V=pi/4*D^2*hV =1.0e+003 *Columns 1 through 92.3011 2.2540 2.2133 2.1698 2.1358 2.0959 2.0654 2.0271 1.9946Columns 10 through 181.9546 0 02.5729 2.4968 2.4278 2.36272.2954 2.2373Columns 19 through 272.1829 2.1213 2.0597 2.0053 1.9546 0 2.5729 2.5184 2.4620Column 282.4207表2 水塔中水的体积>> t1=t(1:10);>> t2=t(13:23);>> t3=t(25:28);>> V1=V(1:10);>> V2=V(13:23);>> V3=V(25:28);>> v=-[gradient(V1,t1),gradient(V2,t2),gradient(V3,t3)]v =Columns 1 through 951.1204 47.6090 41.5072 38.2242 36.4474 34.6895 33.8858 34.9411 36.9837Columns 10 through 1838.4487 70.5862 72.5251 72.7683 65.3094 61.7918 60.9942 57.2190 55.7095Columns 19 through 2557.2190 58.3251 57.5553 59.0599 54.6395 48.1906 44.8752表3 水塔中水流速度(近似为用水速度)>> t=[t1 t2 t3];>> ti=0:0.01:25.908;>> vi=interp1(t,v,ti,'spline');>> plot(t,v,'+',ti,vi,'g')0510********>> ti=0:0.01:24;>> vi=interp1(t,v,ti,'spline');>> I=trapz(ti,vi)I =1.2560e+003稳定性分析:>> ti=0.2:0.01:24.2;>> vi=interp1(t,v,ti,'spline');>> I=trapz(ti,vi)I =1.2565e+003>> ti=0.4:0.01:24.4;>> vi=interp1(t,v,ti,'spline');>> I=trapz(ti,vi)I =1.2567e+003>> ti=1:0.01:25;>> vi=interp1(t,v,ti,'spline'); >> I=trapz(ti,vi)I =1.2572e+003检验:第一段用水量>> ti=0:0.01:8.967;>> vi=interp1(t,v,ti,'spline'); >> I1=trapz(ti,vi)I1 =345.2792第二段用水量>> ti=10.954:0.01:20.839; >> vi=interp1(t,v,ti,'spline'); >> T2=trapz(ti,vi)T2 =618.3992第三段用水量>> ti=22.958:0.01:25.908; >> vi=interp1(t,v,ti,'spline'); >> I3=trapz(ti,vi)I3 =152.0959水泵第一次充水时用水量>> ti=8.967:0.01:10.954; >> vi=interp1(t,v,ti,'spline'); >> I=trapz(ti,vi)I =107.6730水泵第二次充水时用水量>> ti=20.839:0.01:22.958; >> vi=interp1(t,v,ti,'spline'); >> I=trapz(ti,vi)I =123.9158。
案例6 估计水塔水流量

f ( t )dt 335329 (加仑) f ( t )dt 336480 (加仑)
25.5 1.5
相差只约1%
[0,24]区间内检验
第一次充水 前总用水量 第一次充水后, 第二次充水前 总用水量 第一次充水 期间用水量 第二次充水 期间用水量
V1= 606125-514872=91253(加仑)
充水时间约为2.1189小时
3. 由Vi—ti关系产生水流量 fi—ti的关系
注:亦可以由Vi—ti关系拟合 V(t),再求微商得到 f(t)
关于水流量 fi
Vi 1 Vi f i f (t i ) t i 1 t i V i V i 1 与 f i f (t i ) t i t i 1
水体积的误差为0.5% 用样条逼近的用水量其误差可用抽样计算得5.1%
一天 总量 误差
2 2 2 2 SV [ SV0 SV8.9678 SV p SV10.9542 SV20.8392
1
2 2 2 2 SV p SV 22.9581 SV23.88 SV[ 23.88 , 24 ] ]1 2
水泵工作的时间为32284秒(8.9678 小时); 水泵结束时间为39435秒(10.9542小时); 充水时间约为1.9864小时
水泵工作的时间为75021秒(20.8392 小时),水 位26.97英尺 第 二 次 充 水 水泵结束时间为82649秒(22.9581小时), 补充水位35.50英尺
水流量值(表3)
时
(小时)
间
水 流 量
(加仑/小时)
时
(小时)
间
水流量
(加仑/小时)
时
估计水塔的水流量
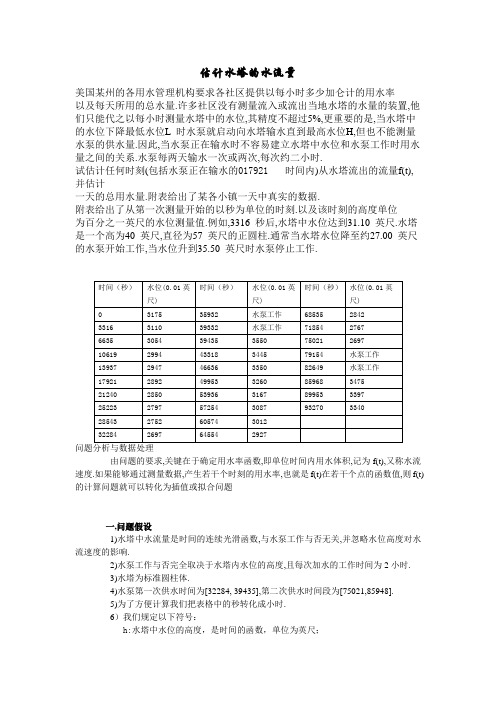
估计水塔的水流量美国某州的各用水管理机构要求各社区提供以每小时多少加仑计的用水率以及每天所用的总水量.许多社区没有测量流入或流出当地水塔的水量的装置,他们只能代之以每小时测量水塔中的水位,其精度不超过5%,更重要的是,当水塔中的水位下降最低水位L 时水泵就启动向水塔输水直到最高水位H,但也不能测量水泵的供水量.因此,当水泵正在输水时不容易建立水塔中水位和水泵工作时用水量之间的关系.水泵每两天输水一次或两次,每次约二小时.试估计任何时刻(包括水泵正在输水的017921 时间内)从水塔流出的流量f(t),并估计一天的总用水量.附表给出了某各小镇一天中真实的数据.附表给出了从第一次测量开始的以秒为单位的时刻.以及该时刻的高度单位为百分之一英尺的水位测量值.例如,3316 秒后,水塔中水位达到31.10 英尺.水塔是一个高为40 英尺,直径为57 英尺的正圆柱.通常当水塔水位降至约27.00 英尺的水泵开始工作,当水位升到35.50 英尺时水泵停止工作.问题分析与数据处理由问题的要求,关键在于确定用水率函数,即单位时间内用水体积,记为f(t),又称水流速度.如果能够通过测量数据,产生若干个时刻的用水率,也就是f(t)在若干个点的函数值,则f(t)的计算问题就可以转化为插值或拟合问题一,问题假设1)水塔中水流量是时间的连续光滑函数,与水泵工作与否无关,并忽略水位高度对水流速度的影响.2)水泵工作与否完全取决于水塔内水位的高度,且每次加水的工作时间为2小时.3)水塔为标准圆柱体.4)水泵第一次供水时间为[32284, 39435],第二次供水时间段为[75021,85948].5)为了方便计算我们把表格中的秒转化成小时.6)我们规定以下符号:h:水塔中水位的高度,是时间的函数,单位为英尺;v:水塔中水的体积,是时间的函数,单位为加仑; t:时间,单位为小时;f:模型估计的水塔水流量,是时间的函数,单位为加仑/小时p:水泵工作时的充水水流量,也是时间的函数,单位为加仑/小时。
水塔流量估计的数学建模

水塔流量估计的数学建模1. 引言水塔是现代城市供水系统中至关重要的组成部分,其作用是通过储存水源来保障城市居民日常用水,并且在有紧急情况时提供应急用水。
为了更好地保障全社会的用水需求,并降低供水系统建设和运营成本,对水塔的流量进行准确的估计和预测具有重要意义。
本文将探讨如何利用数学建模的方法对水塔流量进行估计和预测。
2. 水塔流量的影响因素水塔流量的大小受到多种因素的影响,主要包括以下几个方面:2.1 水塔容积水塔的容积越大,其流量也就越大。
因此,在进行水塔流量估计时,首先需要考虑其容积。
2.2 外部水压水塔的流量受到外部水压的影响。
如果外部水压较大,则水塔的流量也将较大。
2.3 水泵功率水泵功率的大小直接影响到水塔的流量大小。
水泵功率越大,水塔的流量也就越大。
2.4 关阀状态水塔流量还受到管道关阀状态的影响。
如果关阀状态较大,则水塔流量也将减小。
3. 水塔流量的数学建模方法水塔流量的数学建模方法主要包括以下几个步骤:3.1 收集数据收集水塔流量的相关数据,并对其进行初步的整理和分析。
3.2 设计建模方程根据已收集到的数据,设计合适的建模方程。
建模方程需要考虑到水塔容积、外部水压、水泵功率、关阀状态等多种因素。
3.3 参数估计利用已有的数据对建模方程中的参数进行估计。
参数估计是非常重要的一步,其准确性直接影响到模型的准确性和可靠性。
3.4 模型检验和优化使用已有的数据来对所建立的模型进行检验和优化。
检验过程中需要对模型的精度、准确性、鲁棒性等进行评估,如果出现问题,需要进行适当的调整。
4. 案例分析为了说明水塔流量估计的数学建模方法,我们以某市几座水塔为例进行分析。
4.1 收集数据在该市的几座水塔中,我们选取了其中一座水塔进行了数据的收集,主要包括该水塔的容积、水泵功率、外部水压等基本信息。
4.2 设计建模方程根据收集到的数据,我们设计了一个基础的建模方程,其中各项参数分别为:Q为流量,V为水塔容积,P为外部水压,H为水泵的扬程,K为关阀系数。
水塔水流量的估计

水塔水流量的估计一.实验问题某居民区有一供居民用水的圆柱形水塔,一般可以通过测量其水位来估计水的流量。
但面临的困难是,当水塔水位下降到设定的最低水位时,水泵自动启动向水塔供水,到设定的最高水位时停止供水,这段时间无法测量水塔的水位和水泵的供水量。
通常水泵每天供水一次,每次约2h。
水塔是一个高为12.2m,直径为17.4m的正圆柱。
按照设计,水塔水位降至约8.2m时,水泵自动启动,水位升到约10.8m时水泵停止工作。
表1是某一天的水位测量纪录(符号“//”表示水泵启动),试估计任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量。
表1 水位测量纪录二.问题分析根据以上数据的形式和以往经验,适合采用线性拟合的方式进行数据处理。
对第1、2、3未供水时段可直接进行用五次多项式进行拟合。
对第1、2供水时段分别在两端各取两个点用前后时刻的流速拟合得到。
结果可以用分段函数表示分为5段,分别是第一未供水时段,第一供水时段,第二未供水时段,第二供水时段,第三未供水时段。
得出流速之后再乘以水塔横截面积即得任何时刻与水塔流出水流量的关系,即流速与时间的关系。
对流速进行分段积分并求和,即得一天的总水流量。
三.程序的设计与求解方法1.数据的单位转换水塔的横截面积为A=(17.4)^2*pi/4=237.0661(平方米)。
2.拟合水位——时间函数(1)对第1未供水时段的数据进行拟合。
t=[0 0.92 1.84 2.90 3.87 4.98 5.90 7.00 7.93 8.97 10.95 12.03 12.95 13.88 14.98 15.90 16.83 17.93 19.04 19.96 20.84 23.88 24.99 25.91]h=[ 9.68 9.48 9.31 9.13 8.98 8.81 8.69 8.52 8.39 8.22 10.82 10.50 10.21 9.94 9.65 9.41 9.18 8.92 8.66 8.43 8.22 10.59 10.35 10.18] f1=polyfit(t(1:10),h(1:10),5); tm1=0:0.1:9.0; y1=polyval(f1,tm1); plot(tm1,y1)01234567898.28.48.68.899.29.49.69.8(2)对第2未供水时段的数据进行拟合。
水塔水流量估计问题
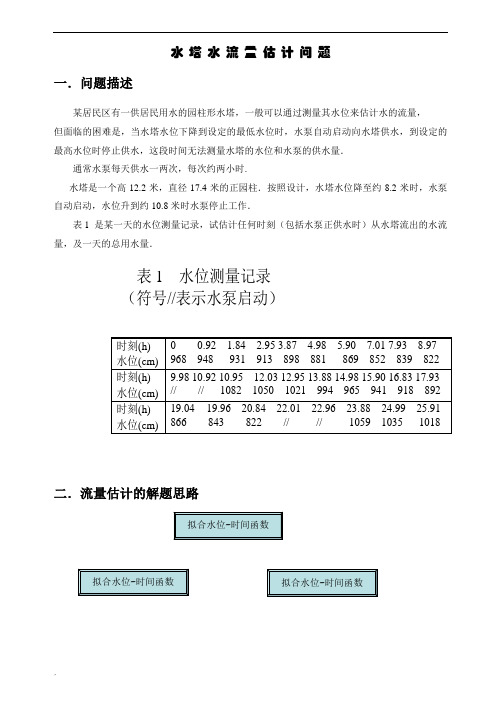
水塔水流量估计问题一.问题描述某居民区有一供居民用水的园柱形水塔,一般可以通过测量其水位来估计水的流量,但面临的困难是,当水塔水位下降到设定的最低水位时,水泵自动启动向水塔供水,到设定的最高水位时停止供水,这段时间无法测量水塔的水位和水泵的供水量.通常水泵每天供水一两次,每次约两小时.水塔是一个高12.2米,直径17.4米的正园柱.按照设计,水塔水位降至约8.2米时,水泵自动启动,水位升到约10.8米时水泵停止工作.表1 是某一天的水位测量记录,试估计任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量.表1 水位测量记录(符号//表示水泵启动)二.流量估计的解题思路1.拟合水位~时间函数测量记录看,一天有两个供水时段(以下称第1供水时段和第2供水时段),和3个水泵不工作时段(以下称第1时段t=0到t=8.97,第2次时段t=10.95到t=20.84和第3时段t=23以后)。
对第1、2时段的测量数据直接分别作多项式拟合,得到水位函数.为使拟合曲线比较光滑,多项式次数不要太高,一般在3~6.由于第3时段只有3个测量记录,无法对这一时段的水位作出较好的拟合。
2.确定流量~时间函数对于第1、2时段只需将水位函数求导数即可,对于两个供水时段的流量,则用供水时段前后(水泵不工作时段)的流量拟合得到,并且将拟合得到的第2供水时段流量外推,将第3时段流量包含在第2供水时段内. 3.一天总用水量的估计总用水量等于两个水泵不工作时段和两个供水时段用水量之和,它们都可以由流量对时间的积分得到。
三.算法设计与编程1、拟合第1时段的水位,并导出流量设t ,h 为已输入的时刻和水位测量记录(水泵启动的4个时刻不输入),第1时段各时刻的流量可如下得:1) c1=polyfit (t (1:10),h (1:10),3);%用3次多项式拟合第1时段水位,c1输出3次多项式的系数2)a1=polyder (c1);% a1输出多项式(系数为c1)导数的系数3)tp1=0:0.1:9;x1=-polyval (a1,tp1);% x1输出多项式(系数为a1)在tp1点的函数值(取负后边为正值),即tp1时刻的流量4)流量函数为:1079.227173.22356.0)(2-+-=t t t f2、拟合第2时段的水位,并导出流量设t ,h 为已输入的时刻和水位测量记录(水泵启动的4个 时刻不输入),第2时段各时刻的流量可如下得: 1) c2=polyfit(t(10.9:21),h(10.9:21),3);%用3次多项式拟合第2时段水位,c2输出3次多项式的系数2) a2=polyder(c2);% a2输出多项式(系数为c2)导数的系数3)tp2=10.9:0.1:21;x2=-polyval(a2,tp2); % x2输出多项式(系数为a2)在tp2点的函数值(取负后边为正值),即tp2时刻的流量4)流量函数为:1994.349045.152173.10284.0)(23+-+-=t t t t f3、拟合供水时段的流量在第1供水时段(t=9~11)之前(即第1时段)和之后(即第2时段)各取几点,其流量已经得到,用它们拟合第1供水时段的流量.为使流量函数在t=9和t=11连续,我们简单地只取4个点,拟合3次多项式(即曲线必过这4个点),实现如下:xx1=-polyval(a1,[8 9]);%取第1时段在t=8,9的流量xx2=-polyval(a2,[11 12]);%取第2时段在t=11,12的流量xx12=[xx1 xx2];c12=polyfit([8 9 11 12],xx12,3);%拟合3次多项式tp12=9:0.1:11;x12=polyval(c12,tp12);% x12输出第1供水时段各时刻的流量拟合的流量函数为:在第2供水时段之前取t=20,20.8两点的流水量,在该时刻之后(第3时段)仅有3个水位记录,我们用差分得到流量,然后用这4个数值拟合第2供水时段的流量如下:dt3=diff(t(22:24));%最后3个时刻的两两之差dh3=diff(h(22:24));%最后3个水位的两两之差dht3=-dh3./dt3;%t(22)和t(23)的流量t3=[20 20.8 t(22) t(23)];1.10785049.3368448.341731.1)(23+-+-=ttttfxx3=[-polyval(a2,t3(1:2)),dht3];%取t3各时刻的流量c3=polyfit(t3,xx3,3);%拟合3次多项式tp3=20.8:0.1:24;x3=polyval(c3,tp3);% x3输出第2供水时段(外推至t=24)各时刻的流量拟合的流量函数为:4、一天总用水量的估计第1、2时段和第1、2供水时段流量的积分之和,就是一天总用水量.虽然诸时段的流量已表为多项式函数,积分可以解析地算出,这里仍用数值积分计算如下:y1=0.1*trapz(x1);%第1时段用水量(仍按高度计),0.1为积分步长y2=0.1*trapz(x2);%第2时段用水量y12=0.1*trapz(x12);%第1供水时段用水量y3=0.1*trapz(x3);%第2供水时段用水量8.44966844.6158430.274181.0)(23-+-=ttttfy=(y1+y2+y12+y3)*237.8*0.01; %一天总用水量 (L m 1033)计算结果:y1=146.1815, y2=266.4409, y12=48.5004, y3=74.8064,y=1274.45、流量及总用水量的检验计算出的各时刻的流量可用水位记录的数值微分来检验.用水量y1可用第1时段水位测量记录中下降高度968-822=146来检验,类似地,y2用1082-822=260检验.供水时段流量的一种检验方法如下:供水时段的用水量加上水位上升值260是该时段泵入的水量,除以时段长度得到水泵的功率(单位时间泵入的水量),而两个供水时段水泵的功率应大致相等.第1、2时段水泵的功率可计算如下:p1=(y12+260)/2; %第1供水时段水泵的功率(水量仍以高度计) tp4=20.8:0.1:23;xp2=polyval (c3,tp4); % xp2输出第2供水时段各时刻的流量 p2=(0.1*trapz(xp2)+260)/2.2;%第2供水时段水泵的功率(水量仍以高度计) 计算结果:p1=154.2502 ,p2=142.3670四.计算结果(3,4)流量函数为:(56)流量函数为:画图(n1,n2)y1 y2 y12 y3 y p1 p2 (3,4) 146.1815 266.4409 48.5004 74.8064 1274.4 154.2502 142.3670 (5,6) 146.5150 265.5417 46.1317 72.6057 1262.2 153.0659 141.4479⎪⎪⎩⎪⎪⎨⎧≤≤-+-<≤+-+-<≤+-+-<≤-+-=24218.44966844.6158430.274181.021111.10785049.3368448.341731.11191994.349045.151.21730284.091079.227173.22356.0)(2323232tttttttttttttttt f⎪⎪⎩⎪⎪⎨⎧≤≤-+<≤++-<≤+++-<≤-++-=24214.3551490.560022.3526-3382.021114974.362112.7045-11.80653930.01198447.20.8873-0.10780.0065-0.00020.000098296.235.71081.5878-0.22240120.0)(23232345234tttttttttttttttttttt fn=(3,4)n=(5,6)。
数学建模估计水塔的流量用数学软件求解拟合问题

算法设计与编程
1. 拟合第1、2时段的水位,并导出流量
2. 拟合供水时段的流量
3. 估计一天总用水量
4. 流量及总用水量的检验
1. 拟合第1时段的水位,并导出流量 设t,h为已输入的时刻和水位测量记录(水泵启动的4个时刻不输入),第1时段各 时刻的流量可如下得: 1) c1=polyfit(t(1:10),h(1:10),3); %用3次多项式拟合第1时段水位,c1输出3次多项式的系数 2)a1=polyder(c1); % a1输出多项式(系数为c1)导数的系数
m 3 103 L
MATLAB(llgjz)
4. 流量及总用水量的检验
计算出的各时刻的流量可用水位记录的数值微分来检验.用水量y1可用第1时段水位测 量记录中下降高度968-822=146来检验,类似地,y2用1082-822=260检验. 供水时段流量的一种检验方法如下:供水时段的用水量加上水位上升值 260是该时段泵入 的水量,除以时段长度得到水泵的功率(单位时间泵入的水量),而两个供水时段水泵的 功率应大致相等.第1、2时段水泵的功率可计算如下: p1=(y12+260)/2; %第1供水时段水泵的功率 (水量仍以高度计) tp4=20.8:0.1:23; xp2=polyval(c3,tp4); % xp2输出第2供水时段 各时刻的流量 p2=(0.1*trapz(xp2)+260)/2.2; %第2供水时段水泵的功率 (水量仍以高度计) 计算结果:p1=154.5 ,p2=140.1
用非线性最小二乘拟合c(t)-用lsqcurvefit
1. 用M文件curvefun3.m定义函数
function f=curvefun3(x,tdata) d=300 f=(x(1)\d)*exp(-x(2)*tdata) % x(1)=v; x(2)=k
水塔流量估计的数学建模

水塔流量估计的数学建模水塔是城市供水系统中的重要组成部分,它们储存着大量的水资源,为城市居民提供生活用水。
在城市供水系统中,水塔的流量是一个非常重要的参数,它直接影响着供水系统的运行效率和水资源的利用率。
因此,如何准确地估计水塔的流量是一个非常重要的问题。
水塔的流量估计可以通过数学建模来实现。
首先,我们需要了解水塔的基本结构和工作原理。
水塔通常由水箱、进水管、出水管、溢流管等组成。
当水箱内的水位下降时,进水管会自动打开,将外部的水源引入水箱中,同时出水管会自动关闭,防止水箱内的水流失。
当水箱内的水位上升到一定高度时,溢流管会自动打开,将多余的水流出水箱,以保持水箱内的水位稳定。
在水塔的运行过程中,我们可以通过测量进水管和出水管的水流速度来估计水塔的流量。
根据流量的定义,流量等于单位时间内通过某一截面的液体体积。
因此,我们可以通过测量进水管和出水管的截面积和水流速度来计算水塔的流量。
具体地,假设进水管的截面积为A1,出水管的截面积为A2,进水管的水流速度为v1,出水管的水流速度为v2,则水塔的流量Q可以表示为:Q = A1v1 - A2v2其中,A1v1表示进水管的流量,A2v2表示出水管的流量。
由于进水管和出水管的截面积和水流速度可能会随着时间的变化而发生变化,因此我们需要不断地对它们进行测量和调整,以保证水塔的流量估计的准确性。
除了测量进水管和出水管的水流速度外,我们还可以通过其他的方法来估计水塔的流量。
例如,我们可以通过测量水塔内部的水位变化来估计水塔的流量。
具体地,我们可以安装水位传感器在水塔内部,通过测量水位的变化来计算水塔的流量。
这种方法的优点是不需要对进水管和出水管进行测量,但是需要安装水位传感器,成本较高。
水塔流量估计的数学建模是一个非常重要的问题。
通过测量进水管和出水管的水流速度或者测量水塔内部的水位变化,我们可以准确地估计水塔的流量,从而保证城市供水系统的正常运行。
估计水塔的水流量
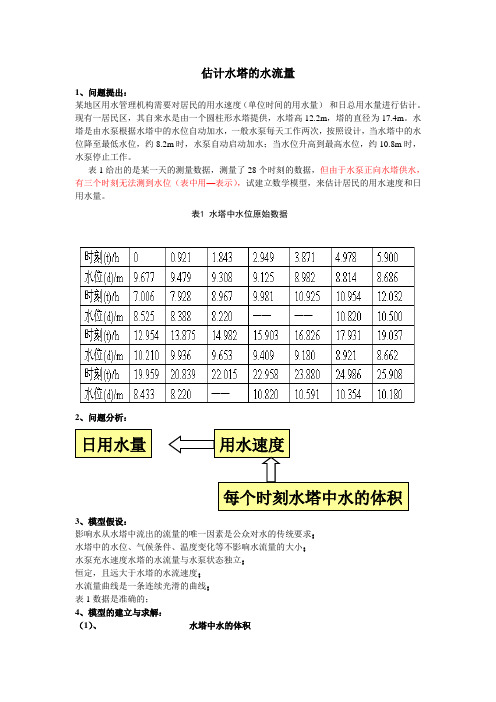
估计水塔的水流量1、问题提出:某地区用水管理机构需要对居民的用水速度(单位时间的用水量)和日总用水量进行估计。
现有一居民区,其自来水是由一个圆柱形水塔提供,水塔高12.2m,塔的直径为17.4m。
水塔是由水泵根据水塔中的水位自动加水,一般水泵每天工作两次,按照设计,当水塔中的水位降至最低水位,约8.2m时,水泵自动启动加水;当水位升高到最高水位,约10.8m时,水泵停止工作。
表1给出的是某一天的测量数据,测量了28个时刻的数据,但由于水泵正向水塔供水,有三个时刻无法测到水位(表中用—表示),试建立数学模型,来估计居民的用水速度和日用水量。
表1 水塔中水位原始数据2、问题分析:日用水量用水速度每个时刻水塔中水的体积3、模型假设:影响水从水塔中流出的流量的唯一因素是公众对水的传统要求;水塔中的水位、气候条件、温度变化等不影响水流量的大小;水泵充水速度水塔的水流量与水泵状态独立;恒定,且远大于水塔的水流速度;水流量曲线是一条连续光滑的曲线;表1数据是准确的;4、模型的建立与求解:(1)、水塔中水的体积其中, ,(r 为底面半径,d 为水面高度)(2)在Matlab 命令窗口直接运行(不包括未知三点)>>t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,10.954,12.032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.959,20.839,22.958,23.880,24.986,25.908];>>v=[2301.1,2254,2213.3,2169.8,2135.8,2095.9,2065.4,2027.1,1994.6,1954.6,2572.9,2496.8,2427.8,2362.7,2295.4,2237.3,2182.9,2121.3,2059.7,2005.3,1954.6,2572.9,2518.4,2462.0,2420.7]; >> scatter(t,v)得到水塔中水体积的散点图 0510********19002000210022002300240025002600(3)在Matlab 中编写脚本文件(不包括未知三点)采用数值微分的一阶微商的两点公式(末位处近似为sd(n)=sd(n-1))t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,10.954,12.032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.959,20.839,22.958,23.880,24.986,25.908];v=[2301.1,2254,2213.3,2169.8,2135.8,2095.9,2065.4,2027.1,1994.6,1954.6,2572.9,2496.8,2427.8,2362.7,2295.4,2237.3,2182.9,2121.3,2059.7,2005d r V 2π=.3,1954.6,2572.9,2518.4,2462.0,2420.7];for i=1:9sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));endsd(10)=sd(9);for i=11:20sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));endsd(21)=sd(20);for i=22:24sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));endsd(25)=sd(24);scatter(t,sd)hold onplot(t,sd)得到水塔中水流速度的散点图及光滑图0510********(4)预测水塔中的未知流速[1]在Matlab中运行脚本文件(不包括未知三点):采用数值微分的一阶微商的两点公式(末位处近似为sd(n)=sd(n-1))t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,10.954,12. 032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.959,20.839,22 .958,23.880,24.986,25.908];v=[2301.1,2254,2213.3,2169.8,2135.8,2095.9,2065.4,2027.1,1994.6,1954. 6,2572.9,2496.8,2427.8,2362.7,2295.4,2237.3,2182.9,2121.3,2059.7,2005 .3,1954.6,2572.9,2518.4,2462.0,2420.7];for i=1:9sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));endsd(10)=sd(9);for i=11:20sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));endsd(21)=sd(20);for i=22:24sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));endsd(25)=sd(24);sd得到速度(不包括未知三点)sd =Columns 1 through 951.1401 44.1432 39.3309 36.8764 36.0434 33.0803 34.6293 35.2495 38.4986Columns 10 through 1838.4986 70.5937 74.8373 70.6840 60.7949 63.0836 58.9382 55.7466 55.6962Columns 19 through 2559.0022 57.6136 57.6136 59.1106 50.9946 44.7939 44.7939 [2]采用拉格朗日插值法估计未知三点的速度:在Matlab命令窗口直接运行>> x0=[7.928,8.967];>> y0=[38.4968,38.4968];>> lglr3(x0,y0,9.981)ans =38.4968>> x0=[8.967,9.981];>> y0=[38.4968,38.4968];>> lglr3(x0,y0,10.925)ans =38.4968>> x0=[19.959,20.839];>> y0=[57.6136,57.6136];>> lglr3(x0,y0,22.015)ans =57.6136[3]在Matalb中运行脚本文件t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,9.981,10.9 25,10.954,12.032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.959,20.839,22.015,22.958,23.880,24.986,25.908];sd=[51.1401,44.1432,39.3309,36.8764,36.0434,33.0803,34.6293,35.2495,3 8.4986,38.4968,38.4968,38.4986,70.5937,74.8373,70.6840,60.7949,63.083 6,58.9382,55.7466,55.6962,59.0022,57.6136,57.6136,57.6136,59.1106,50. 9946,44.7939,44.7939];scatter(t,sd)hold onplot(t,sd)得到水塔中水流速度的散点图及光滑图(new)757065605550454035300510********(4)a、通过曲线拟合,拟合出上述函数(f1)b、通过数值积分(梯形,辛普森)求出用水量(f2)5、模型检验:应该另外测试一批数据检验模型(f1,f2)6、模型分析:(1) 4.(3)中末位处近似为sd(n)=sd(n-1)可以改进,比如先采用数值微分求1----(n-1)的速度,再采用拉格朗日插值法求末位n的速度;(2)拉格朗日插值可以改用其他更为精确的插值法(3)数值微分法可以采用其他的更为精确的方法(而不是一阶微商的两点公式)(4) 4.(4)中的两部暂时不会(5)模型假设处可能有一些瑕疵7、附录:。
水塔流量问题(专业教学)

本科生课程设计报告
实习课程数值分析
学院名称管理科学学院
专业名称
学生姓名
学生学号
指导教师
实验地点
实验成绩
二〇一六年六月二〇一六年六月
估计水塔的水流量
摘要
水塔流量的估计是一个较为经典的数学建模问题,本问题最大的困难在于不知泵启动时水位的变化和向外水流的速度.解决该问题,先确定近似流速,利用中点数值求导公式计算出每个时间点出的流速,再利用插值与拟合计算出流速与时间的函数,对0到24小时积分可得总用水量,这是第一种方法.第二种方法,水泵没有开动时利用高度差计算用水量,水泵开动时利用积分,这样计算出的结果较为准确,2种方法比较,可得出误差.
关键词:中点数值求导;插值与拟合;积分
目录
第1章前言 (1)
1.1 内容及要求 (1)
1.2 研究思路及结构安排 (2)
第2章模型建立与求解 (3)
2.1模型假设 (3)
2.2确定近似流速 (3)
2.3 确定水泵启动时的流量及总流量曲线 (4)
2.4确定总用水量 (4)
第3章算法步骤 (6)
3.1 中点数值求导函数步骤及流程图 (6)
3.2 三次样条插值函数步骤及流程图 (7)
第4章算法实现 (7)
4.1 程序总体结构 (7)
4.2 源程序清单 (8)
4.3 程序运行 (12)
第5章误差分析 (15)
第6章模型的评价和改进 (16)
6.1 优点 (16)
6.2 缺点 (16)
6.3 模型的改进方向 (16)
参考文献 (16)。
估计水塔水流量的求解模型要点

估计水塔水流量的求解模型摘要由所给的题目可知,本问题是一个关于如何计算居民用水的问题,由题目给出的表格,可知不同时刻的水位,根据所要求的不同时刻水位的不同入手,此计算问题就可以转化为插值或拟合问题。
这里主要考虑采用插值的方法,可以利用MATLAB软件进行插值和曲线拟合计算并解决一些具体的实际问题。
根据题目建立模型并采用插值的方法进行求解,推算出任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量。
关键词:用水规律与水泵的工作功率原始数据用水规律与水泵的工作功率一、问题重述1.1基本情况某居民区有一供居民用水的圆柱形水塔,一般可以通过测量其水位来估计水的流量。
面临的困难是,当水塔水位下降到设定的最低水位时,水泵自动启动向水塔供水,到设定的最高水位的时候停止供水,这段时间无法测量水塔的水位和水泵的供水量。
通常水泵每天供水一两次,每次约3h. 已知水塔是一个高为12.2m,直径为17.4m的正圆柱。
1.2 所要解决的问题现在需要了解该居民区用水规律与水泵的工作功率。
按照设计,当水塔的水位降至最低水位,约8.2米时,水泵自动启动加水;当水位升高到一个最高水位,约10.8米时,水泵停止工作。
可以考虑采用用水率(单位时间的用水量)来反映用水规律,并通过间隔一段时间测量水塔里的水位来估算用水率。
表1是某一天的测量记录数据,测量了28个时刻,但是由于其中有4个时刻遇到水泵正在向水塔供水,而无水位记录(表中用符号//表示)。
所要解决的问题就是,要估计任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量。
表1水位测量记录(符号//表示水泵启动)二、问题背景1991年的美国大学生数学建模竞赛A题(AMCM1991A),由于它是水库调度、自来水管理、公共场所的人流量估计等问题的代表,因此有许多文献对其进行了研究,但一般都是采用差分与拟合的方法。
而由于居民何时用水是无法准确的预报的,可能引起的水位的变化是随机事件,因此,可以以水容量作为随机变量,建立一个随机数学模型,不仅可以给出了水塔流量函数,同时还可以讨论水容量函数的数学期望。
估计水塔的水流量(AMCM91

估计水塔的水流量(AMCM911.实验问题某地的用水管理机构要求各社区提供用水率(以每小时多少加仑计,英制单位下,1加仑=4.54596dm3,美制单位下,1加仑=3.78533dm3)以及每天所用的总用水量,但许多社区并没有测量流入或流出当地水塔的水量的设备,而只能以每小时测量水塔的水位代替,其精度在0.5%以内。
更为重要的是,无论什么时候,只要水塔中的水位下降到某一最低水位L时,水泵就启动向水塔重新充水直至某一最高水位H,但也无法得到水泵的供水量的测量数据。
因此,在水泵正在工作时,不容易建立水塔中水位与水泵工作时用水量之间的关系。
水泵每天向水塔充水一次或两次,每次大约2小时。
试估计在任何时候,甚至包括水泵正在工作的时间内从水塔流出的流量,并估计一天的总用水量。
水塔是一个垂直圆柱体,高为40英尺,直径为57英尺。
下表给出了某个小镇某一天的真实数据。
表:某小镇某天的水塔水位(1m=3.281英尺)2.实验分析2.1 计算中将流量定义为单位时间流出的水的高度乘以水塔横截面积。
2.2 把时间分成5段:第1未供水段、水泵开启第1段、第2未供水段、水泵开启第2段、第3未供水段。
2.3 先直接对第1、2、3未供水段进行5次曲线拟合。
2.4 再对得到的曲线分别求导,取得流速(即单位时间内流出的水的高度)。
2.5 水泵开启第1、2段,分别在两端各取两个点,用时刻流速进行拟合得到这两段的流速。
2.6 流速乘以水塔横截面积就得到任何时刻的水流量。
2.7 对其进行分段积分,求和得到一天的总水流量。
3.程序设计与求解方法3.1 对表中数据进行处理数据的单位转换:46636,49953,53936,57254,60574,64554,68535,71854,75021,85968,89953,932 70];y=[31.75,31.10,30.54,29.94,29.55,28.92,28.50,27.87,27.52,26.97,35.50, 34.45,33.50,32.67,31.56,30.81,30.12,29.27,28.42,27.67,26.97,34.75,33. 89,33.40];t=x/3600; %时间单位为小时h=y/3.281; %水位高度单位为米水塔横截面积为a=pi*(57/2)^2;3.2 对第1段未供水段进行5次拟合x1=t(1:10);y1=h(1:10);f1=polyfit(x1,y1,5);t1=0:0.01:t(10);h1=polyval(f1,t1);plot(x1,y1,'o',t1,h1,'k');xlabel('时间(h)');ylabel('水位(m)');title('第一未供水时段的时间水位图')3.3 对第2段未供水段进行5次拟合x2=t(11:21);y2=h(11:21);f2=polyfit(x2,y2,5);t2=t(11):0.01:t(21);h2=polyval(f2,t2);plot(x2,y2,'o',t2,h2,'r');xlabel('时间(h)');ylabel('水位(m)');title('第二未供水时段的时间水位图 ')3.4 对第3段未供水段进行5次拟合x3=t(22:24);y3=h(22:24);f3=polyfit(x3,y3,5);t3=t(22):0.01:t(24);h3=polyval(f3,t3);plot(x3,y3,'o',t3,h3,'r');xlabel('时间(h)');ylabel('水位(m)');title('第三未供水时段的时间水位图 '3.5 对1、2、3未供水段进行求导,得到流速,再乘以水塔横截面积得流量b1=polyder(f1);%求导b2=polyder(f2);%求导b3=polyder(f3);%求导g1=-polyval(b1,t1)*a;%流速值再乘以水塔横截面积得流量g11=-polyval(b1,x1)*a;g2=-polyval(b2,t2)*a;%流速值再乘以水塔横截面积得流量g22=-polyval(b2,x2)*a;g3=-polyval(b3,t3)*a;%流速值再乘以水塔横截面积得流量g33=-polyval(b3,x3)*a;plot(x1,g11,'*',t1,g1,'c') %第一未供水段时间流量图plot(t2,g2) %第二未供水段时间流量图plot(t3,g3) %第三未供水段时间流量图3.6 求水泵开启第一段的时间流量图,取那段的前后两端各两个点的流速进行拟合,再乘以水塔横截面积得流量。
水塔水流量问题的广义线性回归解法
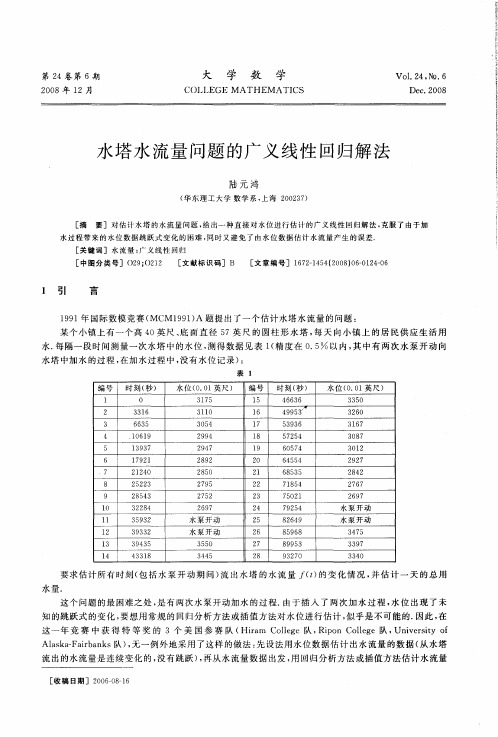
[ 摘
要] 对 估 计 水 塔 的 水 流 量 问 题 , 出一 种 直 接 对 水 位 进 行估 计 的 广义 线 性 回归 解 法 , 服 了 由于 加 给 克
水 过 程 带 来 的水 位 数 据 跳 跃 式 变 化 的 困难 , 时 又 避 免 了 由水 位 数 据 估 计 水 流 量 产 生 的 误 差. 同
知的跳跃 式 的变化 , 要想用 常规 的 回归分析 方法或插 值方 法对 水位进 行估计 , 似乎 是不 可能 的. 因此 , 在 这一年 竞 赛 中 获 得 特 等 奖 的 3个 美 国 参 赛 队 ( rm C l g Hi ol e队 , io olg a e R p n C l e队 , iest f e Unvri o y Als aF i a k 队 )无 一例 外地采 用 了这样 的做法 : ak — ar n s , b 先设 法用水 位数据 估 计 出水流 量 的数 据 ( 从水 塔
流 出的水 流量是 连续 变化 的 , 没有 跳跃 ) 再从 水流量 数据 出发 , 回归分析 方法 或插值 方法估 计水 流量 , 用
[ 稿 日期 ] 2 0—81 收 0 60—6
第 6期
陆元鸿 : 水塔 水 流量 问题 的广义 线性 回归解 法
15 2
- 的变 化. 们 的做法 , 厂 ) ( 他 虽然 也能 得 到问题 的解 , 是 , 于他 们 的水 流 量数 据 是估 计 出 来 的 , 但 由 比起 原 始数 据来 , 显然 多 了一重误 差 , 在此基 础 上再进 行 回归或 插值 , 结果 必然误 差很 大 , 以 , 样做 , 所 这 显然 不
为了简化 问题 , 我们 先不 考虑 加水 过程 , 假定 自始 至终 水塔 中只有 水流 出 , 没有 水加 入.
水塔水流量估计模型与数据插值总结

一
数据插值
给定n个数据点 ( x1 , y1 ), ( x2 , y2 ),, ( xn , yn ),
试求一个较为简单的函 数P ( x ),使得P ( x )满足 yi P ( xi ), i 1,2,, n
称P(x)为插值函数。也即求解一条严格通过各数 据点的曲线,用它来进行分析研究和预测,这种 方法常称为数据插值法。
称为牛顿插值公式,最后一项称为牛顿插值余项, 记为Rn(x),余项前的多式称为插值多项式,记 为Pn(x)。
牛顿插值多项式具有以下特点:
(1)在插值结点处与拉格朗日插值一样,误差 为零; (2)多项式k次项的系数是f(x)的k阶差商; (3)增加插值节点时,只增加最后一项,不必 像拉格朗日插值公式那样需要重新计算系数。 在做牛顿插值时,一般先做出差商表,然后套 用公式。
n 1 1
解为X A1Y .
可以证明,对于n+1个不同结点,必存在唯一的次 数不超过n的满足条件的多项式,这个多项式称为 插值多项式,这种方法称为n次多项式插值(或代 数插值。
为了以后使用方便,先编制一个Lagrange插值函数程序: function p=lagrange(x,y) L=length(x); A=ones(L); for j=2:L A(:,j)=A(:,j-1).*x'; end X=inv(A)*y'; for i=1:L p(i)=X(L-i+1); end
5
4
3
2
1
0
-1
1
1.5
2
2.5
3
3.5
4
4.5
5
从结果可以看到,所插值的4次多项式曲线较好地连接了5个 数据点,从而可以用此多项式曲线作为这5个数据的一个近 似变化。
(完整word版)计算水塔水流量(word文档良心出品)

一、课程设计目的:1.训练学生灵活应用所学数值分析知识,独立完成问题分析,结合数值分析理论知识,编写程序求解指定问题。
2.初步掌握解决实际问题过程中的对问题的分析、系统设计、程序编码、测试等基本方法和技能;3.提高综合运用所学的理论知识和方法独立分析和解决问题的能力;4.训练用数值分析的思想方法和编程应用技能模拟解决实际问题,巩固、深化学生的理论知识,提高学生对数值分析的认知水平和编程水平,并在此过程中培养他们严谨的科学态度和良好的工作作风二、课程设计任务与要求:课程设计题目:计算水塔的水流量【问题描述】某居民区的民用自来水是由一个圆柱形的水塔提供,水塔高12.2米,直径17.4米。
水塔是由水泵根据水塔内水位高低自动加水,一般每天水泵工作两次,现在需要了解该居民区用水规律与水泵的工作功率。
按照设计,当水塔的水位降至最低水位,约8.2米时,水泵自动启动加水;当水位升高到一个最高水位,约10.8米时,水泵停止工作。
可以考虑采用用水率(单位时间的用水量)来反映用水规律,并通过间隔一段时间测量水塔里的水位来估算用水率,原始数据表是某一天的测量记录数据,测量了28个时刻,但是由于其中有3个时刻遇到水泵正在向水塔供水,而无水位记录。
试建立合适的数学模型,推算任意时刻的用水率、一天的总用水量。
进一步:可自己增加一些新的计算功能。
【问题假设】1.水塔中水流量是时间的连续光滑函数,与水泵工作与否无关,并忽略水位高度对水流速度的影响。
2.水泵工作与否完全取决于水塔内水位的高度。
3.水塔为标准的圆柱体。
体积V=PI*D*D*h/4 其中D为底面直径,h为水位高。
4.水泵第一次供水时间段为[8.967,10.954],第二次供水时间段为[20.839,22.958]。
【实验数据】原始数据(单位:时刻(小时),水塔中水位(米))【实现提示】由问题的要求,关键在于确定用水率函数,即单位时间内用水体积,记为f(t),又称水流速度。
数学建模基础 12.4估计水塔的水流量

(**)
2
对于第一型插值问题,取 λ 0=1,μ n=1,
6 y1 y0 d0 ( y0 ' ), h1 h1
yn yn1 6 dn ( yn ' ) hn hn
对于第二型插值问题,取λ 0=0,μ n=0
d0 2 y0 ' ' ,
dn 2 yn ' '
对于第三型插值问题,利用周期性,可导出
10619
13937 17921
2994
2947 2892
43318
46636 49953
3445
3350 3260
79154
82649 85968
水泵工作
水泵工作 3475
21240
25223 28543
2850
2797 2752
53936
57254 60574
3167
3087 3012
89953
三次样条插值问题加上第i型边界条件称为第i型插值问题( i=1,2,3).可以证明第 i 型插值问题的解是存在且唯 一的。他们对应如下的三对角方程组: 2 λ 0 μ1 2 λ 1 . . . . . . . . . μ n-1 2 λ μ
n
n-1
M0 M1 . . = . Mn-1 Mn
d0 d1 . . . dn-1 dn
, M i+1
三次样条函数的构造
S”(x) M i
构造三次样条插值函数的方法有很多,这里介绍一个常用 的方法:三弯矩插值法 记Mi = S″(xi), f(xi)= fi= yi ,考虑它在任一区间[xi,xi+1]上的 形式.根据三次样条的定义可知 ,S(x)的二阶导数S″(x)在每一个 子区间[xi,xi+1] ( i=0,1,2,,n-1)上都是线性函数. 于是在[xi,xi+1] 上S(x)=Si(x)的二阶导数表示成
水塔水流量估计

答卷编号(参赛学校填写):答卷编号(竞赛组委会填写):论文题目: 98年A组别:本科参赛队员信息(必填):参赛学校:承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):估计水塔的流量一、问题重述某居民区有一供居民用水的圆柱形水塔,一般可以通过测量其水位来估计水的流量,但面临的困难是,当水塔水位下降到设定的最低水位时,水泵自动启动向水塔供水,到设定的最高水位时停止供水,这段时间无法测量水塔的水位和水泵的供水量.通常水泵每天供水一两次,每次约两小时.水塔是一个高12.2米,直径17.4米的正圆柱.按照设计,水塔水位降至约8.2米时,水泵自动启动,水位升到约10.8米时水泵停止工作.表1 是某一天的水位测量记录,试估计任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量.二、模型假设1、假设该水塔为标准的圆柱形。
2、水塔的流量只取决水塔内水位的差值,与其水位的高低无关且该流量应看做连续光滑的变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
估计水塔的水流量
1、问题提出:
某地区用水管理机构需要对居民的用水速度(单位时间的用水量)和日总用水量进行估计。
现有一居民区,其自来水是由一个圆柱形水塔提供,水塔高12.2m,塔的直径为17.4m。
水塔是由水泵根据水塔中的水位自动加水,一般水泵每天工作两次,按照设计,当水塔中的水位降至最低水位,约8.2m时,水泵自动启动加水;当水位升高到最高水位,约10.8m时,水泵停止工作。
表1给出的是某一天的测量数据,测量了28个时刻的数据,但由于水泵正向水塔供水,有三个时刻无法测到水位(表中用—表示),试建立数学模型,来估计居民的用水速度和日用水量。
表1 水塔中水位原始数据
2、问题分析:
日用水量用水速度
每个时刻水塔中水的体积
3、模型假设:
影响水从水塔中流出的流量的唯一因素是公众对水的传统要求;
水塔中的水位、气候条件、温度变化等不影响水流量的大小;
水泵充水速度水塔的水流量与水泵状态独立;
恒定,且远大于水塔的水流速度;
水流量曲线是一条连续光滑的曲线;
表1数据是准确的;
4、模型的建立与求解:
(1)、水塔中水的体积
其中, ,(r 为底面半径,d 为水面高度)
(2)在Matlab 命令窗口直接运行(不包括未知三点)
>>t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,10.954,12.032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.959,20.839,22.958,23.880,24.986,25.908];
>>v=[2301.1,2254,2213.3,2169.8,2135.8,2095.9,2065.4,2027.1,1994.6,1954.6,2572.9,2496.8,242
7.8,2362.7,2295.4,2237.3,2182.9,2121.3,2059.7,2005.3,1954.6,2572.9,2518.4,2462.0,2420.7]; >> scatter(t,v)
得到
水塔中水体积的散点图 0510********
1900
2000
2100
2200
2300
2400
2500
2600
(3)在Matlab 中编写脚本文件(不包括未知三点)
采用数值微分的一阶微商的两点公式(末位处近似为sd(n)=sd(n-1))
t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,10.954,12.032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.959,20.839,22.958,23.880,24.986,25.908];
v=[2301.1,2254,2213.3,2169.8,2135.8,2095.9,2065.4,2027.1,1994.6,1954.6,2572.9,2496.8,2427.8,2362.7,2295.4,2237.3,2182.9,2121.3,2059.7,2005d r V 2π=
.3,1954.6,2572.9,2518.4,2462.0,2420.7];
for i=1:9
sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));
end
sd(10)=sd(9);
for i=11:20
sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));
end
sd(21)=sd(20);
for i=22:24
sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));
end
sd(25)=sd(24);
scatter(t,sd)
hold on
plot(t,sd)
得到
水塔中水流速度的散点图及光滑图
0510********
(4)预测水塔中的未知流速
[1]在Matlab中运行脚本文件(不包括未知三点):
采用数值微分的一阶微商的两点公式(末位处近似为sd(n)=sd(n-1))
t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,10.954,12. 032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.959,20.839,22 .958,23.880,24.986,25.908];
v=[2301.1,2254,2213.3,2169.8,2135.8,2095.9,2065.4,2027.1,1994.6,1954. 6,2572.9,2496.8,2427.8,2362.7,2295.4,2237.3,2182.9,2121.3,2059.7,2005 .3,1954.6,2572.9,2518.4,2462.0,2420.7];
for i=1:9
sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));
end
sd(10)=sd(9);
for i=11:20
sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));
end
sd(21)=sd(20);
for i=22:24
sd(i)=abs((v(i+1)-v(i))/(t(i+1)-t(i)));
end
sd(25)=sd(24);
sd
得到
速度(不包括未知三点)
sd =
Columns 1 through 9
51.1401 44.1432 39.3309 36.8764 36.0434 33.0803 34.6293 35.2495 38.4986
Columns 10 through 18
38.4986 70.5937 74.8373 70.6840 60.7949 63.0836 58.9382 55.7466 55.6962
Columns 19 through 25
59.0022 57.6136 57.6136 59.1106 50.9946 44.7939 44.7939 [2]采用拉格朗日插值法估计未知三点的速度:
在Matlab命令窗口直接运行
>> x0=[7.928,8.967];
>> y0=[38.4968,38.4968];
>> lglr3(x0,y0,9.981)
ans =
38.4968
>> x0=[8.967,9.981];
>> y0=[38.4968,38.4968];
>> lglr3(x0,y0,10.925)
ans =
38.4968
>> x0=[19.959,20.839];
>> y0=[57.6136,57.6136];
>> lglr3(x0,y0,22.015)
ans =
57.6136
[3]在Matalb中运行脚本文件
t=[0,0.921,1.843,2.949,3.871,4.978,5.900,7.006,7.928,8.967,9.981,10.9 25,10.954,12.032,12.954,13.875,14.982,15.903,16.826,17.931,19.037,19.
959,20.839,22.015,22.958,23.880,24.986,25.908];
sd=[51.1401,44.1432,39.3309,36.8764,36.0434,33.0803,34.6293,35.2495,3 8.4986,38.4968,38.4968,38.4986,70.5937,74.8373,70.6840,60.7949,63.083 6,58.9382,55.7466,55.6962,59.0022,57.6136,57.6136,57.6136,59.1106,50. 9946,44.7939,44.7939];
scatter(t,sd)
hold on
plot(t,sd)
得到
水塔中水流速度的散点图及光滑图(new)
75
70
65
60
55
50
45
40
35
30
0510********
(4)a、通过曲线拟合,拟合出上述函数(f1)
b、通过数值积分(梯形,辛普森)求出用水量(f2)
5、模型检验:
应该另外测试一批数据检验模型(f1,f2)
6、模型分析:
(1) 4.(3)中末位处近似为sd(n)=sd(n-1)可以改进,比如先采用数值微分求1----(n-1)的速度,再采用拉格朗日插值法求末位n的速度;
(2)拉格朗日插值可以改用其他更为精确的插值法
(3)数值微分法可以采用其他的更为精确的方法(而不是一阶微商的两点公式)(4) 4.(4)中的两部暂时不会
(5)模型假设处可能有一些瑕疵
7、附录:。
