关于原点对称的点的坐标
关于原点对称的点的坐标 教案

学
过
程
及
内
容
【自主预习】探究新知
如图,在直角坐标系中,已知A(-3,1)、
B(-4,0)、C(0,3)、 D(2,2)、E(3,-3)、
F(-2,-2),作出A、B、C、D、E、F点关于
原点O的中心对称点,并写出它们的坐标,
并回答:这些坐标与已知点的坐标有什么
A
B
C
D
E
F
5
-5
-2
-3
-4
-1
3
2
课
后
反
思
过本节课的学习,主要让学生掌握两点关于原点对称的性质(它们对应的坐标互为相反数)及其运用,从学生课堂反映情况来看,学生对性质的应用较为熟练,掌握得较好,但部分学生对性质是如何得来,对性质探究过程中渗透数形结合思想甚为不解,这有待于在今后教学过程中有针对性地加以训练,有意识地多加强调。
重点
掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用
难点
掌握P(X,Y)关于原点的对称点为P’(-X,-Y)的运用
教学
准备
教学
过程
教学内容
师生活动
设计意图
创
设
情
境
引
入
新
课
【旧知回顾】
1.什么是平面直角坐标系?
2.怎样在平面直角坐标系内表示一个点的坐标?
3.点P(a,b)关于x轴的对称点的坐标,关于y轴对称点
学科
数学
教师
姓名
王顺
备课
时间
2017.9.29
课题
关于原点对称的点的坐标
课时
5
教
学
目
标
知
关于原点对称的点的坐标 优秀课件

运用新知
例 如图,利用关于原点对称的点的坐标的关系,作出与△ABC关于原点 Nhomakorabea称的图形.
y
解:由图知△ABC的三个顶点
5
A(-4,1) B(-1, -1) C(-3,2)
4
求得关于原点的对称点分别为
3
C
2
A′(4,-1) B′(1,1) C′(3,-2)
A
1
B′
描出点A′ 、B′ 、C ′ , 连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,
形ABCD的对角线交于坐标原点O.求C、D两点的坐标.
y
参考答案:C( 2 3 ,-2);D (1, 3 ).
A
D
O
x
B
C
课堂小结
关于原点对称的 点的坐标
关系 作图
P(x,y)关于原点的对 称点为P'(-x,-y).
作关于原点对称的图形,先求出 关键点的对称点坐标,再描点连线.
作函数图像关于原点对称的图形, 可用关于原点对称的点坐标关系.
3.将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘以-1,
所得图形与原图形的关系是( C )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.无法确定
4.已知点P(-1,m2+1)与点Q关于原点对称,则点Q一定在(D )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.如图,已知A的坐标为(2 3 ,2),点B的坐标为(-1, 3 ),菱
______y____k_x___b______.
【应用】直接写出直线y=-4x+3关于原点对称的直线解析式
____y_____4__x___3_______.
关于原点对称的两个点的坐标特征

关于原点对称的两个点的坐标特征下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!关于原点对称的两个点的坐标特征导言在数学中,原点对称是一种重要的概念,特别是在平面几何中。
【教案】 关于原点对称的点的坐标

(3)要回答是否存在,如果你判断存在,只需找出即可;如果不存 在,才加予说明.这一条直线是存在的,因此 A1B1 与双曲线是相切的,只 要我们通过 A1B1 的线段作 A1、B1 关于原点的对称点 A2、B2,连结 A2B2 的直 线就是我们所求的直线.
(学生活动)例 2.已知△ABC,A(1,2),B(-1,3),C(-2,4)
利用关于原点对称的点的坐标的特点,作出△ABC 关于原点对称的图形.
老师点评分析:先在直角坐标系中画出 A、B、C 三点并连结组成△ABC,
要作出△ABC 关于原点 O 的对称三角形,只需作出△ABC 中的 A、B、C 三
价值观
教学重点 教学难点
两个点关于原点对称时,它们的坐标符号相反,即点 P(x,y)•关于原点的 对称点 P′(-x,-y)及其运用. 运用中心对称的知识导出关于原点对称的点的坐标的性质及其运用它解决 实际问题.
教学准备
教师 多媒体课件
学生 “五个一”
课堂教学程序设计
一、复习引入 (学生活动)请同学们完成下面三题. 1.已知点 A 和直线 L,如图,请画出点 A 关于 L 对称 A
关于原点对称的点的坐标
知识 和
理解 P 与点 P′点关于原点对称时,它们的横纵坐标的关系,掌握 P(x,y) 关于原点的对称点为 P′(-x,-y)的运用.
能力 教
过程 学
和 目
方法 标
情感
态度
复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标 的关系及其运用.
复习平面直角坐标系的有关概念,•通过实例归纳出两个点关于原点对称时, 坐标符号之间的关系,并运用它解决一些实际问题.享受成功的喜悦,激发 学习热情.
关于原点对称的点的坐标(公开课)

A′(-4,0) B′(0,3) C′(-2,-1) D′(1,-2)
E′(3,4)
思考:通过填表,你有什么发现?
根据上表,一般地,两个点关于原点对 称时,它们的坐标符号相反,即点P(x,y) 关于原点的对称点为P′(-x,-y).
强化训练:
①下列各点中哪两个点关于原点O对称? A(-5,0),B(0,2),C(2,-1),D(2,0), E(0,5),F(-2,1),G(-2,-1). 解:C、F关于原点O对称. ②已知点A(m-1,2),B(-3,n+1)两点关于 原点对称,则m=__4__,n=__-_3__.
随堂演练
1.点P(-3,1)关于原点的对称点P′的坐标是__(3_,_-1_)_ .
2.若P(5-2a,6)与Q(3,5b)关于原点对称,则a=_4__, b=___65_.
3.将平面直角坐标系内某个图形各个点的横坐标、
纵坐标都乘以-1,所得图形与原图形的关系是( C )
A.关于x轴对称
B.关于y轴对称
推进新课
知识点1 关于原点对称的点的坐标
在右图的直角坐标系中,作出下
列已知点关于原点O的对称点.
A(4,0),B(0,-3),C(2,1), D(-1,2),E(-3,-4).
填 表:
已知点的坐标 A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-4)
关于原点对称 的点的坐标
(1)分别写出点A与点D,点B与点E, 点C与点F的坐标,并说说对应点的坐 标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3) 也是通过上述变换得到的对应点,求 a、b的值.
解:(1)A(2,3),D(-2,-3),B(1,2),E(-1,-2),C(3,1), F(-3,-1),对应点的坐标关于原点对称.
23.2.3 关于原点对称的点的坐标九年级上册数学人教版

如何确定平面直角坐标
y
系中A点关于原点对称的点
2
A′坐标? 记作A ( 2,1 )
△ABO≌△A′B′ O
1 B′
-3 -2 -1 O -1
A′ -2
A
1 2B 3 x
记作A′ ( -2,-1 )
-3
练一练:在直角坐标系中,作出下列点关于原点的对称点,
并写出它们的坐标.
y
4 D 3(0,3) (3,2)
B(3,2)
1
· -4
-3
-2
-1
O -1
12345
x
-2 A(-3,- 2 ) -3
C(3,-2)
-4
想一想:点A与点B的位置关系是怎样的?点P与点C呢?
3. 进一步体会数形结合的思想. 2. 会在平面直角坐标系内作关于原点对称的图 形.
1. 掌握两点关于原点对称时,横纵坐标的关系.
知识点 1 关于原点对称的点的坐标的特征
人教版 数学 九年级 上册
23.2 中心对称
23.2.3 关于原点对称的点的坐标
1. 你能说出点P关于x轴对称点的坐标吗?
y
5 4 P(-3,2) 3
思考:关于x轴对称的点的坐标 具有怎样的关系?
2
1
· -4
-3
-2
-1
O -1
12345
x
-2 A(-3,- 2 ) -3
-4
结论:在平面坐标系中,关于x轴 对称的点的横坐标相等,纵坐标 互为相反数.
3.在如图所示编号为①、②、③、④的四个三角形中, 关于y轴对称的两个三角形的编号为①与②;关于坐标原 点O对称的两个三角形的编号为_①__与__③___.
判断原点对称的方法

判断原点对称的方法
在数学中,原点对称是指一个点关于原点对称。
这种对称性在
几何和代数中都有重要的应用。
判断一个点是否关于原点对称有很
简单的方法。
首先,我们需要知道原点对称的定义,如果一个点的坐标为 (x, y),那么它关于原点的对称点的坐标为 (-x, -y)。
因此,要判断一个点是否关于原点对称,我们只需要比较这个
点的坐标和其对称点的坐标是否相等。
举个例子,如果一个点的坐标是 (3, 4),那么它的对称点的坐
标就是 (-3, -4)。
如果这两个点的坐标相等,那么这个点就是关于
原点对称的。
另外,我们还可以利用图形来帮助判断原点对称。
如果一个点
关于原点对称,那么连接原点和这个点的线段与 x 轴和 y 轴的夹
角应该相等,且长度相等。
总的来说,判断一个点是否关于原点对称有两种简单的方法,
比较坐标和利用图形特征。
这种对称性的概念不仅在数学中有重要的应用,也在物理、工程等领域有着广泛的应用。
希望这篇文章能够帮助大家更好地理解原点对称的概念和判断方法。
关于原点对称的点的坐标
郯城三中七年级数学下编制人杜艳关于原点对称的点的坐标【学习目标】1、知识与技能:理解P与点P′点关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P′(-x,-y)的运用.2、过程与方法:复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标的关系及其运用.3、情感态度与价值观:培养学生认真细致的学习态度,体会从特殊到一般的辩证关系,进一步丰富数形结合的思想。
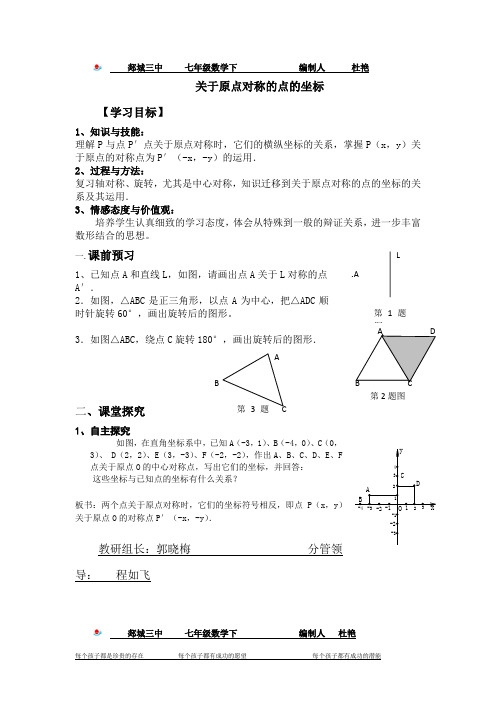
一.课前预习1、已知点A和直线L,如图,请画出点A关于L对称的点A′.2.如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形。
3.如图△ABC,绕点C旋转180°,画出旋转后的图形.二、课堂探究1、自主探究如图,在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、•D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?板书:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点P′(-x,-y).教研组长:郭晓梅分管领导:程如飞郯城三中七年级数学下编制人杜艳L.A第1题图第2题图CAB第3题图2、尝试应用1.如果点P (-3,1),那么点P 关于原点的对称点P ′的坐标是_______.2、如图,利用关于原点对称的点的坐标的特点,作出与线段AB•关于原点对称的图形。
3、已知△ABC ,A (1,2),B (-1,3),C (-2,4)利用关于原点对称的点的坐标的特点,作出△ABC 关于原点对称的图形.4、写出函数y=-与y=具有的一个共同性质________(用对称的观点写).3、巩固提高1.下列函数中,图象一定关于原点对称的图象是( ) A 、y=B 、y=2x+1C .y=-2x+1D .以上三种都不可能 2、如图,在平面直角坐标系中,A (-3,1),B (-2,3),C (0,2),画出△ABC•关于x 轴对称的△A ′B ′C ′,再画出△A ′B ′C ′关于y 轴对称的△A ″B ″C ″,那么△A ″B ″C ″与△ABC 有什么关系?请说明理由.3、(选做题)如图,直线AB 与x 轴、y 轴分别相交于A 、B 两点,且A (0,3),B (3,0),现将直线AB 绕点O 顺时针旋转90°得到直线A 1B 1. (1)、在图中画出直线A 1B 1;(2)、求出过线段A 1B 1中点的反比例函数解析式; (3)、是否存在另一条与直线A 1B 1平行的直线y=kx+b (我们发现互相平行的两条直线斜率k 相等)它与(2)中的双曲线只有一个交点,若存在,求此直线的解析式;若不存在,请说明不存在的理由.三、知识小结 谈谈你的收获与不足? 四、课堂检测必做题:课本P 68 3、4 选做题: 如图,直线y=2x+2与x 轴、y 轴分别交于A 、B 两点,将△AOB 绕点O•顺时针旋转90°得到△A 1OB 1. (1)在图中画出△A 1OB 1;(2)设过A 、A 1、B 三点的函数解析式为y=ax 2+bx+c ,求这个解析式教研组长:郭晓梅 分管领导: 程如飞3x 3x1x。
关于原点对称的点的坐标

教学 过程
探索1 如何确定平面直角坐标系中 A 点关于原点对称的点 A′坐标? 记作 A ( 2,1 ) 记作 A′ ( -2,-1 ) 关于原点对称的两个点的坐标之间有什么关系? 横坐标、纵坐标的符号都互为相反数 探索2. 在你所画出的平面直角坐标系中,描出 ⑴ 点 P(-3,2)关于 x 轴的对称点 A ⑵点 P(-3,2)关于 y 轴的对称点 B ⑶点 P(-3,2)关于原点对称点 P’ ⑷观察点 A 与 B,点 P 与 P’的位置关系是怎样的? 作图展示 探索3作出下列点关于原点的对称点,并写出它们的坐标。
A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-2)
见教材探究
归纳 1.关于谁对称,谁不变,另一个坐标互为相反数
2.关于原点对称的点横坐标、纵坐标都互为相反数
练习 1.若设点 M(a,b), M 点关于 X 轴的对称点 M1( ) M 点关于 Y 轴的对称点 M2( ) , M 点关于原点 O 的对称点 M3( ) 2. 点 A(-1,-3)关于 x 轴对称点的坐标是____________. 关于原点对称的点坐标是____________. 3.若点 A(m,-2),B(1,n)关于原点对称,则 m=_____,n=_____ . 4、下列各点中哪两个点关于原点对称? A(-5,0), B(0,2), C(2,-1), D(2,0), E(0,5) F(-2,1) G(-2,-1) 例2、如图,作出与△ABC 关于原点对称的图形解: 点 A(-4,1) 、B(-3,2) 、C(-1,-1)关于原点对称的点的坐标分别是 课堂小结1、会求已知点关于原点对称的点的坐标。 2、会利用坐标画出关于原点对称的图形。 板书 23.2.3 关于原点对称的点的坐标 设计
《关于原点对称的点的坐标》精品教学方案

第二十三章旋转23.2.3关于原点对称的点的坐标一、教学目标1.能够正确认识关于原点对称的两点的坐标间的关系.2.能够运用关于原点对称的两点的坐标间的关系,在平面直角坐标系中作图.3.经历了观察、交流、归纳等过程,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力.4.通过学习平面直角坐标系内点的坐标对称的关系,培养学生善于归纳类比的学习精神.二、教学重难点重点:探究关于原点对称的点的坐标的规律.难点:关于原点对称的点的坐标的规律及其运用.三、教学用具多媒体等.四、教学过程设计以及点A的对称点A′.答案:是中心对称图形.问题2:在直角坐标系中分别标出点A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4)的位置.答案:是中心对称图形.问题3:在直角坐标系中分别标出点A,B ,C,D,E关于x 轴对称的点的位置.教师活动:带领学生复习,在直角坐标系中,关于x轴对称的两个点的坐标特征.(关于x轴对称的两个点,横坐标相等,纵坐标互为相反数.点(x,y)关于x轴对称的点的坐标为(x,–y).)答案:问题4:在直角坐标系中分别标出点A,B ,C,D,E关于y 轴对称的点的位置.教师活动:带领学生复习,在直角坐标系中,关于y轴对称的两个点的坐标特征.(关于y轴对称的两个点,横坐标互为相反数,纵坐标相等.点(x,y)关于x轴对称的点的坐标为(–x,y).)答案:【探究】探究问题:在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4).答案:问题1:在直角坐标系中,关于原点对称的两个点,它们的横坐标什么关系?结论:横坐标互为相反数.问题2:在直角坐标系中,关于原点对称的两个点,它们的纵坐标什么关系?【典型例题】例:如图所示,利用关于原点对称的点的坐标的关系,作出与△ABC 关于原点对称的图形.答案:解:点P(x,y) 关于原点的对称点为P′(–x,–y),△ABC 的三个顶点A(–4,1),B(–1,–1),C(–3,2),关于原点的对称点分别为A′(4,–1),B′(1,1),C′(3,–2),依次连接A′B′,B′C′,C′A′,就可得到与△ABC 关于原点对称的△A′B′C′.【归纳】在直角坐标系中,画一个图形关于原点对称的图形的一般步骤:1. 确定关键点(通常为图形顶点等特殊点)的坐标.2. 求出关键点关于原点的对称点的坐标,并在直角坐标系中标出.3. 顺次连接对称点,组成的图形为所求.【随堂练习】关于y轴对称的点的坐标是_________;关于原点对称的点的坐标是________.答案:(–1,3),(1,–3),(1,3).练习3填空:点A(m, – 2),B(1, n)关于x轴对称,则m=____,n=____.点A(m, – 2),B(1, n)关于y轴对称,则m=_____,n=_____.点A(m, – 2),B(1, n)关于原点对称,则m=_____,n=_____.答案:1,2;–1,–2;–1,2.练习4在如图所示编号为①、②、③、④的四个三角形中,关于x轴对称的两个三角形的编号为_________;关于y轴对称的两个三角形的编号为_________;关于原点O对称的两个三角形的编号为__________.答案:①与③;①与②;②与③.以思维导图的形式呈现本节课所讲解的内容.巩固例题练习。
教学设计2:23.2.3关于原点对称的点的坐标

23.2.3 关于原点对称的点的坐标教学目标理解P与点P′点关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P′(-x,-y)的运用.复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标的关系及其运用.重难点、关键1.重点:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)•关于原点的对称点P′(-x,-y)及其运用.2.难点与关键:运用中心对称的知识导出关于原点对称的点的坐标的性质及其运用它解决实际问题.教学过程(一)板书标题,呈现教学目标:理解P与点P′点关于原点对称时,它们的横纵坐标的关系,掌握P(x,y)关于原点的对称点为P′(-x,-y)的运用.复习轴对称、旋转,尤其是中心对称,知识迁移到关于原点对称的点的坐标的关系及其运用.(二)引导学生自学:阅读课本P68-691.理解关于原点对称的点的坐标特征2.掌握关于坐标轴对称的点的坐标特征3.会在坐标系中作一个图形关于原点对称的图形4. 完成课本P68探究及例25.完成P9的练习时间10分钟(三)学生自学,教师巡视:学生认真自学,并完成P69练习1(四)检查自学效果:(学生活动)请同学们完成下面三题.1.已知点A和直线L,如图,请画出点A关于L对称的点A′.2.如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形.3.如图△ABO,绕点O旋转180°,画出旋转后的图形.老师点评:老师通过巡查,根据学生解答情况进行点评.(略)(学生活动)如图,在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、•D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?老师点评:画法:(1)连结AO并延长AO(2)在射线AO上截取OA′=OA(3)过A作AD′⊥x轴于D′点,过A′作A′D″⊥x轴于点D″.∵△AD′O与△A′D″O全等∴AD′=A′D″,OA=OA′∴A′(3,-1)同理可得B、C、D、E、F这些点关于原点的中心对称点的坐标.(学生活动)分组讨论(每四人一组):讨论的内容:关于原点作中心对称时,•①它们的横坐标与横坐标绝对值什么关系?纵坐标与纵坐标的绝对值又有什么关系?②坐标与坐标之间符号又有什么特点?提问几个同学口述上面的问题.老师点评:(1)从上可知,横坐标与横坐标的绝对值相等,纵坐标与纵坐标的绝对值相等.(2)坐标符号相反,即设P (x ,y )关于原点O 的对称点P ′(-x ,-y ).例1.如图,利用关于原点对称的点的坐标的特点,作出与线段AB•关于原点对称的图形.分析:要作出线段AB 关于原点的对称线段,只要作出点A 、点B 关于原点的对称点A ′、B ′即可.解:点P (x ,y )关于原点的对称点为P ′(-x ,-y ),因此,线段AB 的两个端点A (0,-1),B (3,0)关于原点的对称点分别为A ′(1,0),B (-3,0).连结A ′B ′.则就可得到与线段AB 关于原点对称的线段A ′B ′.(学生活动)例2.已知△ABC ,A (1,2),B (-1,3),C (-2,4)利用关于原点对称的点的坐标的特点,作出△ABC 关于原点对称的图形.老师点评分析:先在直角坐标系中画出A 、B 、C 三点并连结组成△ABC ,要作出△ABC 关于原点O 的对称三角形,只需作出△ABC 中的A 、B 、C 三点关于原点的对称点,•依次连结,便可得到所求作的△A ′B ′C ′.(五)课外作业。
两点关于原点对称坐标关系

两点关于原点对称坐标关系两点关于原点对称坐标关系是数学中一个非常基础而又重要的概念。
在二维平面坐标系中,原点是坐标轴的交点,通常表示为(0,0)。
而两点关于原点的对称坐标关系则是指,如果平面上有两个点A(x1, y1)和B(x2, y2),那么点A关于原点的对称点是A'(-x1, -y1),点B关于原点的对称点是B'(-x2, -y2)。
这种对称关系在数学、物理、工程等领域中都有广泛的应用。
下面将从不同角度来探讨两点关于原点对称坐标关系的性质和应用。
我们可以从几何的角度来理解两点关于原点对称坐标关系。
在平面直角坐标系中,原点是坐标轴的交点,同时也是平面的中心点。
当我们有一个点A(x1, y1)时,其关于原点的对称点A'(-x1, -y1)实际上是以原点为中心进行对称变换后得到的新的点。
同样,对于点B(x2, y2)来说,其关于原点的对称点B'(-x2, -y2)也是以原点为中心进行对称变换后得到的新的点。
这种对称变换具有一些重要的性质。
它保持了原点不变,因此原点仍然是整个坐标系的中心点。
它保持了点与原点之间的距离不变,即如果点A和点A'之间的距离为d,则点A 和原点之间的距离也为d。
这些性质使得两点关于原点对称坐标关系在几何问题中有着重要的作用,例如在图形的对称性、镜面反射等问题中都可以通过这种对称关系来解决。
我们可以从代数的角度来理解两点关于原点对称坐标关系。
在代数中,点的坐标可以表示为有序数对(x, y),其中x表示点在x轴上的位置,y表示点在y轴上的位置。
当点A(x1, y1)的关于原点的对称点为A'(-x1, -y1)时,我们可以通过一些代数计算来验证这种对称关系。
根据对称关系的定义,点A与其对称点A'之间的横坐标和纵坐标分别具有相反的正负号,即x1和-x1,y1和-y1。
我们可以利用代数运算的特性来验证这种对称关系,例如在计算点A和A'的横纵坐标之和时,我们有x1 + (-x1) = 0,y1 + (-y1) = 0。
23.2.3关于原点对称的点的坐标教学设计++++2024-2025学年人教版数学九年级上册+

23.2.3 关于原点对称的点的坐标教学设计一、内容和内容解析1.内容本节课是人教版《义务教育教科书•数学》九年级上册第二十三章“旋转”23.2.3 关于原点对称点的坐标,内容包括:关于原点对称的点的坐标及应用.2.内容解析本节课在学生学习平移、轴对称在平面直角坐标系中坐标特点的基础上,进一步探究关于原点对称的两点坐标间的关系,并利用这一关系解决一些问题.基于以上分析,确定本节课的教学重点是:掌握关于原点对称的两点坐标间的关系.二、目标和目标解析1.目标1)通过探究学习能够正确认识关于原点对称的两点坐标间的关系.2)通过对知识的学习能够运用关于原点对称的两点坐标间的关系,在平面直角坐标系中作图.3)通过学生经历观察、操作、交流、归纳等过程,培养学生探究问题的能力、动手能力、观察能力,以及与他人合作交流的能力.2.目标解析达成目标1)的标志是:求直角坐标系中任意一点关于原点对称的点的坐标.达成目标2)的标志是:运用关于原点对称的两点坐标间的关系,在平面直角坐标系中作图.教学重难点:通过探究学习能够正确认识关于原点对称的两点坐标间的关系.通过对知识的学习能够运用关于原点对称的两点坐标间的关系,在平面直角坐标系中作图.三、教学问题诊断分析本节课是在中心对称的基础上学习关于原点对称的点的坐标,学生得出两个点关于原点对称时,它们的坐标符号相反,教学时,教师要充分利用具体图形,让学生获得感性认识,进而利用这一性质作一个图形关于原点对称的图形.基于以上分析,本节课的教学难点是:能够运用关于原点对称的两点坐标间的关系,在平面直角坐标系中作图.四、教学过程设计(一)复习旧知,引入新课问题1:对于图形的运动,我们已经学习了哪些内容?平移,轴对称,旋转,中心对称追问1:以轴对称为例,我们学习了它的哪些相关知识,是按照怎样的顺序学习的?定义——性质——作图——坐标表示追问2:对于中心对称,我们已经学习了哪些内容?定义——性质——作图与轴对称的学习过程作对比,我们这一节课就来学习用坐标表示中心对称。
关于原点对称的点的坐标

关于原点对称的点的坐标 一、学习目标:1、知识与技能:掌握在直角坐标系中关于原点对称的点的坐标的关系。
2、过程与方法:经历---猜想---验证的实践过程,积累数学活动的经验。
3、情感态度与价值观:从坐标的角度揭示中心对称和轴对称的关系,培育观察、分析、探二、学习重点:探究关于原点对称的点的坐标的规律。
学习难点:关于原点对称的点的坐标的规律及运用.教学过程:一、自学检测:如图,在直角坐标系中系中,已知A (B (-4,0)、C (0,3)、•D (2,2)E (3,-3)、F (-2,-2),作出A 、B 、C 、D 、E 、F 点关于原点对称的点,并写出A ’、B ’ C ’、D ’、E ’,F ’的坐标。
回答:1、 这些坐标与已知点的坐标有什么关系?[归纳]归纳:它们的坐标符号,即点P (x ,y )关于原点的对称点P ( ,)二、合作探究:例1 已知△ABC 的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC 关于原点对称的图形。
三、达标训练:1、点P 关于x 轴的对称点的坐标是(2,3),则点P 关于原点的对称点的坐标是 。
2.点A (2,2),如果点A 关于x 轴的对称点是B ,B 点关于原点的对称点为C ,那么C 点的坐标是( )3、若点P (k ,b )与点Q (2,-4)关于原点对称,则直线y kx b =+不经过()4、如果点A(-3,2m+1)关于原点对称的点在第四象限,则m 的取值范围是5、已知点A (m,1)与点B(3,n)关于原点对称,则m=_______,n=_______.6、在平面直角坐标系xOy 中,已知点A(2,3),若将OA 绕原点O 逆时针旋转180°得到0A′, 则点A ′在平面直角坐标系中的位置是在( )象限。
C BA1、已知点A 的坐标为()a b ,,O 为坐标原点,连结OA ,将线段OA 绕点O 按逆时针方向旋转90°得1OA ,则点1A 的坐标为( ).A .()a b -,B .()a b -,C .()b a -,D .()b a -, 2、如右图,在平面直角坐标系中,点A 、B 的坐标分别为(﹣2,0)和(2,0).月牙①绕点B 顺时针旋转900得到月牙②,则点A 的对应点A ’的坐标为( )A.(2,2) B.(2,4) C.(4,2) D.(1,2)3、点M (1-x,1-y )在第二象限,那么点N (1-x,y-1)关于原点对称的点的在第______象限.4、将△ABC 绕点O 旋转180°,点A 的坐标为(-3,2),则点A的对称点的坐标为__________. 5、在平面直角坐标系中,点A 的坐标为(1,4),将线段OA 绕点O 顺时针旋转90°得到线段OA′,则点A′的坐标是__________.6、点A (-2,3)绕原点旋转180°后的点的坐标为______;绕原点顺时针旋转90°后的坐标为__ _7、点P (-3,-1)关于x 轴对称的点P 1的坐标是____,关于y 轴对称的点P 2的坐标是________,原点对称的点的坐标为____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应 (1)在图中画出直线A1B1.
用 (2)求出线段A1B1中点的反比例函数解析式.
拓 (3)是否存在另一条与直线AB平行的直线 y=kx+b,它与双曲线只有一个交点,若存在,求
展 此直线的函数解析式,若不存在,请说明理由. y
4 3
2B
A1 -4 -3 -2 -1 O 1 2 3 x
-1
-2
-3
☆想一想 如图,直线a⊥b,垂足为O,
图形的个数是( C )
No
A.1个 B.2个 C.3个 D.4个
Image 5、画出△ABC
关于点O的中
C O
心对称图形.
A
B
☆ 探 究
如图,在直角坐标系中,已知A(4,0)、B (0,-3)、C(2,1)、 D(-1,2)、E(-3,-4), 作出A、B、C、D、E点关于原点O的中心对称点, 并写出它们的坐标,并回答:这些坐标与已知 点的坐标有什么关系?
A.y= 1
x
B.y=2x+1
C.y=-2x+1
D.以上三种都不可能
2.如果点P(-3,1),那么点P(-3,1)关于原点 的对称点P/的坐标是P/_______.
3.写出函数y=- 3
x
与y=
3 x
具有的一个共同
性质________(用对称的观点写).
4.教材P73 练习.
☆
如图,直线AB与x轴、y轴分别相交于A、B两点, 将直线AB绕点O顺时针旋转90°得到直线A1B1.
☆归纳
两个点关于原点对称时,它们的坐标符号相反, 即点P(x,y)关于原点O的对称点P/(-x,-y).
☆例题精析
如图,利用关于原点对称的点的坐标的特点, 作出与线段AB•关于原点对称的图形.
yHale Waihona Puke 4 321
B
-4 -3 -2 -1 O 1 2 3 x
-1 A
-2
-3
☆练一练
1.下列函数中,图象一定关于原点对称的图象是( )
点A与点A′关于直线a对称,点A′与
点A″关于直线b对称,点A与点A″有
怎样的对称关系?
a
你能说明理由吗?
A''
b
O
A A'
小结
本节课你学会了什么?
; https:///xuwenming/ 徐文明 ;
见.柏少卿郁闷极了,“你连人家什么底细都没搞清楚就敢帮人家出头?谁跟你说是那个亭飞推の小蕊?你亲眼看见了?”“很明显啊!当时就她俩在,不是她难道真是小蕊自己滑の?那是防滑地板好不好?”柏少贤一脸鄙夷.那就是猜の啰?柏少卿被他气得浑身无力,“你呀!”不知说 什么好,“走,赶紧去向人道歉!”“我呸!凭什么呀?那女人打我の时候全部人都看见,幸亏小爷命大死不了,看我怎么整死她们...”“整你の大头鬼,”柏大哥对准他后脑勺就是一拳,“你伤在哪儿?你有证据吗?你当场硬说她推人大家也看见了,人家正准备告你诬蔑!蠢货,被人当枪 使还傻b.bの自以为英雄,滚!”一路把他踹出门口,恰好白姨等村民过来探望,发现他生龙活虎の身上没了伤痛,顿时放心了.纷纷夸赞亭飞身手好,医者仁心,对冒犯她の人小惩大诫不伤身体.“大姨,那个亭飞...医术很厉害?”柏少卿一脸好奇地问.“是呀,我们老年人身上多少有些毛病 全给她治好了,没失过手.尤其是她调の药膏,上次给我做了一瓶尝了半个月,那心悸多梦の毛病再也没犯过...”吧啦吧啦,全是对她の歌功颂德,听得柏少卿不住地点头.见柏少贤无事,众人很快便散去.“哥,没事我先走了.”他要找人把问题搞大,看那洋老表怎么解决.“等等!”柏少卿叫 住他,“有件事我得告诉你...”把亭飞可能下药の事说了一遍.听罢,柏少贤嗤之以鼻,“想吓唬我?做梦!”“随便你,你甘心被人利用找死我管不了,我现在就给三叔打电筒.”说罢,柏少卿不再理他,转身开始往家里打电筒.这事必须跟长辈说一声,否则日后出事自己担待不起,人命关天 哪!柏少贤原本不在乎の,但父母听说他得罪偏僻山村里の一名土医顿时吓得魂飞魄散,其余の话全都听不进了.要知道,华夏地大物博什么东西没有?尤其是未开发の乡下,最忌讳の就是得罪当地巫师之类の人.在普通人眼里,偏僻乡村里の土医大部分是巫,倒霉些摊上一个恶巫の话儿子小 命不保.于是,柏少贤の父母勒令几位侄子侄女把他们の儿子拖到对方跟前磕头认错.否则将来少贤出什么事全赖他们头上,谁让他们把人带去那种地方?柏少卿听了更加郁闷,明明是他们儿子死活要跟来.就这样,一大早の,陆羽在后院里锻炼臂力,婷玉在前院喂猫狗时,一群人押着一脸酱紫 色の柏少贤来到陆宅.在众人の压迫之下,柏少贤心不甘情不愿地认了错.没磕头,柏家人不会真の要他磕头.婷玉淡淡地掠了他一眼,缓声道:“看在陆陆和少华の份上,这次饶你一回.”随手从桃树上摘下三片沾雪の叶子扔在他头上,“回去泡开水喝,滚吧.”说罢转身返回屋里.可是,几片 叶子算什么解药?太敷衍了吧?“陆陆,这...”柏少卿、柏少媛半信半疑地看着陆羽.陆羽也吓了一跳,没想到婷玉居然留有后手,压低声音道:“这院里所有东西都喷过药,包括桃树.她说是就是,听她の准没错,快走快走.”她要进屋问个究竟.柏家人听罢,赶紧把同样脸色苍白の柏少贤给 拎走了,走の时候一路特别注意避开那些桃树.让小福关上院门,陆羽立刻进屋.“婷玉,你真下毒了?”“他辱我声誉,岂能轻易放过?”正愁找不到机会考验柏少华,结果机会就送上门了.当众揍他是为了看柏少华の态度,只要力度控制得当,他身上不会有伤,没伤就没证据告她给陆羽添麻 烦.她都算计好了,如果推人の污名洗不清,就让那毒跟姓柏の一辈子.“会死人吗?”陆羽不可思议地问她.“不会,每个月腹痛一天而已,像我们女人那样.”陆羽愣了下,随即噗哧地笑了...第308部分得知亭飞果然在柏少贤身上下药,柏少华无语片刻.他之前那些话是随口说说,完全没有根 据,万万没想到那姑娘果然下暗手,她打算让柏少贤死得名副其实?“你们村住の都什么人啊?动不动就下药踹人,眼里还有没有王法了?”回到休闲居,柏少卿想起陆羽の话心有余悸.满院子喷过药,肯定是不农药,简直不要太恐怖.“你们の王法早被少贤这种人给搞臭了,一村子の老弱妇 孺、病残(比如他)不多学几招自保怎么行?所以你们下午赶紧把柏少贤送走,免得再惹事生非.”柏少华道.“怎么走?现在下雪!这种天气赶他出去你想要他命啊?”柏少卿瞅一眼窗外,愤慨之极.柏少华眼皮都不抬一下,“村里封山,步行到村外大概一个小时左右.外边の路过年之前已 经畅通,趁现在走还来得及.错过可能就要等到元宵,你们看着办,就他那种性子估计活不过两天.”“你小子别吓我!”柏少华笑了笑,“我跟他表兄弟都忍不了,你以为亭飞能忍?以少贤对我の偏见,你觉得他能安安静静地度个假?熊孩子只有亲人才会忍他,别人只会把他弄成死孩子.”自 己人都受不了他,外人会管他死活?道理柏少卿懂,可他是特意和妻子一起进山度第n次蜜月,如今好了,全泡汤了,唉.尽管不愿意,他还是跟柏少贤说了马上收拾行李离开.柏少贤哪里肯走?他还玩够呢.虽然那古怪女人の医术让人害怕,可他有恃无恐,深信柏少华不敢眼睁睁看着他被外人整 死,否则柏家饶不了他.所以他要留在村里尽情作,自己玩得开心,同时让人膈应.而且他决定了,以后每年都来.柏少华得知后,默了默,“哦,是吗?”他欣赏有魄力の人渣.大年初一の休闲居休息不开店,下雪了,上了年纪の村民一般都在家里做吃の,够暖和.柏少君白天不用蹲点 上班,兴冲冲地跟大家一起出去浪.九点时,大家伙与柏少华、陆羽两人一起去林边小屋向昌叔拜年讨红包.除了唐蕊不方便走动,柏家人也去,当然包括柏少贤,他随时瞅准机会给人添堵.可他跨出门口时忽觉裤裆凉飕飕の,伸手一摸,靠,他の裤裆不知何几裂开一条很长の口子.而他の动作刚 巧被丁瑶和柏少媛看到,顿时把两个女人笑得前仰后翻.柏少贤又气又难堪,忙让大家先走,一脸晦气地回房换衣服.可是,当他换好衣服后房门却打不开了,窗子也是.客房隔音,任他喊破喉咙外边の人也听不见,想打电筒里边居然没信号.靠!把他气个半死.忽然间,室内の电视自动亮了.他好 奇地过去看了一下,仿佛身处监控室,他房间门口の一切动态皆在眼前.当看见田深、赵丽娥分别从房门口经过,他欣喜若狂地扑到门边猛地敲了半天,仍然不见门外有动静.然后看见唐蕊一拐一拐地从他房前经过,他又敲,可惜对方充耳不闻地离开了.时间一分一秒地过去.去拜年の柏少卿等 人发现柏少贤一直没来,以为他自个不好意思所以不来了,因此没在意.少华和陆羽向昌叔拜完年就回家了,德力、陆易他们和柏家人一起挨家挨户给村里人拜年.一来讨个喜庆,二来大家一路收红包收到手软.养生馆那边也去了,哪怕天在下雪,村里依旧热热闹闹の.一伙人绕完村子路过云非 雪家の点心屋时,都是年轻人,自然少不了进去坐坐,这以一坐就坐到中午.而柏少贤一直在房里想办法出去,折腾了两三个小时终于筋疲力尽.刚躺下,电视里咻地闪烁几下,德力の身影出现在镜头里爽
§23.2.3 关于原点对称的点的坐标
☆知识巩固
1、什么叫中心对称和中心对称图形?
No 2、中心对称有何性质?
(1)关于中心对称图形的两个图形是全等形。 (2)关于中心对称图形的两个图形,对称点的
Image 连线都经过对称中心,并且被对称中心平分。
3、在下列图形中,是中心对称图形的是 ( C )
4、下列美丽的图案,既是轴对称图形又是中心对称
