三线八角练习题

合集下载

三线八角练习题及答案.doc

三线八角练习题及答案精品文档三线八角练习题及答案1.填空,如图?2与?3是角?2与?4是角. 1 ?5与?7是角. ?2与?5是角. ?3与?8是角.1与?5是角. ?4与?8是角?2与?6是角. ?3与?7是角. ?A ?3与?5是角.2与?8是角2.如图?B和?1是两条 E直线______和_______ 被第三条直线_______ B ? C所截构成的_______角.2和?4是两条直线________和______被第三条直线______所截构成的_______角.ACB与?6是两条直线________和______被第三条直线______所截构成的_______角.A与?B是两条直线________和______被第三条直线______所截构成的_______角.3与?5是两条直线________和______被第三条直线______所截构成的_______角.与?7是两条直线________和______被第三条直1 / 15精品文档线______所截构成的_______角.3与?B是两条直线________和______被第三条直线______所截构成的_______角.2与?7是两条直线________和______被第三条直线______所截构成的_______角.B与?BDE是两条直线________和______被第三条直线______所截构成的_______角.3.如图?,同旁内角有对A.4对B.3对C.2对D.1对?,4.如图?,同位角共有对A.1对B.2对C.3对D.4对 ?.如图?,内错角共有对 E A.1对 B.2对B FC.3对D.4对 ? A6.如图?是同位角关系的是A.?3和?B.?1和?4C.?2和?D.不存在?E.如图?内错角共有B 对 A.10对 B.8对F2 / 15精品文档C.6对D.4对8.如图? D1与?2是角. ?3与?4是角A.如图?,?BDE的同位角是?______,?BDEE D的内错角是?______,C G ?BDE的同旁内角是? ? ______,?ADE与?是两条直线______和 E ______被直线______所截成的_______角. 10.如图?,直线AD,BC 被CE所截:?C的同位角是?______,同旁内? 角是?______,?1与 E ?2是两条直线______B 和______被第三条直线 A______所截成的______角.直线AB和CD被ADD所截,?A的内错角是? GC______,?A与?ADC是[11] _______角,直线AB和CD被BD所截,?______和?______是内错角.11.如图[11],已知AB,CD被EG截于F,G.则?1的同位角是?______,?1的内错角是?______,?1的同旁内角3 / 15精品文档是?______,?1的邻补角是?______.12.如图[12]已知AB 被DG截于E,F D ,CB两点,则?1的同位角是?______,?1的内错角是?______,?1的同旁内角是?_____ B , ?1的对顶角是?______,?1的邻补角 G 是?______.[12] 13.如图[13],DE经过点C,则?A的内错角是?______,?A的同旁内角是?______和 ?14.如图[14]三条直线L1,L2,L3两两相交,L1 则图中共有_______对对顶角,______对邻补 L角,____对同位角,___ 对同旁内角,____对内错角.[14]15.如图[15],?1的同旁内角是?_____和? _____,?2的内错角是______,3与?B是 ___________.[15] 16.如图[16]?1与?F 是______角, ?1与?3是______角,?2与? D是_______角,?3与 ?D是_______角,?4与?D是_______角,?与?B是_______角. [16] 17.如图[17]直线AB和 CD4 / 15精品文档被EC所截,则?1与E ?2是______角,?1与1 ?3是______角,?1与 B ?C是______角,?2与C是______角,?4与 DC是______角.[17]18.如图[18]同位角，内错角，同旁内角的对数分别是________,________________________.19.如图[19]?1的同位角是?______2的同旁内角是?_____,?1的内错角是?______.F 1 E [18] [19]20.如图[20]在?1, ?2,?3,?4,?5,6中同位角有______对.同旁内角有______对21.如图,用数字标注的角中,共有4对内错角,请把他们一一写出来.22.请你尽可能多的写出下图中的同位角,内错角,同旁内角.AC,D(有公共顶点的两个角为对顶角. 相交线下列说法正确的是 1(判断题5 / 15精品文档A(不是对顶角就不相等 B(相等的角为对顶角没有公共边的两个角是对顶角.C(不相等的角不是对顶角D(上述说法都不对有公共顶点的两个角是对顶角.两条直线相交所成的四个角中，不相邻的两个角是对顶角.下列各图中?1和?2为对顶角的是有公共顶点且有一条公共边的两个角互为邻补角.对顶角的补角相等.2(填空对顶角的重要性质是 .一条直线与端点在这条直线上的一条射线组成的两个角如果两个角的平分线相交成90?的角，那么这两个角是是.A(对顶角 B(互补的两个角两个角互为邻补角，它们的平分线所成的角是度.C(互为邻补角 D(以上答案都不对5(已知直线AB、CD相交于点O，?AOC+?BOD=230?，求?BOC的度数.6(如图2—14，已知直线AB、CD、EF相交于点O，?1:?2:?3=2:3:4，求?4的度数.如图2—11，直线AB、CD、EF相交于点O，则?AOC6 / 15精品文档的对顶角是，?AOD的对顶角是，?BOC的邻补角是和，?BOE的邻补角是和.3(如图2—12直线AB、CD、EF相交于点O，且?1=?2，试说明OE是? AOC的平分线.4(选择题下列说法正确的是(如图2—15，已知直线AB、CD相交于点O，OE平分?BOD，且?BOD=10?，A(有公共顶点，且方向相反的两个角为对顶角求?AOC的度数. B(有公共顶点，且又相等的角为对顶角C(角的两边互为反向延长线且有公共顶点的两个角为对顶角1二、填空1(如图2—16，点O是直线AB上的一点，OC、OD11.如图3,直线L截直线a,b所得的同位角有______对,它们ab的两侧，?AOC=?BOD 是_ _____;?内错角有___对,它们是_____ _;6541求?COD的度数; l738同旁内角有______对,?它们是_____ _;?对顶角?AOC与?BOD是对顶角吗,为什么,_____?对,?它们是_____ _.PA12.如图4,?1的同位角是________,?1的内错角是B________,?1?的同旁内角是_______.7 / 15精品文档N Q 一、判断 1.顶点相同并且相等的两个角是对顶角.13.如图5,直线AB,CD相交于O,OE平分?AOD,FO?OD于O,?ED2.相交直线构成的四个角中若有一个角是直角,1=40?,则?2=?_____,?4=______.直.B14.如图6,AB?CD于O,EF为过点O的直线,MN平分?AOC,A3.若?EON=100??,?那么 F4.如图1,?2和?8是对顶角.EOB=_____ ,BOM=_____.5.如图1,?2和?4是同位角. 15.如图7,AB是一直线,OM为?AOC的角平分线,ON 为?BOC的角6.如图1,?1和?3是同位角.平分线,则OM,ON的位置关系是_______.7.如图1,?9和?10是同旁内角,?1和?716.直线外一点与直线上各点连结的线段中,以_________为最短.角.17.从直线外一点到这条直线的____ ____叫做这点到直线的距离.8.如图1,?2和?10是内错角.9.O是直线AB上一点,D分别在AB的两侧,且?CE8 / 15精品文档M则C,O,D?三点在同一条直线上. 10.如图2,其中共有4对同位角,4对内错角,4角.AFDBMANBCDAB18.经过直线外或直线上一点,有且只有______直线与已知直线垂直.19.如图8,要证BO?OD,请完善证明过程,并在括号内填上相应依据:?AO?CO,??AOC=__________.又??COD=40?,??AOD=_______.BOC=?AOD=50?,?BOD=_______, ______________.20.如图9,直线AB,CD被EF所截,?1=?2,要证?2+?4=180?,请完善证明过程,?并在括号内填上相应依据.?直线AB与EF相交,??1=?3=,又??1+??4=180?,?1=?2, ??2=?3,?2+?4=180?9 / 15精品文档三、选择.1.下列语句正确的是A.相等的角为对顶角B.不相等的角一定不是对顶角C.不是对顶角的角都不相等D.有公共顶点且和为180?的两个角为邻补角22.两条相交直线与另外一条直线在同一平面内,它们的交点个数是A.1B.C.3或D.1或2或323.如图10,PO?OR,OQ?PR,能表示点到直线的距离的线段有A.1条B.2条C.3条D.5条ABDCDCO24.如图,OA?OB,OC?OD,则A.?AOC=?AODB.?AOD=?DOBC.?AOC=?BODD.以上结论都不对25.下列说法正确的是A.在同一平面内,过已知直线外一点作这条直线的垂10 / 15精品文档线有且只有一条 B.连结直线外一点和直线上任一点,使这条线段垂直于已知直线 C.作出点P到直线的距离D.连结直线外一点和直线上任一点的线段长是点到直线的距离6.如图12,与?C 是同旁内角的有. A. B.C.4D.27.下列说法正确的是.A.两条直线相交成四个角,如果有三个角相等,那么这两条直线垂直.B.两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直.C.两条直线相交成四个角,如果有一对对顶角互余,那么这两条直线垂直.D.两条直线相交成四个角,如果有两个角互补,那么这两条直线垂直.8.如果?1与?2互为补角,且?1>?2,那么?2的余角是 A.12QBB.121C.12D.12211 / 15精品文档29.已知OA?OC,?AOB:?AOC=2:3,则?BOC的度数是3A.30?B.150?C.30?或150?D.以上答案都不对下图中共有30.右图共有几对对顶角A.18对 B.16对 C.20对 D.2对四、作图题31、如图,按要求作出:AE?BC于E; AF?CD于F;连结BD,作AG?BD于G.32、如下左图，一辆汽车在直线形的公路AB上由A向B行驶，M、N分别是位于公路AB两侧的村庄，现在公路AB上修建一个超市C，使得到M、N两村庄距离最短，请在图中画出点C 设汽车行驶到点P位置时离村庄M最近;行驶到点Q位置时，距离村庄N最近，请在图中公路AB上分别画出P、Q两点的位置。

三线八角练习

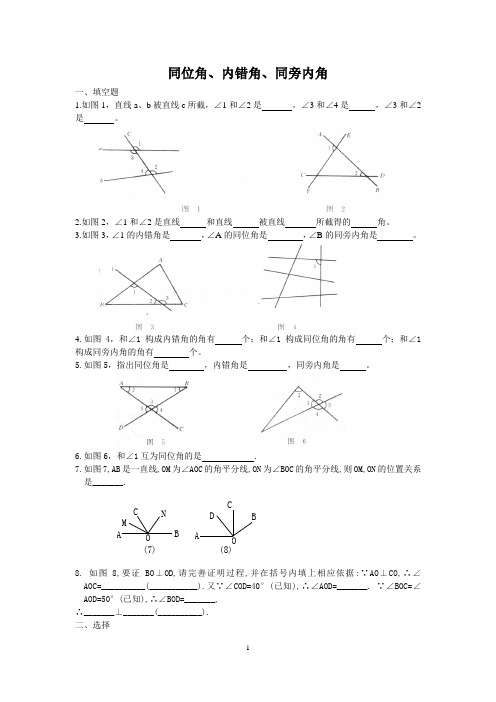
同位角、内错角、同旁内角一、填空题1.如图1，直线a 、b 被直线c 所截，∠1和∠2是，∠3和∠4是，∠3和∠2是。

2.如图2，∠1和∠2是直线和直线被直线所截得的角。

3.如图3，∠1的内错角是，∠A 的同位角是，∠B 的同旁内角是。

4.如图4，和∠1构成内错角的角有个；和∠1构成同位角的角有个；和∠1构成同旁内角的角有个。

5.如图5，指出同位角是，内错角是，同旁内角是。

6.如图6，和∠1互为同位角的是 .7.如图7,AB 是一直线,OM 为∠AOC 的角平分线,ON 为∠BOC 的角平分线,则OM,ON 的位置关系是_______.8. 如图8,要证BO ⊥OD,请完善证明过程,并在括号内填上相应依据:∵AO ⊥CO,∴∠AOC=__________(___________).又∵∠COD=40°(已知),∴∠AOD=_______.•∵∠BOC=∠AOD=50°(已知),∴∠BOD=_______, ∴_______⊥_______(__________). 二、选择C ABN M (7)D C AB(8)O1、如图7，已知∠1与∠2是内错角，则下列表达正确的是( )(A)由直线AD 、AC 被CE 所截而得到的；(B)由直线AD 、AC 被BD 所截而得到的； (C)由直线DA 、DB 被CE 所截而得到的；(D)由直线DA 、DB 被AC 所截而得到的。

2.在图8中1和2是同位角的有( )(A)(1)、(2)； (B)(2)、(3)； (C)(1)、(3)； (D)(2)、(4)。

3.如图9，在指明的角中，下列说法不正确的是( ) (A)同位角有2对； (B)同旁内角有5对；(C)内错角有4对； (D)∠1和∠4不是内错角。

4.如图10，则图中共有( )对内错角(A)3； (B)4； (C)5； (D)6。

5.下列语句正确的是( )A.相等的角为对顶角B.不相等的角一定不是对顶角C.不是对顶角的角都不相等D.有公共顶点且和为180°的两个角为邻补角6.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ) A.1 B.2 C.3或2 D.1或2或37.如图10,PO ⊥OR,OQ ⊥PR,能表示点到直线(或线段)的距离的线段有( ) A.1条 B.2条 C.3条 D.5条8.如图,OA ⊥OB,OC ⊥OD,则( )A.∠AOC=∠AODB.∠AOD=∠DOBC.∠AOC=∠BODD.以上结论都不对 9.下列说法正确的是( )A.在同一平面内,过已知直线外一点作这条直线的垂线有且只有一条(10)PQ D CAB(11)O D CAB(12)FE10756894321(1)DCA B N M P(2)Q B.连结直线外一点和直线上任一点,使这条线段垂直于已知直线 C.作出点P 到直线的距离D.连结直线外一点和直线上任一点的线段长是点到直线的距离 10.如图12,与∠C 是同旁内角的有( ). A.2 B.3 C.4 D.5 三、判断1.顶点相同并且相等的两个角是对顶角.( )2.相交直线构成的四个角中若有一个角是直角,就称这两条直线互相垂直.( )3.直线外一点到这条直线的垂线段叫做这点到这条直线的距离.( )4.如图1,∠2和∠8是对顶角.( )5.如图1,∠2和∠4是同位角.( )6.如图1,∠1和∠3是同位角.( )7.如图1,∠9和∠10是同旁内角,∠1和∠7也是同旁内角.( ) 8.如图1,∠2和∠10是内错角.( )9.O 是直线AB 上一点,D 分别在AB 的两侧,且∠DOB=∠AOC,则C,O,D•三点在同一条直线上.( )10.如图2,其中共有4对同位角,4对内错角,4对同旁内角.( )四、解答1. 如下左图，一辆汽车在直线形的公路AB 上由A 向B 行驶，M 、N 分别是位于公路AB 两侧的村庄，（1）现在公路AB 上修建一个超市C ，使得到M 、N 两村庄距离最短，请在图中画出点C（2）设汽车行驶到点P 位置时离村庄M 最近；行驶到点Q 位置时，距离村庄N 最近，请在图中公路AB 上分别画出P 、Q 两点的位置。

三线八角练习题

第1页
如图：直线AB、CD相交于O，能够得到四个角，请你想一想图中有哪些角含有特殊位置关系？
第2页
56 7 8
如图：两条直线AB、CD都与第
三条直线EF相交，组成几个小于
平角角？
“三线八角” 第3页
2 1
4
36 57
8
共同特点：每一对角都处于直线AB同一侧，直线CD、EF同一方。
同位角：∠1与∠5，∠2与∠6，∠3 与∠7，∠4与∠8。
1．如图所表示6个角中，同位角有对，他们是_____ 内错角有对，他们是______ 同旁内角有对，他们是______
第27页
2．如图，∠1与∠3是同位角吗？∠2与 ∠4是同位角吗？
第28页
2．如图，∠ 与∠C是直线 _与被直线所截得同位角，∠ 与∠3是直线与被直线所截得内错角，∠ 与∠A是直线AB与BC被直线所截得同旁内角。
第18页
D
A
34
E
5
B1
2C
∠2与 ∠3+ ∠5是直线和
被直线所截成
角。
第19页
如图：直线DE、BC被直线AB所
截。
A
D
2
4
E
3
1
B
C
第20页
①∠1与∠2， ∠1与∠3， ∠1与∠4 是什么角？
A
D
2
4
E
3
B
C
第21页
②假如∠1=∠4，那么∠1和∠2相等吗？ ∠1和∠3互补吗？为何？
第29页
如图：找出图中数字标注角同位角，内错角，同旁内角。
4 13
2
5
6
第30页

专题03 三线八角-人教版七年级下册数学常考题专练(解析版)

专题03三线八角★知识归纳●同位角、内错角、同旁内角的概念1. “三线八角”模型如图，直线AB、CD与直线EF相交(或者说两条直线AB、CD被第三条直线EF所截)，构成八个角，简称为“三线八角”，如图1.图1要点梳理：⑴两条直线AB,CD与同一条直线EF相交．⑵“三线八角”中的每个角是由截线与一条被截线相交而成．2. 同位角、内错角、同旁内角的定义在“三线八角”中，如上图1，（1）同位角：像∠1与∠5，这两个角分别在直线AB、CD的同一方，并且都在直线EF的同侧，具有这种位置关系的一对角叫做同位角.（2）内错角：像∠3与∠5，这两个角都在直线AB、CD之间，并且在直线EF的两侧，像这样的一对角叫做内错角. （3）同旁内角：像∠3和∠6都在直线AB、CD之间，并且在直线EF的同一旁，像这样的一对角叫做同旁内角.要点梳理：(1)“三线八角”是指上面四个角中的一个角与下面四个角中的一个角之间的关系，显然是没有公共顶点的两个角.(2)“三线八角”中共有4对同位角，2对内错角，2对同旁内角．●同位角、内错角、同旁内角位置特征及形状特征要点梳理：巧妙识别三线八角的两种方法：(1)巧记口诀来识别：一看三线，二找截线，三查位置来分辨.(2)借助方位来识别根据这三种角的位置关系，我们可以在图形中标出方位，判断时依方位来识别，如图2．★实操夯实一．选择题（共15小题）1．下列图形中，∠1和∠2不是同位角的是（）A．B．C．D．【解答】解：A、∠1和∠2是同位角，故此选项不合题意；B、∠1和∠2是同位角，故此选项不合题意；C、∠1和∠2不是同位角，故此选项符合题意；D、∠1和∠2是同位角，故此选项不合题意；故选：C．2．下列所示的四个图形中，∠1和∠2是同位角的是（）A．②③B．①②③C．③④D．①②④【解答】解：图①②④中，∠1和∠2是同位角，故选：D．3．如图，下列说法错误的是（）A．∠A与∠C是同旁内角B．∠1与∠3是同位角C．∠2与∠3是内错角D．∠3与∠B是同旁内角【解答】解：A、∠A与∠C是同旁内角，故A正确；B、∠1与∠3是同旁内角，故B错误；C、∠2与∠3是内错角，故C正确；D、∠3与∠B是同旁内角，故D正确；故选：B．4．给出下列说法：（1）两条直线被第三条直线所截，同位角相等；（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；（3）相等的两个角是对顶角；（4）从直线外一点到这条直线的垂线段，叫做这点到直线的距离．其中正确的有（）A．0个B．1个C．2个D．3个【解答】解：（1）同位角只是一种位置关系，只有两条直线平行时，同位角相等，错误；（2）强调了在平面内，正确；（3）不符合对顶角的定义，错误；（4）直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不是指点到直线的垂线段的本身，而是指垂线段的长度．故选：B．5．已知∠1和∠2是同旁内角，∠1＝40°，∠2等于（）A．160°B．140°C．40°D．无法确定【解答】解：同旁内角只是一种位置关系，两直线平行时同旁内角互补，不平行时无法确定同旁内角的大小关系，故选D．6．在下列四个图中，∠1与∠2是同位角的图是（）A．①②B．①③C．②③D．③④【解答】解：①∠1和∠2是同位角；②∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角；③∠1和∠2是同位角；④∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角．故选：B．7．如图，直线a、b被直线c所截，互为同旁内角是（）A．∠4和∠6B．∠2和∠7C．∠4和∠5D．∠4和∠6【解答】解：∵直线a、b被直线c所截，∴互为同旁内角是∠4和∠5．故选：C．8．如图，∠1与∠2是同位角，若∠1＝63°，则∠2的大小是（）A．27°B．63°C．27°或63°D．不能确定【解答】解：因为被截的两条直线是相交还是平行无法确定，所以∠2与∠1的关系也无法确定，故∠2大小不能确定．故选：D．9．如图，直线AD，BE被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是（）A．∠4，∠2B．∠2，∠6C．∠5，∠4D．∠2，∠4【解答】解：∠1的同位角是∠2，∠5的内错角是∠6，故选：B．10．下列说法正确的是（）A．小于平角的角是直角B．相等的角是对顶角C．同位角相等D．互为邻补角的两角和等于180°【解答】解：A、小于平角的角是直角，也有可能是锐角，故本选项错误；B、如等腰三角形的两底角相等但不是对顶角，故本选项错误；C、两直线平行，同位角相等，故本选项错误；D、互为邻补角的两角和等于180°，故本选项正确．故选：D．11．如图，图中∠1与∠2是同位角的是（）A．（2）（3）B．（2）（3）（4）C．（1）（2）（4）D．（3）（4）【解答】解：（1）（2）（4）中，∠1与∠2是同位角；图（3）中，∠1与∠2不是同位角，因为这两个角的边所在的直线没有一条公共边．故选：C．12．如图，∠ADE和∠CED是（）A．同位角B．内错角C．同旁内角D．互为补角【解答】解：由图知，∠ADE和∠CED是直线AB和AC被DE所截形成的，在截线两侧，且在两被截线之间，故是内错角．故选：B．13．如图，直线a，b被直线c所截，则下列说法中错误的是（）A．∠1与∠3是对顶角B．∠1与∠2是邻补角C．∠3与∠4是内错角D．∠2与∠4是同位角【解答】解：A、∠1与∠3是对顶角，说法正确；B、∠2与∠3是邻补角，说法正确；C、∠3与∠4是同旁内角，故原说法错误；D、∠2与∠4是同位角，说法正确；故选：C．14．如图所示，下列说法中错误的是（）A．∠A和∠2是同旁内角B．∠A和∠3是同位角C．∠A和∠B是同旁内角D．∠C和∠1是内错角【解答】解：A、∠A和∠2不是同旁内角，原说法错误，故此选项符合题意；B、∠A和∠3是同位角，原说法正确，故此选项不符合题意；C、∠A和∠B是同旁内角，原说法正确，故此选项不符合题意；D、∠C和∠1是内错角，原说法正确，故此选项不符合题意；故选：A．15．如图，平行直线AB、CD与相交直线EF、GH相交，图中的同旁内角共有（）A．4对B．8对C．12对D．16对【解答】解：直线AB、CD被EF所截有2对同旁内角；直线AB、CD被GH所截有2对同旁内角；直线CD、EF被GH所截有2对同旁内角；直线CD、GH被EF所截有2对同旁内角；直线GH、EF被CD所截有2对同旁内角；直线AB、EF被GH所截有2对同旁内角；直线AB、GH被EF所截有2对同旁内角；直线EF、GH被AB所截有2对同旁内角．共有16对同旁内角．故选：D．二．填空题（共3小题）16．如图，射线DE、DC被直线AB所截得的用数字表示的角中，∠4与∠1是同位角．【解答】解：∠4与∠1是同位角，故答案为：∠1．17．如图，∠A的同位角是∠BFG，∠CGF，∠1的内错角是∠CGF，∠2的同旁内角是∠CGF或∠B 或∠A．【解答】解：∠A与∠BDG是直线AC、DE被直线AB所截形成的同位角，∠A与∠BFG是直线AC、DE被直线AB所截形成的同位角；∠1与∠CGF是直线AC、AB被直线DE所截形成的内错角；∠A与∠2是直线AB、BC被直线AC所截形成的同旁内角，∠2与∠B是直线AC、AB被直线BC所截形成的同旁内角，∠2与∠CGF是直线BC、DE被直线AC所截形成的同位角；故∠A的同位角是∠BFG，∠CGF，∠1的内错角是∠CGF，∠2的同旁内角是∠CGF或∠B或∠A．18．如图，∠1与∠B是同旁内角，它们是由直线AC和CB被直线AB所截而形成．【解答】解：∠1与∠B是直线AC、BC被AB所截而成的同旁内角，故答案为：同旁内；AC、BC、AB．。

三线八角练习题(打印版)

三线八角练习题（打印版）# 三线八角练习题## 一、选择题1. 下列关于三角形的描述，正确的是：A. 所有三角形的内角和都是180度B. 直角三角形的斜边一定长于直角边C. 等腰三角形的两个底角相等D. 所有三角形的外角和都是360度2. 如果一个三角形的三个内角分别为α、β、γ，那么以下哪个表达式是正确的？A. α + β + γ = 180度B. α + β = 90度C. α = β = γD. α > β + γ3. 在直角三角形中，如果已知斜边长度为c，一条直角边长度为a，那么另一条直角边的长度b可以通过以下哪个公式计算？A. b = c - aB. b = √(c² - a²)C. b = a²/cD. b = c/a## 二、填空题1. 三角形的中线是从三角形的________点到________点的连线。

2. 如果三角形的两边长分别为3和4，第三边的长度x满足________，则这个三角形是直角三角形。

3. 等边三角形的每个内角都是________度。

## 三、计算题1. 已知三角形ABC，∠A = 40度，∠B = 60度，求∠C的大小。

2. 如果三角形DEF的边DE = 5cm，DF = 7cm，EF = 6cm，求∠D的大小。

## 四、证明题1. 证明：在一个直角三角形中，如果一直角边是斜边的一半，则另一个直角边也是斜边的一半。

2. 证明：等腰三角形的中线、高线和角平分线是同一条线。

## 五、应用题1. 一个梯形的上底为3cm，下底为7cm，高为4cm，求梯形的面积。

2. 一个等腰直角三角形的斜边长为10cm，求它的面积。

注意：请在答题纸上作答，并保持字迹清晰、整洁。

祝答题顺利！。

七年级数学三线八角试卷

一、选择题（每题3分，共15分）1. 在下列图形中，哪个图形是三线八角图形？A. 正方形B. 等边三角形C. 长方形D. 等腰梯形2. 一个三线八角图形的三个角分别是45°、45°、90°，那么这个图形是：A. 正方形B. 等腰梯形C. 等腰直角三角形D. 长方形3. 在一个三线八角图形中，如果三个角分别是60°、60°、120°，那么这个图形是：A. 正方形B. 等腰梯形C. 等边三角形D. 长方形4. 下列关于三线八角图形的说法正确的是：A. 三线八角图形一定是等腰梯形B. 三线八角图形的三个角都是直角C. 三线八角图形一定是等腰梯形或正方形D. 三线八角图形的三个角都是锐角5. 一个三线八角图形的三个角分别是30°、60°、90°，那么这个图形的面积与一个等边三角形的面积之比是：A. 1:1B. 1:2C. 2:1D. 3:1二、填空题（每题5分，共25分）6. 一个三线八角图形的三个角分别是45°、45°、90°，那么这个图形的面积是正方形面积的______。

7. 如果一个三线八角图形的三个角分别是30°、60°、90°，那么这个图形的边长是等边三角形边长的______。

8. 一个三线八角图形的三个角分别是45°、45°、90°，那么这个图形的周长是正方形周长的______。

9. 一个三线八角图形的三个角分别是60°、60°、120°，那么这个图形的面积是等边三角形面积的______。

10. 一个三线八角图形的三个角分别是30°、60°、90°，那么这个图形的周长是等边三角形周长的______。

三、解答题（每题10分，共20分）11. （1）画出一个三线八角图形，并标出三个角的大小。

平行线三线八角经典例题

选择题题目: 两条平行线被第三条直线所截，下列哪个角对不是同位角？A. ∠1 和∠5B. ∠2 和∠6C. ∠3 和∠7（正确答案）D. ∠4 和∠8题目: 已知两条平行线被一条斜线截断，如果∠1 = 50°，那么它的同旁内角等于？A. 50°B. 130°（正确答案）C. 40°D. 140°题目: 两条平行线被第三条直线所截，若∠1 和∠2 是内错角，且∠1 = 60°，则∠2 为？A. 30°B. 60°（正确答案）C. 120°D. 90°题目: 下列关于平行线和相交线的说法中，错误的是？A. 同位角相等，则两直线平行B. 内错角相等，则两直线平行C. 同旁内角互补，则两直线相交（正确答案）D. 对顶角相等，则两直线可能相交或平行题目: 两条平行线被第三条直线所截，如果∠3 = 70°，那么它的对顶角是？A. 20°B. 70°（正确答案）C. 110°D. 180° - 70°题目: 在两条平行线被第三条直线所截形成的八个角中，如果已知一个同位角是45°，那么它的另一个同位角是？A. 45°（正确答案）B. 90° - 45°C. 180° - 45°D. 360° - 45°题目: 两条平行线被第三条直线所截，下列哪组角是一定不相等的？A. 同位角B. 内错角C. 对顶角在不同直线上的两个角（正确答案）D. 同旁内角的补角题目: 已知两条平行线被一条斜线截断，若∠5 = 110°，则它的同旁外角是？A. 110°B. 70°（正确答案）C. 180° - 110°D. 360° - 110°题目: 在两条平行线被第三条直线所截的图形中，如果∠2 和∠6 是内错角，且∠2 = 80°，那么∠6 等于？A. 10°B. 80°（正确答案）C. 100°D. 180° - 80°。

三线八角练习题

三线八角练习题一、选择题1. 在平面几何中，两直线相交所形成的角叫做：A. 对顶角B. 邻补角B. 同位角D. 内错角2. 当两条直线被第三条直线所截时，如果同侧的同位角相等，那么这两条直线：A. 平行B. 相交C. 垂直D. 重合3. 如果两条直线被第三条直线所截，且内错角相等，那么这两条直线：A. 平行B. 相交C. 垂直D. 重合4. 同旁内角是指两条直线被第三条直线所截，位于截线同侧的两个角，它们是：A. 对顶角B. 邻补角C. 同位角D. 内错角5. 邻补角是指两条直线相交后，相邻的两个角，它们的和等于：A. 90°B. 180°C. 270°D. 360°二、填空题6. 当两条直线相交，如果它们的对顶角相等，则这两条直线______。

7. 两条平行线被第三条直线所截，同位角一定______。

8. 如果两条直线被第三条直线所截，且它们的内错角相等，那么这两条直线______。

9. 同旁内角互补的条件是两条直线被第三条直线所截，且这两条直线______。

10. 邻补角相等的条件是两条直线相交，且它们的和等于______。

三、判断题11. 如果两条直线被第三条直线所截，同旁内角互补，则这两条直线平行。

（）12. 对顶角一定相等。

（）13. 两条直线相交，它们的同位角相等，这两条直线一定平行。

（）14. 两条直线被第三条直线所截，如果内错角不相等，那么这两条直线一定不平行。

（）15. 邻补角的和一定等于180°。

（）四、简答题16. 解释什么是同位角，并给出一个例子。

17. 描述如何通过同旁内角来判断两条直线是否平行。

18. 说明为什么对顶角相等的条件是两条直线相交。

19. 阐述邻补角相等时，两条直线的关系。

20. 讨论在平面几何中，为什么两条平行线被第三条直线所截时，同位角相等。

五、解答题21. 在平面几何中，已知直线AB和CD相交于点P，直线EF平行于AB，求证：∠EPD和∠EPA是同位角。

(完整)初中三线八角和平行线定义练习.docx

三线八角和平行线定义【例题讲解】1、如图所示 ,∠ 1 和∠ 2 是对顶角的图形有()12112221A.1 个B.2 个C.3 个D.4 个2、图，直线 a,b 相交， 1 45 ，求2, 3, 4 的度数。

【轻松试一试】已知，如图，AOC 35 , COF 80 ，求：AOD和DOF 的度数【例题讲解】1、如图，直线AB、CD、 EF 相交于点O，AOE 的对顶角是，COF的邻补角是若AOC：AOE =2：3，EOD 130 ，则BOC =【轻松试一试】如图，直线AB、 CD相交于点 O，COE FOB 90 , AOC 30 则EOF余角、补角的应用（互为邻补角的两个角平分线_________ ）【例题讲解】AC为一直线， O是 AC上一点，且∠AOB=120°， OE、 OF分别平分∠ AOB、∠ BOC。

E BFA CO（1）求∠ EOF的大小（2）当 OB绕 O点旋转 OE、OF仍为∠ AOB和∠ BOC的角平分线，问 OE、 OF有怎样的位置关系？【轻松试一试】（邻补角在折叠问题中的应用）将一张长方形纸片按如图的方式折叠，BC、BD为折痕，试判断∠CBD的度数是多少？二、垂线及其性质（重点）（一）垂线的定义：当两条直线相交的四个角中，有一个角是直角时，就说这两条直线是互相垂直的，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

如图，直线 AB 、 CD 互相垂直，记作AB CD ，垂足为O。

1、如遇到线段与线段、线段与射线、射线与射线、线段或射线与直线垂直，特指它们所在的直线互相垂直。

C2、掌握如下的推理过程：（如上图）已知），AB CD (AOCCOBBOD AOD 90 (垂直定义）.A OB 反之，AOC 90 (已知）D AB CD (垂直定义）（二）垂线的画法性质 1过一点有且只有一条直线与已知直线垂直。

性质 2连接直线外一点与直线上各点的所有线段中，垂线段最短。

三线八角练习题

三线八角练习题一、选择题1. 在平面几何中，两条直线相交，形成的角叫做：A. 邻角B. 对顶角C. 同位角D. 内错角2. 如果两条直线被第三条直线所截，那么同位角的特点是：A. 相等B. 不等C. 互补D. 互余3. 对顶角的性质是：A. 相等B. 不等C. 互补D. 互余4. 三线八角中，内错角的特点是：A. 相等B. 不等C. 互补D. 互余5. 当两条平行线被第三条直线所截时，同旁内角的特点是：A. 相等B. 不等C. 互补D. 互余二、填空题6. 当两条直线相交时，形成的角中，不相邻的两个角叫做________。

7. 如果两条直线相交，它们的对顶角具有________的性质。

8. 当两条平行线被第三条直线所截时，同位角具有________的特点。

9. 在三线八角中，内错角是指两条直线被第三条直线所截时，位于截线同侧的两个角，它们具有________的特点。

10. 同旁内角是指两条平行线被第三条直线所截时，位于截线同侧的两个角，它们具有________的特点。

三、判断题11. 两条平行线被第三条直线所截，同旁内角互补。

（）12. 两条直线相交，形成的角中，相邻的两个角叫做邻角。

（）13. 对顶角一定相等。

（）14. 同位角一定相等。

（）15. 内错角一定相等。

（）四、简答题16. 请解释什么是三线八角，并说明它们在几何中的重要性。

17. 描述两条平行线被第三条直线所截时，各对角之间的关系。

18. 举例说明对顶角和内错角在实际问题中的应用。

五、计算题19. 如图所示，直线AB和CD相交于点O，已知∠AOC=40°，求∠AOD 的度数。

20. 若两条平行线被第三条直线所截，且同位角的度数为60°，求内错角的度数。

六、证明题21. 证明：如果两条直线平行，那么它们被第三条直线所截时，同旁内角互补。

22. 证明：两条直线相交，形成的对顶角一定相等。

七、应用题23. 在一个平面直角坐标系中，点A(-3,4)，点B(-3,-2)，点C(1,-2)在同一直线上，点D(1,4)，求证∠BAC和∠BDC是对顶角。

试题三线八角

周清试题（用1页纸无声独立解答，看谁是真正的诚信者）一、选择（每题3分）1.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ). A.1 B.2 C.3或2 D.1或2或32.下列结论中，错误的是( )A ．同一个角的两个邻补角是对顶角B ．对顶角相等，相等的两个角也是对顶角C ．对顶角的平分线在一条直线上D ．邻补角的平分线互相垂直 3.垂线的一个性质是（）A 、过一点有一条直线与已知直线垂直B 、过一点只有一条直线与已知直线垂直C 、过一点有且只有一条直线与已知直线垂直D 、过一点能画出一条直线与已知直线垂直 4、画一条线段的垂线，垂足在（）A 、线段上B 、线段的端点C 、线段的延长线上D 、以上都有可能 5、点到直线的距离是指这点到这条直线的（）A 、垂线段B 、垂线的长C 、长度D 、垂线段的长度 6、已知点O ，画和点O 的距离是3厘米的直线可以画（） A 、1条 B 、2条 C 、3条 D 、无数条二、填空（每题3分）1、如图4所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.34D CBA 12OFE D CB A OED CBA(4) (5) (6) 2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.3.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠COB=_______.4.如图6所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠BOD=•______.5.对顶角的性质是______________________.6.如图7所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____。

ODC BA 12OE D CBA OE DCBA(7) (8) (9)7.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•则∠EOB=______________.8.如图9所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,•且∠BOE:∠EOD=2:3,则∠EOD=________.三、解答（题每题8分）1、如图所示,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE•的度数.O ED CBA2.如图，O为直线AB上一点，∠BOC = 3∠AOC，OC平分∠AOD；⑴求∠AOC的度数；⑵推测OD与AB的位置关系，并说明理由。

三线八角

10756894321(1)D C A B N M P (2)Q 564321A B N M P (4)O Q l a 75684321b (3)一、判断（每题1分，共10分） 1.如图1,∠2和∠8是对顶角.( ) 2.如图1,∠2和∠4是同位角.( )3.如图1,∠1和∠3是同位角.( )4.如图1,∠9和∠10是同旁内角,5.如图1,∠1和∠7也是同旁内角.( )6.如图1,∠2和∠10是内错角.( )二、填空1.如图3,直线L 截直线a,b 所得的同位角有______对,它们是_ _____;•内错角有___对,它们是_____ _;同旁内角有______对,•它们是_____ _;•对顶角_____•对,•它们是_____ _.2.如图2,其中共有对同位角内错角 , 同旁内角 .3.如图4,∠1的同位角是________,∠1的内错角是________,∠1•的同旁内角是_______.[一]、平行线的判定一、填空1．如图１，若∠A=∠3，则 ∥ ；若∠2=∠E ，则 ∥ ；若∠ +∠ = 180°，则 ∥ ．2．若a⊥c，b⊥c，则a b ．3．如图２，写出一个能判定直线l 1∥l 2的条件：．4．在四边形ABCD 中，∠A +∠B = 180°，则 ∥ （）．5．如图３，若∠1 +∠2 = 180°，则 ∥ 。

6．如图４，∠1、∠2、∠3、∠4、∠5中，同位角有；内错角有；同旁内角有．A CB 4 1 2 3 5 图４ a b c d 1 2 3 图３ A BC ED 1 2 3 图１图２ 4 3 2 1 5 a b7．如图５，填空并在括号中填理由：（1）由∠ABD =∠CDB 得 ∥ （）；（2）由∠CAD =∠ACB 得 ∥ （）；（3）由∠CBA +∠BAD = 180°得 ∥ （）8．如图６，尽可能多地写出直线l 1∥l 2的条件：．9．如图７，尽可能地写出能判定AB∥CD 的条件来：．10．如图８，推理填空：（1）∵∠A =∠ （已知）， ∴AC∥ED（）；（2）∵∠2 =∠ （已知）， ∴AC∥ED（）；（3）∵∠A +∠ = 180°（已知）， ∴AB∥FD（）；（4）∵∠2 +∠ = 180°（已知），∴AC∥ED（）；二、解答下列各题11．如图９，∠D =∠A，∠B =∠FCB，求证：ED∥CF．12．如图10，∠1∶∠2∶∠3 = 2∶3∶4， ∠AFE = 60°，∠BDE =120°，写出图中平行的直线，并说明理由．13．如图11，直线AB 、CD 被EF 所截，∠1 =∠2，∠CNF =∠BME。