第5章1、2矩形谐振腔
4.3 矩形谐振腔

(4-31)
第四章 微波谐振器
矩形谐振腔 §4.3 矩形谐振腔
横向场量可以用纵向场量求出来
r 1 ∂ H t = 2 (∇t H z ) K c ∂z r 1 Et = 2 ( jωµ z × ∇t H z ) ˆ Kc v v ˆ Et = − Z TE z × H t
Ex = − jωµ ∂H z 2 K c ∂y
2
λr =2ຫໍສະໝຸດ v 2π = fr K2
m n p + + a b l
λr =
2π 2 = 2 2 2 K m n p + + a b l
(4-37)
第四章 微波谐振器
矩形谐振腔 §4.3 矩形谐振腔
两个传播方向相反的行波叠加时, 两个传播方向相反的行波叠加时,场的表达式为
mπ + E z = E0 sin a mπ − y e − jβ z + E0 sin a nπ x sin b y e jβ z
若z=0处放一短路板,则有边界条件 z=0处放一短路板, 处放一短路板
E x z =l = 0
pπ ( p = 0,1,2,3L) l
βl = pπ 或 β =
则腔体内TM 则腔体内TMmnp模的纵向电场为
矩形谐振腔讲义

五、TE101模的Q值
结合上面三种情况可知
Rs λ2 2 ab bl 1 a l 0 PL = E0 2 + 2 + + 2 8η 2 l a a l
代入Q 代入Q值公式
Q0 =
Rsλ 8η
2 0 2
8 ab 1 a bl l + E 02 2 + 2 + 2 l a a l
四、矩形构
五、TE101模的Q值
W = (We ) max
2 1 1 l b a 2 2 π = ε ∫ E dv = ε ∫ ∫ ∫ E0 sin a 2 V 2 0 0 0
π x sin 2 l
l
1 2 z dxdydz = ablεE0 8
二、品质因数Q0
v2 1 W = We + Wm = ∫ µ| H | dv 2 v
(31(31-7)
而导体壁损耗
1 1 2 PL = ∫ | J s | Rs ds = Rs ∫ | Hτ |2 ds S 2 S 2
ω0µ
s
(31(31-8)
式中R 是表面电阻率, 式中Rs是表面电阻率, R = 2σ , H 为切向磁场。 为切向磁场。 因此, 所对应的谐振腔Q 因此,有限电导率σ所对应的谐振腔Q值
βl = pπ
则有
( p = 1,2,3,L )
(31(31-4)
λ0 =
2 m n p + + a b l
2 2 2
=
1 1 p + λ 2l c
2 2
(31(31-5)
二、品质因数Q0
第5章_高功率微波源

冲功率与连续波功率
5.2.1 发展概况及基本原理
电子回旋脉塞期间包括一大类器件,这 类期间又称为回旋管系列,属于快波器件. 电子回旋脉塞器件能以各种方式在跨越 厘米波,毫米波甚至亚毫米波的范围内产 生高脉冲功率与连续波功率
电子回旋脉塞发展历史
电子回旋脉塞起源于50年代末期,但是有3位学者开始进行电 子回旋脉塞互相作用产生微波的理论研究.
第五章 高功率微波源 Development and Appling of High Power Microwave(HPM)
5.1 引言
5.2 电子回旋脉塞及回旋管系列
5.3 相对论普通微波管系列 5.4 其他高功率微波器件
电磁波谱及主要产生方式
1 高功率微波(high power microwave-HPM)
如果高频场的角频率与电子回旋频率相等,受加 速的电子数等于受减速的电子数 如国高频场的角频率小于电子回旋频率.电磁波 场的旋转速度略慢于电子的旋转速度,则电子的 群聚落入加速场,有更多的电子受到加速而从波 场获得能量,场被电子吸收能量而衰减. 如国高频场的角频率大于电子回旋频率,电磁波 场的旋转速度略大于电子的旋转速度,则电子的 群聚落入波场的减速区.在场的一个周期内,减 速的电子数大于加速的电子数.净效果是电子注 失去能量,将能量交给高频场,波场得到增强,于 是产生微波振荡或放大.
非致命武器1美国陆军实验室正在研制的地面车辆制动装置就是利用微波源产生的脉冲波爆使远处的正在高速行驶的汽车失灵甚至报废2电力分配弹药epdmelectricpowerdistributionmanition当其飞抵目标上方时爆炸释放出大量松散的传导性碳纤维缠丝随风飘落缠绕在高能电缆上使电子设备严重短路3目前正在研制中的隐蔽式眩目激光武器是使用荧光技术其发射出的紫外光照射眼睛后眼睛会产生荧光感应出现视线模糊使人致晕但无致人失明的危险
题库-微波技术与天线

微波技术与天线题库一、填空题1. 驻波比的取值范围为;当传输线上全反射时,反射系数为,此时驻波比ρ等于。
2. γ=α+jβ称为,其中α称为,它表示传输线上的波,β称为,它表示传输线上的波。
3. 特性阻抗50欧的均匀传输线终端接负载Z1为20j欧、50欧和20欧时,传输线上分别形10cm,如图所示:Z in=;Z in=;在z=5cm处的输入阻抗Z in=;2.5cm<z<5cm处,Z in呈性。
ρ=。
5. 无耗传输线的终端短路和开路时,阻抗分布曲线的主要区别是终端开路时在终端处等效为谐振电路,终端短路时在终端处等效为谐振电路。
6. 一段长度为l(0<l<λ/4)短路线和开路线的输入阻抗分别呈纯和纯。
7. 阻抗匹配分为阻抗匹配、阻抗匹配和阻抗匹配,它们反映Z0,根据各点在下图所示的阻抗圆( );( );⑤R<Z0,X=0 ( ); ⑥R=Z0,X=0 ( );⑦Г=0 ( ); ⑧SWR=1 ( );⑨=1Γ( ); ⑩ SWR=∞( ).9. 在导行波中, 截止波长λc最长的电磁波模称为该导波系统的主模。
矩形波导的主模为模, 因为该模式具有场结构简单、稳定、频带宽和损耗小等特点, 所以实用时几乎毫无例外地工作在该模式。
10. 与矩形波导一样,圆波导中也只能传输TE波和TM波;模是圆波导的主模,模是圆波导第一个高次模,而模的损耗最低,这三种模式是常用的模式。
11. 在直角坐标系中,TEM波的分量E z和H z为零;TE波的分量为零;TM波的分量为零。
12. 低频电路是参数电路,采用分析方法,微波电路是参数电路,采用分析方法。
13. 简并模式的特点就是具有相同的和不同的。
14. 微带线的弯区段、宽度上的阶变或接头的不连续性可能会导致电路性能的恶化,主要是因为这种不连续性会引入。
15. 写出下列微波元件的名称。
(a) (b) (c) (d)16. 下图(a)为微带威尔金森功分器,特性阻抗等于,其电长度L等于。
第5章谐振腔

三、谐振腔的几何参数 1、RL参数 参数
R1 L R2
R1、R2:两镜面曲率半径,L:腔长 两镜面曲率半径, : 2、g参数 参数
L g1 =1− R 1 L g2 =1− R2
§2 光线变换矩阵 一、光线坐标矩阵
r θ
θ r
r:光线位置到轴线距离 轴线上方为正 光线位置到轴线距离(轴线上方为正 光线位置到轴线距离 轴线上方为正) 光线方向与轴线方向(水平 所夹锐角(向 水平)所夹锐角 θ: 光线方向与轴线方向 水平 所夹锐角 向 上传播为正) 上传播为正
∴-1< 2g1g2 −1<1
(2) g1=g2=0 证
A= 2g2 −1= −1
B = 2Lg2 = 0
2 C = − (g1 + g2 −2g1g2 ) = 0 L D = 4g1g2 −2g2 −1= −1
−1 0 T = 0 −1
−1 0 −1 0 1 0 T = 0 −1 0 −1 = 0 1
例 稳定: 稳定: 非稳: 非稳:
例 判断谐振腔的稳定性 单位 判断谐振腔的稳定性(单位 单位:mm) (1)R1=80,R2=40,L=100 解
100 1 g1 =1− =− 80 4 g1g2 = 3 8
100 3 g2 =1− =− 40 2
R1 R2
稳定
(2)R1=20, R2=10, L=50 解
ϕ = arccos 1 (A+ D) 2
A、B、C、D:往返一周的光线变换 矩阵元素 ix −ix
e −e sin x = 2i
§3 谐振腔的稳定性 一、稳定腔的概念 1、物理意义 镜面上任一点发出的近轴光线,往返无 镜面上任一点发出的近轴光线, 限次而不逸出 2、数学意义 Tn各元素当 n →∞时,保持有界 保持有界
《矩形谐振腔》课件

矩形谐振腔的设计
1
设计参数
2
包括谐振腔尺寸、波导位置、材料选择
等。
3
一般步骤
确定频率、计算谐振腔尺寸、优化设工具等。
矩形谐振腔的应用
微波和微纳电子学
矩形谐振腔在微波电路和微纳电子学中广泛应用, 用于滤波、频率选择和放大等。
量子计算
矩形谐振腔是量子计算中的关键元件,用于存储和 操作量子比特。
参考文献
相关研究论文
1. "矩形谐振腔的设计与制作",XXX期刊,2020 年。
网络资源
2. "如何设计优秀的矩形谐振腔",微电子论坛, https://www.***.com
谐振模式的定义
谐振模式是矩形谐振腔中特定频率下的电磁场分布形态,不同模式对应不同的场分布和电磁能量分布。
不同谐振模式的特点
TE10
最简单的模式,电场仅沿一个方向震荡。
TM11
电场和磁场都存在,和波导边界垂直。
TE01
场与波导边界垂直,纵向波动不变。
TE20
正方形波导才有的模式,电场沿两个方向震荡。
实验
1
测量共振频率
通过改变谐振腔的尺寸,测量不同谐振
测量Q值
2
模式的共振频率。
通过测量共振峰的宽度,计算谐振腔的 品质因数(Q值)。
结论
1 优点与不足
2 未来发展趋势
矩形谐振腔具有结构简单、易于制作的优点, 但波导的存在会引入损耗。
随着技术的不断进步,矩形谐振腔将在量子 计算和通信领域发挥越来越重要的作用。
《矩形谐振腔》PPT课件
矩形谐振腔是微波和微纳电子学中常见的元件。本课件将详细介绍矩形谐振 腔的定义、工作原理、谐振模式以及设计和应用。
第5章光学谐振腔的基本理论

B sin n
sin
D sin n sin (n 1)
sin
arccos
1 2
(A
D)
1、值是实数(-1<cos<1)时, Tn各元素有界谐
振腔为稳定腔。 2、值有虚部时(-1>cos或者cos>1),旁轴 光线往返有限次后便会逸出谐振腔,谐振腔为非
稳腔。
3、值等于0或者π(cos=±1),Tn各项元素的值
38
§3 谐振腔的衍射理论基础
激光器中所使用的谐振腔是一种开腔, 在这种没有侧面边界的区域内是否存在电磁 场的本征态,即不随时间而变化的稳态场分 布?如何求出这种场分布?这些问题需要用谐 振腔的衍射理论来解决。本节首先给出理想 开腔的模型——孔阑传输线,在此基础上引 入稳态场分布——自再现模的概念。
T
2 R1
10
1 0
L 1
1 2
R2
10
1 0
L 1
1 L 1 L
2 R1
1
2L R1
2 R2
1
2L R2
2L
1 R2
2 R1
2 R2
4L R1R2
2L2
2L R1
2L R2
(1 2L )(1 R1
2L R2
)
=
A C
B
D
15
A
1
2L R2
2(1
L R2
)
1
2g2
1
2L2
L
B 2L R2 2L(1 R2 ) 2Lg2
4L 2 2 2 L L 2L2
C
( )
R1R2 R1 R2
L R1 R2 R1R2
微波谐振腔特性参数的计算和仿真

毕业论文二0一一年六月微波谐振腔特性参数的计算和仿真专业班级:通信工程3班姓名:指导教师:摘要微波谐振腔其内部的电磁场分布在空间三个坐标方向上都将受到限制,均成驻波分布.微波谐振腔在微波电路中起着与低频LC振荡回路相同的作用,是一种具有储能和选频特性的谐振器件.这次主要研究矩形谐振腔和圆柱体谐振腔的特性参数的计算和仿真.计算时用VC++中的MFC编写一个小界面计算工具,当输入变量参数时,类似计算器形式直接输出计算结果,仿真所用软件为HFSS,对矩形谐振腔和圆柱谐振腔进行仿真,输入变量得出仿真结果并与上述结算结果进行比较。
本文首先介绍了微波谐振腔的发展及前景和理论基础知识和MFC,Hfss等软件.然后分别进行了:1.对金属谐振腔中特性参数的特性及计算方式进行深入探讨,学习其基本特性与基本分析方法。
2.矩形谐振腔和圆柱谐振腔特性参数的计算在小界面计算方式方式下表示,并举例输入变量得出计算结果。
3.用Hfss微波技术仿真软件对矩形谐振腔和圆柱谐振腔仿真,与之前的结果进行比较。
4.在小界面计算工具在输入不同尺寸,内部填充不同材料,以及用铜,铁,铝等材料作为谐振腔表面材料等多种情况下计算,得出不同结果,并用仿真软件对矩形及圆柱谐振腔仿真,两组数据比较并得出结果。
本文主要研究金属谐振腔中矩形谐振腔及圆柱谐振腔特性参数的特性及计算方法,对其特性参数的特点,计算方式进行深入研究,然后运用编程软件对其编程,得到一个便捷的计算工具,并对矩形及圆柱谐振腔仿真,计算结果与仿真结果比较来判别计算工具的实用性与便捷性。
关键词:金属谐振腔,特性参数,MFC,小界面,Hfss,仿真AbstractMicrowave resonant cavity of internal electromagnetic field distribution in space three coordinate direction will be limited, all into standing wave distribution. Microwave resonator in microwave circuits plays and low frequency oscillation loop of the same role LC, is one kind has the energy storage and choose the resonance frequency characteristics of the device. The main research rectangular resonant cavity and cylinder of resonance cavity characteristic parameters of the calculation and simulation calculation with vc + +. When the MFC write a small interface calculation tool, when the input variable parameter, similar calculator form output calculation result directly, and the simulation software for HFSS, used for rectangular resonant cavity and cylindrical a rectangular resonant cavity simulation, the input variables that the simulation results and the results were compared with the settlement. This paper first introduces the development of microwave resonator and prospects and theoretical knowledge and MFC, Hfss and software. And then, the:1. To metal in a resonant cavity characteristic parameters of the characteristics and calculation way further discusses the basic characteristics and learning basic analysis method.2. Rectangular resonant cavity and cylindrical resonator parameters calculation in small interface calculated method, and an example is said that the calculation results input variables.3. With Hfss microwave technology simulation software of the rectangular resonant cavity and cylindrical resonant cavity, and the results of the simulation before the comparison.4. In a small interface computing tools in different size, internal filling input, and different material with copper, iron, aluminum and other materials as a resonant cavity surface material, etc cases calculated, different results, and the simulation software of the rectangular cylinder and resonant cavity simulation, two sets of data and compared to obtain the result.This paper makes a study of the metal in a resonant cavity rectangular resonant cavity and cylindrical resonator characteristic parameters of the characteristics and calculation method, and the characteristic parameters of the method for calculating the characteristics, further research and study, and then use of its programming software programming, get a convenient calculation tool, and in rectangular cylinder and resonant cavity simulation, the results and simulation results is discrimination computing tools of practicality and convenience.Keywords:metal resonator, characteristic parameters, MFC, small interface, Hfss,目录第1章绪论 (1)1.1研究背景及概况 (1)1.2谐振腔的发展和应用 (2)1.3本文主要的工作 (3)第2章微波谐振腔的基本理论 (4)2.1 引言 (4)2.2 谐振频率f0的概念与计算方法 (5)2.3 品质因数Q的概念与计算方法 (7)第3章:金属波导型谐振腔 (10)3.1 矩形谐振腔 (10)3.1.1 矩形谐振腔谐振频率f0的计算方法 (13)3.1.2 矩形谐振腔品质因数Q的计算方法 (13)3.2 圆柱谐振腔 (15)第3章微波谐振腔特性参数的计算 (18)4.1 关于MFC (18)4.2 运用MFC进行编写的具体步骤 (18)4.2.1 对矩形腔编程 (19)4.2.2 对圆柱腔编程 (20)4.3 具体数据代入计算 (21)第5章微波谐振腔的仿真 (23)5.1 电磁仿真软件ANSOFT HFSS (23)5.2谐振腔的的仿真步骤 (24)5.2.1 矩形谐振腔的的仿真步骤 (24)5.2.2 圆柱谐振腔的的仿真步骤 (26)5.3 对实验结果进行分析 (27)第6章:总结 (31)参考文献 (32)致谢 (33)微波谐振腔特性参数的计算和仿真第1章绪论1.1研究背景及概况目前,随着移动通信,卫星通信的迅速发展,和通讯设备的进一步向多功能,便携化,全数字化和高集成化方向发展,极大地推动了电子元器件的小型化,片式化和低成本化,以及其间组合化,功能集成化的发展进程。
矩形谐振腔PPT课件

Hx
k2jkzkz2
Hz x
jkz z
Hy
k2jkzkz2
Hz y
jk z
z
Hx
k2
1 kz2
(Hz x z
)
Hy
k2
1 kz2
(Hz y z
)
Ex
j
k2 kz2
Hz y
Ey
j
k2 kz2
Hz x
Ez 0
2020/6/10
.
14
第九章 导行电磁波
H z ( x ,y ,z ) c o s ( m a x ) c o s ( n b y ) ( D 1 e jk z z D 2 e jk z z )
因为随着频率升高,必须减小 LC 谐振电路的电感量和电 容量,但是当 LC 很小时,分布参数的影响不可忽略。电容器 的引线电感、线圈之间以及器件之间的分布电容必须考虑。
随着频率升高,回路的电磁辐射效应显著,电容器中的 介质损耗也随之增加,这些因素导致谐振电路的品质因素 Q 值显著下降。
在米波以上的微波波段,经常使用相应波段的传输线来构 成谐振器件。
衰减常数 Pl
2P
[Np m]
P l 单位长度波导壁的功率损耗
P 单位长度波导壁的传输功率
TE10
b
Rs
[12b( fc)2]
1( fc)2
af
TM
f
11
2020/6/10
电磁场. 理论
3
第九章 导行电磁波
9-5 矩形谐振腔
研究波导谐振腔的意义
在米波以上的微波波段,集总参数的LC谐振电路无法使用。
m 、 n 和 p 取不同的值,可得不同模式的TM波,称为 TMmnp 模式。
《矩形谐振腔》课件

采用遗传算法、粒子群算法等优化算 法,对矩形谐振腔进行优化设计,以 提高其性能。
04
矩形谐振腔的制造工艺
加工工艺流程
切割与成型
使用切割机和成型机对材料进行 精确加工,得到矩形谐振腔的初 步形状。
组装与调试
将各部分组合在一起,并进行必 要的调整和测试,以确保其性能 达标。
01
材料准备
选择合适的材料,如铜、铝或不 锈钢,确保其物理和化学属性满 足谐振腔的设计要求。
03
表面处理不均匀
表面处理过程中可能出现不均 匀的情况,影响电磁性能。解 决策略包括加强工艺控制和增 加后处理工序。
04
组装误差
部件组装时可能出现误差,导 致性能下降。应对措施包括采 用精密的测量设备和严格的组 装流程管理。
05
矩形谐振腔的性能测试与分析
测试设备与方法
01
测试设备
02
高精度频谱分析仪
分析频率响应曲线,确定矩形谐振腔的工作频 带和带宽。
测试结果分析
阻抗匹配
测量矩形谐振腔的输入和输出阻抗。
分析阻抗匹配情况,判断矩形谐振腔是否具有良好的 能量传输效率。
测试结果分析
01
群时延
02
测量矩形谐振腔在不同频率下的群时延。
03 分析群时延曲线,评估矩形谐振腔对信号的畸变 程度。
结果与讨论
雷达制导
在雷达制导系统中,矩形谐振腔可用于信号处理和目标识别,提高制导精度和抗干扰能力。
其他领域的应用
微波测量
矩形谐振腔可用于微波测量领域,如微波频谱分析、微波传感器等。
电子对抗
在电子对抗中,矩形谐振腔可用于信号干扰和欺骗,提高电子设备的抗干扰能力。
激光原理周炳坤-第5章习题答案

第五章 激光振荡特性1、证明: 由谐振腔内光强的连续性,有:I =I 'ηη''=⇒'⋅'=⋅⇒C N CNV N V N 谐振腔内总光子数 )(l L S N NSl -'+=Φ)(l L NS NSl -'+=ηη ηηη/])([l l L NS +-'=η/L NS '= , 其中)(l L l L -'+='ηηRNSl C n dt d τησΦ-∆=Φ21 R L NS NSl C n dt dN L S ητηση'-∆='21 , CL R δτ'=L CNL l CN n dt dN '-'∆=δσ212.长度为10cm 的红宝石棒置于长度为20cm 的光谐振腔中,红宝石谱线的自发辐射寿命3410s s τ-≈⨯,均匀加宽线宽为5210MHz ⨯。
光腔单程损耗0.2δ=。
求(1)阈值反转粒子数t n ∆;(2)当光泵激励产生反转粒子数 1.2t n n ∆=∆时,有多少个纵模可以振荡(红宝石折射率为 解:(1) 阈值反转粒子数为:222212112337217344210 1.764100.2 cm 10(694.310) 4.0610cm H s t n l l πνητδδσλπ----∆∆==⨯⨯⨯⨯⨯⨯=⨯⨯=⨯(2) 按照题意 1.2m t g g =,若振荡带宽为osc ν∆,则应该有22221.222H t t osc H g g ννν∆⎛⎫ ⎪⎝⎭=∆∆⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭ 由上式可以得到108.9410Hz osc H νν∆==⨯相邻纵模频率间隔为10831022( 1.76())2(10 1.7610) 5.4310Hzq c c l l L l ν⨯∆==='⨯+-⨯+=⨯ 所以1088.9410164.65.4310osc q νν∆⨯==∆⨯ 所以有164~165个纵模可以起振。
第5章1、2矩形谐振腔
2016/4/15
第五章 微波谐振腔
5.1 简介
两块相对放置的导体板也可构成微波谐 振腔,如果导体板的尺度远大于微波波长。 r r
这种腔体被称为开放式微波谐振腔。
这两种谐振腔在毫米波、远 红外和光波频段有广泛用途 。 利用介质材料参数的周期性 或非周期性变化,可以构成所谓 分布反馈谐振腔。
2016/4/15
m m n m m n ) sin( x)cos ( y) sin(t z ) D' ( ) sin( x)cos ( y) sin(t z ) a a b a a b
E y ( x, y, z, t ) (
2016/4/15
m m n ) sin ( x)cos( y) D' sin (t z ) D' sin (t z ) a a b
b2
a1
2016/4/15 4
第五章 微波谐振腔
5.1 简介
2a
圆波导
两块相对放置的导体板也可构成微波谐 振腔,如果导体板的尺度远大于微波波长。 这种腔体被称为开放式微波谐振腔。
r
r
当电磁波波长较短时,很容易实现这种 谐振腔。在光学系统中,这种谐振腔称为 FP 腔。 优点是品质因数高(选频特性好)。
(5-2)
(1) 由边界条件 Ex(x,y,z = 0, t) 0 可得:D' = D' = D'
(2) 由边界条件 Ex(x,y,z = l, t) 0 ,和 D' = D' = D' 可得: = p / l
(
(p = 1,2,3, … 是否可取零待定)
m 2 n 2 m 2 n 2 p 2 ) ( ) 2 ( ) ( ) ( ) 2 a b a b l
谐振腔介绍资料

dW PL dt
0W
Q
另外,根据式(31-17),导出
(31-18) (31-19)
dW 2 0Wdt
比较(31-18)和(31-19)很清楚
二、品质因数Q0
1 2Q
(31-20)
这样,引入复频率,可以把谐振频率和值包含 在一个公式之中
1 ~ 0 1 j 2Q
讨论谐振腔的主要指标是谐振频率0、品质因数 Q 和电导 G。谐振腔的讨论思路是 : 理想腔 — 耦合腔 — 非理想腔,如图(31-2)所示。 在研究谐振频率 f0时,采用不计及腔损耗,即腔 壁由理想导体构成。但是,当研究 Q 时 , 则必须考虑 损耗的因素。 耦合腔和实际腔反映了谐振腔的具体应用。
0
i
y
Ey
j
z
0
k
E x E0 0 x 1 E y z z Hx j j 0 sin cos = j sin cos 0 z 0 l a l 2l a l E0 E0 0 1 E y x z x z Hz j j cos cos sin j sin x a a l 2a a l
2
2 E0 0 2 l 2 x 2 z 0 E0 a + 2 cos sin dxdz 0 0 2a a l 8 2 l a
2 1 1 l b a 2 2 2 1 E dv E0 sin x sin z dxdydz ablE02 a l 2 V 2 0 0 0 8
电动力学期末各章复习试题(选择+填空)

电动⼒学期末各章复习试题(选择+填空)第⼀章选择题1. ⽅程/E B t ??=-??的建⽴主要依据哪⼀个实验定律 ( )A 电荷守恒定律B 安培定律C 电磁感应定律D 库仑定律2.已知电极化强度,则极化电荷密度为()A. B. C. D.3.若在某区域已知电位移⽮量,则该区域的电荷体密度为()4.下⾯说法正确的是()A. 空间任⼀点的场强是由该点的电荷密度决定的;B. 空间任⼀点的场强的散度是由所有在场的电荷q决定的; C. 空间任⼀点的场强的散度只与该点的电荷密度有关; D. 空间某点,则该点,可见该点也必为零.5. H Bµ= 是()A .普适的 B. 仅适⽤于铁磁性物质C .仅适⽤于线性⾮铁磁性物质 D. 不适⽤于⾮铁磁性物质6、对任意介质,下列⽅程⼀定正确的有() A.极化强度⽮量E P )(0εε-= B.极化强度⽮量0e P E χε=C.磁化强度⽮量M u B H -=0D.磁化强度⽮量001()M H µµµ=- 7、对于表达式 (I) dv E D W e ?=21和(II )=dv W e ?ρ21,下列说法中正确的有()A .表达式I 和II 在任何电场情况下总是等价的B .I 中的被积函数是电场能量密度,⽽II 中的被积函数则⽆此物理意义C .?ρ21的单位不是能量密度的单位 x y D xe ye =+.2D ρ=-.2A ρε=-.2B ρ=.2C ρε=D . I 中的被积函数不代表电场的能量密度,⽽II 中的被积函数则有此物理意义8、对任意介质,下列⽅程⼀定正确的有()A.极化强度⽮量0P D E ε=-B.极化强度⽮量0e P E χε=C.磁化强度⽮量m M H χ=D.磁化强度⽮量001()M H µµµ=-9、⼀般情况下电磁场切向分量的边值关系为:< >A: ()210n D D ?-=;()210n B B ?-=; B: ()21n D D σ?-=;()210n B B ?-= ; C: ()210n E E ?-=;()210n H H ?-=; D: ()210n E E ?-=;()21n H H α?-=。
43矩形谐振腔

(4-32)
第四章 微波谐振器
§4.3 矩形谐振腔
下面的关系式成立
K 2K c 22, Kc2ma2nb2
K2m a2nb 2pl2
不同的m,n,p对应不同的TEmnp模,m,n不能同时为零。 工作于TEmnp模的矩形腔具有多谐性。
Hm 2a l2 21a4bH l4m 2a2l2al b
第四章 微波谐振器
§4.3 矩形谐振腔
在腔体前后壁(z=0,z=ι)的内表面上
H 1 2H x12H m 2a l2 2si2 n ax
在腔体左右壁(x=0,x=a)的内表面上
H 2 2H z12H m 2si2n lx
第四章 微波谐振器
§4.3 矩形谐振腔
在与z=0相距ι处再放一短路板,形成腔体.
则有边界条件
Exzl 0
所以 lp 或 p (p0 ,1 ,2 ,3 )
l
则腔体内TMmnp模的纵向电场为
E z E m s im a nx s in b ny c o p ls z
第四章 微波谐振器
§4.3 矩形谐振腔
腔体内TMmnp模的其它场分量为
E x K E m c 2p lm ac o m ax s s in b n y s ip ln z E y K E m c 2p ln b s im a n x c o n by s s ip ln z H x jm E K c 2 n bs im a n x c o n by s c o p lz s
H xH ma lsi a nx co lsz
矩形谐振腔讲义课件

电导率
电导率影响电磁波在介质中的传播损耗,进而影响腔体的Q值。
介电常数
介电常数决定了电磁波在介质中的传播速度,从而影响谐振频率。
损耗角正切值
损耗角正切值反映了介质的能量损耗特性,对腔体的Q值有重要影 响。
矩形谐振腔的表面涂层
涂层材料
涂层材料的电导率、介电常数 和磁导率都会影响腔体的性能
。
涂层厚度
涂层厚度需精确控制,以确保 其对电磁波的反射特性的影响
矩形谐振腔讲义课件
contents
目录
• 矩形谐振腔概述 • 矩形谐振腔的基本原理 • 矩形谐振腔的设计与优化 • 矩形谐振腔的制造工艺 • 矩形谐振腔的性能测试与评估 • 矩形谐振腔的应用实例
01
矩形谐振腔概述
定义与特性
定义
矩形谐振腔是一种具有特定边界条件 的空腔,通常由金属壁围成,可以在 其中产生电磁波的共振。
矩形谐振腔可用于微波加热,快速均匀 地加热物质,广泛应用于食品加工和材 料处理。
VS
医疗领域
在医疗领域,矩形谐振腔可用于微波治疗 和诊断,例如肿瘤热疗和微波成像。
THANKS
感谢观看
制造流程
材料准备
根据设计图纸准备相应的材料 ,并进行必要的处理如清洗、 矫直等。
组装调试
将加工好的各个部件进行组装 ,并进行必要的调试和测试, 确保性能符合要求。
设计图纸
根据需求和规格,设计矩形谐 振腔的图纸,包括腔体尺寸、 形状、接口等。
加工成型
按照设计图纸对材料进行加工 ,形成矩形谐振腔的各个部件 。
质量检测
对制造完成的矩形谐振腔进行 质量检测,包括尺寸、外观、 电气性能等方面的检测。
05
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016/4/15
11
第五章 微波谐振腔
5.2 矩形谐振腔
1、矩形腔中 TE 模的解。
根据 2.3 小节,已知矩形金属波导中 TE 波的解和相应的本征值 kc 。 将导体表面边界条件 Et(z = 0,z = l) = 0 或 Hn(z = 0,z = l) = 0 代 入式 (2-34) 中的 Ex,Ey 或 Hz 的表达式中,可以导出谐振腔中电磁场 TE 模 的解。
2016/4/15
7
第五章 微波谐振腔
5.1 简介
微波谐振腔 与 微波传输线
微波谐振腔与微波传输线的相同之处是它们都具有相同类型的横向边 界条件,因而具有相同类型的横向电磁场分布。
各工作模式只有在与激励源之间满足奇偶禁戒规则的条件下才能被激 励。
微波谐振腔与微波传输线的区别是:对于传输线而言,只要它的某个 模式与激励源之间满足奇偶禁戒规则,该模式就能被激励(不一定能传输)。
有 5 个方程可选,只有 2 个待定常数(D、)。因此,可选最简单的 条件方程。即短路面上电场的切向分量方程或磁场的法线分量方程。 m,n
2016/4/15
1
第五章 微波谐振腔
5.1 简介
微波谐振腔是微波系统中经常用到的重要元件。有源微波部件往往都
需要用微波谐振腔实现能量交换。
微波谐振腔在其他领域中也有广泛的用途。例如,电子直线加速器的
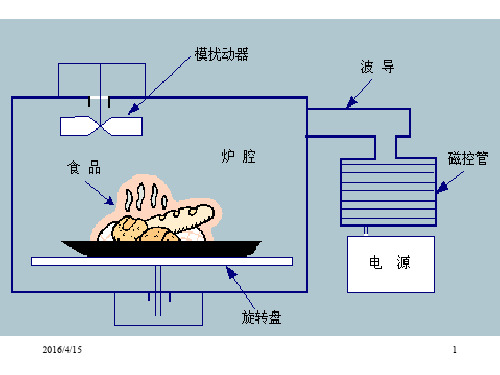
主体是工作在 TM010 模式的圆柱腔,微波炉是一个工作在多模状态的矩形 谐振腔等等。
微波谐振腔能够将特定频率的电磁波限制在一定的几何空间内。也就
8
第五章 微波谐振腔
5.1 简介
微波谐振腔 与 LC 谐振回路
~的相同之处是微波谐振腔与 LC 谐振回路都具有储能和选频的功能。
~的不同之处是 LC 谐振回路只有一个谐振频率 ,一个工作模式 (TEM 模),而微波谐振腔具有无限多个谐振频率,无限多个工作模式。
第五章主要介绍矩形谐振腔,圆柱谐振腔和同轴谐振腔的: 1、谐振频率 2、品质因数 3、模式特征、激励方式
这种腔体被称为开放式微波谐振腔。
r
当电磁波波长较短时,很容易实现这种
谐振腔。在光学系统中,这种谐振腔称为
FP 腔。
优点是品质因数高(选频特性好)。
5
第五章 微波谐振腔
5.1 简介
两块相对放置的导体板也可构成微波谐
振腔,如果导体板的尺度远大于微波波长。
r
r
这种腔体被称为开放式微波谐振腔。
这两种谐振腔在毫米波、远 红外和光波频段有广泛用途。
是说:谐振腔具有存储电磁能量和频率选择的能力。凡是具有这两个特征
的元件都可称作微波谐振腔。
一般说来,用导体边界构成的空腔或低损耗介质块都可以作为微波谐
振腔。
(有什么区别?)
微波频段常用的谐振腔按几何形状分类有:矩形腔、圆柱腔、同轴腔、
开放式谐振腔等;按所用材料分类有:金属腔,介质腔以及复合型腔等。
2016/4/15
2
第五章 微波谐振腔
圆波导
2a
5.1 简介
2a 2b
同轴线
在圆波导两端用导体短路可构成 微波圆柱谐振腔。
D = 4 mm, h = 3.5 mm f0 = 12 GHz,Ku 波段
在同轴线两端用抗流活塞或低通滤波 器短路可构成微波同轴谐振腔。
2016/4/15
D = 11 mm,h = 8 mm f0 = 4.2 GHz ,C 波段
因此,矩形谐振腔中电磁场的通 解形式和横向本征值与矩形波导中的 电磁场完全相同;不同之处在于,矩 形谐振腔在 z 方向上也有齐次边界条 件。
2016/4/15
10
第五章 微波谐振腔
5.2 矩形谐振腔
无论是在谐振腔中还是在波导中,本征方程 kx2+ky2+ 2 = 2,都必 须成立,否则波动方程 (2-6) 没有非零解。
如果激励源的频率高于该模式的截止频率时,该模式就成为传输模式。 如果激励源的频率低于该模式的截止频率时,该模式就成为截止模式。
对于微波谐振腔而言,由于它比传输线多了纵向边界条件,要想在微 波谐振腔中激励起某个模式,激励源不但要与该模式满足奇偶禁戒规则, 而且激励源的频率必须等于该模式的谐振频率。
2016/4/15
3
第五章 微波谐振腔
5.1 简介
YIG 小球与耦合回路构成的谐振腔。 H0(Oe) = f (MHz) /2.8
微带线耦合回路构成的谐振腔。 0 = 2d
b2
2d
2016/4/15
a1
4
第
r
2016/4/15
两块相对放置的导体板也可构成微波谐
振腔,如果导体板的尺度远大于微波波长。
在波导中 kx 和 ky 是由横向边界条件确定的,因此,对于任意工作频 率总存在对应的传播常数,总存在相应的本征解 (也就是说电磁场总能在波导中存
在)。虽然这个解可能是传输状态也可能处于截止状态。
在矩形波导上相距为 l 的两处位置上用理想导体短路,就构成了矩形 谐振腔。
由于理想导体表面电场的切向分量为零 (Et = 0),磁场的法线分量为零 (Hn = 0)。所以,只需将其中一个条件代入矩形波导的电磁场表达式中,解 出相应的传播常数 就可以得到谐振频率和谐振腔中电磁场的表达式。
利用介质材料参数的周期性 或非周期性变化,可以构成所谓 分布反馈谐振腔。
2016/4/15
6
第五章 微波谐振腔
5.1 简介
在研究谐振腔时,我们关心的主要参数有:
(1) 谐振频率 f0,谐振腔只能储存与其谐振频率相同的电磁波能量。 (2) 固有品质因数 Q0,谐振腔储能和谐振腔本身耗能的情况。 (3) 有载品质因数 QL,谐振腔储能和谐振腔及其耦合装置的耗能情况。 (4) 特性阻抗 0,谐振腔耦合口上的电场强度。 微波谐振腔在几何结构上与微波传输线类似,在储能和选频功能方面 与低频 LC 电路类似。
2016/4/15
9
第五章 微波谐振腔
5.2 矩形谐振腔
矩形谐振腔具有与矩形波导完全相同的横向边界条件,它们的区别仅 在于矩形谐振腔在 z 方向上也存在短路边界条件。因此,求解矩形谐振腔 谐振频率和工作模式的方法与求解矩形波导截止频率和工作模式的方法基 本相同。
这是因为矩形谐振腔中的电磁场 所满足的微分方程和横向边界条件与 矩形波导中的电磁场完全相同。
