传热过程计算..
传热过程计算

7
二.总传热系数
T 冷 流 体
T Tw dQ1 i dSi (T Tw ) 1 i dSi
Q dQ2 dSm (Tw t w ) Tw t w b b dSm
15
4.4.3 总传热速率方程和平均温度差法 一.总传热速率方程
m1,t1
dQ KdS(T t )
Q
m2,T1 dS t2
T2
dQ Ktm dS
0 0
S
——总传热速率方程 传热计算的出发点和核心:
Q KStm
K—— 平均总传热系数 tm—— 平均温度差
Q KStm W1c p1 (T1 T2 ) W2c p 2 (t2 t1 )
①总传热系数Ko;
②管外对流传热系数αo增加一倍,总传热系 数有何变化? ③管内对流传热系数αi增加一倍,总传热系 数有何变化?
13
①总传热系数Ko 解:
1 1 Ko 1 16 0.0015 16 1 1 do b do 1 40 14.5 90 i d i d m o 100013 1 80.8W/ m 2 C 0.00123 0.00004 0.01111
Tw 热 体
tw
对流
导热
t w-t dQ3 o dSo (t w-t ) t 1 o dSo 对流
对于稳定传热
dQ dQ1 dQ2 dQ3
T Tw Tw t w tw t T t dQ 1 b 1 1 b 1 8 i dSi dSm o dSo i dSi dSm o dSo
传热过程的计算

[
]
Q = KA∆tm = qm1c p1 (T1 −T2 ) = G2c p2 (t2 − t1 )
3.4.2 平均温度差的计算
一、恒温差传热
∆t m = T − t
二、变温差传热 分单侧变温和双侧变温, 与流体流向有关。 分单侧变温和双侧变温,∆tm还与流体流向有关。
逆流
并流
错流
折流
1. 逆、并流时的∆tm 并流时的∆
(1) α1不变 α2提高到 4W/(m2·K) ) 不变, 提高到10 (2) α2不变 α1提高到 ) 不变, 提高到80W/(m2·K) (3) α2不变 α1提高到 ) 不变, 提高到500W/(m2·K) 计算上面各种情况下的K值 计算上面各种情况下的 值? 强化传热——应提高α小一侧流体的α 应提高 强化传热
Q = qm 1 r + cp1 (Ts − T2 ) = qm 2 cp2 (t 2 − t1 )
• 热负荷 由生产任务决定,对设备换热能力的要求 热负荷—由生产任务决定 由生产任务决定, • 传热速率 设备在一定操作条件下的换热能力 传热速率—设备在一定操作条件下的换热能力 传热过程计算的基础式: 传热过程计算的基础式:
3.4.4 壁温的计算
定态传热
Q = KA∆t m T − TW TW − t W t W − t = = = 1 b 1 α 1 A1 λ Am α 2 A2
t W = TW
bQ − λ Am
TW
Q =T − α 1 A1
tW
Q =t+ α 2 A2
(1)一般情况下 λ大,(b/λAm)小,可认为 tW≈TW )一般情况下, 可认为
K (T − t )dA = −qm 1c p1dT = −qm 2 c p 2dt
传热过程的计算
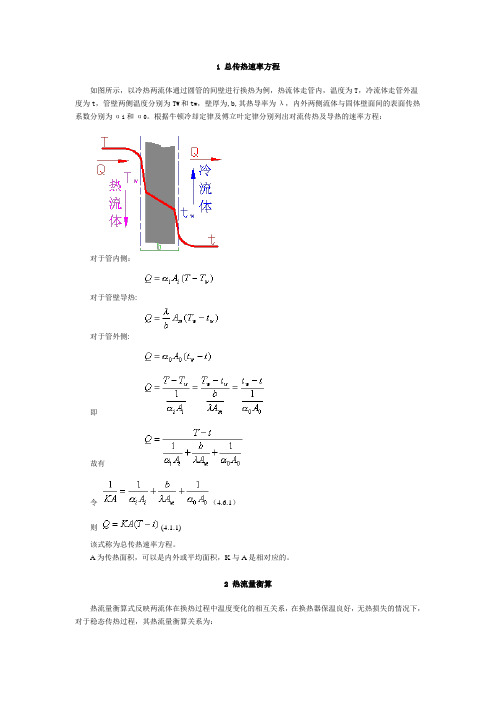
1 总传热速率方程如图所示,以冷热两流体通过圆管的间壁进行换热为例,热流体走管内,温度为T,冷流体走管外温度为t,管壁两侧温度分别为T W和t w,壁厚为,b,其热导率为λ,内外两侧流体与固体壁面间的表面传热系数分别为αi和α0。
根据牛顿冷却定律及傅立叶定律分别列出对流传热及导热的速率方程:对于管内侧:对于管壁导热:对于管外侧:即故有令(4.6.1)则(4.1.1)该式称为总传热速率方程。
A为传热面积,可以是内外或平均面积,K与A是相对应的。
2 热流量衡算热流量衡算式反映两流体在换热过程中温度变化的相互关系,在换热器保温良好,无热损失的情况下,对于稳态传热过程,其热流量衡算关系为:(热流体放出的热流量)=(冷流体吸收的热流量)在进行热衡算时,对有、无相变化的传热过程其表达式又有所区别。
(1)无相变化传热过程式中Q----冷流体吸收或热流体放出的热流量,W;m h,m c-----热、冷流体的质量流量,kg/s;C ph,C pc------热、冷流体的比定压热容,kJ/(kg·K);T1,t1 ------热、冷流体的进口温度,K;T2,t2------热、冷流体的出口温度,K。
(2)有相变化传热过程两物流在换热过程中,其中一侧物流发生相变化,如蒸汽冷凝或液体沸腾,其热流量衡算式为:一侧有相变化两侧物流均发生相变化,如一侧冷凝另一侧沸腾的传热过程式中r,r1,r2--------物流相变热,J/kg;D,D1,D2--------相变物流量,kg/s。
对于过冷或过热物流发生相变时的热流量衡算,则应按以上方法分段进行加和计算。
3 传热系数和传热面积(1)传热系数K和传热面积A的计算传热系数K是表示换热设备性能的极为重要的参数,是进行传热计算的依据。
K的大小取决于流体的物性、传热过程的操作条件及换热器的类型等,K值通常可以由实验测定,或取生产实际的经验数据,也可以通过分析计算求得。
传热系数K可利用式(4.6.1)进行计算。
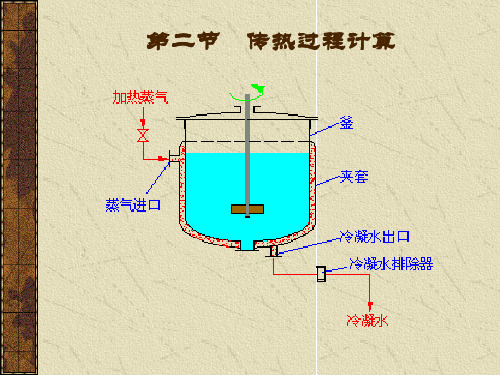
2.2 传热过程计算
Δt
m
Δt 2 Δt ln Δt 2
1
Δt 1
第二节 传热过程计算
二、平均温度差 错流和折流
tm tm'
f (P, R)
R T1 T2 t2 t1
P t2 t1 T1 t1
பைடு நூலகம்
第二节 传热过程计算
三、传热计算的题型
(qmcp)hT
KS tm Q
(qmcp)ct qmhrh
1. 设计型
对于平壁或薄壁: 1 1 b 1 K αi λ αo
第二节 传热过程计算
一、总传热速率 Q KSt
对于平壁或薄壁: 1 1 b 1 K αi λ αo
二、平均温度差
Q KStm
tm: 平均温度差
第二节 传热过程计算
二、平均温度差 流体的流向
逆流
并流
错流
折流
第二节 传热过程计算
二、平均温度差 逆流和并流
Q1=Q2=Q3 =... 一、传导传热
Q λ dt S dn 热通量(密度) 温度梯度 (W/m2) (K/m) 例:求平面壁定态热传导速率的表达式
Q λ t1 t2S
b
第一节 传热基本规律
二、对流传热 膜模型 湍流核心处温度一致 层流膜内符合热传导规律
牛顿冷却定律
S
Q t
,
t
Q St
第二节 传热过程计算
第二节 传热过程计算
第二节 传热过程计算
一、总传热速率 1b 1
R总 , T T t α iSi λ S m α oSo
Q t
Sot
R总 So bS o 1
α iSi λ Sm α o
令: 1 So bS o 1 K α iSi λ S m α o
热传递热量计算公式

热传递热量计算公式
热传递是指热量从一个物体传递到另一个物体的过程。
热传递的计算可以通过多种公式来实现,具体取决于热传递的方式。
以下是一些常见的热传递计算公式:
1. 热传导(导热)的计算公式:
热传导是指热量通过物质内部传递的过程。
其计算公式可以用傅立叶定律来表示:
Q = -kAΔT/Δx.
其中,Q表示传导热量,k表示热导率,A表示传热面积,ΔT表示温度差,Δx表示传热距离。
2. 热对流的计算公式:
热对流是指热量通过流体(气体或液体)对流传递的过程。
其计算公式可以用牛顿冷却定律来表示:
Q = hAΔT.
其中,Q表示对流热量,h表示对流换热系数,A表示传热面积,ΔT表示温度差。
3. 热辐射的计算公式:
热辐射是指热量通过辐射传递的过程。
其计算公式可以用斯特藩-玻尔兹曼定律来表示:
Q = εσA(T₁^4 T₂^4)。
其中,Q表示辐射热量,ε表示发射率,σ表示斯特藩-玻尔兹曼常数,A表示辐射面积,T₁和T₂分别表示两个物体的绝对温度。
以上是一些常见的热传递计算公式,它们分别适用于不同的热传递方式。
在实际问题中,需要根据具体情况选择合适的公式进行计算。
传热过程的计算

必须着力减少控制步骤的热阻,才更易以达到强化传热的目的。 。
实际计算换热管热流量,可依据管壁内表面积或外表面积写出两个方程 内表面: 外表面: Ql=KlA1 (T-t) Q2=K2A2 (T-t) (6-116)
式中,K1、K2分别为以内、外表面积为基准的传热系数,明显两者是不相等的。 但有 K1A1=K2A2 如圆管的内、外直径分别用d1、d2表示,结合式子: K 可导出: K 1
即
Q KAt m
称为传热过程基本方程式
式中
t m
T t 1 T t 2 T t 1 ln T t 2
称为对数平均温差或对数平均推动力。
对数平均推动力
对数平均推动力恒小于算术平均推动力,特别是当换热器两端推动力相差悬 殊时,对数平均值要比算术平均值小得多。 当换热器一端两流体温差接近于零时,对数平均推动力将急剧减小。 对数平均推动力这一特性,对换热器的操作有着深刻的影响。 例如,当换热器两端温差有一个为零时,对数平均温差必为零。 这意味着传递相应的热流量,需要无限大的传热面。 但是,当两端温差相差不大时,如0.5<(T-t)1/(T-t)2<2时,对数平均推动 力可用算术平均推动力代替。
qm1CP1dT=q1dA1=dQ (热流体在微元体内放出的热量) 同样,对冷流体作类似假定,并以微元体内环隙空 间为控制体作热量衡算,可得到 qm2CP2dt=q2dA2=dQ (冷流体在微元体内吸收的热量)
2、传热速率方程式 热流密度q是反映具体传热过程速率 大小的特征量。从理论上讲,根据前面 导热或对流给热规律,热流密度q已可以 计算。但是,这种做法必须引入壁面温 度;而在实际计算时,壁温往往是未知 的。为实用方便,希望能够避开壁温, 直接根据冷、热流体的温度进行传热速 率的计算。 如图所示的套管换热器中,热量序 贯地由热流体传给管壁内侧、再由管壁 内侧传至外侧,最后由管壁外侧传给冷 流体(参见 P201 图 6-35 )。在定态条 件下,并忽略管壁内外表面积的差异, 则各环节的热流量相等,即
传热过程和换热器热计算基础

(m2·℃) / W
多层平壁的传热:
q=
n δi 1 1 +∑ + h1 i =1 λi h2
tf1- tf2
二、圆筒壁的传热 每米长圆筒壁的总传热热阻热阻:
只有管道外径 d 2 超过某一值后包上热绝缘层才能 起到减少单位管长热损失的作用,把此直径称为临界 热绝缘直径,用 d c 表示。
d c 可由求 q1 对热绝缘层外径的一阶导数并令之 等于零而得到,即 d = 2λins c h2 ( d 2 > d c 加绝热层才能减少热损)
式中: 2 ——管道热绝缘层外表面对环境的表面传 h 热系数[W/(m2·K)]; λins ——保温材料的导热系数[W/(m·K)]。
' 肋面平均温度 t w2 (< tw2 )
肋片实际散热量:
h A (t
2
2
'
w2
− tf2
)
2
肋处于肋基温度下的理想散热量: h 肋片效率:
A2 (t w 2 − tf2 )
t w 2 − tf2 实际散热量 h2 A2 t w 2 − tf2 = = η= 理想散热量 h2 A2 (t w 2 − tf2 ) t w 2 − tf2
Φ = Ah2 (t w2 − tf2 )
λ Φ = A (t w1 − t W2 ) δ
Φ tf1 − t W1 = Ah Φ t w1 − t W2 = Aλ / δ Φ t w2 − t f2 = Ah2
传热方程:
A(t f1 − t f2 ) Φ= = KA ∆ t 1 / h1 + λ / δ + 1 / h2
传热过程的计算

第四节 传热过程计算化工原理中所涉及的传热过程计算主要有两类:一类是设计计算,即根据生产要求的热负荷,确定换热器的传热面积;另一类是校核计算,即计算给定换热器的传热量、流体的流量或温度等。
两者都是以换热器的热量衡算和传热速率方程为计算的基础。
应用前述的热传导速率方程和对流传热速率方程时,需要知道壁面的温度。
而实际上壁温常常是未知的,为了避开壁温,故引出间壁两侧流体间的总传热速率方程。
4—4—1 能量衡算对间壁式换热器做能量衡算,以小时为基准,因系统中无外功加入,且一般位能和动能项均可忽略,故实质上为焓衡算。
假设换热器绝热良好,热损失可以忽略时,则在单位时间内换热器中热流体放出的热量等于冷流体吸收的热量,即 , .、)()(1221c c c h h h H H W H H W Q -=-= (4—30)式中 Q —换热器的热负荷,kj/h 或W ;W -流体的质量流量,kg /h ;H -单位质量流体的焓,kJ /kg 。
下标c 、h 分别表示冷流体和热流体,下标1和2表示换热器的进口和出口。
式4-30即为换热器的热量衡算式,它是传热计算的基本方程式,通常可由该式计算换热器的传热量(又称热负荷)。
.若换热器中两流体无相变化,且流体的比热容不随温度而变或可取平均温度下的比热容时,式4-30可表示为Q )()(1221t t c W T T c W pc c ph h -=-= (4-31)式中 c p -流体的平均比热容,kJ /(kg ·℃);t —冷流体的温度,℃;T -热流体的温度,℃。
若换热器中的热流体有相变化,例如饱和蒸气冷凝时,式4-30可表示为Q )(12t t c W r W pc c h -== (4-32)式中 W h —饱和蒸气(即热流体)的冷凝速率,k 2/h ;r —饱和蒸气的冷凝潜热,kJ /kg 。
式4-32的应用条件是冷凝液在饱和温度下离开换热器。
若冷凝液的温度低于饱和温度时,则式4-32变为Q )()]([1221t t c W T T c r W pc c ph h -=-+= (4-33)式中 C ph -冷凝液的比热容,kJ /(kg ·℃);T s —冷凝液的饱和温度,℃。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当两流体在换热过程中均只发生相变时, 热流体温度T和冷流体温度t都始终保持不 变,称为恒温传热。 换热器的传热推动力可取任一传热截面上 的温度差,即Δtm=T-t。 大多数情况下,间壁一侧或两侧的流体温 度沿换热器管长而变化,称为变温传热。 变温传热时,各传热截面的传热温度差各 不相同。由于两流体的流向不同,对平均 温度差的影响也不相同,故需分别讨论。
化学工业出版社
(1) 恒温传热
两侧流体温度恒定:
t m T t 恒定
T t
(2) 变温传热 ① 一侧有温度变化
化学工业出版社
②
两侧流体均有温度变化
t1 T2 t2 T1
t1
T1 t2 T2
化学工业出版社
化学工业出版社
t1 t 2 对数平均温度差:t m t1 ln t 2 说明:
W/(m2·K); S--传热面积,m2; Δtm--换热器的传热推动力,或称传热 平均温度差,K; R=1/(KS)--换热器的总热阻,K/W; R'=1/K--换热器的总热阻, m2·K/W。
化学工业出版社
传热系数K
K Q / St m
K — 传热系数,表示换热设备性能的重要参数
K的物理意义:当冷热两流体之间的温度差为1℃时, 在单位时间内通过单位传热面积的传热量.
化学工业出版社
(3)潜热法(有相变) Qh=qm,hγh Qc=qm,cγc 若无热损失, Qh= Qc 注意:a.通过上式可计算载热体或冷流体的 热量。 b.若有热损失 Q= Qc= Qh+ QL 热损失在热流体一侧 Q= Qh= Qc+ QL 热损失在冷流体一侧
化学工业出版社
三、传热温度差的计算
化学工业出版社
对于一定的传热任务,确定换热器所 需传热面积是选择(或设计)换热器 的主要任务。由传热方程式可知,要 计算传热面积,必须先求得传热速率 Q、传热平均温度差Δtm以及传热系数 K,这些项目的求取涉及到热量衡算、 传热推动力、各种传热方式的规律等 有关理论和计算。
化学工业出版社
二、热负荷的计算
化学工业出版社
3.热负荷的计算方法 (1)焓差法 Qh=qm,h(H1-H2) Qc=qm,c(h2-h1) 若无热损失, Qh= Qc 0℃的液体的焓为零J/kg 蒸汽的焓取0℃的液体的焓为零J/kg作计算基准。 此法使用时受到限制,有些液体的焓很难查到。
化学工业出版社
(2)显热法(无相变时) Qh=qm,hCp,h(T1-T2) Qc=qmcCp,c(t2-t1) 若无热损失, Qh= Qc Cp,h、 Cp,c:冷热流体进出口温度范围 内的平均比热,亦是进出口平均温 度下的比热。
化学工业出版社
t h t h , w t h , w tc , w Q 1 b i Si S m
t c,w t c 1 0 S0
th
th tc 因此,Q 1 b 1 i S i S m 0 S 0
t R
热 流 体
Q
Q
th,w
tc,w
当用传热基本方程式计算整个换热器 的传热速率时,必须使用整个传热面 积上的平均温差。 传热平均温度差的大小及计算方法与 换热器中两流体的相互流动方向及温 度变化情况有关。换热过程中,热流 温度沿程降低,冷流温度沿程升高, 故冷热流体温度差在换热器表面各点 不同。
化学工业出版社
换热器中两流体间有不同的流动型式 。 若两流体的流动方向相同,称为并流; 若两流体的流动方向相反,称为逆流; 若两流体的流动方向垂直交叉,称为 错流;若一流体沿一方向流动,另一 流体反复折流,称为简单折流;若两 流体均作折流,或既有折流,又有错 流,称为复杂折流。
化学工业出版社
(二)热量衡算与热负荷的确定 1、热量衡算 以单位时间为基准 Qh=Qc+QL Qh ——热流体放出的热量,kJ/s或kW Qc ——冷流体吸收的热量,kJ/s或kW QL ——热热损失,kJ/s或kW 2、热负荷的确定 若忽略热损失,热负荷取Qh或Qc 若有热损失,哪种流体走管程,就应取哪种 流体的传热量作为换热器的热负荷。
(一)热负荷与传热速率 1.热负荷:换热器单位时间内冷热流体所交换的热量。 传热速率:单位时间内通过传热面传递的热量。 2.热负荷与传热速率的区别:
热负荷是生产上要求换热器单位时间传递的热量, 是换热器的生产任务。传热速率是换热器单位时 间能够传递的热量,是换热器的生产能力,主要 由换热器自身的性能决定。为保证换热器完成传 热任务,应使换热器的传热速率大于至少等于其 热负荷。
冷 流 体 tc
1 1 b 1 令: R KS S S S i i m 0 0
化学工业出版社
用平均传热温差t m 代替(t h tc)
式中,K — 总传热系数,W/m2· K。 注意: K 与 S 对应,选Si、Sm 或 S0
化学工业出版社
式中
Q--传热速率,W; q--热通量,W/m2; K--比例系数,称为传热系数,
① 逆流: t1 T1 t 2 ② 并流: t1 T1 t1
K的来源: 实验测定;
取生产实际的经验数据; 计算求得。
化学工业出版社
化工过程的传热问题可分为两类:一 类是设计型问题,即根据生产要求, 选定(或设计)换热器;另一类是操 作型问题,即计算给定换热器的传热 量、流体的流量或温度等。两者均以 传热基本方程为基础。下面以设计型 问题为例分析解决传热问题要涉及到 的有关内容。
传热过程计算
化学工业出版社
2.5
总传热速率方程
一、 间壁传热过程:
热量:
热流体 管内壁
对流传热
th
热 流 体
Q
Q
th,w
tc,w
冷 流 体 tc
管外壁
热传导
冷流体
对流传热
化学工业出版社
各部分传热速率方程: 管内侧流体 Qi i Si (t h t h,w ) 管壁导热 Qm S m (t h,w t c,w ) / b 管外侧流体 Q0 0 S0 (t c,w t c ) 对稳态传热 Q Qi Qm Qo
