投影面平行线的投影特性
第二章 直线的投影
2.已知直线 AB 平行直线 CD,试完成直线
例:已知直线AB平行直线CD,试完成直线AB
AB 和 CD 的三面投影。 和CD的三面投影。
题解: c′〝
c
NEW
c
c
b
点C的投影在直线的同面投影上,并 符合点的投影规律。
二、D点不在 直线AB上。
a A d b a b
NEW
a b
D
d
B
d
例:判断点M是否在直线CD 上 解法1:
NEW
点M的投影不符合点在直线上的投影规律, 故M点不在直线CD上。
例:判断点M是否在直线CD 上
直线 水 平 线
直观图
投影图
投影特征 1、水平投影ab 反映实长 及直线的倾角β 和γ 。 2、正面投影a b //o x轴, 侧面投影a"b "//oy w 轴,且 均短于实长。 1、正面投影e f 反映实长 及直线的倾角α 和γ 。 2、水平投影ef //o x轴,侧 面投影e"f "//oz 轴,且均 短于实长。 1、侧面投影e"f" 反映实 长及直线的倾角α 和β 。 2、水平投影e f//oy H 轴,正 面投影e f //oz 轴,且均 短于实长。
• 1. 直线上的点,其投影必在该直线的同面投影上。 • 2. 直线上的点,分割线段之比,在投影后保持不变。
三.直线上的点 (一) 直线上点的投影特性
点C在直线上 AB上
1.直线上的点,
其投影必在该 直线的同面投 影上。
2.直线上的点,
第2章 正投影基础

第2章正投影基础本章提要本章主要介绍投影法的基本概念和构成物体的基本几何元素点、线、面的投影特性、作图原理和方法;直线与直线、直线与平面的相对位置关系。
为解决求直线的实长和平面的实形的问题,还介绍了点、线、面的变换投影面的方法。
2.1投影法及三视图的形成2.1.1投影法在日常生活中人们注意到,当太阳光或灯光照射物体时,墙壁上或地面上会出现物体的影子。
投影法就源自这种自然现象。
如图2-1所示,平面P为投影面,不属于投影面的定点S为投影中心。
过空间点A由投影中心可引直线SA,SA为投射线。
投射线SA与投影面P的交点a,称作空间点A在投影面P上的投影。
同理,点b是空间点B在投影面P上的投影(注:空间点以大写字母表示,其投影用相应的小写字母表示)。
由此可知,投影法是投射线通过物体向预定投影面进行投影而得到图形的方法。
图2-1投影法图图2-2中心投影法2.1.2投影法的分类投影法一般分为中心投影法和平行投影法两类。
1、中心投影法投射线从投影中心出发的投影法,称为中心投影法,所得到的投影称为中心投影,如图2-2所示,通过投影中心S作出△ABC在投影面P上的投影:投射线SA、SB、SC分别与投影面P交于点a、b、c,而△abc就是△ABC在投影面P上的投影。
在中心投影法中,△ABC的投影△abc的大小随投影中心S距离△ABC的远近或者△ABC 距离投影面P的远近而变化。
因此它不适合绘制机械图样。
但是,根据中心投影法绘制的直观图立体感较强,适用于绘制建筑物的外观图。
2、平行投影法投射线相互平行的投影法,称为平行投影法,所得到的投影称为平行投影。
根据投射线与投影面的相对位置,平行投影法又分为:斜投影法和正投影法。
(1)斜投影法投射线倾斜于投影面时称为斜投影法,所得到的投影称为斜投影,如图2-3所示。
(2)正投影法投射线垂直于投影面时称为正投影法,所得到的投影称为正投影,如图2-4所示。
绘制工程图样主要用正投影,今后如不作特别说明,“投影”即指“正投影”。
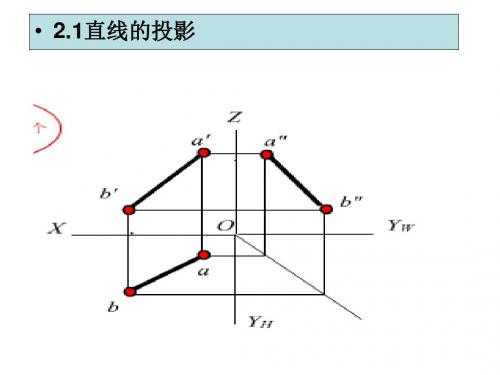
直线的投影

图2-19 判别C点是否在线段AB上 作图:首先过a作一辅助线ab1,使ab1=a'b',ac1=a'c';然后连接b1b,过c1作b1b的 平行线使与ab相交,如果交点与C点的水平投影c重合,则表明C点对AB的分段符合定比 分段法,此时C点在直线段AB上;反之不在直线段AB上。 1.3两直线的相对位置 空间两直线的相对位置有三种情况:平行、相交和交叉。其中平行和相交两直线均在同一 平面上,交叉两直线不在同一平面上,因此,又称为异面直线。 1. 两直线平行: 相同;反之,若两直线的同面投影都平行,则空间两直线互相平行。如图2-20(a)所示, 因为AB∥CD,则ab∥cd、a'b'//c'd',且ab:cd= a'b':c'd'。
1.水平投影积聚为一点 2.正面投影和侧面投影都 平行于Z轴,并反映实长
1.正面投影积聚为一 点2.水平投影和侧面 投影都平行于Y轴,并 反映实长
1.侧面投影积聚为一
侧
点
垂 线
2.正面投影和水平投 影都平行于X轴,并
反映实长
(3) 一般位置直线 一般位置直线与三个投影面都倾斜,因此在三个投影面上的投影都不反映实长,投 影与投影轴之间的夹角也不反映直线与投影面之间的倾角,见图2-17。
影的夹角仍为直角;如果两直线都不平行于某一投影面时,则两直线在该投影面上的投影 不反映直角。如果两直线相交成直角、且其中有一条直线平行于某一投影面,则两直线在 该投影面上的投影仍然反映直角关系。通常称之为直角投影原理。
2-28所示,AB、BC为相交成直角的两直线,其中BC平行于H面(即水平线), AB为一般位置直线。现证明两直线的水平投影ab和bc仍相互垂直,即bc垂直于ab。
直线投影学习

B
A b
a
b a
证明:设
C
因
直角边BC//H面 BC⊥AB, 同时BC⊥Bb
所以 BC⊥ABba平面
c
又因 BC∥bc
H
故 bc ⊥ABba平面
c
因此 bc⊥ab
即 ∠abc 为直角
b a
c
直线在H面上的投影互 相垂直
第23页/共30页
交叉垂直的两直线的投影
第24页/共30页
直角投影定理
条件:①互相垂直的两直线(相交或交叉) ②其中有一条直线平行于某一投影面 则:两直线在该投影面上投影仍互相垂直
c′ a′
X
c
O
b
b″ c″
a″
Y
a
Y
◆若点在直线上, 则点的投影必在直线的同名投影上。
◆点的投影将线段的同名投影分割成与空间线段相同 的比例。即:
AC:CB=ac:cb=ac:cb=ac:cb
第11页/共30页
定比定理
点在直线上的判别方法:
◆若点在直线上, 则点的 投影必在直线的同名投 影上。并将线段的同名
侧垂线
Z
a
a
b
ab
A
B
X
X
a
a
bY
Z b
ab
O
YW
b YH
第8页/共30页
(2) 投影面垂直线
铅垂线
正垂线
侧垂线
a
a c(d)
d c
e
f
e(f)
●
●
b
●
a(b)
b d
c
e
f
投影特性:
① 在其垂直的投影面上,投影有积聚性。
第二节 直线和平面的投影特性
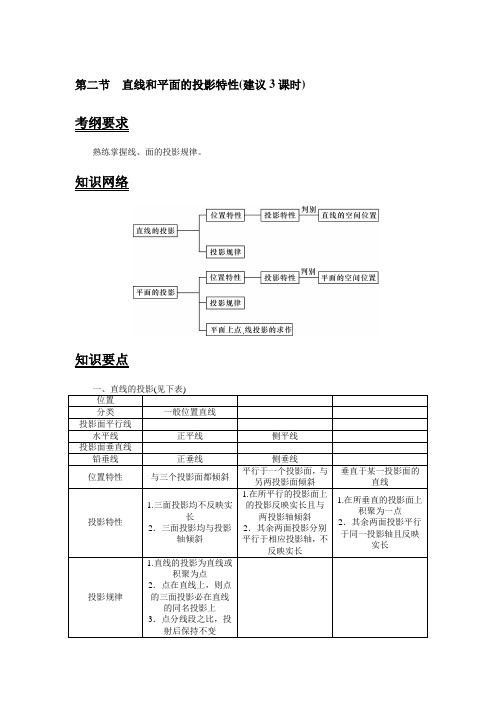
第二节直线和平面的投影特性(建议3课时) 考纲要求熟练掌握线、面的投影规律。
知识网络知识要点二、平面的投影(见表)典型例题【例1】 根据下图中直线的两面投影,判别直线的空间位置。
【解题指导】 (a )图中,直线EF 的正面投影平行OX 轴说明z E =z F ,水平投影也平行于OX 轴说明y E =y F ,则E 、F 两点的侧面投影e ″、f ″为一对重影,即E 、F 两点的侧面投影重合在一起,所以EF 为侧垂线。
同理,(d )图中直线GH 为铅垂线。
(b )图中,直线EF 的正面投影e ′f ′∥OX 轴,则e ′f ′上任一点到OX 轴的距离均相等,即e ′f ′上任一点的z 坐标都相等,所以EF 上任一点到H 面距离均相等,即EF ∥H 面。
由侧面投影及正面投影可知,EF 上任两点的x 、y 坐标值均不相等,所以EF 为水平线。
同理(c )图中直线GH 为一般位置直线。
【答案】 (a )EF 为侧垂线;(b )EF 为水平线;(c )GH 为一般位置直线;(d )GH 为铅垂线 【点评】 根据直线段的两面投影判别其空间位置,首先要熟练掌握各种位置直线的投影特性,其次要分析所给投影的特性,进而判别出直线的空间位置。
如果直线的两面投影都与投影轴平行且平行于同一个投影轴,则该直线为投影面垂直线;如果直线的两面投影平行于不同投影轴,则该直线为投影面平行线。
【例2】判断点M、N是否在平面ABC上。
【解题指导】线是由点构成的,面也是由点构成的。
某点是否在平面上,要先看点是否处于平面内的某一确定的直线上。
粗一看N点的两面投影都在平面的一条直线的投影上,其实N点正面投影与AC边上的1点是重影点,水平投影与BC边上的2点是重影点。
对于M点连接b′m′交a′c′于e′,通过投影关系,可以看出,M点的水平面投影m也在bc 上,所以M点在平面ABC上。
【答案】M点在平面ABC上,N点不在平面ABC上。
【例3】完成平面图形ABCDE的水平投影。
各种位置直线的投影特性

各种位置直线的投影特性按照直线对三个投影面的相对位置,可以把直线分为三类:一般位置直线、投影面平行线、投影面垂直线。
后两类直线又称为特殊位置直线。
1.一般位置直线—与三个投影面都倾斜的直线一般位置直线的投影特性如下(图3-10):1)三面投影都倾斜于投影轴。
2)投影长度均比实长短,且不能反映直线与投影面倾角的真实大小。
直线对H、V、W的倾角分别用α、β、γ表示。
投影面平行线——平行于一个投影面,倾斜于另外两个投影面的直线(1)投影面平行线又可分为三种:平行于V面的直线叫正平线;平行于H面的直线叫水平线;平行于W面的直线叫侧平线。
图3-11 正平线的投影特性(2)正平线的投影特性(图3-11):1)直线平行于V面,则V面投影与直线本身平行且等长,a'b'=AB;2)正平线上各点到V面的距离即Y坐标都相等,则a b∥OX, a"b"∥OZ。
3)AB与H面的倾角为α,由于AB平行V面,所以AB与V面的倾角为0。
又因为AB ∥a'b',a b∥OX轴,所以,a'b'与OX轴的夹角为α,同理a'b'与OZ轴的夹角即为AB与W面的倾角γ。
表3-1为投影面平行线的投影特性。
表3-1 投影面平行线的投影特性名称轴测图投影图投影特性正平线(1)a'b'=AB, 反映α、γ角(2)a b//OX轴, a"b"//OZ轴水平线(1) cd=CD ,反映β、γ角(2)c'd'//OX轴, c"d"//O YW轴侧平线(1) e"f"=EF, 反映α、β角(2)e'f'//OZ轴,ef//O YH轴投影面平行线的投影特性:1.直线在与其平行的投影面上的投影,反映该线段的实长和与其他两个投影面的倾角2.直线在其他两个投影面上的投影分别平行于相应的投影轴,且比线段的实长短投影面垂直线——垂直于一个投影面,平行于另外两个投影面的直线1)投影面垂直线又可分为三种:垂直于V面的直线叫正垂线;垂直于H面的直线叫铅垂线;垂直于W面的直线叫侧垂线。
直线、平面在三面投影体系中的投影特性分析

直线、平面在三面投影体系中的投影特性分析【摘要】建筑制图中直线、平面相对于三个投影面的不同位置关系的分类相同,空间直线按其相对于三个投影面的不同位置关系可分为三种:投影面平行线、投影面垂直线和投影面倾斜线。
【关键词】相对位置;投影特性;分析一、投影面平行线与投影面平行面1.定义的区别(1)投影面平行线:与一个面平行与另外两个面倾斜,按其与水平投影面、正立投影平面、侧立投影平面平行的位置分为水平线、正平线、侧平线。
(2)投影面平行面:与一个面平行与另外两个面垂直,按其与水平投影面、正立投影平面、侧立投影平面平行的位置分为水平面、正平面、侧平面。
2.投影特性的区别(1)投影面平行线:直线在所平行的投影面上的投影反映实长,此投影与投影轴的夹角反映直线与另两个投影面的夹角实形;直线在另两个投影面上的投影,平行于相应的投影轴,但不反映实长。
“开发资产管理应用程序时,我们首要任务之一是帮助客户完全掌控过程知识。
为此,我们首次允许用户灵活地借助收集的情报快速创建自己的资产模型。
”ABB设备管理和资产优化全球产品经理NeilShah说到,“包括根本原因分析在内的资产分析是帮助客户在当今工业市场中保持竞争力的另一个关键因素。
”(2)投影面平行面:平面在它平行的投影面上的投影反映实形,其它两个投影积聚成线段,并且分别平行于相应的投影轴。
3.空间位置的判别(1)投影面平行线:一斜两直线,必为平行线;斜线在哪面,平行哪个面。
(2)投影面平行面:一框两直线,必为平行面;框在哪个面,平行哪个面。
投影面平行线投影图投影面平行面投影图二、投影面垂直线与投影面垂直面1.定义的区别众所周知,信息化条件下的现代战争,武器装备的优劣在很大程度上影响战争的胜败,但是决定战场胜负的主体因素依然是人。
现代战争中的每一项军事行动,都离不开军人良好身体素质的支撑。
良好身体素质的获得自然离不开真、难、严、实的军事训练,而逼近实战的军事训练中也将不可避免的发生军事训练伤。
特殊位置直线的投影

§3-2 特殊位置直线的投影
二、投影面垂直线
空间垂直某一投影面的直线称为投影面垂直线。 投影面垂直线分为三种:
铅垂线 (⊥于H 面,∥于V 面和W 面)。
正垂线
侧垂线
(⊥于V 面,∥于H 面和W 面)。
(⊥于W 面,∥于H 面和V 面)。
§3-2 特殊位置直线的投影
二、投影面垂直线
本节结束
§3-2 特殊位置直线的投影
3.侧平线投影特性Fra bibliotek1)a” b” =AB ;
2)反映α、β实角; 3) ab∥OY 轴,a’b’∥OZ 轴。
Z V
a’ b’ X b a A β B
O
实长
β
a’
b’
Z
a”
β
实长
b” YW
a”
b”
X b a Y
O
YH
§3-2 特殊位置直线的投影
一、投影面平行线
归纳投影面平行线的投影特性: 直线在所平行的投影面上的投影反映实长、 投影与相应轴的夹角反映直线与另外两个投影 面的夹角实际大小; 直线的另两个投影平行于相应的轴,且长度 缩短。
二、投影面平行线
2.正平线
投影特性
Z a’
实长
V b’
1)a’b’ = AB ; 2)反映α 、γ实角; 3)ab ∥OX 轴,a’’b’’∥OZ 轴。
实长
a” b” b’ X b Y α
α B
b
A α O a
a’ O
Z
a” b” YW
X
a YH
§3-2 特殊位置直线的投影
一、投影面平行线
实长
V a‘ A X
第五章 正投影法基础_03
c
b n
50
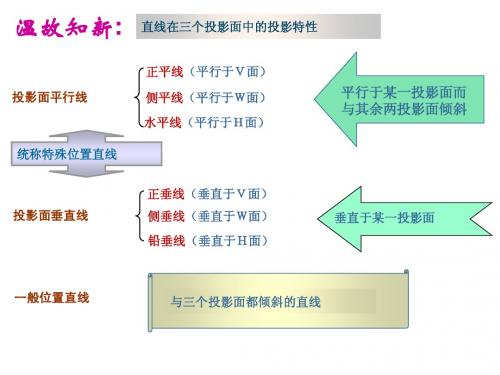
例 试过定点K作特殊位置平面的法线。
h
PV k
SV k h
h
k
k
h
k h h QH
51
k
例 平面由两平行线AB、CD给定,试判断直线MN是否垂直 于定平面。 a c m e f b X m d n O
b
e d
a
c f
n
52
结论:不垂直。
2
两平面垂直
A
P
B
几何条件:若一直线垂直于一定平面,则包含这条直线 的所有平面都垂直于该平面。
A A
Ⅰ Ⅱ
B
Ⅰ
B
Ⅱ
两平面垂直 两平面不垂直
反之,两平面相互垂直,则由属于第一个平面的任意一 点向第二个平面作的垂线必属于第一个平面。
54
例
平面由 BDF给定,试过定点K作已知平面的垂面 h f c g k b
d
a
a c k
●
d b 先作正面投影
(2)直线与平面相交
V
方法一
N B P
积聚性法
A PH a
K
b k Mபைடு நூலகம்
C c H
当直线为一般位置,平面的某个投影具有积聚性时,交 点的一个投影为直线与平面积聚性投影的交点,另一个投影 可在直线的另一个投影上找到。
29
直线可见性的判别
V a k
b N
n
2. 相交问题
(1)熟练掌握特殊位置线、面相交(其中直线或平面的投影具有积 聚性)交点的求法和作两个面的交线(其中一平面的投影具有积聚性)。 (2)熟练掌握一般位置线、面相交求交点的方法;掌握一般位置面 、面相交求交线的作图方法。 ( 3 )掌握利用重影点判别投影可见性的方法。
直线的投影——习题讲解

2.特点 (1)近代中国交通业逐渐开始近代化的进程,铁路、水运和 航空都获得了一定程度的发展。 (2)近代中国交通业受到西方列强的控制和操纵。 (3)地域之间的发展不平衡。 3.影响 (1)积极影响:促进了经济发展,改变了人们的出行方式, 一定程度上转变了人们的思想观念;加强了中国与世界各地的 联系,丰富了人们的生活。 (2)消极影响:有利于西方列强的政治侵略和经济掠夺。
筹办航空事宜
处
三、从驿传到邮政 1.邮政 (1)初办邮政: 1896年成立“大清邮政局”,此后又设 , 邮传邮正传式部脱离海关。 (2)进一步发展:1913年,北洋政府宣布裁撤全部驿站; 1920年,中国首次参加 万国。邮联大会
2.电讯 (1)开端:1877年,福建巡抚在 架台设湾第一条电报线,成为中国自 办电报的开端。
C’
d’ a’
b d
a
a ax
a
az a
ay
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材·填要点]
一、铁路,更多的铁路 1.地位 铁路是 交通建运设输的重点,便于国计民生,成为国民经济 发展的动脉。 2.出现 1881年,中国自建的第一条铁路——唐山 至开胥平各庄铁 路建成通车。 1888年,宫廷专用铁路落成。
正垂线
c(d)
●
d c
xd
c
侧垂线
e f e(f) ●
x
ef
① 投影面垂直线在所垂直的投影面上的投影 必积聚成一个点。
② 另外两个投影 都反映线段实长。且垂直于 相应的投影轴。
2.一般位置直线的投影特性是什么?
b
a
x
a
b
b a
投影特性:
直线的投影 -平行线

与V面的角:β
与W面的夹角:γ
投 影 特 性:
① 在其平行的那个投影面上的投影反映实长,并反映直线 与另两投影面倾角。
② 另两个投影面上的投影平行于相应的投影轴。
内容总结
1、复习点的投影,巩固加深直线的投影。 2、熟练掌握投影面平行线的பைடு நூலகம்影特性。能根据直 线的三面投影判断直线的位置
作业布置
习题集P12 (1、3)
b
YH
2.正平线
b a
Z
B a b
O
Z b b a O YW
a
X
A
X
a
b
Y
a
b
YH
投影特性: 1.ab OX ; a b OZ
2.a b=AB 3.反映、 角的真实大小
3.侧平线
Z
a A a X b a Z a
O
a b
Y
b
b
X
任务二
直线的投影
1
课程介绍
1
直线的投影及分类
2
投影面平行线的投影特性
3
回顾总结与布置作业
一、直线的投影
直线的投影由直线上两点的同面投影的 连线确定 b' b"
a'
a"
b a
3
B
A b a
A B A
B
b
ab a
H
4
直线相对于投 影面的位置可 归结为几类?
直线对三投影面均倾斜 — 一般位置线 直线 // 某一投影面— 投影面平行线
a
b
O
YW
B b YH
投影特性: 1.ab OZ ; ab OYH
第二章投影法基本知识

积聚性:当一线段与投影面垂直时,其正投影积聚为一
点;当一平面图形与投影面垂直时,其正投影积聚为 一直线。
积聚性
类似性:当一线段与投影面倾斜时,其正投影为缩短
的线段; 当一平面图形与投影面倾斜时,其正投影 为缩小的类似图形。
类似性
§2-2 三视图的形成及其对应关系
根据国标规定,用正投影法绘制出物体的图形称为视图。 下图表示的是三个不同形体,在一个投影面上的视图却是完 全相同的。
1、主视图—从前向后投射,在V 面上所得的视图。
2、俯视图—从上向下投射,在H 面上所得的视图。
3、左视图—从左向右投射,在W 面上所得的视图。
三视图的形成
三投影面的展开
V面保持不动,H面绕OX轴向下旋转90°,W面绕 OZ轴向右旋转90°,这样V、H和W三个投影面就摊 平在了同一平面上。
水 平 投 影 面 和侧立投影 面旋转后,OY轴被分成两 条,分别用OYh和OYw 表 示 。
注意:
要细心,不要把点对错了。
§2-4 直线的投影
二、各种位置直线的投影
根据直线在三投影面体系中对投影面的相对位置不同,将
直线分为:
投影面平行线 投影面垂直线
特殊位置直线
投影面倾斜线
一般位置直线
1、一般位置直线 定义:与三个投影面均成倾斜的直线
直线与 H、V、W 投影面的倾角分别用 α、β、γ表示,见图 中的标注。
即 ac:cb=a'c':c'b'=a''c'':c''b''=k
例: 判断图中点是否在直线上。
作图分析: ⑴由于AB直线为一般位置。而给出 的C点的两投影分别在AB线的同面投 影上,故可认定C点从属于AB直线。
各位置直线和平面投影特性总结

13
直角三角形法
直角三角形法的四要素:投影长、坐标差、实长、 倾角。已知四要素中的任意两个,便可确定另外两个。 解题
时,直角三角形画在任何位置都不影响解题结果,但用哪个长 度来作直角边不能搞错。 如图所示,在各个直角三角形中,实长与水平投影的夹角是α, α的对边长一定是Z坐标差;实长与正面投影的夹角是,的 对边长一定是Y坐标差;实长与侧面投影的夹角是, 的对边 一定是X坐标差。直线对H、V、W三投影面的倾角为α、、 。
3、一般位置平面
——与三个投影面都倾斜的平面。
16
(1)正垂面
投影特性:(一线两框)
1、正面投影abcd积聚为一倾斜于投影OX、OZ的直线。 2、abcd、abcd 具有类似性,PH OX轴,PWO轴 3、abcd与OX、OZ轴的夹角反映α、 角的真实大小
Z V
Z
γ
14
(二)各种位置平面的投影特性
在三面投影体系中,根据平面与投影面所处的相 对位置不同有如下分类:
平面
特殊位置平面 一般位置平面
投影面平行面 投影面垂直面
15
各种位置平面的三面投影
平面对H、V、W三投影面的倾角是指平面与投影面之间的
夹角,分别用α、、
1、投影面的垂直面
——与一个投影面垂直,而与另两个倾斜的平面。
X
O
βγ
β γ
H Y
YH
18
(3)侧垂面
投影特性:(一线两框)
1、侧面投影 abcd积聚为一倾斜于投影OYW、OZ的直线。 2、abcd、abcd 具有类似性,PH OYH,PVOZ轴 3、 abcd与OZ、OYW轴的夹角反映、α角的真实大小
《机械制图》第二章 直线的投影

1.cd积聚成一点 2.c′d′⊥OX
c″d″⊥OYW 3.c′d′=c″d″=CD
1.e″f″积聚成一点 2.ef⊥OYH
e′f′⊥OZ 3.ef=e′f′=EF
一般位置直线(投影特点:三条斜线)
b a a
b
b a
投影特性:
三个投影都缩短。 即: 都不反映空间 线段的实长及与三 个投影面夹角的实 大,且与三根投影
1. ab∥OX
影
a″b″∥OZ
特
2. a′b′=AB 3. 反映α 、γ 倾角
性
βγ
1. c′d′∥ OX c″d″∥OYW
2. cd=CD 3. 反映β 、γ 倾角
β α
1.e′f′∥OZ ef∥OY H
2. e″f″=EF 3. 反映α 、β 倾角
2.投影面垂直线
由两点到两个投影面距离相等时的两 点连线构成。该直线垂直于某一投影 面,对另外两个投影面都平行 。
YW
Y
YH
• 在直线所平行的投影面上,投影反映实长,且该投影与相邻 投影轴的夹角反映该直线对另外两个投影面的倾角大小。
• 在另外两个投影面上,线段的投影为缩短的线段,且分别 平行于直线一斜二平)
名称
直 观 图
正平线
水平线
侧平线
投
γ
影
α
图
投
第二章 直线的投影
第三节 直线的投影
一、各种位置直线及投影特性
1.一般位置直线
由一般位置的两点连线构成。 该直线与三个投影面都倾斜。
β
γ
YW
α
Y YH
投影特性: 三个投影都倾斜于投影轴,每个投影既不直接
反映线段的实长,也不直接反映倾角的大小。
直线投影

1、已知直线AB的三面投影
试判别有关性质:
aˊ
(1)AB是 侧平 线
(2)它同V面—倾—斜
bˊ
它同W—平—行
Xa
它同H 倾斜(平行或倾斜)
(3)它在 W 投影面上的投影 b
a〞b〞 反映实长
Z a〞
b〞
O
YW
YH
2、已知直线AB的三面投影,试判别有关性 质:
Z
a'(b')
X
b
b"
O
a"
AB是 正垂 线,
bˊ
a〞 b〞
A X
B O b〞 X
O
YW
a
H
b
a
Y
b
YH
投影特性:1、ab=AB且 ab且倾斜于投影轴(一斜)
2、a′b′、a〞b〞<AB且平行于相应投影轴(二平)
3、侧平线(平行W面且 倾斜V面、H面)
Z
V
aˊ
aˊ A
W a〞
bˊ
bˊ
Z a〞b〞Xa来自OXaO
YW
B
b〞
Hb
b Y
YH
投影特性:1、a〞b〞 =AB且 a′b′且倾斜于投影轴(一斜)
(垂直于投影轴→二垂)
辩认:一点二垂
(三)一般位置直线 这类直线对三个投影面均处于倾斜位置
V
Z
b' B b" W
a'
X
A a b a"
Z b' b"
a'
O a"
X
b
YW
H
Y
a YH
1)直线的三面投影长度均小于实长
各种位置直线的投影特性讲解学习

各种位置直线的投影特性各种位置直线的投影特性按照直线对三个投影面的相对位置,可以把直线分为三类:一般位置直线、投影面平行线、投影面垂直线。
后两类直线又称为特殊位置直线。
1.一般位置直线—与三个投影面都倾斜的直线一般位置直线的投影特性如下(图3-10):1)三面投影都倾斜于投影轴。
2)投影长度均比实长短,且不能反映直线与投影面倾角的真实大小。
直线对H、V、W的倾角分别用α、β、γ表示。
投影面平行线——平行于一个投影面,倾斜于另外两个投影面的直线(1)投影面平行线又可分为三种:平行于V面的直线叫正平线;平行于H面的直线叫水平线;平行于W面的直线叫侧平线。
图3-11正平线的投影特性(2)正平线的投影特性(图3-11):1)直线平行于V面,则V面投影与直线本身平行且等长,a'b'=AB;2)正平线上各点到V面的距离即Y坐标都相等,则a b∥OX, a"b"∥OZ。
3)AB与H面的倾角为α,由于AB平行V面,所以AB与V面的倾角为0。
又因为AB∥a'b',a b∥OX轴,所以,a'b'与OX轴的夹角为α,同理a'b'与OZ轴的夹角即为AB与W面的倾角γ。
表3-1为投影面平行线的投影特性。
表3-1 投影面平行线的投影特性名称轴测图投影图投影特性正平线(1)a'b'=AB, 反映α、γ角(2)a b//OX轴, a"b"//OZ轴水平线(1) cd=CD ,反映β、γ角(2)c'd'//OX 轴, c"d"//O YW轴侧平线(1) e"f"=EF, 反映α、β角(2)e'f'//OZ轴,ef//O YH轴投影面平行线的投影特性:1.直线在与其平行的投影面上的投影,反映该线段的实长和与其他两个投影面的倾角2.直线在其他两个投影面上的投影分别平行于相应的投影轴,且比线段的实长短投影面垂直线——垂直于一个投影面,平行于另外两个投影面的直线1)投影面垂直线又可分为三种:垂直于V面的直线叫正垂线;垂直于H面的直线叫铅垂线;垂直于W面的直线叫侧垂线。
直线和平面的投影

② 另外两个投影,反映线段实长。且垂直 于相应的投影轴。
2021/2/4
1
17
⑶ 一般位置直线
b
b
投影特性:
a
三个投影都缩短。即:
a
都不反映空间线段的实长及
与三个投影面夹角的实大,
a
且与三根投影轴都倾斜。
b (1)ab, a’b’, a’’b’’对于三个投影轴既不平行也 (2) ab, a’b’, a’’b’不’垂都直较空间线段AB缩短了。
2021/2/4
1
19
二、三角形法:一般位置直线的实长求法
YB-YA
b′
ZB-ZA ZB-ZA
V
a
A
b
A0
β
B
α B0
bH
a′
a α
实长
b
2021/2/4
1
20
对H面倾角和实长
a
X
2021/2/4
b
B
|zA-zB|
a
X O
C
A
b
a
a
AB
ab
1
|zA-zB|
b
AB
|zA-zB|
ab
b
AB
|zA-zB |
2021/2/4
d
1
c
实长
d
24
直角三角形法要点
1、角度、投影、坐标差和投影之间的对应关系
α角——水平投影——z坐标差——线段实长 β角——正面投影—— y坐标差——线段实长 γ角——侧面投影——x坐标差——线段实长
2、投影、坐标差、实长和角度四个要素知 道其中二个就可以求其它二个
3、解题时,直角三角形画在任何位置,都不影响 解题结果。但用哪个长度来作直角边不能搞错
2.3 直线的投影

X
c'
O
轴测图 投影图 投影特性:两直线的投影,既不符合平行两直线的投影 特性,又不符合相交两直线的投影特性。同面投影的交 点,就是两直线上各一点形成的对这个投影面的重影点 的重合的投影。
[例题] 检验侧平线AB和一般位置直线CD的相
对位置。 (两种方法)
(a)已知条件 (b)加W面
(c)用直线上的点
b
a
A
a W X
O
YW
X
a b
O
a
b
投影特性: H 1、ɑ/ b/ 反映真长和α、γ角。
Y
YH
2、ɑb // OX,ɑ// b// // OZ,且长度缩短。
水平线(平行H面,同时倾斜于V、W面的直线)
V
a
A
Z b
Z a a b a b
B
X a
O
W b
X a
O
YW
Hb
b YH
2、ab// OYH,a/ b / // OZ,且长度缩短。
二、一般位置直线
1、基本概念 2、一般位置直线的投影特性
1、基本概念
一般位置直线:
既不平行也不垂直于任何一个投影 面,即与三个投影面都处于倾斜位置的 直线。
2、一般位置直线的投影特性:
V
Z b B a X A H a b a X O b
2.3 直线的投影
空间两点可以决定一直线,所以只要
作出线段两端点的三面投影,连接该两点 的同面投影(同一投影面上的投影),即 可得空间直线的三面投影。 直线的投影一般仍为直线。
空间直线与投影面的相对位置有三种:
投影面平行线
特殊位置直线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于投影面平行线的辨认:当直线的投影有两个平行于投影轴,
第三投影与投影轴倾斜时,则该直线一定是投影面平行线,且一定
平行于其投影为倾斜线的那个投影面。
ﻫ
ﻫ
对于投影面垂直线的辨认:直线的投影中只要有一个投影积聚为
一点,则该直线一定是投影面垂直线,且一定垂直于其投影积聚为一
点的那个投影面。
对于一般位置直线的辨认:直线的投影如果与三个投影轴都倾斜,则可判定该直线为一般位置直线。
要求学生必须掌握表2—3中的图例.
对于投影面垂直面的辨认:如果空间平面在某一投影面上的投
影积聚为一条与投影轴倾斜的直线,则此平面垂直于该投影面。
ﻫ
ﻫ
要求学生必须掌握表2-3中的图例。
对于投影面垂直面的辨认:如果空间平面在某一投影面上的投影积聚为一条与投影轴倾斜的直线,则此平面垂直于该投影面。
ﻫ
要求学生必须掌握表2—4中的图例.
对于投影面平行面的辨认:如果空间平面在某一投影面
上反映实形,则此平面平行于该投影面。
ﻫﻫ
ﻫ
ﻫﻫ
对于一般位置平面的辨认:如果平面的三面投影都是类似的
几何图形的投影,则可判定该平面一定是一般位置平面。
