大学数学向量及运算 (1)
(完整版)第八章向量代数与空间解析几何教案(同济大学版高数)(最新整理)

形对角线的交点(。见图 7-5)
图 7-4
解: a
b
AC
2
AM
,于是
MA
1
(a
b)
2
由于 MC MA ,
于是
MC
1
(a
b)
2
又由于
a
b
BD
2 MD
,于是
MD
1
(b
a)
2
由于 MB MD ,
于是
MB
1
(b
a)
2
三、空间直角坐标系
1.将数轴(一维)、平面直角坐标系(二维)进一步推广建立空间直角坐标系(三维)
五、向量的模、方向角、投影
设 a {ax , a y , az } ,可以用它与三个坐
标轴的夹角、、 (均大于等于 0,小
5
于等于 )来表示它的方向,称、、 为非零向量 a 的方向角,见图 7-6,其余弦表示
形式cos、cos 、cos 称为方向余弦。
1. 模
a
a
2 x
a
2 y
a
2 z
2. 方向余弦
PP1 x2 2 2 32 x2 11 PP2 x2 12 12 x2 2
PP为: (1,0,0) , (1,0,0)
四、利用坐标系作向量的线性运算
1.向量在坐标系上的分向量与向 量的坐标
通过坐标法,使平面上或空间的 点与有序数组之间建立了一一对应关 系,同样地,为了沟通数与向量的研 究,需要建立向量与有序数之间的对 应关系。
◆ 任意向量的方向余弦有性质: cos2 cos2 cos2 1
◆ 与非零向量 a 同方向的单位向量为:
a 0 a 1 {a x , a y , a z } {cos, cos , cos } aa
大学数学知识点总结

大学数学知识点总结1. 线性代数1.1 向量和矩阵•向量的定义和运算:加法、数乘、点乘•矩阵的定义和运算:加法、数乘、乘法•向量空间的概念和性质•行列式的计算和性质1.2 线性方程组•线性方程组的解的存在唯一性判断•高斯消元法求解线性方程组•矩阵求逆的方法•矩阵的秩和最简行阶梯型1.3 特征值和特征向量•特征值和特征向量的定义和性质•特征值和特征向量的求解方法•对角化和相似矩阵的概念2. 微积分2.1 极限和连续•函数的极限和连续的定义•无穷小和无穷大的定义•极限的性质和运算法则•常用的极限计算方法2.2 导数和微分•导数的定义和几何意义•导数的基本运算法则•高阶导数和隐函数求导•微分的定义和几何意义2.3 积分•不定积分和定积分的定义•积分的性质和基本公式•分部积分和换元积分法•定积分的几何意义3. 概率统计3.1 概率•概率的基本概念和性质•条件概率和独立事件的概率•随机变量的概率分布•期望、方差和协方差的定义和性质3.2 统计•样本与总体的概念•抽样和抽样分布的基本知识•参数估计和假设检验的基本方法3.3 常用概率分布•正态分布和标准正态分布•二项分布和泊松分布•样本均值的分布和样本比例的分布4. 微分方程4.1 常微分方程•常微分方程的基本概念和分类•一阶常微分方程的解法•高阶线性常微分方程的解法•常微分方程的初值问题和边值问题4.2 偏微分方程•偏微分方程的基本概念和分类•热传导方程、波动方程和拉普拉斯方程的解法•边值问题和本征值问题的求解方法以上是大学数学中的一些重要知识点的总结。
掌握这些数学知识,对于其他学科如物理、工程等都有重要的应用价值。
在学习过程中,还需要通过练习题和实际应用问题的解析深入理解这些知识点。
希望这个总结能够帮助你在学习大学数学时有所指导和帮助。
《线性代数》教案

《线性代数》教案一、前言1. 教学目标:使学生理解线性代数的基本概念、理论和方法,培养学生运用线性代数解决实际问题的能力。
2. 适用对象:本教案适用于大学本科生线性代数课程的教学。
3. 教学方式:采用讲授、讨论、练习相结合的方式进行教学。
二、教学内容1. 第一章:线性代数基本概念1.1 向量及其运算1.2 线性方程组1.3 矩阵及其运算1.4 行列式2. 第二章:线性空间与线性变换2.1 线性空间2.2 线性变换2.3 矩阵与线性变换2.4 特征值与特征向量3. 第三章:特征值与特征向量3.1 特征值与特征向量的定义3.2 矩阵的特征值与特征向量3.3 矩阵的对角化3.4 二次型4. 第四章:线性方程组的求解方法4.1 高斯消元法4.2 克莱姆法则4.3 矩阵的逆4.4 最小二乘法5. 第五章:线性代数在实际应用中的案例分析5.1 线性规划5.2 最小二乘法在数据分析中的应用5.3 线性代数在工程中的应用5.4 线性代数在计算机科学中的应用三、教学方法1. 讲授:通过讲解线性代数的基本概念、理论和方法,使学生掌握线性代数的基础知识。
2. 讨论:组织学生就线性代数中的重点、难点问题进行讨论,提高学生的思维能力和解决问题的能力。
3. 练习:布置适量的练习题,让学生通过自主练习巩固所学知识,提高解题能力。
四、教学评价1. 平时成绩:考察学生的出勤、作业、课堂表现等方面,占总评的30%。
2. 期中考试:考察学生对线性代数知识的掌握程度,占总评的40%。
3. 期末考试:全面测试学生的线性代数知识水平和应用能力,占总评的30%。
五、教学资源1. 教材:推荐使用《线性代数》(高等教育出版社,同济大学数学系编)。
2. 辅助教材:可参考《线性代数教程》(清华大学出版社,谢乃明编著)。
3. 网络资源:推荐学生浏览线性代数相关网站、论坛,拓展知识面。
4. 软件工具:推荐使用MATLAB、Mathematica等数学软件,辅助学习线性代数。
大学经典课件之高等数学——7-3向量的乘法运算

C
1 25 2 2 2 = 15 + 12 + 16 = , 2 2 1 | AC | = 42 + ( −3)2 = 5, S = | AC |⋅ | BD | 2 25 1 ∴| BD |= 5. = ⋅ 5⋅ | BD | 2 2
机动 目录 上页 下页 返回 结束
r r r 例 6 设向量 m , n, p 两两垂直,符合右手规 r r r 则,且| m |= 4 ,| n |= 2 ,| p |= 3 ,计算 r r r ( m × n) ⋅ p .
机动
目录
上页
下页
返回
结束
r r a⋅b r r r r a ⋅ b =| a || b | cosθ ⇒ cos θ = r r , | a || b |
cosθ = a x bx + a y b y + a z bz a x + a y + az
2 2 2
bx + b y + bz
2 2
2
——两向量夹角余弦的坐标表示式 由此可知两向量垂直的充要条件为 r r r r a ⊥ b ⇐⇒ a ⋅ b = 0
( 2) cosθ = a x bx + a y b y + a z bz a x + a y + az
2 2 2
bx + b y + bz
2 2
2
1 =− , 2
r r r r r ( 3 ) a ⋅ b =| b | ( a ) b
3π . ∴θ = 4 r r r r a⋅b ∴ (a )b = r = −3. |b |
2
2 2
b a r a
大学数学向量空间的基本性质与运算

大学数学向量空间的基本性质与运算向量空间是线性代数中的一个基本概念,它是一种由向量和一些基本运算构成的数学结构。
在大学数学中,研究向量空间的基本性质与运算是非常重要的,本文将介绍向量空间的定义、基本性质和运算法则。
一、向量空间的定义向量空间是一个非空集合V,其中包含了两个运算,即向量的加法和数乘运算。
具体而言,对于V中的任意两个向量u、v和任意标量a,满足以下条件:1. 加法运算:对于V中的任意两个向量u和v,定义u+v为V中的一个向量,称为向量u和v的和。
2. 数乘运算:对于V中的任意一个向量u和任意一个标量a,定义au为V中的一个向量,称为向量u的标量倍。
同时,向量空间需要满足以下性质:1. 封闭性:对于V中的任意两个向量u和v,u+v仍然属于V;对于任意向量u和任意标量a,au仍然属于V。
2. 结合律:对于V中的任意三个向量u、v和w,(u+v)+w=u+(v+w);对于任意向量u和任意两个标量a和b,(a+b)u=au+bu。
3. 交换律:对于V中的任意两个向量u和v,u+v=v+u。
4. 零向量:存在一个特殊的向量0,对于V中的任意向量u,有u+0=u。
5. 相反向量:对于V中的任意向量u,存在一个向量-v,使得u+(-v)=0。
以上就是向量空间的基本定义和性质,根据这些性质,我们可以进行向量空间的运算和推导。
二、向量空间的运算在向量空间中,我们可以进行向量的加法和数乘运算。
具体而言,对于V中的任意向量u和v,以及任意标量a和b,有以下运算法则:1. 加法运算:u+v=v+u。
即向量的加法满足交换律。
2. 数乘运算:(a+b)u=au+bu。
即对于两个标量的和,与向量的数乘先后顺序不影响结果。
3. 数乘结合律:a(bu)=(ab)u。
即标量的乘法满足结合律。
4. 数乘单位元:1u=u。
即1乘以任意向量等于该向量本身。
5. 数乘零元:0u=0。
即0乘以任意向量等于零向量。
通过这些运算法则,我们可以进行向量的运算以及证明向量空间的性质。
2020版高考数学大一轮复习-第1节平面向量的概念及线性运算讲义(理)(含解析)新人教A版
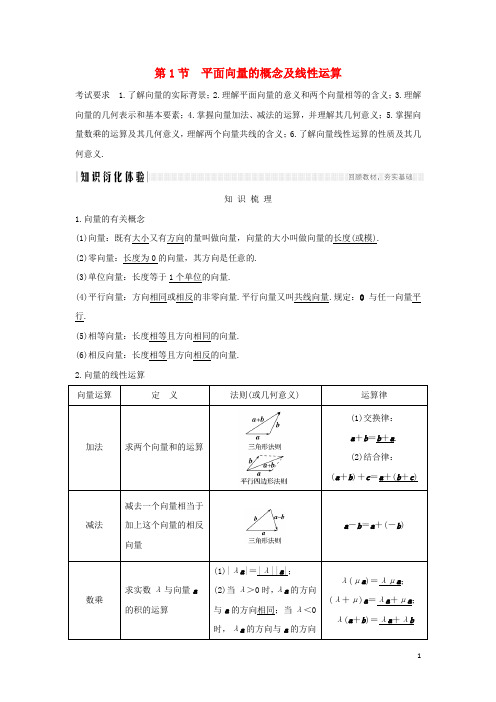
第1节平面向量的概念及线性运算考试要求 1.了解向量的实际背景;2.理解平面向量的意义和两个向量相等的含义;3.理解向量的几何表示和基本要素;4.掌握向量加法、减法的运算,并理解其几何意义;5.掌握向量数乘的运算及其几何意义,理解两个向量共线的含义;6.了解向量线性运算的性质及其几何意义.知识梳理1.向量的有关概念(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的长度(或模).(2)零向量:长度为0的向量,其方向是任意的.(3)单位向量:长度等于1个单位的向量.(4)平行向量:方向相同或相反的非零向量.平行向量又叫共线向量.规定:0与任一向量平行.(5)相等向量:长度相等且方向相同的向量.(6)相反向量:长度相等且方向相反的向量.2.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律:a+b=b+a.(2)结合律:(a+b)+c=a+(b+c)减法减去一个向量相当于加上这个向量的相反向量a-b=a+(-b)数乘求实数λ与向量a的积的运算(1)|λa|=|λ||a|;(2)当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向λ(μa)=λμa;(λ+μ)a=λa+μa;λ(a+b)=λa+λb相反;当λ=0时,λa =03.共线向量定理向量a (a ≠0)与b 共线的充要条件是存在唯一一个实数λ,使得b =λa . [微点提醒]1.一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量,即A 1A 2→+A 2A 3→+A 3A 4→+…+A n -1A n =A 1A n →,特别地, 一个封闭图形,首尾连接而成的向量和为零向量.2.若P 为线段AB 的中点,O 为平面内任一点,则OP →=12(OA →+OB →).基 础 自 测1.判断下列结论正误(在括号内打“√”或“×”) (1)零向量与任意向量平行.( ) (2)若a ∥b ,b ∥c ,则a ∥c .( )(3)向量AB →与向量CD →是共线向量,则A ,B ,C ,D 四点在一条直线上.( ) (4)当两个非零向量a ,b 共线时,一定有b =λa ,反之成立.( ) 解析 (2)若b =0,则a 与c 不一定平行.(3)共线向量所在的直线可以重合,也可以平行,则A ,B ,C ,D 四点不一定在一条直线上. 答案 (1)√ (2)× (3)× (4)√2.(必修4P78A6改编)给出下列命题:①零向量的长度为零,方向是任意的;②若a ,b 都是单位向量,则a =b ;③向量AB →与BA →相等.则所有正确命题的序号是( ) A.①B.③C.①③D.①②解析 根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量AB →与BA →互为相反向量,故③错误. 答案 A3.(必修4P92A12改编)设M 为平行四边形ABCD 对角线的交点,O 为平行四边形ABCD 所在平面内任意一点,则OA →+OB →+OC →+OD →等于( )A.OM →B.2OM →C.3OM →D.4OM →解析 OA →+OB →+OC →+OD →=(OA →+OC →)+(OB →+OD →)=2OM →+2OM →=4OM →. 答案 D4.(2019·东莞调研)如图所示,已知AC →=3BC →,OA →=a ,OB →=b ,OC →=c ,则下列等式中成立的是( )A.c =32b -12aB.c =2b -aC.c =2a -bD.c =32a -12b解析 因为AC →=3BC →,OA →=a ,OB →=b ,所以OC →=OA →+AC →=OA →+32AB →=OA →+32(OB →-OA →)=32OB →-12OA→=32b -12a . 答案 A5.(2018·上海静安区月考)若四边形ABCD 满足AD →=12BC →且|AB →|=|DC →|,则四边形ABCD 的形状是( ) A.等腰梯形 B.矩形 C.正方形D.菱形解析 因为AD →=12BC →,所以AD →∥BC →,且|AD →|=12|BC →|,所以四边形ABCD 为以AD 为上底,BC为下底的梯形.又|AB →|=|DC →|,所以梯形ABCD 的两腰相等.因此四边形ABCD 是等腰梯形. 答案 A6.(2019·菏泽调研)设a 与b 是两个不共线向量,且向量a +λb 与-(b -2a )共线,则λ=________.解析 依题意知向量a +λb 与2a -b 共线,设a +λb =k (2a -b ),则有(1-2k )a +(k +λ)b=0,所以⎩⎪⎨⎪⎧1-2k =0,k +λ=0,解得k =12,λ=-12.答案 -12考点一 平面向量的概念【例1】 (1)设a ,b 都是非零向量,下列四个条件中,一定能使a |a |+b|b |=0成立的是( )A.a =2bB.a ∥bC.a =-13bD.a ⊥b(2)给出下列四个命题: ①若|a |=|b |,则a =b ;②若A ,B ,C ,D 是不共线的四点,则“AB →=DC →”是“四边形ABCD 为平行四边形”的充要条件;③若a =b ,b =c ,则a =c ;④a =b 的充要条件是|a |=|b |且a ∥b . 其中正确命题的序号是( ) A.②③B.①②C.③④D.②④解析 (1)由a |a |+b |b |=0得a |a |=-b |b |≠0,即a =-b|b |·|a |≠0,则a 与b 共线且方向相反,因此当向量a 与向量b 共线且方向相反时,能使a |a |+b|b |=0成立.对照各个选项可知,选项A 中a 与b 的方向相同;选项B 中a 与b 共线,方向相同或相反;选项C 中a 与b 的方向相反;选项D 中a 与b 互相垂直.(2)①不正确.两个向量的长度相等,但它们的方向不一定相同.②正确.∵AB →=DC →,∴|AB →|=|DC →|且AB →∥DC →,又A ,B ,C ,D 是不共线的四点,∴四边形ABCD 为平行四边形;反之,若四边形ABCD 为平行四边形,则|AB →|=|DC →|, AB →∥DC →且AB →,DC →方向相同,因此AB →=DC →.③正确.∵a =b ,∴a ,b 的长度相等且方向相同,又b =c ,∴b ,c 的长度相等且方向相同,∴a ,c 的长度相等且方向相同,故a =c .④不正确.当a ∥b 且方向相反时,即使|a |=|b |,也不能得到a =b ,故|a |=|b |且a ∥b 不是a =b 的充要条件,而是必要不充分条件. 综上所述,正确命题的序号是②③. 答案 (1)C (2)A规律方法 对于向量的有关概念应注意以下几点:(1)平行向量就是共线向量,二者是等价的,它们均与起点无关;非零向量的平行具有传递性;相等向量一定是平行向量,而平行向量未必是相等向量;相等向量具有传递性. (2)向量与数量不同,数量可以比较大小,向量则不能,但向量的模是非负数,可以比较大小.(3)向量可以平移,平移后的向量与原向量是相等向量,解题时,不要把它与函数图象的平移混为一谈.(4)非零向量a 与a |a |的关系:a|a |是与a 同方向的单位向量.【训练1】 (1)如图,等腰梯形ABCD 中,对角线AC 与BD 交于点P ,点E ,F 分别在两腰AD ,BC 上,EF 过点P ,且EF ∥AB ,则下列等式中成立的是( )A.AD →=BC →B.AC →=BD →C.PE →=PF →D.EP →=PF →(2)给出下列说法:①非零向量a 与b 同向是a =b 的必要不充分条件; ②若AB →与BC →共线,则A ,B ,C 三点在同一条直线上; ③a 与b 是非零向量,若a 与b 同向,则a 与-b 反向; ④设λ,μ为实数,若λa =μb ,则a 与b 共线. 其中错误说法的序号是________.解析 (1)根据相等向量的定义,分析可得AD →与BC →不平行,AC →与BD →不平行,所以AD →=BC →,AC →=BD →均错误,PE →与PF →平行,但方向相反也不相等,只有EP →与PF →方向相同,且大小都等于线段EF 长度的一半,所以EP →=PF →.(2)根据向量的有关概念可知①②③正确,④错误. 答案 (1)D (2)④考点二 平面向量的线性运算 多维探究角度1 向量的线性运算【例2-1】 (2018·全国Ⅰ卷)在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB →=( ) A.34AB →-14AC → B.14AB →-34AC →C.34AB →+14AC →D.14AB →+34AC → 解析 ∵E 是AD 的中点,∴EA →=-12AD →,∴EB →=EA →+AB →=-12AD →+AB →,又知D 是BC 的中点, ∴AD →=12(AB →+AC →),因此EB →=-14(AB →+AC →)+AB →=34AB →-14AC →.答案 A角度2 利用向量线性运算求参数【例2-2】 (1)如图,在平行四边形ABCD 中,AC ,BD 相交于点O ,E 为线段AO 的中点.若BE →=λBA →+μBD →(λ,μ∈R ),则λ+μ等于( )A.1B.34C.23D.12(2)在锐角△ABC 中,CM →=3MB →,AM →=xAB →+yAC →(x ,y ∈R ),则x y=________.解析 (1)∵E 为线段AO 的中点, ∴BE →=12BA →+12BO →=12BA →+12×12BD →=12BA →+14BD →=λBA →+μBD →, ∴λ+μ=12+14=34.(2)由题设可得AM →=CM →-CA →=34CB →+AC →=34(AB →-A C →)+AC →=34AB →+14AC →, 则x =34,y =14.故xy =3.答案 (1)B (2)3规律方法 1.解题的关键在于熟练地找出图形中的相等向量,并能熟练运用相反向量将加减法相互转化.2.用几个基本向量表示某个向量问题的基本技巧:(1)观察各向量的位置;(2)寻找相应的三角形或多边形;(3)运用法则找关系;(4)化简结果.【训练2】 (1)如图所示,已知AB 是圆O 的直径,点C ,D 是半圆弧的两个三等分点,AB →=a ,AC →=b ,则AD →=( )A.a -12bB.12a -bC.a +12bD.12a +b(2)设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________.解析 (1)连接CD ,由点C ,D 是半圆弧的三等分点, 得CD ∥AB 且CD →=12AB →=12a ,所以AD →=AC →+CD →=b +12a .(2)DE →=DB →+BE →=12AB →+23BC →=12AB →+23(AC →-AB →)=-16AB →+23AC →,∵DE →=λ1AB →+λ2AC →, ∴λ1=-16,λ2=23,因此λ1+λ2=12.答案 (1)D (2)12考点三 共线向量定理及其应用 【例3】 设两个非零向量a 与b 不共线.(1)若AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ).求证:A ,B ,D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线. (1)证明 ∵AB →=a +b ,BC →=2a +8b ,CD →=3(a -b ).∴BD →=BC →+CD →=2a +8b +3(a -b )=2a +8b +3a -3b =5(a +b )=5AB →.∴AB →,BD →共线,又它们有公共点B , ∴A ,B ,D 三点共线.(2)解 ∵k a +b 与a +k b 共线,∴存在实数λ, 使k a +b =λ(a +k b ),即k a +b =λa +λk b , ∴(k -λ)a =(λk -1)b .∵a ,b 是不共线的两个非零向量,∴k -λ=λk -1=0,∴k 2-1=0,∴k =±1.规律方法 1.证明三点共线问题,可用向量共线解决,但应注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线.2.向量a ,b 共线是指存在不全为零的实数λ1,λ2,使λ1a +λ2b =0成立.【训练3】 (1)已知a ,b 是不共线的向量,AB →=λa +b ,AC →=a +μb ,λ,μ∈R ,则A ,B ,C 三点共线的充要条件为( )A.λ+μ=2B.λ-μ=1C.λμ=-1D.λμ=1(2)(一题多解)已知A ,B ,C 是直线l 上不同的三个点,点O 不在直线l 上,则使等式x 2OA →+xOB →+BC →=0成立的实数x 的取值集合为( )A.{0}B.∅C.{-1}D.{0,-1}解析 (1)因为A ,B ,C 三点共线,所以AB →∥AC →,设AB →=mAC →(m ≠0),则λa +b =m (a +μb ),所以⎩⎪⎨⎪⎧λ=m ,1=mμ,所以λμ=1.(2)法一 若要x 2OA →+xOB →+BC →=0成立,BC →必须与x 2OA →+xOB →共线,由于OA →-OB →=BA →与BC →共线,所以OA →和OB →的系数必须互为相反数,则x 2=-x ,解得x =0或x =-1,而当x =0时,BC →=0,此时B ,C 两点重合,不合题意,舍去.故x =-1.法二 ∵BC →=OC →-OB →,∴x 2OA →+xOB →+OC →-OB →=0, 即OC →=-x 2OA →-(x -1)OB →,∵A ,B ,C 三点共线,∴-x 2-(x -1)=1,即x 2+x =0,解得x =0或x =-1.当x =0时,x 2OA →+xOB →+BC →=0,此时B ,C 两点重合,不合题意,舍去.故x =-1. 答案 (1)D (2)C[思维升华]1.向量线性运算的三要素向量的线性运算满足三角形法则和平行四边形法则,向量加法的三角形法则要素是“首尾相接,指向终点”;向量减法的三角形法则要素是“起点重合,指向被减向量”;平行四边形法则要素是“起点重合”. 2.三个常用结论(1)O 为△ABC 的重心的充要条件是OA →+OB →+OC →=0;(2)四边形ABCD 中,E 为AD 的中点,F 为BC 的中点,则AB →+DC →=2EF →;(3)对于平面上的任一点O ,OA →,OB →不共线,满足OP →=xOA →+yOB →(x ,y ∈R ),则P ,A ,B 共线⇔x +y =1.注意向量共线与三点共线的区别. [易错防范]1.解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.要特别注意零向量的特殊性.2.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.基础巩固题组 (建议用时:35分钟)一、选择题1.已知下列各式:①AB →+BC →+CA →;②AB →+MB →+BO →+OM →;③OA →+OB →+BO →+CO →;④AB →-AC →+BD →-CD →,其中结果为零向量的个数为( )A.1B.2C.3D.4解析 由题知结果为零向量的是①④,故选B. 答案 B2.如图,在正六边形ABCDEF 中,BA →+CD →+EF →=( )A.0B.BE →C.AD →D.CF →解析 由题图知BA →+CD →+EF →=BA →+AF →+CB →=CB →+BF →=CF →. 答案 D3.设a 是非零向量,λ是非零实数,下列结论中正确的是( ) A.a 与λa 的方向相反 B.a 与λ2a 的方向相同 C.|-λa |≥|a |D.|-λa |≥|λ|·a解析 对于A ,当λ>0时,a 与λa 的方向相同,当λ<0时,a 与λa 的方向相反,B 正确;对于C ,|-λa |=|-λ||a |,由于|-λ|的大小不确定,故|-λa |与|a |的大小关系不确定;对于D ,|λ|a 是向量,而|-λa |表示长度,两者不能比较大小. 答案 B4.已知AB →=a +2b ,BC →=-5a +6b ,CD →=7a -2b ,则下列一定共线的三点是( ) A.A ,B ,C B.A ,B ,D C.B ,C ,DD.A ,C ,D解析 因为AD →=AB →+BC →+CD →=3a +6b =3(a +2b )=3AB →,又AB →,AD →有公共点A ,所以A ,B ,D 三点共线. 答案 B5.设D ,E ,F 分别为△ABC 的三边BC ,CA ,AB 的中点,则EB →+FC →=( ) A.BC →B.12AD → C.AD →D.12BC → 解析 如图,EB →+FC →=EC →+CB →+FB →+BC →=EC →+FB →=12(AC →+AB →)=12·2AD →=AD →.答案 C6.(2019·唐山二模)已知O 是正方形ABCD 的中心.若DO →=λAB →+μAC →,其中λ,μ∈R ,则λμ=( ) A.-2B.-12C.- 2D. 2解析 DO →=DA →+AO →=CB →+AO →=AB →-AC →+12AC →=AB →-12AC →,∴λ=1,μ=-12,因此λμ=-2.答案 A7.如图所示,在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M ,N ,若AB →=mAM →,AC →=nAN →,则m +n 的值为( )A.1B.2C.3D.4解析 ∵O 为BC 的中点,∴AO →=12(AB →+AC →)=12(mAM →+nAN →)=m 2AM →+n 2AN →, ∵M ,O ,N 三点共线,∴m 2+n2=1,∴m +n =2. 答案 B8.在△ABC 中,点D 在线段BC 的延长线上,且BC →=3CD →,点O 在线段CD 上(与点C ,D 不重合),若AO →=xAB →+(1-x )AC →,则x 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,12B.⎝ ⎛⎭⎪⎫0,13C.⎝ ⎛⎭⎪⎫-12,0D.⎝ ⎛⎭⎪⎫-13,0 解析 设CO →=yBC →,因为AO →=AC →+CO →=AC →+yBC →=AC →+y (AC →-AB →)=-yAB →+(1+y )AC →. 因为BC →=3CD →,点O 在线段CD 上(与点C ,D 不重合),所以y ∈⎝ ⎛⎭⎪⎫0,13, 因为AO →=xAB →+(1-x )AC →,所以x =-y ,所以x ∈⎝ ⎛⎭⎪⎫-13,0. 答案 D 二、填空题9.如图,点O 是正六边形ABCDEF 的中心,在分别以正六边形的顶点和中心为始点和终点的向量中,与向量OA →相等的向量有________个.解析 根据正六边形的性质和相等向量的定义,易知与向量OA →相等的向量有CB →,DO →,EF →,共3个.答案 310.设向量a ,b 不平行,向量λa +b 与a +2b 平行,则实数λ=____________. 解析 ∵向量a ,b 不平行,∴a +2b ≠0,又向量λa +b 与a +2b 平行,则存在唯一的实数μ,使λa +b =μ(a +2b )成立,即λa +b =μa +2μb ,则得⎩⎪⎨⎪⎧λ=μ,1=2μ,解得λ=μ=12.答案 1211.在△ABC 中,点M ,N 满足AM →=2MC →,BN →=NC →.若MN →=xAB →+yAC →,则x +y =________. 解析 由题中条件得,MN →=MC →+CN →=13AC →+12CB →=13AC →+12(AB →-AC →)=12AB →-16AC →=xAB →+yAC →, 所以x =12,y =-16,因此x +y =12-16=13.答案 1312.(2019·清华大学自主招生能力测试)设O 在△ABC 的内部,D 为AB 的中点,且OA →+OB →+2OC →=0,则△ABC 的面积与△AOC 的面积的比值为________. 解析 ∵D 为AB 的中点, 则OD →=12(OA →+OB →),又OA →+OB →+2OC →=0,∴OD →=-OC →,∴O 为CD 的中点. 又∵D 为AB 的中点,∴S △AOC =12S △ADC =14S △ABC ,则S △ABCS △AOC=4.答案 4能力提升题组 (建议用时:15分钟)13.已知点O ,A ,B 不在同一条直线上,点P 为该平面上一点,且2OP →=2OA →+BA →,则( ) A.点P 在线段AB 上B.点P 在线段AB 的反向延长线上C.点P 在线段AB 的延长线上D.点P 不在直线AB 上解析 因为2OP →=2OA →+BA →,所以2AP →=BA →,所以点P 在线段AB 的反向延长线上,故选B. 答案 B14.(2019·青岛二模)设D ,E ,F 分别为△ABC 三边BC ,CA ,AB 的中点,则DA →+2EB →+3FC →=( ) A.12AD → B.32AD → C.12AC →D.32AC → 解析 因为D ,E ,F 分别为△ABC 三边BC ,CA ,AB 的中点,所以DA →+2EB →+3FC →=12(BA →+CA →)+2×12(AB →+CB →)+3×12×(AC →+BC →)=12BA →+AB →+CB →+32BC →+32AC →+12CA →=12AB →+12BC →+AC →=12AC →+AC →=32AC →.答案 D15.已知△ABC 和点M 满足MA →+MB →+MC →=0,若存在实数m 使得AB →+AC →=mAM →成立,则m =________.解析 由已知条件得MB →+MC →=-MA →,如图,延长AM 交BC 于D 点,则D 为BC 的中点.同理E ,F 分别是AC ,AB 的中点,因此点M 是△ABC 的重心, ∴AM →=23AD →=13(AB →+AC →),则m =3.答案 316.(2019·郑州模拟)设e 1与e 2是两个不共线向量,AB →=3e 1+2e 2,CB →=k e 1+e 2,CD →=3e 1-2k e 2,若A ,B ,D 三点共线,则k 的值为________.解析 由题意,A ,B ,D 三点共线,故必存在一个实数λ,使得AB →=λBD →. 又AB →=3e 1+2e 2,CB →=k e 1+e 2,CD →=3e 1-2k e 2, 所以BD →=CD →-CB →=3e 1-2k e 2-(k e 1+e 2) =(3-k )e 1-(2k +1)e 2,所以3e 1+2e 2=λ(3-k )e 1-λ(2k +1)e 2, 又e 1与e 2不共线,所以⎩⎪⎨⎪⎧3=λ(3-k ),2=-λ(2k +1),解得k =-94.答案 -94新高考创新预测17.(多填题)在△ABC 中有如下结论:“若点M 为△ABC 的重心,则MA →+MB →+MC →=0.”设a ,b ,c 分别为△ABC 的内角A ,B ,C 的对边,点M 为△ABC 的重心. 若aMA →+bMB →+33cMC →=0,则内角A 的大小为________,当a =3时,△ABC 的面积为________.解析 由aMA →+bMB →+33cMC →=aMA →+bMB →+33c (-MA →-MB →)=⎝ ⎛⎭⎪⎫a -33c MA →+⎝ ⎛⎭⎪⎫b -33c MB →=0,且MA →与MB →不共线,∴a -33c =b -33c =0,∴a =b =33c .△ABC 中,由余弦定理可求得cosA =32,∴A =π6.若a =3,则b =3,c =33,S △ABC =12bc sin A =12×3×33×12=934. 答案 π6 934。
线性代数大一上知识点讲解

线性代数大一上知识点讲解线性代数是一门研究向量空间及其相关运算的数学学科。
它是大学数学课程中的重要组成部分,对于培养学生的逻辑思维能力和抽象思维能力具有重要意义。
本文将对线性代数大一上的一些关键知识点进行讲解。
一、向量与向量空间向量是线性代数的基本概念之一,它可以用有序数对或有序数组来表示。
向量空间则是由一组向量所张成的集合,具有加法和数乘两种运算,同时满足一定的性质。
大一上学期主要学习的向量与向量空间的内容包括向量的加法与数乘、线性组合、线性相关与线性无关、子空间等概念和性质。
二、矩阵与行列式矩阵是线性代数中非常重要的概念,它是由数构成的矩阵元按照一定的规则排列而成的矩形数组。
矩阵可以表示线性方程组,并通过矩阵运算实现对线性方程组的求解。
行列式是与矩阵相对应的一个重要概念,它是一个数,可以通过一定的计算规则对给定的矩阵进行求解。
三、线性方程组的求解线性方程组是线性代数中的重要内容之一,它是由线性方程构成的方程组。
线性代数的一个重要应用就是求解线性方程组,大一上学期主要学习的方法有高斯消元法、矩阵的逆与克拉默法则等。
四、特征值与特征向量特征值与特征向量是矩阵理论中的重要概念,它们在线性代数中有着广泛的应用。
大一上学期主要学习的内容包括特征值与特征向量的定义、求解特征值与特征向量的方法以及特征值与特征向量的性质。
五、线性变换与矩阵的相似性线性变换是线性代数中的另一个重要概念,它是指将一个向量空间映射到另一个向量空间的变换。
矩阵的相似性是线性代数中矩阵的重要性质之一,两个矩阵相似意味着它们具有相同的特征值和特征向量。
总结:通过本文对线性代数大一上的知识点进行讲解,我们可以看到线性代数作为一门重要的数学学科,对于培养学生的逻辑思维能力和抽象思维能力具有重要意义。
大一上学期主要学习的内容包括向量与向量空间、矩阵与行列式、线性方程组的求解、特征值与特征向量、线性变换与矩阵的相似性等。
这些知识点的学习有助于我们理解和解决实际问题,为后续学习提供了基础。
同济大学(高等数学)-第八章-向量代数与解析几何

第五篇 向量代数与空间解析几何第八章 向量代数与空间解析几何解析几何的基本思想是用代数的方法来研究几何的问题,为了把代数运算引入几何中来,最根本的做法就是设法把空间的几何结构有系统的代数化,数量化. 平面解析几何使一元函数微积分有了直观的几何意义,所以为了更好的学习多元函数微积分,空间解析几何的知识就有着非常重要的地位.本章首先给出空间直角坐标系,然后介绍向量的基础知识,以向量为工具讨论空间的平面和直线,最后介绍空间曲面和空间曲线的部分内容.第1节 空间直角坐标系1.1 空间直角坐标系用代数的方法来研究几何的问题,我们需要建立空间的点与有序数组之间的联系,为此我们通过引进空间直角坐标系来实现.1.1.1 空间直角坐标系过定点O ,作三条互相垂直的数轴,这三条数轴分别叫做x 轴(横轴)、y 轴(纵轴)、z 轴(竖轴),它们都以O 为原点且具有相同的长度单位. 通常把x 轴和y 轴配置在水平面上,而z 轴则是铅垂线;它们的正方向要符合右手规则:右手握住z 轴,当右手的四指从x 轴的正向转过2角度指向y 轴正向时,大拇指的指向就是z 轴的正向,这样就建立了一个空间直角坐标系(图8-1),称为Oxyz 直角坐标系,点O 叫做坐标原点.图8-1在Oxyz 直角坐标系下,数轴Ox ,Oy ,Oz 统称为坐标轴,三条坐标轴中每两条可以确定一个平面,称为坐标面,分别为xOy ,yOz ,zOx ,三个坐标平面将空间分为八个部分,每一部分叫做一个卦限(图8-2),分别用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ表示.图8-21.1.2 空间点的直角坐标设M 为空间中的任一点,过点M 分别作垂直于三个坐标轴的三个平面,与x 轴、y 轴和z 轴依次交于A 、B 、C 三点,若这三点在x 轴、y 轴、z 轴上的坐标分别为x ,y ,z ,于是点M 就唯一确定了一个有序数组(, , )x y z ,则称该数组(, , )x y z 为点M 在空间直角坐标系Oxyz 中的坐标,如图8-3.x ,y ,z 分别称为点M 的横坐标、纵坐标和竖坐标.yxzO图8-3反之,若任意给定一个有序数组(, , )x y z ,在x 轴、y 轴、z 轴上分别取坐标为x ,y ,z 的三个点A 、B 、C ,过这三个点分别作垂直于三个坐标轴的平面,这三个平面只有一个交点M ,该点就是以有序数组(, , )x y z 为坐标的点,因此空间中的点M 就与有序数组(, , )x y z 之间建立了一一对应的关系.注:A 、B 、C 这三点正好是过M 点作三个坐标轴的垂线的垂足.1.2 空间中两点之间的距离设两点111(, , )M x y z ,222(, , )N x y z ,则M 与N 之间的距离为212212212)()()(z z y y x x d -+-+-= (8-1-1)事实上,过点M 和N 作垂直于xOy 平面的直线,分别交xOy 平面于点1M 和1N ,则1MM ∥1NN ,显然,点1M 的坐标为11(, , 0)x y ,点1N 的坐标为22(, , 0)x y (如图8-4).图8-4由平面解析几何的两点间距离公式知,1M 和1N 的距离为:21221211)()(||y y x x N M -+-=.过点M 作平行于xOy 平面的平面,交直线1NN 于2N ,则11M N ∥2MN ,因此2N 的坐标为221(, , )x y z ,且212212112)()(||||y y x x N M MN -+-==,在直角三角形N MN 2中,||||122z z N N -=,所以点M 与N 间的距离为2122122122222)()()(||||z z y y x x N N MN d -+-+-=+=.例1 设(1, 2, 0)A -与(1, 0, 2)B --为空间两点,求A 与B 两点间的距离. 解 由公式(8-1-1)可得,A 与B 两点间的距离为d ==例2 在z 轴上求与点(3, 5, 2)A -和(4, 1, 5)B -等距的点M .解 由于所求的点M 在z 轴上,因而M 点的坐标可设为(0, 0, )z ,又由于MA MB =,由公式(8-1-1),得222222)5(1)4()2(53z z -++-=--++.从而解得72=z ,即所求的点为2(0, 0, )7M .习题8-11.讨论空间直角坐标系的八个卦限中的点的坐标的符号. 2.在坐标轴上的点和在坐标平面上的点的坐标各有何特点?3.在空间直角坐标系中,画出下列各点:(2, 0, 0)A ;(0, 3, 0)B -;(3, 0, 1)C ;(3, 2, 1)D -. 4.求点(1, 2, 3)-关于各坐标平面对称的点的坐标. 5.求点(1, 2, 3)关于各坐标轴对称的点的坐标. 6.求下列各对点间的距离: (1) (0, 1, 3)A -与(2, 1, 4)B ;(2) (1, 4, 2)C -与D(2, 7, 3).7.在坐标平面yOz 上求与三点(3, 1, 2)A 、(4, 2, 2)B --和(0, 5, 1)C 等距的点. 8.求点(12, 3, 4)A -与原点、各坐标平面和各坐标轴的距离.9. 证明以()()()A 4,3,1,B 7,1,2,C 5,2,3为顶点的三角形△ABC 是一等腰三角形.第2节 空间向量的代数运算2.1 空间向量的概念在日常生活中,我们经常会遇到一些量,如质量、时间、面积、温度等,它们在取定一个度量单位后,就可以用一个数来表示.这种只有大小没有方向的量,叫做数量(或标量).但有一些量,如力、位移、速度、电场强度等,仅仅用一个实数是无法将它们确切表示出来,因为它们不仅有大小,而且还有方向,这种既有大小又有方向的量,叫做向量(或矢量).在数学上,我们用有向线段AB u u u r来表示向量,A 称为向量的起点,B 称为向量的终点,有向线段的长度就表示向量的大小,有向线段的方向就表示向量的方向.通常在印刷时用黑体小写字母a ,b ,c ,…来表示向量,手写时用带箭头的小写字母, ,,a b c r r rL 来记向量.向量的长度称为向量的模,记作a 或AB u u u r,模为1的向量叫做单位向量,模为0的向量叫做零向量,记作0,规定:零向量的方向可以是任意的.本章我们讨论的是自由向量,即只考虑向量的大小和方向,而不考虑向量的起点,因此,我们把大小相等,方向相同的向量叫做相等向量,记作a =b .规定:所有的零向量都相等.与向量a 大小相等,方向相反的向量叫做a 的负向量(或反向量),记作 a . 平行于同一直线的一组向量称为平行向量(或共线向量).平行于同一平面的一组向量,叫做共面向量,零向量与任何共面的向量组共面.2.2 向量的线性运算2.2.1 向量的加法我们在物理学中知道力与位移都是向量,求两个力的合力用的是平行四边形法则,我们可以类似地定义两个向量的加法.定义1 对向量a ,b ,从同一起点A 作有向线段AB u u u r 、AD u u u r分别表示a 与b ,然后以AB u u u r 、AD u u u r 为邻边作平行四边形ABCD ,则我们把从起点A 到顶点C 的向量AC u u u r称为向量a 与b 的和(图8-5),记作a +b .这种求和方法称为平行四边形法则.图8-5 图8-6若将向量b 平移,使其起点与向量a 的终点重合,则以a 的起点为起点,b 的终点为终点的向量c 就是a 与b 的和(图8-6),该法则称为三角形法则.多个向量,如a 、b 、c 、d 首尾相接,则从第一个向量的起点到最后一个向量的终点的向量就是它们的和a +b +c +d (图8-7).图8-7对于任意向量a ,b ,c ,满足以下运算法则: (1) a +b =b +a (交换律).(2) ()()a +b +c =a +b +c (结合律). (3) 0a +=a .2.2.2 向量的减法定义2 向量a 与b 的负向量-b 的和,称为向量a 与b 的差,即()--a b =a +b .特别地,当b =a 时,有()-0a +a =.abcda +b +c +dabCabc =a +b由向量减法的定义,我们从同一起点O 作有向线段OA u u u r ,OB u u u r分别表示a ,b ,则()OA OB OA OB --=+-u u u r u u u r u u u r u u u ra b =OA BO BA =+=u u u r u u u r u u u r .也就是说,若向量a 与b 的起点放在一起,则a ,b 的差向量就是以b 的终点为起点,以a 的终点为终点的向量(图8-8).图8-82.2.3数乘向量定义3 实数λ与向量a 的乘积是一个向量,记作λa ,λa 的模是λa ,方向: 当0λ>时,λa 与a 同向;当0λ<时,λa 与a 反向;当0λ=时,λ0a =.对于任意向量a ,b 以及任意实数λ,μ,有运算法则: (1) ()()λμλμa =a . (2) ()+λμλμ+a =a a .(3)()+λλλ+a b =a b .向量的加法、减法及数乘向量运算统称为向量的线性运算,λμa +b 称为a ,b 的一个线性组合(, )R λμ∈.特别地,与❒a 同方向的单位向量叫做❒a 的单位向量,记做a ,即aa e a ρρρ=.上式表明:一个非零向量除以它的模的结果是一个与原向量同方向的单位向量.aabb-a bBAC例1 如图8-9,在平行六面体///ABCD B C D /—A 中,设/=AA u u u u r ,a AD =u u u r b AB =u u u r c ,试用,,a b c 来表示对角线向量//,.AC A C u u u u r u u u u raC'B'A'D'DAC图8-9解 ''AC AB BC CC =++u u u u r u u u u r u u u r u u u r 'AB BC AA =++u u u r u u u r u u u r a b c =++;'''AC A A AB BC AA AB AD =++=-++u u u r u u u r u u u r u u u r u u u r u u u r u u u r a b c =++.由于向量λa 与a 平行,所以我们通常用数与向量的乘积来说明两个向量的平行关系.即有,定理1 向量a 与非零向量b 平行的充分必要条件是存在一个实数λ,使得λa =b .2.3 向量的坐标表示2.3.1向量在坐标轴上的投影设A 为空间中一点,过点A 作轴u 的垂线,垂足为'A ,则'A 称为点A 在轴u 上的投影(图8-10).图8-10若M 为空间直角坐标系中的一点,则M 在x 轴、y 轴、z 轴上的投影为A 、B 、C ,如图8-11所示.图8-11设向量AB u u u r的始点与终点B 在轴u 的投影分别为A '、B ',那么轴u 上的有向线段uuuu rA B ''的值A B ''叫做向量AB u u u r 在轴u 上的投影,记作u u u r u prj AB A B ''=,轴u 称为投影轴.图8-12当uuuu r A B ''与轴u 同向时,投影取正号,当A B ''u u u u r 与轴u 反向时,投影取负号.注 (1) 向量在轴上投影是标量.(2) 设MN u u u u r为空间直角坐标系中的一个向量,点M 的坐标为111(, , )x y z ,点N 的坐标为222(, , )x y z ,显然,向量MN u u u u r在三个坐标轴上的投影分别为12x x -,12y y -,12z z -.2.3.2向量的坐标表示取空间直角坐标系Oxyz ,在x 轴、y 轴、z 轴上各取一个与坐标轴同向的单位向量,依次记作, , i j k ,它们称为坐标向量.yxzOA B CM空间中任一向量a ,它都可以唯一地表示为, , i j k 数乘之和.事实上,设MN u u u u ra =,过M 、N 作坐标轴的投影,如图8-13所示.MN =MA+AP +PN =MA+MB +MC u u u u r u u u r u u u r u u u r u u u r u u u r u u u u r a =.由于MA u u u r 与i 平行,MB u u u r与j 平行,MC u u u u r 与k 平行,所以,存在唯一的实数, , x y z ,使得MA x =u u u r i ,MB y =u u u rj ,MC z =u u u u r k ,即x y z a =i +j +k . (8-2-1)图 8-13我们把(8-2-1)式中, , i j k 系数组成的有序数组(, , )x y z 叫做向量a 的直角坐标,记为{, , }x y z a =,向量的坐标确定了,向量也就确定了.显然,(8-2-1)中的, , x y z 是向量a 分别在x 轴、y 轴、z 轴上的投影.因此,在空间直角坐标系中的向量a 的坐标就是该向量在三个坐标轴上的投影组成的有序数组.例2 在空间直角坐标系中设点(3, 1, 5)M -,(2, 3, 1)N -,求向量MN u u u u r 及NM u u u u r 的直角坐标.解 由于向量的坐标即为向量在坐标轴上的投影组成的有序数组,而向量的各投影即为RPQM 1M 2xyzγβα终点坐标与起点坐标对应分量的差.所以向量MN u u u u r 的坐标为{5, 4, 4}--,向量NM u u u u r的坐标为{5, 4, 4}-.例3(定比分点公式) 设111(,,)A x y z 和222(,,)B x y z 为两已知点,有向线段AB u u u r 上的点M 将它分为两条有向线段AMu u u u r和MB u u u r ,使它们的值的比等于数(1)λλ≠-,即AMMBλ=,求分点(,,)M x y z 的坐标. 图8-14解 如图8-14,因为AM u u u u r 与MB u u u r 在同一直线上,且同方向,故AM MB λ=⋅u u u u r u u u r,而122{,,}AM x x y y z z =---u u u u r, 222{,,}MB x x y y z z =---u u u r222{(),(),()}MB x x y y z z λλλλ=---u u u r所以 12()x x x x λ-=-,12()y y y y λ-=-,12()z z z z λ-=- 解得121212,,.111x x y y z z x y z λλλλλλ+⋅+⋅+⋅===+++当=1, 点M 的有向线段→AB 的中点, 其坐标为221x x x += 221y y y +=221z z z +=. 2.3.3向量的模与方向余弦的坐标表示式向量可以用它的模与方向来表示,也可以用它的坐标式来表示,这两种表示法之间的是有联系的.设空间向量12a M M =u u u u u ur r 与三条坐标轴的正向的夹角分别为,,αβγ,规定:0,0,0απβπγπ≤≤≤≤≤≤,称,,αβγ为向量a的方向角.图8-15因为向量❒a 的坐标就是向量在坐标轴上的投影,因此12cos cos x a M M a αα=⋅=⋅u u u u u u r r12cos cos y a M M a ββ=⋅=⋅u u u u u u r r(8-2-2)12cos cos z a M M a γγ=⋅=⋅u u u u u u r r公式(8.2.2)中出现的cos ,cos ,cos αβγ称为向量❒a 的方向余弦.而{,,}{cos ,cos ,cos }x y z a a a a a a a αβγ==⋅⋅⋅v v v v{cos ,cos ,cos }a a a e αβγ=⋅=⋅r r u u r{cos ,cos ,cos }a e αβγ=u u r 是与向量❒a 同方向的单位向量.而❒a =M M =12u u u u u ur,,x y z M P a M Q a M R a ===111,故向量a r 的模为a =r(8-2-3)从而向量a r的方向余弦为cos a αβγ===(8-2-4)并且 222cos cos cos 1αβγ++=.例4已知两点1M 和()21,3,0M ,求向量12M M u u u u u u r的模、方向余弦和方向角.解12(12,32,0(1,1,M M =--=-u u u u u ur2)2(1)1(222=-++-=;11cos ,cos ,cos 222αβγ=-==-;23,,334πππαβγ===. 例5 已知两点(4,0,5)A 和(7,1,3)B ,求与AB u u u r同方向的单位向量e r .解 因为{74,10,35}{3,1,2},u u u rAB =---=-所以 AB ==u u u r于是 }.e =r2.4 向量的数量积在物理中我们知道,一质点在恒力F 的作用下,由A 点沿直线移到B 点,若力F 与位移向量AB u u u r的夹角为θ,则力F 所作的功为||||cos W F AB θ=⋅⋅u u u r.类似的情况在其他问题中也经常遇到.由此,我们引入两向量的数量积的概念. 定义1 设a ,b 为空间中的两个向量,则数cos ,a b a b叫做向量a 与b 的数量积(也称内积或点积),记作⋅a b ,读作“a 点乘b ”.即cos ,⋅a b =a b a b (8-2-5)其中,a b 表示向量a 与b 的夹角,并且规定0, π≤≤a b .两向量的数量积是一个数量而不是向量,特别地当两向量中一个为零向量时,就有0⋅a b =.由向量数量积的定义易知: (1) 2⋅a a =a ,因此=a(2) 对于两个非零向量a ,b ,a 与b 垂直的充要条件是它们的数量积为零,即⊥a b ⇔0⋅a b =.注 数量积在解决有关长度、角度、垂直等度量问题上起着重要作用. 数量积的运算满足如下运算性质:对于任意向量a ,b 及任意实数λ,有 (1) 交换律:⋅⋅a b =b a .(2) 分配律:()⋅⋅⋅a b +c =a b +a c .(3) 与数乘结合律:()()()λλλ⋅⋅=⋅a b =a b a b . (4) 0⋅≥a a 当且仅当0a =时,等号成立.例6 对坐标向量i ,j ,k ,求⋅i i ,⋅j j ,⋅k k ,⋅i j ,⋅j k ,⋅k i . 解 由坐标向量的特点及向量内积的定义得1⋅⋅⋅i i =j j =k k =, 0⋅⋅⋅i j =j k =k i =.例7 已知2=a ,3=b ,2, 3π=a b ,求a b ⋅,(2)()-+a b a b ⋅,+a b . 解 由两向量的数量积定义有2cos , 23cos 3π⋅=⨯⨯a b =a b a b 123()=32=⨯⨯--.(2)()=22-⋅+⋅⋅-⋅-⋅a b a b a a +a b b a b b22=2-⋅-a a b b 222(3)23=11=---⨯-.2()()+=⋅+a b a +b a b =⋅⋅+⋅+⋅a a +a b b a b b222=+⋅+a a b b2222(3)3=7=+⨯-+,因此+=a b在空间直角坐标系下,设向量111{,,}x y z a =,向量222{,,}x y z b =,即111x y z ++a =i j k , 222x y z ++b =i j k .则111222()()x y z x y z ⋅++⋅++a b =i j k i j k121212()()+()x x x y x z ⋅+⋅⋅=i i i j i k 121212()()+()y x y y y z ⋅+⋅⋅+j i j j j k 121212()()+()z x z y z z ⋅+⋅⋅+k i k j k k .由于1⋅⋅⋅i i =j j =k k =, 0⋅⋅⋅i j =j k =k i =,所以121212x x y y z z ⋅++a b =. (8-2-6)也就是说,在直角坐标系下,两向量的数量积等于它们对应坐标分量的乘积之和. 同样,利用向量的直角坐标也可以求出向量的模、两向量的夹角公式以及两向量垂直的充要条件,即设非零向量111{,,}x y z a =,向量222{,,}x y z b =,则==a (8-2-7)cos ||||⋅=a ba,b a b=. (8-2-8)⊥a b ⇔1212120x x y y z z ++=. (8-2-9)例8 在空间直角坐标系中,设三点(5, 4, 1)A -,(3, 2, 1)B ,(2, 5, 0)C -.证明:ABC ∆是直角三角形.证明 由题意可知{2, 6, 0}AB =-u u u r ,={3, 1, 1}AC ---u u u r,则(2)(3)6(1)0(1)0AB AC ⋅=-⨯-+⨯-+⨯-=u u u r u u u r,所以AB AC ⊥u u u r u u u r .即ABC ∆是直角三角形.2.5向量的向量积在物理学中我们知道,要表示一外力对物体的转动所产生的影响,我们用力矩的概念来描述.设一杠杆的一端O 固定,力F 作用于杠杆上的点A 处,F 与OA u u u r的夹角为θ,则杠杆在F 的作用下绕O 点转动,这时,可用力矩M 来描述.力F 对O 的力矩M 是个向量,M 的大小为||||||sin OA OA =u u u r u u u rM F ,F .M 的方向与OA u u u r 及F 都垂直,且OA u u u r,F ,M 成右手系,如图8-16所示.图8-162.5.1向量积的定义在实际生活中,我们会经常遇到象这样由两个向量所决定的另一个向量,由此,我们引入两向量的向量积的概念.定义2 设a ,b 为空间中的两个向量,若由a ,b 所决定的向量c ,其模为sin , c =a b a b . (8-2-10)其方向与a ,b 均垂直且a ,b ,c 成右手系(如图8-17),则向量c 叫做向量a 与b 的向量积(也称外积或叉积).记作⨯a b ,读作“a 叉乘b ”.注 (1) 两向量a 与b 的向量积⨯a b 是一个向量,其模⨯a b 的几何意义是以a ,b 为邻边的平行四边形的面积.(2)⨯0a a =这是因为夹角θ=0,所以⨯0a a = 图8-17(3)对两个非零向量a 与b ,a 与b 平行(即平行)的充要条件是它们的向量积为零向量.a ∥b ⇔⨯0a b =.向量积的运算满足如下性质: 对任意向量a ,b 及任意实数λ,有 (1) 反交换律:⨯-⨯a b =b a . (2) 分配律: ()⨯⨯⨯a b +c =a b +a c ,()⨯⨯⨯a +b c =a c +b c .(3) 与数乘的结合律:()()()λλλ⨯⨯⨯a b =a b =a b .例9 对坐标向量i ,j ,k ,求⨯i i ,⨯j j ,⨯k k ,⨯i j ,⨯j k ,⨯k i . 解 ⨯⨯⨯0i i =j j =k k =.⨯i j =k ,⨯j k =i ,⨯k i =j .2.5.2向量积的直角坐标运算在空间直角坐标系下,设向量111{, , }x y z a =,向量222{, , }x y z b =,即111x y z ++a =i j k ,222x y z ++b =i j k ,因为⨯⨯⨯0i i =j j =k k =. ⨯i j =k ,⨯j k =i ,⨯k i =j , ⨯-j i =k ,⨯-k j =i ,⨯-i k =j .则111222()()x y z x y z ⨯++⨯++a b =i j k i j k121212()()+()x x x y x z ⨯+⨯⨯=i i i j i k 121212()()+()y x y y y z ⨯+⨯⨯+j i j j j k 121212()()+()z x z y z z ⨯+⨯⨯+k i k j k k121212121212()()+()()()()x y y x y z z y x z z x -⨯-⨯--⨯=i j j k k i 121212121212()()+()y z z y x z z x x y y x ----=i j k .为了便于记忆,借助于线性代数中的二阶行列式及三阶行列式有111111222222y z x z x y y z x z x y ⨯-a b =i j +k 111222x y z x y z =ij k . 注 设两个非零向量111{, , }x y z a =,222{, , }x y z b =,则a ∥b ⇔⨯0a b =,⇔212121z z y y x x ==. 若某个分母为零,则规定相应的分子为零.例10 设向量{1,2,1}--a =,{2,0,1}b =,求⨯a b 的坐标.解211112121012120201----⨯--=-i j ka b =i j +k 234=--i j +k . 因此⨯a b 的直角坐标为{2, 3, 4}--.例11 在空间直角坐标系中,设向量{3, 0, 2}a =,{1, 1, 1}--b =,求同时垂直于向量a 与b 的单位向量.解 设向量⨯c =a b ,则c 同时与a ,b 垂直.而32111⨯--ij kc =a b =23=-+i j +k ,所以向量c 的坐标为{2, 1, 3}-.再将c 单位化,得02,1,3}={=-c ,即{与-- 为所求的向量.例12 在空间直角坐标系中,设点(4, 1, 2)A -,(1, 2, 2)B -,(2, 0, 1)C ,求ABC∆的面积.解 由两向量积的模的几何意义知:以AB u u u r 、AC u u u r为邻边的平行四边形的面积为AB AC ⨯u u u r u u u r,由于{3, 3, 4}AB =--u u u r ,{2, 1, 1}AC =--u u u r,因此33453211AB AC ⨯=--=++--u u u r u u u ri j ki j k ,所以AB AC ⨯==u u u r u u u r故ABC ∆的面积为235=∆ABC S .2.6向量的混合积定义3 给定空间三个向量,,a b c r r r,如果先作前两个向量a r 与b r 的向量积,再作所得的向量与第三个向量c r 的数量积,最后得到的这个数叫做三向量,,a b c r r r的混合积,记做()a b c ⨯⋅r r r 或abc ⎡⎤⎣⎦r r r.说明:三个不共面向量,,a b c r r r 的混合积的绝对值等于以,,a b c r r r为棱的平行六面体的体积V .定理 如果111a X i Y j Z k =++r r r r ,222b X i Y j Z k =++r r r r ,333c X i Y j Z k =++r r r r, 那么 111222333.X Y Z abc X Y Z X Y Z ⎡⎤=⎣⎦r r r 习题8-21.,,,,,().ABCD AB AD AC DB MA M ==u u u r u u u r u u u r u u u r u u u r设为一平行四边形试用表示为平行四边形对角线的交点a b.a b12.,().2M AB O OM OA OB =+u u u r u u u u r u u u r u u u r设为线段的中点,为空间中的任意一点证明2223.?(1)()();(2)();(3)()().==⨯=⨯g g g g g g 对于任意三个向量与判断下列各式是否成立a,b c,a b c b c a a b a b a b c c a b4.:(1);(2)(3).利用向量证明三角形的余弦定理正弦定理;勾股定理5.设,,a b c r r r为单位向量,且满足0a b c ++=r r r r ,求.a b b c c a ++r r r r r r gg g 6.1(3,2,2),(1,3,2),(8,6,2),322a b c a b +c.求=-==-- 7.已知三点(3,0,2),A B AB ==u u u r求的坐标、模、方向余弦和方向角.8.一向量的终点在点B(2,-1,7),它在x 轴、y 轴和z 轴上的投影依次为4,-4和7.求这向量的起点A 的坐标.9.设2=a ,4=b ,3πa,b =,求⋅a b ,(2)-⋅a b b ,-a b .10.设向量a ,b ,c 两两垂直,且1=a ,2=b ,3=c ,求向量d =a +b +c 的模及d,a .11.在空间直角坐标系中,已知{1,2,3}-a = ,{2,2,1}-b = ,求: (1) ⋅a b ;(2) 25⋅a b ;(3) a ;(4) cos a,b .12.已知向量2332和,,a i j k b i j k c i j =-+=-+=-,计算(1)gg ()();a b c a c b -(2)()();a b b c +⨯+(3)()a b c ⨯g . 13.设向量a ,b 的直角坐标分别为{1, 3, 2}--和{2, 4, }k -,若a b ⊥,求k 的值.14.设向量{2, 1, 1}-a =,{1, 3, 0}-b =,求以、a b 为邻边构造的平行四边形面积.15.求同时垂直于向量{3, 2, 4}-a =和纵轴的单位向量.16.已知三角形三个顶点(4, 1, 2)A -,(3, 0, 1)B -,(5, 1, 2)C ,求ABC ∆的面积.第3节 空间中的平面与直线方程在本节我们以向量为工具,在空间直角坐标系中讨论最简单的曲面和曲线——平面和直线.3.1平面及其方程首先利用向量的概念,在空间直角坐标系中建立平面的方程,下面我们将给出几种由不同条件所确定的平面的方程.3.1.1平面的点法式方程若一个非零向量n 垂直于平面π,则称向量n 为平面π的一个法向量.显然,若n 是平面π的一个法向量,则λn (λ为任意非零实数)都是π的法向量,即平面上的任一向量均与该平面的法向量垂直.由立体几何知识知道,过一个定点0000(, , )M x y z 且垂直于一个非零向量{, , }A B C n =有且只有一个平面π.设(, , )M x y z 为平面π上的任一点,由于π⊥n ,因此0M M ⊥u u u u u u rn .由两向量垂直的充要条件,得00M M =⋅u u u u u u rn ,而0000{, , }M M x x y y z z =---u u u u u u r,{, , }A B C n =,所以可得0)()()(000=-+-+-z z C y y B x x A . (8-3-1)由于平面π上任意一点(, , )M x y z 都满足方程(8-3-1),而不在平面π上的点都不满足方程(8-3-1),因此方程(8-3-1)就是平面π的方程.由于方程(8-3-1)是给定点0000(, , )M x y z 和法向量{, , }A B C n =所确定的,因而称式(8-3-1)叫做平面π的点法式方程.图8-18例1 求通过点0(1, 2, 4)M -且垂直于向量{3, 2, 1}-n =的平面方程.解 由于{3, 2, 1}-n =为所求平面的一个法向量,平面又过点0(1, 2, 4)M -,所以,由平面的点法式方程(6-14)可得所求平面的方程为3(1)2(2)1(4)=0x y z --⋅++⋅-,整理,得32110x y z -+-=.例2 求过三点()12,1,4M -,()2M 1,3,2--,()3M 0,2,3 的平面π的方程. 解 所求平面π的法向量必定同时垂直于12u u u u u u r M M 与13u u u u u u r M M .因此可取12u u u u u u r M M 与13u u u u u u rM M 的向量积1213u u u u u u r u u u u u u rM M M M ⨯为该平面的一个法向量n .即1213n =u u u u u u r u u u u u u r M M M M ⨯.由于12{3, 4, 6}u u u u u u r M M =--,13{2, 3, 1}u u u u u u rM M =--,因此1213-631i jkn =u u u u u u r u u u u u u rM M M M =342⨯---149i j k,=+-,因此所求平面π的方程为0419214=--++-)()()(z y x ,化简得.015914=--+z y x一般地,过三点(,,)(1,2,3)k k k k M x y z k =的平面方程为1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 称为平面的三点式方程。
向量的线性运算

1.4 在共线共面问题上的应用
于是 C 和A, B 共线 AC // AB 存在实数s, 使得AC = s AB
即 OC OA = s (OB OA) 存在实数s, 使得OC = (1s) OA + s OB OC 对OA, OB 可分解, 且分解系数之和为1. 充分性. 设OC = r OA + s OB, 其中r + s = 1, 于是 OC = (1s) OA + s OB, 即 AC = s AB. 因此 AC // AB, 从而 C 和A, B共线.
设又有 = , 则( ) = = 0.
又 0 , 故 = 0 , 即 = .
充分性由平行定义易知.
注: 为方便, 将这里的数 记为
1.3 向量的分解
(2) 存在性. 从同一起点 O 作
OA = , OB = , OC = .
过 C 作 CD // OB, 且与直线 OA 交于 D.
1.4 在共线共面问题上的应用
由于上述结论, 使得向量的线性运算可以用 来解决有关点的共线、共面问题以及线段的 定比分割问题等.
命题1.2 假设O, A, B不共线, 则点C 和A, B共线 的充分必要条件是: 向量OC 对OA, OB 可分解, 并且分解系数之和等于1. 证明: 必要性. 由于O, A, B不共线, 所以OA, OB不平行, 且AB 0.
注: 向量组共线就是其中任何两个向量平行, 向量组共面就是其中任何三个向量共面. 于是判别“两向量是否平行”, “三向量是否共面” 成为基本问题.
1.3 向量的分解
定理1.1 (向量分解定理)
(1) 设 为非零向量, 则 // (与共线) 当且 仅当存在唯一实数, 使得 = . (2) 若向量 , , 共面, 并且 与 不平行, 则 存在唯一的一对实数, 使得 = + .
高等数学-第8章-空间解析几何与向量代数
-。
b与a的差b a.向量加法的性质〔运算律〕②结合律+的模一般地不等于a的模加b的模,而有a b a ba b+≤+,即三角形两边之和大于等于第三向量与数的乘法Array、向量的定义:向量a与数m的乘积是一个向量,它的模等于m a,方向与a相同〔假设反〔假设m<0〕。
、向量与数量乘法的性质(运算律)②分配律≠,则向量b平行于a得充分必要条件是:存在唯一实数λ,使b=λa。
a0在实际问题中,有些向量与其起点有关,有些向量与其起点无关。
由于一切向量的共性是它们都有大小和方向,所以在数学上我们研究与起点无关的向量,并称这种向量为自由向量〔以后简称向量〕,即只考虑向量的大小和方向,而不管它的起点在什么地方。
当遇到与起点有关的向量时〔例如,谈到某一质点的运动速度时,这速度就是与所考虑的那一质点的位置有关的向量〕,可在一般原则下作特别处理。
上的射影。
投影向量的定义:AB 的始点A B ''就定义AB 在轴u 上的投影向量。
向量在轴上的投影:向量A B ''在轴AB 在轴u 上的投影,记为投影AB 。
向量在轴上的投影性质:性质1〔投影定理〕AB =cos AB ϕ与向量AB 的夹角。
推论:相等矢量在同一轴上的射影相等。
性质2:Prj(12a a +)=Prj 1a +Prj 2a 。
性质2可推广到有限个向量的情形。
性质3:Prj u λa =λPrj u a 。
向量在坐标轴上的分向量与向量的坐标:向量a 在坐标轴上的投影向量,,y z i a j a k 称为向量在坐标轴上的分向量。
向量a 在三条坐标轴上的投影,y z a a 叫做向量的坐标,记为:a ={,,x y a a 由向量在轴上的投影定义,a 在直角坐标系Oxyz 中的坐标{,,x y z a a a a ,由此可知,向量的投影具有与坐标相同的性质。
利用向量的坐标,可得向量的加法、减法以及向量与数的乘法的运算如下:a ={,x y a a ,{,,}x y zb b b b =利用向量加法的交换律与结合律,以及向量与数乘法的结合律与分配律,有{,x y z z a b a b b a b +=+++{x a b a b -=-{,}x y a a a λλλ=由此可见,对向量进行加、减及与数相乘,只须对向量的各个坐标分别进行相应的数量运算就行了。
第2章-n维向量

请双面打印/复印,节约纸张。
第二章 n维向量第一节 n维向量及其运算 第二节 向量组的秩和线性相关性 第三节 向量组线性相关性的 等价刻画 第四节 向量组的极大线性无关组 第五节 向量空间 第六节 内积与正交矩阵第二章 n维向量§2.1 n维向量及其运算第二章 n维向量§2.1 n维向量及其运算§2.1 n维向量及其运算 一. 历史古希腊的亚里士多德(Aristotle): 二力合成的平行四边形法则 法国数学家笛卡尔(René Descartes): 解析几何 1831年, 德国数学家高斯 (Johann Carl Friedrich Gauss): 复平面的概念 1844年, 德国数学家格拉斯曼 (Hermann Günter Grassmann): n 维向量 英国物理学家数学家亥维赛(Oliver Heaviside): 向量分析 1888年, 意大利数学家皮亚诺(Giuseppe Peano): 以公理的方式定义了有/无限维向量空间三皇 五帝 夏朝 商朝 周朝 春秋 战国 秦朝 西楚 西汉 新朝 玄汉 东汉 三国约前?世纪-约前30世纪初 约前30世纪初-前2029年 前2070-前1600 前1600-前1046 前1046-前256 前770-前476 前475-前221 前221-前206 前206-前202 前202-公元9年 公元8年12月-23年10月 亚里士多德[希腊] (前384~前322.3.7) 23-25 25-220 220-280第二章 n维向量§2.1 n维向量及其运算第二章 n维向量§2.1 n维向量及其运算笛卡尔[法] (1596.3.31~1650.2.11)明朝1368-1644 顺治1644-1662 康熙1662-1723 雍正1723-1736 乾隆1736-1796 嘉庆1796-1821 道光1821-1851 咸丰1851-1862 同治1862-1875 光绪1875-1908 宣统1908-1911高斯[德] (1777.4.30~1855.2.23)顺治1644-1662 康熙1662-1723 雍正1723-1736 乾隆1736-1796 嘉庆1796-1821 道光1821-1851 咸丰1851-1862 同治1862-1875 光绪1875-1908 宣统1908-1911东南大学-张小向 272365083@1请双面打印/复印,节约纸张。
解析几何大学数学

§1.5 标架与坐标 §1.7 向量的数量积 §1.9 三向量的混合积
§1.1 向量的概念
• 量的分类 :标量、向量(矢量)、张量等
定义 集合 相互关系
§1.1 向量的概念
定义1.1.1 既有大小又有方向的量叫做向量, 或称矢量.
向量的几何表示: 有向线段
M2 a
有向线段的长度表示向量的大小,
a2 A2
a1 O
A1 a3 c
A4
an1
An-1
An
这种求和的方法叫做多边形法则.
a4 A3
Back
三、向量的减法
定义1.2.2 当向量 b 与向量 c 的和等于向量 a ,即 b c a 时,我们把向量 c 叫做向量 a 与 b 的差, 并记做 c a b.
向量减法的定义:a b a (b).
相反.我们把这种运算叫做数量与向量的乘法,简称为数乘.
设 是一个数,向量a与 的乘积a规定为
(1) 0, (2) 0,
aa与a0同向,|
a
|
|
a
|
(3) 0, a与a 反向,| a || | | a |
a
2a
1
a
2
下一页
返回
定理1.3.1 数与向量的乘积符合下列运算规律:
(1)
B
a
C a (a) 0.
A
a
b
b
c
a
A
O
O a bc a b c C
二、向量加法的运算规律
有限个向量 a1, a2, an 相加可由向量的三角形求和法则推广: 自任意点 O 开始,依次引OA1 a1, A1A2 a2, , An1An an , 由此得一折线 OA1A2 An,于是向量 OAn a 就是 n 个向量 a1, a2 , , an 的和,即OA OA1 A1A2 An1An .
《毕业论文《向量》》word版

摘要向量在中学教学和研究中占有比较重要的地位,如何用向量的知识去解决平面几何问题是比较重要的利用向量解决一些数学问题,将大大简化解题的步骤,使学生多掌握一种行之有效的数学工具.本文首先回顾了向量的一些基本性质,接着分别从证明线段平行,证明垂直问题,求夹角问题,求长度问题总结归纳向量在解决一系列数学问题中的应用并举例说明使用向量更加快捷直观地解决一些较复杂的数学问题.关键词向量平面几何方法Abstract vector occupy an important position in middle school teaching and research, knowledge of how to use vector plane geometry to solve problems using vector to solve some mathematical problems is more important, will greatly simplify the problem-solving steps, enable students to master a proven mathematical tools. First of all, this article reviews some basic properties of vector, then proof from line segments parallel to prove that the vertical issues, angle problems, and the length problem summary application of vector in solving a series of mathematical problems faster, and gives examples of using vector and intuitive solution to some of the more complex mathematical problems.Keywords vector, plane geometry, method目录前言 (3)1 向量基本性质回顾 (3)1.1向量的概念 (3)1.2向量的几何表示 (3)1.3相等向量与共线向量 (3)1.4向量的运算 (4)1.5向量的数量积 (5)1.6平面向量的基本定理 (5)2 证明线段平行问题 (6)3 证明垂直问题 (7)4 求夹角问题 (8)5 求线段的长度 (9)结束语 (12)致谢 (13)参考文献 (14)前言向量作为中学数学的必修内容,在知识体系中占的比例也较大,在中学平面几何中有着广泛的应用.向量的加法运算与全等、平行,数量的向量积与相似,距离、夹角之间有密切的联系.因此,利用向量可以解决中学平面几何中的相关问题.向量是沟通代数、三角、几何等内容的桥梁之一,利用向量可以解决一些数学问题,将大大化简解题的步骤,使学生掌握一些行之有效的数学工具。
大学向量知识点总结归纳

大学向量知识点总结归纳一、向量的定义在几何学中,向量通常指的是具有大小和方向的物理量。
在数学中,向量通常用一组有序数对或者n元组表示。
向量的定义可以从几何的角度和代数的角度来理解。
在几何的角度,向量可以看成是具有大小和方向的箭头,箭头的长度表示向量的大小,箭头的方向表示向量的方向。
在代数的角度,向量可以看成是n个实数组成的有序数组。
在这个意义上,向量可以表示为(a1, a2, ..., an),其中a1, a2, ..., an分别表示向量在各个坐标轴上的分量。
例如在二维平面上,一个向量可以表示为(a, b),其中a和b分别表示向量在x轴和y轴上的分量。
在三维空间中,可以表示为(a, b, c),其中a、b和c分别表示向量在x轴、y轴和z轴上的分量。
根据这个定义,向量的大小可以用勾股定理来表示。
在二维平面上,向量(a, b)的大小记作||(a, b)||,可以用勾股定理来表示:||(a, b)|| = √(a² + b²)。
在三维空间中,向量(a, b, c)的大小记作||(a, b, c)||,可以用勾股定理来表示:||(a, b, c)|| = √(a² + b² + c²)。
根据这个定义,向量的大小是一个非负的实数,向量的大小为0时,向量被称为零向量。
向量的方向可以用单位向量来表示,单位向量是指大小为1的向量。
二、向量的表示在数学中,向量可以用不同的表示方法来表示。
常见的表示方法有:1. 符号表示法向量通常用字母加箭头的方式来表示,如→AB。
这里的箭头表示向量的方向,字母表示向量的名称,向量的起点通常写在上面,终点写在下面。
例如上图中向量→AB可以表示为向量a,记作→AB = vector a。
向量→AB和向量→CD是相等的,这里的相等表示两个向量的大小和方向都相等。
例如:→AB = →CD。
2. 坐标表示法向量还可以用坐标表示法来表示,这种表示方法通常用于研究向量的运算。
大学数学易考知识点向量的叉乘运算

大学数学易考知识点向量的叉乘运算大学数学易考知识点:向量的叉乘运算向量的叉乘是大学数学中的一个重要知识点,在向量运算中起到了至关重要的作用。
本文将详细介绍向量的叉乘运算及其相关概念和性质,帮助读者更好地理解和掌握这一知识点。
一、向量的定义及表示方法向量是用来表示具有大小和方向的量的数学工具,常用于几何和物理问题的描述和求解。
在二维平面中,向量通常用有序数对表示;在三维空间中,向量通常用有序数列表示。
在二维平面中,用向量AB表示从点A到点B的有向线段,其表示方法为:AB = (x2 - x1) i + (y2 - y1) j其中,i和j分别表示x轴和y轴的单位向量,(x1, y1)和(x2, y2)分别表示点A和点B的坐标。
在三维空间中,用向量AB表示从点A到点B的有向线段,其表示方法为:AB = (x2 - x1) i + (y2 - y1) j + (z2 - z1) k其中,i、j和k分别表示x轴、y轴和z轴的单位向量,(x1, y1, z1)和(x2, y2, z2)分别表示点A和点B的坐标。
二、向量的叉乘运算向量的叉乘,也称为向量积或叉积,是一种二元运算。
对于给定的两个向量u和v,在三维空间中进行叉乘运算的结果是另一个向量w,表示为:w = u × v叉乘的结果向量w的大小等于向量u和v构成的平行四边形的面积,方向垂直于u和v所在平面,并符合右手规则。
三、叉乘运算的定义和性质叉乘的定义如下:u × v = |u| |v| sinθ n其中,|u|和|v|分别表示向量u和v的模,θ表示u和v之间的夹角(0° ≤ θ ≤ 180°),n表示垂直于u和v构成的平面上的单位法向量。
叉乘运算具有以下几个重要性质:1. 叉乘的结果是一个向量。
2. 叉乘满足反交换律,即 u × v = - (v × u)。
3. 叉乘满足分配律,即 (ku) × v = k(u × v),u × (kv) = k(u × v),其中k为常数。
大学__数学专业__空间解析几何__第一章__向量代数

证 必要性 设三矢量 a, b , c可 以 构成三角形 ABC, 即 有AB a , BC
A B
b, CA c, 那 么AB+BC+CA=AA 0, 即a b c 0
充 分性 设a b c 0 , 作AB a , BC b, 那 么AC a b, 所 以AC c 0, 从 而c是 AC的 反矢 量, 因 此 c= CA ,所以 a, b , c可 构成 一个 三 角形 ABC .
平行于同一直线的一组矢量
a // b
零矢量与任何共线的矢量组共线.
定义1.1.5 平行于同一平面的一组矢量 叫做共面矢量. 零矢量与任何共面的矢量组共面.
a
c d
§1.2、向量的加法
定 义1.2.1 设 已 知 矢 量 a、 b ,以空间任意一点 O为 始 点 接连作矢量 OA a, AB b得 一 折 线 OAB, 从 折 线 的 端 点 O到 另 一 端 点 B的 矢 量 OB c , 叫 做 两 矢 量 a与b的 和 , 记 做 cab
a
M
M2
1
a 或 M1 M 2 以 M 1 为起点,M 2 为终点的有向线段. 向量的大小. | a | 或 | M 1 M 2 向量的模长: |, a
向量的大小. | a | 或 | M 1 M 2 向量的模长: |
a
M
M2
特别:
模长为1的向量A OA n OA 1 A1 A2 An 1 An .
A1 A2 O An-1 An A4 A3
这种求和的方法叫做多边形法则.
ab a b
O
a
A
b
B
三角不等式
大学数学-线性代数-向量组

向量组的线性组合
向量组的线性组合是指 通过给定向量组中的向 量以及标量系数的线性 运算得到的新向量。
线性组合的系数可以是 实数或复数,也可以是 标量或向量。
线性组合的结果是一个 新的向量,其分量是原 向量分量与系数的线性 组合。
线性组合满足交换律、 结合律和分配律。
秩的性质
定理
若矩阵A经过有限次初等行变换 得到矩阵B,则矩阵A和B的秩相 等。
若向量组中的向量个数等于向 量的维数,则该向量组线性无 关;若向量组中的向量个数小 于向量的维数,则该向量组线 性相关。
05
向量组的正交性
正交向量的定义
正交向量的定义
两个向量$vec{a}$和$vec{b}$是正交 的,如果它们的点积为0,即$vec{a} cdot vec{b} = 0$。
向量组线性相关的充要条件是该向量组构成的矩阵的 秩小于向量的个数。
如果向量组中任何一个向量是其余向量的线性组合, 则该向量组线性相关。
04
向量组的秩
向量组的秩的定义
秩的定义
向量组的秩是指该向量组中线性无关向量的最大数量。
线性无关的定义
如果向量组中的向量个数等于向量的维数,则该向量组线性无关。
向量组中线性无关向量的判断
02
向量组的定义与表示
向量组的定义
向量组是由一组有序数列构成的集合,每个数列称为一个向量, 每个向量由若干个数(分量)组成。
向量组中向量的个数称为向量组的维数,所有向量中分量的个数 必须相同。
向量组的表示方法
通常使用黑体字母表示向量,如 $mathbf{a}$、$mathbf{b}$、 $mathbf{c}$等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反向时取负号, 则 b 与 a 同向, 且
b
故 b a. 再证数 的唯一性 . 设又有 b= a , 则 ( ) a 0 故 0, 即 .
目录 上页 下页 返回 结束
“ ” 已知 b= a , 则
b=0
a , b 同向
a∥b
a , b 反向
例1. 设 M 为 ABCD 对角线的交点,
a ( ax , ay , az )
平行向量对应坐标成比例:
当 a 0 时,
bx by bz ax ay az
bx ax by ay
bz az
目录 上页 下页 返回 结束
例2. 求解以向量为未知元的线性方程组
5x3y a
①
3x2y b
②
其中a (2,1,2), b (1,1, 2).
第八章
空间解析几何与向量代数
第一部分 向量代数 第二部分 空间解析几何
在三维空间中: 空间形式 — 点, 线, 面
数量关系 — 坐标, 方程(组) 基本方法 — 坐标法; 向量法
第一节
第八章
向量及其线性运算
一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影
当 1时, 点 M 为 AB 的中点 ,于是得
M B
o
A
中点公式:
x1
2
x2
,
B
y1
2
y2
,
z1 z2 2
M
目录 上页 下页 返回 结束
五、向量的模、方向角、投影
1. 向量的模与两点间的距离公式
设 r (x, y, z ), 作 OM r, 则有 r OM ONP ONQM OR
规定 :
总之:
a a
运算律 : 结合律 ( a ) ( a) a
分配律
可见 1a a
1a a ;
(a b) a b
则有单位向量 ea
1 a
a. 因此 a a ea
目录 上页 下页 返回 结束
定理1. 设 a 为非零向量 , 则
a∥b
( 为唯一实数)
证: “ ”. 设 a∥b , 取 =± , a , b 同向时取正号
2. 向量的坐标表示
以在空i ,间j ,直k 分角别坐标表系示下x,,
任意向量 r 可用向径 OM 表示.
y , z 轴上的单位向量 , 设点 M
的坐标为 M (x , y , z), 则
z C
OM ON NM OA OB OC r x i y j z k 记 (x, y , z )
三角形法则可推广到多个向量相加 .
目录 上页 下页 返回 结束
s a1 a2 a3 a4 a5
a4
a5
a3 s
a2 a1
目录 上页 下页 返回 结束
2. 向量的减法 三角不等式
a
目录 上页 下页 返回 结束
3. 向量与数的乘法
是一个数 , 与 a 的乘积是一个新向量, 记作 a .
原点 O(0,0,0) ; 坐标轴上的点 P, Q , R ;
坐标面上的点 A , B , C
z
R(0,0, z)
B(0, y, z)
C(x,0, z)
r
O
x P(x,0,0)
M y
Q(0, y,0)
A(x, y,0)
目录 上页 下页 返回 结束
z
O x
坐标面 :
坐标轴 :
y
目录 上页 下页 返回 结束
试用a 与b 表示 MA, MB , MC , MD.
解: a b AC
2 MA
D
C
b a BD
2 MB
bM
MA
1 2
(
a
b)
MB
1 2
(baFra bibliotek)A
a
B
MC
1 2
(
a
b
)
MD
1 2
(b
a
)
目录 上页 下页 返回 结束
三、空间直角坐标系
1. 空间直角坐标系的基本概念
过空间一定点 O ,由三条互相垂直的数轴按右手规则
解: 2×① -3×② , 得
x 2a 3b (7,1,10)
代入②得 y 1 (3 x b) (11, 2,16) 2
目录 上页 下页 返回 结束
例3. 已知两点 在AB所在直线上求一点 M , 使
及实数 1,
解: 设 M 的坐标为
如图所示
AM MB
AM OM OA MB OB OM
k
O Ai
x
M r jB
y N
此式称为向量 r 的坐标分解式 ,
沿三个坐标轴方向的分向量,
目录 上页 下页 返回 结束
四、利用坐标作向量的线性运算
设 a ( ax ,ay ,az ), b (bx ,by ,bz ), 为实数,则
a b (ax bx , ay by , az bz )
组成一个空间直角坐标系.
• 坐标原点
Ⅲ
z z 轴(竖轴)
Ⅱ
• 坐标轴
Ⅳ
• 坐标面
• 卦限(八个) Ⅶ
x
x轴(横轴)
Ⅷ
yOz 面
O xOy面
Ⅴ
Ⅰ
y
y轴(纵轴)
Ⅵ
目录 上页 下页 返回 结束
在直角坐标系下
点 M 11 有序数组 (x, y, z) 11 向径 r
(称为点 M 的坐标) 特殊点的坐标 :
OM O A (OB OM )
A
M B
o
A
得 即
OM
1
1
(OA
OB
B
1
1
(x1 x2 , y1 y2 , z1 z2 )
M
目录 上页 下页 返回 结束
说明: 由
1
1
(x1 x2 , y1 y2 , z1 z2 )
得定比分点公式:
A
x1 x2 1
,
y1 y2 1
,
z1 z2 1
目录 上页 下页 返回 结束
一、向量的概念
向量: 既有大小, 又有方向的量称为向量 (又称矢量).
表示法: 有向线段 M1 M2 , 或 a , 或 a .
向量的模 : 向量的大小,
自由向量: 与起点无关的向量. 单位向量: 模为 1 的向量, 记作 e 或e . 零向量: 模为 0 的向量,
M2 M1
目录 上页 下页 返回 结束
若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a=b ;
若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行,记作 a∥b ; 规定: 零向量与任何向量平行 ;
与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作-a ;
因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 .
若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 .
目录 上页 下页 返回 结束
二、向量的线性运算
1. 向量的加法 平行四边形法则:
b ab
(a b) c
c
bc
a (b c)
a
三角形法则:
abc ab b
ab b
a
a 运算规律 : 交换律 a b b a
结合律 ( a b ) c a (b c ) a b c
