9练习题参考答案
3、假设检验的结论为什么不能绝对化
因为统计推断的结论都是具有概率性的， 因为统计推断的结论都是具有概率性的，不 管是否拒绝H0，都有可能发生推断错误， 管是否拒绝 ，都有可能发生推断错误， 尤其当P值较接近检验水准时 值较接近检验水准时， 即 α 或β ，尤其当 值较接近检验水准时， 即样本统计量在界值上下波动时， 即样本统计量在界值上下波动时，作推断结 论时应慎重，在报告结论时， 论时应慎重，在报告结论时，最好列出检验 统计量的值，尽量写出P值的确切范围 值的确切范围， 统计量的值，尽量写出 值的确切范围，以 便读者与同类研究进行比较。 便读者与同类研究进行比较。
2、假设检验的基本思想与步骤
在进行均数比较时，如果两个均数不等有 在进行均数比较时， 两种可能性：（ 由于抽样误差所致；（ ：（1 ；（2 两种可能性：（1）由于抽样误差所致；（2） 二者来自不同的总体。如何作出判断呢？ 二者来自不同的总体。如何作出判断呢？ 按照逻辑推理，如果第一种可能性较大， 按照逻辑推理，如果第一种可能性较大， 可以接受它，统计上称差异无统计意义； 可以接受它，统计上称差异无统计意义； 如果第一种可能性较小， 如果第一种可能性较小，可以拒绝它而接 受后者，统计上称差异有统计意义。 受后者，统计上称差异有统计意义。假设 检验就是根据反证法和小概率事件的思想 建立起来的。 建立起来的。
练习题参考答案
计算分析题
1、某药厂原来生产的一种安眠药，经临床使用测得平均 某药厂原来生产的一种安眠药， 睡眠时间为18.6小时 小时。 睡眠时间为18.6小时。该厂技术人员为增加睡眠时间改 进了旧工艺，改进工艺后生产的安眠药经10名受试者试 进了旧工艺，改进工艺后生产的安眠药经10名受试者试 睡眠时间为： 用，睡眠时间为：23.4 25.6 24.3 21.2 21.0 26.0 25.5 26.2 24.3 24.0 。 指出资料类型。 （1）指出资料类型。 计量资料 改进工艺后安眠药的平均睡眠时间为多少？ （2）改进工艺后安眠药的平均睡眠时间为多少？
4、 t 检验，P <0.001，是否能说明两总 检验， <0.001， 体均数之间差别很大，为什么？ 体均数之间差别很大，为什么？
P值 的大小只能说明差异是否 有统计学意义， 值越小， 有统计学意义，P值越小，只能说 明有很大把握认为两总体均数有差 别，而不能误解为所分析的指标间 差异很大， 差异很大，或在医学上有明显的实 用价值。 用价值。
x ± 2.58s = 3.29 ± 2.58 × 0.44 = (2.15 ~ 4.42)kg
该男孩体重超出正常值范围，属于巨大儿。 该男孩体重超出正常值范围，属于巨大儿。 （2）请估计全市男孩出生体重均数95％可信区间。 请估计全市男孩出生体重均数95％可信区间。
x ± 1.96 s X = 3.29 ± 1.96 × 0.039 = (3.21 ~ 3.37)kg
x=
∑ x = 23.4 + 25.6 + ... + 24.0 = 24.5
n 10
（3）改进工艺后生产的安眠药是否提高了疗效？ 改进工艺后生产的安眠药是否提高了疗效？
解：本例：n=10, X =24.5, S =1.85, 本例：n=10, 24.5, 1.85, 10 1.建立假设 确定检验水准α 建立假设、 1.建立假设、确定检验水准α
Σ( X − X )2 计算公式 S= n −1
用途 ①表示样本均数代表性 ②描述正态分布资料的 分布特征 ③利用正态分布法计算 正常值范围 计算变异系数CV和 ④计算变异系数CV和 均数的标准误
1、标准差与均数标准误的区别 标准差与均数 均数标准误的区别
S SX = n
①表示样本均数的可靠性 ②计算总体均数的可信 区间 ③进行两均数的假设检验
差异无统计学意义,尚不能认为两地正常成年男子红细胞数有差别。 H0， 差异无统计学意义,尚不能认为两地正常成年男子红细胞数有差别。
(S x ) 标准差（ 标准差（ s） 均数标准误 均数标准误 概念 描述个体值的变异程度 描述样本均数的变异程度 意义 表示一组正态变量值的 表示样本均数抽样误差大 变异程度指标 小的指标
（4）该地成年男子红细胞数的95%正常值范围： 该地成年男子红细胞数的95%正常值范围 正常值范围：
X ±1.96S = 479.38 ±1.96× 40.91 = (399.20,559.56)
名正常成年男子， 立方毫米， ⑸在另一地区随机抽取 125 名正常成年男子，测得其红细胞数的均数为 480.23 万/立方毫米， 立方毫米，问两地正常成年男子红细胞数有无差别？ 标准差为 41.68 万/立方毫米，问两地正常成年男子红细胞数有无差别？
3.查相应界值表， 3.查相应界值表，确定 P 值， 查相应界值表 界值表 0.05， 查 t 界值表， t0.05,9 = 2.262 , t > t0.05,9 ，P <0.05， 4.推断结论 4.推断结论 推断 的检验水准上， 差异有统计学意义， 在α=0.05 的检验水准上，拒绝 H0，接受 H1，差异有统计学意义，即可以认为 改进工艺后生产的安眠药疗效与以前不同 疗效提高了。 不同， 改进工艺后生产的安眠药疗效与以前不同，疗效提高了。
2．随机抽样调查129名上海市区男孩出生体重，均数为 随机抽样调查129名上海市区男孩出生体重 名上海市区男孩出生体重， 3.29kg，标准差为0.44kg， 3.29kg，标准差为0.44kg，问：
（1）理论上99%男孩出生体重在什么范围？若某男孩出生体重4.51kg，怎么 理论上99%男孩出生体重在什么范围 若某男孩出生体重4.51kg， 男孩出生体重在什么范围？ 评价？ 评价？
假设检验的基本步骤
1、建立假设，确定单侧检验或是双侧检验 建立假设，
H0：无效假设（零假设），差别由抽样误差引起。 无效假设（零假设） 差别由抽样误差引起。 H1：备择假设，差别是本质上存在的。 备择假设，差别是本质上存在的。 2 、 确定检验水准 （ 显著性水准 ） α， 指进行假设检 确定检验水准（ 显著性水准） 验发生假阳性的概率， 05。 验发生假阳性的概率，多取α＝0.05。
3、根据资料性质及类型，选定检验方法和计算统计 根据资料性质及类型， 等统计量。 量，如计算t、u、x2等统计量。 4、根据样本检验统计量，确定概率P。 根据样本检验统计量， 5、 做出推断结论 ： 以检验水准 α判断 H0是否成立 ， 做出推断结论： 是否成立， 结合专业知识做出结论。 结合专业知识做出结论。
（3）郊区抽查男童100人的出生体重，得均数3.23(kg)，标准差0.47(kg)，问市 郊区抽查男童100人的出生体重 得均数3.23(kg)，标准差0.47(kg)， 人的出生体重， 区和郊区男孩出生体重均数是否不同？ 区和郊区男孩出生体重均数是否不同？ （4）以前上海市区男孩平均出生体重为3kg，问现在出生的男童是否更重些 以前上海市区男孩平均出生体重为3kg， 了？
综合练习综合练习-选择题
选择题一： 选择题一：
1-5 BBCDB 6-10 CBDBD
选择题二
1-5 CCACA 6-10 CBDCB
1.某医师观察新药对肺炎的疗效，并与旧药组相比，得两组的退热天数见下表，试问新药 某医师观察新药对肺炎的疗效，并与旧药组相比，得两组的退热天数见下表， 某医师观察新药对肺炎的疗效 疗效是否优于旧药？ 疗效是否优于旧药？ 分组 病例数 平均退热天数 标准差 25 3.8 0.8 新药组 23 5.2 0.9 旧药组
450~ 470~ 490~ 510~ 530~ 550~ 570~590 合计
22 25 21 17 9 4 1 130
（1）正态分布 ） （2）算术均数与标准差 ）
X=
S=
f1X1 + f2 X2 +⋅⋅⋅+ fk Xk 2×380 + 4× 400 +... +1×580 = = 479.38 f1 + f2 +⋅⋅⋅+ fk 2 + 4 + 9 +... + 4 +1
= 5.7
下结论。 3.查相应界值， 3.查相应界值，确定 P 值，下结论。 查相应界值 0.05， 查表 t0.05,50 = 2.009 , t > t0.05,50 ，P < 0.05，拒绝 H0，接受 H1，差异有 统计学意义，可以认为新药与旧药疗效不同，新药优于旧药。 统计学意义，可以认为新药与旧药疗效不同，新药优于旧药。
130， 479.38， 40.91， 解：本例： n1 =130， X1 =479.38， S1 =40.91， 本例： n2 =125， X 2 =480.23， S2 =41.68 125， 480.23， 1.建立假设 建立假设、 1.建立假设、确定检验水准α。 H0： µ1 = µ2 两地正常成年男子红细胞数无差别 H1： µ1 ≠ µ2 两地正常成年男子红细胞数有差别 α=0.05 2.计算检验统计量 计算检验统计量。 2.计算检验统计量。
µ0 =18.6
H0： µ = µ0 改进工艺后药效与以前相同。 改进工艺后药效与以前相同。 H1： µ ≠ µ0 改进工艺后药效与以前不同。 改进工艺后药效与以前不同。
双侧检验，检验水准: 双侧检验，检验水准:α=0.05 2.计算检验统计量 2.计算检验统计量 t 值
| x − µ0 | | 24.5 −18.6| t= = = 9.57 , ν = n −1 = 10 −1 = 9 s/ n 1.85/ 10
∑ fx
2
− (∑ fx) / ∑ f
2
∑ f −1
=
∑30091200 − 62320 /130 = 40.91
2
Hale Waihona Puke 129可信区间： （3）总体均数的 ）总体均数的95%可信区间： 可信区间
部编语文七(上)第9课《从百草园到三味书屋》练习题及参考答案
部编语文七（上）第9课《从百草园到三味书屋》练习题及参考答案基础知识1.下列加点字的注音无误的一项是( )A.确凿．(zuó) 觅．食(mì)秕．谷(bǐ) 人声鼎．沸(dǐng)B.菜畦．(qí) 油蛉．(líng)蝉蜕．(tuō) 风流倜．傥(tì)C.缠络．(lào) 捕．获(bǔ)锡箔．(bó) 人头攒．动(cuán)D.盔．甲(kuī) 宿儒．(rú)斑蝥．(máo) 朝．花夕拾(zhāo)2.用恰当的词语替换句中画线部分的内容。
(1)清晨的里约热内卢国际机场人声喧闹,来自世界各地的记者、球迷们陆续赶到这里。
( )(2)湖南五彩谷有“江南坝上”之称,是个少有人来的地方,也是一个令你怦然心动的天堂。
( )(3)书生自然吓得要死,而那老和尚却道无妨,给他一个小盒子,说只要放在枕边,便可垫高了枕头睡觉。
( )3.根据原文在下列横线处填写恰当的动词。
薄薄的雪,是不行的;总须积雪盖了地面一两天,鸟雀们久已无处觅食的时候才好。
开一块雪,露出地面,用一枝短棒起一面大的竹筛来,下面些秕谷,棒上一条长绳,人远远地着,看鸟雀下来啄食,走到竹筛底下的时候,将绳子一,便住了。
4.下列语句中,没有运用修辞手法的一项是( )A.油蛉在这里低唱,蟋蟀们在这里弹琴。
B.如果不怕刺,还可以摘到覆盆子,像小珊瑚珠攒成的小球,又酸又甜,色味都比桑椹要好得远。
C.碧绿的菜畦,光滑的石井栏,高大的皂荚树,紫红的桑椹。
D.最好的工作是捉了苍蝇喂蚂蚁,静悄悄地没有声音。
5.“我就只读书,正午习字,晚上对课。
”这是鲁迅先生回忆在三味书屋读书时的情景。
对课就是对对子、拟对联。
请你根据课文内容,为下面的上联拟出下联。
上联:百草园里赏景捕鸟听故事,其乐无穷下联:。
外研版英语四年级下册Module 9 课课练习题含答案
Module 9 Unit 1 Did he live in New York?一、单项选择。
( ) 1. It's a postcard ________ my friend.A. inB. fromC. at( ) 2. Do your parents live ________ New York?A. inB. onC. at( ) 3. We ________ here by train yesterday.A. comeB. cameC. comes( ) 4. Did you ________ to Hong Kong last year?A. goB. wentC. goes( ) 5. They want ________ Beijing .A. visitB. visitedC. to visit二、根据图片提示，从方框中选择正确的答语。
( ) 1 . Did he visit the Great Wall ？( ) 2 . Did Daming travel by plane?( ) 3 . Does he live in New York?( ) 4 . Did they play football yesterday?( ) 5 . What did they do last week?三、用正确的介词填空。
1. We live ________ Changsha.2. Welcome ________ our school.3. It's a postcard ________ my friend.4. Tom travelled ________ train last year.5. My parents are ________ holiday in Sanya.四、根据所给图片判断句子或对话的对(√)错(×)。
() 1. I came here by plane.() 2. —Did he travel by train —No, he didn’t. He travelled by bus.() 3. —Did Fangfang visit Beijing?—Yes, she did.() 4. Welcome to England!考答案一、1. B 2. A 3. B 4. A 5. C二、1. B 2. E 3. A 4. C 5 . D三、1. in 2. to 3. from 4. by 5. on四、1.√ 2.× 3.√ 4.×Module 9 Unit 2 Did you have a nice holiday?一、根据汉语提示完成句子。
新目标八年级上册英语Unit 9 Section B (3a-Self Check)练习题及答案一
新目标八年级上册英语Unit 9 Section B (3a-Self Check)练习题及答案一Part1根据句意及所给首字母或汉语提示完成句子1．Would you like to a________ Helen's present?2．Hurry up, and you can ________(赶上) the early bus.3．Tomorrow I will________(闲逛) with my friends.4．I'm afraid Ted can't join us. He ___________(正准备数学考试)．5．Anna i________ Wilson to her party yesterday.6．—I'm not feeling well and I have a fever.—Maybe you have the________(流感)．You'd better see a doctor.7．I get up early to ________(赶上) the bus.8．He gave me a gift, but I didn't ________(接受)．9．Don't ________ (拒绝) to help the people in trouble. 10．Tom won't be________(有空的)this weekend. He has to look after his little cousin.11．(阜康、米泉)I'll i________ some good friends to come to my birthday party this Sunday.12．Are you going to a piano c________ or an English party?13．Look at the c________ for this week. And find a time to g o there.14．He can prepare his party well in the d________．15．Would you like to come to the o________ of the big hotel？16．Can you use paper and ________(胶水) to make a model plane?17．This article is too long. Please ________(删除) some words.18．Peter said ________(再见) to his classmates and left.19．I must go and dress up before all the ________(客人) arrive.20．What ________(悲伤的) news！Lots of people lost their lives in the earthquake in Nepal.21．Mark only works on ________(工作日)，not on weekends.22．The workers are ________(印刷) newspapers in the factory.23．Look at the ________(日历)．It is December 4th today.24．I am very ________(高兴的) to meet you and your parents.25．There will be two ________(音乐会) next month.26．All the g________ had a good time at the party.27．The No.9 bus is coming in five minutes.Can we c________ it?28．Lang Lang gave a piano c________ in our city last month.29．How do you often c________ your parents' birthday?30．I can't r________ her invitation，so I'll go to her party.Part2拒绝邀请时说明理由的动词短语1．准备考试________________2．看医生________________3．得了流感________________4．帮我的父母________________5．见我的朋友________________6．太多的作业________________7．骑自行车________________8．为考试学习________________9．去看电影________________ 10．和……打网球________________ 11．帮助某人做某事________________ 12．在某方面帮助某人________________ 13．去旅行________________14．照顾；照料________________ (二)时间短语1．在星期六________________2．这个周末________________3．在这个月末________________4．去年秋天________________5．放学后________________6．后天________________7．下一次________________8．前天________________9．到下周五为止________________ 10．28日，周五________________(三)其他短语1．有空的________________2．为……感谢________________3．多好的主意啊！________________4．一个惊喜派对________________5．乔迁派对________________6．招待食物与饮料________________7．期待做某事________________8．收到某人的来信________________9．邀请某人做某事/到某地________________ 10．想要做某事________________11．直到……才……________________ 12．计划做某事________________13．有空做某事________________14．拒绝________________15．外出闲逛________________16．书面形式回复________________17．经过努力，成功；胜利________________ 18．来参加我的聚会________________Part3用方框中所给词的适当形式填空with，invite，surprise，reply，weekday1．All the students must go to school on__________.2．I have to study for my test，so I can't accept your__________. 3．We can't live on the earth________water.4．He didn't________to her question right away.5．She must be________when she sees the gift.Part4选词或短语填空1．“________(When/What) are you going to have the party？”“On Sunday morning.”2．“Did your mother ________(accept/receive) your advice？”“No，she didn't.”3．It's rainy today. I __________(must/have to) stay at home. 4．He spends ____________(too many/too much) time playing football with his friends every day.5．Can you give me ________(the other/another) glass? I don't like this one.Part5仿照例句，完成句子。
人教七年级英语上册Unit 9 My favorite subject is science.单元练习题含答案
Unit 9 My favorite subject is science.单元测试一、单项填空1. —_______ do you like music?—Because it is relaxing.A. WhyB. WhatC. WhoD. When2. This English-Chinese dictionary is very useful _______ the students.A. toB. withC. forD. of3. It is very _______ for us to eat fruit and vegetables every day.A. freeB. usefulC. busyD. happy4. He likes science ______it's very interesting.A. andB. soC. becauseD. but5. All my classes finish _____ 4:00 p.m.A. inB. onC. forD. at6. — Is Helen’s favorite day Friday?— ______.A. No, it isB. Yes, she isC. Yes, it isD. No, she isn’t7. —______ is your music teacher?—Mr. Smith is our music teacher.A. WhoB. WhyC. WhatD. How8. _______ is the last day of a week.A. MondayB. SundayC. SaturdayD. Friday9. — _______ do you like history?— Because it is fun.A. HowB. WhyC. WhenD. What10. We have ________ every day.A. a ChineseB. ChineseC. the ChineseD. an Chinese11.— ____ does he like blue?— Because the color makes him happy.A. WhatB. WhenC. WhyD. How12. The teacher it is useful.A. saysB. tellC. speakD. talk13. —Why do you like Friday?—Because day is Saturday.A. firstB. lastC. nextD. the next14. Science is difficult _______ interesting.A. butB. andC. orD. to15. Frank wants to go to China ____ April 2nd.A. onB. atC. inD. for16. We all go to school _______. What about you?A. from Monday to FridayB. from a Monday to FridayC. from the Monday to the FridayD. from monday to friday17. —When do you _______?—_______ Monday, Wednesday and Friday.A. have a math; OnB. have a math; AtC. have math; AtD. have math; On18. _______ favorite day is Tuesday because he _______ P.E.A. Tom’s; isB. Tom’s; hasC. Tom; hasD. Tom; does19. My sister gets up ______ seven _______ Saturday morning.A. in; atB. at; onC. at; inD. on; on20. I’m very _______. I can’t play with you now.A. freeB. goodC. busyD. well21. —_____ is the T-shirt, please?—Five dollars.A. How muchB. How aboutC. How oldD. How many22. My friend ______ a Chinese lesson every day.A. haveB. hasC. isD. does23. —_______ do you have P.E.?—On Monday afternoon.A. WhyB. HowC. WhenD. Where24. _______ favorite day is Monday, because he _______ P.E.A. Jim’s, isB. Jim’s, hasC. Tom, hasD. Tom, does25. I don’t like history because it’s ________.A. interestingB. relaxingC. excitingD. boring二、完形填空AMy dear friends, let me tell you something about my timetable (时间表). I 1 at7:00 and I go to 2 at 8:00. I have science at 3 and then I have math at 10:00.4 is my favorite subject. I like math because it’s5 . Mr. Dai is our math6 . I like him very much. I eat7 at 12:00 and then I have music at 1:00. I have history at 2:00. I8 like history because it is boring. But I9 like art. I have art 10 Wednesday at 2:00.1. A. come on B. get up (起床) C. play games D. play with2. A. home B. store C. school D. room3. A. six B. nine C. eleven D. twelve4. A. Music B. History C. English D. Math5. A. boring B. difficult C. interesting D. free6. A. teacher B. student C. classmate D. friend7. A. breakfast B. dinner C. lunch D. supper8. A. not B. doesn’t C. don’t D. am not9. A. well B. really C. surely D. good10. A. at B. in C. for D. onBI have many friends, and they have all kinds of favorite subjects. John’s favorite subjectis computer because he 1 computer can help him a lot in 2 study. He is a computer 3 . He likes playing computer games 4 much, and he is good at playing it. Jack likes art best 5 he likes drawing pictures a lot. Mary likes 6 because her father is Chinese. Her father 7 her Chinese at home. She loves China very much, and she 8 to know more about China. Bob thinks math is very 9 , so he likes math best. David likes P. E. because he likes 10 sports. He is good at playing basketball and soccer.1. A. thinks B. thanks C. talks D. sees2. A. him B. his C. he D. her3. A. fan (迷) B. student C. man D. boy4. A. too B. to C. but D. very5. A. so B. also C. because D. then6. A. computer B. game C. Chinese D. English7. A. teaches B. likes C. learns D. has8. A. gets B. wants C. helps D. buys9. A. boring B. interesting C. difficult D. relaxing10. A. going B. coming C. getting D. doing三、阅读理解A下面是一张Jack所在班级的课程表，每节课为45分钟。
会计学原理-郝振平-课后习题答案-第9章长期负债
第9章长期负债练习题参考答案练习一1、P=40000×(P/F, 8%, 5) =40000×0.68 = 27200 (元)2、P = 1000×(P/A, 8%, 5) + 40000×(P/F, 8%, 5)= 1000×3.992 + 40000×0.68= 3992 + 27200 = 31192(元)3、P = 2000×(P/A, 6%, 6) =2000×4.917 = 9834(元)4、P = 50000×(P/F, 10%, 6) =50000×0.564 = 28200 (元)5、P = 2000×(P/A, 6%, 6) + 50000×(P/F, 10%, 6)= 2000×4.917 + 50000×0.564= 9834 + 28200 = 38034(元)习题二20x5年1月1日取得借款时：借：银行存款350,000贷：长期借款350,00020x5年12月31日计提利息21,000元(350,000 ×6%)时：借：财务费用21,000贷：应付利息21,00020x6年12月31日计提利息22,260元(371,000 ×6%)时：借：财务费用22,260贷：应付利息22,26020x7年12月31日计提利息23,595.6元(393,260 ×6%)时：借：财务费用23,595.6贷：应付利息23,595.620x8年12月31日到期还本付息时，计提当年的利息25,011.34元(416,855.6 ×6%)，然后归还本息：借：财务费用25,011.34贷：应付利息25,011.34借：长期借款350,000应付利息91,866.94贷：银行存款441,866.94习题三1. 若当时资金市场的市场利率为7%，则按折价发行，有关计算如下：P = 480,000×(P/A, 7%, 5) + 8,000,000×(P/F, 7%, 5)= 480,000×4.100 + 8,000,000×0.713 = 9,337,200= 1,968,000 + 5,704,000 = 7,672,00020x5年1月1日债券发行后应作如下分录：借：银行存款7,672,000应付债券—利息调整328,000贷：应付债券—面值8,000,0002. 若当时资金市场的市场利率为5%，则按溢价发行，有关计算如下：P = 480,000×(P/A, 5%, 5) + 8,000,000×(P/F, 5%, 5)= 480,000×4.329 + 8,000,000×0.783= 2,077,920 + 6,264,000 = 8,341,92020x5年1月1日债券发行后应作如下分录：借：银行存款8,341,920贷：应付债券—面值8,000,000应付债券—利息调整341,9203. 按直线法对折价进行摊销的摊销额和实际利息费用为：每期票面利息支出= 8,000,000×6% = 480,000（元）每期折价摊销额= 328,000 ÷ 5 = 65,600（元）每期实际利息费用= 480,000 + 65,600 = 545,600（元）在每年的付息日：借：财务费用545,600贷：银行存款480,000应付债券—利息调整65,6004. 按实际利率法对溢价进行摊销，编制债券溢价摊销表，并编制第一个付息日的会计分录；债券溢价摊销表━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━日期应付利息利息费用利息调整未摊销溢价摊余成本───────────────────────────────20x5. 1. 1 341920 834192020x5.12.31 480000 417096 62904 279016 827901620x6.12.31 480000 413951 66049 212967 821296720x7.12.31 480000 410648 69352 143615 814661520x8.12.31 480000 407181 72819 70796 807079620x9.12.31 480000 409204 70796 —8000000 ────── ────── ──────2400000 2058080 341920======= ======= =======━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━付息日应做会计分录，20x5年12月31日：借：财务费用417,096应付债券—利息调整62,904贷：银行存款480,0005.编制债券到期偿还的分录：借：应付债券—面值8,000,000 贷：银行存款8,000,000。
《宏观经济学》课后练习题参考答案9
第9章总供给一、选择题二、名词解释1、不完全信息模型：不完全信息模型是阐述经济主体在做出经济决策时，并不能掌握所有相关信息从而影响总供给的模型。
不完全信息模型假设市场出清，即所有工资和价格自由调整使供求平衡，短期和长期总供给曲线的不同是因为对价格暂时的错觉。
此外，该模型还假设，经济中的每个供给者生产一种单一产品并消费许多产品。
由于产品数量如此之多，供给者无法在所有时间中观察到所有价格。
他们密切注视他们所生产的产品的价格，但对他们消费的所有产品的价格关注较不密切。
由于信息不完全，他们有时混淆了物价总水平的变动与相对价格的变动。
这种混淆影响了供给多少的决策，并导致物价水平与产出之间在短期的正相关关系。
当物价水平发生了未预期到的上升时，经济中所有供给者都观察到了自己所生产的产品价格的上升。
他们都理性而错误地推断，他们生产的产品的相对价格上升了。
他们更努力地工作，并生产得更多。
总之，不完全信息模型说明，当实际物价超过预期物价时，供给者增加其产出。
由Y=Y+α（P-P e）可知，当产出背离预期物价水平时，产出背离自然率。
2、黏性价格模型：性价格模型即阐述黏性价格对总供给影响的模型。
黏性价格指不能迅速反映产品市场供求的变动，只能缓慢地根据产品市场状况改变而调整的价格。
该模型假设市场是完全竞争的，完全竞争企业是价格接受者，而不是价格制定者。
该模型表示为Y=Y+α（P-P e ），说明了产出与自然率的背离和物价水平与预期物价水平的背离是正相关的。
3、菲利普斯曲线：菲利普斯曲线是表示货币工资变动率与失业率之间交替关系的曲线。
它是英国经济学家菲利普斯根据1861～1957年英国的失业率和货币工资变动率的经验统计资料提出来的，故称之为菲利普斯曲线。
这条曲线表示，当失业率高时，货币工资增长率低；反之，当失业率低时，货币工资增长率高。
因此，如图9-2-1所示，横轴代表失业率（U），纵轴代表货币工资增长率（W），菲利普斯曲线（PC）是一条向右下方倾斜的曲线。
九年级数学练习题及答案
九年级数学练习题及答案【篇一：初中数学中考模拟题及答案(一)】>一、选择题（本大题有7题，每小题3分，共21分．每小题有四个选项，其中有且只有一个选项正确）1．下面几个数中，属于正数的是（） a．3b．?12c． d．0a． b． c． d．（第2题）a．平均数b．众数c．中位数d．方差鞋店经理最关心的是，哪种型号的鞋销量最大．对他来说，下列统计量中最重要的是（）4．已知方程|x|?2，那么方程的解是（） a．x?2b．x??2c．x1?2，x2??2d．x?45、如图（3），已知ab是半圆o的直径，∠bac=32o，d是弧ac 的中点，那么∠dac的度数是（）6．下列函数中，自变量x的取值范围是x?2的函数是（） a．y? b．y?c．y? d．y??7．在平行四边形abcd中，?b?60，那么下列各式中，不能成立的是（）．．a．?d?60?b．?a?120?c．?c??d?180 d．?c??a?180??8．在四川抗震救灾中，某抢险地段需实行爆破．操作人员点燃导火线后，要在炸药爆炸前跑到400米以外的安全区域．已知导火线的燃烧速度是1.2厘米/秒，操作人员跑步的速度是5米/秒．为了保证操作人员的安全，导火线的长度要超过（） a．66厘米b．76厘米c．86厘米d．96厘米二、填空题（每小题3分，共24分）9．2008年北京奥运圣火在厦门的传递路线长是17400米， 10．一组数据：3，5，9，12，6的极差是 11??2x??412．不等式组?的解集是．x?3?0?13．如图，在矩形空地上铺4块扇形草地．若扇形的半径均为r米，圆心角均为90?，则铺上的草地共有平方米．14．若?o的半径为5厘米，圆心o到弦ab的距离为3厘米，则弦长ab为厘米．15．如图，在四边形abcd中，p是对角线bd的中点，e，f分别是ab，cd的中点，ad?bc，?pef?18，则?pfe的度数是．?（第14题）bbe e（第16题）（第17题）16．如图，点g是△abc的重心，cg的延长线交ab于d，ga?5cm，gc?4cm，gb?3cm，将△adg绕点d旋转180?得到△bde，则de?cm，△abc的面积?cm2．三、解答题（每题8分，共16分） 17．已知a?18.先化简，再求值四、解答题（每题10分，共20分）19．四张大小、质地均相同的卡片上分别标有1，2，3，4．现将标有数字的一面朝下扣在桌子上，然后由小明从中随机抽取一张（不放回），再从剩下的3张中随机取第二张．（1）用画树状图的方法，列出小明前后两次取得的卡片上所标数字的所有可能情况；（2）求取得的两张卡片上的数字之积为奇数的概率．xx?1213?1，b?13?1，求ab???ab?b??的值。
单位内部认证机械工程制图考试练习题及答案9_2022_背题版
***************************************************************************************试题说明本套试题共包括1套试卷每题均显示答案和解析单位内部认证机械工程制图考试练习题及答案9(500题)***************************************************************************************单位内部认证机械工程制图考试练习题及答案91.[单选题]平行于侧面的平面称为______。
A)水平面B)正平面C)侧平面答案:C解析:2.[单选题]图纸基本幅面尺寸最小的代号是______。
A)A1B)A3C)A4答案:C解析:3.[单选题]当一条线垂直于一个投影面时，必（ ）于另外两个投影面A)平行B)垂直C)倾斜答案:A解析:4.[单选题]当机件外形比较简单,内形比较复杂而且又不对称时,常采用A)全剖视图B)半剖视图C)局部剖视图答案:A解析:5.[单选题]尺寸线和尺寸界线用______绘制。
A)粗实线B)细实线6.[单选题]如果已知点C（30，20，7），那么C的Z坐标是______。
A)30B)20C)7答案:C解析:7.[单选题]标注线性尺寸时，尺寸线必须与所标注的线段（ ）。
A)平行B)相交C)交叉答案:A解析:8.[单选题]在半剖视图中，剖视图部分与视图部分的分界线为（ ）A)细点画线B)粗实线C)双点画线答案:A解析:9.[单选题]机械制图中一般不标注单位,默认单位是( )A)㎜B)㎝C)m答案:A解析:10.[单选题]如果已知点B（5，7，20），那么B的Y坐标是______。
A)5B)7C)20答案:B解析:11.[单选题]简单的装配图中的零件除标准件外,其余零件一 般应称为(A)非标准件B)专用件12.[单选题]比例标注为2：1时，是 比例。
【合集】螺纹连接练习题及答案9
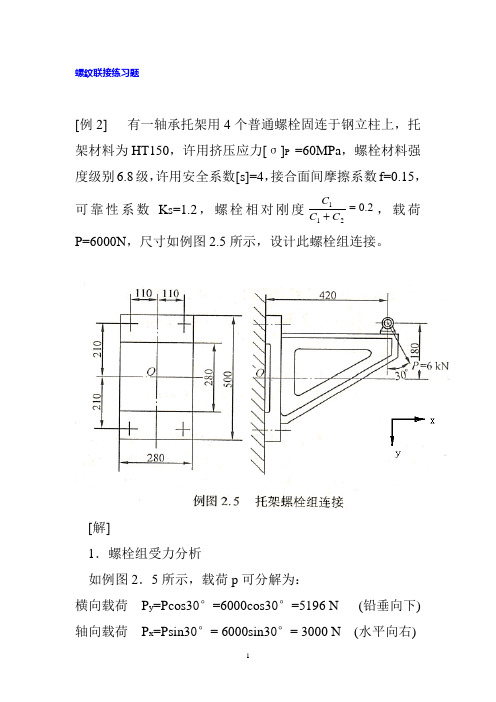
A．升角小，单线三角形螺纹D．升角大，双线三角形螺纹
C．升角小，单线梯形螺纹D．升角大，双线矩形螺纹
[题5]用于薄壁零件连接的螺纹，应采用( )。
A．三角形细牙螺纹B．梯形螺纹
C.锯齿形螺纹D．多线的三角形粗牙螺纹
[题6]当螺栓组连接承受横向载荷或旋转力矩时，该螺栓组中的螺栓( )。
[题3] [解]
1．计算螺栓组连接允许传递的最大转矩
该铰制孔用螺栓连接所能传递的转矩大小受到螺栓剪切强度和配合面挤压强度的制约。因此可按螺栓剪切强度条件来计算Tmax，然后校核配合面挤压强度，也可按螺栓剪切
强度和配合面挤压强度分别求出Tmax，取其值小者。本解按第一种方法计算。
校核螺栓与孔壁配合面间的挤压强度
2．改为普通螺栓连接，计算螺栓小径d1
(1)计算螺栓所需的预紧力F'，。按接合面间不发生相对滑移的条件，则有
(2)计算螺栓小径d1
螺纹连接测试题
一、单项选择题(从给出的A、B、C、D答案中选一)
[题1]当螺纹公称直径、牙型角、螺纹线数相同时，细牙螺纹的自锁性能比粗牙螺纹的自锁性能( )。
A．好B．差C．相同
[题15]工作时仅受预紧力F'作用的紧螺栓连接，其强度校
核公式为 ，式中的系数1.3是考虑( )。
A．可靠性系数B.安全系数
C．螺栓在拧紧时，同时受拉伸与扭转联合作用的影响
[题16]紧螺栓连接在按拉伸强度计算时，应将拉伸裁荷增加到原来的1．3倍，这是考虑( )的影响。
A．螺纹的应力集中B．扭转切应力作用
显然该螺栓组连接受横向载荷Py、轴向载荷Px和倾覆力矩M三种简单载荷的共同作用。
(1)确定受力最大螺栓的轴向工作载荷。首先确定在轴向载荷Px作用下，每个螺栓受到的轴向工作载荷
免疫学练习题09(第10~11章)答案
第十章T淋巴细胞参考答案一、单项选择题1、C2、B3、A4、C5、B6、D7、B8、C9、A 10、C 11、D 12、C 13、B 14、C 15、C 16、B 17、A 18、C 19、B 20、C 21、D 22、A 23、D 24、B 25、B 26、D 27、D 28、D 29、A 30、C 31、A 32、B二、名词解释1、T细胞库：在免疫系统中，每个T细胞克隆通过其TCR特异性识别相应抗原，所有T 细胞克隆组成了T细胞库。
2、（胸腺的）阳性选择：在胸腺皮质中，同胸腺上皮细胞表面抗原肽-MHCⅠ类或Ⅱ类分子复合物以适当亲和力发生结合的DP细胞可继续分化为CD8+或CD4+的单阳性（SP）细胞，而亲和力不足或过高的DP细胞则发生凋亡。
3、（胸腺的）阴性选择：SP细胞在胸腺皮髓质交界处及髓质区，与胸腺树突状细胞、巨噬细胞表面自身抗原肽-MHCⅠ类或Ⅱ类分子复合物发生高亲和力结合者，则被清除，而不结合的SP细胞进一步发育成熟。
4、TCR-CD3：由TCR与CD3分子以非共价键结合，形成TCR-CD3复合物，表达于T细胞表面。
其中，TCR的作用是能特异性识别APC或靶细胞表面的抗原肽-MHC分子复合物，CD3分子的功能是传导TCR识别抗原所产生的活化信号。
5、ITAM：即免疫受体酪氨酸活化基序。
是免疫细胞某些跨膜分子胞浆内特定的氨基酸序列（含保守序列YxxL/V），易被PTK作用而发生磷酸化，在免疫细胞信号传导和活化中起重要作用。
6、CTLA-4：表达在活化的T细胞表面，配体是APC或靶细胞表面的B7分子。
CTLA-4与B7分子结合产生抑制性信号（胞浆区有ITIM），终止T细胞活化。
三、填空题1、功能性TCR的表达，自身MHC限制性，自身免疫耐受2、TCR胚系基因重排，阳性选择，阴性选择3、抗原肽-MHC分子复合物，TCR识别抗原所产生的活化信号4、MHCⅡ类分子，MHCⅠ类分子，B7(CD80,CD86)，B7(CD80,CD86)，CD40，LFA-3(CD58)，ICAM-1，LFA-15、初始T细胞，效应T细胞，记忆T细胞四、简答题1、简述 T细胞的表面标志、抗原识别等特点及主要生物学作用。