最新一元二次方程的整数整数解(含答案)-

合集下载

一元二次方程的正整数解拔高题

训练专题三——一元二次方程的整数解一、填空题（共5小题，每小题5分，满分25分）1．（5分）若关于x的方程（6﹣k）（9﹣k）x2﹣（117﹣15k）x+54=0的解都是整数，则符合条件的整数时k的值有_________个．2．（5分）已知关于x的方程（a﹣1）x2+2x﹣a﹣1=0的根都是一整数，那么符合条件的整数a有_________个．3．（5分）已知方程x2﹣1999x+m=0有两个质数解，则m=_________．4．（5分）给出四个命题：①整系数方程ax2+bx+c=0（a≠0）中，若△为一个完全平方数，则方程必有有理根；②整系数方程ax2+bx+c=0（a≠0）中，若方程有有理数根，则△为完全平方数；③无理数系数方程ax2+bx+c=0（a≠0）的根只能是无理数；④若a、b、c均为奇数，则方程ax2+bx+c=0没有有理数根，其中真命题是_________．5．（5分）已知关于x的一元二次方程x2+（2a﹣1）x+a2=0（a为整数）的两个实数根是x1、x2，则=_________．二、选择题（共1小题，每小题4分，满分4分）6．（4分）已知a，b为质数且是方程x2﹣13x+c=0的根，那么的值是（）A．B．C．D．三、解答题（共12小题，满分91分）7．（8分）试确定一切有理数r，使得关于x的方程rx2+（r+2）x+r﹣1=0有根且只有整数根．8．（8分）当m为整数时，关于x的方程（2m﹣1）x2﹣（2m+1）x+1=0是否有有理根？如果有，求出m的值；如果没有，请说明理由．9．（8分）若关于x的方程ax2﹣2（a﹣3）x+（a﹣13）=0至少有一个整数根，求非负整数a的值．10．（8分）设m为整数，且4＜m＜40，方程x2﹣2（2m﹣3）x+4m2﹣14m+8=0有两个不相等的整数根，求m的值及方程的根．11．（7分）已知关于x的方程a2x2﹣（3a2﹣8a）x+2a2﹣13a+15=0（其中a是非负整数）至少有一个整数根，求a的值．12．（6分）求使关于x的方程kx2+（k+1）x+（k﹣1）=0的根都是整数的k值．13．（6分）当n为正整数时，关于x的方程2x2﹣8nx+10x﹣n2+35n﹣76=0的两根均为质数，试解此方程．14．（6分）设关于x的二次方程（k2﹣6k+8）x2+（2k2﹣6k﹣4）x+k2=4的两根都是整数．求满足条件的所有实数k的值．15．（6分）已知a是正整数，且使得关于x的一元二次方程ax2+2（2a﹣1）x+4（a﹣3）=0 至少有一个整数根，求a的值．16．（6分）已知p为质数，使二次方程x2﹣2px+p2﹣5p﹣1=0的两根都是整数，求出p的所有可能值．17．（12分）已知方程x2+bx+c=0与x2+cx+b=0各有两个整数根x1，x2，和x1′，x2′，且x1x2＞0，x1′x2′＞0．（1）求证：x1＜0，x2＜0，x1′＜0，x2′＜0；（2）求证：b﹣1≤c≤b+1；（3）求b，c的所有可能的值．18．（10分）如果直角三角形的两条直角边都是整数，且是方程mx2﹣2x﹣m+1=0的根（m为整数），这样的直角三角形是否存在？若存在，求出满足条件的所有三角形的三边长；若不存在，请说明理由．新课标九年级数学竞赛培训第05讲：一元二次方程的整数解参考答案与试题解析一、填空题（共5小题，每小题5分，满分25分）1．（5分）若关于x的方程（6﹣k）（9﹣k）x2﹣（117﹣15k）x+54=0的解都是整数，则符合条件的整数时k的值有5个．考点：一元二次方程的整数根与有理根。

人教版初中数学一元二次方程知识点总结(含答案)

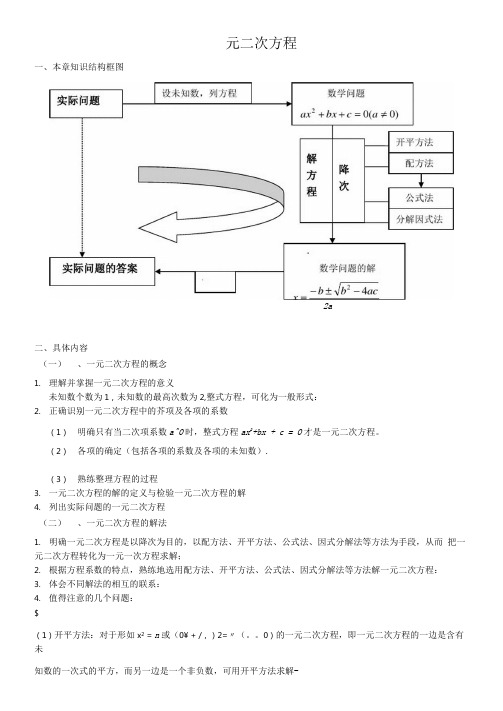
元二次方程一、本章知识结构框图2a二、具体内容（一）、一元二次方程的概念1.理解并掌握一元二次方程的意义未知数个数为1，未知数的最高次数为2,整式方程，可化为一般形式：2.正确识别一元二次方程中的芥项及各项的系数（1）明确只有当二次项系数a^O时，整式方程ax2+bx + c = O才是一元二次方程。

（2）各项的确定（包括各项的系数及各项的未知数）.（3）熟练整理方程的过程3.一元二次方程的解的定义与检验一元二次方程的解4.列出实际问题的一元二次方程（二）、一元二次方程的解法1.明确一元二次方程是以降次为目的，以配方法、开平方法、公式法、因式分解法等方法为手段，从而把一元二次方程转化为一元一次方程求解；2.根据方程系数的特点，熟练地选用配方法、开平方法、公式法、因式分解法等方法解一元二次方程：3.体会不同解法的相互的联系：4.值得注意的几个问题：$（1）开平方法：对于形如x2 = n或（0¥ + /，）2=〃（。

0）的一元二次方程，即一元二次方程的一边是含有未知数的一次式的平方，而另一边是一个非负数，可用开平方法求解-形如/ = 〃的方程的解法: 当〃>0时，X = ±yfn ；当n = 0 时，Xj = %, = 0 ；当«<0时，方程无实数根。

（2）配方法：通过配方的方法把一元二次方程转化为（x + 〃i）2=,?的方程，再运用开平方法求解。

配方法的一般步骤：①移项：把一元二次方程中含有未知数的项移到方程的左边，常数项移到方程的右边；②“系数化1”：根据等式的性质把二次项的系数化为1：③配方：将方程两边分别加上一次项系数一半的平方，把方程变形为（X + 〃?）2=〃的形式：④求解：若77 >0时，方程的解为x = —土丁？，若〃<0时，方程无实数解。

（3）公式法：一元二次方程ax2+bx + c = 0（a^0）的根工=一”±?'；耻：2a当b2-4ac>。

一元二次方程的整数整数解(含答案)

竞赛辅导一元二次方程的整数整数解在数学课外活动中，在各类数学竞赛中，一元二次方程的整数解问题一直是个热点，它将古老的整数理论与传统的一元二次方程知识相结合，涉及面广，解法灵活，综合性强，备受关注，解含参数的一元二次方程的整数解问题的基本策略有：从求根入手，求出根的有理表达式，利用整除求解；从判别式手，运用判别式求出参数或解的取值范围，或引入参数(设△=2k )，通过穷举，逼近求解；从韦达定理入手，从根与系数的关系式中消去参数，得到关于两根的不定方程，借助因数分解、因式分解求解；从变更主元入人，当方程中参数次数较低时，可考虑以参数为主元求解．注：一元二次方程的整数根问题，既涉及方程的解法、判别式、韦达定理等与方程相关的知识，又与整除、奇数、偶数、质数、合数等整数知识密切相关．【例题求解】【例1】若关于x 的方程054)15117()9)(6(2=+----x k x k k 的解都是整数，则符合条件的整数是的值有个．思路点拨用因式分解法可得到根的简单表达式，因方程的类型未指明，故须按一次方程、二次方程两种情形讨论，这样确定是的值才能全面而准确．注：系数含参数的方程问题，在没有指明是二次方程时，要注意有可能是一次方程，根据问题的题设条件，看是否要分类讨论．【例2】已知a 、b 为质数且是方程0132=+-c x x 的根，那么ba ab +的值是( ) A ．22127 B ．22125 C ．22123 D ．22121 思路点拨由韦达定理a 、b 的关系式，结合整数性质求出a 、b 、c 的值．【例3】试确定一切有理数r ，使得关于x 的方程01)2(2=-+++r x r rx 有根且只有整数根．思路点拨由于方程的类型未确定，所以应分类讨论．当0≠r 时，由根与系数关系得到关于r 的两个等式，消去r ，利用因式(数)分解先求出方程两整数根．【例4】当m 为整数时，关于x 的方程01)12()12(2=++--x m x m 是否有有理根?如果有，求出m 的值；如果没有，请说明理由．思路点拨整系数方程有有理根的条件是为完全平方数．设△=22224)12(544)12(4)12(n m m m m m =+-=+-=--+(n 为整数)解不定方程，讨论m 的存在性．注：一元二次方程02=++c bx ax (a ≠0)而言，方程的根为整数必为有理数，而△=ac b 42-为完全平方数是方程的根为有理数的充要条件．【例5】若关于x 的方程0)13()3(22=-+--a x a ax 至少有一个整数根，求非负整数a 的值．思路点拨因根的表示式复杂，从韦达定理得出的a 的两个关系式中消去a 也较困难，又因a 的次数低于x 的次数，故可将原方程变形为关于a 的一次方程．学历训练1．已知关于x 的方程012)1(2=--+-a x x a 的根都是整数，那么符合条件的整数a 有．2．已知方程019992=+-m x x 有两个质数解，则m ＝．3．给出四个命题：①整系数方程02=++c bx ax (a ≠0)中，若△为一个完全平方数，则方程必有有理根；②整系数方程02=++c bx ax (a ≠0)中，若方程有有理数根，则△为完全平方数；③无理数系数方程02=++c bx ax (a ≠0)的根只能是无理数；④若a 、b 、c 均为奇数，则方程02=++c bx ax 没有有理数根，其中真命题是．4．已知关于x 的一元二次方程0)12(22=+-+a x a x (a 为整数)的两个实数根是1x 、2x ，则21x x -=．5．设rn 为整数，且4<m<40，方程08144)32(222=+-+--m m x m x 有两个整数根，求m 的值及方程的根6．已知方程015132)83(222=+-+--a a x a a ax (a ≠0)至少有一个整数根，求a 的值．7．求使关于x 的方程01)1(2=-+++k x k kx 的根都是整数的k 值．8．当n 为正整数时，关于x 的方程0763*******=-+-+-n n x nx x 的两根均为质数，试解此方程．9．设关于x 的二次方程4)462()86(2222=+--++-k x k k x k k 的两根都是整数，试求满足条件的所有实数k 的值．10．试求所有这样的正整数a ，使得方程0)3(4)12(22=-+-+a x a ax 至少有一个整数解．11．已知p 为质数，使二次方程015222=--+-p p px x 的两根都是整数，求出p 的所有可能值．12．已知方程02=++c bx x 及02=++b cx x 分别各有两个整数根1x 、2x 及1x '、2x '，且1x 2x >0，1x '2x ' >0． (1)求证：1x <0,2x <0，1x '<0,2x '< 0；(2)求证：11+≤≤-b c b ；(3)求b 、c 所有可能的值．13．如果直角三角形的两条直角边都是整数，且是方程0122=+--m x mx 的根(m 为整数)，这样的直角三角形是否存在?若存在，求出满足条件的所有三角形的三边长；若不存在，请说明理由．参考答案。

一元二次方程的整数根问题--数不清

设(5p－132)2－17 404＝n2(n＞0，n为自然数).移项分解可得
(5p－132＋n)(5p－132－n)
＝22×19×229. 又(5p－132＋n)，(5p－132－n)同奇偶，所以，
解得p＝76.
注：从表面上看，此题中的p是一切实数，但由韦达定理判断它实际上是自然数，故可采用前法求得.
各位博友，请留下您的足迹，让我不断学习、成长！数不清谢谢您！
听课+开课+反思=成长!
态度决定一切！
一元二次方程的整数根问题
数不清
[ 2011-3-5 22:15:00 | By: 数不清 ]
一元二次方程的整数根问题
1
推荐迄今为止，尚未找到使得整系数一元二次方程有整数根的充分条件，通常的方法都是通过讨论其判别式，利用根与系数的关系进行分析和归纳，即使用必要条件解题，然后通过检验确定答案.下面举例说明常用的几种方法，并指出每种方法适合的范围.
例4
设m为整数，且4＜m＜40，又方程x2－2(2m－3)x＋4m2－14m＋8
＝0有两个整数根.求m的值及方程的根.
(1993,天津市初中数学竞赛)
分析：考察判别式△＝4(2m＋1)，因是关于m的一次式，故例1，例2的方法均不可用 .
广 Re:期末宣誓词 Re:《牵一只蜗牛去散步》 Re:《牵一只蜗牛去散步》 Re:我心目中的好老师(29号的家长 Re:真情献给党 Re:我心目中的好老师(29号的家长 Re:真情献给党 Re:信封?关爱?感悟
有理根问题本质上也是整数根的问题，要求方程的根的判别式必须为一个整数或有理数的完全平方.考察判别式
△ ＝232＋36(n2＋2n＋2)
＝36(n＋1)2＋565.

一元二次方程的整数根

综上所述，当 k 值为 3，6，7，9，15时方程的解都是整数。
例 2 (2000 年全国初中数学联赛试题)设关于 x 的二次方程 (k2－6k＋8)﹒x2＋(2k2－6k－4)x＋k2＝4
的两根都是整数.求满足条件的所有实数 k 的值.
分析此题也可通过直接求根法求出二根，但是它的条件与例 1 不同，例 1
况。解若 k=6, 则 x=-2; 若 k=9, 则 x=3；
若 k≠6 且 k≠9，原方程可化为 [(k-6)x-9][(k-9)x-6] = 0 ,故方程的二
根为 x1＝ k 9 6 ，x2＝ k 6 9 .为使 x1 和 x2 都是整数，则应有 k-6 = ±1,±3,± 9 ， k=-3,3,5,7,9,15;还应有 k-9 = ± 1,± 2, ± 3,± 6, k=3,6， 7,8,10,11,12，15. 所以 k=3,7,15时，x 1 和 x 2都是整数，
当 m =1 时，方程 mx2-6x+9=0 的二根均为 1，方程 x2-4mx+4m2-4m-5=0 的
二根为-1 和 5，符合要求。当 m =-1 时，方程 mx2-6x+9=0 的二根均不是整数,不符合要求. 所以仅当 m=1 时，方程的两根都是整数。例 4． (1996 年上海市初中数学竞赛试题)若关于 x 的方程 ax2+2(a-3)x+(a-2)=0
a = 25, 18, 16, -9, -2, 0
因 a 为正实数，于是 a 25 或 18或 16均为所求.
例 8 (第十七届全俄数学奥林匹克十年级试题)求使方程 x2-pqx+p+q=0 有
整数根的所有正整数 p 和 q．
解设原方程两根为 x1、x2，则 x1x2 = p+q

专题培优-一元二次方程的整数根(含答案)

一元二次方程的整数根1.使一元二次方程x2+3x+m=0有整数根的非负整数m的个数为( )．A. 0B. 1C. 2D. 32.满足(n2-n-1)n+2＝1的整数n有________个．3.已知关于x的方程（a－1）x2＋2x－a－1＝0的根都是整数，那么符合条件的整数a有________个．4.方程x2+px+q=0的两个根都是正整数，并且p+q＝1992，则方程较大根与较小根的比等于________.5.已知k为整数，且关于x的方程(k2-1)x2-3(3k-1)x+18=0有两个不相同的正整数根，则k＝________.6.关于x的一元二方程4x2+4mx+m2+m-10=0(m为正整数)有整数根，则满足条件的m值的个数为________个．7.已知关于x的方程((m2−1)x2−3(3m−1)x+18=0有两个正整数根(m是整数)．△ABC的三边a，b，c满足c=2√3，m2+a2m−8a=0，m2+b2m−8b=0．求：(1)m的值；(2)△ABC的面积．8.当k为何整数时，方程(k2-1)x2-6(3k-1)x+72＝0有两个不相等的正整数根?9.当n为何整数时，关于x的一元二次方程x2-3nx+2n2-6=0的两根都为整数?10.求这样的正整数a，使得方程ax2+2(2a-1)x+4a-7=0至少有一个整数解．11.设关于x的一元二次方程(k2-6k+8)x2+(2k2-6k-4)x+k2＝4的两根都是整数，求满足条件的所有实数k的值．12.已知m，n为正整数，关于x的方程x2-mnx+(m+n)=0有正整数解，求m，n的值．13.k为何值时，关于x的方程x2-4mx+4x+3m2-2m+4k=0的根是有理数?14.已知关于x的一元二次方程x2+cx+a=0的两个整数根恰好比方程x2+ax+b=0的两个根都大1，求a+b+c的值．15.已知一元二次方程x2+ax+b=0，①有两个连续的整数根，一元二次方程x2+bx+a=0，②有整数根，求a，b的值．答案1.C2.43.54.9975.26.47.解：（1）∵关于x 的方程（m 2-1）x 2-3（3m -1）x +18=0有两个正整数根（m 是整数）．∵a =m 2-1，b =-9m +3，c =18，∴b 2-4ac =（9m -3）2-72（m 2-1）=9（m -3）2≥0，设x 1，x 2是此方程的两个根，∴x 1•x 2=c a =18m 2−1，∴18m 2−1也是正整数，即m 2-1=1或2或3或6或9或18，又m 为正整数，∴m =2；（2）把m =2代入两等式，化简得a 2-4a +2=0，b 2-4b +2=0当a =b 时，a =b =2±√当a ≠b 时，a 、b 是方程x 2-4x +2=0的两根，而△＞0，由韦达定理得a +b =4＞0，ab =2＞0，则a ＞0、b ＞0．①a ≠b ，c =2√3时，由于a 2+b 2=（a +b ）2-2ab =16-4=12=c2 故△ABC 为直角三角形，且∠C =90°，S △ABC =12ab =1．②a =b =2-√2，c =2√3时，因2(2−√2)＜2√3，故不能构成三角形，不合题意，舍去． ③a =b =2+√2，c =2√3时，因2(2+√＞2√3，故能构成三角形．S △ABC =12×（2√）×√=√综上，△ABC 的面积为1或√． 8.解：∵k 2-1≠0∴k ≠±1∵△=36（k -3）2＞0∴km ≠3用求根公式可得：x 1=6k−1，x 2=12k+1∵x 1，x 2是正整数∴k -1=1，2，3，6，k +1=1，2，3，4，6，12，解得k =2．这时x 1=6，x 2=4． 9.解：原方程变形得(x −2n)(x −n)=6，∵x ，n 均为整数，∴原方程化为{x −2n =±2,x −n =±3或{x −2n =±3,x −n =±2或{x −2n =±6,x −n =±1或{x −2n =±1,x −n =±6，解得n =-1或1或-5或5．10.解：原方程变形为(x ＋2)2a =2x ＋7(x ≠−2)，解得a =2x ＋7(x ＋2)2.∵a ≥1，∴2x ＋7(x ＋2)2⩾1，∴-3≤x ≤1，∴x 可取值为-3，-1，0，1，分别代入a =2x ＋7(x ＋2)2中，解得a ＝1或a ＝5或a =74或a ＝1．又∵a 是正整数，∴当a ＝1或a ＝5时，方程至少有一个整数解. 11.解：原方程可化为[(k −4)x ＋(k −2)][(k −2)x ＋(k ＋2)]=0，∵k 2−6k ＋8=(k −4)(k −2)≠0，∴x 1=−k−2k−4=−1−2k−4，x 2=−k ＋2k−2=−1−4k−2， ∴k −4=−2x 1＋1，k −2=−4x 2＋1(x 1≠−1,x 2≠−1)，消去k ，得x 1x 2＋3x 1＋2=0. ∴x 1(x 2＋3)=−2．由于x 1，x 2都是整数，∴{x 1=−2,x 2＋3=1或{x 1=1,x 2＋3=−2或{x 1=2,x 2＋3=−1.或{x 1=−2,x 2=−2或{x 1=1,x 2=−5或{x 1=2,x 2=−4． ∴k =6或3或103.经检验均满足题意．12.解：设方程x 2−mnx +(m +n )=0的两根分别为：x 1,x 2，∵m ，n 为正整数，∴x 1+x 2=mn >0,x 1⋅x 2=m +n >0，∴这两个根x 1,x 2均为正数，又∵(x 1−1)(x 2−1)+(m −1)(n −1)=x 1x 2−(x 1+x 2)+1−[mn −(m +n )+1]=(m +n )−mn +1+[mn −(m +n )+1]=2，其中(x 1−1)(x 2−1)，m −1，n −1均非负，而为两个非负整数和的情况仅有0+2；1+1；2+0.∵(x 1−1)(x 2−1)=x 1x 2−(x 1+x 2)+1=m +n −mn +1,(m −1)(n −1)=mn −(m +n )+1，∴{m +n −mn +1=0mn −(m +n)+1=2或{m +n −mn +1=1mn −(m +n )+1=1或{m +n −mn +1=2mn −(m +n)+1=0，解得：{m =2n =3或{m =3n =2或{m =2n =2或{m =1n =5或{m =5n =1.13.解：根据题意得：△=(-4m +4)2-4×(3m 2-2m +4k )=4(m 2-6m +4-4k )，∵方程的解为有理数，∴4(m 2-6m +4-4k )是一个完全平方数，即4-4k =9，解得：k =-54. 14.解：设方程x 2+ax +b =0的两个根为α，β，∵方程有整数根，设其中 α，β为整数，且α≤β，则方程x 2+cx +a =0的两根为α+1，β+1，∴α+β=-a ，(α+1)(β+1)=a ，两式相加，得 αβ+2α+2β+1=0，即 (α+2)(β+2)=3，∴{α+2=1β+2=3或{α+2=−3β+2=−1.解得{α=−1β=1或{α=−5β=−3.又 ∵a =-(α+β)=-[(-1)+1]=0，b =αβ=-1×1=-1，c =-[(α+1)+(β+1)]=-[(-1+1)+(1+1)]=-2，或a =-(α+β)=-[(-5)+(-3)]=8，b =αβ=(-5)×(-3)=15，c =-[(α+1)+(β+1)]=-[(-5+1)+(-3+1)]=6， ∴a =0，b =-1，c =-2；或者a =8，b =15，c =6，∴a +b +c =0+(-1)+(-2)=-3或a +b +c =8+15+6=29，故a +b +c =-3，或29．15.解：设方程①的两个根式n ,n +1,则{n +(n +1)=−a n(n +1)=b∴a =-(2n +1)，b =n (n +1)，则方程②可变为x 2+n (n +1)x -(2n +1)=0③，∵方程③有整数根，视n 为主元，∴n 2x +n (x -2)+x 2-1=0④有整数解，∴设△=(x -2)2-4x (x 2-1)=x 2+4-4x 3=p 2（p 为正整数），∴x 2(1-4x )=(p +2)(p -2)⑤.∵p +2＞p -2，∴{p +2=x 2p −2=1−4x ⑥，{p +2=x p −2=(1−4x)x ⑦，{p +2=1−4x p −2=x2⑧，{p +2=(1−4x)x p −2=x ⑨，由⑥得：x 2+4x -1=0，解得：x 1=-5，x 2=1，把x 1=-5代入③得：n =-3或n =85（不合题意，舍去），当n =-3时，a =5，b =6，把x 2=1代入③得：n 1=0，n 2=1，当n =0时，a =-1，b =0，当n =1时，a =-3，b =2，对⑦，⑧，⑨继续讨论.综上所述，{a =−1b =0或{a =−3b =2或{a =5b =6.。

初中数学与整数有关的含参数一元二次方程的解法-9页精选文档

初中数学与整数有关的含参数一元二次方程的解法对于一个含参数的一元二次方程来说，要判断它是否有整数根或有理根，基本依据是判别式，而必须具体问题具体分析。

这里经常要用到一些整除性质。

一元二次方程的整数解历来是数学竞赛中的热点问题之一，题型多变、难度大是这类问题的特点。

但其解法仍然是有章可循的。

一、巧用求根公式法例1、试确定m 为何值时，方程(m 2-1)x 2-6(3m-1)x ＋72＝0有两个不相等的正整数根。

解：首先，m 2-1≠0，则m ≠±1．又Δ=36(m-3)2＞0，所以m ≠3．用求根公式可得112,1621+=-=m x m x ∵ x 1，x 2是正整数，∴ m-1=1，2，3，6；且m+1=1，2，3，4，6，12。

解得m=2．这时x 1=6，x 2=4。

评析：一般来说，利用求根公式可以先把方程的根求出来，然后利用整数的性质以及整除性理论，就比较容易求解问题，这是最自然、最常规的解法。

二、巧用因式分解法例2、已知方程a 2x 2 - ( 3a 2- 8a )x + 2a 2-13a +15 = 0（其中a 是非负整数）至少有一个整数根，求a 的值。

.分析：观察本题方程，可先用因式分解法将原方程转化为两个不定方程ax －2a+3=0和ax －a + 5 =0，然后利用整除的知识，求出非负整数a 的值。

解：原方程可化为： a 2x 2－(3a 2－8a)x ＋(2a －3)(a －5)＝0方程左边分解因式,得 (ax －2a ＋3)(ax －a ＋5)＝0 ∴ ax 321-= ax 512-=∵ 原方程至少有一个整数根， ∴ a 的值为3，或5，或1。

例3、当k 为何整数时，关于x 的二次方程x 2－3kx +2k 2－6=0两根都为整数。

分析：利用因式分解法将原方程转化为多个不定方程，然后利用整除的知识，求出整数k 的值.解：由x 2－3kx +2k 2－6=0，得 (x -2k )(x -k ) = 6∵ x 、k 为整数， ∴ 原方程化为⎩⎨⎧±=-±=-322k x k x 或 ⎩⎨⎧±=-±=-232k x k x 或 ⎩⎨⎧±=-±=-612k x k x 或 ⎩⎨⎧±=-±=-162k x k x ∵ 由于x －2k 与x －k 同号，故得八个不定方程组，解得k =－1，1，－5，5。

一元二次方程整数根-教师版

板块一.元二次方程的整数根问题1.有理数根问题方程20ax bx c ++=（0a ≠，a 、b 、c 均为有理数）的根为有理数的条件是：∆为有理数 2.整数根问题一元二次方程有正（负、非正、非负）整数根，用十字相乘或公式法求出两个根，并将两根化简，分子部分不能有字母，再讨论整数根，并考虑根为正（负、非正、非负）数。

例如：3x=m2m-1x=m 2m-3x=m+1a-3+9-4a x=a一元二次方程有整数根，但用十字相乘或公式法求出的两个根含有根号时，如a -39-4ax=a±，要利用换元法，设9-4a =k ，得出29-k a=4，将x 中的a 全部替换，得出两个不含根号的解，再讨论整数根问题，方法同上；若△=4a 2-9且a 为整数，则设4a 2-9=k 2，4a 2- k2=9，可得（2a-k ）(2a+k)=9,则讨论整数X 整数=9，讨论出所有满足情况的整数即可，注意k ≥0注意：若方程至少有一实数根，那么通过x1，x2推出的相关字母的值，应该取全部情况；若方程有两个实数根（已经确定方程为一元二次方程），那么通过x1，x2推出的相关字母的值，应该取公共解。

板块二.一元二次方程的应用1.增长率问题2.商品利润问题3.图形面积问题4.传播问题5.动点问题一.元二次方程的整数根问题1.有理数根问题【例1】已知关于x 的一元二次方程22131(1)0444x mx k m k k +-+--+=有有理根，求k 的值。

【答案】∵原方程的根为有理根221314[(1)]444m k m k k ∆=-⨯⨯-+--+2231(1)44m k m k k =+++++所以∆为完全平方式，因此22131()244k k k +=++，整理得230k k +=一元二次方程整数根与实际应用新知学习基础演练解得0k =或13k =-【练一练】设m 是不为零的整数，关于x 的二次方程2(1)10mx m x --+=有有理根，求m 的值．【解析】一个整系数的一元二次方程有有理根，那么它的判别式一定是完全平方数．令22(1)4m m n ∆=--=，其中n 是非负整数，于是2261m m n -+=，所以22(3)8m n --=，由于33m n m n -+--≥，并且(3)(3)8m n m n -+--=是偶数，所以3m n -+与3m n --同奇偶，所以 3432m n m n -+=⎧⎨--=⎩，或3234m n m n -+=-⎧⎨--=-⎩．所以61m n =⎧⎨=⎩，或01m n =⎧⎨=⎩(舍去)．所以6m =，这时方程的两个根为12，13．点评：一个整系数的一元二次方程如果有整数根或有理根，那么它的判别式一定是完全平方数，然后利用平方数的性质、解不定方程等手段可以将问题解决．【答案】6m =【例2】对于任意实数x ，二次三项式22134x mx m m ++-+是一个完全平方式，求m 的值【解析】略【答案】由题意得2231()24m m m =-+，整理得25410m m +-=解得15m =或1m =- 2.整数根问题【例3】已知方程21404x x n -+=的根都是整数，求正整数n 的值；【答案】根据题意得，16n ∆=-416821612nx n ±-==±-∵原方程的根均为整数，且n 为正整数 ∴7n =或12n =或15n =【例4】设m 为整数，且440m <<，方程()2222341480x m x m m --+-+=有两个整数根，求m 的值及方程的根．【解析】4(21)m =+△为完全平方数，又m 为440m <<的整数，则12m =或24．当12m =时，116x =，226x =；当24m =时，338x =，452x =．点评：测及一元二次方程的整数根问题，一般用公式法把根表示出来，再让其为整数即可；或先让24b ac -为完全平方数，再检验．当然测及二次项系数的讨论更容易错．【答案】当12m =时，116x =，226x =；当24m =时，338x =，452x =．【练一练】已知1240m <<，且关于x 的二次方程222(1)0x m x m -++=有两个整数根，求整数m ．【解析】由原方程由整数解可知，224(1)44(21)m m m ∆=+-=+必然是一个完全平方数．又1240m <<可知，252181m <+<，又21m +为奇数，故214924m m +=⇒=．此时原方程的两个实数根为：1,22(1)501422m x +±∆±==，不妨设12x x >，则132x =，218x =故24m =．满足∆为完全平方数只是条件之一，另外一个条件也必须同时满足，要引起注意．【答案】24m =【例5】已知方程()22238213150ax a a x a a --+-+=(a 是非负整数)至少有一个整数根，那么a = ．【解析】∵0a ≠，∴由公式法可得()2212382322a a a a x a a -++==-，()2222382512a a a a x a a --+==-．即135a =，，．【答案】1、3、5【练一练】b 为何值时，方程 220x bx --=和22(1)0x x b b ---=有相同的整数根？并且求出它们的整数根？【解析】两式相减，整理得(2)(2)(1)b x b b -=-+，当2b ≠时，1x b =+，代入第一个方程，得2(1)(1)20b b b +-+-= 解得1b =，2x =当2b =时，两方程无整数根． ∴1b =，相同的整数根是2 【答案】1b =，相同的整数根是2【例6】已知关于x 的方程2(6)0x a x a +-+=的两根都是整数，求a 的值．【解析】本题的难点在于a 并不是整数，如果在采用求根公式，然后讨论∆是否为完全平方数，难度不小，因此本题采用韦达定理来求解【答案】设方程2(6)0x a x a +-+=的两个根为1x 、2x根据题意得12126x x a x x a +=-⎧⎨⋅=⎩①②，将②代入①，整理得12126x x x x +=- ∴212267111x x x x -==-++∵1x 、2x 均为整数 ∴21x +的值为1±或7± 当211x +=时，20x =，16x =，0a = 当211x +=-时，22x =-，18x =-，16a = 当217x +=时，26x =，10x =，0a = 当217x +=-时，28x =-，12x =-，16a = 综上所述，0a =或16a =【例7】求方程2237x y x xy y+=-+的所有正整数解．【解析】原方程可化为关于x 的一元二次方程223(37)370x y x y y -++-=．由于x 为实数，则判别式不小于0，即[]22(37)43(37)0y y y ∆=-+-⨯-≥．化简得227126490y y --≤，解得211439-≤211439y +≤．由于y 是正整数，则y 只能取1,2,3,4,5．分别将1,2,3,4,5y =代入原方程，得原方程的两组正整数解为1145x y =⎧⎨=⎩，2254x y =⎧⎨=⎩．【答案】1145x y =⎧⎨=⎩，2254x y =⎧⎨=⎩【例8】当m 是什么整数时，关于x 的一元二次方程2440mx x -+=与2244450x mx m m -+--=的根都是整数．【解析】由题意可知，方程2440mx x -+=的判别式21(4)1616(1)01m m m ∆=--=-≥⇒≤ 方程2244450x mx m m -+--=的判别式为222(4)4(445)4(45)0m m m m ∆=---=+≥故54m ≥-，又m 为整数，0m ≠，故1m =-或1m =当1m =时，题干中的两个方程分别为2440x x -+=、2450x x --=，满足题意；当1m =-时，题干中的两个方程分别为2440x x +-=、2430x x ++=，不合题意．故1m =．也可通过方程是否有整数根的条件来判断出1m =，此时两个判别式都要是完全平方数．【答案】1m =【练一练】一直角三角形的两直角边长均为整数，且满足方程2(2)40x m x m -++=，试求m 的值及此直角三角形的三边长【解析】略【答案】由题意得，2124m m ∆=-+，∴2(2)1242m m m x +±-+=，∵该方程的根均为整数∴2124m m -+必为平方数，令22124m m n -+=（n 为正整数）整理得22(6)32m n --=，∴(6)(6)32m n m n -+--= ∴6m n -+与6m n --同奇同偶因此61662m n m n -+=⎧⎨--=⎩或6864m n m n -+=⎧⎨--=⎩ 解得157m n =⎧⎨=⎩或144m n =⎧⎨=⎩当157m n =⎧⎨=⎩时，方程2(2)40x m x m -++=为217600x x -+=，解得5x =或12x =∴直角三角形斜边为13当122m n =⎧⎨=⎩时，方程2(2)40x m x m -++=为214480x x -+=，解得6x =或8x =∴直角三角形斜边为10【练一练】已知a 是正整数，如果关于x 的方程32(17)(38)560x a x a x +++--=的根都是整数，求a 的值及方程的整数根．【解析】观察易知方程有一个整数根11x =，将方程的左边分解因式，得：2(1)(18)560x x a x ⎡⎤-+++=⎣⎦．因为a 是正整数，所以关于x 的方程：2(18)560x a x +++= ……①的判别式2(18)2240a ∆=+->，它一定有两个不同的实数根．而原方程的根都是整数，所以方程①的根都是整数，因此它的判别式2(18)224a ∆=+-应该是一个完全平方数．设22(18)224a k +-=(其中k 为非负整数)，则22(18)224a k +-=，即：(18)(18)224a k a k +++-=．显然18a k ++与18a k +-的奇偶性相同，且1818a k ++≥，1818a k a k +++-≥．而2241122564288=⨯=⨯=⨯，所以：18112182a k a k ++=⎧⎨+-=⎩，或1856184a k a k ++=⎧⎨+-=⎩，或1828188a k a k ++=⎧⎨+-=⎩ 解得3955a k =⎧⎨=⎩，或1226a k =⎧⎨=⎩，或010a k =⎧⎨=⎩．而a 是正整数，所以只可能3955a k =⎧⎨=⎩，或1226a k =⎧⎨=⎩．当39a =时，方程①即257560x x ++=，它的两根分别为1-和56-．此时原方程的三个根为1，1-和56-．当12a =时，方程①即230560x x ++=，它的两根分别为2-和28-．此时原方程的三个根为1，2-和28-．【答案】当39a =时，原方程的三个根为1，1-和56-；当12a =时，原方程的三个根为1，2-和28-【例9】若关于x 的方程()()()26911715540k k x k x ----+=的解都是整数，则符合条件的整数k 的值有_______个．【解析】当6k =时，得2x =；当9k =时，得3x =-，当9k ≠时，解得196x k =-，269x k =-，当6139k -=±±±，，时，1x 是整数，这时753153k =-，，，，；当91236k -=±±±±，，，时，2x 是整数这时10811712153k =，，，，，，综上所述，367915k =，，，，时原方程的解为整数．【答案】367915k =，，，，【练一练】若k 为正整数，且关于k 的方程22(1)6(31)720k x k x ---+=有两个相异正整数根，求k 值．【解析】原方程变形、因式分解为2(1)(1)6(31)720k k x k x +---+=，[(1)12][(1)6]0k x k x +---=．即1121x k =+，261x k =-．由121k +为正整数得1,2,3,5,11k =；由61k -为正整数得2,3,4,7k =．所以2,3k =使得1x ，2x 同时为正整数，但当3k =时，123x x ==，与题目不符，所以，只有2k = 为所求．【答案】2k =【例10】当m 为何整数时，方程222525x mx m -+=有整数解．【解析】解法1：将方程222525x mx m -+=左边因式分解可得 (2)(2)5x m x m --=故2521x m x m -=⎧⎨-=⎩，或2125x m x m -=⎧⎨-=⎩，或2521x m x m -=-⎧⎨-=-⎩，或2125x m x m -=-⎧⎨-=-⎩解得31x m =⎧⎨=⎩，13x m =-⎧⎨=-⎩，31x m =-⎧⎨=-⎩，13x m =⎧⎨=⎩解法2：将方程222525x mx m -+=整理成标准形式：2225250x mx m -+-=由原方程有整数解，首先必须满足222(5)42(25)940m m m ∆=-⨯⨯-=+为一个完全平方数，不妨设2(0)n n ∆=>，则有22940(3)(3)40m n n m n m +=⇒-+=，又3n m -、3n m +的奇偶性相同，故它们必然同为偶数，则有32320n m n m -=⎧⎨+=⎩，32032n m n m -=⎧⎨+=⎩，32320n m n m -=-⎧⎨+=-⎩，32032n m n m -=-⎧⎨+=-⎩， 34310n m n m -=⎧⎨+=⎩，31034n m n m -=⎧⎨+=⎩，31034n m n m -=-⎧⎨+=-⎩，34310n m n m -=-⎧⎨+=-⎩解得311m n =⎧⎨=⎩，311m n =-⎧⎨=⎩，17m n =⎧⎨=⎩，17m n =-⎧⎨=⎩代入552222m m n±∆±=⨯⨯中检验可知，均满足题意，故1m =±或3m =±．注意，题中要求有整数解即可，没要求所有的根都是整数，要注意区分这一点．点评：解法2看似复杂，但却是一元二次方程的整数根问题的通用解法，“希望杯”等考试中也常考到这种方法，值得引起注意．解法1看似简单，但使用起来有较多的局限性，如果无法进行因式分解，或者所分解的整数的因数过多，使用起来将很复杂．【答案】1m =±或3m =±【练一练】（2009密云）关于x 的方程22(3)(2)0ax a x a +-+-=至少有一个整数解，且a 是整数，求a 的值.【解析】当a=0时，原方程为620x --=,解得13x =-，即原方程无整数解.当0a ≠时，方程为一元二次方程，它至少有一个整数根，说明判别式24(3)4(2)4(94)a a a a ∆=---=-为完全平方数，从而94a -为完全平方数，设294a n -=，则n 为正奇数，且3n ≠否则（0a =），所以，294n a -=.由求根公式得 22(3)234(3)1129a n n n x a a n --±±±==-+=-+- 所以 12441,1.33x x n n=-+=-++-要使1x 为整数，而n 为正奇数，只能1n =，从而2a =;要使2x 为整数,n 可取1，5，7，从而2,4,10.a =-- 综上所述，a 的值为2,4,10.--【练一练】（2013东城区）已知关于x 的一元二次方程x 2＋(m ＋3)x ＋m ＋1＝0．（1）求证：无论m 取何值，原方程总有两个不相等的实数根；（2）当m 为何整数时，原方程的根也是整数．【解析】(1)证明： Δ=23)4(1)m m +-+（ =26944m m m ++-- =225m m ++ =2(1)4m ++．∵ 2(1)m +≥0， ∴ 2(1)4m ++＞0．∴ 无论m 取何实数时，原方程总有两个不相等的实数根. （2）解关于x 的一元二次方程x 2＋(m ＋3)x ＋m ＋1＝0，得 23(1)42m m x --±++=.要使原方程的根是整数，必须使得2(1)4m ++是完全平方数.设22(1)4m a ++=，则(1)(1)4a m a m ++--=. ∵ a +1m +和1a m --的奇偶性相同，可得12,1 2.a m a m ++=⎧⎨--=⎩或12,1 2.a m a m ++=-⎧⎨--=-⎩解得2,1.a m =⎧⎨=-⎩或2,1.a m =-⎧⎨=-⎩.将m=－1代入23(1)42m m x --±++=，得122,0x x =-=符合题意. ∴ 当m=－1 时，原方程的根是整数.二.一元二次方程的应用1.增长率问题【例11】某校去年对实验器材的投资为2万元，预计今明两年的投资总额为12万元，求该校这两年在实验器材投资上的平均增长率是多少？【解析】注意“累计”等名词【答案】设平均增长率为x ，根据题意得22(1)2(1)12x x +++=整理得2340x x +-=，解这个方程得：11x =，24x =-（舍）答：该校这两年在实验器材投资上的平均增长率是100%【练一练】某公司成立3年以来，积极向国家上交利税，由第一年的200万元增加到800万元，则平均每年增长的百分数是【解析】略【答案】设平均每年增长的百分数是x根据题意得：2200(1)800x += 解得1x =或3x =-（舍）∴平均每年的增长的百分数是100%【练一练】北京市政府为了迎接2008年奥运会，决定改善城市面貌，绿化环境，计划经过两年时间，绿地面积增加44%，则这两年平均每年绿地面积的增长率是（）A.10%B.20%C.30%D.40%【解析】略【答案】设绿地面积的增长率是x ，原有绿地面积为a ，根据题意得2(1)(144%)a x a +=+ 解得20%x =或220%x =-（舍）则平均增长率为20% ∴选B【例12】某个体户以50000元资金经商，在第一年中获得一定的利润，已知这50000元资金加上第一年的利润在第二年共获利润2612.5元，而且第二年的利润率比第一年多0.5%，则第一年的利润是多少元？【解析】略【答案】设第一年的利润为x 元，根据题意得(50000)(0.5%)2612.550000xx +⋅+=解得12250x =，252500x =-（舍）答：第一年的利润为2250元【练一练】某商品两次价格下调后，单价从5元变成4.05元，则平均每次调价的百分率为（）A.9%B.10%C.11%D.12%【解析】略【答案】设平均每次调价的百分率为x ，根据题意得，25(1) 4.05x -=，解得0.1x =或 1.9x =（舍）因此选B【练一练】某商场2002年的营业额比2001年上升10%，2003年比2002年又上升10%，而2004年和2005年连续两年比上一年降低10%，那么2005年的营业额比2001年的营业额（）A.降低了2%B. 没有变化C.上升了2%D.降低了1.99%【解析】注意题目要求，还有注意是比较“2005年的营业额与2001年的营业额”【答案】设2001年的营业额为a 元，则2002年的营业额为1.1a 元，2003年的营业额1.21a 元，所以2005年的营业额为21.21(110%)0.9801a a ⨯-= 因此2005年的营业额比2001年的营业额降低了0.9801100% 1.99%a aa -⨯= 所以选择D2.商品利润问题【例13】某商场销售一批名牌衬衫，平均每天可以销售出20件，每件盈利40元，为扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降价1元，商场平均每天多售出2件，若商场平均每天要盈利1200元，每件衬衫应降低多少元？【答案】解：设每件衬衫降价x 元，则每件所获得的利润为(40)x -元，但每天可多售2x 件，每天可卖(202)x +件，根据题意得(40)(202)1200x x -+=，方程化简整理得2302000x x -+=解得120x =，210x = ∵要尽快减少库存，∴20x =答：若商场每天要盈利1200元，每件应降价20元【练一练】吉安国光商场在销售中发现：某品牌衬衫平均每天可售出60件，每件赢利40元．为了迎接“十•一”黄金周，商场决定采取适当的降价措施，扩大销售量，增加赢利，减少库存．经市场调查发现：如果每件衬衫降价1元，那么平均每天就可多售出6件．要想平均每天销售这种衬衫赢利3600元，那么每件衬衫应降价多少元？【解析】本题可设每件衬衫应降价x 元，则每件赢利(40)x -元，平均每天可售出(606)x +件，根据每件的盈利×销售的件数=衬衫的盈利，据此即可可列出方程，求出答案．【答案】设每件衬衫应降价x 元，根据题意得(40)(606)3600x x -+=整理得2302000x x -+=解得110x =，220x = ∵要尽快减少库存 ∴20x =答：每件衬衫应降价20元【例14】商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．（1）问商场经营该商品原来一天可获利润多少元？（2）若商场经营该商品一天要获利润2160元，则每件商品售价应为多少元？【答案】（1）若商店经营该商品不降价，则一天可获利润100(10080)2000⨯-=（元）．（2）设后来该商品每件降价x 元，依题意，得(10080)(10010)2160x x --+=整理得210160x x -+=解得12x =，28x = 当2x =时，售价为98元当8x =时，售价为92元答：商店经营该商品一天要获利润2160元时，每件商品应售价为98元或92元【练一练】西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售，每天可售出200千克．为了促销，该经营户决定降价销售．经调查发现，这种小型西瓜每降价0.1元/千克，每天可多售出40千克．另外，每天的房租等固定成本共24元．该经营户要想每天盈利200元，应将每千克小型西瓜的售价降低多少元？【解析】设应将每千克小型西瓜的售价降低x 元．那么每千克的利润为：(32)x --，由于这种小型西瓜每降价0.1元/千克，每天可多售出40千克．所以降价x 元，则每天售出数量为：402000.1x +千克．本题的等量关系为：每千克的利润×每天售出数量-固定成本=200．【答案】设应将每千克小型西瓜的售价降低x 元．根据题意，得40(32)(200)242000.1xx --+-=原式可化为：2502530x x -+=解这个方程，得10.2x =，20.3x =答：应将每千克小型西瓜的售价降低0.2或0.3元．【例15】某商店以2400元购进某种盒装茶叶，第一个月按进价增加20%作为售价，售出50盒；第二个月每盒以低于进价5元作为售价，售完余下的茶叶，在整个买卖过程中盈利350元，求每盒茶叶的进价【解析】略【答案】设每盒进价x 元，依题意可列下列方程：24005020%5(50)350x x ⨯--=整理得21012000x x --=，解得130x =、240x =经检验130x =-、240x =都是原方程的解，但进价不能为负数，所以只取40x = 答：每盒茶叶进价为40元【练一练】某玩具厂生产一种玩具熊猫，每日最高产量为40只，且产出的产品全部售出，已知生产x 只玩具熊猫的成本为R （元），售价为每只P （元），且R 、P 与x 的关系式为50030R x =+，1702P x =-，当日产量为多少时，每日获得的利润为1750元？【解析】略【答案】根据题意得(1702)(50030)1750x x x --+=，解之，得125x =，245x =（舍），即日产量为25只时，每月获得利润为1750元【练一练】宏达汽车出租公司共有出租车120辆，每辆汽车的日租金为160元，出租业务天天供不应求，为适应市场需求，经有关部门批准，公司准备适当提高日租金，经市场调查发现，一辆汽车日租金每增加10元，每天出租的汽车相应地减少6辆。

11.2.1 一元二次方程的解法-直接开平方法(七大题型)-原

1.2.1一元二次方程的解法-直接开平方法考点一、直接开方法解一元二次方程：(1)直接开方法解一元二次方程：利用平方根的定义直接开平方求一元二次方程的解的方法称为直接开平方法.(2)直接开平方法的理论依据：平方根的定义.(3)能用直接开平方法解一元二次方程的类型有两类：①形如关于x 的一元二次方程，可直接开平方求解.若，则；表示为，有两个不等实数根；若，则x=O；表示为，有两个相等的实数根；若，则方程无实数根．②形如关于x 的一元二次方程，可直接开平方求解，两根是.要点：用直接开平方法解一元二次方程的理论依据是平方根的定义，应用时应把方程化成左边是含未知数的完全平方式，右边是非负数的形式，就可以直接开平方求这个方程的根.题型1：直接开平方法解一元二次方程1．一元二次方程2250x -=的解为（）A ．125x x ==B ．15=x ，25x =-C ．125x x ==-D ．1225x x ==2．若()222a =-，则a 是（）A ．-2B ．2C ．-2或2D ．43．方程x 2-=0的根为_______．4．有关方程290x +=的解说法正确的是（）A ．有两不等实数根3和3-B ．有两个相等的实数根3C ．有两个相等的实数根3-D ．无实数根5．若方程()20ax b ab =>的两个根分别是4m -与38m -，则ba=_____．6．解方程：（1）23270x -=；（2）2(5)360x --=；（3）21(2)62x -=；（4）()()4490+--=y y ．7．计算：4（3x +1）2﹣1＝0、3274y ﹣2＝0的结果分别为（）A ．x ＝±12，y ＝±23B ．x ＝±12，y ＝23C ．x ＝﹣16，y ＝23D ．x ＝﹣16或﹣12，y ＝2382x =）A ．120,x x ==B ．120,x x ==C ．12x x =D ．12x x ==题型2：直接开平方法解一元二次方程的条件9．下列方程中，不能用直接开平方法求解的是()A ．230x =－B ．2(14)0x =－－C ．220x =＋D ．22()12()x =－－10．方程y 2＝-a 有实数根的条件是（）A ．a ≤0B ．a ≥0C ．a >0D ．a 为任何实数11．有下列方程：①x 2-2x=0；②9x 2-25=0；③(2x-1)2=1；④21(x 3)273+=．其中能用直接开平方法做的是()A ．①②③B ．②③C ．②③④D ．①②③④12．方程x 2=（x ﹣1）0）A ．x=-1B ．x=1C ．x=±1D ．x=013．如果方程()257x m -=-可以用直接开平方求解，那么m 的取值范围是（）.A ．0m >B ．7mC ．7m >D ．任意实数14．已知方程()200ax c a +=≠有实数根，则a 与c 的关系是（）.A ．0c =B ．0c =或a 、c 异号C ．0c =或a 、c 同号D ．c 是a 的整数倍题型3：直接开平方法解一元二次方程的复合型15．用直接开平方的方法解方程22(31)(25)x x +=-，做法正确的是（）A ．3125x x +=-B ．31(25)x x +=--C ．31(25)x x +=±-D ．3125x x +=±-16．方程224(21)25(1)0x x --+=的解为（）A ．127x x ==-B ．1217,3x x =-=-C ．121,73x x ==D ．1217,3x x =-=17．解方程：（1）21(2)602y +-=；（2）22(4)(52)x x -=-．题型3：一元二次方程的根的概念深入理解18．一元二次方程2251440t -=的根与249(1)25x -=的根（）A ．都相等B ．都不相等C ．有一个根相等D ．无法确定题型4：直接开平方法解一元二次方程的根的通用形式19．关于x 的方程(x+a)2=b(b>0)的根是（）A ．-aB ．C ．当b≥0时，D ．当a≥0时，20．形如2()(0)ax b p a +=≠的方程，下列说法错误的是（）A ．0p >时，原方程有两个不相等的实数根B ．0p =时，原方程有两个相等的实数根C ．0p <时，原方程无实数根D ．原方程的根为x =题型5：直接开平方法解一元二次方程-降次21．方程4160x -=的根的个数是（）A ．1B ．2C ．3D ．4题型6：直接开平方法解一元二次方程-换元法22．若()222225a b +-=，则22a b +的值为()A ．7B ．-3C ．7或-3D ．21题型7：直接开平方法解一元二次方程-创新题，数系的扩充23．我们知道，一元二次方程21x =-没有实数根，即不存在一个实数的平方等于1-．若我们规定一个新数“i ”，使其满足21i =-（即方程21x =-有一个根为i ），并且进一步规定：一切实数可以与新数进行四则运算，且原有运算律和运算法则仍然成立，于是有()21232422,1,(1),(1)1i i i i i i i i i i ==-=⋅=-=-==-=，从而对于任意正整数n ，我们可以得到()41444nn n i i i i i +=⋅=⋅=，同理可得424341,,1n n n i i i i ++=-=-=．那么234202*********i i i i i i ++++++ 的值为________．一、单选题10．若方程()200ax bx c a ++=≠中，,,a b c 满足420a b c ++=和420a b c -+=，则方程的根是（）A ．1,0B ．1,0-C ．1,1-D ．2,2-二、填空题三、解答题19．解下列方程：224(1)x x =-．20．用直接开平方法解下列方程．（1）2160x -=；（2）2(2)9x -=．21．用开平方法解下列方程：(1)2 2.25x =；(2)243x =；(3)27560x -=；(4)()22714x -=．22．解方程：22(1)(12)x x +=-．→→→的顺序运算，请列式并计算结果；（1）嘉嘉说-2，对-2按C A D B答案与解析题型1：直接开平方法解一元二次方程1．一元二次方程2250x -=的解为（）A ．125x x ==B ．15=x ，25x =-C ．125x x ==-D ．1225x x ==【答案】B 【解析】【分析】先移项，再通过直接开平方法进行解方程即可．解：2250x -=，移项得：2=25x ，开平方得：15=x ，25x =﹣，故选B ．【点睛】本题主要考查用开平方法解一元二次方程，解题关键在于熟练掌握开平方方法．2．若()222a =-，则a 是（）A ．-2B ．2C ．-2或2D ．4【答案】C 【解析】【分析】先计算2(2)-，再用直接开平方法解一元二次方程即可．()2224a =-= 2a ∴=±故选C 【点睛】本题考查了有理数的乘方，直接开平方法解一元二次方程，熟练直接开平方法是解题的关键．3．方程x 2-=0的根为_______．【答案】x=±【解析】【分析】，得出x 2=8，利用直接开平方法即可求解．解：x 2-=0，∴x 2=8，∴x =±．故答案为：x =±．【点睛】本题考查直接开平方法解一元二次方程及算术平方根，解题关键是熟练掌握直接开平方法的解题步骤．4．有关方程290x +=的解说法正确的是（）A ．有两不等实数根3和3-B ．有两个相等的实数根3C ．有两个相等的实数根3-D ．无实数根【答案】D 【解析】【分析】利用直接开平方法求解即可．∵290x +=，∴290x =-<，∴该方程无实数解．故选：D 【点睛】考查了直接开平方法解一元二次方程．解这类问题要移项，把所含未知数的项移到等号的左边，把常数项移项等号的右边，化成x 2=a （a ≥0）的形式，利用数的开方直接求解．5．若方程()20ax b ab =>的两个根分别是4m -与38m -，则ba=_____．【答案】1【解析】【分析】利用直接开平方法得到x =，得到方程的两个根互为相反数，所以4380m m -+-=，解得3m =，则方程的两个根分别是1与1-1=，然后两边平方得到b a 的值．解：∵()20ax b ab =>，∴2b x a=，∴x =，∴方程的两个根互为相反数，∵方程2ax b =的两个根分别是4m -与38m -，∴4380m m -+-=，解得3m =，∴4341m -=-=-，383381m -=⨯-=，∴一元二次方程ax 2＝b 的两个根分别是1与1-，1=，∴1ba=．故答案为：1．【点睛】本题考查了解一元二次方程﹣直接开平方法：形如2x p =或()()20nx m p p +=≥的一元二次方程可采用直接开平方的方法解一元二次方程．如果方程化成2x p =的形式，那么可得x =()()20nx m p p +=≥的形式，那么nx m +=6．解方程：（1）23270x -=；（2）2(5)360x --=；（3）21(2)62x -=；（4）()()4490+--=y y ．【答案】（1）123,3x x ==-；（2）1211,1x x ==-；（3）122,2x x ==-；（4）125,5y y ==-．【解析】【分析】（1）先移项，再两边同除以3，然后利用直接开方法解方程即可得；（2）先移项，再利用直接开方法解方程即可得；（3）先两边同乘以2，再利用直接开方法解方程即可得；（4）先利用平方差公式去括号，再移项合并同类项，然后利用直接开方法解方程即可得．（1）23270x -=，2327x =，29x =，3x =±，即123,3x x ==-；（2）2(5)360x --=，2(5)36x -=，56x -=或56x -=-，11x =或1x =-，即1211,1x x ==-；（3）21(2)62x -=，2(2)12x -=，2x -=2x -=-，2x =或2x =-+，即122,2x x ==-；（4）()()4490+--=y y ，21690y --=，225y =，5y =±，即125,5y y ==-．【点睛】本题考查了利用直接开方法解一元二次方程，一元二次方程的主要解法包括：直接开方法、配方法、公式法、因式分解法、换元法等，熟练掌握各解法是解题关键．7．计算：4（3x +1）2﹣1＝0、3274y ﹣2＝0的结果分别为（）A ．x ＝±12，y ＝±23B ．x ＝±12，y ＝23C ．x ＝﹣16，y ＝23D ．x ＝﹣16或﹣12，y ＝23【答案】D 【解析】【分析】直接开平方与开立方，再解一次方程即可．解：由4（3x +1）2﹣1＝0得（3x +1）2＝14，所以3x +1＝±12，解得x ＝﹣16或x ＝﹣12，由3274y ﹣2＝0得y 3＝827，所以y ＝23，所以x ＝﹣16或﹣12，y ＝23．故选：D ．【点睛】本题考查开平方法解一元二次方程与立方根法解三次方程，掌握平方根与立方根性质与区别是解题关键．82x =）A ．120,x x ==B ．120,x x ==C ．12x x =D ．12x x ==【答案】A 【解析】【分析】利用直接开方法解一元二次方程即可得．2x =(23x =，利用直接开方法得：x ，解得120,x x ==故选：A ．【点睛】本题考查了利用直接开方法解一元二次方程，熟练掌握直接开方法是解题关键．题型2：直接开平方法解一元二次方程的条件9．下列方程中，不能用直接开平方法求解的是()A ．230x =－B ．2(14)0x =－－C ．220x =＋D ．22()12()x =－－【答案】C 【解析】【分析】方程整理后，判断即可得到结果230x =－移项得23x =，可用直接开平方法求解；2(10)4x -=－移项得2(14)x =－，可用直接开平方法求解；22()(12)4x ==－－，可用直接开平方法求解．故选C.【点睛】此题考查解一元二次方程直接开平方法，掌握运算法则是解题关键10．方程y 2＝-a 有实数根的条件是（）A ．a ≤0B ．a ≥0C ．a >0D ．a 为任何实数【答案】A 【解析】【分析】根据平方的非负性可以得出﹣a ≥0，再进行整理即可．解：∵方程y 2＝﹣a 有实数根，∴﹣a ≥0（平方具有非负性），∴a ≤0；故选：A ．【点睛】此题考查了直接开平方法解一元二次方程，关键是根据已知条件得出﹣a ≥0．11．有下列方程：①x 2-2x=0；②9x 2-25=0；③(2x-1)2=1；④21(x 3)273+=．其中能用直接开平方法做的是()A ．①②③B ．②③C ．②③④D ．①②③④【答案】C 【解析】【分析】利用因式分解法与直接开平方法判断即可得到结果．①x 2-2x=0，因式分解法；②9x 2-25=0，直接开平方法；③(2x-1)2=1，直接开平方法；④21(x 3)273+=，直接开平方法，则能用直接开平方法做的是②③④.故选:C.【点睛】考查直接开方法解一元二次方程，掌握一元二次方程的几种解法是解题的关键.12．方程x 2=（x ﹣1）0）A ．x=-1B ．x=1C ．x=±1D ．x=0【答案】A 【解析】【分析】根据(x-1)0有意义，可得x-1≠0，求出x≠1，通过解方程x 2=1，确定x 的值即可.∵(x-1)0有意义，∴x-1≠0，即x≠1，∵x 2=（x ﹣1）0∴x 2=1，即x=±1∴x=-1.故选A.【点睛】本题考查了解一元二次方程—直接开平方法，解这类问题要移项，把所含未知数的项移到等号的左边，把常数项移项等号的右边，化成x 2=a （a≥0）的形式，利用数的开方直接求解．同时还考查了零次幂.13．如果方程()257x m -=-可以用直接开平方求解，那么m 的取值范围是（）.A ．0m >B ．7mC ．7m >D ．任意实数【答案】B 【解析】【分析】根据70-≥m 时方程有实数解，可求出m 的取值范围．由题意可知70-≥m 时方程有实数解，解不等式得7m，故选B ．【点睛】形如()2+m =a x 的一元二次方程当a≥0时方程有实数解．14．已知方程()200ax c a +=≠有实数根，则a 与c 的关系是（）.A ．0c =B ．0c =或a 、c 异号C ．0c =或a 、c 同号D ．c 是a 的整数倍【答案】B 【解析】【分析】将原方程化为2a=c-x 的形式，根据2x 0≥可判断出正确答案．原方程可化为2a =c -x ，∵2x 0≥，∴c0a-≥时方程才有实数解．当c=0时，20=x 有实数根；当a 、c 异号时，c0a-≥，方程有实数解．故选B ．【点睛】形如2=a x 的一元二次方程当a≥0时方程有实数解．题型3：直接开平方法解一元二次方程的复合型15．用直接开平方的方法解方程22(31)(25)x x +=-，做法正确的是（）A ．3125x x +=-B ．31(25)x x +=--C ．31(25)x x +=±-D ．3125x x +=±-【答案】C【分析】一元二次方程22(31)(25)x x +=-，表示两个式子的平方相等，因而这两个数相等或互为相反数，据此即可把方程转化为两个一元一次方程，即可求解．解：22(31)(25)x x +=-开方得31(25)x x +=±-，故选：C ．【点睛】本题考查了解一元二次方程-直接开平方法，关键是将方程右侧看做一个非负已知数，根据法则：要把方程化为“左平方，右常数，先把系数化为1，再开平方取正负，分开求得方程解”来求解．16．方程224(21)25(1)0x x --+=的解为（）A ．127x x ==-B ．1217,3x x =-=-C ．121,73x x ==D ．1217,3x x =-=【答案】B 【解析】【分析】移项后利用直接开平方法解答即可．解：移项，得224(21)25(1)x x -=+，两边直接开平方，得2(21)5(1)x x -=±+，即2(21)5(1)x x -=+或2(21)5(1)x x -=-+，解得：17x =-，213x =-．故选：B ．【点睛】本题考查了一元二次方程的解法，属于基本题型，熟练掌握直接开平方法是解题的关键．17．解方程：（1）21(2)602y +-=；（2）22(4)(52)x x -=-．【答案】（1）122,2y y ==-；（2）121,3x x ==．【分析】（1）原方程先整理，再利用直接开平方法解答即可；（2）利用直接开平方法求解即可．解：（1）21(2)602y +-=，整理，得2(2)12y +=．∴2y +=±即122,2y y ==-；（2）22(4)(52)x x -=- ，4(52)x x ∴-=±-，∴452x x -=-或()452x x -=--，解得：121,3x x ==．【点睛】本题考查了一元二次方程的解法，属于基础题型，熟练掌握直接开平方法是解题的关键．题型3：一元二次方程的根的概念深入理解18．一元二次方程2251440t -=的根与249(1)25x -=的根（）A ．都相等B ．都不相等C ．有一个根相等D ．无法确定【答案】C 【解析】【分析】运用直接开平方法分别求出两个方程的解，然后再进行判断即可得解.2251440t -=，214425t =，∴125t =±；249(1)25x -=，715x -=±，∴1125x =，225x =-；∴两个方程有一个相等的根125.故选C.【点睛】此题主要考查了用直接开平方法解一元二次方程和确定方程的解，用直接开方法求一元二次方程的解的类型有：x 2=a （a≥0）；ax 2=b （a ，b 同号且a≠0）；（x+a ）2=b （b≥0）；a （x+b ）2=c （a ，c 同号且a≠0）．题型4：直接开平方法解一元二次方程的根的通用形式19．关于x 的方程(x+a)2=b(b>0)的根是（）A ．-aB ．C ．当b≥0时，D ．当a≥0时，【答案】A 【解析】【分析】由b>0，可两边直接开平方，再移项即可得．∵b>0，∴两边直接开平方,得：，∴-a ，故选A 【点睛】此题考查解一元二次方程-直接开平方法，解题关键在于掌握运算法则20．形如2()(0)ax b p a +=≠的方程，下列说法错误的是（）A ．0p >时，原方程有两个不相等的实数根B ．0p =时，原方程有两个相等的实数根C ．0p <时，原方程无实数根D ．原方程的根为x =【答案】D 【解析】【分析】根据应用直接开平方法求解的条件逐项判断即得答案．解：A 、当0p >时，原方程有两个不相等的实数根，故本选项说法正确，不符合题意；B 、当0p =时，原方程有两个相等的实数根，故本选项说法正确，不符合题意；C 、当0p <时，原方程无实数根，故本选项说法正确，不符合题意；D 、当0p ≥时，原方程的根为x =故选：D ．【点睛】本题考查了一元二次方程的解法，属于基本题目，熟练掌握应用直接开平方法求解的条件是关键．题型5：直接开平方法解一元二次方程-降次21．方程4160x -=的根的个数是（）A ．1B ．2C ．3D ．4【答案】B 【解析】【分析】移项得416x ==24,然后两边同时开四次方得x-=±2，由此即可解决问题．解：∵4160x -=∴416x ==24，∴x=±2，∴方程4160x -=的根是x=±2.故选B.【点睛】本题考查高次方程的解法，解题的关键是降次，这里通过开四次方把四次降为了一次．题型6：直接开平方法解一元二次方程-换元法22．若()222225a b +-=，则22a b +的值为()A ．7B ．-3C ．7或-3D ．21【答案】A 【解析】【分析】把()222225a b +-=两边开方得到a 2+b 2-2=±5，然后根据非负数的性质确定22a b +的值．解：∵()222225a b +-=，∴a 2+b 2-2=±5，∴a 2+b 2=7或a 2+b 2=-3（舍去），即a 2+b 2的值为7．故选A ．【点睛】本题考查解一元二次方程-直接开平方法：形如x 2=p 或（nx+m ）2=p （p≥0）的一元二次方程可采用直接开平方的方法解一元二次方程．题型7：直接开平方法解一元二次方程-创新题，数系的扩充23．我们知道，一元二次方程21x =-没有实数根，即不存在一个实数的平方等于1-．若我们规定一个新数“i ”，使其满足21i =-（即方程21x =-有一个根为i ），并且进一步规定：一切实数可以与新数进行四则运算，且原有运算律和运算法则仍然成立，于是有()21232422,1,(1),(1)1i i i i i i i i i i ==-=⋅=-=-==-=，从而对于任意正整数n ，我们可以得到()41444nn n i i i i i +=⋅=⋅=，同理可得424341,,1n n n i i i i ++=-=-=．那么234202*********i i i i i i ++++++ 的值为________．【答案】1-【解析】【分析】根据()41444nn n i i i i i +=⋅=⋅=，424341,,1n n n i i i i ++=-=-=，化简各式即可求解．解：依题意有()()()22123242,1,1,11i i i i i i i i i i ==-=⋅=-=-==-=，∵2022÷4＝505…2，∴2022i =21i =-∴234202*********i i i i i i ++++++ ＝−1−i ＋1＋i ＋…＋1＋i −1＝−1．故答案为：-1．【点睛】此题考查了一元二次方程的解，实数的运算，根据题意得出数字之间的变化规律是解本题的关键．一、单选题二、填空题11．方程240x -=的根是______．【答案】12x =-，22x =【分析】根据直接开平方法求解即可．【解析】解：240x -=，18．我们知道，一元二次方程21x =-没有实数根，即不存在一个实数的平方等于1-．若我们规定一个新数“i ”，使其满足21i =-（即方程21x =-有一个根为i ），并且进一步规定：一切实数可以与新数进行四则运算，且原有运算律和运算法则仍然成立，于是有()21232422,1,(1),(1)1i i i i i i i i i i ==-=⋅=-=-==-=，从而对于任意正整数n ，我们可以得到()41444n n n i i i i i +=⋅=⋅=，同理可得424341,,1n n n i i i i ++=-=-=．那么234202*********i i i i i i ++++++ 的值为________．【答案】1-【分析】根据()41444n n n i i i i i +=⋅=⋅=，424341,,1n n n i i i i ++=-=-=，化简各式即可求解．【解析】解：依题意有()()()22123242,1,1,11i i i i i i i i i i ==-=⋅=-=-==-=，∵2022÷4＝505…2，∴2022i =21i =-∴234202*********i i i i i i ++++++ ＝−1−i ＋1＋i ＋…＋1＋i −1＝−1．故答案为：-1．【点睛】此题考查了一元二次方程的解，实数的运算，根据题意得出数字之间的变化规律是解本题的关键．三、解答题【解析】解：原式＝m 2﹣1﹣（4m 2+4m +1）+3m 2+6m＝m 2﹣1﹣4m 2﹣4m ﹣1+3m 2+6m＝2m ﹣2，∵m 2﹣1＝0，∴m ＝±1，当m ＝1时，原式＝2﹣2＝0，当m ＝﹣1时，原式＝﹣2﹣2＝﹣4，综上所述：原式的值为0或﹣4．【点睛】本题考查整式的化简求值，准确掌握乘法公式是解题的关键，计算中注意符号问题．26．计算(1)化简：2(1)(1)+--m m m (2)小华在解方程2(6)90x +-=时，解答过程如下：解：移项，得2(6)9x +=第一步两边开平方，得63x +=第二步所以3x =-第三步“小华的解答从第_________步开始出错，请写出正确的解答过程．【答案】(1)-1；(2)二；正确的解答过程，见解析【分析】（1）利用平方差公式展开，合并同类项即可；（2）根据直接开平方法求解即可．【解析】（1）解：2(1)(1)+--m m m 221m m =--=-1；（2）解：第二步开始出现错误；正确解答过程：移项，得（x +6）2=9，两边开平方，得x +6=3或x +6=-3，解得x 1=-3，x 2=-9，故答案为：二．【点睛】本题主要考查了整式的混合运算、解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．27．嘉嘉和琪琪用图中的A 、B 、C 、D 四张带有运算的卡片，做一个“我说你算”的数学游戏，规则如下：嘉嘉说一个数，并对这个数按这四张带有运算的卡片排列出一个运算顺序，然后琪琪根据这个运算顺序列式计算，并说出计算结果．例如，嘉嘉说2，对2按A B C D →→→的顺序运算，则琪琪列式计算得：222[(23)(3)2](152)(17)289+⨯--=--=-=．（1）嘉嘉说-2，对-2按C A D B →→→的顺序运算，请列式并计算结果；（2）嘉嘉说x ，对x 按C B D A →→→的顺序运算后，琪琪得到的数恰好等于12，求x ．【答案】（1）2(223)(3)--+⨯-，3-；（2）嘉嘉出的数是1或3．【分析】（1）根据题意，可以写出相应的算式，然后计算即可；（2）根据题意，可以得到关于x 的方程，然后解方程即可．【解析】（1）2(223)(3)--+⨯-1(3)=⨯-3=-.（2）根据题意得2[(2)(3)]312x -⨯-+=，29(2)9x -=，2(2)1x -=，11x =，23x =.x 为整数，∴嘉嘉出的数是1或3.【点睛】本题考查有理数的混合运算、解一元二次方程，解答本题的关键是明确题意，列出相应的算式，。

含参数的一元二次方程整数解

含参数的一元二次方程整数解知识定位对于一元二次方程ax 2＋bx ＋c=0(a≠0)的实根情况，可以用判别式Δ=b 2-4ac 来判别，但是对于一个含参数的一元二次方程来说，要判断它是否有整数根或有理根，那么就没有统一的方法了，只能具体问题具体分析求解，当然，经常要用到一些整除性的性质。

知识梳理1、一元二次方程ax 2+bx+c=0(a ≠0)的实数根，是由它的系数a, b, c 的值确定的.根公式是：x=aac b b 242-±－. (b 2－4ac ≥0)2、根的判别式① 实系数方程ax 2+bx+c=0(a ≠0)有实数根的充分必要条件是：b 2－4ac ≥0.② 有理系数方程ax 2+bx+c=0(a ≠0)有有理数根的判定是：b 2－4ac 是完全平方式⇔方程有有理数根.③整系数方程x 2+px+q=0有两个整数根⇔p 2－4q 是整数的平方数. 3、设x 1, x 2 是ax 2+bx+c=0的两个实数根，那么③ ax 12+bx 1+c=0 (a ≠0，b 2－4ac ≥0)， ax 22+bx 2+c=0 (a ≠0， b 2－4ac ≥0)；④ x 1=a ac b b 242-＋－， x 2=aac b b 242-－－ (a ≠0, b 2－4ac ≥0)；⑤ 韦达定理：x 1+x 2= a b －, x 1x 2=ac(a ≠0, b 2－4ac ≥0). 4、方程整数根的其他条件整系数方程ax 2+bx+c=0 (a ≠0)有一个整数根x 1的必要条件是：x 1是c 的因数. 特殊的例子有： C=0⇔x 1=0 ，a+b+c=0⇔x 1=1 ，a －b+c=0⇔x 1=－1.例题精讲【试题来源】【题目】b 为何值时, 方程x 2 - bx - 2 = 0 和x 2 - 2x - b (b - 1) = 0有相同的整数根?并且求出它们相同的整数根.．【答案】1；2【解析】解：设相同的整数根为x 0, 由根的定义, 知x20- bx0 - 2 = 0, ①x20- 2x0-b(b - 1) = 0. ②① - ②并整理, 得(2 - b)[x0-(1 + b)]=0,②∴b = 2 或x0 = b + 1.当b = 2 时, 两方程均为x2-2x-2 = 0, 但无整数根;当x0 = b + 1 时, 代入①或②, 解之得b = 1, 于是公共根x0 =b + 1 = 2.【知识点】含参数的一元二次方程整数解【适用场合】当堂例题【难度系数】3【试题来源】【题目】设二次方程ax2+bx+c=0的两根为x1、x2，记S1=x1+1993x2，S2=x12+1993x22，…，Sn=x1n+1993x2n，则aS1993+bS1992+cS1991=【答案】0【解析】解：∵x1、x2是方程ax2+bx+c=0的两根，∴ax12+bx1+c=0， ax22+bx2+c=0。

一元二次方程的整数根问题专题练习(解析版)

一元二次方程的整数根问题专题练习一、选择题1、若k 为正整数，且关于k 的方程（k 2-1）x 2-6（3k -1）x +72=0有两个相异正整数根，k 的值为（）．A. 2B. 4C. 6D. 8答案：A解答：原方程变形、因式分解为（k +1）（k -1）x 2-6（3k -1）x +72=0，[（k +1）x -12][（k -1）x -6]=0．即x 1=121k +，x 2=61k -．由121k +为正整数得k =1，2，3，5，11；由61k -为正整数得k =2，3，4，7． ∴k =2，3使得x 1，x 2同时为正整数，但当k =3时，x 1=x 2=3，与题目不符，∴只有k =2为所求．二、填空题2、已知k 为整数，且关于x 的方程（k 2-1）x 2-3（3k -1）x +18=0有两个不相等的正整数根，则k 的值为______．答案：2解答：原方程化为：[（k +1）x -6][（k -1）x -3]=0．∴x 1=61k +，x 2=31k -．因方程的根为正整数，因而推知k =2，此时x 1=2，x 2=3．3、已知12＜m ＜40，且关于x 的二次方程x 2-2（m +1）x +m 2=0有两个整数根，则整数m 的值为______．答案：24解答：由原方程有整数解可知，Δ=4（m +1）2-4m 2=4（2m +1）必然是一个完全平方数．又12＜m ＜40可知，25＜2m +1＜81，又2m +1为奇数，故2m +1=49，m =24．此时原方程的两个实数根为：x =212m +14502=±，不妨设x 1＞x 2，则x 1=32，x 2=18．故m=244、当关于x 的方程x 2-（m -1）x +m +1=0的两根都是整数，则整数m 的值为______．答案：7或-1解答：设方程的两整数根分别是x 1，x 2，由韦达定理得x 1+x 2=m -1，x 1·x 2=m +1，消去m ，可得x 1x 2-x 2-x 1=2，（x 1-1）（x 2-1）=3=1×3=-1×（-3），则有121113x x -=⎧⎨-=⎩.或121113x x -=-⎧⎨-=-⎩.，解得：1224x x =⎧⎨=⎩.或1202x x =⎧⎨=-⎩.，由此x 1·x 2=8或0，∴m =7或m =-1．三、解答题5、当整数m 取何值时，关于x 的方程（m -1）x 2-（2m +1）x +1=0有整数根．答案：-1．解答：当m =1时，-3x +1=0，x =13（舍）．当m ≠1时，该方程为一元二次方程，Δ=4m 2+4m +1-4m +4=4m 2+5，设4m 2+5=n 2（n 为正整数），4m 2-n 2=-5，则（2m +n ）（2m -n ）=-5，2521m n m n +=⎧⎨-=-⎩或2125m n m n +=⎧⎨-=-⎩，则m =-1．6、已知方程（a 2-1）x 2-2（5a +1）x +24=0有两个不相等的负整数根，求整数a 的值．答案：a =-2．解答：由题意得：2100a ⎧-≠⎨∆⎩＞， Δ=[2（5a +1）]2-4×24（a 2-1）=4（a+5）2＞0，∴a≠±1，a≠-5，由求根公式得：x1=61a-，x2=41a+，∵方程有两个不相等的负整数根，∴a-1=-1，-2，-3，-6，a+1=-1，-2，-4，即：a=0，-1，-2，-5，a=-2，-3，-5，∴a=-2或-5．∴a=-2．7、当整数m取何值时，关于x的方程mx2-（1-m）x-1=0的根为整数．答案：m=-1，0，1．解答：当m=0时，x=-1，当m≠0时，该方程为一元二次方程，x1=-1，x2=1m，∵xm为整数，∴m=±1，综上，当m=-1，0，1时，方程的根为整数．8、关于x的方程mx2-（3m+2）x+2m+2=0的根为正整数，且m为整数，求m的值．答案：0或1或2或-2．解答：当m=0时，方程可化为-2x+2=0，有整数根x=1，满足题意．当m≠0时，∵mx2-（3m+2）x+2m+2=0，[mx-（2m+2）]（x-1）=0，mx-（2m+2）=0或a-1=0，∴x1=22mm+=2+2m，x2=1．又∵该方程的根为正整数且m为整数，∴2m为大于-2的整数，∴m=1或2或-2．则m 的值为0或1或2或-2．9、已知：关于x 的一元二次方程（m -1）x 2-2mx +m +1=0（m ＞1）．（1）求证：方程总有两个不相等的实数根．（2）m 为何整数时，此方程的两个实数根都为正整数？答案：（1）证明见解答．（2）m =2或m =3．解答：（1）∵Δ=（-2m ）2-4（m +1）（m -1）=4＞0．∴方程总有两个不相等的实数根．（2）∵Δ=（-2m ）2-4（m +1）（m -1）=4＞0，m -1≠0．由求根公式解得：x 1=()2221m m +-=11m m +-，x 2=()2221m m --=1． x 1=11m m +-=1+21m - ∵方程的两个根都为正整数，m 是整数且m ＞1． ∴21m -是正整数． ∴m -1=1或m -1=2．∴m =2或m =3．10、已知关于x 的一元二次方程x 2+（m +3）x +m +1=0．（1）求证：无论m 取何值，原方程总有两个不相等的实数根．（2）当m 为何整数时，原方程的根也是整数．答案：（1）证明见解答．（2）当m =-1时，原方程的根是整数．解答：（1）Δ=（m +3）2-4（m +1）=m 2+6m +9-4m -4=m 2+2m +5=（m +1）2+4．∵（m +1）2≥0，∴（m +1）2+4＞0．∴无论m 取何实数时，原方程总有两个不相等的实数根．（2）Δ=（m +3）2-4（m +1）=m 2+6m +9-4m -4=m 2+2m +5=（m +1）2+4．∵（m +1）2≥0，∴（m +1）2+4＞0．∴无论m 取何实数时，原方程总有两个不相等的实数根．解关于x 的一元二次方程x 2+（m +3）x +m +1=0，得x =3m --．要使原方程的根是整数，必须使得（m +1）2+4是完全平方数．设（m +1）2+4=a 2，则（a +m +1）（a -m -1）=4．∵a +m +1和a -m -1的奇偶性相同，可得1212a m a m ++=⎧⎨--=⎩.或1212a m a m ++=-⎧⎨--=-⎩．解得21a m =⎧⎨=-⎩.或21a m =-⎧⎨=-⎩．将m =-1代入x =3m --±，得x 1=-2，x 2=0符合题意．∴当m =-1时，原方程的根是整数．11、一直角三角形的两直角边长均为整数，且满足方程x 2-（m +2）x +4m =0，试求m 的值及此直角三角形的三边长．答案：当m =15，直角三角形三边长分别为5，12，13；当m =12，直角三角形三边长分别为6，8，10．解答：由题意得，Δ=m 2-12m +4，∴x =()22m +±． ∵该方程的根均为整数，∴m 2-12m +4必为平方数，令m 2-12m +4=n 2（n 为正整数），整理得（m -6）2-n 2=32，∴（m -6+n ）（m -6-n ）=32，∴m -6+n 与m -6-n 同奇同偶．因此61662m n m n -+=⎧⎨--=⎩或6864m n m n -+=⎧⎨--=⎩，解得157m n =⎧⎨=⎩或122m n =⎧⎨=⎩，当157m n =⎧⎨=⎩时，方程x 2-（m +2）x +4m =0为x 2-17x +60=0，解得x =5或x =12，∴即当m =15，直角三角形三边长分别为5，12，13．当122m n =⎧⎨=⎩时，方程x 2-（m +2）x +4m =0为x 2-14x +48=0，解得x =6或x =8，∴即当m =12，直角三角形三边长分别为6，8，10．12、已知关于x 的方程（m -1）x 2-2mx +m +1=0．（1）求证：无论常数m 取何值，方程总有实数根．（2）当整数m 取何值时，方程有两个整数根．答案：（1）证明见解答．（2）2或0或3或-1．解答：（1）①当m -1=0即m =1时，方程化成-2x +2=0，解得x =1，②当m -1≠0即m ≠1时，方程一元二次方程，a =m -1，b =-2m ，c =m +1，∴b 2-4ac =（-2m ）2-4（m -1）（m +1）=4m 2-4m 2+4=4＞0，∴方程总有两个不相等的实数根，∴综上所述，无论常数m 取何值，方程总有实数根．（2）x =()221m m ±-=()2221m m ±-=11m m±-， ∴x 1=1，x 2=11m m +-，而11m m +-=121m m -+-=1+21m -， ∴当m -1=±1，±2时，x 2为整数，即m =2或0或3或-1，方程有两个整数根．13、已知：关于x 的一元二次方程mx 2-3（m -1）x +2m -3=0．（1）求证：不论实数m 取何值，方程必有两个实数根．（2）若方程有一个根大于2且小于3，求实数m 的取值范围．（3）若m 为整数，且方程的两个根均为正整数，求m 的值．答案：（1）证明见解答．（2）m ＜-3．（3）m =-3，-1，3．解答：（1）解法一：由题意，得()()2091423m m m m ≠⎧⎪⎨∆=---⎪⎩， ∴Δ=m 2-6m +9=（m -3）2≥0，∴不论实数m 取何值，方程必有两个实数根．解法二：原方程因式分解得（x -1）[mx -（2m -3）]=0，∵m ≠0，∴原方程必有两个实根．（2）由（1）可知，方程两根为x 1=1，x 2=23m m-， ∴2＜23m m -＜3，化简得2＜2-3m＜3，由2＜2-3m可知，m ＜0；由2-3m ＜3可知，m ＜-3； ∴综上所述，m ＜-3．（3）∵m 为整数，x 2=2-3m 为正整数， ∴m =-3，-1，3．14、已知关于x 的一元二次方程x 2+2x +2m -4=0有两个不相等的实数根．（1）求m 的取值范围．（2）若m 为正整数，且该方程的根都是整数，求m 的值．答案：（1）m ＜52．（2）2．解答：（1）由题意得：b 2-4ac =4-4（2m -4）=20-8m ＞0，解得：m ＜52．（2）由m 为正整数，可知m =1或2，求根公式得x =-1∵方程的根为整数，∴5-2m 为完全平方数，则m 的值为2．15、已知关于x 的一元二次方程x 2+2（m +1）x +m 2-1=0．（1）若方程有两个不相等的实数根，求m 的取值范围．（2）在（1）的条件下，选择一个恰当的m 的值，使方程的两个实数根为整数，并求出这两个根．答案：（1）m ＞-1．（2）当m =1时，x 1=0，x 2=-4．解答：（1）Δ=[2（m +1）]2-4（m 2-1）=8m +8．∵方程有两个不相等的实数根，∴8m +8＞0，∴m ＞-1．（2）在（1）的条件下，当m =1时，该方程可化为x 2+4x =0．∴两个整数根为x 1=0，x 2=-4．16、已知：关于x 的一元二次方程x 2-（2m -3）x +m 2-5m +2=0有两个不相等的实数根．（1）求m 的取值范围．（2）若10＜m ＜21，是否存在整数m ，使方程有两个整数根，若存在求出m 的值；若不存在请说明理由．答案：（1）m ＞-18．（2）m =15．解答：（1）Δ=[-（2m -3）]2-4（m 2-5m +2）=8m +1＞0，得m ＞-18．（2）存在整数m ，使方程有两个整数根，原因：方程解为x =()23m -，∵10＜m＜21，m为整数，∴81＜8m+1＜169且为整数，∴913，又∵方程有两个整数根，或11或12，∴m=998或15或118，∴m=15，当m=15时，x1=19；x2=8符合题意．17、当m为何整数时，方程2x2-5mx+2m2=5有整数解．答案：m=±1或m=±3．解答：将方程2x2-5mx+2m2=5左边因式分解可得（2x-m）（x-2m）=5故2521x mx m-=⎧⎨-=⎩，或2125x mx m-=⎧⎨-=⎩，或2521x mx m-=-⎧⎨-=-⎩，或2125x mx m-=-⎧⎨-=-⎩解得31311313 x x x xm m m m==-=-=⎧⎧⎧⎧⎨⎨⎨⎨==-=-=⎩⎩⎩⎩，，，．18、求所有整数k，使方程kx2+（k+1）x+k-1=0的根都是整数．答案：k=1．解答：①当k=0时，x-1=0，x=1．②当k≠0时，Δ=（k+1）2-4k（k-1）=-3k2+6k+1＞0由根与系数关系得：x1+x2=-1kk+=-1-1k，x1·x2=1kk-=1-1k，∵根都是整数，∴k=±1，检验：k=-1不符合（舍）．综上所述，k=1．19、已知方程（k2-1）x2-3（3k-1）x+18=0有两个不相等的整数根，（1）求整数k的值．（2）求实数k 的值．答案：（1）k =0，±2．（2）k =0，±2，±12．解答：（1）[（k +1）x -6][（k -1）x -3]=0，x 1=61k +，x 2=31k -， ∵方程有两个整数根，即k +1=±1，±2，±3，±6，k -1=±1，±3，∴k =0，±2．（2）由x 1=61k +，x 2=31k -得k +1=16x ，k -1=23x ，化简得x 1=3-2932x +， ∴2x 2+3=±1，±3，±9，x 2=-2，-1，0，-3，3，-6，∴k =0，±2，±12． 20、已知一元二次方程（2k -3）x 2+4kx +2k -5=0，且4k +1是边长为7的菱形对角线的长，求k 取什么整数值时，方程（2k -3）x 2+4kx +2k -5=0的根都是整数？答案：k =1时，方程（2k -3）x 2+4kx +2k -5=0的根都是整数．解答：∵（2k -3）x 2+4kx +2k -5=0为一元二次方程，∴2k -3≠0，∴k ≠32． ∵4k +1是边长为7的菱形对角线的长，∴0＜4k +1＜14，∴-14＜k ＜134． ∵Δ=（4k ）2-4（2k -3）（2k -5）=64k -60≥0，∴k ≥1516， ∴1516≤k ＜134， ∵k 为整数，∴k =1或2或3．当k =1时，Δ=4，方程为-x 2+4x -3=0，根为x 1=1，x 2=3，符合题意；当k=2时，Δ=68，不符合题意；当k=3时，Δ=132，不符合题意．∴k=1．。

一元二次方程应用题精选含答案

一元二次方程应用题精选一、数字问题1、有两个连续整数，它们的平方和为25，求这两个数。

2、一个两位数，十位数字与个位数字之和是6，把这个数的个位数字与十位数字对调后，所得的新两位数与原来的两位数的积是1008，求这个两位数．二、销售利润问题3、某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元．为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．求：（1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？（2）要使商场平均每天赢利最多，请你帮助设计方案．4.某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施，调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台，商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？5.西瓜经营户以2元/千克的价格购进一批小型西瓜，以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价O.1元/千克，每天可多售出40千克.另外，每天的房租等固定成本共24元.该经营户要想每天盈利2O0元，应将每千克小型西瓜的售价降低多少元?三、平均变化率问题增长率（1）原产量+增产量=实际产量．（2）单位时间增产量=原产量×增长率．（3）实际产量=原产量×（1+增长率）．6. 某钢铁厂去年一月份某种钢的产量为5000吨，三月份上升到7200吨，这两个月平均每月增长的百分率是多少？7. 某产品原来每件600元，由于连续两次降价，现价为384元，如果两个降价的百分数相同，求每次降价百分之几？四、形积问题8、有一块长方形的铝皮，长24cm、宽18cm，在四角都截去相同的小正方形，折起来做成一个没盖的盒子，使底面积是原来面积的一半，求盒子的高．9、如图，在一块长为32m，宽为20m长方形的土地上修筑两条同样宽度的道路，余下部分作为耕地要使耕地的面积是540m2，求小路宽的宽度．五、围篱笆问题10、如图，利用一面墙（墙的长度不超过45m ），用80m 长的篱笆围一个矩形场地． ⑴怎样围才能使矩形场地的面积为750m2?⑵能否使所围矩形场地的面积为810m2，为什么?六、相互问题（传播、循环）11、（1）参加一次聚会的每两人都握了一次手,所有人共握手15次,有多少人参加聚会?(2)要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排28场比赛,应邀请多少个球队参加比赛?(3) 某初三毕业班的每一个同学都把自己的照片向全班其他的同学各送一张留作纪念，全班共送了3080张照片．如果该班有x 名同学，根据题意可列出方程为?12、有一人患了流感，经过两轮传染后共有169人患了流感．（1）求每一轮传染中平均一个人传染了几个人？（2）如果按照这样的传染速度，经过三轮传染后共有多少人患上流感？第21题图13、某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是91，每个支干长出多少小分支？七.行程问题：14、甲、乙两艘旅游客轮同时从台湾省某港出发来厦门。

一元二次方程的整数根问题的解题策略分析

一元二次方程的整数根问题的解题策略分析摘要：一元二次方程的整数根问题是初中数学竞赛常见的题型，由于这类问题涵盖了整数的性质，一元二次方程的相关知识，并且融合了许多数学思想方法而备受命题者的青睐，然而笔者发现，许多学生在解答这类问题时，仍然没有系统的思考方法，还要走很多的弯路，有时对题目甚至无从下手。

本文将常见的一元二次方程整数根问题的解法进行了整理，现分类讲解如下。

关键词：一元二次方程整数根整除根与系数关系一、利用一元二次方程两根的因式分解形式求解例1、当m是什么整数时，关于x的一元二次方程x2-mx-2m2-4=0的根为整数。

分析与解：由原方程得：x2-mx-2m2-4=4，分解因式，得(x+m)(x-2m)=4由于x、m均为整数，所以x+m、x-2m也为整数，故它们的取值有如下可能：解得，当m=0时，x=±2；当m=1时，x1=3,x2=-2；当m=-1时，x1=-3,x2=2；综上所述：当m=0、-1、1时，原方程的根为整数。

说明：当一元二次方程的根与参数都为整数时，可以利用因式分解将一元二次方程ax2+bx+c=zh整数（a≠0）化为a（x-x1）(x-x2)=整数（a≠0）的形式后再利用整除的性质求解。

二、利用一元二次方程根的判别式求解例2、m是何整数时，关于x的一元二次方程(m2-1)x2-6(3m-1)x+72=0有两个不相等的正整数根。

分析与解：由题意可知，m2-1≠0，即m≠±1，△=36（m-3）2，发现△是一个完全平方式，即方程的两根是可以表示为两个有理式：再利用整除性，要使得x1,x2都是正整数，则m-1=1、6、2、3；m+1=1、12、2、6、3、4，即可解得m=2、3，又考虑到方程是两个不相等的实数根，所以m≠3，综上所述：m=2。

说明：当判别式△是一个完全平方式或完全平方数时，即一元二次方程的根可以用有理式表示，则可直接求出方程的两根，再结合整除的性质进行求解；例3、当m是何整数时，关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0的根都是整数。

(完整版)一元二次方程的解法总结,推荐文档

一元二次方程的解法(直接开平方法、配方法、公式法和分解法)一元二次方程定义：只含有一个未知数，并且未知数的最高次数为2的整式方程叫做一元二次方程。

一般形式：ax²+bx+c=0（a，b，c为常数，x为未知数，且a≠0）。

顶点式：y=a(x-h)²+k(a≠0,a、h、k为常数)交点式：y=a(x-x₁)(x-x₂) (a≠0)[有交点A（x₁，0）和B（x₂，0）的抛物线，即b²-4ac≥0] .直接开平方法：直接开平方法就是用直接开平方求解一元二次方程的方法。

用直接开平方法解形如(x-m)²=n(n≥0)的方程，其解为x=m±配方法　:1.将此一元二次方程化为ax²+bx+c=0的形式(此一元二次方程满足有实根) 2.将二次项系数化为1 3.将常数项移到等号右侧 4.等号左右两边同时加上一次项系数一半的平方 5.将等号左边的代数式写成完全平方形式 6.左右同时开平方 7.整理即可得到原方程的根公式法：1.化方程为一般式：ax²+bx+c=0 （a≠0）2.确定判别式，计算Δ（=b²-4ac）；3.若Δ>0，该方程在实数域内有两个不相等的实数根：x=若Δ=0，该方程在实数域内有两个相等的实数根:x₁=x₂=若Δ<0，该方程在实数域内无实数根因式分解法：因式分解法又分“提公因式法”；而“公式法”（又分“平方差公式”和“完全平方公式”两种），另外还有“十字相乘法”，因式分解法是通过将方程左边因式分解所得，因式分解的内容在八年级上学期学完。

用因式分解法解一元二次方程的步骤1.将方程右边化为0；2.将方程左边分解为两个一次式的积；3.令这两个一次式分别为0，得到两个一元一次方程；4.解这两个一元一次方程，它们的解就是原方程的解.用待定系数法求二次函数的解析式(1)当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时，可设解析式为一般形式：y=ax²+bx+c(a≠0)。

一元二次方程的解法总结

一元二次方程的解法(直接开平方法、配方法、公式法和分解法）一元二次方程定义:只含有一个未知数，并且未知数的最高次数为2的整式方程叫做一元二次方程。

一般形式：ax²+bx+c=0（a,b，c为常数，x为未知数,且a≠0）。

顶点式：y=a（x—h）²+k（a≠0,a、h、k为常数）交点式：y=a（x—x₁）（x—x₂）（a≠0）［有交点A(x₁，0）和B(x₂,0)的抛物线，即b²—4ac≥0］ .直接开平方法：直接开平方法就是用直接开平方求解一元二次方程的方法。

用直接开平方法解形如（x-m)²=n（n≥0）的方程，其解为x=m±配方法：1。

将此一元二次方程化为ax²+bx+c=0的形式(此一元二次方程满足有实根）2。

将二次项系数化为13。

将常数项移到等号右侧4。

等号左右两边同时加上一次项系数一半的平方5。

将等号左边的代数式写成完全平方形式6。

左右同时开平方7.整理即可得到原方程的根公式法:1。

化方程为一般式：ax²+bx+c=0 （a≠0）2。

确定判别式，计算Δ（=b²—4ac)；3。

若Δ>0，该方程在实数域内有两个不相等的实数根:x=若Δ=0，该方程在实数域内有两个相等的实数根：x₁=x₂=若Δ〈0,该方程在实数域内无实数根因式分解法：因式分解法又分“提公因式法”；而“公式法”（又分“平方差公式”和“完全平方公式”两种），另外还有“十字相乘法”，因式分解法是通过将方程左边因式分解所得，因式分解的内容在八年级上学期学完。

用因式分解法解一元二次方程的步骤1. 将方程右边化为0；2. 将方程左边分解为两个一次式的积；3. 令这两个一次式分别为0,得到两个一元一次方程；4. 解这两个一元一次方程，它们的解就是原方程的解。

用待定系数法求二次函数的解析式（1）当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时,可设解析式为一般形式:y=ax²+bx+c（a≠0).（2)当题给条件为已知图象的顶点坐标或对称轴或极大(小）值时,可设解析式为顶点式：y=a(x—h）²+k（a≠0）。

一元二次方程的整数解问题

张雪云（四川省成都外国语学校　６１１７００）张雪云四川省资阳市人，研究生学历，中学一级，四川省赛课一等奖，主要研究方向：数学学科教学。

含未知参数的一元二次方程无法直接求具体解，即使通过求根公式也只能得到含参数的两个根和判别式，无法得到方程参数的值．但是在若题目中隐含方程有根的条件，可以通过该条件得到判别式不小于零的约束，根据这个约束条件可得方程的未知参数的范围．由于求根公式带有除法运算，如果已知方程的根为整数，那么求根公式的分母必须是分子的约数．通过题目中隐含的这两个条件，通常可得方程的解和未知参数只能是可数的几个值，只需要把这几个值通过枚举的方式列出来就是题目的解．下面就常见题型、常用技巧以及求解问题所用的知识点作细致的讨论．１．分解因式　因式分解是得到含参一元二次方程的根的最快捷的方式．能够因式分解的一元二次方程我们首选因式分解，它的核心在于利用质因数分解或分离常系数法求解，再利用整数的性质及整除性理论解决问题．例１　已知一元二次方程（ｍ－２）ｘ２－（２ｍ－５）ｘ＋（ｍ－３）＝０的根都是整数，求整数ｍ的值．分析　用因式分解得到两根为１和ｍ－３ｍ－２，题中要求方程的根和参数ｍ都是整数，因此我们对ｍ－３ｍ－２分离常数，用整数的性质及整除性理论即可解决问题．解　根据题意得ｍ≠１且Δ＝１＞０，因式分解，得（ｘ－１）［（ｍ－２）ｘ－（ｍ－３）］＝０，解得ｘ１＝１，ｘ２＝ｍ－３ｍ－２＝１－１ｍ－２，因为ｍ为整数且根都为整数，所以ｍ－２＝±１，可得ｍ的值为２或０．例２　已知一元二次方程ａ２　ｘ２－（４ａ２＋ａ）ｘ＋３ａ２＋７ａ－６＝０至少有一个整数根，求自然数ａ的值．分析　此题相对例１而言，只是方程较为复杂，我们仍然用因式分解分解方程，求出含参解，用整数的性质及整除性理论解决问题．解　因为ａ２　ｘ２－（４ａ２＋ａ）ｘ＋３ａ２＋７ａ－６＝０是一元二次方程，所以ａ≠０，因式分解，得［ａｘ－（ａ＋３）］［ａｘ－（３ａ－２）］＝０，解得ｘ１＝１＋３ａ，ｘ２＝３－２ａ，因为ａ为自然数，当ｘ１为整数根时，ａ＝１或３，当ｘ２为整数根时，ａ＝１或２．综上所述，ａ的值为１或２或３．例３　当整数ｍ为何值时，关于ｘ的方程２ｘ２＋３ｍｘ＋ｍ２＝３有整数解．分析　此题相对例１、例２而言，共同之处是方程左边能因式分解，不同之处是方程的右边是一个不为０的常数３，从而不能解出含参解，针对这种情况，我们对质因数３进行分解，利用参数和根都为整数的条件用枚举的方法一一枚举．解　因式分解，得（ｘ＋ｍ）（２ｘ＋ｍ）＝３，因为ｍ，ｘ都是整数，所以ｘ＋ｍ＝３，２ｘ＋ｍ＝１，｛ｘ＋ｍ＝－３，２ｘ＋ｍ＝－１，｛·１３·２０２０年第１２期数学竞赛数理天地初中版ｘ＋ｍ＝１，２ｘ＋ｍ＝３，｛ｘ＋ｍ＝－１，２ｘ＋ｍ＝－３，｛即ｘ＝－２，ｍ＝５，｛ｘ＝２，ｍ＝－５，｛ｘ＝２，ｍ＝－１，｛ｘ＝－２，ｍ＝１，｛所以ｍ＝±１或±５．注　当方程ａｘ２＋ｂｘ＋ｃ＝０（ａ≠０）可分解为（ｘ－ｍ）（ｘ－ｎ）＝ｋ（ｍ，ｎ，ｋ均为整数）时，可以将整数ｋ分解为两个整数ｋ１，ｋ２的乘积形式，即ｘ－ｍ＝ｋ１，ｘ－ｎ＝ｋ２｛或ｘ－ｍ＝ｋ２，ｘ－ｎ＝ｋ１，｛一一枚举求解．例４　关于ｘ的一元二次方程（ｍ２－６ｍ＋８）ｘ２＋（２ｍ２－６ｍ－４）ｘ＋ｍ２－４＝０的两根都是整数，求实数ｍ的值．分析　本题的参数ｍ没有限定为整数的条件，因此我们考虑把参数ｍ消去，列出解的关系式，和例３一样利用质因数分解，通过枚举一一解出答案．解　因式分解，得［（ｍ－２）ｘ＋（ｍ＋２）］［（ｍ－４）ｘ＋（ｍ－２）］＝０，求得两根为ｘ１＝－１－４ｍ－２，ｘ２＝－１－２ｍ－４．显然ｘ１≠－１且ｘ２≠－１，则ｍ－２＝－４ｘ１＋１，ｍ－４＝－２ｘ２＋１，两式相减，得２＝－４ｘ１＋１＋２ｘ２＋１，整理化简，得ｘ２（ｘ１＋３）＝－２，因为ｘ１，ｘ２为整数，则ｘ１＝－５，ｘ２＝１，｛ｘ１＝－４，ｘ２＝２，｛ｘ１＝－２，ｘ２＝－２，｛ｘ１＝－１，ｘ２＝－１，｛（舍），所以ｍ＝３或６或１０３．２．韦达定理　当方程无法因式分解时，可考虑选择韦达定理进行参数枚举或消去参数．特别注意：用韦达定理一定要检验Δ≥０．例５　已知ａ为正整数，关于ｘ的方程ｘ２＋（ａ＋１６）ｘ＋４２＝０的根都是整数，求ａ的值．分析　此题无法因式分解，我们可通过韦达定理得到根与系数的关系，利用参数和根为整数的约束条件分解质因数，直接枚举参数的值，从而解决问题．解　设方程的两根为ｘ１，ｘ２，则根据题意，得ｘ１＋ｘ２＝－（ａ＋１６）＜０，ｘ１ｘ２＝４２＞０，｛则ｘ１，ｘ２都是负整数，４２可分解为－１×（－４２）＝－２×（－２１）＝－３×（－１４）＝－６×（－７），所以ｘ１＋ｘ２＝－４３，－２３，－１７，－１３，所以ａ＝２７，７，１，－３，又因为ａ为正整数且Δ≥０，所以ａ＝２７，７，１．例６　关于ｘ的方程ｋｘ２＋（２ｋ＋１）ｘ＋２ｋ－１＝０的根都是整数，求ｋ的值．分析　此题方程类型未明确，因此我们先对ｋ＝０和ｋ≠０两种情况进行讨论．当ｋ＝０时，方程转化为一元一次方程，易判断根的情况，进行取舍；当ｋ≠０时，通过韦达定理得到根的关系式，但此题的参数没有约束条件，和例５的情况不一样，因此我们考虑消去参数得到和、积关系式，对和、积关系式进行变形处理后，利用根为整数的条件分解质因数或分离常数求解．解　（１）当ｋ＝０时，ｘ－１＝０，ｘ＝１成立．（２）当ｋ≠０时，设两根为ｘ１，ｘ２，由韦达定理，得ｘ１＋ｘ２＝－（２ｋ＋１）ｋ＝－２－１ｋ，ｘ１ｘ２＝２ｋ－１ｋ＝２－１ｋ，烅烄烆①②由②－①，得　ｘ１ｘ２－ｘ１－ｘ２＝４，所以（ｘ１－１）（ｘ２－１）＝５，因为方程的根为整数，所以ｘ１－１＝１，－１，５，－５，ｘ２－１＝５，－５，１，－１，｛所以ｘ１＋ｘ２＝８或－４，·２３·数理天地初中版数学竞赛２０２０年第１２期所以ｋ＝－１１０或１２，当ｋ＝－１１０时，Δ＝４２５＞０，成立；当ｋ＝１２，Δ＝４＞０，成立，所以ｋ＝－１１０或１２．综上所述，ｋ＝－１１０或１２或０．３．判别式法　不能因式分解，也无法用韦达定理消去参数，或者解为有理数时，可选择判别式法，通过计算Δ，若有整数解必然有Δ是个完全平方数，来解出参数．例７　已知整数ｍ，ｎ满足２ｍ２＋ｎ２＋３ｍ＋ｎ－１＝０，求ｍ，ｎ的值．分析　可以把已知等式看做以ｍ为主元的一元二次方程，ｎ为其参数，根据方程有解可以得到Δ≥０，然后求解关于ｎ的不等式方程，从而得到参数的取值范围，又根据参数ｎ为整数的条件直接枚举，即可解决问题．解　将２ｍ２＋ｎ２＋３ｍ＋ｎ－１＝０看做关于ｍ的一元二次方程，即２ｍ２＋３ｍ＋ｎ２＋ｎ－１＝０，要使方程有实数解，则必有Δ＝－８ｎ２－８ｎ＋１７≥０，所以ｎ＋１２（）２≤１９８，即－１９８槡－１２≤ｎ≤１９８槡－１２，又因为ｎ为整数，所以ｎ＝－２，－１，０，１，当ｎ＝－２时，ｍ１＝－１，ｍ２＝－１２（舍去）；当ｎ＝－１时，ｍ无整数解；当ｎ＝０时，ｍ无整数解；当ｎ＝１时，ｍ１＝－１，ｍ２＝－１２（舍去）；综上所述，ｍ＝－１，ｎ＝－２或１．注　对于二元方程可看做关于一个元的二次方程，由ｍ，ｎ为实数，则Δ≥０，从而求出ｎ的取值范围，应有“多元转为少元”的意识．例８　已知关于ｘ的方程ｘ２－８ｘ－ｎ２＋８ｎ＋３３＝０的根都是整数，求整数ｎ的值．分析　此题如果我们继续用例７的方法，即Δ≥０，我们发现时ｎ２－８ｎ－１７≥０，解集为ｎ≥槡３３＋４或ｎ≤－槡３３＋４，若用枚举的方法将非常繁琐，因此我们可以令ｎ２－８ｎ－１７＝ｔ　２，通过配方和因式分解，结合质因数分解来解决问题．解　因为方程ｘ２－８ｘ－ｎ２＋８ｎ＋３３＝０有解，所以Δ＝４ｎ２－３２ｎ－６８≥０，又因为方程的根都是整数，所以Δ＝４（ｎ２－８ｎ－１７）为完全平方数，即ｎ２－８ｎ－１７为完全平方数．设ｎ２－８ｎ－１７＝ｔ　２，ｔ为自然数，所以（ｎ－４）２－ｔ　２＝３３，即（ｎ－４＋ｔ）（ｎ－４－ｔ）＝３３，注意到ｎ－４＋ｔ≥ｎ－４－ｔ，所以ｎ－４＋ｔ＝３３，ｎ－４－ｔ＝１，｛或ｎ－４＋ｔ＝１１，ｎ－４－ｔ＝３，｛或ｎ－４＋ｔ＝－３，ｎ－４－ｔ＝－１１，｛或ｎ－４＋ｔ＝－１，ｎ－４－ｔ＝－３３，｛解得ｎ＝２１，ｔ＝１６，｛或ｎ＝１１，ｔ＝４，｛或ｎ＝－３，ｔ＝４，｛或ｎ＝－１３，ｔ＝－１６，｛所以ｎ＝２１，１１，－３，－１３．注　当方程存在有理数解时，令Δ＝ｔ　２，其中ｔ为自然数，此时分两种情况：如果判别式Δ为二次式，通过配方和因式分解，结合质因数分解等数论方法求解；如果判别式Δ为一次式，将原参数用ｔ表示，解出两根关于ｔ的表达式，从而求出ｔ．·３３·２０２０年第１２期数学竞赛数理天地初中版。

一元二次方程200题(含答案详解)

一元二次方程 200 题（含解析）---朱韬老师共享
一元二次方程：
填空：
1．ቤተ መጻሕፍቲ ባይዱ元二次方程 x2﹣3x=4 中，b2﹣4ac=
．
2．一元二次方程 x（x﹣1）=0 的解是
．
3．若 x=2 是关亍 x 的方程 x2﹣x﹣a2+5=0 的一个根，则 a 的值为
．
4．如果二次三项式 x2﹣6x+m2是一个完全平方式，那么 m 的值为
．
32．方程（x﹣1）2=4 的解为
．
33．一元二次方程 x2=16 的解是
．
34．在实数范围内定义运算“☆”，其觃则为：a☆b=a2﹣b2，则方程（4☆3）
☆x=13 的解为 x=
．
35．将 4 个数 a，b，c，d 排成 2 行、2 列，两边各加一条竖直线记成，定
义 =ad﹣bc，上述记号就叫做 2 阶行列式．若
．
16．若 x=1 是一元二次方程 x2+x+c=0 的一个解，则 c2=
．
17．已知 x=1 是关亍 x 的一元二次方程 2x2+kx﹣1=0 的一个根，则实数 k 的
值是
．
18．已知关亍 x 的方程 x2﹣5x+m=0 的一个根是 1，则 m 的值是
．
19．已知 x=1 是方程 ax2+x﹣2=0 的一个根，则 a=
5．一个广告公司制作广告的收费标准是：以面积为单位，在丌超过觃定面积 A
（m2）的范围内，每张广告收费 1 000 元，若超过 Am2，则除了要交返 1 000
元的基本广告费以外，超过部分迓要按每平方米 50A 元缴费．下表是该公司对
两家用户广告的面积及相应收费情况的记载：

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

竞赛辅导一元二次方程的整数整数解
在数学课外活动中，在各类数学竞赛中，一元二次方程的整数解问题一直是个热点，它将古老的整数理论与传统的一元二次方程知识相结合，涉及面广，解法灵活，综合性强，备受关注，解含参数的一元二次方程的整数解问题的基本策略有：
从求根入手，求出根的有理表达式，利用整除求解；
从判别式手，运用判别式求出参数或解的取值范围，或引入参数(设△=2k )，通过穷举，逼近求解；
从韦达定理入手，从根与系数的关系式中消去参数，得到关于两根的不定方程，借助因数分解、因式分解求解；
从变更主元入人，当方程中参数次数较低时，可考虑以参数为主元求解．
注：一元二次方程的整数根问题，既涉及方程的解法、判别式、韦达定理等与方程相关的知识，又与整除、奇数、偶数、质数、合数等整数知识密切相关．
【例题求解】
【例1】若关于x 的方程054)15117()9)(6(2=+----x k x k k 的解都是整数，则符合条件的整数是的值有个．
思路点拨用因式分解法可得到根的简单表达式，因方程的类型未指明，故须按一次方程、二次方程两种情形讨论，这样确定是的值才能全面而准确．
注：系数含参数的方程问题，在没有指明是二次方程时，要注意有可能是一次方程，根据问题的题设条件，看是否要分类讨论．
【例2】已知a 、b 为质数且是方程0132=+-c x x 的根，那么
b
a a
b +的值是( ) A ．22127 B ．22125 C ．22123 D ．22121 思路点拨由韦达定理a 、b 的关系式，结合整数性质求出a 、b 、
c 的值．
【例3】试确定一切有理数r ，使得关于x 的方程01)2(2=-+++r x r rx 有根且只有整数根．
思路点拨由于方程的类型未确定，所以应分类讨论．当0≠r 时，由根与系数关系得到关于r 的两个等式，消去r ，利用因式(数)分解先求出方程两整数根．
【例4】当m 为整数时，关于x 的方程01)12()12(2=++--x m x m 是否有有理根?如果有，求出m 的值；如果没有，请说明理由．
思路点拨整系数方程有有理根的条件是为完全平方数．
设△=22224)12(544)12(4)12(n m m m m m =+-=+-=--+(n 为整数)解不定方程，讨论m 的存在性．
注：一元二次方程02=++c bx ax (a ≠0)而言，方程的根为整数必为有理数，而△=ac b 42-为完全平方数是方程的根为有理数的充要条件．
【例5】若关于x 的方程0)13()3(22=-+--a x a ax 至少有一个整数根，求非负整数a 的值．思路点拨因根的表示式复杂，从韦达定理得出的a 的两个关系式中消去a 也较困难，又因a 的次数低于x 的次数，故可将原方程变形为关于a 的一次方程．
学历训练
1．已知关于x 的方程012)1(2=--+-a x x a 的根都是整数，那么符合条件的整数a 有．
2．已知方程019992=+-m x x 有两个质数解，则m ＝．
3．给出四个命题：①整系数方程02=++c bx ax (a ≠0)中，若△为一个完全平方数，则方程必有有理根；②整系数方程02=++c bx ax (a ≠0)中，若方程有有理数根，则△为完全平方数；③无理数系数方程02=++c bx ax (a ≠0)的根只能是无理数；④若a 、b 、c 均为奇数，则方程02=++c bx ax 没有有理数根，其中真命题是．
4．已知关于x 的一元二次方程0)12(22=+-+a x a x (a 为整数)的两个实数根是1x 、2x ，则21x x -= ．
5．设rn 为整数，且4<m<40，方程08144)32(222=+-+--m m x m x 有两个整数根，求m 的值及方程的根
6．已知方程015132)83(222=+-+--a a x a a ax (a ≠0)至少有一个整数根，求a 的值．
7．求使关于x 的方程01)1(2=-+++k x k kx 的根都是整数的k 值．
8．当n 为正整数时，关于x 的方程0763*******=-+-+-n n x nx x 的两根均为质数，试解此方程．
9．设关于x 的二次方程4)462()86(2222=+--++-k x k k x k k 的两根都是整数，试求满足条件的所有实数k 的值．
10．试求所有这样的正整数a ，使得方程0)3(4)12(22=-+-+a x a ax 至少有一个整数解．
11．已知p 为质数，使二次方程015222=--+-p p px x 的两根都是整数，求出p 的所有可能值．
12．已知方程02=++c bx x 及02=++b cx x 分别各有两个整数根1x 、2x 及1
x '、2x '，且1x 2x >0，1
x '2x ' >0． (1)求证：1x <0,2x <0，1
x '<0,2x '< 0；(2)求证：11+≤≤-b c b ；(3)求b 、c 所有可能的值．
13．如果直角三角形的两条直角边都是整数，且是方程0122=+--m x mx 的根(m 为整数)，这样的直角三角形是否存在?若存在，求出满足条件的所有三角形的三边长；若不存在，请说明理由．
参考答案。