圆柱表面积练习题ppt课件
合集下载
《圆柱体的表面积》ppt课件

在几何图形中,圆柱体表面积的计算有助于理解立体图形的构造和性质,为解决 更复杂的几何问题提供基础。
在日常生活中的应用
圆柱体在日常生活中随处可见,如水桶、饮料瓶、水管等。 这些物品的表面积决定了它们的外观和包装方式,对于生产 制造、物流运输和销售都有重要意义。
圆柱体表面积的计算有助于优化产品设计,降低生产成本, 提高经济效益。
代数法
总结词
代数法是通过代数运算来计算圆柱体的表面积。这种方法需 要一定的代数基础和计算能力。
详细描述
首先,将圆柱体的侧面积表示为2πr|h|,其中|h|是高度的一半。 然后,将两个底面的面积表示为2πr^2。最后,将侧面积和两 个底面积相加,得到圆柱体的总表面积。
微积分法
总结词
微积分法是通过微积分的基本定理来 计算圆柱体的表面积。这种方法需要 一定的微积分基础和计算能力。
侧面积 $S_{侧} = C times h = 2pi rh$。
圆柱体的底面积计算公式
底面积计算公式
$S_{底} = pi r^{2}$
解释
其中,$S_{底}$表示圆柱体的底面积,$pi$是圆周率,$r$是圆柱 底面圆的半径。
底面积计算公式推导
根据圆的面积公式,圆的面积 $A = pi r^{2}$,所以底面积 $S_{底} = A = pi r^{2}$。
圆柱体的全面积计算公式
全面积计算公式
$S_{全} = S_{侧} + S_{底}$
解释
其中,$S_{全}$表示圆柱体的全面积,$S_{侧}$是圆柱体的侧面积, $S_{底}$是圆柱体的底面积。
全面积计算公式推导
全面积就是侧面积加上两个底面积,即 $S_{全} = S_{侧} + 2S_{底} = 2pi rh + 2pi r^{2}$。
在日常生活中的应用
圆柱体在日常生活中随处可见,如水桶、饮料瓶、水管等。 这些物品的表面积决定了它们的外观和包装方式,对于生产 制造、物流运输和销售都有重要意义。
圆柱体表面积的计算有助于优化产品设计,降低生产成本, 提高经济效益。
代数法
总结词
代数法是通过代数运算来计算圆柱体的表面积。这种方法需 要一定的代数基础和计算能力。
详细描述
首先,将圆柱体的侧面积表示为2πr|h|,其中|h|是高度的一半。 然后,将两个底面的面积表示为2πr^2。最后,将侧面积和两 个底面积相加,得到圆柱体的总表面积。
微积分法
总结词
微积分法是通过微积分的基本定理来 计算圆柱体的表面积。这种方法需要 一定的微积分基础和计算能力。
侧面积 $S_{侧} = C times h = 2pi rh$。
圆柱体的底面积计算公式
底面积计算公式
$S_{底} = pi r^{2}$
解释
其中,$S_{底}$表示圆柱体的底面积,$pi$是圆周率,$r$是圆柱 底面圆的半径。
底面积计算公式推导
根据圆的面积公式,圆的面积 $A = pi r^{2}$,所以底面积 $S_{底} = A = pi r^{2}$。
圆柱体的全面积计算公式
全面积计算公式
$S_{全} = S_{侧} + S_{底}$
解释
其中,$S_{全}$表示圆柱体的全面积,$S_{侧}$是圆柱体的侧面积, $S_{底}$是圆柱体的底面积。
全面积计算公式推导
全面积就是侧面积加上两个底面积,即 $S_{全} = S_{侧} + 2S_{底} = 2pi rh + 2pi r^{2}$。
《圆柱的表面积》练习2课件

1、填空 (1)下列物体都是圆柱。在计算下列情境中物体的表面 积时,应该算圆柱的哪些面。 ① 做一个没有盖的桶( 侧面+1个底面 ). ②通风管( 侧面 ) ③铅笔的油漆面( 侧面 ) ④压路机滚筒滚动一周的压路面积( 侧面 )
(2)一个底面直径是4分米,高是4分米的圆柱形通风管, 需要铁皮(50.24 )平方分米。
50cm
10cm
6、一个圆柱底面半径是4cm,高是6cm,沿这个圆柱 的底面直径将圆柱平均分成两份(如图),这时表面 积比原来增加多少平方厘米?
4cm
6cm
7、一个圆柱侧面展开后是一个边长为 31.4cm的正方形,这个圆柱的表面积是 多少?
8、一个圆柱的侧面积是18.84cm2,底 面周长是6.28cm,求这个圆柱的表面积?
9、一个圆柱的侧面积是188.4cm2,底 面半径是2cm,它的高是多少?
10、一个圆柱被截去5cm后,圆柱的表面积减 少了31.4cm2,求原来圆柱的表面积?
5cm
20cm
C. 它的侧面展开图一定是正方形
(2)一个圆柱的侧面展开后是正方形,这个圆柱的高和底 面直径比是( A )
A. π∶1 B. 1∶π C. 1∶1
3、求下列各图形的表面积
15cm
6cm
5Байду номын сангаасm
9cm
10cm
6cm
4、书P18第17题
10cm
10cm
5、要将路灯座(如右图) 漆上白色的油漆,要漆多 少平方米?
(3)一个圆柱体,它的底面半径是2厘米,高是5厘米,它的 底面积是( 12.56cm2),它的底面周长是( 12.56cm),它的 侧面积是( 62.8cm2),它的表面积是( 87.92cm2 )
(2)一个底面直径是4分米,高是4分米的圆柱形通风管, 需要铁皮(50.24 )平方分米。
50cm
10cm
6、一个圆柱底面半径是4cm,高是6cm,沿这个圆柱 的底面直径将圆柱平均分成两份(如图),这时表面 积比原来增加多少平方厘米?
4cm
6cm
7、一个圆柱侧面展开后是一个边长为 31.4cm的正方形,这个圆柱的表面积是 多少?
8、一个圆柱的侧面积是18.84cm2,底 面周长是6.28cm,求这个圆柱的表面积?
9、一个圆柱的侧面积是188.4cm2,底 面半径是2cm,它的高是多少?
10、一个圆柱被截去5cm后,圆柱的表面积减 少了31.4cm2,求原来圆柱的表面积?
5cm
20cm
C. 它的侧面展开图一定是正方形
(2)一个圆柱的侧面展开后是正方形,这个圆柱的高和底 面直径比是( A )
A. π∶1 B. 1∶π C. 1∶1
3、求下列各图形的表面积
15cm
6cm
5Байду номын сангаасm
9cm
10cm
6cm
4、书P18第17题
10cm
10cm
5、要将路灯座(如右图) 漆上白色的油漆,要漆多 少平方米?
(3)一个圆柱体,它的底面半径是2厘米,高是5厘米,它的 底面积是( 12.56cm2),它的底面周长是( 12.56cm),它的 侧面积是( 62.8cm2),它的表面积是( 87.92cm2 )
《圆柱的表面积》课件PPT

圆柱的表面由上、下两个底面和一个侧面组成。
圆柱的表面积=侧面积+两个底面的面积 S圆=πr²
2、圆柱的底面积容易求,圆柱的侧面积怎 么求呢?
底面 底面
底面 底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
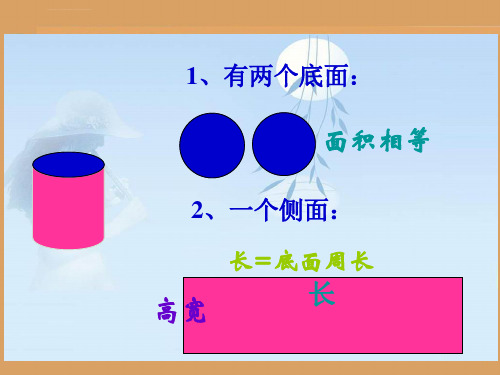
长方形的长等于圆柱底面的长, 宽等于圆柱的高。
底面的周长 高
底面
你会求 侧面的面 积吗?
长方形的面积=长×宽 圆柱的侧面积=底面周长×高
S侧=Ch S圆=πr² S圆柱=S侧+S底×2
(1)侧面积:2 ×3.14 ×10 ×30=1884(平方厘米) (2)底面积:3.14 ×102 =314(平方厘米) (3)表面积:1884+314 × 2=2512(平方厘米)
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径 是5cm,高是20cm。这张商标纸的面积是多少?
求商标纸的面积就是求什么?
侧面积:2 ×3.14 ×5 ×20=628(平方厘米)
帽子侧面积: 3.14×20×28=1758.4(cm2)
帽顶的面积: 3.14×(20÷2)2 =314 (cm2)
所用面料:
1758.4+314=2072.4 (cm2) =2080 (cm2)
答:做这样一顶帽子至少需要用2080平方厘米面料。
9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 ) 答:这个圆柱体的表面积是102.86 cm2。
2、一个圆柱体的侧面积是226.08 cm2,底面半径4 cm,它的高是多少?
圆柱的表面积=侧面积+两个底面的面积 S圆=πr²
2、圆柱的底面积容易求,圆柱的侧面积怎 么求呢?
底面 底面
底面 底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
长方形的长等于圆柱底面的长, 宽等于圆柱的高。
底面的周长 高
底面
你会求 侧面的面 积吗?
长方形的面积=长×宽 圆柱的侧面积=底面周长×高
S侧=Ch S圆=πr² S圆柱=S侧+S底×2
(1)侧面积:2 ×3.14 ×10 ×30=1884(平方厘米) (2)底面积:3.14 ×102 =314(平方厘米) (3)表面积:1884+314 × 2=2512(平方厘米)
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径 是5cm,高是20cm。这张商标纸的面积是多少?
求商标纸的面积就是求什么?
侧面积:2 ×3.14 ×5 ×20=628(平方厘米)
帽子侧面积: 3.14×20×28=1758.4(cm2)
帽顶的面积: 3.14×(20÷2)2 =314 (cm2)
所用面料:
1758.4+314=2072.4 (cm2) =2080 (cm2)
答:做这样一顶帽子至少需要用2080平方厘米面料。
9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 ) 答:这个圆柱体的表面积是102.86 cm2。
2、一个圆柱体的侧面积是226.08 cm2,底面半径4 cm,它的高是多少?
8.3.2 圆柱、圆锥、圆台、球表面积和体积(课件)2022-2023学年高一下学期数学(人教A版2

解:当球内切于正方体时用料最省 此时棱长=直径=5cm
答:至少要用纸150cm2
练习
解析 设球 O 的半径为 r,则圆柱的底面半径为 r, 高为 2r,所以VV12=π43rπ2·r23r=32.
三、课堂小结:
1.圆柱、圆锥、圆台的表面积公式
1).圆柱 2).圆锥
S 2r 2 rl
S r 2 rl
如果圆台的上、下底面半径分别为r和R,母线长为l,你能计算它的
表面积吗?
r O’
RO
圆台的侧面展开图是扇环
x x
r 'O’
rO
xl r x r' l rr' x r'
xl 1 r 1 x r'
x r' l r r'
∵圆台侧面展开图是一个扇环
S侧面积
1 2
2 r( x
l)
1 2
2 r
'
x
r( x l ) r ' x rx rl r ' x
A
B
D
C
A1 D1
B1 C1
变式 球的内接长方体的长、宽、高分别为3、2、 3 ,求此球体的表面积 和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们 中心重合,则长方体对角线与球的直径相等。
内切球问题
例题3 把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸? 分析:用料最省时,球与正方体有什么位置关系? 球内切于正方体
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2) 所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
答:至少要用纸150cm2
练习
解析 设球 O 的半径为 r,则圆柱的底面半径为 r, 高为 2r,所以VV12=π43rπ2·r23r=32.
三、课堂小结:
1.圆柱、圆锥、圆台的表面积公式
1).圆柱 2).圆锥
S 2r 2 rl
S r 2 rl
如果圆台的上、下底面半径分别为r和R,母线长为l,你能计算它的
表面积吗?
r O’
RO
圆台的侧面展开图是扇环
x x
r 'O’
rO
xl r x r' l rr' x r'
xl 1 r 1 x r'
x r' l r r'
∵圆台侧面展开图是一个扇环
S侧面积
1 2
2 r( x
l)
1 2
2 r
'
x
r( x l ) r ' x rx rl r ' x
A
B
D
C
A1 D1
B1 C1
变式 球的内接长方体的长、宽、高分别为3、2、 3 ,求此球体的表面积 和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们 中心重合,则长方体对角线与球的直径相等。
内切球问题
例题3 把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸? 分析:用料最省时,球与正方体有什么位置关系? 球内切于正方体
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2) 所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
《圆柱的表面积练习》PPT课件

④一根长2米、底面直径是4厘米的圆柱形 木料,把它锯成同样长的4段,表面积比原 来增加了多少平方厘米?
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
14
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
人教新课标六年级数学下册
教学目标
• 1.通过练习使同学们进一步理解和掌 握圆柱侧面积和表面积的计算方法, 能正确地计算圆柱的侧面积和表面积。
• 2.培养同学们观察、比较、分析、推 理的能力,并会根据实际问题灵活解 答。
判断:
1. 圆柱侧面展开图只能是长方形或
正方形。
(× )
2. 圆柱体的侧面展开可以得到一个
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A 宽等于圆柱的高。( × )
3. 圆柱体上、下两个底面之间的距
离叫做它的高。
(√ )
填空:
1.把圆柱体的侧面展开, 可能得到一 个( 长方 )形, 也可能得到一个 ( 正方 )形。
2. 把一个圆柱体侧面展开, 可以得到 一个长方形, 这个长方形的长等于圆柱 的( 底面周长 ), 宽等于圆柱的( 高 )。
3. 圆柱两底面之间的( 距离 )叫做它 的高, 它的高有(无数 )条。
4.圆柱的侧面积等于底面的( 周长)乘以 ( 高 )。
5. 一个圆柱的侧面展开是一个正方形,边长 是15.7厘米,这个圆柱的底面直径是
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
14
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
人教新课标六年级数学下册
教学目标
• 1.通过练习使同学们进一步理解和掌 握圆柱侧面积和表面积的计算方法, 能正确地计算圆柱的侧面积和表面积。
• 2.培养同学们观察、比较、分析、推 理的能力,并会根据实际问题灵活解 答。
判断:
1. 圆柱侧面展开图只能是长方形或
正方形。
(× )
2. 圆柱体的侧面展开可以得到一个
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A 宽等于圆柱的高。( × )
3. 圆柱体上、下两个底面之间的距
离叫做它的高。
(√ )
填空:
1.把圆柱体的侧面展开, 可能得到一 个( 长方 )形, 也可能得到一个 ( 正方 )形。
2. 把一个圆柱体侧面展开, 可以得到 一个长方形, 这个长方形的长等于圆柱 的( 底面周长 ), 宽等于圆柱的( 高 )。
3. 圆柱两底面之间的( 距离 )叫做它 的高, 它的高有(无数 )条。
4.圆柱的侧面积等于底面的( 周长)乘以 ( 高 )。
5. 一个圆柱的侧面展开是一个正方形,边长 是15.7厘米,这个圆柱的底面直径是
圆柱的表面积优秀课件ppt
要包装100个圆柱形易拉罐的侧面, 至少共需要多少平方分米的广告
纸?(得数保留整数)
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
一台压路机的滚 筒宽1.2米,直径为 0.8米。如果它滚动 10周,压路的面积 是多少平方米?
A: 6
B: 12
C: 24
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
冬天护林工人给圆柱形 的树干的下端涂防蛀涂 料,那么粉刷树干的面
积是指树的( B ). A.底面积 B.侧面积 C.表面积 D.体积
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
长方形的长=圆柱的底面周长,长方形的宽=圆柱的高。
圆柱的侧面积=底面周长×高
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
做一个笔筒所需塑料面积
加油啊!
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
圆柱在木板上滚过的轨迹是什么形状?
往柱子上涂漆,求 涂漆部分面积。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
纸?(得数保留整数)
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
一台压路机的滚 筒宽1.2米,直径为 0.8米。如果它滚动 10周,压路的面积 是多少平方米?
A: 6
B: 12
C: 24
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
冬天护林工人给圆柱形 的树干的下端涂防蛀涂 料,那么粉刷树干的面
积是指树的( B ). A.底面积 B.侧面积 C.表面积 D.体积
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
长方形的长=圆柱的底面周长,长方形的宽=圆柱的高。
圆柱的侧面积=底面周长×高
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
做一个笔筒所需塑料面积
加油啊!
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
圆柱在木板上滚过的轨迹是什么形状?
往柱子上涂漆,求 涂漆部分面积。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
第三单元圆柱表面积练习课(课件)-六年级下册数学人教版

在一个零件(如图)的表面涂一层防锈材料。这个零件是由Байду номын сангаас
两个圆柱组成的,小圆柱的底面直径是4cm,高是2cm;大圆
柱的底面直径是6cm,高是5cm。这个零件涂防锈材料的面积
是多少平方厘米?
方法一:
小圆柱的表面积 大圆柱的表面积
- 小圆柱的两个 底面积
在一个零件(如图)的表面涂一层防锈材料。这个零件是由 两个圆柱组成的,小圆柱的底面直径是4cm,高是2cm;大圆 柱的底面直径是6cm,高是5cm。这个零件涂防锈材料的面积 是多少平方厘米?
下面是一张长方形纸板,剪下的阴影部分刚好能做成一个圆柱 (接头处忽略不计),做成的圆柱的表面积是多少?
d h C底 =πd
51.4cm
d
S表=2S底 + S侧
r r、h
或d、h
2d + πd =51.4
下面是一张长方形钢板,剪下的阴影部分刚好能做成一个圆 柱形带盖的水桶(接头处忽略不计),这个水桶表面积是多少?
h
d
C底 =πd
20.7dm
圆柱表面积 拓展练习
P 课本 19 4、如下图,上排图中切完后的截面或剪完后展开的
侧面分别是什么形状?请与下排图连一连。
横切
纵切
一根圆柱形状的木料,底面直径是10厘米,高是12厘米。 把这块木料分成相等的两块,原木料的表面积增加了多少?
课本P19
11、一根圆柱形木料的底面半径是0.5m,长是2m。如图所
5cm 12cm
把一个圆柱体木块过底面圆心从上到下劈成两半,表面积增 加64平方厘米。这个圆柱体木块原来的侧面积是多少平方厘米?
一个圆柱体木块,底面半径5cm,沿直径切成两个完全相同 的半圆柱,表面积增加160cm2。原来这个圆柱体木块的表面 积是多少平方厘米?
《圆柱的表面积》PPT教学课件

答:剩下铝板的面积是458.24平方厘米。
4. 李师傅用白铁皮制作直径是1分米、长是1米的烟 囱。制作25节,大约需要白铁皮多少平方米? (接缝处按1厘米计算)
只有1个侧面,没有底面长是1m,宽是1cm的长方形
1分米=0.1米
1厘米=0.01米
1节烟囱需要白铁皮:3.14×0.1×1 + 0.01×1 = 0.324(平方米)
列综合算式: 5×2×3.14×14+3.14×52×2
= 439.6+2×78.5 =596.6(平方厘米) 答:它的表面积是596.6平方厘米。
r=5cm
14cm
返回
1个侧面+1个底面
一个无盖的圆柱形铁皮水桶(如右图)。
做这个水桶至少要用多少平方厘米铁皮?
不考虑水桶接缝处的重叠部分。 侧面积: 30×35×3.14 = 3297(平方厘米) 底面积: 3.14×(30÷2)2 = 706.5(平方厘米) 表面积: 3297+706.5 = 4003.5(平方厘米)
冀教版 数学 六年级 下册
4 圆柱和圆锥
圆柱的表面积
情境导入
探究新知
课堂练习
课堂小结
课后作业
情境导入
圆柱的展开图是什么样子?
返回
圆柱的侧面积加上两个底面的面积就是圆柱的表面积。
怎样求圆柱的表面积?
返回
探究新知
圆柱的表面积公式
S底=πr2
S侧=Ch=πdh=2πrh
圆柱的表面积公式: S表=S侧+2S底=2πrh+2πr2
25节烟囱需要白铁皮:25×0.324 = 8.1(平方米) 答:制作25节烟囱大约需要白铁皮8.1平方米。
变式题
4. 李师傅用白铁皮制作直径是1分米、长是1米的烟 囱。制作25节,大约需要白铁皮多少平方米? (接缝处按1厘米计算)
只有1个侧面,没有底面长是1m,宽是1cm的长方形
1分米=0.1米
1厘米=0.01米
1节烟囱需要白铁皮:3.14×0.1×1 + 0.01×1 = 0.324(平方米)
列综合算式: 5×2×3.14×14+3.14×52×2
= 439.6+2×78.5 =596.6(平方厘米) 答:它的表面积是596.6平方厘米。
r=5cm
14cm
返回
1个侧面+1个底面
一个无盖的圆柱形铁皮水桶(如右图)。
做这个水桶至少要用多少平方厘米铁皮?
不考虑水桶接缝处的重叠部分。 侧面积: 30×35×3.14 = 3297(平方厘米) 底面积: 3.14×(30÷2)2 = 706.5(平方厘米) 表面积: 3297+706.5 = 4003.5(平方厘米)
冀教版 数学 六年级 下册
4 圆柱和圆锥
圆柱的表面积
情境导入
探究新知
课堂练习
课堂小结
课后作业
情境导入
圆柱的展开图是什么样子?
返回
圆柱的侧面积加上两个底面的面积就是圆柱的表面积。
怎样求圆柱的表面积?
返回
探究新知
圆柱的表面积公式
S底=πr2
S侧=Ch=πdh=2πrh
圆柱的表面积公式: S表=S侧+2S底=2πrh+2πr2
25节烟囱需要白铁皮:25×0.324 = 8.1(平方米) 答:制作25节烟囱大约需要白铁皮8.1平方米。
变式题
六年级下册数学《圆柱的表面积》(17张PPT)

圆柱的侧面积
圆柱的侧面积和一个底面积
圆柱的侧面积和两个底面积
学习检测
一、基础训练1、一台压路机的滚筒宽1.2米,直径为0.8米。它滚动1周,压路的面积是多少平方米?2、一个圆柱的底面半径5厘米,高10厘米,它的一个底面积是( )平方厘米,侧面积是( )平方厘米,表面积是( )平方厘米。二、提高练习(选做) 一个圆柱形的无盖铁皮桶,底面直径4分米,高4.5分米。为了防止生锈,要在桶的里外都涂上防锈漆,涂漆的面积是多少平方分米?
课堂总结
我们认识了圆柱的表面积、学习了圆柱表面积的计算方法,希望同学们能灵活运用,解决生活中的实际问题。
同学们再见!
授课老师:
时间:2024年9月1日
2024课件
同学们再见!
授课老师:
时间:2024年9月1日
帽子的侧面积:3.14×20×30=1884(cm2)
帽顶的面积:3.14×(20÷2)2=314(cm2)
需要用的面料:1884+314=2198≈2200(cm2)
答:做这样一顶帽子大约要用2200cm2的面料。
巩固练习
一、下面这些生活中的问题实际求的是圆柱的什么?想一想,选一选。A底面积 B侧面积 C表面积 D一个底面+侧面积1.制作一节通风管需要的铁皮面积。( )2.求圆柱形水池的占地面积。( )3.求做一个无盖的圆柱形塑料水桶,需要的塑料面积。( )4.做一个圆柱形茶叶桶,需要的硬纸板的面积。( )10 Nhomakorabea罐头
S侧=ch = 2×5×3.14×10 =314(平方厘米)答:商标纸的面积是314平方厘米。
5
圆柱的表面积=侧面积+两个底面的面积
S表 =S侧+2S底
S表=S侧+2S底
圆柱的侧面积和一个底面积
圆柱的侧面积和两个底面积
学习检测
一、基础训练1、一台压路机的滚筒宽1.2米,直径为0.8米。它滚动1周,压路的面积是多少平方米?2、一个圆柱的底面半径5厘米,高10厘米,它的一个底面积是( )平方厘米,侧面积是( )平方厘米,表面积是( )平方厘米。二、提高练习(选做) 一个圆柱形的无盖铁皮桶,底面直径4分米,高4.5分米。为了防止生锈,要在桶的里外都涂上防锈漆,涂漆的面积是多少平方分米?
课堂总结
我们认识了圆柱的表面积、学习了圆柱表面积的计算方法,希望同学们能灵活运用,解决生活中的实际问题。
同学们再见!
授课老师:
时间:2024年9月1日
2024课件
同学们再见!
授课老师:
时间:2024年9月1日
帽子的侧面积:3.14×20×30=1884(cm2)
帽顶的面积:3.14×(20÷2)2=314(cm2)
需要用的面料:1884+314=2198≈2200(cm2)
答:做这样一顶帽子大约要用2200cm2的面料。
巩固练习
一、下面这些生活中的问题实际求的是圆柱的什么?想一想,选一选。A底面积 B侧面积 C表面积 D一个底面+侧面积1.制作一节通风管需要的铁皮面积。( )2.求圆柱形水池的占地面积。( )3.求做一个无盖的圆柱形塑料水桶,需要的塑料面积。( )4.做一个圆柱形茶叶桶,需要的硬纸板的面积。( )10 Nhomakorabea罐头
S侧=ch = 2×5×3.14×10 =314(平方厘米)答:商标纸的面积是314平方厘米。
5
圆柱的表面积=侧面积+两个底面的面积
S表 =S侧+2S底
S表=S侧+2S底
人教版六年级数学下册第三单元第4课《圆柱的表面积》整理复习课件

一个圆柱的侧面积是188.4 dm2,底面半径是2 dm。 它的高是多少?
根据3.14×圆柱的底面半径×2×高=圆柱的侧面积
188.4÷(3.14×2×2)=15(dm)
侧面积 ÷ 底面周长 = 高
答:这个圆柱的高是15dm。
一根圆柱形木料的底面半径是0.5m,长是2m。如图所示, 将它截成4段,这些木料的表面积之和比原木料的表面积增 加了多少平方米?
正方形的边长
圆柱的底面周长 =圆柱的高
解:设圆柱的底面直径为d,底面周长为dπ。 直径与高的比 d∶πd =1∶π
答:这个圆柱底面直径与高的比是1∶π。
这节课你们都学会了哪些知识?
圆柱的表面积计算 1.计算方法:
圆柱的表面积=侧面积+两个底面积
2πrh
2×πr2
2.解决问题时要根据实际情况判断。
圆柱表面积的意义 1.填一填。 (1)圆柱的表面积是指圆柱的( 侧面积 )和
求用了多少彩纸,需要用圆 柱的表面积减去上下底面中 间留出的口的面积。
(1)侧面积:3.14×20×30=1884(cm2 ) (2)两个底面的面积:3.14×(20÷2)2 ×2=628(cm2 ) (3)需要用的彩纸:1884+628-78.5×2=2355(cm2 )
答:他用了2355cm2的彩纸。
3 圆柱与圆锥
练习四
说一说:圆柱展开图是什么样的。
用手摸一摸,圆的表面积是哪Fra bibliotek? 圆柱的表面积是指圆柱的侧面积和两个底面积 的面积和。
用字母怎么表示呢?
圆柱的表面积=侧面积+两个底面积
底面是圆形 S底= πr 2
S表=S侧 +2S底
长方形的面积= 长 × 宽
人教版六年级数学下册3.2《圆柱的表面积》课件

小试牛刀 (选题源于教材P22做一做第1题)
求下面各圆柱的侧面积。 (1)底面周长是1.6m,高是0.7m。
1.6×0.7=1.12( m2 ) 答:圆柱的侧面积是1.12m2 。 (2)底面半径是3.2dm,高是5dm。
2×3.14×3.2 ×5=100.48(dm2 ) 答:圆柱的侧面积是100.48dm2。
3 圆柱与圆锥
圆柱的表面积(1)
口头回答下面的问题。
(1)一个圆形花池,直径是5m,周长是多少? (2)长方形的面积怎样计算?
长方形的面积=长×宽。
探究点 1 圆柱的表面积的意义和计算公式
圆柱的表面积指的是什么?
底面
底面的周长 底面
底面
底面的
周长 高
底面
圆柱的表面积=圆柱的侧面积 +两个底面的面积
4.一个圆柱的展开图是一个正方形,求这个圆柱的 底面直径与高的比。(选题源于教材P24第14*题)
底面直径×π=高, 所以底面直径:高=1:π
夯实基础
1.填空。 (1)已知圆柱的底面直径是3 cm,高也是3 cm,把它沿高
展开后得到的图形的长是( 9.42 )cm,宽是( 3 )cm。 (2)把一个底面半径是2 cm,高是5 cm的圆柱沿高展开,
(1)帽子的侧面积:3.14×20×30=884(cm2 ) (2)帽顶的面积:3.14×(20÷2)2=314(cm2 ) (3)需要用的面料:1884+314=198≈2200(cm2 ) 为什么最后的结果取2200,而不取2190呢?
628÷10÷3.14÷2=10(cm) 3.14×102×2+3.14×10×2×(10+15)=2198(cm2)
6.一根圆柱形木头的长是3 m,底面直径是8 cm, 如果将它截成3段,表面积增加了多少平方厘米?
【课件】圆柱、圆锥、圆台、球表面积和体积课件高一下学期数学人教A版(2019)必修第二册

例析
例2 如右图,圆柱的底面直径和高都等于球的直径, 求球与圆
柱的体积之比.
解:(1)设球的半径为R,则圆柱的底面半径
为R,高为2R.
4 3
因为 V球
R ,V 圆柱
R2 2R 2 R3
3
所以 V球 : V圆柱
2
3
问题:球的表面积与圆柱的侧面积之比呢?
R O
练习
题型一:圆柱、圆锥、圆台的表面积
例1.(1)已知圆柱的上、下底面的中心分别为1 ,2 ,过直线1 2 的平面截该圆
)
2.若圆柱的底面圆的直径与圆柱的高相等,则圆柱的侧面展开图是正方形. (
答案:√,×.
辨析2:若圆柱的底面半径为1,母线长为2,则它的侧面积为(
A.2
答案:D.
B.3
C.
D.4
).
)
新知探索
割 圆 术
早在公元三世纪,我国数学家刘徽为推
导圆的面积公式而发明了“倍边法割圆术”.
他用加倍的方式不断增加圆内接正多边形的
∴ = 5,∴ = × (2 + 6) × 5 + × 22 + × 62 = 40 + 4 + 36 = 80.
练习
题型二:圆柱、圆锥、圆台的体积
例2.(1)若一个圆柱与圆锥的高相等,且轴截面面积也相等,则圆柱与圆锥的体积
之比是(
).
A.1
B.1:2
C. 3:2
D.3:4
的夹角为60°,轴截面中的一条对角线垂直于腰,则圆台的体
积为_____.
解:设上、下底面半径,母线长分别为,,.
作1 ⊥ 于点,则1 = 3,∠1 = 60°.
又∠1 = 90°,∴∠1 = 60°,∴ =
圆柱表面积练习PPT课件

3.14×10=31.4(平方米)
CHENLI
10
2、学校食堂要用铁皮做一根横 截面半径是3分米,高是3米的圆 柱形烟囱,至少需要多少平方米 的铁皮? 2×3.14×0.3×3
=6.28×0.3×3
=1.884×3
=5.652(平方米)
CHENLI
11
3、一个底面直径为2分米, 高5分米的圆柱体,它的侧面 积是多少?
计算下现各圆柱的表面积。 (单位:厘米)
CHENLI
4
侧面积:3.14 ×12 ×16 = 602.88 底面积:3.14 ×(12÷2)²× 2=226.08 表面积:602.88+226.08=828.96
CHENLI
5
侧面积:3.14 ×5 ×20 = 314 底面积:3.14 ×(5÷2)²× 2=39.25 表面积:314+39.25=353.25
2×3.14×5 =6.28×5 =31.4(平方分米)
CHENLI
12
CHENLI
13
1、一个圆柱,底面周长是 100厘米,高是25厘米,求它 的侧面积。
100×25=2500(平方厘米)
答:它的侧面积是2500平方厘米。
CHENLI
14
2、一个圆柱,底面直径是2 分米,高是10分米,求它的 表面积。
=37.68(平方米)
答:抹水泥的面积是37.68平方米
CHENLI
16
(1)圆形水池的占地面积; (2)做一节烟囱所需铁皮的面积; (3)做一个无盖水桶所需铁皮的面积; (4)做一个油桶所需铁皮的面积; (5)求易拉罐上商标纸的面积;
(6)在水池的内壁和底面抹水泥,求抹水泥部 分的面积
(7)往大厅的柱子上涂漆,求涂漆部分的面积 ; (8)压路机的滚筒转动一CHE周NLI ,求压路的面积.3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:这个圆柱体的表面积是471平方厘米。
4
5. 一个圆柱体的表面积是1884平方 厘米,底面半径是10厘米,它的高
是多少?
• 先求出底面积,从表面积中减去两个底面积,剩 下的面积是侧面积,由此求出圆柱体的高。
• 底面积=10×10×3.14=314(平方厘米) • 底面周长=(10+10)×3.14=62.8(厘米) • 圆柱侧面积=表面积-底面积×2=1884-
• (6)一个圆柱体的侧面积是37.68平方厘米, 底面半径是3厘米,它的高是多少厘米?
7
• (7)一个圆柱形,侧面展开是一个边长为 62.8厘米的正方形,这个圆柱形的表面积是 多少平方厘米?
• (8) 做5节底面直径是2分米,长8分米的圆 柱形通风管,至少需要多少铁皮?
• (9) 某宾馆大堂有6根圆柱形大柱,高10米, 大柱周长25.12分米,要全部涂上油漆,如 果按每平方米的油漆费为80元计算,需用 多少钱?
圆柱表面积练习题
1. 把一个底面半径6分米,高1米的圆柱切成 3个小圆柱,表面积增加了多少?
切成3段后增加了4个底面积。 S底=πrr=6×6×3.14=113.04(平方分米) 增加的表面积=4S底 =4×113.04=452.16(平方分米)
1
• 2. 工人叔叔把一根高1米的圆柱形木料,沿 与底面平行的方向锯成两段,这时表面积 比原来增加了25.12平方分米,求这根料的 底面半径是多少?
8
• (10) 一个没有盖的圆柱形铁皮水桶,高是24厘米, 底面直径是20厘米,做这个水桶至少要用铁皮多 少平方厘米?(接口处不计,得数保留整百平方 厘米)
• (11) 压路机的滚筒是一个圆柱。它的横截面半径 是0.5米,长是2米,它滚一周能压过多大的路面? 如果它滚100周,压过的路面又有多大?
• (15) 一个无盖的圆柱形铁皮水桶,底面直径是0.4 米,高是0.8米,要在水桶里、外两面都漆防锈漆, 油漆的面积大约是多少平方米?(得数保留一位 小数)
10
3
4. 把一棱长10厘米的正方形木块, 削成一个最大的圆柱体,这个圆柱
体的表面积是多少?
圆柱体的高和底面直径等于正方体棱长10厘 米。
圆柱体侧面积=高×周长=10×10×3.14=314 (平方厘米)
圆柱体底面积=(10÷2)×(10÷2) ×3.14=78.5(平方厘米)
圆柱体表面积=侧面积+底面积×2=314+ 78.5×2=471(平方厘米)
314×2=1256(平方厘米) • 圆柱体高=侧面积÷周长=1256÷62.8=20(厘米)
5
• (1)用一张长2.5米, 宽1.5米的铁皮做一个圆柱 形烟筒, 这个烟筒的侧面积是多少? (接口处忽 略不计)
• (2)一个圆柱形无盖的水桶,底面的直径是60 厘米,高是40厘米,做这样一个水桶,需要 多少平方分米的铁皮?(得数保留整数)
• (3)一个圆柱形水池,底面半径是2米,高是 1.5米,在池内周围和底面抹上水泥,抹水泥 的面积是多少?
6
• (4)一个圆柱形铁皮盒,底面半径是2分米, 高5分米,在这个盒子的侧面帖上商标纸, 需多少平方米的纸?
• (5)一个压路机的滚筒横截面的直径是1米, 长是1.8米,转一周能压路多少平方米?如 果每分钟转8周,半小时能压路多少平方米?
增加的表面积是2个底面积, 圆柱底面积=25.12÷2=12.56(平方分米) 根据S=rrπ 知 rr=S/π=12.56÷3.14=4 r=2(分米) 答:这根料的底面半径是2分米
2
• 3. 一圆柱底面直径是4米,高是6米,沿着 底面直径把圆柱切成两半,求这个圆柱的 表面积增加多少?
【解】 增加两2个以直径和高形成的矩 形。 矩形面积=4×6=24(平方分米) 增加的表面积=矩形面积×2=24×2=48 (平方分米) 答:这个圆柱的表面积增加48平方分 米。
• (12) 一个圆柱,它的高增加1厘米,它的侧面积 就增加50.24平方厘米,这个圆柱的底面半径是多 少厘米?
9
• (13) 一根长2米,底面积半径是4厘米的圆柱形木 段,把它据成同样长的4根圆柱形的木段。表面积 比原来增加了多少平方厘米?
• (14) 学校走廊上有10根圆柱形柱子,每根柱子底 面半径是4分米,高是2.5分米,要油漆这些柱子, 每平方米用油漆0.3千克,共需要油漆多少千克?
4
5. 一个圆柱体的表面积是1884平方 厘米,底面半径是10厘米,它的高
是多少?
• 先求出底面积,从表面积中减去两个底面积,剩 下的面积是侧面积,由此求出圆柱体的高。
• 底面积=10×10×3.14=314(平方厘米) • 底面周长=(10+10)×3.14=62.8(厘米) • 圆柱侧面积=表面积-底面积×2=1884-
• (6)一个圆柱体的侧面积是37.68平方厘米, 底面半径是3厘米,它的高是多少厘米?
7
• (7)一个圆柱形,侧面展开是一个边长为 62.8厘米的正方形,这个圆柱形的表面积是 多少平方厘米?
• (8) 做5节底面直径是2分米,长8分米的圆 柱形通风管,至少需要多少铁皮?
• (9) 某宾馆大堂有6根圆柱形大柱,高10米, 大柱周长25.12分米,要全部涂上油漆,如 果按每平方米的油漆费为80元计算,需用 多少钱?
圆柱表面积练习题
1. 把一个底面半径6分米,高1米的圆柱切成 3个小圆柱,表面积增加了多少?
切成3段后增加了4个底面积。 S底=πrr=6×6×3.14=113.04(平方分米) 增加的表面积=4S底 =4×113.04=452.16(平方分米)
1
• 2. 工人叔叔把一根高1米的圆柱形木料,沿 与底面平行的方向锯成两段,这时表面积 比原来增加了25.12平方分米,求这根料的 底面半径是多少?
8
• (10) 一个没有盖的圆柱形铁皮水桶,高是24厘米, 底面直径是20厘米,做这个水桶至少要用铁皮多 少平方厘米?(接口处不计,得数保留整百平方 厘米)
• (11) 压路机的滚筒是一个圆柱。它的横截面半径 是0.5米,长是2米,它滚一周能压过多大的路面? 如果它滚100周,压过的路面又有多大?
• (15) 一个无盖的圆柱形铁皮水桶,底面直径是0.4 米,高是0.8米,要在水桶里、外两面都漆防锈漆, 油漆的面积大约是多少平方米?(得数保留一位 小数)
10
3
4. 把一棱长10厘米的正方形木块, 削成一个最大的圆柱体,这个圆柱
体的表面积是多少?
圆柱体的高和底面直径等于正方体棱长10厘 米。
圆柱体侧面积=高×周长=10×10×3.14=314 (平方厘米)
圆柱体底面积=(10÷2)×(10÷2) ×3.14=78.5(平方厘米)
圆柱体表面积=侧面积+底面积×2=314+ 78.5×2=471(平方厘米)
314×2=1256(平方厘米) • 圆柱体高=侧面积÷周长=1256÷62.8=20(厘米)
5
• (1)用一张长2.5米, 宽1.5米的铁皮做一个圆柱 形烟筒, 这个烟筒的侧面积是多少? (接口处忽 略不计)
• (2)一个圆柱形无盖的水桶,底面的直径是60 厘米,高是40厘米,做这样一个水桶,需要 多少平方分米的铁皮?(得数保留整数)
• (3)一个圆柱形水池,底面半径是2米,高是 1.5米,在池内周围和底面抹上水泥,抹水泥 的面积是多少?
6
• (4)一个圆柱形铁皮盒,底面半径是2分米, 高5分米,在这个盒子的侧面帖上商标纸, 需多少平方米的纸?
• (5)一个压路机的滚筒横截面的直径是1米, 长是1.8米,转一周能压路多少平方米?如 果每分钟转8周,半小时能压路多少平方米?
增加的表面积是2个底面积, 圆柱底面积=25.12÷2=12.56(平方分米) 根据S=rrπ 知 rr=S/π=12.56÷3.14=4 r=2(分米) 答:这根料的底面半径是2分米
2
• 3. 一圆柱底面直径是4米,高是6米,沿着 底面直径把圆柱切成两半,求这个圆柱的 表面积增加多少?
【解】 增加两2个以直径和高形成的矩 形。 矩形面积=4×6=24(平方分米) 增加的表面积=矩形面积×2=24×2=48 (平方分米) 答:这个圆柱的表面积增加48平方分 米。
• (12) 一个圆柱,它的高增加1厘米,它的侧面积 就增加50.24平方厘米,这个圆柱的底面半径是多 少厘米?
9
• (13) 一根长2米,底面积半径是4厘米的圆柱形木 段,把它据成同样长的4根圆柱形的木段。表面积 比原来增加了多少平方厘米?
• (14) 学校走廊上有10根圆柱形柱子,每根柱子底 面半径是4分米,高是2.5分米,要油漆这些柱子, 每平方米用油漆0.3千克,共需要油漆多少千克?
