时间序列分析作业及答案

合集下载

统计基础知识第五章时间序列分析习题及答案

第五章时间序列分析一、单项选择题1.构成时间数列的两个基本要素是( C )（2012年1月）A.主词和宾词B.变量和次数C.现象所属的时间及其统计指标数值D.时间和次数2．某地区历年出生人口数是一个( B )（2011年10月）A．时期数列 B.时点数列C.分配数列D.平均数数列3.某商场销售洗衣机，2008年共销售6000台，年底库存50台，这两个指标是( C ) （2010年10）A.时期指标B.时点指标C.前者是时期指标，后者是时点指标D.前者是时点指标，后者是时期指标4.累计增长量( A ) （2010年10）A.等于逐期增长量之和B.等于逐期增长量之积C.等于逐期增长量之差D.与逐期增长量没有关系5.某企业银行存款余额4月初为80万元，5月初为150万元，6月初为210万元，7月初为160万元，则该企业第二季度的平均存款余额为（ C ）（2009年10）万元万元万元万元6.下列指标中属于时点指标的是( A ) （2009年10）A.商品库存量B.商品销售量C.平均每人销售额D.商品销售额7.时间数列中，各项指标数值可以相加的是( A ) （2009年10）A.时期数列B.相对数时间数列C.平均数时间数列D.时点数列8.时期数列中各项指标数值（ A ）（2009年1月）A.可以相加B.不可以相加C.绝大部分可以相加D.绝大部分不可以相加10.某校学生人数2005年比2004年增长了8%，2006年比2005年增长了15%，2007年比2006年增长了18%，则2004-2007年学生人数共增长了（ D ）（2008年10月）％+15％+18％％×15％×18％C.（108％+115％+118％）-1 ％×115％×118％-1二、多项选择题1.将不同时期的发展水平加以平均而得到的平均数称为( ABD )（2012年1月）A.序时平均数B.动态平均数C.静态平均数D.平均发展水平E.一般平均数2．定基发展速度和环比发展速度的关系是( BD )（2011年10月）A．相邻两个环比发展速度之商等于相应的定基发展速度B.环比发展速度的连乘积等于定基发展速度C.定基发展速度的连乘积等于环比发展速度D.相邻两个定基发展速度之商等于相应的环比发展速度E.以上都对3.常用的测定与分析长期趋势的方法有( ABC ) （2011年1月）A.时距扩大法B.移动平均法C.最小平方法D.几何平均法E.首末折半法4.时点数列的特点有( BCD ) （2010年10）A.数列中各个指标数值可以相加B.数列中各个指标数值不具有可加性C.指标数值是通过一次登记取得的D.指标数值的大小与时期长短没有直接的联系E.指标数值是通过连续不断的登记取得的5.增长1%的绝对值等于（ AC ）（2010年1）A.增加一个百分点所增加的绝对量B.增加一个百分点所增加的相对量C.前期水平除以100D.后期水平乘以1%E.环比增长量除以100再除以环比发展速度6.计算平均发展速度常用的方法有（ AC ）（2009年10）A.几何平均法(水平法)B.调和平均法C.方程式法(累计法)D.简单算术平均法E.加权算术平均法7.增长速度（ ADE ）（2009年1月）A.等于增长量与基期水平之比B.逐期增长量与报告期水平之比C.累计增长量与前一期水平之比D.等于发展速度-1E.包括环比增长速度和定基增长速度8.序时平均数是（ CE ）（2008年10月）A.反映总体各单位标志值的一般水平B.根据同一时期标志总量和单位总量计算C.说明某一现象的数值在不同时间上的一般水平D.由变量数列计算E.由动态数列计算三、判断题1.职工人数、产量、产值、商品库存额、工资总额指标都属于时点指标。

8章时间序列分析练习题参考答案

A
35.采用几何平均法计算平均发展速度的理由是（）。
A.各年环比发展速度之和等于总速度B.各年环比发展速度之积等于总速度
C.各年环比增长速度之积等于总速度D.各年环比增长速度之和等于总速度
B
36.计算平均发展速度应用几何平均法的目的在于考察（）。
A.最初时期发展水平B.全期发展水平
C.最末时期发展水平D.期中发展水平
B
3.发展速度属于( )
A比例相对数B比较相对数C动态相对数D强度相对数
C
4.计算发展速度的分母是( )
A报告期水平B基期水平C实际水平D计划水平
B
5.某车间月初工人人数资料如下：
月份
1
2
3
4
5
6
7
月初人数(人)
280
284
280
300
302
304
320
则该车间上半年的平均人数约为( )
A 296人B 292人C 295人D 300人
A.0.33倍B.0.50倍C.0.75倍D.2倍
D
16.已知一个数列的环比增长速度分别为3%、5%、8%，则该数列的定基增长速度为（）
A.3%×5%×8%B.103%×105%×108%
C.（3%×5%×8%）＋1D.（103%×105%×108%）－1
D
17.企业生产的某种产品2002年比2001年增长了8%，2003年比2001年增长了12%，则2003年比2002年增长了（）。
时间第一年第二年第三年第四年第五年销售额万元10001100130013501400根据上述资料计算的下列数据正确的有a第二年的环比增长速度二定基增长速度10b第三年的累计增长量二逐期增长量200万元c第四年的定基发展速度为135d第五年增长1绝对值为14万元e第五年增长1绝对值为135万元ace7

第7章时间序列分析习题解答

第七章时间序列分析思考与练习一、选择题1.已知2000-2006年某银行的年末存款余额，要计算各年平均存款余额，该平均数是:（ b ）a. 几何序时平均数；b.“首末折半法”序时平均数；c. 时期数列的平均数；d.时点数列的平均数。

2.某地区粮食增长量1990—1995年为12万吨，1996—2000年也为12万吨。

那么，1990—2000年期间，该地区粮食环比增长速度（ d ）a.逐年上升b.逐年下降c.保持不变d.不能做结论上表资料中，是总量时期数列的有（ d ）a. 1、2、3b. 1、3、4c. 2、4d. 1、34.利用上题资料计算零售额移动平均数（简单，4项移动平均），2001年第二季度移动平均数为（a ）a. 47.5b. 46.5c. 49.5d. 48.4二、判断题1.连续12个月逐期增长量之和等于年距增长量。

2.计算固定资产投资额的年平均发展速度应采用几何平均法。

3.用移动平均法分析企业季度销售额时间序列的长期趋势时，一般应取4项进行移动平均。

4.计算平均发展速度的水平法只适合时点指标时间序列。

5.某公司连续四个季度销售收入增长率分别为9%、12%、20%和18%，其125126环比增长速度为0.14%。

正确答案：（1）错；（2）错；（3）对；（4）错；（5）错。

三、计算题：1．某企业2000年8月几次员工数变动登记如下表：试计算该企业8月份平均员工数。

解：该题是现象发生变动时登记一次的时点序列求序时平均数，假设员工人数用y 来表示，则： 1122n 12y y ...y y=...nnf f f f f f ++++++121010124051300151270311260()⨯+⨯+⨯+=≈人该企业8月份平均员工数为1260人。

2. 某地区“十五”期间年末居民存款余额如下表：试计算该地区“十五”期间居民年平均存款余额。

解：居民存款余额为时点序列，本题是间隔相等的时点序列，运用“首末折半法”计算序时平均数。

人大版统计学习题加答案第七章时间序列分析

第七章时间序列分析一、填空1、下表为两个地区的财政收入数据:则A地区财政收入的增长速度是,B地区财政收入的增长速度是,A 地区财政收入的增长1%的绝对值为,B地区财政收入的增长1%的绝对值为。

2、已知环比增长速度为7.1%、3.4%、3.6%、5.3%,则定基增长速度是。

3、年劳动生产率r(千元和职工工资y (元之间的回归方程为110x=,这意味着120y+年劳动生产率每提高1千元时,职工工资平均。

4、拉氏价格或销售量指数的同度量因素都是选期,而派许指数的同度量因素则选期。

5、动态数列的变动一般可以分解为四部分,即趋势变动、变动、变动和不规则变动。

二、选择题1.反映了经济现象在一个较长时间内的发展方向,它可以在一个相当长的时间内表现为一种近似直线的持续向上或持续向下或平稳的趋势。

A长期趋势因素B季节变动因素C周期变动因素D不规则变动因素2.是经济现象受季节变动影响所形成的一种长度和幅度固定的周期波动。

A长期趋势因素B季节变动因素C周期变动因素D不规则变动因素3、时间序列在一年内重复出现的周期性波动称为(A、趋势B、季节性C、周期性D、随机性4、在使用指数平滑法进行预测时,如果时间序列比较平稳,则平滑系数α的取值(A、应该小些B、应该大些C、等于0D、等于15、某银行投资额2004年比2003年增长了10%,2005年比2003年增长了15%,2005年比2004年增长了(A、15%÷10%B、115%÷110%C、(110%×115%+1D、(115%÷110%-1三、判断1、若1998年的产值比1997年上涨10%,1999年比1998年下降10%,则1999年的产值比1997年的产值低。

(2、若三期的环比增长速度分别为9%、8%、10%,则三期的平均增长速度为9% (。

3、去年物价下降10%,今年物价上涨10%,今年的1元钱比前年更值钱。

(。

4、若平均发展速度大于100%,则环比发展速度也大于100%。

时间序列分析试卷及答案3套

时间序列分析试卷及答案3套时间序列分析试卷1⼀、填空题（每⼩题2分，共计20分）1. ARMA(p, q)模型_________________________________，其中模型参数为____________________。

2. 设时间序列{}t X ，则其⼀阶差分为_________________________。

3. 设ARMA (2, 1)：1210.50.40.3t t t t t X X X εε---=++-则所对应的特征⽅程为_______________________。

4. 对于⼀阶⾃回归模型AR(1): 110t t t X X φε-=+＋，其特征根为_________，平稳域是_______________________。

5. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-，当a 满⾜_________时，模型平稳。

6. 对于⼀阶⾃回归模型MA(1):10.3t t t X εε-=-，其⾃相关函数为______________________。

7. 对于⼆阶⾃回归模型AR(2):120.50.2t t t t X X X ε--=++则模型所满⾜的Yule-Walker ⽅程是______________________。

8. 设时间序列{}t X 为来⾃ARMA(p,q)模型：1111t t p t p t t q t q X X X φφεθεθε----=++++++L L则预测⽅差为___________________。

9. 对于时间序列{}t X ，如果___________________，则()~t X I d 。

10. 设时间序列{}t X 为来⾃GARCH(p ，q)模型，则其模型结构可写为_____________。

⼆、（10分）设时间序列{}t X 来⾃()2,1ARMA 过程，满⾜()()210.510.4ttB B X B ε-+=+,其中{}t ε是⽩噪声序列，并且()()2t t 0,E Var εεσ==。

时间序列分析作业及答案

年份 1993 甲厂产量 3500 乙厂产量 4800 1994 3550 4750 1995 3720 4950 1996 3880 5200 1997 3800 5250 1998 3900 5360 1999 4000 5500
（3） 5500 4000 (1 x ) 5 5500 x 106.58% 甲厂平均发展速度需 106.58% 4000
a1 a2 a3 a4 a5 1 解 : x x 1 x 1 5 a0 a1 a2 a3 a 4
n
5 (1 5.2%) (1 4.8%) (1 3.8%) (1 3.5%) (1 2.4%) 1
平均每年的降低率： x 96.05% 1 3.95%
lg1.375 0.13830 n 14.32年 15年后可达到乙厂水平 lg1.0225 0.00966
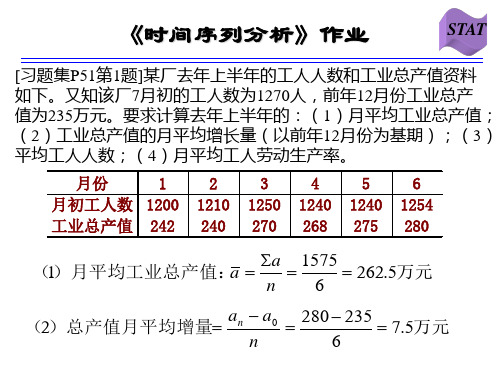
《时间序列分析》作业
STAT
[习题集P53第8题]甲、乙两厂各年产量资料如下。要求：（1）分别计算两厂的平均发展速度；（2）按现在甲厂平均发展速度，要几年才能达到乙厂1999年的水平？（3）如要求甲厂从1999年起，在五年内达到乙厂1999年的水平，则甲厂的平均发展速度必须达到多少？
a1990 25(1 4%)5 30.42 a2000 30.42(1 4.5%)10 47.24
a2000 25(1 4%)5 (1 4.5%)10 47.24 （万吨）
（2）已知：a2000 3 25 75 75 25(1 4%)5 (1 x )10
5
《时间序列分析》作业
STAT
[习题集P54第10题]某地区1995~2001年财政收入资料如下（单位：亿元）。根据该资料：（1）用最小平方法的简捷式配合直线趋势方程；（2）根据直线趋势方程预测2002年的财政收入。

应用时间序列分析习题标准答案

应⽤时间序列分析习题标准答案第⼆章习题答案2.1（1）⾮平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本⾃相关图2.2（1）⾮平稳，时序图如下（2）-（3）样本⾃相关系数及⾃相关图如下：典型的同时具有周期和趋势序列的样本⾃相关图2.3（1）⾃相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）⽩噪声序列2.4，序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。

显著性⽔平=0.05不能视为纯随机序列。

2.5（1）时序图与样本⾃相关图如下（2）⾮平稳（3）⾮纯随机 2.6（1）平稳，⾮纯随机序列（拟合模型参考：ARMA(1,2)）（2）差分序列平稳，⾮纯随机第三章习题答案3.1 解：1()0.7()()t t t E x E x E ε-=?+0)()7.01(=-t x E 0)(=t x E t t x ε=-）B 7.01(t t t B B B x εε)7.07.01()7.01(221 +++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ3.2 解：对于AR （2）模型：=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ解得：==15/115/721φφ3.3 解：根据该AR(2)模型的形式，易得：0)(=t x E原模型可变为：t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ??=-====015.06957.033222111φφφρφ 3.4 解：原模型可变形为：t t x cB B ε=--)1(2由其平稳域判别条件知：当1||2<φ，112<+φφ且112<-φφ时，模型平稳。

人大版应用时间序列分析(第5版)习题答案

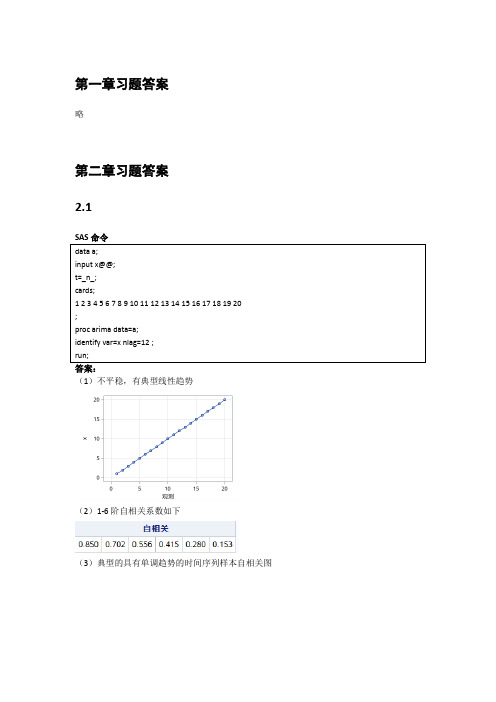
第一章习题答案略第二章习题答案2.1答案：（1）不平稳，有典型线性趋势（2）1-6阶自相关系数如下（3）典型的具有单调趋势的时间序列样本自相关图2.2答案：（1）不平稳（2）延迟1-24阶自相关系数（3）自相关图呈现典型的长期趋势与周期并存的特征2.3答案：（1）1-24阶自相关系数（2）平稳序列（3）非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。

由于延迟1-12阶Q统计量的P值均显著大于0.05，所以该序列为纯随机序列。

2.5答案（1）绘制时序图与自相关图（2）序列时序图显示出典型的周期特征，该序列非平稳（3）该序列为非白噪声序列2.6答案（1）如果是进行平稳性图识别，该序列自相关图呈现一定的趋势序列特征，可以视为非平稳非白噪声序列。

如果通过adf检验进行序列平稳性识别，该序列带漂移项的0阶滞后P值小于0.05，可以视为平稳非白噪声序列（2）差分后序列为平稳非白噪声序列2.7答案（1）时序图和自相关图显示该序列有趋势特征，所以图识别为非平稳序列。

（2）单位根检验显示带漂移项0阶延迟的P值小于0.05，所以基于adf检验可以认为该序列平稳（3）如果使用adf检验结果，认为该序列平稳，则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳，那么一阶差分后序列为平稳非白噪声序列2.8答案（1）时序图和自相关图都显示典型的趋势序列特征（2）单位根检验显示该序列可以认为是平稳序列（带漂移项一阶滞后P值小于0.05）（3）一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--（） 221112() 1.96110.7t Var x φ===--（） 22213=0.70.49ρφ==（）12122221110.490.7=0110.71ρρρφρρ-==-（4） 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有：,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=（）1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=（） 1112223340.70.15=0φρφφφ====-（）3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩（）（）模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩（） 3.5证明:该序列的特征方程为：320c c λλλ--+=，解该特征方程得三个特征根：11λ=，2λ=3λ=无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。

时间序列分析试题

第九章时间序列分析一、单项选择题1、乘法模型是分析时间序列最常用的理论模型。

这种模型将时间序列按构成分解为（）等四种成分，各种成分之间( )，要测定某种成分的变动，只须从原时间序列中（）。

A. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；除去其他影响成分的变动D.长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；除去其他影响成分的变动答案：C2、加法模型是分析时间序列的一种理论模型。

这种模型将时间序列按构成分解为（）等四种成分，各种成分之间( )，要测定某种成分的变动，只须从原时间序列中（）。

A. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动；保持着相互依存的关系；除去其他影响成分的变动D.. 长期趋势、季节变动、循环波动和不规则波动；缺少相互作用的影响力量；除去其他影响成分的变动答案：B3、利用最小二乘法求解趋势方程最基本的数学要求是（）。

A.∑=-任意值2)ˆ(t Y Y B. ∑=-min )ˆ(2t Y Y C. ∑=-max )ˆ(2t Y Y D. 0)ˆ(2∑=-t Y Y 答案：B4、从下列趋势方程t Y t86.0125ˆ-=可以得出（）。

A. 时间每增加一个单位，Y 增加0.86个单位B. 时间每增加一个单位，Y 减少0.86个单位C. 时间每增加一个单位，Y 平均增加0.86个单位D. 时间每增加一个单位，Y 平均减少0.86个单位答案：D.5、时间序列中的发展水平（）。

统计学习题答案第9章时间序列分析

第9章时间序列分析——练习题●1. 某汽车制造厂2003年产量为30万辆。

（1）若规定2004—2006年年递增率不低于6%，其后年递增率不低于5%，2008年该厂汽车产量将达到多少？（2）若规定2013年汽车产量在2003年的基础上翻一番，而2004年的增长速度可望达到7.8%，问以后9年应以怎样的速度增长才能达到预定目标？（3）若规定2013年汽车产量在2003年的基础上翻一番，并要求每年保持7.4%的增长速度，问能提前多少时间达到预定目标？解：设i 年的环比发展水平为x i ，则由已知得：x 2003＝30，（1）又知：320042005200620032004200516%x x x x x x ≥+（），2200720082006200715%x x x x ≥+（），求x 2008由上得32200820072008200320032007(16%)(15%)x x x x x x =≥++ 即为3220081.061.0530x ≥，从而2008年该厂汽车产量将达到得 x 2008≥30× 31.06×21.05= 30×1.3131 = 39.393（万辆）从而按假定计算，2008年该厂汽车产量将达到39.393万辆以上。

（2）规定201320032x x ＝，20042003x x ＝1+7.8％由上得＝107.11%==可知，2004年以后9年应以7.11％的速度增长，才能达到2013年汽车产量在2003年的基础上翻一番的目标。

（3）设：按每年7.4%的增长速度n 年可翻一番，则有 201320031.0742na a == 所以 1.074log 20.30103log 29.70939log1.0740.031004n ====（年）可知，按每年保持7.4%的增长速度，约9.71年汽车产量可达到在2003年基础上翻一番的预定目标。

原规定翻一番的时间从2003年到2013年为10年，故按每年保持7.4%的增长速度，能提前0.29年即3个月另14天达到翻一番的预定目标。

(完整word版)时间序列分析基于R__习题答案及解析

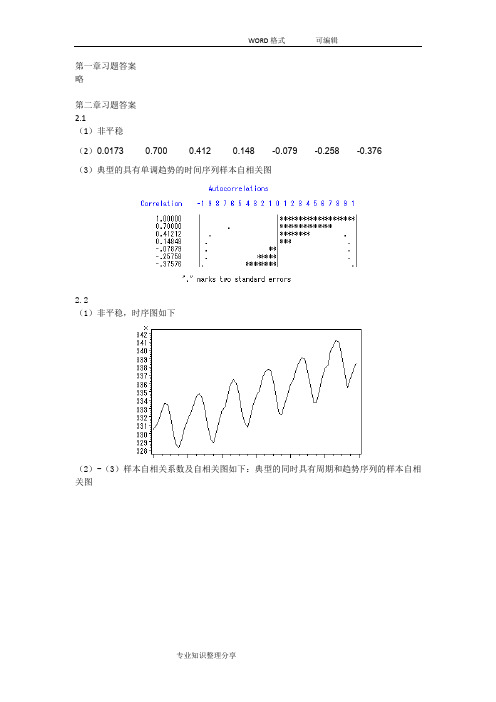
第一章习题答案略第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1）自相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）白噪声序列2.4，序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。

显著性水平=0.05不能视为纯随机序列。

2.5（1）时序图与样本自相关图如下（2）非平稳（3）非纯随机 2.6（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)）（2）差分序列平稳，非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为：32--c 0c λλλ+=，解该特征方程得三个特征根：11λ=，2c λ=3c λ=-无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。

时间序列分析试卷及答案

时间序列分析试卷及答案时间序列分析试卷1一、填空题（每小题2分, 共计20分）1.ARMA(p,q)模型是一种常用的时间序列模型, 其中模型参数为p和q。

2.设时间序列{Xt}, 则其一阶差分为Xt-Xt-1.3.设ARMA (2.1): Xt=0.5Xt-1+0.4Xt-2+εt-0.3εt-1, 则所对应的特征方程为1-0.5B-0.4B^2+0.3B。

4.对于一阶自回归模型AR(1):Xt=10+φXt-1+εt, 其特征根为φ, 平稳域是|φ|<1.5.设ARMA(2.1):Xt=0.5Xt-1+aXt-2+εt-0.1εt-1, 当a满足|a|<1时, 模型平稳。

6.对于一阶自回归模型Xt=φXt-1+εt, 其平稳条件是|φ|<1.7.对于二阶自回归模型AR(2):MA(1):Xt=εt-0.3εt-1, 其自相关函数为Xt=0.5Xt-1+0.2Xt-2+εt, 则模型所满足的XXX-Walker方程是ρ1-0.5ρ2=0.2, ρ2-0.5ρ1=1.8.设时间序列{Xt}为来自ARMA(p,q)模型: Xt=φ1Xt-1+。

+φpXt-p+εt+θ1εt-1+。

+θqεt-q, 则预测方差为σ^2(1+θ1^2+。

+θq^2)。

9.对于时间序列{Xt}, 如果它的差分序列{ΔXt}是平稳的, 则Xt~I(d)。

10.设时间序列{Xt}为来自GARCH(p,q)模型, 则其模型结构可写为σt^2=α0+α1εt-1^2+。

+αpεt-p^2+β1σt-1^2+。

+βqσt-q^2.二、（10分）设时间序列{Xt}来自ARMA(2,1)过程, 满足(1-B+0.5B^2)Xt=(1+0.4B)εt, 其中{εt}是白噪声序列, 并且E(εt)=0, Var(εt)=σ^2.1）判断ARMA(2,1)模型的平稳性。

根据特征方程1-φ1B-φ2B^2, 求得其根为0.5±0.5i, 因此模型的平稳条件是|φ1-0.5i|<1和|φ1+0.5i|<1, 即-1<φ1<1.因为0.5i不在实轴上, 所以模型不是严平稳的, 但是是宽平稳的。

8章时间序列分析练习题参考答案

8章时间序列分析练习题参考答案第八章时间数列分析一、单项选择题1.时间序列与变量数列()A都是根据时间顺序排列的B都是根据变量值大小排列的C前者是根据时间顺序排列的，后者是根据变量值大小排列的D前者是根据变量值大小排列的，后者是根据时间顺序排列的C2.时间序列中，数值大小与时间长短有直接关系的是()A平均数时间序列B时期序列C时点序列D相对数时间序列B3.发展速度属于()A比例相对数B比较相对数C动态相对数D强度相对数C4.计算发展速度的分母是()A报告期水平B基期水平C实际水平D计划水平B则该车间上半年的平均人数约为()A296人B292人C295人D300人C6.某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为()A150万人B150．2万人C150．1万人D无法确定C7.由一个9项的时间序列可以计算的环比发展速度()A有8个B有9个C有10个D有7个A8.采用几何平均法计算平均发展速度的依据是()A各年环比发展速度之积等于总速度B各年环比发展速度之和等于总速度C各年环比增长速度之积等于总速度D各年环比增长速度之和等于总速度A9.某企业的科技投入，2022年比2005年增长了58．6％，则该企业2006—2022年间科技投入的平均发展速度为()A5%6.58B5%6.158C6%6.58D6%6.158B10.根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是()A简单平均法B几何平均法C加权序时平均法D首末折半法D11.在测定长期趋势的方法中，可以形成数学模型的是()A时距扩大法B移动平均法C最小平方法D季节指数法12.动态数列中，每个指标数值相加有意义的是（）。

A.时期数列B.时点数列C.相对数数列D.平均数数列A13.按几何平均法计算的平均发展速度侧重于考察现象的（）A.期末发展水平B.期初发展水平C.中间各项发展水平D.整个时期各发展水平的总和A14.累计增长量与其相应的各逐期增长量的关系表现为（）A.累计增长量等于相应各逐期增长量之和B.累计增长量等于相应各逐期增长量之差C.累计增长量等于相应各逐期增长量之积D.累计增长量等于相应各逐期增长量之商A15.已知某地区2022年的粮食产量比2000年增长了1倍，比2005年增长了0.5倍，那么2005年粮食产量比2000年增长了（）。

时间序列分析试卷及答案

时间序列分析试卷1一、填空题（每小题2分，共计20分）1. ARMA(p, q)模型_________________________________，其中模型参数为____________________。

2. 设时间序列{}t X ，则其一阶差分为_________________________。

3. 设ARMA (2, 1)：1210.50.40.3t t t t t X X X εε---=++-则所对应的特征方程为_______________________。

4.—5.对于一阶自回归模型AR(1): 110t t t X X φε-=+＋，其特征根为_________，平稳域是_______________________。

6. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-，当a 满足_________时，模型平稳。

7. 对于一阶自回归模型MA(1):10.3t t t X εε-=-，其自相关函数为______________________。

8. 对于二阶自回归模型AR(2):120.50.2t t t t X X X ε--=++则模型所满足的Yule-Walker 方程是______________________。

9. 设时间序列{}t X 为来自ARMA(p,q)模型：1111t t p t p t t q t q X X X φφεθεθε----=++++++则预测方差为___________________。

10. 对于时间序列{}t X ，如果___________________，则()~t X I d 。

11. 设时间序列{}t X 为来自GARCH(p ，q)模型，则其模型结构可写为_____________。

二、（10分）设时间序列{}t X 来自()2,1ARMA 过程，满足()()210.510.4ttB B X B ε-+=+,其中{}t ε是白噪声序列，并且()()2t t 0,E Var εεσ==。

时间序列分析作业及答案

统计基础知识第五章时间序列分析习题及答案

8章 时间序列分析练习题参考答案

第7章时间序列分析习题解答

人大版统计学 习题加答案第七章 时间序列分析

时间序列分析试卷及答案3套

时间序列分析作业及答案

应用时间序列分析习题标准答案

人大版应用时间序列分析(第5版)习题答案

时间序列分析试题

统计学习题答案 第9章 时间序列分析

(完整word版)时间序列分析基于R__习题答案及解析

时间序列分析试卷及答案

8章时间序列分析练习题参考答案

时间序列分析试卷及答案

8章时间序列分析练习题参考答案

人大版统计学习题加答案第七章时间序列分析

统计学习题答案第9章时间序列分析