第三章 流体静力学
第三章 流体力学

完全不可压缩的无粘滞流体称为理想流体。
液体不易被压缩,而气体的可压缩性大。但当气体可自由流 动时,微小的压强差即可使气体快速流动,从而使气体各部 分的密度差可以忽略不计。
流体内各部分间实际存在着内摩擦力,它阻碍着流体各部分 间的相对运动,称为粘滞性。但对于很“稀”的流体,可近 似看作是无粘滞的。
4l
dQ=vdS
流量
R
Q R4 ( P1 P2 )
8l
泊肃叶定律推导(略)
流速分布: r
r
v P1 P2 ( R2 r 2 )
4l
各流层流速沿径向呈抛 物线分布
v 管轴中心处,流速最大
vmax
P1 P2
4l
R2
管壁处,流速最小 vmin 0
v
平均速度 v P1 P2 R2
由伯努利方程:
p0
gh
p0
1 2
v2
由上式求得:
v 2 gh
p0
A h
B p0 v
习例题题5-1:1 直径为0.10m,高为0.20m的圆筒形容器底部有1cm2的小 孔。水流入容器内的流量为1.4×10-4m3/s 。求:容器内水面能
上升多高?
D
由伯努利方程: v 2 gh
h 当水面升至最高时: QV v S S 2 ghm
若1 < 2 , 小球(气泡)上浮
1 2
V
v
2 1
gh2V
gh1V
即:
p1
1 2
v
2 1
gh1
流体力学第三章习题

第三章 流体动力学基础3-1 已知速度场为k z x j y x i y x u)()()(2-+-++= (m/s),求(2,3,1)点的速度和加速度。
已已知知::z x u y x u y x u -=-=+=z y x )(2,, 解析:(1) (2,3,1)点的速度为m/s 1m/s 1m/s 10)(2z y x =-=-=-==+=z x u y x u y x u ,, s /m 10.101)1(102222z 2y 2x =+-+=++=u u u u (2) (2,3,1)点的加速度为2x z x y x x x x m/s 1832262602)(2)(20=⨯+⨯=+=+⨯-+⨯++=∂∂+∂∂+∂∂+∂∂=y x y x y x zuu y u u x u u u a τ2y zy yy xy y m/s 1133230)1()(1)(20=⨯+=+=+-⨯-+⨯++=∂∂+∂∂+∂∂+∂∂=y x y x y x zu u yu u xu u u a τ2z z z y z x z z m/s 913222)1()(01)(20=+⨯+=++=-⨯-++⨯++=∂∂+∂∂+∂∂+∂∂=z y x z x y x zu u y u u x u u u a τ22222z 2y 2x s /m 93.2291118=++=++=a a a a3-2 已知速度场为k z y j y i x u )34()(2)3(2-+-++=ττ (m/s),求τ=2秒时,位于(2,2,1)点的速度和加速度。
已已知知::z y u y u x u )34()(23z 2y x -=-=+=,,ττ解析:(1) τ=2秒、位于(2,2,1)点的速度为m/s 5)34(m/s 4)(2m/s 83z 2y x =-=-=-==+=z y u y u x u ,,ττ s /m 25.105)4(82222z 2y 2x =+-+=++=u u u u (2) τ=2秒、位于(2,2,1)点的加速度为2x z x y x x x x m/s 251)223(31)3(3003)3(1=++⨯⨯=++=++⨯++=∂∂+∂∂+∂∂+∂∂=τττx x zuu y u u x u u u a2222y zy yy xy y m/s 342)22(282)(80)4()(202=+-⨯⨯=+-=+-⨯-++=∂∂+∂∂+∂∂+∂∂=τττy y y y zu u yu u xu u u a2222222z z z y z x z z m/s 91)324()22(18)34()(8)34(4)(200=⨯-⨯+-⨯⨯=-+-=-+⨯-++=∂∂+∂∂+∂∂+∂∂=z y y z zy z y zuu y u u x u u u a τττ22222z 2y 2x s /m 15.4393425=++=++=a a a a3-3 已知二维流场的速度分布为j x y i x y uττ)96()64(-+-= (m/s)。
第三章流体静力学

作用在平面上总压力的计算方法有两种: 解析法
图解法
第二十六页,共八十九页。
1.平面总压力大小
o
设有一与水平面成α夹角的倾斜平面 ab,其面积为A,左侧受水压力, 水面大气压强为p0,在平板表面所 在的平面上建立坐标,原点o取在 平板表面与液面的交线上,ox轴与
hD hC yb
整理 p2p1gh
液体静力学基本方程式为 pp0 gh
第八页,共八十九页。
二.流体静力学基本方程的意义
1.A点的压强
p p 0g h p 0g (z 0 z )
整理
p
g
z
p0
g
z0
常数
意义:
Z——单位重量液体的位置势能(简称比位能);
——p 静止液体中单位质量液体的压力能(简称比压能)
g
,比位能与比压能之和称为总比能。
3.运动流体是理想流体时,不会产生切应力,所以理想流体
动压强呈静水压强分布特性,即
第七页,共八十九页。
第二节 重力场中流体的平衡
一.流体静压强的基本方程
静止液体所受的力除了液体重力外 ,还有液面上的压力和固体壁面作 用在液体上的压力,其受力情况如 图所示。
1.受力平衡方程
p 2 A p 1 A g l A co 0 s
D
sin y2dA sinyc AyD
式中 y2dA 为受压面对ox轴的惯性矩 I X
所以
yD
Ix ycA
第三十二页,共八十九页。
根据平行移轴定理:
I X IC yC2 A
∴
yD
yc
Ic ycA
ohD hC h源自αa yyb
流体力学_第三章_伯努利方程及动量方程
23
第三节 恒定总流的伯努利方程
例 用直径d=100mm的水管从水箱引水,水管水面与
管道出口断面中心高差H=4m,水位保持恒定,水头 损失hw=3m水柱,试求水管流量,并作出水头线 解:以0-0为基准面,列1-1、2-2断面的伯努利方程
第三节 恒定总流的伯努利方程
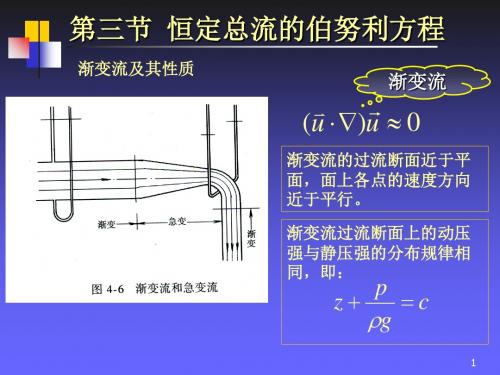
渐变流及其性质
渐变流
(u )u 0
渐变流的过流断面近于平 面,面上各点的速度方向 近于平行。 渐变流过流断面上的动压 强与静压强的分布规律相 同,即:
p z c g
1
第三节 恒定总流的伯努利方程
大小的变化 流速的变化 方向的变化
出现直线惯性力 压强沿流向变化
微小圆柱体的力平衡
p1dA ldA cos p2 dA l cos Z1 Z 2 p1 (Z1 Z 2 ) p2
Z1 p1 Z2 p2
4
第三节 恒定总流的伯努利方程
Z1 p1
Z2
p2
均匀流过流断面上压强 分布服从水静力学规 律
40
2
,
2
第三节 恒定总流的伯努利方程
( a )( z2 z1 ) ( a )( z2 z1 ) ( a )
单位体积气体所受有效浮力
v1 2 gh d1 1 d 2
4
4
2 1
2 1
30
第三节 恒定总流的伯努利方程
Q v1
4
d
2 1
4
d
2 1
2 gh d1 d 1 2
流体力学基础-第三章-一维流体动力学基础

1Q1dt 2Q2dt
1. 微小流束连续性方程
1Q1 2Q2 11dA1 22dA2
对不可压缩流体:
1 2 , Q1 Q2 1dA1 2dA2
1. 微小流束连续性方程 推而广之,在全部流动的各个断面上:
Q1 Q2 ~ Q
拉格朗日法(Lagrange method)—“跟踪”法
拉格朗日法是将流场中每一流体质点作为研究对象, 研究每一个流体质点在运动过程中的位置、速度、加 速度及密度、重度、压强等物理量随时间的变化规律。 然后将所有质点的这些资料综合起来,便得到了整 个流体的运动规律。即将整个流体的运动看作许多流 体质点运动的总和。
d 2 4A d 4R d x
非圆形截面管道的当量直径 x
D 4A 4R x
R
关于湿周和水力半径的概念在非圆截面管道的水力计算中常常用到。
五、一维流动模型
一维流动: 流动参数是一个坐标的函数; 二维流动: 流动参数是两个坐标的函数; 三维流动: 流动参数是三个坐标的函数。
二维流动→一维流动
(1)(a,b,c)=const ,t 为变数,可以 得出某个指定质点在任意时刻所处的位置。 (2)(a,b,c)为变数,t =const,可以得 出某一瞬间不同质点在空间的分布情况。
流体质点速度为: x a,b,c,t
流体质点加速度为:
v x x a,b,c,t a x t t 2 v y 2 y a,b,c,t a y 2 t t vz 2 z a,b,c,t a z t 2 t
动方向的横断面, 如图中的 1-1,2-2 断面。又称为有效 截面,在流束中与各流线相垂直,在每一个微元流束的过 水断面上,各点的速度可认为是相同的。
第三章 流体的运动(幻)

二、 稳定流动
研究流体运动通常有两种方法: 拉格朗日法——以流体的各个质元为 研究对象,根据牛顿定律研究每个质 元的运动状态随时间的变化。
5
欧拉法——研究各个时刻在流体流经过 的空间每一个点上流体质元的运动速度 的分布。
1、 稳定流动
流体在流动过程中的任一时刻,流体所占 据的空间中的每一个点都具有一定的流速, 其函数表达式为υ(x,y,z,t)。
Sυ是单位时间内通过任一截面S的
流体体积,常称为体积流量。
所以上式又称体积流量守恒定律。
13
对于不可压缩的流体来说,不仅质 量流量守恒,体积流量也是守恒的。 体积流量又可简称为流量,用Q来表示 Q=Sυ Q —— 指单位时间内通过流管中任一截 面的流体体积,其单位为(m3·-1)。 s
四、血流速度分布
1 1 2 2 p1 1 gh P2 2 2 2
则液体从小孔处流出的速度 为:
2 2 gh
与其从高度为h处自由下落时的速度 相等。上式就称为“托里折利公式”。
33
第三节 粘性流体的流动 一、 层流和湍流
粘性——实际流体在流动过程中总 是具有内摩擦力,表现出粘滞性, 简称粘性。因而它在流动过程中需 要克服内摩擦力作功而消耗能量。 粘性流体在运动时主要具有层流、湍 流和过渡流动三种运动形态。
2 gh
30
3、体位对血压的影响
若流体在等截面管中流动,若 其流速不变,由 伯努利方程得
P gh1 P2 gh2 1
P +ρgh = 常量
结论:高处的压强较小,而低处的 压强则较大。
31
压强与高度间的关系,可用来解释体 位因素对血压的影响。
32
第三章流体静力学(流体的平衡)

1.流体的平衡:绝对平衡、相对平衡 2.流体平衡时的压强 3.流体平衡的条件 3.1.平衡的微分方程 ∂ p dx ∂ p dx −∂ p dydz − p dydz = dxdydz ∂x 2 ∂x 2 ∂x 表面力: −∇ p dxdydz d 体积力: f b =∇ p 绝对平衡方程: f x 方向表面力: p −
∫ gy sin dA= g sin ∫ y dA= g y c sin A= P c A
A A
设压力中心坐标为
x D , y D = x C f , y C e ,其中 f 和 e 称为纵向和横向偏心矩。
则总合力对形心坐标轴的力矩:
F e =∫ dF = g sin ∫ y dA F f =∫ dF = g sin ∫ y dA∇ p d r =0
d 考虑到绝对平衡方程,得出等压面的微分方程: f b r = 0 ,即在等压面上体力处处与等压面 垂直。
3.3.流体平衡的必要条件
b =∇× 由绝对平衡方程得 ∇× f 1 −1 ∇ p = 2 ∇ ×∇ p
−1 ∇ p⋅∇ ×∇ p =0 3 ⋅∇ × f =0 流体平衡的必要条件 f b b b⋅∇ × f b = 于是 f
均质流体 =constant
≡0 ∇× f b
−∇ =
1 ∇p
=
−p
非均质流体:正压流体 = p ,如等温或绝热气体 定义压力函数 P p : ∇ P =
=∇ P 由绝对平衡方程得, f b 4.流体静力学基本方程(静力学规律)
由 P =− gz C 得
∇p p ≡0 ,故 f 有势,势函数 =− P p ∇× f b b
液压传动第三章 流体力学基础

1、理想流体和恒定流动
理想流体:既无粘性,又无压缩性的假想液体。
实际流体:有粘性,又有压缩性的液体。
恒定流动:液体在流动时,通过空间某一点的压力、速度和密度等运
动参数只随位置变化,与时 间无关。
非恒定流:液体在流动时,通过空间某一点的压力、速度和密度等
运动参数至少有一个是随时 间变化的。
2、流线 流管、流束、通流截面
dqdt
u22 2
dqdt
u12 2
势能:ΔEP gdqh2dt gdqh1dt
外力做的功=能量变化:
W ΔE ΔEK ΔEP
p1
g
u12 2g
h1
p2
g
u22 2g
h2
1.理想流体的能量方程
p1
g
u12 2g
h1
p2
g
u22 2g
h2
2、实际流体伯努利方程
实际流体:有粘性、可压缩、非恒定流动 速度修正:动能修正系数
正确设计和使用液压泵站。 液压系统各元部件的连接处要密封可靠,严防
空气侵入。 采用抗腐蚀能力强的金属材料,提高零件的机
械强度,减小零件表面粗糙度值。
第六节 液 压 冲 击
一、管内液流速度突变引起的液压冲击
有一液位恒定并能保持 液面压力不变的容器如 图3-40所示。
二、运动部件制动所产生的液压冲击
第四节 孔口和缝隙液流
一、薄壁小孔
➢ 薄壁小孔是指小孔的长度和直径之比l/d<0.5的孔, 一般孔口边缘做成刃口形式,如图3-25所示。
➢薄壁小孔的流量计算
对于图所示的通过薄壁小孔的液体,取小孔前后截面1-1和2-2列伯努利方程
p1
g
v12 2g
工程流体力学 第三章 流体静力学(孔珑 第三版)

Δp pA pB 2 gh 1 gh2 1 gh1 2 1 gh
如果被测流体为气体:
21
1 gh 0
2013年9月21日
《工程流体力学》 樊小朝 电气学院
4.倾斜微压计
玻璃管倾斜角
,截面积 A1
宽广容器截面积 A2
微压计存在压差 p2 p1
F mg pe 13263 Pa 2 d 4
液柱显示的压强:
pe gH h
联立方程,解得:
H 0.8524 m
24
2013年9月21日
《工程流体力学》 樊小朝 电气学院
P30例题3-2 如图所示,为测压装置。假设容器 A 中水面上的计 h 示压强 pe 2.45 104 Pa , h 500 mm ,h1 200mm , 2 100mm 3 3 h3 300mm ,水的密度 1 1000kg m ,酒精的密度 2 800kg m B 中气体的计示压强。 水银的密度 3 13600kg m3 ,试求容器
16
2013年9月21日
《工程流体力学》 樊小朝 电气学院
三、绝对压强 计示压强 p26 绝对压强:以真空为基准计量的压强。
p pa gh pa ——大气压强
计示压强:以当地大气压强为基准计量的压强。
pe p pa gh (测压计显示压强)
真空:绝对压强小于当地大气压
pV pa p pe (又称负压)
1 p fx 0 x
同理:
1 p fy 0 y 1 p fz 0 z
——流体平衡方程式(欧拉方程)
5
2013年9月21日
《工程流体力学》 樊小朝 电气学院
高等流体力学第3讲

第三讲 流体静力学一、 静止流体中的应力特性静止流体中,流体质点之间没有相对运动,切应力必然为0,又由于流体分子之间的引力很小,流体质点之间几乎不能承受拉力。
因此,在静止流体中,只能存在指向作用面的法向应力。
即n p =-p n (3-1)式中的p n 就是工程流体力学中的流体静压力。
上式也可以写成张量形式P ==000000p p p -⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦=p 00000011⎡⎤⎢⎥1⎢⎥⎢⎥⎣⎦= p I (3-2) 式中I 为单位张量。
静止流体中任意一点处的应力无论来自何方均相等,即任意一点处的静压力与作用方向无关。
二、 欧拉平衡方程惯性坐标系中,任何流体处于静止状态的必要条件是:作用在物体上的合外力为0,即0∑=F (4-3)在静止流场中任取一个流体团作为研究对象,作用在其上的质量力可表示为d ρττ⎰⎰⎰f (a ) 表面力可表示为d d AAp A p A -=-⎰⎰⎰⎰n n (b )根据第一个平衡条件(3-3)可得d d =0Aρτp A τ-⎰⎰⎰⎰⎰f n (c ) 根据高斯定理可知,若物理量p 在封闭空间τ中连续且存在连续的一阶导数,则有d =d Ap A p ττ∇⎰⎰⎰⎰⎰n (d )将(d)式代入(c)式则可得d 0ρp ττ-∇=⎰⎰⎰()f 由于流体团是任意选取的,所以要使上式成立,则被积函数在该体积内任意点上的数值必须为0,于是有=0ρp -∇f或1=p ρ∇f (3-4)这就是欧拉平衡微分方程式,其在直角坐标系中可写为111x yzp f ρx pf ρy p f ρz ⎧∂=⎪∂⎪⎪∂=⎨∂⎪⎪∂=⎪∂⎩(3-5) 同时,合力矩为0是自动满足的。
三、 静压流场的质量力条件(自学)对于所有的静止流体,(3-4)式均成立,现对其两端同时取旋度可得1111==+=p p p p ρρρρ⎛⎫⎛⎫⎛⎫∇⨯∇⨯∇∇⨯∇∇⨯∇∇⨯∇ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()f上式中应用了标量函数梯度的旋度为0这一结论,现证明之p ∇⨯∇()=p p p xy z ⎛⎫∂∂∂∇⨯++ ⎪∂∂∂⎝⎭i j k=x y z p p p xy z∂∂∂∂∂∂∂∂∂∂∂∂ij k =p p p p p p y z z y x z z x x y y x ⎛⎫⎛⎫∂∂∂∂∂∂∂∂∂∂∂∂⎛⎫---+-⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭i j k =0(矢量) 将上式与(3-4)式进行点乘则有()1=p p ρρ⎡⎤⎛⎫∇∇⨯∇⨯∇⎢⎥ ⎪⎝⎭⎣⎦f f 上式右端为矢量的混合积,由混合积的定义可知由于三个矢量中有两个同名,所以其值为0,可得()=0∇⨯f f (3-6)由此可以得出结论:流体静止的必要条件是质量力必须满足()=0∇⨯ff 。
《化工原理》流体静力学

p1
p1
pa
pa
表压
真空度
2. 指示液的选取: 指示液与被测流体不互溶,不发生化学反应; 其密度要大于被测流体密度。 应根据被测流体的种类及压差的大小选择指示液。
思考:若U形压差计安装在倾斜管路中,此时读数 R反映了什么?
p1 z1
p2
z2 p1 gz1 p2 gz2
(0 )gR
R A A’
——静力学基本方程
讨论:
(1)适用于重力场中静止、连续的同种不可压缩性 流体;
(2)物理意义:
zg ——单位质量流体所具有的位能,J/kg;
p
——单位质量流体所具有的静压能,J/kg。
在同一静止流体中,处在不同位置流体的位
能和静压能各不相同,但二者可以转换,其总和
保持不变 。
(3)在静止的、连续的同种流体内,处于同一水平 面上各点的压力处处相等。压力相等的面称为等压 面。
表 压 = 绝对压力 - 大气压力
真空度 = 大气压力 - 绝对压力
p1
表压
大气压
真空度
绝对压力
p2
绝对压力
绝对真空
【例1-2】*已知某离心泵进口真空表读数为76kPa,出 口压力表读数为245kPa,试求离心泵进出口的绝对压 力及压差。(大气压力为1标准大气压)
解:进口处绝对压力
pi绝 1atm pi真空度 101300 76000 25300 Pa
(4)压力具有传递性:液面上方压力变化时,液体 内部各点的压力也将发生相应的变化。
【例1-3】*如图所示,将大气视为静止流体,且认为从海
平面到20000m高度间是等温状态,试计算20000m高度处
的大气压强。假设海平面处p1= 101.3kPa, ρ1 = 1.205kg/m3,
第三章 流体静力学

条件:r 0,z 0,p pa
因此: C pa
p pa g (
2r 2
2g
z)
实例2:封闭容器装满液体, 顶盖边缘开口通大气
1 2 2 p ( r gz ) C 2
条件:r R,z 0,p pa
圆柱体底面上各点所受到的计 示压强为:
F mg pe d2 4
pe H h g
pe g H h
例3-2 假设容器A中水面上的计示压强为pe,已知h,h1, h2,h3,水的密度ρ1,酒精的密度ρ3,试求容器B中气体 的计示压强。
p1e pe 1 g h h1 p2 e p1e 3 gh1 pe 1 g h h1 3 gh1 pe 1 g h h1 3 gh1 2 gh2 pe 1 g h h1 3 gh1 2 gh2 3 gh3
EXIT
一、水平等加速运动容器中液体的相对平衡 装着液体的车以等加速度a向右行驶,液面上气体压强为p0, 达到相对平衡后,液面与水平面间的夹角α。
• 液体静压强分布规律
p ax gz C
• 等压面方程
ax gz C1
•自由液面方程
ax gzs (几何) 0 (压力) p p 0 1 =-tan a g
第三节 重力场中流体的 平衡帕斯卡原理
一、绝对压强 计示压强 (1)绝对压强p:以完全真空(p=0)为基准计量的压强。 (2)计示压强pe:以当地大气压(pa)为基准计量的压强。 (3)真空pv:绝对压强小于当地大气压强的负计示压强。 绝对压强 计示压强 p=pa+ρgh pe=p-pa= ρgh
流体静力学原理

流体静力学原理流体静力学是研究流体静止状态下的力学性质和规律的学科,它在工程学、物理学和地质学等领域都有着广泛的应用。
本文将介绍流体静力学的基本原理,包括压力、密度、浮力等概念,以及这些原理在实际中的应用。
首先,我们来讨论流体静力学中的基本概念,压力和密度。
压力是单位面积上的力,它可以用公式P=F/A来表示,其中P表示压力,F表示作用在单位面积上的力,A表示面积。
而密度则是单位体积内的质量,通常用ρ来表示,可以用公式ρ=m/V来表示,其中ρ表示密度,m表示质量,V表示体积。
这两个概念是流体静力学中非常重要的基础,对于理解流体的性质和行为至关重要。
其次,我们将讨论浮力的原理。
浮力是指物体浸没在液体中时,液体对物体的支持力。
根据阿基米德原理,浮力的大小等于物体排开的液体的重量,方向与重力方向相反。
这意味着,当物体浸没在液体中时,液体会对物体产生一个向上的浮力,这个浮力的大小与物体在液体中排开的液体的重量相等。
浮力的大小与物体的密度和排开液体的体积有关,这也是为什么密度小的物体会浮在液体表面,密度大的物体会沉在液体底部的原因。
最后,我们将讨论流体静力学原理在实际中的应用。
在工程学中,流体静力学原理被广泛应用于水压力的计算、水坝的设计、船舶的浮力计算等方面。
在物理学中,流体静力学原理被用来解释气球漂浮、液压系统的工作原理等现象。
在地质学中,流体静力学原理被用来研究地下水的运动规律、地下石油和天然气的储存等问题。
总之,流体静力学原理是一个非常重要的学科,它不仅有着广泛的理论意义,还有着丰富的实际应用价值。
通过对流体静力学原理的深入理解,我们可以更好地理解自然界中的许多现象,同时也能够更好地应用这些原理来解决实际问题。
希望本文的介绍能够帮助读者更好地理解流体静力学原理,并对其应用有更深入的认识。
工程流体力学第三章

则总压力P 则总压力P为: 其中 代入上式,则: 代入上式,
(1)
对于本例即
它表明作用在平面 A 的液体总压力,等于浸水面积 A 与形心点 的液体总压力, 的静压力 γhc的乘积。 的乘积。 可理解为一假想体积的液重,即以浸水面积 A 为底,面积 A 的 为底, 可理解为一假想体积的液重, 形心淹没深度h 为高的这样一个体积包围的液体重量。 形心淹没深度hc为高的这样一个体积包围的液体重量。
一点的质量力必然垂直于通过该点的等压面。 一点的质量力必然垂直于通过该点的等压面。 等压面概念对解决许多流体平衡问题很有用处, 等压面概念对解决许多流体平衡问题很有用处,它是液柱式压力计测压原理的重 要基础。 要基础。 根据等压面性质,我们可以在已知质量力的方向,去确定等压面的形状, 根据等压面性质,我们可以在已知质量力的方向,去确定等压面的形状,或已知 等压面的形状去确定质量力的方向。 等压面的形状去确定质量力的方向。
根据等压面的特性可以更普遍地证明:两种不同流体处于平衡状态时,其 根据等压面的特性可以更普遍地证明:两种不同流体处于平衡状态时, 相互接触的(但互不相混)分界面必然是等压面。 相互接触的(但互不相混)分界面必然是等压面。
( 4 )正压流场 流体的密度只是压力的函数的流场称之为正压流场,即在正压流场中 流体的密度只是压力的函数的流场称之为正压流场,
§3 . 3 某些流体静力学基本问题
在工程技术中,许多的工业过程与流体静力学相关,研究这些问 在工程技术中,许多的工业过程与流体静力学相关, 题就需要流体静力学的知识。 题就需要流体静力学的知识。 一、压力分布与受力分析 对于流体静力学基本方程: 对于流体静力学基本方程:
∂P = ρ fx; ∂x ∂P = ρ fy; ∂y
流体静力学

称为流体平衡微分方程的综合式。
1 p fx 0 x
1 p fy 0 y
1 p fz 0 z
对常密度流体,对式坐标交错求偏导,整理得: f z f x f y f z f x f y x z y x z y ——力作功与路径无关的充分必要条件
流体的平衡微分方程 (欧拉平衡方程)
1 f p 0
1 p fz 0 z
1 p fx 0 x
1 p fy 0 y
1 p fz 0 z
1 f p 0
平衡微分方程的物理意义:
1、单位质量流体所受的表面力与单位质量力分量彼此 对应相等。
力学基本方程的两种表 达式。
其中:p 为任一点静止液体的压强;p0 为液体表面的压强,如果 液面为通大气的开口容器,则p0 = pa;h 为该点距液面的淹没深 度;z 为该点在坐标平面以上的高度。
p p0 gh
z p
g
C
若1点的压强为p1、坐标为z1; 2 点的压强为p2、坐标为z2:
p1 pA 1gh1
p1 p2 3 gh2
p3 p2 2 gh3
p3 p4 3 gh4
将上式逐个代入下一个式子: pA pB 1gh1 3 gh2 2 gh3 3 gh4 1g h5 h4 整理后得A,B两点的压强差:
§2-3 重力作用下流体静压强的分布
流体静力学基本方程式:
重力场中,取xoy为水平面,z轴垂直 向上,在该坐标系中单位质量力的 分量为:
fx fy 0
1 p fx 0 x
f z g
1 p fy 0 y
1 p fz 0 z
高中物理奥林匹克竞赛专题---流体力学(共88张PPT)

压强视为平均压强。因此,垂直于x轴的左、右两微元面上
的总压力分别为:
p1 pdxdydz 2 x
和
p1 p dxdydz 2 x
同理,可得到垂直于y轴的下、上两个微元面上的总压力分别
为:
p
1 2
p y
dydxdz
和
p
1 2
pp(x,y,z)
2019/9/6
6
第二节 流体平衡方程式
一、流体平衡微分方程式
在静止流体中任取一边长为 dx,dy和dz的微元平行六面体
的流体微团,现在来分析作用在这流体微团上外力的平衡条 件。作用在微元平行六面体的表面力只有静压强。设微元平 行六面体中心点处的静压强为p,则作用在六个平面中心点 上的静压强可按泰勒(G.I.Taylor)级数展开,在垂直于X轴 的左、右两个平面中心点上的静压强分别为:
p y
dydxdz
2019/9/6
9
垂直于轴的后、前两个微元面上的总压力分别为:
p1pdzdxdy p1pdzdxdy
2z
2z
作用在流体微团上的外力除静压强外,还有质量力。
若流体微团的平均密度为ρ,则质量力沿三个坐标轴的分
量为
fxdxdydz fydxdydz fzdxdydz
(2)由于绝大多数气体的性质是气体绝对压强的函
数,如正压性气体ρ=ρ(p),所以气体的压强都用
绝对压强表示。而液体的性质几乎不受压强的影响, 所以液体的压强常用计示压强表示,只有在汽化点 时,才用液体的绝对压强。
2019/9/6
30
压强的三种量度单位
(1)压强的基本定义
1 a ( 标 准 t 大 气 压 m ) 1 . 0 1 5 P 1 7 0 m 3 a 6 1 . 3 m m 0 2 O 0 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单位质量力在各坐标轴上的分力为
fx 0
2014-3-25
fy 0
24
fz g
1. 方程推导
fx 0
fy 0
代入
fz g
dp ( f x dx f y dy f z dz )
得
dp gdz
积分,ρ=const
F
x
0
F
y
0
F
z
0
流体微团受力分析
x方向受力分析
1 dydz 表面力: P p x x2
1 p dydz P cos p dAn cos n2 n n
1 质量力: W x ( dxdydz ) f x 6
流体微团质量
X方向单位质量力
因为流体平衡
x方向受力分析
质量力——
f x dxdydz
表面力—— 只有静压强 如何求解是关键
2014-3-25
15
作用在六个平面中心点上的静压强可按泰勒级数展开
在垂直于x轴的左、右两个平面中心点上的静压强分别为
p d x 1 2 p dx 1 3 p dx p 2 3 x 2 2 x 2 6 x 2
流体平衡微分方程式
欧拉平衡微分方程式
写成矢量形式
适用范围: 静止或相对静止状态的可压缩和不可压缩流体。 物理意义:在静止流体中,某点单位质量流体的质量力 与静压强的合力相平衡。
压强差公式 (1)
fx
fy
1 p 0 x
1 p 0 y
乘以dx
乘以dy 乘以dz
f x dx
第三章 流体静力学
流体静压强及其特性 流体平衡方程式 重力场中流体的平衡 帕斯卡原理 液柱式测压计 液体的相对平衡 静止液体作用在平面上的总压力 静止液体作用在曲面上的总压力 静止液体作用在潜体和浮体上的浮力 阿基米德原理
2014-3-25
1
(1) 其内部的压强分布规律;
dp dz 0 g
流体静力学 基本方程
p z c g
适用范围: 重力作用下的平衡状态, 均质 不可压缩流体
2. 物理意义
p z c g
在重力作用下静止流体中各点的单位重量流体的 总势能是相等的。
z
p / g
单位重量流体对某一基准面的位势能
单位重量流体的压强势能
位势能和压强势能之和称为单位重量流体的总势能
f x dx f y dy f z dz 0
性质:在静止流体中,作用于任意点的质量力垂直于经 过该点的等压面。 写成矢量形式
由矢量代数可知,这两个矢量必然垂直
等压面(2)
举例说明
液体与气体的分界面,即液体的自由液面就是等压 面,其上各点的压强等于在分界面上各点气体的压强。
互不掺混的两种液体的分界面也是等压面。 等压面
1. 静压强定义
问题1. 水流方向垂直于容器壁 面,为什么?
问题2. 如图所示的平面壁转折处B点, 对于不同方位的作用面而言,其静压 力方向不同,静压力的大小呢?
2. 静压强的两个特征及其证明
2014-3-25 4
第一节 流体静压强及其特性
一、静压强定义 流体处于静止或相对静止状态时,在流体内部或流体与 固体壁面间存在的单位面积上负的法向表面力。 给出方向——负法向 给出大小——表面力
h=z0-z 静止流体中任意点在自由 液面下的深度
2 淹深为 、密度为
的流体柱产生的压强
该式还表明: 均质不可压缩的重力流体处于平衡状态时,自由液面上的 压强对内部任意点上的影响是相同的,即施加与自由液面上的压强,将 以同样的大小传递到液体内部任意点上—帕斯卡原理。
2014-3-25 29
布莱士·帕斯卡
p x pn
p y pn
p z pn
p x p y pz pn
n的方向可以任意选择,从而证明了在静止流体 中任一点上来自各个方向的流体静压强都相等。
第一节 流体静压强及其特性
二、静压强两个特征(几点说明)
(1) 静止流体中不同点的静压强一般是不等的,是空间坐标的连续 函数。同一点的各向静压强大小相等。 (2) 运动状态下的实际流体,流体层间若有相对运动,则由于粘 性 会产生切应力,这时同一点上各法向应力不再相等。
本章导论
(2) 流体与其它物体间的相互作用力。
研究内容:流体在外力作用下处于平衡状态的规律及其 在工程实际中的应用。 静止含义: 以地球作为惯性参考坐标系 绝对静止:流体相对于惯性坐标系静止 相对静止:流体相对于非惯性参考坐标系静止 适用范围: 静止状态
0
2
0
实际流体、理想流体都是适用的。
A
完全真空
A 静水头线
p2 / g
p1 / g
p0
p2
2
p1
z1
1
z2
基准面
在重力作用下静止流体中各点的静水头都是相等的 静水头线是水平直线
2014-3-25 28
帕斯卡原理
对淹深为h的a点和压强为p0的自由 液面上的点,列静力学基本方程
Z
p0
A
p
h
z0
OzBiblioteka Y上式表明:不可压缩的重力流体处于平衡 状态时,流体内部的静压强由两部分构成 1 自由表面的压强
两式相减
因为
2014-3-25
水
dp
1 1 dp 0 1 2 1 2 dp
dp=0
23
1 2 0
第三节 重力作用下的流体平衡
一、重力作用下的静力学基本方程式 1. 方程推导 静止容器上取直角坐标系
G = mg
P0
假设
一、流体平衡微分方程式(推导)
1 p dx dydz p 2 x
A
C p
B
1 p dx dydz p 2 x
½ dx
图2-3 微元平行六面体x方向的受力分析
一、流体平衡微分方程式(推导)
在静止流体中任取一平行六面体的流体微团, 边长为 dx,dy,dz的微元,中心点静压强为p(x,y,z)
1 p dx 0 x
1 p f y dy dy 0 y
f z dz 1 p dz 0 z
1 p fz 0 z
三式相加,整理
p p p ( f x dx f y dy f z dz ) dx dy dz x y z
p f ( x, y, z )
求静压强分布规律 研究平衡状态的一般情况 推导平衡微分方程式 流体静力学 最基本方程组
2014-3-25 12
第二节 流体平衡微分方程
本章的重点,内容包括:
1.
流体的平衡微分方程
意义 适用范围
2.
3.
压强差公式 等压面
2014-3-25
13
第二节 流体平衡微分方程
c
2014-3-25
26
3. 几何意义 单位重量流体具有的能量用液柱高度来表示称为水头。
p z c g
z
p / g
单位重量流体的位置水头 单位重量流体的压强水头 位置水头和压强水头之和称为静水头
c
在重力作用下静止流体中各点的静水头都是相等的。
2014-3-25 27
p z c g
2014-3-25
【学习重点、难点】
重点:
1. 静压强及其特性,点压强的计算,静压强分布。 2. 作用于平面上液体总压力。 3. 作用于曲面上液体总压力,压力体的画法。
难点:
1. 应用静力学基本定律计算作用在平面、曲面上的总压力; 2. 不同高度的液体对固体壁面总压力的计算。
2014-3-25
3
第一节 流体静压强及其特性
2 3
f ( x0 ) f ( x ) f ( x0 ) f ( x0 )( x x0 ) ( x x0 ) 2 2! f n ( x0 ) ...... ( x x0 ) n n!
p dx 1 2 p d x 1 3 p dx p 2 3 x 2 2 x 2 6 x 2
压强差公式的物理意义:在静止流体中,空间点的坐标增量 为dx、dy、dz时,相应的流体静压强增加dp,压强的增量 取决于质量力。
20
等压面(1)
1. 在流体中,压强相等的各点所组成的面称为等压面。 dp=0
对不同的等压面,其常数值是不同的。 流体中任意一点只能有一个等压面通过。
2. 微分形式的等压面方程
2014-3-25 19
压强差公式(2)
( f x dx f y dy f z dz )
p p p dx dy dz x y z
流体静压强是空间坐标的连续函数,它的全微分为
p p p dp dx dy dz x y z
所以
dp ( f x dx f y dy f z dz )
p p0
p p0
等压面
油 水
等压面(3)
证明 互不掺混的两种液体的分界面也是等压面。 分界面上取两点1和2 点1——点2的压强增量
p p0
1 油 2
等压面
dp 1 ( f x dx f y dy f z dz ) dp 2 ( f x dx f y dy f z dz )
F
x
0
在轴方向上力的平衡方程为 把 Px ,Pn和Wx的各式代入得
Px Pn cos W x 0
