初中数学菱形的性质及判定
八年级菱形知识点总结

八年级菱形知识点总结在初中数学中,菱形是一种常见的图形,学生需要掌握它的性质和用法。
本文将总结八年级菱形的知识点,包括面积、周长、对角线、中线等方面,希望对初中数学学习有所帮助。
一、菱形的定义和性质菱形是四边形的一种,它有如下性质:1. 四条边相等,即AB=BC=CD=DA,其中AB代表菱形上的任意一条边;2. 对角线互相垂直,且相互平分,即AC⊥BD并且AC=BD;3. 对角线的中点连线互相垂直,即AE⊥BF,CE⊥DF,其中E 和F分别是AC和BD的中点;4. 菱形内角和为360度,即∠ABC+∠BCD+∠CDA+∠DAB=360度。
二、菱形的周长和面积1. 周长由于菱形的四条边相等,因此它的周长可以用任意一条边a来表示,即P=4a。
2. 面积菱形面积的公式是S=(d1×d2)/2,其中d1和d2分别是对角线长,可以使用勾股定理计算,即d1²=d²+a²/4,d2²=d²+b²/4。
其中a和b分别是菱形两边的长度,d是菱形的对角线长度。
三、菱形的对角线和中线1. 对角线的长度由于菱形的对角线互相平分,因此可以用勾股定理求出对角线的长度,即d=√(a²+b²)。
2. 对角线的中点连线菱形的对角线的中点连线被称为菱形的中线,分别用e和f表示,它们互相垂直,长度相等。
中线长度的公式为e=f=√(a²+b²)/2。
四、菱形的应用1. 建筑设计在建筑设计中,常常需要设计菱形形状的窗户和门,因为这样可以在视觉上改变建筑物的形状。
2. 拼贴艺术拼贴艺术是一种非常受欢迎的艺术形式,它可以使用各种材料进行创作,包括彩纸、糊纸、墙纸等。
在拼贴艺术中,菱形形状也经常被使用。
3. 数学应用菱形在数学中有着广泛的应用,包括概率、统计、几何等方面。
例如,在概率计算中,会使用菱形图来表示事件的可能性。
在统计学中,会使用菱形图来表示一组数据的分布情况。
新人教部编版初中八年级数学18.2.2 第2课时 菱形的判定

证一证
已知:如图,四边形ABCD是平行四边形,对角线AC
与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.
证明: ∵四边形ABCD是平行四边形.
B
∴OA=OC.
O
又∵AC⊥BD,
A
C
∴BD是线段AC的垂直平分线.
D
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
长冲中学数学组-“四学一测”活力课堂
长冲中学数学组-“四学一测”活力课堂
长冲中学活力课堂
典例精析
例3 如图,在△ABC中, AD是角平分线,点E、F分别在 AB、 AD上,且AE=AC,EF = ED. 求证:四边形CDEF是菱形.
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD, ∴ △ACD≌ △AED (SAS).
A
21 F
求证:四边形ABCD是菱形.
证明:∵ OA=4,OB=3,AB=5,
D
∴ AB2=OA2+OB2,
∴△AOB是直角三角形, A
O
C
即AC⊥BD,
B
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
长冲中学数学组-“四学一测”活力课堂
长冲中学活力课堂
例2 如图,矩形ABCD的对角线AC的垂直平分线与边AD、 BC分别交于点E、F,求证:四边形AFCE是菱形.
A
FD BE C
请补充完整的 证明过程
分析:易知四边形ABCD是平行四边形,只需证一 组邻边相等或对角线互相垂直即可进一步判断. 由题意可知BC边上的高和CD边上的高相等, 然后通过证△ABE≌△ADF,即得AB=AD.
长冲中学数学组-“四学一测”活力课堂
(初中)数学《菱形的性质与判定》中考专项复习训练典型试题梳理汇总

(初中)数学《菱形的性质与判定》中考专项复习训练典型试题梳理汇总菱形的性质与判定基础同步过关知识点一:菱形的性质定理1.如图,四边形ABCD的对角线互相平分,则添加下列条件之一,不能使它成为菱形的是()A.AB=ADB.AC=BDC.BD平分∠ABCD.AC∠BD2.如图,顺次连接四边形ABCD各边的中点得到四边形EFGH,要使四边形EFGH为菱形,应添加的条件是。
3.如图,下列对菱形ABCD表述正确的有。
∠AC=BD;∠∠OAB=∠OBA;∠AC∠BD;∠有4条对称轴;∠AD=BD;∠∠OAB=∠OAD。
4.如图,四边形ABCD是菱形,AC BD相交于点O,AC=8,BD=6,DH∠AB于点H,则DH的长为。
第1题图第2题图第3题图第4题图5.如图,在菱形ABCD中,AB=2,∠ABC=120°,则菱形ABCD的面积是。
6.如图,在菱形ABCD中,对角线AC与BD交于点O,OE∠AB,垂足为E,若∠ADC=128°,则∠AOE的度数为()A.62°B.52°C.68°D.64°7.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG的长度为()B.3第5第6题图第7题图知识点二:菱形的判定定理8.已知四边形ABCD中,AC∠BD,再补充一个条件使得四边形ABCD为菱形,这个条件可以是()A.AC=BDB.AB=BCC.AC与BD互相平分D.∠ABC=90°9.如图,将∠ABC沿BC方向平移得到∠DCE,连接AD.下列条件中,能够判定四边形ACED为菱形的是()A .AB=BC B. AC=BC C.∠ABC=60° D.∠ACB=60°10.AC,BD相交于点O,点E,F,G,H分别是OA,OB,OC,OD的中点,若要使四边形EFGH成为菱形,(写出一种即可)11.折纸游戏一直很受大家的欢迎,小丽同学要用一张矩形纸片折出一个菱形,她用沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图)。
北师大课标版初中数学九年级上册1.1菱形的性质与判定说课稿

菱形的判定说课稿一、说教材1、教材的地位和作用本节课选自北师大九年级上册第一章第一节《菱形的性质与判定》的第二课时,主要内容是菱形的判定,尝试从不同角度寻求菱形的判定方法,并能有效地解决问题。
它是在探究平行四边形之后,一个特殊四边形判定方法的探索,它不仅是三角形、四边形知识的延伸,更为探索矩形的性质与判定指明了方向。
学习本课时,通过观察猜想,归纳证明,培养学生的推理能力和演绎能力,为以后圆等知识的学习奠定基础。
2、教学目标根据本节课的教学内容,结合新课标理念, 我制定了以下教学三维目标:知识目标:理解菱形的判别条件及其证明,并能利用这两个定理解决一些简单的问题。
能力目标:(1)经历运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,发展抽象思维.(2)经历实际操作,探索菱形判定定理的证明过程,发展合情推理能力和初步的演绎推理的能力;(3)在具体问题的证明过程中,有意识地渗透实验论证、逆向思维的思想,提高学生的能力。
情感态度价值观(1)积极参与数学学习活动,对数学有好奇心和求知欲.(2)通过“实验—猜想—证明—应用“的数学活动提升科学素养.3、教学重点、难点基于本节课的主要内容是围绕着菱形的判定方法而展开的,菱形的判定方法在本节课中处于核心地位,所以我确定本节课的教学重点为菱形判定方法的探究。
由于学生还没有具备辨证分析问题的能力,所以我确定本节课的教学难点是菱形判定方法的探究及灵活运用。
4、教材处理根据教学目标,为突出重点,突破难点,在探索菱形的有关对角线的判定定理时,用教具演示,四边形的两条对角线在保持互相平分的前提下进行转动,当它们的位置关系是垂直时,平行四边形变为菱形,给学生以直观感受,印象深刻;在探索菱形的另一个判定定理时,让学生根据它的特殊点去猜想边之间满足的关系,从而得出定理,拓展学生的思维空间。
二、说教法1、创设问题情境,恰当设疑,引发学生兴趣。
2、采用直观操作和几何论证相结合的探究式的教学方法。
初中数学菱形的性质及判定

初中数学菱形的性质及判定1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.2.菱形的性质菱形是特殊的平行四边形,它具有平行四边形的所有性质,? 还具有自己独特的性质:①边的性质:对边平行且四边相等.②角的性质:邻角互补,对角相等.③对角线性质:对角线互相垂直平分且每条对角线平分一组对角.④对称性:菱形是中心对称图形,也是轴对称图形.菱形的面积等于底乘以高,等于对角线乘积的一半.点评:其实只要四边形的对角线互相垂直,其面积就等于对角线乘积的一半.3.菱形的判定判定①:一组邻边相等的平行四边形是菱形.判定②:对角线互相垂直的平行四边形是菱形.判定③:四边相等的四边形是菱形.4.三角形的中位线中位线:连结三角形两边的中点所得的线段叫做三角形的中位线.也可以过三角形一边的中点作平行于三角形另外一边交于第三边所得的线段也是中位线.以上是中位线的两种作法,第一种可以直接用中位线的性质,第二种需要说明理由为什么是中位线,再用中位线的性质.定理:三角形的中位线平行第三边且长度等于第三边的一半.重点是菱形的性质及判定定理。
菱形是在平行四边形的前提下定义的,首先她是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法。
菱形的这些性质和判定定理即是平行四边形性质与判定的延续,又是以后要学习的正方形的基础。
难点是菱形性质的灵活应用。
由于菱形是特殊的平行四边形,所以它不但具有平行四边形的性质,同时还具有自己独特的性质。
如果得到一个平行四边形是菱形,就可以得到许多关于边、角、对角线的条件,在实际解题中,应该应用哪些条件,怎样应用这些条件,常常让许多学生手足无措,教师在教学过程中应给予足够重视。
板块一、菱形的性质菱形的两条对角线将菱形分成全等三角形的对数为考点】菱形的性质及判定题型】填空难度】2 星关键词】解析】根据菱形的性质可知:共有8 对答案】8在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是【考点】菱形的性质及判定【题型】填空【难度】2 星【关键词】【解析】根据菱形的性质可知:应当旋转至少180【答案】180如图2,一活动菱形衣架中,菱形的边长均为16cm 若墙上钉子间的距离AB BC16cm ,则1 度.考点】菱形的性质及判定题型】填空难度】2 星关键词】2009 年,江西中考解析】由题意可知:构成三角形为等边三角形答案】120如图,在菱形ABCD 中,A 60 ,E 、F 分别是AB 、AD 的中点,若EF 2 ,则菱形ABCD 的边长是______________________ .AC【考点】菱形的性质及判定【题型】填空【难度】2 星【关键词】2009 年,漳州中考【解析】省略【答案】4如图,E 是菱形ABCD 的边AD 的中点,EF AC 于H ,交CB 的延长线于F ,交AB 于P ,证明:AB与EF 互相平分.考点】菱形的性质及判定,平行四边形的性质和判定题型】解答难度】3 星关键词】解析】省略答案】连接BD、AF、EB菱形ABCD 中BD AC ,EF AC ,∴ BD ∥ EF∵ AD ∥ FC ,∴四边形BDEF 是平行四边形,∴ ED FB 又∵ AE∥FB,∴四边形AFBE 是平行四边形∴ AB 与EF 互相平分如图1 所示,菱形ABCD 中,对角线AC 、BD 相交于点O,H 为AD 边中点,菱形ABCD 的周长为24 ,则OH 的长等于AE ED ,∴ AE FB考点】菱形的性质及判定 题型】填空 难度】 2 星 关键词】 2009 年,本溪中考 解析】省略 答案】 3如图,已知菱形 ABCD 的对角线 AC 8cm ,BD 4cm ,DE BC 于点 E ,则 DE 的长 为 【考点】菱形的性质及判定 【题型】填空 【难度】 2 星【关键词】 【解析】省略 【答案】8 5cm 5菱形周长为 52cm , 一条对角线长为 10cm ,则其面积为 【考点】菱形的性质及判定 【题型】填空 【难度】 2 星 【关键词】D图1【解析】菱形的边长为52 4 13 cm ,由勾股数和菱形对角线的性质得另一对角线长为24 cm ,故面积为120 cm2【答案】120菱形的周长为20cm ,两邻角度数之比为2:1 ,则菱形较短的对角线的长度为【考点】菱形的性质及判定【题型】填空【难度】2 星【关键词】【解析】省略【答案】5如图2,在菱形ABCD 中,AC 6,BD 8,则菱形的边长为()A.5 B .10 C .6 D .8考点】菱形的性质及判定题型】选择难度】2 星关键词】2009 年,重庆江津中考解析】由菱形的对角线互相垂直平分及勾股数可知选A答案】A如图3,在菱形ABCD 中,A 110 ,E 、F 分别是边AB 和BC 的中点,EP 于点P ,则FPC ()A.35 B .45 C .50 D .55CDD考点】菱形的性质及判定 题型】选择 难度】 2 星 关键词】 2009 年,杭州市中考 解析】省略 答案】 D如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一 个锐角为 60 的菱形,剪口与折痕所成的角 的度数应为( ) 考点】菱形的性质及判定 题型】选择 难度】 2 星 关键词】 2009 年,绵阳市中考 解析】省略 答案】 D菱形 ABCD 中, E 、F 分别是 BC 、CD 的中点,且 AE BC ,AF CD , 那么 等于 . 【考点】菱形的性质及判定 题型】填空 难度】 2 星 关键词】A . 15 或 30B . 30 或 45C . 45 或 60DEAFE BP C图330解析】省略 答案】 60已知菱形的一个内角为 60 ,一条对角线的长为 2 3 ,则另一条对角线的 长为 _________________ . 【考点】菱形的性质及判定 【题型】填空 【难度】 2 星【关键词】 2009 年,辽宁朝阳中考 【解析】省略 【答案】 2 或 6如图,将一个长为 10cm ,宽为 8cm 的矩形纸片对折两次后,沿所得矩形 两邻边中点的连线 (虚线)剪下,再打开, A . 10cm 2B . 20cm 2C . 40cm 2考点】菱形的性质及判定 题型】选择 难度】 3 星 关键词】 2009 年,南宁市中考 解析】省略 答案】 A已知菱形 ABCD 的两条对角线 AC ,BD 的乘积等于菱形的一条边长的平方, 则菱形的一个钝角的大小是 【考点】菱形的性质及判定得到的菱形的面积为 ( ) D . 80cm 2C2【题型】填空 【难度】 4 星【关键词】希望杯邀请赛【解析】如图,过点 A 作 AE BC 于 E ,则 1AC BD BC AE ,又 AC BD AB 2,2得AE 1AB , ABC 30 , BAD 1502答案】 150如图,菱形花坛 ABCD 的周长为 20m , ABC 60 , ? 沿着菱形的对角线修 建了两条小路 AC 和 BD ,求两条小路的长和花坛的面积.考点】菱形的性质及判定 题型】解答 难度】 3 星 关键词】 解析】 ∵四边形 ABCD 是菱形∴ AB BC CD DA 5 ∵ABC 60∴ ABC 和 ADC 都是等边三角形 ∴ AC 5 又∵ AC BD在 Rt ABO 和 Rt ADO 中可得53BO DODA图2∴BD 5 3∴ S ABCD1 AC BD 25 3 ABCD 2 2点评:内角为60 和120 的菱形学生必须掌握,这是考试的热点模型.【答案】见解析如图,在菱形ABCD 中,AB 4a ,E 在BC 上,BE 2a ,BAD 120 ,P 点在BD 上,则PE PC 的最小值为【考点】菱形的性质及判定【题型】填空【难度】3 星【关键词】【解析】A,C 关于BD对称,连AE 交BD 于P ,且AE BC ,BAE 30 ,PE PC AE 4a 2 2a 2 2 3a 为最小值【答案】2 3a已知,菱形ABCD中,E、F 分别是BC 、CD上的点,若AE AF EF AB,求C的度数.考点】菱形的性质及判定题型】解答难度】4 星关键词】解析】∵ AE AB ∴ B AEBD同理D AFD∵四边形 ABCD 是菱形考点】菱形的性质及判定 题型】解答 难度】 4 星 关键词】 解析】连接 AC ,∵ 四边形 ABCD 为菱形AB BC CD AD△ABC 和 △ ACD 为等边三角形AB AC , B ACD BAC 60 EAF 60 BAE CAF△ ABE ≌△ ACF AE AFEAF 60△AEF 为等边三角形AEF 60∵AEC B BAE AEF CEF∴ CEF 18 分析:在矩形、菱形的定理题中,有时也常连对角线,把四边形问题 转∴ AD ∥ BC , B D , BAD C , AEB AFDB D ∴ BAE DAFDE EF AF ,∴ △ AEF 是等边三角形,∴EAF 60AD ∥BC ,xB BAD 180 ,∴ 90 60 2x 1802∴x 20 ∴C【答案】 100BAD 60 2 x 100已知,菱形 ABCD 中, E 、 F 分别是 BC 、 BAE 18 .求: CEF 的度数.CD 上的点,且B EAF 60 ,化为三角形问题.【答案】18板块二、菱形的判定如图,如果要使平行四边形ABCD 成为一个菱形,需要添加一个条件,那么你添加的条件是.考点】菱形的性质及判定题型】填空难度】2 星关键词】2007 年,四川成都解析】AB AD,AC BD 等;答案】AB AD,AC BD如图,在ABC 中,BD 平分ABC ,BD 的中垂线交AB 于点E ,交BC 于点F ,求证:四边形BEDF 是菱形考点】菱形的性质及判定题型】解答难度】3 星关键词】解析】省略答案】∵ EF 是BD 的中垂线∴BE DE ,BF DF ,∴DBE BDE∵ EBD DBF∴ DBF EDB ,所以BC∥ DE 同理AB∥ DF 所以四边形BEDF 是菱形如图,在ABC 中,AB AC ,D是BC 的中点,连结AD,在AD 的延长线上取一点E,连结BE ,CE .当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.【考点】菱形的性质及判定【题型】解答【难度】3 星【关键词】2009 年,娄底中考【解析】当AE 2AD (或AD DE 或DE 1 AE )时,四边形ABEC 是菱形2理由如下:∵ AE 2AD ,∴ AD DE又点D 为BC 中点,∴ BD CD∴四边形ABEC 为平行四形边∵ AB AC∴四边形ABEC 为菱形【答案】见解析已知:如图,平行四边形ABCD 的对角线AC的垂直平分线与边AD 、BC 分别相交于E 、F . 求证:四边形AFCE 是菱形.【考点】菱形的性质及判定【题型】解答【难度】3 星【关键词】2006 年,盐城中考【解析】省略【答案】∵ EF 垂直平分AC,∴ EF AC,AO CO .o∴ AOE COF 90o.又∵ ABCD 平行四边形,∴ EAO FCO .∴ AOE ≌COF .∴OE OF .∴四边形AECF 是平行四边形.又由AC EF 可知,四边形AECF 是菱形.如图,在梯形纸片ABCD 中,AD //BC ,AD CD ,将纸片沿过点D 的直线折叠,使点C 落在AD上的点C处,折痕DE交BC于点E,连结CE. 求证:四边形CDC E 是菱形.考点】菱形的性质及判定题型】解答难度】3 星关键词】2007 年,云南双柏解析】省略答案】根据题意可知CDE C'DE则CD C'D,C'DE CDE ,CE C'E .∵ AD / /BC ,∴ C DE CDE .∴ CDE CED ,∴ CD CE .∴ CD C D CE CE ,∴四边形CDC E为菱形.如图,E 是菱形ABCD 的边AD 的中点,EF AC 于H ,交CB 的延长线于F ,交AB 于P ,证明:AB 与EF 互相平分【考点】菱形的性质及判定,平行四边形的性质和判定【题型】解答【难度】3 星【关键词】【解析】省略【答案】连结BD,AF ,EB,因为菱形ABCD 中BD AC ,又因为EF AC ,所以BD ∥ EF ,因为AD ∥ FC ,所以四边形BDEF 是平行四边形,可得ED FB ,因为AE ED,所以AE FB,从而AE∥ FB ,AE FB ,因此四边形AFBE 是平行四边形,所以AB与EF互相平分已知:如图,在平行四边形ABCD 中,AE 是BC边上的高,将ABE沿BC 方向平移,使点E与点C重合,得GFC .若B 60 ,当AB与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.B E F C考点】菱形的性质及判定题型】解答难度】3 星关键词】2009 年,山东青岛市解析】省略答案】当BC 3AB 时,四边形ABFC 是菱形.2AB∥GF ,AG∥ BF 四边形ABFG 是平行四边形∵ Rt ABE 中, B 60∴ BAE 30∴ BE1 AB2∵ BE CF ,BC3 AB2∴ EF1 AB2∴ AB BF∴四边形ABFG是菱形如图,在ABC 中,AB AC ,M 是BC 的中点.分别作MD AB于D ,ME AC 于E,DF AC 于F ,EG AB 于G.DF、EG 相交于点P .求证:四边形DMEP 是菱形.【考点】菱形的性质及判定【题型】解答【难度】3 星【关键词】【解析】省略【答案】∵ MD AB,EG AB.∴ MD ∥ EG ,同理ME ∥ DF ,∴四边形MFPD 是平行四边形AB AC ,BCo∵ BM MC , BDM CEM 90o,∴ BDM ≌ CEM ∴ DM EM ,∴四边形 DMEP 是菱形如图, ABC 中, ACB 90 ,AD 是 BAC 的平分线, 交 BC 于 D ,CH 是 AB 边上 的高,交 AD 于 F , DE AB 于 E ,求证:四边形 CDEF 是菱形.考点】菱形的性质及判定 题型】解答 难度】 3 星 关键词】 解析】省略 答案】 ∵ CH AB ,∴ HAF AFH 90ACB 90 ,∴ CAD ADC 90AD 平分 CAB ,∴ CAD HAF ,∴ AFH CDF AFH CFD ,∴ CDF CFD ,∴ CF CD AD 平分 CAB , DC AC , DE AB∴CD DE ,∴ CF DE 又∵ CH AB ,DE AB∴ CF ∥ DE , 故四边形 ABCD 是平行四边形∵ CD DE , ∴四边形 ABCD 是菱形 如图, M 是矩形 ABCD 内的任意一点,将 MAB 沿 AD 方向平移,使 AB 与 DC 重合,点 M 移动到点 M '的位置 ⑴画出平移后的三角形;⑵连结 MD ,MC ,MM ' ,试说明四边形 MDM 'C 的对角线互相垂直,且长度分 别等于AB ,AD 的长;⑶当 M 在矩形内的什么位置时, 在上述变换下, 四边形 MDM 'C是菱形?为什么?AD AM D M'BC【考点】菱形的性质及判定 【题型】解答 【难度】 3 星【关键词】 【解析】省略 【答案】⑴如图, DCM '就是所要作的三角形⑵因为 AM 平移到 DM ' ,所以 AM ∥DM '且AM DM ',四边形 DAMM' 是平行四边形,所以AD ∥MM ',矩形 ABCD 中,AD CD , 所以 MM ' CD ,又因为 AD MM ' , CD AB ,所以四边形 MDM 'C 的对角线互相垂直, 且长度分别等于 AB ,AD 的 长⑶当点 M 是 AC ,BD 的交点时,四边形 MDM 'C 是菱形,理由:如 图,矩形ABCD 中,AM BM MC MD , 又因为 AM D'M ,BM CM ' , 可得 MD MC CM ' DM ' , 所以 四边形 MDM 'C 是菱形 如图, ACD 、 ABE 、 BCF 均为直线 BC 同侧的等边三角形.已知 ABAC . ⑴ 顺次连结 A 、D 、F 、 E四点所构成的图形有哪几类?直接写出构成 图形的类型和相应 的条件.⑵ 当 BAC 为度时,四边形 ADFE 为正方形.考点】菱形的性质及判定题型】解答【难度】 3 星【关键词】 2008 年,佛山市中考改编DBC【解析】省略【答案】⑴ 构成的图形有两类,一类是菱形,一类是线段.当图形为菱形时,∠ BAC≠60°(或A与F不重合、△ ABC不为正三角形)(若写出图形为平行四边形时,不给分)当图形为线段时,∠BAC= 60°(或A与F重合、△ ABC为正三角形).⑵ 150 .三、与菱形相关的几何综合题已知等腰△ABC 中,AB AC ,AD 平分BAC交BC 于D点,在线段AD 上任取一点P(A点除外),过P点作EF ∥ AB ,分别交AC 、BC于E 、F点,作PM∥AC,交AB于M 点,连结ME .⑴求证四边形AEPM 为菱形⑵当P 点在何处时,菱形AEPM 的面积为四边形EFBM 面积的一半?M考点】菱形的性质及判定题型】解答难度】3 星关键词】解析】省略答案】⑴∵ PM ∥AC,EF∥ AB∴四边形AEPM 为平行四边形∵ AB AC ,AD平分CAB∴ CAD BADAD BC,BAD EPACAD EPAEA EPS 四边形 EFBM2 ∵四边形 AEPM 为菱形, ∴ AD EM∵AD BC ∴EM ∥BC 又 EF ∥AB ∴四边形 EFBM 为平行四边形问题:如图 1,在菱形 ABCD 和菱形 BEFG 中,点 A ,B ,E 在同一条直线上, P 是线段 DF 的中点,连结 PG ,PC .若 ABC BEF 60 ,探究 PG 与 PC 的位置 关系及 PG的值.PC小聪同学的思路是:延长 GP 交 DC 于点 H ,构造全等三角形,经过推理 使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题: ⑴ 写出上面问题中线段 PG 与 PC 的位置关系及 PG的值;PC⑵ 将图 1 中的菱形 BEFG 绕点 B 顺时针旋转,使菱形 BEFG 的对角线 BF 恰 好与菱形ABCD 的边 AB 在同一条直线上,原问题中的其他条件不变(如 图 2).你在⑴中得到的两个结论是否发生变化?写出你的猜想并加以 证明. ⑶ 若图 1 中 ABC BEF 2 0 90 ,将菱形 BEFG 绕点 B 顺时针旋转任【考点】菱形的性质及判定,全等三角形的性质和判定,旋转的性 质 题型】解答 难度】 5 星【关键词】 2008 年,北京中考 【解析】省略【答案】⑴ 线段 PG 与 PC 的位置关系是 PG PC ;PG3 .PC∴四边形 AEPM 为菱形 ⑵当 P 为 EF 中点时,S意角度,原问题中的其他条件不变,求 PG 的值(用含的式子表示) .F⑵ 猜想:⑴中的结论没有发生变化.证明:如图,延长 GP 交 AD 于点 H ,连结 CH ,CG .∵ P 是线段 DF 的中点, ∴ FP DP .由题意可知 AD ∥FG .∴ GFP HDP . 又∵ GPF HPD ,∴ GFP ≌ HDP ,∴ GP HP , GF HD .∵四边形 ABCD 是菱形,∴ CD CB , HDC ABC 60 . 由ABC BEF 60 ,且菱形 BEFG 的对角线 BF 恰好与菱形 ABCD 的边 AB 在同 一条直线上,可得 GBC 60 . ∴ HDC GBC . ∵四边形 BEFG 是菱形,∴ GF GB ,∴ HD GB .∴ HDC ≌ GBC ,∴ CH CG , DCHBCG . ∴ DCH HCB BCG HCB 120 ,即 HCG 120 .∵CHCG, PH PG , ∴ PG PC , GCP HCP 60 .∴ PG3.PC⑶PGtan 90 .证明过程略.PC本题是一道探究性的几何综合题,本题的题干是以阅读材料的形式呈 现,从而降低了题目的难度, 本题应该是在 05 年大连中考压轴题的基 础上改进而来的.四、中位线与平行四边形顺次连结面积为 20 的矩形四边中点得到一个四边形,再顺次连结新四 边形四边中点得到一个 ,其面积为 . 【考点】三角形的中位线 【题型】填空 【难度】 3 星【关键词】【解析】理由:由中位线得 EF FG GH HE 1AD 即可.2【答案】 AD BC .如图,在四边形 ABCD 中, AB CD , E 、 F 、 G 、 H 分别是 AB 、 BD 、 CD 、 AC 的中点,要使四边形 EFGH 是菱形,四边形 ABCD 还满足的一个条件 是 ,并说明理由.考点】菱形的性质及判定,三角形的中位线 题型】填空 难度】 3 星 关键词】2009 年,上海模拟 解析】理由:由中位线得 EF FG GH HE 1AD 即可.2 答案】 AD BC .在四边形 ABCD 中, AB CD , P , Q 分别是 AD 、 BC 的中点, M , N 分别是 对角线AC , BD 中点,证明:PQ 与MN互相垂直.考点】菱形的性质及判定,三角形的中位线题型】解答难度】4 星关键词】解析】连接PN , NQ , MQ , PM .证明PNQM 为菱形.答案】见解析四边形ABCD 中,R、P 分别是BC 、CD 上的点,点,当点P在CD上从C向D移动而点R不动时,()A.线段EF 的长逐渐增大B.线段EF 的长逐渐减小C.线段EF 的长不变D.线段EF 的长与点P的位置有关考点】三角形的中位线题型】选择难度】4 星关键词】解析】连结AR ,利用三角形的中位线可得答案】CE、F 分别是AP、RP的中那么下列结论成立的是EF 12 AR与点P无关.如图,ABC 中,AD 是BAC 的平分线,CE AD 于 E ,M 为BC 的中点,AB 14cm ,AC 10cm,则ME 的长为【考点】三角形的中位线【题型】填空【难度】3 星【关键词】【解析】延长CE 交AB 于点线可得14 10 2 cm .2【答案】2N .利用中位线的性质和直角三角形斜边中如图,四边形ABCD 中,AB长,分别交BA,CDCD ,的延长线于点的中点,连结EF 并延CHEBC,ADBGEE,F 分别是G ,H ,求证:【考点】三角形的中位线【题型】解答【难度】4 星【关键词】【解析】省略【答案】连结BD,取BD中点P ,连结PE,PF ,BDC ,DBA 的中位线,所以PE∥DC,PF ∥BA,且PE 所以PE PF ,所以PEF PFE ,由PE∥ DC 可得:所以BGE CHEPE PF ,PFEBGE ,由条件易得1DC ,PF2PEF1BA2CHEPE,PF 分别是,因为AB CD ,,同理可得如图,已知 BE 、 CF 分别为 ABC 中 B 、 C 的平分线, AM BE 于 M,AN CF 于 N ,求证:MN ∥ BC.【考点】三角形的中位线 【题型】解答 【难度】 4 星 【关键词】【解析】延长 AM 、 AN 交 BC 于点 Q 、 R . 由等腰三角形三线合一可得 AM QM 、 ANRN 再由三角形中位线可得 MN ∥ BC .【答案】见解析如图,四边形 ABCD 中,E ,F 分别是边 AB ,CD 的中点,【考点】三角形的中位线 【题型】选择 【难度】 3 星 【关键词】【解析】连结 BD ,取 BD 的中点 P ,连结 FP ,EP ,由三角形的中位线可知 选B 【答案】 B则 AD ,BC 和 EF 的关系是( )A . AD BC 2EFBC .AD BC 2EF DAD BC ≥ 2EF AD BC ≤ 2EF已知如图所示,E、F 、G 、H分别是四边形ABCD 的四边的中点,求证:四边形EFGH 是平行四边形.【考点】平行四边形的性质和判定,三角形的中位线【题型】解答【难度】3 星【关键词】【解析】连接AC .∵ H 、G 分别为AD 、DC 中点∴ HG 1 AC ,HG ∥ AC2 又∵ E、F 分别为AB、BC 中点∴ EF 1 AC ,EF ∥ AC ,∴ HG EF ,HG ∥ EF2 ∴四边形EFGH 为平行四边形【答案】见解析如图,在四边形ABCD 中,E为AB 上一点,ADE 和BCE 都是等边三角形,AB、BC 、CD 、DA的中点分别为P、Q、M 、N ,证明四边形PQMN 为平行四边形且PQ PN .D考点】平行四边形的性质和判定,三角形的中位线题型】解答难度】4 星关键词】2009 年,兰州中考解析】如图,连结AC 、BD .∵ PQ 为 ABC 的中位线 ∴ PQ ∥ AC 且 PQ 1AC2同理 MN ∥ AC 且 MN 1AC2∴ MN ∥ PQ 且 MN PQ∴四边形 PQMN 为平行四边形. 在 AEC 和 DEB 中AE DE , EC EB , AED 60 CEB 即 AEC DEB ∴ AEC ≌ DEB∴AC BD ∴ 1 1.∴ PQ AC BD PN .22【答案】见解析如图,四边形 ABCD 中,AB CD ,E ,F ,G ,H 分别是 AD ,BC ,BD ,AC 的中点,求证: EF ,GH相互垂直平分【考点】菱形的性质及判定,三角形的中位线 【题型】解答 【难度】 3 星 【关键词】【解析】连结 EG ,GF ,FH ,HE ,根据题意, EG ,HF 分别是 DAB , CAB 的中位线, 所 以 EG HF 1AB , 同 理 可 证 : GF EH 1CD , 因为 AB CD , 所以 22EG HF GF EH , 则四边形 EGFH 是菱形,所以 EF ,GH 相互垂直 【答案】见解析ABC 的三条中线分别为 AD 、BE 、CF ,H 为 BC 边外一点,且 BHCF 为平行 四边形,求证: AD ∥ EH.C考点】平行四边形的性质和判定,三角形的中位线题型】解答难度】4 星关键词】【解析】此题解法很多,仅供两种解法参考.方法一:连结DE 、DH .(如图1)∵四边形BHCF 为平行四边形∴CH BF AF 且CH ∥ AF由中位线可得DE 12 AB AF∴ CH DE∴四边形DECH 为平行四边形∴DH ∥ CE 且DH CE AE∴四边形DHEA 为平行四边形∴ AD ∥ EH方法二:连结DE .(如图2)通过中位线和平行四边的性质可得DE HC ,AB∥ DE ∥HC∴ AED ECH 又∵ AE EC显然ADE ≌EHC ∴DAE HEC ∴ AD ∥ EH 【答案】见解析在平行四边形ABCD 的对角线BD上取一点 E ,使BE1 DE ,连接AE 并延长3与DC 的延长线交于F ,则CF 2 AB .OR ∥CD ∥ AB,【考点】三角形的中位线 【题型】解答 【难度】 5 星 【关键词】【解析】法 1:如图 2,取 BD 之中点 O ,由 O 引 OM ∥ AF 交 DF 于 M ,再由 C 引CG ∥FE交BD 于 G .∵ AB CD , ABE CDG , BAE DCG ,∴ ABE ≌ CDG , BE DG , 则 O 为 EG 的中点, ∴ EO OG . 又∵ DG BE 1DE ,3 1∴ EO OG DE ,3即 G 、 O 是 DE 的三等分点. ∵ CG ∥ OM ∥ AF ,∴C 、M 是 DF 的三等分点,有 CF 2CD . 而 CD AB ,∴ CF 2AB .法 2 :如图 3,连接 AC 交 BD 于 O ,则 O 为 AC 、BD 的中点,取 AF 的中点 R , 连接 AC 交 BD 于 O ,则 O 为 AC 、 BD 的中点,取 AF 的中点 R ,连接 OR ,则 1 OR ∥ CF .2图3∴ABE ROE ,BAE ORE.又∵ BE OE OD ,BE 1 DE 1 (OE OD),33由此可得BE 1OD,OE 1DE ,23BE OE ,ABE ≌ROEAB OR.即AB1OR CF ,∴CF2AB.2法3:如图1,∵AB∥DF ,AB BE 1,DF DE 3即DF3AB.又AB CD ,CF DF CD 3 AB AB,即CF2AB.答案】见解析如图,ABC中,E、F分别是AB 、BC的中点,G、H是AC的三等分点,连结并延长EG 、FH交于点D.求证:四边形ABCD是平行四边形.【考点】平行四边形的性质和判定,三角形的中位线【题型】解答【难度】4 星【关键词】【解析】连接BG 、BH 、BD ,设BD 与AC 相交与点O∵E、F 分别是AB 、BC 的中点,∴ EG ∥ BH ,同理FH ∥ BG ∴四边形BHDG 是平行四边形,∴ OB OD ,OG OH∵ AG HC ,∴ OA OC∴四边形ABCD 是平行四边形【答案】见解析如图,在四边形 ABCD 中, M 、 N 分别为 AD 、BC 的中点, BD AC ,BD 和 AC 相交于点O , MN 分别与 AC 、 BD 相交于 E 、 F ,求证 : OE OF .【考点】三角形的中位线 【题型】解答 【难度】 3 星 【关键词】【解析】取 AB 中点 P ,连结 MP 、 NP . 利用中位线可得MP 1BD NP 1AC22∴PMN PNM ∵ MP ∥BD ,NP ∥ AC∴ OFE OEF ∴ OE OF【答案】见解析 如图,线段 AB ,CD 相交于点 O ,且 AB CD , 连结 AD ,BC , E ,F 分别是 AD ,BC的中点, EF 分别交 AB ,CD 于 M ,N ,求证: OM ON考点】三角形的中位线 题型】解答 难度】 4 星关键词】解析】连结 BD ,取 BD 中点 P ,连结 PE ,PF ,由条件易得 PE ,PF 分别是答案】见解析 如图,梯形 ABCD 中,AD ∥ BC ,AB CD ,对角线 AC ,BD 相交于点 O , AOD 60 ,E ,F ,G 分别是 OA ,OB ,CD 的中点,求证 : EFG 是等边三角形【考点】三角形的中位线,直角三角形斜边上的中线等于斜边的一 半,等腰梯形的性质和判定 【题型】解答 【难度】 4 星 【关键词】【解析】省略【答案】 连结 DE ,由等腰梯形对角线相等, 且 AOD 60 ,可证 AOD 是等 边三角形,因为 E 是 OA 中点,所以 DE AC , 在 Rt DCE 中, G 是 DC 中点, 所以 EG 1DC ,同理可证 FG 1DC ,因为 E ,F 分别是 OA ,OB 的中点,所以 22 EF 1AB ,因为 AB DC , 所以 EG FG EF ,即 EFG 是等边三角形2如图,求证:四边形两组对边中点连线与两对角线中点连结这三条线 共点.DBA , BDC 的中位线,所以 PE ∥ BA ,PF ∥ DC , 且 PE 1 BA ,PF 2所以 PE PF ,所以 PEFPFE ONM , 所以 OMNPFE ,由 PE ∥ BA 可得ONM , 所以 OM ONPEF1DC , 因为 AB CD ,2OMN ,同理可得DLD【考点】三角形的中位线【题型】解答 【难度】 5 星 【关键词】【解析】方法一:设 N ,H ,M ,L ,F ,E 分别为 AB ,BC ,CD ,DA ,AC ,BD 的中点, 要证明 EF ,LH ,及MN 三线共点.因为 LF ∥DC 且 LF 1DC ,2所以 EF ∥ DC 且 EF 1DC ,2LF ∥ EH 且 LF EH ,从而四边形 EHFL 为平行四边形,故 LH 与EF 互相平分.设 LH 与 EF 的交点为 O ,则 LH 经过 EF 中点 O (当然也是 LH 中点).同理, MN 也过EF 中点 O .所以, EF ,LH ,MN 三线共点于 O .说明:本题证明的关键是平行四边形 EHFL 的获得(它是通过三角形中 位线定理来证明的) .由此可见,在某些四边形的问题中,通过构造平行四边形去解题是一 种常用的技巧. 请看下例.方法二:应用中点公式法 可设 A x 1,y 1 ,B x 2,y 2 ,C x 3,y 3 ,D x 4 ,y 4 那 么 AC 线 段 的 中 点 坐 标 为 Fx1 x3,y1 y3, BD 线 段 的 中 点 坐 标 为 22Ex 2 x 4 ,y 2 y 4E2 ,2 那么 EF 线段的中点坐标为 x 1 x 2 x3 x4,y 1 y 2 y 3 y422同理可得: MN ,LH的中点坐标也为x1 x2 x3 x4,y1 y2 y3 y422 所以可知: EF , LH , MN 三线共点于 O【答案】见解析如图, O 是平行四边形 ABCD 内任意一点, E , F , G , H 分别是 OA , OB ,OC , OD 的中点.若 DE , CF 交于 P ,DG ,AF 交于 Q , AH , BG 交于 R ,BE ,CH 交 于 S ,求证 :A ENOFHPQ SR .【考点】平行四边形的性质和判定,三角形的中位线【题型】解答【难度】6 星【关键词】【解析】设法证明四边形PORS 为平行四边形.因为F ,G 分别为OB ,OC 的中点,所以FG∥BC,且FG 21BC,FG ∥ AD ,且FG 1 AD ,2从而F 是AQ 中点.同理可证,F 是PC 的中点(EF 是PCD 的中位线).所以四边形APQC 为平行四边形,PQ∥AC,PA AC.同理,RS∥ AC,RS = AC.因此PQ ∥ RS,PQ =RS,即四边形PQRS 为平行四边形,故PQ RS .说明本题证明显示了用平行四边形证题的技巧,平行四边形PQRS ,APQC ,ACRS 像三座互相连接的桥梁一样沟通了条件与结论之间的道路.事实上,由于PQRS 为平行四边形,我们还可得到PQ∥SR,PS∥QR,PS QR,SQ与PR互相平分等等一系列结论.F为AQ的中点(同样G 为DQ 的中点)的断言可以证明于下:取AD 中点M ,连MF ,则FG ∥ MD 且FG MD ,所以四边形MFGD 为平行四边形,MF ∥ DG .因此F 为AQ 的中点.答案】见解析。
自学初中数学资料-菱形的性质及判定(资料附答案)

自学资料一、菱形及其性质【知识探索】1.有一组邻边相等的平行四边形叫做菱形.【说明】菱形的面积还可用对角线乘积除以2求得.2.菱形的性质:(1)菱形的四条边都相等;(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角.【说明】(1)菱形具有平行四边形的所有性质;(2)菱形既是中心对称图形,又是轴对称图形.1个对称中心,对称中心是其对角线的交点;2条对称轴,对称轴是其对角线所在的直线.【错题精练】第1页共16页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训例1.(2002•杭州)如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD等于()A. 4B. 3C. 2D. 1【解答】C【答案】C【举一反三】1.菱形在平面直角坐标系中的位置如图所示,若,,则点的坐标是__________。
【解答】二、菱形的判定【知识探索】1.菱形的判定:(1)对角线互相垂直的平行四边形是菱形;(2)四条边都相等的四边形是菱形.第2页共16页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训【错题精练】例1.如图.若要使平行四边形ABCD成为菱形.则需要添加的条件是()A. AB=CDB. AD=BCC. AB=BCD. AC=BD【解答】C【答案】C例2.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH 是菱形,四边形ABCD还应满足的一个条件是__________.【解答】菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.据此四边形ABCD还应满足的一个条件是AD=BC.等.答案不唯一.例3.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.(1)求证:四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.第3页共16页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训【答案】例4.△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.(1)如图(a)所示,当点D在线段BC上时.①求证:△AEB≌△ADC;②探究四边形BCGE是怎样特殊的四边形?并说明理由;(2)如图(b)所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立;第4页共16页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训(3)在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.【解答】此题要熟练多方面的知识,特别是全等三角形和平行四边形和菱形的判定.证明:(1)①∵△ABC和△ADE都是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAC=60°.(1分)又∵∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD,∴∠EAB=∠DAC,∴△AEB≌△ADC(SAS).(3分)②方法一:由①得△AEB≌△ADC,∴∠ABE=∠C=60°.又∵∠BAC=∠C=60°,∴∠ABE=∠BAC,∴EB∥GC.(5分)又∵EG∥BC,∴四边形BCGE是平行四边形.(6分)方法二:证出△AEG≌△ADB,得EG=AB=BC.(5分)∵EG∥BC,∴四边形BCGE是平行四边形.(6分)(2)①②都成立.(8分)(3)当CD=CB (∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.(9分)理由:方法一:由①得△AEB≌△ADC,∴BE=CD(10分)又∵CD=CB,∴BE=CB.(11分)由②得四边形BCGE是平行四边形,∴四边形BCGE是菱形.(12分)方法二:由①得△AEB≌△ADC,∴BE=CD.(9分)又∵四边形BCGE是菱形,∴BE=CB(11分)∴CD=CB.(12分)方法三:∵四边形BCGE是平行四边形,∴BE∥CG,EG∥BC,∴∠FBE=∠BAC=60°,∠F=∠ABC=60°(9分)∴∠F=∠FBE=60°,∴△BEF是等边三角形.(10分)第5页共16页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训又∵AB=BC,四边形BCGE是菱形,∴AB=BE=BF,∴AE⊥FG(11分)∴∠EAG=30°,∵∠EAD=60°,∴∠CAD=30度.(12分)例5.如图,四边形ABCD中,AD∥BC,AD=DC=BC,过AD的中点E作AC的垂线,交CB的延长线于F.求证:(1)四边形ABCD是菱形.(2)BF=DE.【解答】(1)有一组邻边相等的平行四边形为菱形,AD和BC既平行又相等,所以四边形ABCD为平行四边形,而AD=DC=BC,所以平行四边形ABCD为菱形;(2)要证BF=DE,而在原题中已知AE=DE,所以证明的方向就变为证BF=AE,而证BF=AE则可以通过证△FBM≌△EAM来实现.证明:(1)∵AD∥BC,AD=BC(已知),∴四边形ABCD为平行四边形.又邻边AD=DC,∴四边形ABCD为菱形;(3分)(2)证法一:如图:记EF与AC交点为G,EF与AB的交点为M.由(1)证得四边形ABCD为菱形,所以对角线AC平分∠A,即∠BAC=∠DAC.又∵EF⊥AC,AG=AG,∴△AGM≌△AGE,∴AM=AE.(6分)又∵E为AD的中点,四边形ABCD为菱形,∴AM=BM.∠MAE=∠MBF.又∵∠BMF=∠AME,∴△BMF≌△AME.∴BF=AE.第6页共16页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训∴BF=DE.(8分)证法二:如图:连接BD∵四边形ABCD为菱形∴BD⊥AC∵EF⊥AC∴EF∥BD∵BF∥DE∴四边形BDEF是平行四边形∴BF=DE(8分)【举一反三】1.如图,下列条件之一能使平行四边形ABCD是菱形的为()①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.A. ①③B. ②③C. ③④D. ①②③【答案】A2.(2002•咸宁)如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4.梯形的高DH与中位线EF交于点G,则下列结论中:①△DGF≌△EBH;②四边形EHCF是菱形;③以CD为直径的圆与AB相切于点E.正确的有()A. 1个B. 2个C. 3个第7页共16页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训D. 0个【解答】C【答案】C3.如图,在等腰梯形ABCD中,AD∥BC,BD⊥CD,点E是BC的中点且DE∥AB,则∠BCD的度数是__________.【解答】首先根据BD⊥CD,点E是BC的中点可知DE=BE=EC=BC,又知DE∥AB,AD∥BC,可知四边形ABED是菱形,于是可得到AB=DE,再根据四边形ABCD是等腰梯形,可得AB=CD,进而得到DC=BC,然后可求出∠DBC=30°,最后求出∠BCD=60°.4.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是__________.【解答】菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.据此四边形ABCD还应满足的一个条件是AD=BC.等.答案不唯一.5.如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.(1)求△ABC所扫过的图形的面积;(2)试判断AF与BE的位置关系,并说明理由;(3)若∠BEC=15°,求AC的长.第8页共16页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训【解答】(1)根据题意:易得△ABC≌△EFA,BA∥EF,且BA=EF,进而得出S平行四边形ABFE=2S△EAF,故可求出△ABC扫过图形的面积为S平行四边形ABFE;(2)根据平移的性质,可得四边形ABFE为菱形,故AF与BE互相垂直且平分;(3)根据题意易得:所以∠AEB=∠ABE=15°,BD•AC=3,可得AC•AC=3,进而可得AC的长度.6.如图,在∠ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.(1)求证:四边形BDEF是菱形;(2)若AB=12cm,求菱形BDEF的周长.【解答】(1)可根据菱形的定义“一组邻边相等的平行四边形是菱形”,先证明四边形BFED是平行四边形,然后再证明四边形的邻边相等即可.(2)F是AB的中点,有了AB的长也就求出了菱形的边长BF的长,那么菱形BDEF的周长也就能求出了.(1)证明:∵D、E、F分别是BC、AC、AB的中点,∴DE∥AB,EF∥BC,∴四边形BDEF是平行四边形,又∵DE=AB,EF=BC,且AB=BC,∴DE=EF,∴四边形BDEF是菱形;(2)7.如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E.DF平分∠ADC交BC于F.第9页共16页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训(1)求证:△ABE≌△CDF;(2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.【解答】(1)由平行四边形ABCD可得出的条件有:①AB=CD,②∠A=∠C,③∠ABC=∠CDA;已知BE、CD分别是等角∠ABD、∠CDA的平分线,易证得∠ABE=∠CDF④;联立①②④,即可由ASA 判定所求的三角形全等;(2)由(1)的全等三角形,易证得DE=BF,那么DE和BF平行且相等,由此可判定四边形BEDF是平行四边形,根据对角线垂直的平行四边形是菱形即可得出EBFD的形状.(1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AB=CD,∠ABC=∠ADC,∵BE平分∠ABC,DF平分∠ADC,∴∠ABE=∠CDF(2分),∴△ABE≌△CDF(ASA);(4分)(2)1.如图,在菱形ABCD中,BC=3,点是BD的中点,延长BD到点E,使得BD=DE=2,连结CE,点M是CE的中点,则OM=.【答案】√17.22.如图,将矩形ABCD沿对角线BD翻折,点C落在C′处,BC′交AD于点E,DF∥BE交BC于点F.第10页共16页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训(1)求证:四边形BEDF是菱形.(2)若AB=4,AD=8,请求出菱形BEDF的边长.【解答】(1)证明:∵四边形ABCD是矩形,∴AB=CD,∠A=∠C=90∘,AD∥BC,∵DF∥BE,∴四边形BEDF是平行四边形,由折叠,得∠Capos;=∠C,DCapos;=DC,∴∠A=∠Capos;,AB=DCapos;,又∵∠AEB=∠Capos;ED,∴△AEB≌△C′ED(AAS),∴EB=ED,∴四边形BEDF是菱形;(2)解:设AE=x,则BE=8−x,在Rt△ABE中,由勾股定理,得42+x2=(8−x)2,解得x=3,∴BE=8−3=5,即菱形BEDF的边长为5.【答案】(1)略;(2)5.3.如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABC沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:①若∠A=70∘,则∠ABC=35∘;②若点F是CD的中点,则S△ABE=1S ABCD3下列判断正确的是()A. ①,②都对;B. ①,②都错;C. ①对,②错;D. ①错,②对.【答案】A4.如图,点E,F分别在▱ABCD的边BC,AD上.(1)若BE=DF,求证:四边形AECF是平行四边形;(2)请在图2中用圆规和直尺画出四边形AECF,使得四边形AECF是菱形.(不写作法,保留作图痕迹)【解答】(1)证明:四边形AECF为平行四边形.∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,又∵BE=DF,∴AF=CE,∴四边形AECF为平行四边形;(2)解:如图,四边形AECF就是所求作的菱形.【答案】略.5.如图,在正三角形网格中,菱形M经过旋转变换能得到菱形N,下列四个点中能作为旋转中心的是()A. 点A;B. 点B;C. 点C;D. 点D.【答案】D6.如图,已知在Rt△ABC中,∠ACB=90∘,AC=6,BC=8,BE平分∠ABC交AC于点E,EF⊥AB,垂足为F.(1)求EF的长度;(2)作CD⊥AB,垂足为D,CD与BE相交于G,试说明:CE=CG;(3)连接FG,试说明:四边形CEFG是菱形.【解答】(1)解:∵BE平分∠ABC,∠ACB=90∘,EF⊥AB,垂足为F,∴EF=CE.在△BFE与△BCE中,∠C=∠BFE=90∘,{BE=BE,EF=EC∴△BFE≌△BCE,∴BF=BC=8.∵在Rt△ABC中,∠ACB=90∘,AC=6,BC=8,∴AB=10,∴AF=AB−BF=2.设EF=x,则CE=x,AE=6−x,在直角△AEF中,由勾股定理,得AE2=EF2+AF2,∴(6−x)2=x2+22,解得x=8;3(2)证明:∵在△BCE中,∠CEB=90∘−∠CBE,∠CGE=∠DGB=90∘−∠DBG,∴∠CEB=∠CGE,∴CE=CG;(3)证明:CD⊥AB,EF⊥AB,∴CD∥EF,∵EF=CE,CE=CG,∴EF=CG,∴四边形CEFG是平行四边形,又∵CE=CG,∴CEFG是菱形.;(2)略;(3)略.【答案】(1)837.如图,已知在Rt△ABC中,∠ACB=90∘,AC=6,BC=8,BE平分∠ABC交AC于点E,EF⊥AB,垂足为F.(1)求EF的长度;(2)作CD⊥AB,垂足为D,CD与BE相交于G,试说明:CE=CG;(3)连接FG,试说明:四边形CEFG是菱形.【解答】(1)解:∵BE平分∠ABC,∠ACB=90∘,EF⊥AB,垂足为F,∴EF=CE.在△BFE与△BCE中,∠C=∠BFE=90∘,{BE=BE,EF=EC∴△BFE≌△BCE,∴BF=BC=8.∵在Rt△ABC中,∠ACB=90∘,AC=6,BC=8,∴AB=10,∴AF=AB−BF=2.设EF=x,则CE=x,AE=6−x,在直角△AEF中,由勾股定理,得AE2=EF2+AF2,∴(6−x)2=x2+22,解得x=8;3(2)证明:∵在△BCE中,∠CEB=90∘−∠CBE,∠CGE=∠DGB=90∘−∠DBG,,∴∠CEB=∠CGE,∴CE=CG;(3)证明:CD⊥AB,EF⊥AB,∴CD∥EF,∵EF=CE,CE=CG,∴EF=CG,∴四边形CEFG是平行四边形,又∵CE=CG,∴CEFG是菱形.【答案】(1)8;(2)略;(3)略.3● 矩形。
最全初中数学知识点总结及公式(可打印)

最全初中数学知识点总结及公式(可打印)最全初中数学知识点总结1.菱形的定义:一组相邻边相等的平行四边形称为菱形。
2、菱形的性质:⑴ 矩形具有平行四边形的一切性质;⑵ 菱形的四条边都相等;⑶ 菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
⑷ 菱形是轴对称图形。
提示:利用菱形的性质可证得线段相等、角相等,它的对角线互相垂直且把菱形分成四个全等的直角三角形,由此又可与勾股定理联系,可得对角线与边之间的关系,即边长的平方等于对角线一半的平方和。
3.因式分解的定义:把一个多项式变换成几个代数表达式的乘积,叫做这个多项式的因式分解。
4、因式分解要素:①结果必须是整式②结果必须是积的形式③结果是等式④因式分解与整式乘法的关系:m(a+b+c)5.公因式:多项式的每一项所包含的公因式称为这个多项式的每一项的公因式。
6、公因式确定方法:①系数是整数时取各项最大公约数。
②相同字母取最低次幂③系数最大公约数与相同字母取最低次幂的积就是这个多项式各项的公因式。
7、提取公因式步骤:①确定公因式。
②确定商式③公因式与商式写成积的形式。
8、平方根表示法:一个非负数a的平方根记作,读作正负根号a。
a叫被开方数。
9、中被开方数的取值范围:被开方数a≥010、平方根性质:①一个正数的平方根有两个,它们互为相反数。
②0的平方根是它本身0。
③负数没有平方根开平方;求一个数的平方根的运算,叫做开平方。
11.平方根和算术平方根的区别:定义不同,表述不同,数字不同,取值范围不同。
12、联系:二者之间存在着从属关系;存在条件相同;0的算术平方根与平方根都是013、含根号式子的意义:表示a的平方根,表示a的算术平方根,表示a的负的平方根。
14、求正数a的算术平方根的方法;完全平方数类型:①想谁的平方是数a。
②所以a的平方根是多少。
③用式子表示。
求正数a的算术平方根,只需找出平方后等于a的正数。
初中数学知识点总结及公式1、一元二次方程解法:(1)配方法:(X±a)²=b(b≥0)注:二次项系数必须化为1(2)公式法:aX²+bX+C=0(a≠0)确定a,b,c的值,计算b²-4ac≥0若b²-4ac>0则有两个不相等的实根,若b²-4ac=0则有两个相等的实根,若b²-4ac<0则无解若b²-4ac≥0则用公式X=-b±√b²-4ac/2a注:必须化为一般形式(3)分解因式法①提公因式法:ma+mb=0→m(a+b)=0平方差公式:a²-b²=0→(a+b)(a-b)=0②运用公式法:完全平方公式:a²±2ab+b²=0→(a±b)²=0③十字相乘法2、锐角三角函数定义锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
菱形的性质与判定之八大考点(解析版)--初中数学专题训练 (1)

菱形的性质与判定之八大考点【考点导航】目录【典型例题】【考点一利用菱形的性质求角度】【考点二利用菱形的性质求线段长】【考点三利用菱形的性质求面积】【考点四利用菱形的性质证明】【考点五添一个条件使四边形是菱形】【考点六证明四边形是菱形】【考点七根据菱形的性质与判定求角度、线段长】【考点八根据菱形的性质与判定求面积】【过关检测】【典型例题】【考点一利用菱形的性质求角度】1(2023秋·陕西汉中·九年级统考期末)如图,在菱形ABCD中,对角线AC、BD相交于点O,若∠BAD =110°,则∠OBC的度数为________.【答案】35°##35度【分析】根据菱形的性质进行求解即可.【详解】解:∵四边形ABCD是菱形,∴AD∥BC,∠OBA=∠OBC=1∠ABC,2∵∠BAD=110°,∴∠ABC=180°-∠BAD=70°,∴∠OBC=1∠ABC=35°,2故答案为:35°.【点睛】本题主要考查了菱形的性质,熟知菱形的对角线平分一组对角是解题的关键.【变式训练】1(2023春·重庆渝中·八年级重庆巴蜀中学校考阶段练习)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若∠BCD=50°,则∠DHO的度数为.【答案】25°##25度【分析】根据菱形的性质求出∠BDA=∠ABD=65°,再根据斜边中线等于斜边一半得出∠BDH=∠OHD=25°即可.【详解】解:∵四边形ABCD是菱形,∴OD=OB,AB=AD,∠BCD=∠BAD=50°,∴∠BDA=∠ABD=65°∵DH⊥AB,∴OH=OD=OB,∠ADH=40°,∴∠BDH=∠OHD=25°,故答案为:25°.【点睛】本题考查了菱形的性质和直角三角形的性质,解题关键是根据菱形和直角三角形的性质得出角之间的关系.2(2023春·八年级单元测试)如图,在菱形ABCD中,∠ABC=40°,点E为对角线BD上一点,F为AD边上一点,连接AE、CE、FE,若AE=FE,∠BEC=58°,则∠AFE的度数为.【答案】38°##38度【分析】根据四边形的性质,得出∠ABD=∠CBD=12∠ABC=20°,根据SAS证明△ABE≌△CBE,得出∠AEB=∠BEC=58°,根据三角形内角和得出∠BAE=180°-∠ABE-∠AEB= 102°,根据平行线的性质,得出∠BAD=180°-∠ABC=140°,得出∠EAF=∠BAD-∠BAE=38°,根据等腰三角形的性质,即可得出答案.【详解】解:∵四边形ABCD为菱形,∠ABC=40°,∴AB=BC=AD,AD∥BC,∠ABD=∠CBD=12∠ABC=20°,∵在△ABE和△CBE中AB=BC∠ABE=∠CBE BE=BE,∴△ABE≌△CBE,∴∠AEB=∠BEC=58°,∴∠BAE=180°-∠ABE-∠AEB=102°,∵AD∥BC,∴∠BAD =180°-∠ABC =140°,∴∠EAF =∠BAD -∠BAE =38°,∵AE =FE ,∴∠AFE =∠EAF =38°.故答案为:38°.【点睛】本题主要考查了菱形的性质,平行线的性质,三角形全等的判定和性质,等腰三角形的性质,解题的关键是熟练掌握菱形的性质,证明△ABE ≌△CBE .【考点二利用菱形的性质求线段长】1例题:(2023·辽宁鞍山·统考一模)如图,在菱形ABCD 中,对角线AC ,BD 分别为8和6,DE ⊥AB ,垂足为E ,则DE 的长为______.【答案】245【分析】利用菱形的性质,求出菱形的边长,再用等积法求出线段DE 的长即可.【详解】解:设AC ,BD 交于点O ,∵在菱形ABCD 中,对角线AC ,BD 分别为8和6,∴AC ⊥BD ,OA =12AC =4,OB =12BD =3,∴AB =32+42=5,∵DE ⊥AB ,∴菱形ABCD 的面积=12AC ⋅BD =AB ⋅DE ,即:12×8×6=5DE ,∴DE =245;故答案为:245.【点睛】本题考查菱形的性质.熟练掌握菱形的对角线互相垂直平分,是解题的关键.【变式训练】1(2023·广东东莞·东莞市东莞中学初中部校考一模)如图,菱形ABCD 对角线AC 、BD 相交于点O ,AC =8,BD =6,则菱形的边长为.【答案】5【分析】根据菱形的对角线互相垂直及勾股定理即可求解.【详解】解:依题意可知BD⊥AC,AO=4,BO=3∴AB=32+42=5,故答案为:5.【点睛】此题主要考查菱形的性质,勾股定理,解题的关键是熟知菱形的对角线垂直.2(2022秋·陕西榆林·九年级校考期末)如图,已知四边形ABCD是菱形,且AE⊥BC于点E,AF⊥CD于点F.(1)求证:AE=AF;(2)若AB=10,CE=4,求菱形ABCD的面积.【答案】(1)证明见解析(2)80【分析】(1)根据菱形的性质,得AB=AD,∠B=∠D;根据AE⊥BC于点E,AF⊥CD于点F,则△ABE≅△ADF,即可;(2)根据菱形的性质,得AB=BC,根据AB=10,CE=4,勾股定理,求出AE,即可求出菱形的面积.【详解】(1)证明,如下:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,∵AE⊥BC于点E,AF⊥CD于点F,∴∠AEB=∠AFD=90°,∴△ABE≅△ADF,∴AE=AF.(2)∵四边形ABCD是菱形,∴AB=BC,∵AB=10,CE=4,∴BE=6,∴AE=AB2-BE2=102-62=8,∴菱形ABCD的面积为:BC×AE=10×8=80.【点睛】本题考查菱形的知识,解题的关键是掌握菱形的性质,勾股定理,全等三角形的知识.【考点三利用菱形的性质求面积】1(2023春·广东韶关·八年级校考期中)如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AC =7,BD =4,则菱形ABCD 的面积为_______.【答案】14【分析】根据菱形的面积等于对角线乘积的一半即可解答.【详解】解:∵四边形ABCD 是菱形,AC =7,BD =4,∴菱形ABCD 的面积=12AC ⋅BD =12×7×4=14,故答案为:14.【点睛】本题主要考查了菱形的性质,熟练掌握菱形的面积等于对角线乘积的一半,是解题的关键.【变式训练】1(2023春·广东惠州·八年级校考阶段练习)菱形的两条对角线长为6和8,则菱形的边长为,面积为.【答案】 524【分析】根据菱形的对角线平分且垂直的性质,先计算边长,由对角线乘积的一半求得面积.【详解】解∵菱形的两条对角线长分别为6和8,∴由勾股定理得,菱形的边长=32+42=5,∵菱形的面积=对角线乘积的一半,∴菱形的面积=6×8÷2=24.故答案为:5,24.【点睛】本题主要考查了菱形的性质,菱形的面积公式,勾股定理等知识点,灵活运用性质进行计算是解此题的关键.2(2023春·浙江·八年级专题练习)如图,菱形ABCD 中,对角线AC 与BD 相交于点O ,若AB =25cm ,AC =4cm ,则BD 的长为__cm ,菱形ABCD 的面积为cm 2.【答案】 816【分析】利用菱形对角线互相垂直且平分的性质结合勾股定理得出BD 的长,再根据菱形面积等于对角线乘积的一半即可得出答案.【详解】解:∵菱形ABCD 中,对角线AC ,BD 相交于点O ,AC =4cm ,∴AC ⊥BD ,BO =OD =12BD ,AO =OC =12AC =2cm ,∵AB =25cm ,∴BO =AB 2-AO 2=4cm ,∴BD =2BO =8cm ,∴菱形面积为12AC ⋅BD =12×4×8=16,故答案为:8,16.【点睛】此题主要考查了菱形的性质以及勾股定理的应用,熟练掌握菱形的性质,运用勾股定理解直角三角形,是解题关键.【考点四利用菱形的性质证明】1(2023春·湖北襄阳·八年级统考阶段练习)如图,四边形ABCD 是菱形,点E ,F 分别在边AB ,AD 的延长线上,且BE =DF ,连接CE ,CF .求证:CE =CF .【答案】证明见解析【分析】根据菱形的性质得到BC =CD ,∠ADC =∠ABC ,根据SAS 证明△BEC ≌△DFC ,可得CE =CF .【详解】解:∵四边形ABCD 是菱形,∴BC =CD ,∠ADC =∠ABC ,∴∠CDF =∠CBE ,在△BEC 和△DFC 中,BE =DF∠CBE =∠CDF BC =CD,∴△BEC ≌△DFC SAS ,∴CE =CF .【点睛】本题考查了菱形的性质,全等三角形的判定和性质,解题的关键是根据菱形得到判定全等的条件.【变式训练】1(2023·浙江嘉兴·统考中考真题)如图,在菱形ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,连接EF(1)求证:AE =AF ;(2)若∠B =60°,求∠AEF 的度数.【答案】(1)证明见解析(2)60°【分析】(1)根据菱形的性质的三角形全等即可证明AE =AF .(2)根据菱形的性质和已知条件可推出∠BAD 度数,再根据第一问的三角形全等和直角三角形的性质可求出∠BAE 和∠DAF 度数,从而求出∠EAF 度数,证明了等边三角形AEF ,即可求出∠AEF 的度数.【详解】(1)证明:∵菱形ABCD ,∴AB =AD ,∠B =∠D ,又∵AE ⊥BC ,AF ⊥CD ,∴∠AEB =∠AFD =90°.在△AEB 和△AFD 中,∠AEB =∠AFD∠B =∠D AB =AD,∴△ABE ≌△ADF (AAS ).∴AE =AF .(2)解:∵菱形ABCD ,∴∠B +∠BAD =180°,∵∠B =60°,∴∠BAD =120°.又∵∠AEB =90°,∠B =60°,∴∠BAE =30°.由(1)知△ABE ≌△ADF ,∴∠BAE =∠DAF =30°.∴∠EAF =120°-30°-30°=60°.∵AE =AF ,∴△AEF 等边三角形.∴∠AEF =60°.【点睛】本题考查了三角形全等、菱形的性质、等边三角形的性质,解题的关键在于熟练掌握全等的方法和菱形的性质.2(2023春·广东肇庆·八年级校考期中)如图,在菱形ABCD 中,AB 的垂直平分线交对角线AC 于点F ,交AB 于点E ,连接DF.(1)求证:AF =DF ;(2)若∠BAD =70°,求∠FDC 的度数.【答案】(1)证明见解析(2)∠FDC =75°【分析】(1)连接BF ,由线段垂直平分线的性质得AF =BF ,再证△BCF ≌△DCF (SAS ),得BF =DF ,即可得出结论;(2)由全等三角形的性质得∠FDC =∠FBC ,再由菱形的性质得∠BCF =∠DCF =∠BAC ,∠ABC =180°-∠BAD =110°,然后求出∠FBA =∠BAC =35°,则∠FBC =∠ABC -∠ABF =75°,即可得出答案.【详解】(1)证明:连接BF ,如图所示:∵EF 是线段AB 的垂直平分线,∴AF =BF ,∵四边形ABCD 是菱形,∴BC =DC ,∠BCF =∠DCF ,在△BCF 和△DCF 中,BC =DC∠BCF =∠DCF CF =CF,∴△BCF ≌△DCF (SAS ),∴BF =DF ,∴AF =DF ;(2)解:由(1)知△BCF ≌△DCF (SAS ),∴∠FDC =∠FBC ,∵四边形ABCD 是菱形,∴AB =BC ,∠BAC =12∠BAD =12×70°=35°,AD ∥BC ,∴∠BCF =∠DCF =∠BAC ,∠ABC =180°-∠BAD =180°-70°=110°,∵EF 是线段AB 的垂直平分线,∴AF =BF ,∴∠FBA =∠BAC =35°,∴∠FBC =∠ABC -∠ABF =110°-35°=75°,∴∠FDC =∠FBC =75°.【点睛】本题考查了菱形的性质、全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的性质等知识;熟练掌握菱形的性质,证明△BCF ≌△DCF (SAS )是解题的关键.【考点五添一个条件使四边形是菱形】1(2023·黑龙江牡丹江·统考二模)如图,四边形ABCD 是平行四边形.请添加一个条件_______,使平行四边形ABCD 为菱形.(只填一种情况即可)【答案】AB=AD(符合题意即可)【分析】根据菱形的判定定理进行求解即可.【详解】解:∵四边形ABCD是平行四边形.∴添加AB=AD,则可得ABCD为菱形.(一组邻边相等的平行四边形是菱形)故答案为:AB=AD(符合题意即可)【点睛】本题考查了菱形的判定,熟练掌握菱形的判定是解题的关键.【变式训练】1(2023·安徽·校联考一模)如图,四边形ABCD的对角线AC,BD相交于点O,若AB∥CD,AO= CO,想要判断四边形ABCD是菱形,则可以添加一个条件是.【答案】AB=AD(答案不唯一)【分析】根据菱形的判定方法进行解答即可.【详解】解:∵AB∥CD,∴∠OAB=∠OCD,∠OBA=∠ODC,∵AO=CO,∴△AOB≌△COD,∴AB=CD,∵AB∥CD,∴四边形ABCD为平行四边形,如果添加AB=AD,可以通过有一组邻边相等的平行四边形是菱形,判断四边形ABCD为菱形;故答案为:AB=AD(答案不唯一).【点睛】本题主要考查了三角形全等的判定和性质,平行四边形的判定,平行线的性质,菱形的判定,解题的关键是熟练掌握菱形的判定方法.2(2023春·湖南永州·八年级统考期中)如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC 的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是.【答案】AD=BC【分析】菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.据此四边形ABCD还应满足的一个条件是AD=BC等.答案不唯一.【详解】解:条件是AD=BC.∵EH,GF分别是△ABC、△BCD的中位线,∴EH∥BC,EH=12BC,GF∥BC,GF=12BC,∴EH∥GF,EH=GF,∴四边形EFGH是平行四边形.∵HG是△ACD的中位线,∴HG=12AD,∵AD=BC,∴EH=HG,∴四边形EFGH是菱形.故答案为:AD=BC【点睛】此题主要考查三角形的中位线定理和菱形的判定,正确理解三角形的中位线的性质及菱形的判定定理是解题的关键.【考点六证明四边形是菱形】1(2023·吉林长春·统考一模)如图,在四边形ABCD中,AB∥CD,AD∥BC.过点D分别作DE⊥AB 于点E,DF⊥BC于点F,且DE=DF.求证:四边形ABCD是菱形.【答案】见解析【分析】根据AB∥CD,AD∥BC,得出四边形ABCD是平行四边形,进而证明△ADE≌△CDF AAS得出AD=DC,即可证明四边形ABCD是菱形.【详解】证明:∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∴∠A=∠C,∵DE⊥AB于点E,DF⊥BC于点F,∴∠AED=∠CFD=90°,∵DE=DF,∴△ADE≌△CDF AAS,∴AD=DC,∴四边形ABCD是菱形.【点睛】本题考查了菱形的判定,全等三角形的性质与判定,熟练掌握菱形的判定定理是解题的关键.【变式训练】1(2023春·广东惠州·八年级校考期中)▱ABCD的对角线AC的垂直平分线与边AD、BC分别交于E,F,求证:四边形AFCE是菱形?【答案】是菱形,见解析【分析】根据“对角线互相垂直的平行四边形”证明即可.【详解】证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAO=∠FCO,∠AEO=∠CFO,∵EF垂直平分AC,∴OA=OC,∴△AOE≌△COF AAS,∴OE=OF,∴四边形AFCE是平行四边形,∵EF⊥AC,∴四边形AFCE是菱形.【点睛】本题主要考查了平行四边形的性质、菱形的判定、全等三角形的判定与性质.关键是根据题意推出OE=OF,题目比较典型,难度适中.2(2023·吉林长春·统考二模)如图,AC为▱ABCD的对角线,点E、F分别在边AB、AD上,AE= AF,连接EF交AC于点G.若AC⊥EF,求证.四边形ABCD是菱形.【答案】见解析【分析】根据AE=AF和AC⊥EF得到∠BAC=∠DAC,然后结合平行四边形的性质得到BA= BC,进而证明出四边形ABCD是菱形.【详解】∵AE=AF,∴∠AEF=∠AFE.∵AC⊥EF,∴∠BAC=∠DAC.∵四边形ABCD是平行四边形,∴AD∥BC.∴∠CAD=∠ACB.∴∠BAC=∠BCA.∴BA=BC.∴四边形ABCD是菱形.【点睛】此题考查了平行四边形的性质,菱形的性质和判定等知识,解题的关键是熟练掌握以上知识点.【考点七根据菱形的性质与判定求角度、线段长】1(2023春·全国·八年级专题练习)如图,BD是△ABC的角平分线,过点D作DE⎳BC交AB于点E,DF⎳AB交BC于点F.(1)求证:四边形BEDF是菱形;(2)如果∠A=80°,∠C=30°,求∠BDE的度数.【答案】(1)证明见解析;(2)∠BDE=35°.【分析】(1)由题意可证BE=DE,四边形BEDF是平行四边形,即可证四边形BEDF为菱形;(2)先根据三角形的内角和定理得出∠ABC=180°-80°-30°=70°,再由菱形的性质可求解.【详解】(1)证明:∵DE⎳BC,DF⎳AB,∴四边形DEBF是平行四边形,∵DE⎳BC,∴∠EDB=∠DBF,∵BD平分∠ABC,∠ABC,∴∠ABD=∠DBC=12∴∠ABD=∠EDB,∴DE=BE,又四边形BEDF为平行四边形,∴四边形BEDF为菱形.(2)∵∠A=80°,∠C=30°,∴∠ABC=180°-80°-30°=70°,∵四边形BEDF为菱形,∴∠EDF=∠ABC=70°,∠EDF=35°.∴∠BDE=12【点睛】本题考查了菱形的判定和性质,等腰三角形的判定等知识,掌握菱形的判定定理是本题的关键.【变式训练】1(2023春·广东惠州·九年级校考开学考试)如图,△ABC中,∠ACB的平分线交AB于点D,作CD的垂直平分线,分别交AC、DC、BC于点E、G、F,连接DE、DF.(1)求证:四边形DFCE是菱形;(2)若∠ABC=60°,∠ACB=45°,BD=2,试求BF的长.【答案】(1)见解析(2)1+3【分析】(1)根据垂直平分线的性质可得DE=CE,DF=FC,根据角平分线的性质可得∠ECG=∠FCG,根据全等三角形的判定和性质可得GE=GF,根据平行四边形的判定可得四边形DFCE是平行四边形,根据菱形的判定可得四边形DFCE是菱形;(2)过D作DH⊥BC于H,构建直角三角形,根据30°的直角三角形性质可得BH=1,根据勾股定理可得DH=3,根据菱形的性质可得DF∥AC,根据平行线的性质可得∠DFB=∠ACB=45°,推得△DHF是等腰直角三角形,可得DH=FH=3,从而得结论.【详解】(1)证明:∵EF是DC的垂直平分线,∴DE=CE,DF=FC,∠EGC=∠FGC=90°,DG=CG∵CD平分∠ACB,∴∠ECG=∠FCG,∵CG=CG,∴△CGE≌△CGF ASA,∴GE=GF,∴四边形DFCE是平行四边形,∵DE=CE,∴四边形DFCE是菱形;(2)解:过D作DH⊥BC于H,则∠DHF=∠DHB=90°,∵∠ABC=60°,∴∠BDH=30°,BD=1,∴BH=12在Rt△DHB中,DH=22-12=3,∵四边形DFCE是菱形,∴DF∥AC,∴∠DFB=∠ACB=45°,∴△DHF是等腰直角三角形,∴DH=FH=3,∴BF=BH+FH=1+3.【点睛】本题考查了垂直平分线的性质,角平分线的性质,全等三角形的判定和性质,平行四边形的判定,菱形的判定和性质,等腰直角三角形的判定和性质,平行线的性质,30度角的直角三角形的性质,熟练掌握菱形的判定是解题的关键.2(2023·广东广州·校考二模)如图,在平行四边形ABCD中,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=10,BD=2,求OE的长度.【答案】(1)证明见解析;(2)3【分析】(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DCA,得出CD=AD=AB=BC,即可得出结论;(2)先判断出OE=OA=OC,再求出OB=1,利用勾股定理求出OA=3,即可得出结论.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,AD=BC∴∠OAB=∠DCA,∵AC平分∠BAD,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD=AB=BC,∴四边形ABCD是菱形;(2)解:∵四边形ABCD是菱形,∴OA=OC,BD⊥AC,∵CE⊥AB,AC=OA=OC,∴OE=12∵BD=2,BD=1,∴OB=12在Rt△AOB中,AB=10,OB=1,∴OA=AB2-OB2=102-12=3,∴OE=OA=3.【点睛】本题考查了平行四边形的性质,角平分线的定义,等腰三角形的判定,菱形的判定与性质,直角三角形的性质,勾股定理等知识,熟练掌握菱形的判定与性质是解答本题的关键.3(2023春·全国·八年级专题练习)如图,平行四边形ABCD中,AD=BD,过点C作CE∥BD,交AD的延长线于点E.(1)求证:四边形BDEC 是菱形;(2)连接BE ,若AB =6,AD =9,则BE 的长为.【答案】(1)见解析(2)122【分析】(1)根据已知条件得出四边形BDEC 是平行四边形,根据BD =BC 即可得证;(2)连接BE 交CD 于O ,在Rt △BDO 中,得出BO =62,根据BE =2BO ,即可求解.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,AB =CD ,∵AD =BD ,∴BD =BC ,∵CE ∥BD ,AD ∥BC ,∴四边形BDEC 是平行四边形,又∵BD =BC ,∴四边形BDEC 是菱形;(2)解:如图,连接BE 交CD 于O ,∵四边形BDEC 是菱形,CD =AB =6,∴DO =CO =12CD =3,BO =12BE ,CD ⊥BE 在Rt △BDO 中,AD =BD =9,∴BO =BD 2-DO 2=92-32=62∴BE =2BO =122故答案为:122.【点睛】本题考查了菱形的性质与判定,勾股定理,掌握菱形的性质与判定是解题的关键.【考点八根据菱形的性质与判定求面积】1(2023春·北京海淀·八年级校考期中)如图,在平行四边形ABCD 中,过点A 作AE ⊥BC 于点E ,AF ⊥DC 于点F ,且BE =DF .(1)求证:平行四边形ABCD 是菱形(2)若∠EAF =60°,CF =2,求菱形ABCD 的面积.【答案】(1)证明见解析(2)83【分析】(1)证△AEB≌△AFD,得AB=AD,即可得出结论;(2)连接AC,证△ACD是等边三角形,得CD=AC,再由含30°角的直角三角形的性质得AC=2CF=4,则CD=AC=4,AF=23,即可求解.【详解】(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D.∵AE⊥BC,AF⊥DC,∴∠AEB=∠AFD=90°,又∵BE=DF,∴Rt△AEB≅Rt△AFD ASA.∴AB=AD,∴四边形ABCD是菱形.(2)如图,连接AC,∵AE⊥BC,AF⊥DC,∴∠AEF=∠AFE=90°∵∠EAF=60°,∴∠ECF=120°,∵四边形ABCD是菱形,∴∠ACF=60°,AD=CD∴△ACD是等边三角形∵AF⊥DC∴∠CAF=30°∴AC=2CF=2×2=4在Rt△CFA中,AF=AC2-CF2=42-22=23.∴菱形ABCD的面积=4×23=83.【点睛】本题考查了菱形的判定与性质、平行四边形的性质、全等三角形的判定与性质、等边三角形的判定与性质、含30°角的直角三角形的性质等知识,熟练掌握菱形的判定与性质,证明△ABE≌△ADF是解题的关键,属于中考常考题型.【变式训练】1(2023·四川南充·四川省南充高级中学校考三模)如图,在△ABC中,AC=BC,点D、E、F分别是AB、AC、BC的中点,连接DE、DF.(1)求证:四边形DFCE是菱形;(2)若∠A=75°,AC=8,求菱形DFCE的面积.【答案】(1)见解析(2)8【分析】(1)根据三角形的中位线的性质和菱形的判定定理即可得到结论;(2)过E作EG⊥BC于G,根据等腰三角形和直角三角形的性质即可得到结论.【详解】(1)∵点D、E、F分别是AB、AC、BC的中点,∴DE∥CF,DE=12BC,DF∥CE,DF=12AC,∴四边形DFCE是平行四边形,∵AC=BC,∴DE=DF,∴四边形DFCE是菱形;(2)过E作EG⊥BC于G,∵AC=BC,∠A=75°,∴∠B=∠A=75°,∴∠C=30°,∵点E是AC的中点,AC=8,∴CE=12AC=4,∵EG⊥BC,∴EG=12CE=14AC=2,∵四边形DFCE是菱形,∴CF=CE=4∴S菱形DFCE=CF∙EG=2×4=8.【点睛】本题考查了菱形的判定和性质,等腰三角形的性质,三角形的中位线的性质,菱形的面积,熟练掌握菱形的判定定理是解题的关键.2(2023春·广东珠海·八年级珠海市紫荆中学校考期中)如图,在平行四边形ABCD中,两条对角线相交于点O,EF经过O且垂直于AC,分别与边AD、BC交于点F、E.(1)求证:四边形AECF为菱形;(2)若AD=3,CD=2,且∠ADC=60°,求菱形AECF的面积.【答案】(1)见解析(2)734【分析】(1)先证明△AOF≌△COE,得出AF=CE,证明四边形AECF为平行四边形,根据EF是对角线AC的垂直平分线,得出AF=CF,即可求证;(2)过C作CH⊥AD于H,则∠CHD=∠CHF=90°,根据∠ADC=60°,得出∠HCD=30°,求HD=12CD=1,根据勾股定理求出CH=CD2-HD2=3,进而得到AH=2,在Rt△CHF中,由勾股定理可得AF =CF =74,即可求解.【详解】(1)证明:∵四边形ABCD 为平行四边形,∴OA =OC ,AD ∥BC ,∴∠FAC =∠ACE ,∠AFE =∠CEF ,∴△AOF ≌△COE ,∴AF =CE ,∴四边形AECF 为平行四边形,∵EF 经过O 且垂直于AC ,∴EF 是对角线AC 的垂直平分线,∴AF =CF ,∴四边形AECF 为菱形;(2)解:过C 作CH ⊥AD 于H ,则∠CHD =∠CHF =90°,∵∠ADC =60°,∴∠HCD =30°,∴HD =12CD =1,∴CH =CD 2-HD 2=3,∵AD =3,∴AH =2,∵四边形AECF 是菱形,∴AF =CF ,设AF =CF =x ,则FH =2-x ,在Rt △CHF 中,由勾股定理得:CF 2=FH 2+CH 2,即x 2=2-x 2+3 2,解得:x =74,∴AF =CF =74,∴菱形AECF 的面积为:AF ×CH =74×3=734.【点睛】本题主要考查了菱形的判定和性质,勾股定理,全等三角形的判定和性质,平行四边形的性质等知识,熟练掌握菱形的判定和性质,勾股定理,全等三角形的判定和性质,平行四边形的性质是解题的关键.3(2023·黑龙江哈尔滨·哈尔滨市萧红中学校考模拟预测)如图,矩形ABCD 的对角线AC 的垂直平分线EF 与AD 、AC 、BC 分别交于点E 、O 、F .(1)求证:四边形AFCE是菱形;(2)若AB=5,BC=12,EF=6,求:①BO的长;②菱形AFCE的面积.【答案】(1)见解析(2)①6.5;②39【分析】(1)根据线段垂直平分线的性质可得AE=CE,AO=CO,再由矩形的性质可得AE∥CF,从而得到∠CAE=∠ACF,∠AEO=∠CFO,再证明△AOE≌△COF,可得AE=CF,从而得到四边形AFCE是平行四边形,即可求证;①根据矩形的性质可得AC=2BO,∠ABC=90°,再由勾股定理求出AC=13,即可求解;②根据菱形的面积等于对角线长度乘积的一半,即可求解.【详解】(1)证明:∵EF垂直平分AC,∴AE=CE,AO=CO,∵四边形ABCD是矩形,∴AE∥CF,∴∠CAE=∠ACF,∠AEO=∠CFO,在△AOE和△COF中,∵∠CAE=∠ACF,∠AEO=∠CFO,AO=CO,∴△AOE≌△COF,∴AE=CF,∴四边形AFCE是平行四边形,∵AE=CE,∴四边形AFCE是菱形;(2)解:①∵四边形ABCD是矩形,点O为AC的中点,∴AC=2BO,∠ABC=90°,∵AB=5,BC=12,∴AC=AB2+BC2=13,∴BO=12AC=6.5;②∵四边形AFCE是菱形,EF=6,∴菱形AFCE的面积12AC×EF=12×13×6=39.【点睛】本题主要考查了矩形的性质,菱形的性质和判定,勾股定理,熟练掌握矩形的性质,菱形的性质和判定,勾股定理是解题的关键.【过关检测】一、选择题1(2023春·江西上饶·八年级统考阶段练习)如图,BD为菱形ABCD的对角线,已知∠A=50°,则∠BDC的度数为()A.130°B.50°C.55°D.65°【答案】D【分析】由菱形的性质得出AB ∥CD ,∠ADB =∠CDB ,利用平行线的性质求出∠ADC 的度数,从而即可求得∠BDC 的大小.【详解】解:∵四边形ABCD 是菱形,∴AB ∥CD ,∠ADB =∠CDB ,∴∠A +∠ADC =180°,又∠A =50°,∴∠ADC =130°,∴∠ADB =∠CDB =12∠ADC =65°.故选:D .【点睛】本题考查了菱形的性质、平行线的性质等知识,熟练掌握菱形的性质是解题的关键.2(2023·浙江·统考中考真题)如图,在菱形ABCD 中,AB =1,∠DAB =60°,则AC 的长为()A.12B.1C.32D.3【答案】D 【分析】连接BD 与AC 交于O .先证明△ABD 是等边三角形,由AC ⊥BD ,得到∠OAB =12∠BAD =30°,∠AOB =90°,即可得到OB =12AB =12,利用勾股定理求出AO 的长度,即可求得AC 的长度.【详解】解:连接BD 与AC 交于O .∵四边形ABCD 是菱形,∴AB ∥CD ,AB =AD ,AC ⊥BD ,AO =OC =12AC ,∵∠DAB =60°,且AB =AD ,∴△ABD 是等边三角形,∵AC ⊥BD ,∴∠OAB=12∠BAD=30°,∠AOB=90°,∴OB=12AB=12,∴AO=AB2-OB2=12-12 2=123,∴AC=2AO=3,故选:D.【点睛】此题主要考查了菱形的性质、勾股定理、等边三角形的判定和性质、30°角所对直角边等于斜边的一半,关键是熟练掌握菱形的性质.3(2023春·湖北武汉·八年级校考阶段练习)如图,在菨形ABCD中,过顶点C作CE⊥BC交对角线BD于E点,已知∠A=134°,则∠BEC的大小为()A.67°B.57°C.33°D.23°【答案】A【分析】根据菱形的性质得出∠CBE=23°,再根据直角三角形两个锐角互余,即可求解.【详解】解:∵四边形ABCD为菱形,∴AD∥BC,∴∠ABC=180°-∠A=46°,则∠CBE=12∠ABC=23°,∵CE⊥BC,∴∠BEC=90°-∠CBE=67°,故选:A.【点睛】本题主要考查了菱形的性质,解题的关键是掌握菱形的对角线平分菱形内角,直角三角形两个锐角互余.4(2023春·黑龙江哈尔滨·八年级校考期中)如图,在菱形ABCD中,对角线BD=43,∠BAD= 120°,则菱形ABCD的面积是()A.83B.8C.163D.43【答案】A【分析】根据菱形性质求出AO=12AC,BO=12BD=23,AC⊥BD,∠BAO=12∠BAD=60°,根据勾股定理得AB2-AO2=BO2,即2AO2-AO2=232,求出AO=2,根据菱形面积得出1 2AC⋅BD=12×4×43=83.【详解】解:∵四边形ABCD为菱形,∴AO=12AC,BO=12BD=23,AC⊥BD,∠BAO=12∠BAD=60°,∴∠AOB=90°,∴∠ABO=90°-60°=30°,∴AB=2AO,在Rt△AOB中根据勾股定理得:AB2-AO2=BO2,∴2AO2-AO2=232,解得:AO=2,负值舍去,∴AC=2×2=4,∴菱形ABCD的面积=12AC⋅BD=12×4×43=83,故A正确.故选:A.【点睛】本题主要考查了菱形的性质,直角三角形的性质.解题的关键是注意数形结合与方程思想的应用,注意菱形的面积等于其对角线乘积的一半.5(2023春·黑龙江哈尔滨·八年级校考期中)如图,菱形ABCD中,∠A=60°,E,F分别是边AB,AD的中点,DE,BF相交于G,连接CG,以下结论正确的有( )个①∠BGD=120°;②SΔADE:SΔGBC=2:3;③BG+DG=CG;④S菱形ABCD=32AB2A.1B.2C.3D.4【答案】C【分析】解:①连接BD,证明△ABD为等边三角形,DE⊥AB,BF⊥AD,∠GDB=∠GBD=30°,从而可判断①;证明GD=GB,设菱形的边长为4m,则AE=2m=BE,DE=23m,再分别求解两个三角形的面积可判断②;证明Rt△CDG≌Rt△CBG,可得DG=BG=12CG,可判断③;设菱形的边长为4m,则AE=2m=BE,DE=23m,再求解菱形的面积可判断④.【详解】解:①连接BD,∵四边形ABCD为菱形,∴AD =AB ,且∠A =60°,∴△ABD 为等边三角形,又∵E 、F 分别是AB 、AD 的中点,∴DE ⊥AB ,BF ⊥AD ,∠GDB =∠GBD =30°,∴∠BGD =180°-2×30°=120°,GD =GB ,∴①符合题意;同理可得:∠ADE =30°=∠ABF ,设菱形的边长为4m ,则AE =2m =BE ,DE =23m ,∴S △ADE =12×2m ×23m =23m 2,∵∠ABF =30°,DE ⊥AB ,∴BG =2GE ,∴BG 2=12BG 2+2m 2,∴BG =433m ,同理可得:△BCD 为等边三角形,∴∠GBC =60°+60°-30°=90°,∴S △BCG =12×4m ×433m =833m ,∴S ΔADE :S ΔGBC =3:4,故②不符合题意;∵四边形ABCD 为菱形,∴AB ∥CD ,AD ∥BC ,∴∠CDG =∠CBG =90°,∵CD =CB ,CG =CG ,∴Rt △CDG ≌Rt △CBG ,∴∠DCG =∠BCG =30°,∴DG =BG =12CG ,∴DG +BG =CG ,∴③符合题意;设菱形的边长为4m ,则AE =2m =BE ,DE =23m ,∵△ABD 为等边三角形,△BCD 为等边三角形,∴S 菱形ABCD =2S △ABD =2×12×4m ×23m =83m 2,而32AB 2=32×4m 2=83m 2,∴S菱形ABCD =32AB2,故④符合题意;综上:正确的有①②④;故选C【点睛】本题考查的是等边三角形的判定与性质,勾股定理的应用,全等三角形的判定与性质,菱形的性质,熟练的利用基本图形的性质解题是关键.二、填空题6(2023春·天津滨海新·八年级校考期中)如图,已知菱形ABCD,AC=6,面积等于24,则菱形ABCD的周长等于.【答案】20【分析】设AC与BD交于点O,由菱形的性质得AB=BC=CD=AD,OA=OC=3,OB=OD,AC⊥BD,再由菱形的面积得BD=8,则OB=OD=4,然后由勾股定理求解即可.【详解】解:如图,设AC与BD交于点O,∵四边形ABCD是菱形,AC=6,∴AB=BC=CD=AD,OA=OC=12AC=3,OB=OD,AC⊥BD,∵菱形ABCD的面积是24,∴12AC×BD=24,∴BD=24×26=8,∴OB=OD=12BD=4,在Rt△AOB中,由勾股定理得:AB=OA2+OB2=5,∴菱形ABCD的周长=4AB=20,故答案为:20.【点睛】本题考查了菱形的性质以及勾股定理等知识,熟练掌握菱形的性质,求出BD的长是解题的关键.7(2023春·北京海淀·八年级校考期中)如图,菱形ABCD中,AB=10,AC,BD交于点O,若E是边AD的中点,∠ABO=32°,则OE的长等于,∠ADO的度数为.【答案】532°【分析】根据菱形的性质得出BO=DO,AB=AD,AB∥CD,根据等边对等角可得∠ADO=AB=5.∠ABO=32°,由三角形中位线定理得出OE=12【详解】∵四边形ABCD是菱形,∴BO=DO,AB=AD,AB∥CD,∴∠ADO=∠ABO=32°,∵E是边AD的中点,BO=DO,∴OE是△ABD的中位线,AB=5.∴OE=12故答案为:5,32°.【点睛】本题考查了菱形的性质,等边对等角,三角形中位线定理,,证明出OE是△ABD的中位线是本题的关键.8(2023·全国·八年级假期作业)如图,已知菱形ABCD的顶点A和B的坐标分别为-2,0,、3,0点C在y轴的正半轴上.则点D的坐标是.【答案】-5,4【详解】根据菱形的性质和点的坐标求出OB,DC=AB=BC=5,根据勾股定理求出OC,再求出点D的坐标即可.【解答】解:∵A-2,0,四边形ABCD是菱形,,B3,0∴OB=3,CD=BC=AB=3--2=5,∴OC=BC2-OB2=52-32=4,又∵CD∥AB,CD=5,∴点D的坐标为:-5,4.故答案为:-5,4.【点睛】本题考查菱形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.9(2023·河南新乡·统考三模)如图,菱形ABCD中,∠ABC=120°,AB=2,点E是AB的中点,点F在AC上.若∠BEF=45°,则线段FG的长为.。
初中数学人教版 菱形的性质与判定 人教版

你图能片举中出有一你些熟生悉活的中图菱形形吗的?例子吗?与同伴交流。
想一想
(1)菱形是特殊的平行四边形,它具有一般平行 四边形的所有性质。你能列举一些这样的性质 吗?
菱形的对边平行且相等,对角相等,对角线互相 平分。中心对称图形。
(2)你认为菱形还具有哪些特殊的性质?与同 伴交流。
做一做 用菱形纸片折一折,回答下列问题:
通过上面的折纸活动,我们可以发现菱形的四条 边相等,对角线互相垂直。下面我们证明这些结 论。
已知:如图,在菱形ABCD中,AB=AD,对角线AC与 BD相交于点O. 求证:(1)AB=BC=CD=AD;(2)AC⊥BD.
证明:(1)∵四边形ABCD是菱形, ∴AB = CD,AD= BC (菱形的对边相等) 又∵AB=AD ∴AB=BC=CD=AD
第二重境界是“衣带渐宽终不悔,为伊消得人憔悴”。事情是需要去做才能成的,成越大的事业,需要越大的努力和付出,甚至要经受越大的磨难和困苦。这个世间,从来都是“艰难困苦,玉汝于成”;所以无论如何,都要“天行健,君子”。这说的是历经磨难而逐渐成熟、成长,最终豁然贯通、水到渠成。这其中蕴含一个重要道理,就是苏东坡所说的“厚积而薄发”。只有厚积才能薄发,人要做的,就是不断厚积,等待薄发。这就是拿得起的完整路径,也是事业成功的完整过程。 跟佛家学放得下 。佛家是追求出世、讲究清净的,要求能看到《金刚经》所言的“一切有为法,如梦幻泡影”,做到《心经》所言的“照见五蕴皆空”。概括为三个字,就是“放得下”。 什么是“放得下”?且看这个“佛”字——左边一个“人”,右边一个“弗”,弗的意思是“不”,合起来就是“不人”和“人不”。不人就是无人,也就是放下自我,摆脱私心的困缚;人不就是懂得拒绝,也就是放下欲望,超脱对外物的追逐。这两点能做到,就是放得下。
人教初中数学八下 18.2.2 菱形课件2 【经典初中数学课件汇编】

∴ 152+82=172
∴这个三角形是直角三角形
24
课堂练习
判断由线段a、b、c组成的三角形是不是直角三角形: (1)a=15,b=8,c=17; (2)a=m2-n2,b=m2+n2,c=2mn(m>n,m、n是正整数)
解;(1)∵a2 = 225, (2)∵a2 = (m2 - n2 )2 = m4 - 2m2n2 + n4,
a2 + b2 = c2
那么这个三角形是直角三角形。且边 C所对的角为直角。
勾股定理
互逆命定题理
如果直角三角形两直角边分别为a,b,
斜边为c,那么 a2 + b2 = c2
22
勾股定理的逆命题证明
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2
求证:△ ABC是直角三角形
证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b
思维训练
6、△ABC三边a,b,c为边向外作 正方形,正三角形,以三边为 直则径作是半直圆角,三若角S形1+吗S2?=S3成立,
C
S2
A
b
ca
S1
B
S3
C
S2 b
S1
a
c
A
B
S3
பைடு நூலகம்
32
知识运用:
8如图:在正方形ABCD中,E是BC的中点,F是CD上一点,
1
且CF= 4 CD.猜想△AEF的形状,并证明你的结论.
解: △AEF是直角三角形;
D
FC
理由:设正方形ABCD的边长是a,则:
B E C E 1 a,C F 1 a, D F 3 a,
菱形的性质及判定

初中数学菱形的性质及判定1.菱形的定义:有一组邻边相等的平行四边形叫做菱形. 2.菱形的性质菱形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:① 边的性质:对边平行且四边相等. ② 角的性质:邻角互补,对角相等.③ 对角线性质:对角线互相垂直平分且每条对角线平分一组对角. ④ 对称性:菱形是中心对称图形,也是轴对称图形.菱形的面积等于底乘以高,等于对角线乘积的一半.点评:其实只要四边形的对角线互相垂直,其面积就等于对角线乘积的一半. 3.菱形的判定判定①:一组邻边相等的平行四边形是菱形. 判定②:对角线互相垂直的平行四边形是菱形. 判定③:四边相等的四边形是菱形.板块一、菱形的性质☆ ⑴菱形的两条对角线将菱形分成全等三角形的对数为 ⑵在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是⑴如图2,一活动菱形衣架中,菱形的边长均为,若墙上钉子间的距离,则 度.16cm 16cm AB BC ==1∠=⑵如图,在菱形中,,、分别是、的中点,若,则菱形的边长是______.如图,是菱形的边的中点,于,交的延长线于,交于,证明:与互相平分.☆ 如图1所示,菱形中,对角线、相交于点,为边中点,菱形的周长为,则的长等于 .☆如图,已知菱形的对角线于点,则的长为图21CBA ABCD 60A ∠=︒E F AB AD 2EF =ABCD E ABCD AD EF AC ⊥H CB F AB P AB EF P HFE DCBAABCD AC BD O H AD ABCD 24OH 图1HO DC BAABCD 8cm 4cm AC BD DE BC ==⊥,,E DE E F DBCA☆ 菱形的周长为,两邻角度数之比为,则菱形较短的对角线的长度为如图2,在菱形中,,,则菱形的边长为( ) A . B . C . D .如图3,在菱形中,,、分别是边和的中点,于点,则( )A .B .C .D .☆如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为的菱形,剪口与折痕所成的角的度数应为( ) A .或 B .或 C .或 D .或菱形中,、分别是、的中点,且,,那么等于 .如图,将一个长为,宽为的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( ) A . B . C . D .20cm 2:1ABCD 6AC =8BD =51068图2DCBAABCD 110A ∠=︒E F AB BC EP CD ⊥P FPC ∠=35︒45︒50︒55︒图3E DP CF BA 60︒α15︒30︒30︒45︒45︒60︒30︒60︒ABCD E F BC CD AE BC ⊥AF CD ⊥EAF ∠10cm 8cm 210cm 220cm 240cm 280cm☆已知菱形的两条对角线的乘积等于菱形的一条边长的平方,则菱形的一个钝角的大小是如图,菱形花坛的周长为,,•沿着菱形的对角线修建了两条小路和,求两条小路的长和花坛的面积.已知,菱形中,、分别是、上的点,若,求的度数.板块二、菱形的判定如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是 .☆如图,在中,平分,的中垂线交于点,交于点,求证:四边形是菱形图1DCBA ABCD AC BD ,ABCD 20m 60ABC ∠=︒ACBD 图2ABCD E F BC CD AE AF EF AB ===C ∠FEDCBAABCD DCAB ABC ∆BD ABC ∠BD ABE BCF BEDF已知:如图,平行四边形的对角线的垂直平分线与边、分别相交于 、.求证:四边形是菱形.如图,在梯形纸片中,,,将纸片沿过点 的直线折叠,使点落在上的点处,折痕交于点,连结.求证:四边形是菱形.☆如图,是菱形的边的中点,于,交的延长线于,交于,证明:与互相平分☆已知:如图,在平行四边形中,是边上的高,将沿方向平移,使点与点重合,得.若,当与满足什么数量关系时,四边形是菱形?证明你的结论.如图,在中,,是的中点.分别作于,于,于,于.相交于点.求证:四边形是菱形.FEDCBAABCD AC AD BC E F AFCE ODEFC ABABCD //AD BC AD CD >D C AD C DE BC E C E 'CDC E 'C'DCB A EE ABCD AD EF AC ⊥H CB F AB P AB EF AB CDEF P PF EDC B A ABCD AE BC ABE ∆BC E C GFC ∆60B ∠=︒AB BC ABFG GF E DCBAABC ∆AB AC =M BC MD AB ⊥D ME AC ⊥E DF AC ⊥F EG AB ⊥G DF EG 、P DMEP如图,中,,是的平分线,交于,是边上的高,交于,于,求证:四边形是菱形.☆如图,是矩形内的任意一点,将沿方向平移,使与重合,点移动到点的位置 ⑴画出平移后的三角形;⑵连结,试说明四边形的对角线互相垂直,且长度分别等于的长; ⑶当在矩形内的什么位置时,在上述变换下,四边形是菱形?为什么?三、与菱形相关的几何综合题已知等腰中,,平分交于点,在线段上任取一点(点除外),过点作,分别交、于、点,作,交于点,连结. ⑴求证四边形为菱形⑵当点在何处时,菱形的面积为四边形面积的一半?PMF E DG CBABC ∆90ACB ∠=︒AD BAC ∠BC D CH AB AD F DE AB ⊥E CDEF HF DECBAM ABCD MAB ∆AD AB DC M 'M 'MD MC MM ,,'MDM C AB AD ,M 'MDM C M'M DC BAABC △AB AC =AD BAC ∠BC D AD P A P EF AB ∥AC BC E F PM AC ∥AB M ME AEPM P AEPM EFBM菱形周长为,一条对角线长为,则其面积为 . 如图,在菱形中,在上,点在上,则的最小值为已知菱形的一个内角为,一条对角线的长为则另一条对角线的长为________.已知,菱形中,、分别是、上的点,且,.求:的度数.如图,在中,,是的中点,连结,在的延长线上取一点,连结,.当与满足什么数量关系时,四边形是菱形?并说明理由.如图,、、均为直线同侧的等边三角形.已知. ⑴ 顺次连结、、、四点所构成的图形有哪几类?直接写出构成MPFABDE 52cm 10cm ABCD 4AB a E =,BC 2120BE a BAD P =∠=︒,,BD PE PC +PDCBA60︒3ABCD E F BC CD 60B EAF ∠=∠=︒18BAE ∠=︒CEF ∠FEDCBAABC ∆AB AC =D BC AD AD E BE CE AE AD ABEC EDCB AACD ∆ABE ∆BCF ∆BC AB AC =A D F E 课后练习图形的类型和相应 的条件.⑵ 当为 度时,四边形为正方形.如图,已知、分别为中、的平分线,于,于,求证:.BAC ∠ADFE FEDCBABE CF ABC ∆B ∠C ∠AM BE ⊥M AN CF ⊥N MN BC ∥NMEFCBA。
【复习】:初中数学九年级上册.菱形(基础)知识讲解+练习

专项训练年度:菱形(基础)【学习目标】1. 理解菱形的概念.2. 掌握菱形的性质定理及判定定理.【要点梳理】【高清课堂特殊的平行四边形(菱形)知识要点】要点一、菱形的定义有一组邻边相等的平行四边形叫做菱形.要点诠释:菱形的定义的两个要素:①是平行四边形.②有一组邻边相等.即菱形是一个平行四边形,然后增加一对邻边相等这个特殊条件.要点二、菱形的性质菱形除了具有平行四边形的一切性质外,还有一些特殊性质:1.菱形的四条边都相等;2.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.3.菱形也是轴对称图形,有两条对称轴(对角线所在的直线),对称轴的交点就是对称中心.要点诠释:(1)菱形是特殊的平行四边形,是中心对称图形,过中心的任意直线可将菱形分成完全全等的两部分.(2)菱形的面积有两种计算方法:一种是平行四边形的面积公式:底×高;另一种是两条对角线乘积的一半(即四个小直角三角形面积之和).实际上,任何一个对角线互相垂直的四边形的面积都是两条对角线乘积的一半.(3)菱形可以用来证明线段相等,角相等,直线平行,垂直及有关计算问题.要点三、菱形的判定菱形的判定方法有三种:1.定义:有一组邻边相等的平行四边形是菱形.2.对角线互相垂直的平行四边形是菱形.3.四条边相等的四边形是菱形.要点诠释:前两种方法都是在平行四边形的基础上外加一个条件来判定菱形,后一种方法是在四边形的基础上加上四条边相等.【典型例题】类型一、菱形的性质1、(2015•石景山区一模)如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.(1)求证:四边形EGBD是平行四边形;(2)连接AG,若∠FGB=30°,GB=AE=1,求AG的长.【思路点拨】(1)连接AC,再根据菱形的性质得出EG∥BD,根据对边分别平行证明是平行四边形即可.(2)过点A作AH⊥BC,再根据直角三角形的性质和勾股定理解答即可.【答案与解析】(1)证明:连接AC,如图1:∵四边形ABCD是菱形,∴AC平分∠DAB,且AC⊥BD,∵AF=AE,∴AC⊥EF,∴EG∥BD.又∵菱形ABCD中,ED∥BG,∴四边形EGBD是平行四边形.(2)解:过点A作AH⊥BC于H.∵∠FGB=30°,∴∠DBC=30°,∴∠ABH=2∠DBC=60°,∵GB=AE=1,∴AB=AD=2,在Rt△ABH中,∠AHB=90°,∴AH=,BH=1.∴GH=2,在Rt△AGH中,根据勾股定理得,AG=.【总结升华】本题考查了菱形性质,关键是根据菱形的性质和平行四边形的判定以及直角三角形的性质解题.举一反三:【变式1】(2015•温州模拟)如图,在菱形ABCD中,点E是AB上的一点,连接DE交AC于点O,连接BO,且∠AED=50°,则∠CBO= 度.【答案】50;解:在菱形ABCD 中,AB ∥CD ,∴∠CDO=∠AED=50°, CD=CB ,∠BCO=∠DCO , ∴在△BCO 和△DCO 中,,∴△BCO ≌△DCO (SAS ), ∴∠CBO=∠CDO=50°.【变式2】菱形ABCD 中,∠A ∶∠B =1∶5,若周长为8,则此菱形的高等于( ).A.21B.4C.1D.2【答案】C ;提示:由题意,∠A =30°,边长为2,菱形的高等于12×2=1. 类型二、菱形的判定2、如图所示,在△ABC 中,CD 是∠ACB 的平分线,DE ∥AC ,DF ∥BC ,四边形DECF 是菱形吗?试说明理由.【思路点拨】由菱形的定义去判定图形,由DE ∥AC ,DF ∥BC 知四边形DECF 是平行四边形,再由∠1=∠2=∠3得到邻边相等即可. 【答案与解析】解:四边形DECF 是菱形,理由如下: ∵ DE ∥AC ,DF ∥BC∴ 四边形DECF 是平行四边形. ∵ CD 平分∠ACB ,∴ ∠1=∠2 ∵ DF ∥BC , ∴ ∠2=∠3, ∴ ∠1=∠3.∴ CF =DF ,∴ 四边形DECF 是菱形.【总结升华】在用菱形的定义判定一个四边形是菱形时,首先判定这个四边形是平行四边形,再由一对邻边相等来判定它是菱形.举一反三:【变式】如图所示,AD是△ABC的角平分线,EF垂直平分AD,分别交AB于E,交AC 于F,则四边形AEDF是菱形吗?请说明理由.【答案】解:四边形AEDF是菱形,理由如下:∵EF垂直平分AD,∴△AOF与△DOF关于直线EF成轴对称.∴∠ODF=∠OAF,又∵AD平分∠BAC,即∠OAF=∠OAE,∴∠ODF=∠OAE.∴AE∥DF,同理可得:DE∥AF.∴四边形AEDF是平行四边形,∴EO=OF又∵AEDF的对角线AD、EF互相垂直平分.∴AEDF是菱形.3、如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,CE平分∠ACD,交AD 于点G,交AB于点E,EF⊥BC于点F.求证:四边形AEFG是菱形.【思路点拨】由角平分线性质易知AE=EF,欲证四边形AEFG是菱形,只要再证四边形AEFG是平行四边形或AG=GF=AE即可.【答案与解析】证明:方法一:∵CE平分∠ACB,∠BAC=90°,EF⊥BC,∴AE=EF,∠1+∠3=90°,∠4+∠2=90°.∵∠1=∠2,∴∠3=∠4.∵EF⊥BC,AD⊥BC,∴EF∥AD.∴∠4=∠5.∴∠3=∠5.∴AE=AG.∴EF AG.∴四边形AEFG是平行四边形.又∵AE=AG,∴四边形AEFG是菱形.方法二:∵CE平分∠ACB,∠BAC=90°,EF⊥BC,∴AE=EF,∠1+∠3=90°,∠4+∠2=90°.∴∠3=∠4.∵EF⊥BC,AD⊥BC,∴EF∥AD.∴∠4=∠5.∴∠3=∠5.∴AE=AG.在△AEG和△FEG中,AE=EF,∠3=∠4,EG=EG,∴△AEG≌△FEG.∴AG=FG.∴AE=EF=FG=AG.∴四边形AEFG是菱形.【总结升华】判定一个四边形是菱形,关键是把已知条件转化成判定方法所需要的条件.举一反三:【变式】如图所示,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A 点作AG∥DB交CB的延长线于点G.(1)求证:DE∥BF;(2)若∠G=90°,求证四边形DEBF是菱形.【答案】证明:(1)ABCD中,AB∥CD,AB=CD∵E、F分别为AB、CD的中点∴DF=12DC,BE=12AB∴DF∥BE.DF=BE∴四边形DEBF为平行四边形∴DE∥BF(2)证明:∵AG∥BD∴∠G=∠DBC=90°∴△DBC为直角三角形又∵F为边CD的中点.∴BF=12DC=DF又∵四边形DEBF为平行四边形∴四边形DEBF是菱形类型三、菱形的应用4、如图所示,是一种长0.3m,宽0.2m的矩形瓷砖,E、F、G、H分别为矩形四边BC、CD、DA、AB的中点,阴影部分为淡黄色花纹,中间部分为白色,现有一面长4.2 m,宽2.8m的墙壁准备贴如图所示规格的瓷砖.试问:(1)这面墙最少要贴这种瓷砖多少块?(2)全部贴满后,这面墙壁会出现多少个面积相同的菱形?【答案与解析】解:墙壁长4.2m,宽2.8m,矩形瓷砖长0.3m,宽0.2m,4.2÷0.3=14,2.8÷0.2=14,则可知矩形瓷砖横排14块,竖排14块可毫无空隙地贴满墙面.(1)则至少需要这种瓷砖14×14=196(块).(2)每块瓷砖中间有一个白色菱形,则共有196个白色的菱形,它的面积等于瓷砖面积的一半.另外在同一个顶点处的瓷砖能够拼成一个淡黄色花纹的菱形,它的面积也等于瓷砖面积的一半,有花纹的菱形横排有13个,竖排也有13个,则一共有淡黄色花纹菱形13×13=169个,面积相等的菱形一共有196+169=365(个).【总结升华】菱形可以看作是由直角三角形组成的,因而铺满墙面后,要计算空白菱形的个数和阴影菱形的个数.将相同的图形拼在一起,在顶点周围的几个图形也能拼成一定的图案,不要忽略周围图形的拼接.【巩固练习】一.选择题1.(2015•潍坊模拟)下列说法中,错误的是()A. 平行四边形的对角线互相平分B. 对角线互相平分的四边形是平行四边C.菱形的对角线互相垂直 D. 对角线互相垂直的四边形是菱形2.顺次连结对角线相等的四边形各边中点,所得四边形是( )A.矩形B.平行四边形C.菱形 D.任意四边形3.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD 的周长是( )A.4B.8C.12D.164.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于()A.20 B.15 C.10 D.55.如图,在菱形ABCD中,AC、BD是对角线,若∠BAC=50°,则∠ABC等于()A.40°B.50°C.80°D.100°6.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )A.1B. 2C. 2D. 3二.填空题7.已知菱形的周长为40cm,两个相邻角度数之比为1∶2,则较长对角线的长为______cm.8.(2015•南充)如图,菱形ABCD的周长为8cm,高AE长为cm,则对角线AC长和BD长之比为 .9. 已知菱形ABCD两对角线AC =8cm, BD =6cm, 则菱形的高为________.10.如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是____cm.11. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为_____.12.如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则C点的坐标为_______.三.解答题13.如图,在菱形ABCD中,∠ABC=120°,E是AB边的中点,P是AC边上一动点,PB +PE的最小值是3,求AB的值.14.如图,在平行四边形ABCD中,E、F分别为边AB,CD的中点,连接DE、BF、BD.若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.15(2015春•泰安校级期中)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C 作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:BD=DF;(2)求证:四边形BDFG为菱形;(3)若AG=13,CF=6,求四边形BDFG的周长.【答案与解析】一.选择题 1.【答案】D ; 2.【答案】C ; 3.【答案】D ;【解析】BC =2EF =4,周长等于4BC =16. 4.【答案】B ;【解析】∵∠BCD=120°,∴∠B=60°,又∵ABCD 是菱形,∴BA=BC ,∴△ABC 是等边三角形,故可得△ABC 的周长=3AB=15.5.【答案】C ;【解析】∵四边形ABCD 是菱形,∴∠BAC =12∠BAD ,CB ∥AD ,∵∠BAC =50°,∴∠BAD =100°,∵CB ∥AD ,∴∠ABC +∠BAD =180°,∴∠ABC =180°-100°=80°.6.【答案】D ;【解析】∠DAF =∠FAO =∠OAE =30°,所以2BE =CE =AE ,3BE =3,BC BE =3. 二.填空题7.【答案】【解析】由题意,菱形相邻内角为60°和120°,较长对角线为=8.【答案】1:;【解析】如图,设AC ,BD 相较于点O ,∵菱形ABCD 的周长为8cm , ∴AB=BC=2cm , ∵高AE 长为cm ,∴BE==1(cm ),∴CE=BE=1cm , ∴AC=AB=2cm , ∵OA=1cm ,AC ⊥BD , ∴OB==(cm ),∴BD=2OB=2cm ,∴AC :BD=1:.9.【答案】245cm ; 【解析】菱形的边长为5,面积为168242⨯⨯= ,则高为245cm .10.【答案】4;【解析】在菱形ABCD 中,BD 是∠ABC 的平分线,∵PE ⊥AB 于点E ,PE =4cm ,∴点P 到BC 的距离=PE =4cm .11.【答案】60;【解析】因为菱形的对角线互相垂直及互相平分就可以在Rt △AOB 中利用勾股定理求出OB =12,BD =2OB =24,DE =2OC =10,BE =2BC =26,△BDE 的周长为60.12.【答案】(3,4);【解析】过B 点作BD ⊥OA 于D ,过C 点作CE ⊥OA 于E ,BD =4,OA =x ,AD =8-x ,()22284x x =-+,解得5x =,所以OE =AD =8-5=3,C 点坐标为(3,4).三.解答题13.【解析】解:∵∠ABC =120°∴∠BCD =∠BAD =60°;∵菱形ABCD 中, AB =AD∴△ABD 是等边三角形;又∵E 是AB 边的中点, B 关于AC 的对称点是D ,DE ⊥AB连接DE ,DE 与AC 交于P ,PB =PD ;DE 的长就是PB +PE 的最小值3;设AE =x ,AD =2x ,DE ==1x =,AB =22x =.14.【解析】四边形BFDE 是菱形,证明:∵AD ⊥BD ,∴△ABD 是直角三角形,且AB 是斜边,∵E 为AB 的中点,∴DE =12AB =BE ,∵四边形ABCD 是平行四边形,∴DC ∥AB ,DC =AB ,∵F 为DC 中点,E 为AB 中点,∴DF =12DC ,BE =12AB ,∴DF =BE ,DF ∥BE ,∴四边形DFBE 是平行四边形,∵DE =EB ,∴四边形BFDE 是菱形.15.【解析】证明:∵∠ABC=90°,BD 为AC 的中线,∴BD=AC ,∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形,∵CF⊥BD,∴CF⊥AG,又∵点D是AC中点,∴DF=AC,∴BD=DF;(2)证明:∵BD=DF,∴四边形BGFD是菱形,(3)解:设GF=x,则AF=13﹣x,AC=2x,∵在Rt△ACF中,∠CFA=90°,∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,∴四边形BDFG的周长=4GF=20.。
1菱形的性质与判定-初中九年级上册数学(教案)(北师大版)

a.有一组邻边相等的平行四边形是菱形;
b.对角线互相垂直平分的四边形是菱形;
c.四边相等的四边形是菱形。
3.菱形的应用:运用菱形的性质与判定方法解决实际问题,如求菱形的面积、周长等。
二、核心素养目标
《菱形的性质与判定》-初中九年级上册数学(教案):
1.培养学生的几何直观能力,通过观察和分析菱形的结构特征,提高学生对几何图形的认识和把握。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《菱形的性质与判定》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否见过具有对称美感的图形?”(如风筝、窗户等)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索菱形的奥秘。
在实践活动和小组讨论中,我发现学生们能够将所学的菱形知识应用到解决实际问题中。他们通过讨论、实验操作,不仅加深了对菱形性质的理解,还学会了如何与他人合作。但在这一过程中,我也注意到有些学生在操作过程中还存在一些困难,这让我意识到在以后的教学中,需要更加关注学生的个体差异,给予他们更多的指导和支持。
另外,我发现在学生小组讨论环节,有些学生表现得比较内向,不太愿意表达自己的观点。为了鼓励他们,我尝试提出一些开放性的问题,并给予积极的反馈。我觉得在以后的教学中,应该更多地关注这部分学生,创造一个让他们敢于表达、勇于尝试的学习氛围。
2.培养学生的逻辑推理能力,在探索菱形性质与判定的过程中,学会运用归纳、演绎等方法进行推理,形成严谨的数学思维。
3.培养学生的空间想象力和创新意识,运用菱形知识解决实际问题时,能够灵活运用所学知识,提出不同的解决方案。
4.培养学生的数学建模能力,将现实问题抽象为菱形模型,运用数学语言和符号进行表述,为解决现实问题提供数学支持。
人教版八下数学课件第18章18.2.2第1课时菱形的性质

解 : 当 四 边 形 EDD′F 为 菱 形 时 , △A′DE 是 等 腰 三 角 形 , △A′DE≌△EFC′.理由:∵△BCA 是直角三角形,∠ACB=90°,AD=
DB,∴CD=DA=DB,∴∠DAC=∠DCA,∵A′C∥AC,∴∠DA′E=
∠A , ∠DEA′ = ∠DCA , ∴∠DA′E = ∠DEA′ , ∴DA′ = DE ,
7.如图,AC、BD 是菱形 ABCD 的对角线,那么下列结论一定正确的是( B ) A.△ABD 与△ABC 的周长相等 B.△ABD 与△ABC 的面积相等 C.菱形的周长等于两条对角线之和的两倍 D.菱形的面积等于两条对角线之积的两倍
灿若寒星
8.如图,在菱形 ABCD 中,∠BAD=120°,AB=4.
初中数学课件
灿若寒星*****整理制作
八年级数学(下册)·人教版
第十八章 平行四边形
18.2.2 菱形 第1课时 菱形的性质
灿若寒星
1.定义:四条边相等的四边形 叫做菱形.菱形是轴对称图形,它的对称 轴是 两条对角线所在的直线 . 2.性质:①菱形的四条边 相等 ;②菱形的对角线 互相垂直平分 ,并且 每条对角线 平分 一组对角. 3.菱形的面积等于两对角线长的乘积的 一半 .
解:∵四边形 ABCD 为菱形,∴AC⊥BD,OA=12AC=8cm,OD=21BD= 6cm.∴AD= 62+82=10,∴C 菱形=4AD=40cm.由 S 菱形=AB×DE=12 ×AC×BD,即 10×DE=12×16×12,∴DE=9.6cm.
灿若寒星
5.如图,将一张直角三角形 ABC 纸片沿斜边 AB 上的中线 CD 剪开,得到 △ACD,再将△ACD 沿 DB 方向平移到△A′C′D′的位置,若平移开始后 点 D′,未到达点 B 时,A′C′交 CD 于 E,D′C′交 CB 于点 F,连接 EF,当四边形 EDD′F 为菱形时,试探究△A′DE 的形状,并判断△A′DE 与△EFC′是否全等?请说明理由.
第1讲:菱形的性质与判定_教案
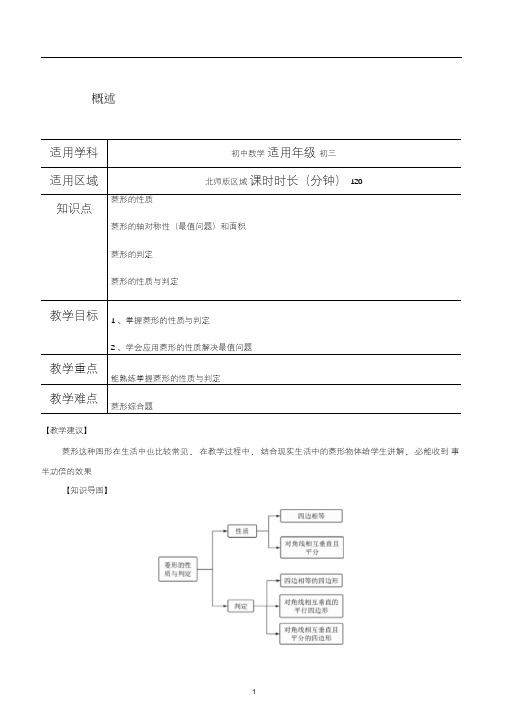
概述【教学建议】菱形这种图形在生活中也比较常见,在教学过程中,结合现实生活中的菱形物体给学生讲解,必能收到事半功倍的效果.【知识导图】教学过程、导入教学建议】在这一部分知识的学习中,要重视学生灵活运用所学知识点的能力培养.在七八年级的学习中我们已经学习过了平行四边形的性质和判定,在本讲中我们将会学习平行四边形中的特殊图形之一——菱形,它在初中数学四边形题型中占据了非常重要的位置.、知识讲解考点 1 菱形的定义和性质定义:一组邻边对应相等的平行四边形叫做菱形.性质:除具备一般平行四边形的性质外,还具备四条边相等,对角线互相垂直,并且每条对角线平分一组对角.考点 2 菱形的判定让学生拿出准备好的长方形纸片,剪出一个四边都相等的四边形,根据这个条件首先证它是平行四边形,再由一组邻边相等,依定义即知为菱形.菱形判定定理1:四边都相等的四边形是菱形1、已知:如图,在ABCD 中,BD⊥AC,O 为垂足.求证:ABCD 是菱形.启发:在已知是平行四边形的情况下,要证明是菱形,只要证明一组邻边相等.证明:∵四边形ABCD 是平行四边形,∴AO =CO(平行四边形的对角线互相平分)∵BD ⊥AC ,∴AD =CD∴ ABCD 是菱形(菱形的定义).结论:菱形判定定理2:对角线互相垂直的平行四边形是菱形.2、猜想:对角线互相垂直平分的四边形是不是菱形?启发:通过四个直角三角形的全等得到四条边相等.结论:对角线互相垂直平分的四边形是菱形.三、例题精析类型一菱形的定义与性质例题 1如图,菱形ABCD的周长为24cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等B.4cmC.2.5cmD.2cm解析】A.∵菱形ABCD的周长为24cm,∴边长AB=24÷4=6cm.∵对角线AC、BD相交于O点,∴ BO=DO.又∵E是AD的中点,∴ OE是△ ABD的中位线. ∴OE=1 AB=1×6=3(cm) 2总结与反思】此题运用了菱形的定义与性质:四边相等、类型二菱形的轴对称性(最值问题)和面积例题 1. 故选 A.对角线相互平分如图,已知菱形ABCD中,∠ ABC=60°,AB=8,过线段BD上的一个动点P(不与B、 D 重合)分别向直线A.3cmAB、AD作垂线,垂足分别为E、F.(1)BD的长是___(2)连接PC,当PE+PF+PC取得最小值时,此时PB的长是___ 【解析】8 3;4 3.(1)连接AC,交BD与点O,∵四边形ABCD是菱形,∠ ABC=60°,【解析】 A首先根据平移的性质得出 AB 平行且等于 CD ,得出四边形 ABCD 为平行四边形,根据邻边相等的平行四边形 是菱形可得添加条件 AB=BC 即可即可.试题解析:∵将△ ABC 沿 BC 方向平移得到△ DCE ,∴AB 平行且等于 CD ,∴四边形 ABCD 为平行四边形,当 AB=BC 时,平行四边形 ACED 是菱形.∴△ ABC 为等边三角形, AC=AB=8,1根据菱形性质得: AO=CO= AC=4,OB=O ,D AC ⊥ BD ,2根据勾股定理得: BD=2OB=×2 82 -42 =8 3 ; (2)延长FP 交 BC 于点 M ,则 FM ⊥ BC .∴PE+PF=PF+PM=F ,M又∵ S 菱形 ABCD =AC?BD=BC?FM ,∴ 1 ×8×8 3 =8?FM ,即 FM=4 3 ,2∴要使 PE+PF+PC 取最小值,只要 PC 取最小值. 当CP ⊥ BD ,即点 P 与点 O 重合时, PE+PF+PC 的值最小.1此时 PB=BO=DO= BD=4 3 .2总结与反思 】 此题是对菱形定义和性质的灵活运用,通过菱形性质求出了最值类型三 菱形的判定例题 1如图,将△ ABC 沿 BC 方向平移得到△ DCE ,连接 AD ,下列条件能够判定四边形 ABCD 为菱形的是( ) A 、 AB=BC B 、AC=BC C 、∠ B=60° D 、∠ ACB=60°故选A.总结与反思】先证明四边形是平行四边形,再由邻边相等证明四边形是菱形四、课堂运用基础1. 在菱形ABCD中,若∠ ADC=120°,对角线AC=6,则菱形的周长是()A.4 3 B .24 C .8 3 D .24 32. 如图,菱形ABCD中,P为对角线AC上一动点,E,F 分别为AB、BC中点,若AC=8,BD=6,则PE+PF的最设AC交BD于O,作E 关于AC 的对称点N,连接NF,交AC 于P,则此时EP+FP的值最小,∴PN=PE,∵四边形ABCD是菱形,∴∠ DAB=∠BCD,AD=AB=BC=C,DOA=OC,OB=OD,AD∥BC,∵E 为AB的中点,∴N 在AD上,且N为AD的中点,∵AD∥CB,∴∠ ANP=∠CFP,∠ NAP=∠ FCP,∵AD=BC,N为AD中点,F为BC中点,答案与解析1. 【答案】 C【解析】试题分析:先根据菱形的性质求得∠角形可得AB的长,从而求得结果.∵菱形ABCD,∠ ADC=120°,AC=6,∴AB=AD,∠ BAD=60°,AO=3,∠AOB=90° ∴△ ABD为等边三角形,∠BAO=30°,∴AB=2BO,∵ AB2AO2BO2,解得AB 2 3,∴菱形的周长是8 3 ,故选 C.2. 【答案】1、5BAD=60°,AO=3,即可得到△ ABD为等边三角形,根据等边三【解析】设AC交BD于O,作 E 关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,根据菱形的性质推出N是AD中点,P 与O重合,推出PE+PF=NF=A,B根据勾股定理求出AB的长即小值为__________∴AN=CF,在△ ANP和△ CFP中∠ANP=∠ CFP,AN=CF,∠ NAP=∠ CFP,∴△ ANP≌△ CFP(ASA),∴AP=CP,即P 为AC中点,∵O为AC中点,∴P、O重合,即NF 过O点,∵AN∥BF,AN=BF,∴四边形ANFB是平行四边形,∴NF=AB,∵菱形ABCD,AC=8,BD=6,∴AC⊥BD,OA=4,OB=3,AB OA2OB 25,则PE+PF的最小值为5.巩固2答案与解析251. 【答案】( 8, 0)和( 25 ,0)8【解析】由在菱形 ABCD 中,AC=12,BD=16,E 为 AD 中点,根据菱形的性质与直角三角形的性质,易求得的长,然后分别从①当 OP= OE 时,②当 OE=PE 时,③当 OP=EP 时去分析求解即可求得答案.∵四边形 ABCD 是菱形, AC=12, BD=16,11∴AC ⊥BD ,OA= AC=6, OD= BD=8,22∴在 Rt △AOD 中, ADOA 2 OD 2 10∵E 为 AD 中点, 1∴OE= AD=5,2① 当 OP=OE 时, P 点坐标( -5 ,0)和( 5,0);② 当 OE=PE 时,此时点 P 与 D 点重合,即 P 点坐标为( 8,③ 如图,当 OP=EP 时,过点 E作EK ⊥BD 于 K ,作 OE 的垂直平分线 PF ,交 OE 于点 F ,交 x 轴于点 P ,∴EK ∥OA ,∴EK :OA=ED :AD=1:2,11. 如图,在菱形 ABCD 中,对角线 AC 、 BD 相交于点 O , AC=12, BD=16, E 为AD 中点,点 P 在x 轴上移动 .小POE 为等腰三角形的 P 点坐标( -5,0 )和( 5,0 ).请你写出其余所有符合这个条件的2.如图所示, 在 Rt △ABC 中,AD 平分∠BAC ,交BC 于 D ,CH ⊥AB 于H ,交 AD 于F ,DE ⊥AB 垂足为 E ,求证:明同学写出了两个使△ P 点坐标∴ OK OE 2 EK 2 4∵∠ PFO=∠EKO=9°0 ,∠ POF=∠ EOK,∴△ POF∽△ EOK,∴OP:OE=OF:OK,即OP:5= 5:4,2 解得OP25,825 ∴P 点坐标为(,0).825 ∴其余所有符合这个条件的P 点坐标为:(8,0)或(25,0)82. 【答案】证明:∵ AD平分∠ BAC,∴∠ 1=∠ 2,∵在Rt △ABC中,CH⊥ AB于H,∴∠ 1+∠ AFH=90°,∠ 2+∠4=90°,∵∠ 3=∠ AFH,∠ 1=∠2,∴∠ 3=∠ 4,∴FC=CD,∵DE⊥AB垂足为E,∠ ACD=90°,∠ 1=∠2,∴CD=DE,∴ FC=DE,∵CH⊥AB,DE⊥AB,∴FC∥DE,∴四边形CFED是平行四边形,∵FC=CD,∴四边形CFED是菱形拔高1.如图,边长为4 的菱形ABCD中,∠ DAB=60°,E是AD上的动点(与且A,D不重合), F 是CD上的动点,AE+CF=4.(1)求证:不论点E,F 的位置如何变化,△ BEF是正三角形;(2)设AE=x,△ BEF的面积是S,求S与x 的函数关系式.2. 已知AC是菱形ABCD的对角线,∠ BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠ EAG=60°,连接CG,当点E在线段BC上时(如图1)易证:AB=CG+C.E当点在E线段BC的延长线上时(如图2),猜想AB、CG、CE之间的关系并证明;当点在E 线段CB的延长线上时(如图3),猜想AB、CG、CE之间的关系.答案与解析1. 【答案】见解析【解析】(1)证明:连接BD,∵四边形ABCD是菱形,∠ DAB=60°,∠ADC=120°,∴△ ABD是正三角形.∴∠ ABD=∠ADB=60°,AB=BD,又因AE+CF=4,DF+CF=4,∴AE=DF,而∠ FDB=∠ADC-∠ ADB=60°=∠DAB,∴△ AEB≌△ DBF,∴BE=BF,∠ ABE=∠ DBF,∵∠ EBF=∠EBD+∠ DBF=∠EBD+∠ABE=∠ABD=60°∴△ BEF是正三角形.(2)解:过 E 作EG⊥ AB于点G,∵AE=x,∠ DAB=60°,31∴EG= x,AG= x,22BG=4- 1 x,2BE2=EG2+BG2=(3x)2+(4- 1x)2=x2 4x 1622作FH⊥EB 垂足为点H,S△ BEF=1 BE?FH=1 BE? 3 BE= 3BE2= 3( x2 4x 16)2 2 2 4 42. 【答案】见解析解析】(1)AB=CG-CE证明:∵ AC是菱形ABCD的对角线且∠BAC=60°,∴AC=AD.∵四边形AEFG菱形,∴∠ DAC=∠GAE=60°,∴∠ DAG=∠CAE.在△ ACE和△ ADG中∴△ ACE≌△ ADG( SAS),∴CE=DG.∴AB=CD=CG-DG=CG-;CE (2)AB=CE-CG.同理可证△ ACG≌△ ABE,∴BE=CG.∴AB=CB=CE-BE=CE-C.G五、课堂小结本节的重要内容:菱形的性质与判定.①四边都相等的四边形是菱形;②在已知是平行四边形的情况下,要证明是菱形,只要证明一组邻边相等;③对角线互相垂直平分的四边形是菱形.六、课后作业基础1. 如图所示,在菱形 ABCD 中,对角线 AC=10, BD=24, AE ⊥ BC 于 E ,则 AE 的长是( )2. 如图,四边形 ABCD 是对角线互相垂直的四边形,且 OB=O ,D 请你添加一个适当的条件使四边形 ABCD 成为菱形 . (只需添加一个条件即可)3. 如图,在菱形 ABCD 中,∠ B=60°,点 E 、 F 分别在边 AB 、AD 上,且 AE=DF .1)试猜想△ ECF 的形状,并说明理由.否存在最小值?如果存在,请求出来;如果不存在,请说明理由.答案与解析1. 【答案】 A【解析】根据菱形的性质得出 BO 、CO 的长,在 RT △ BOC 中求出 BC ,利用菱形面积等于对角线乘积的一半, 也等于 BC ×AE ,可得出 AE 的长度. ∵四边形 ABCD 是菱形, AC=10, BD=24,11∴CO= AC=5,BO= BD=12, AO ⊥BO ,22∴ BCBO 2 CO 2 13 ,1S 菱形 ABCD AC BD BC AE∵ 2 ,12060 C.240 13A. 13B. 13110 24 13AE ,解得AE2 13 故选A.2. 【答案】OA=OC(答案不唯一)【解析】根据菱形的判定,平行的性质,全等三角形的判定和性质,由已知,添加OA=OC或AD=BC或AD//BC 或AB=BC等即可判定ABCD成为菱形.3. 【答案】见解析.【解析】△ ECF是等边三角形.证明:连接AC,∵∠ B=60°,∴AC=AB=C,D ∠ D=∠CAE=60°又∵ AE=FD,∴△ CDF≌△ CEA(SAS),∴CE=EF,∠ ACE=∠ DCF,而∠ DCF+∠FCA=60°,∴∠ ACE+FCA=6°0 =∠ ECF,∴△ ECF是等边三角形.(2)存在.很明显当CE⊥ AB时长度最小,此时CE=BCsin∠ B=5 ,∴最小周长=15 .巩固1. 如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2= .1202. (2011?福州)已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF 的长;(2)如图2,动点P、Q分别从A、C两点同时出发,沿△ AFB和△ CDE各边匀速运动一周.即点P自A→F→B→A 停止,点Q自C→D→E→C停止.在运动过程中,① 已知点P 的速度为每秒5cm,点Q 的速度为每秒4cm,运动时间为t 秒,当A、C、P、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P、Q的运动路程分别为a、b(单位:cm,ab≠ 0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.答案与解析1. 【答案】36.【解析】如图,连接EF,FG,GH,EH,EG与FH相交于点O. ∵E、H分别是AB、DA的中点,∴ EH是△ ABD 的中位线.1∴EH= BD=3.211同理可得EF=GH= AC=3,FG= BD=3.22∴EH=EF=GH=FG=3∴. 四边形EFGH为菱形.∴EG⊥ HF,且垂足为O.∴ EG=2OE,FH=2OH.在Rt △ OEH中,根据勾股定理得:OE2+OH2=EH2=9. 等式两边同时乘以4 得:4OE2+4OH2=×9 4=36.∴(2OE)2+(2OH)2=36,即EG2+FH2=36.2. 【答案】见解析.解析】(1)证明:①∵四边形ABCD是矩形,∴AD∥BC,∴∠ CAD=∠ACB,∠ AEF=∠ CFE,∵EF垂直平分AC,垂足为O,∴OA=OC,∴△ AOE≌△ COF,∴OE=OF,∴四边形AFCE为平行四边形,又∵ EF⊥ AC,∴四边形AFCE为菱形,②设菱形的边长AF=CF=xcm,则BF=(8﹣x)cm,在Rt △ ABF中,AB=4cm,由勾股定理得42+(8﹣x)2=x2,解得x=5 ,∴AF=5cm.(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形.因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,∵点P 的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t 秒,∴PC=5t,QA=12﹣4t ,∴5t=12 ﹣4t ,44解得t= ,∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t= 秒.33②由题意得,以A、C、P、Q四点为顶点的四边形是平行四边形时,点P、Q在互相平行的对应边上.分三种情况:i )如图1,当P 点在AF 上、Q点在CE上时,AP=CQ,即a=12﹣b,得a+b=12;ii )如图2,当P点在BF上、Q点在DE上时,AQ=CP,即12﹣b=a,得a+b=12;iii )如图3,当P点在AB上、Q点在CD上时,AP=CQ,即12﹣a=b,得a+b=12.综上所述,a 与b 满足的数量关系式是a+b=12(ab≠ 0).拔高EF.(1)若 E 是线段 AC 的中点,如图 1,求证: BE=EF ;(2)若 E 是线段 AC 或 AC 延长线上的任意一点,其它条件不变,如图 2、图 3,线段 BE 、 EF 有怎样的数2.如图①,在菱形 ABCD 和菱形 BEFG 中,点A 、B 、E 在同一条直线上, P 是线段 DF 的中点,连接 PG ,PC .若BD GE 3AC BF(1)请写出线段 PG 与 PC 所满足的关系;并加以证明.(2)若将图①中的菱形 BEFG 饶点 B 顺时针旋转,使菱形 BEFG 的对角线 BF 恰好与菱形 ABCD 的边 AB 在同 一条直线上,原问题中的其他条件不变,如图②.那么你在( 1)中得到的结论是否发生变化?若没变化,直接写出结论,若有变化,写出变化的结果.3)若将图①中的菱形 BEFG 饶点 B 顺时针旋转任意角度,原问题中的其他条件不变,请猜想(1)中的结论有没有变化?1.在菱形 ABCD 中,∠ ABC=60°, E 是对角线 AC 上一点,F 是线段 BC 延长线上一点,且 CF=AE ,连接BE 、答案与解析1. 【答案】见解析【解析】(1)延长GP交DC于H,∵DC∥GF,∴∠ DHP=∠PGF,∠ DPH=∠ GPF,∵DP=PF,∴△ DHP≌△ PGF,∴HD=GF,∵四边形ABCD和四边形GFEB是菱形,∴DC=CB,FG=G,B∴DH=GB ∴DC-DH=CB-G,B∴CH=CG,∴△ CHG就是等腰三角形且CP是底边即可得出CP⊥ PG;∴线段PG与PC的位置关系是PG⊥ PC;(2)线段PG与PC的位置关系是PG⊥PC;证明:如图②,延长GP到H,使PH=PG,连接CH,CG,DH,∵P 是线段DF的中点,∴FP=DP,∵∠GPF=∠HPD,∴△ GFP≌△ HDP,∴GF=HD,∠ GFP=∠ HDP,∵ BD GE 3,AC BF∴∠ ADC=∠ABC=60°,∠ GBF=60°,∵四边形ABCD是菱形,∴CD=CB,∠ ADC=∠ABC=60°,点A、B、F 又在一条直线上,∴∠ FBC=120°,∴∠ HDC=∠CBG=60°,∵四边形BEFG是菱形∴GF=GB,CD BC ∴HD=GB,即在△ HDC与△ GBC中,HDC CBGDH BG∴△ HDC≌△ GBC(SAS),∴∠ DCH+∠HCB=∠BCG+∠HCB=120°,∵CH=CG,PH=PG,3)将图①中的菱形BEFG饶点B 顺时针旋转任意角1)中的结论没有变化,PG⊥ PC.2. 【答案】见解析解析】(1)图2:BE=EF.图3.图2 证明如下:过点E 作EG∥ BC,交AB 于点G,AB=BC.又∵∠ ABC=60°,∴△ ABC是等边三角形.∴AB=AC,∠ ACB=60° .又∵ EG∥ BC,∴∠ AGE=∠ABC=60° .又∵∠ BAC=60°,∴△ AGE是等边三角形. ∴ AG=AE.∴BG=CE.又∵ CF=AE,∴ GE=CF.又∵∠ BGE=∠ECF=120°,∴△ BGE≌△ ECF(SAS). ∴ BE=EF.2)图2,过点E作EG∥ BC,交AB于点G,再求出△ AGE是等边三角形,根据等边三角形的性质得到根据等边三角形的性质得到AB=AC,∠ ACB=60°,AG=AE,从而可以求出BG=CE,再根据等角的补角相等求出∠ BGE=∠ ECF=120°,然后利用“边角边”证明△BGE和△ ECF 全等,根据全等三角形对应边相等即可得证.图3,证明思路与方法与图2 完全相同,证明如下:过点E作EG∥ BC交AB延长线于点G,∵四边形ABCD为菱形,∴ AB=BC. 又∵∠ ABC=60°,∴△ ABC 是等边三角形∴AB=AC∠ ACB=60°.又∵ EG∥ BC,∴∠ AGE=∠ABC=60° .又∵∠ BAC=60°,∴△ AGE是等边三角形. ∴ AG=AE.∴BG=CE. 又∵ CF=AE,∴ GE=CF.又∵∠ BGE=∠ECF=60°,∴△ BGE≌△ ECF(SAS).∴BE=EF.七、教学反思。
第1讲:菱形的性质与判定_教案

∵在Rt△ABC中,CH⊥AB于H,
∴∠1+∠AFH=90°,∠2+∠4=90°,
∵∠3=∠AFH,∠1=∠2,
∴∠3=∠4,
∴FC=CD,
∵DE⊥AB垂足为E,∠ACD=90°,∠1=∠2,
∴CD=DE,∴FC=DE,
∵CH⊥AB,DE⊥AB,
∴FC∥DE,
∴四边形CFED是平行四边形,
【解析】根据菱形的判定,平行的性质,全等三角形的判定和性质,由已知,添加OA=OC或AD=BC或AD//BC或AB=BC等即可判定ABCD成为菱形.
3.【答案】见解析.
【解析】△ECF是等边三角形.
证明:连接AC,
∵∠B=60°,
∴AC=AB=CD,∠D=∠CAE=60°
又∵AE=FD,
∴△CDF≌△CEA(SAS),
A.4 B.24 C.8 D.24
2.如图,菱形ABCD中,P为对角线AC上一动点,E,F分别为AB、BC中点,若AC=8,BD=6,则PE+PF的最小值为___________.
答案与解析
1.【答案】C
【解析】试题分析:先根据菱形的性质求得∠BAD=60°,AO=3,即可得到△ABD为等边三角形,根据等边三角形可得AB的长,从而求得结果.
A. D.8
2.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件,
使四边形ABCD成为菱形.(只需添加一个条件即可)
3.如图,在菱形ABCD中,∠B=60°,点E、F分别在边AB、AD上,且AE=DF.
(1)试猜想△ECF的形状,并说明理由.
(2)若AB=10,那么△ECF的周长是否存在最小值?如果存在,请求出来;如果不存在,请说明理由.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学菱形的性质及判定1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.2.菱形的性质菱形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:① 边的性质:对边平行且四边相等.② 角的性质:邻角互补,对角相等.③ 对角线性质:对角线互相垂直平分且每条对角线平分一组对角.④ 对称性:菱形是中心对称图形,也是轴对称图形.菱形的面积等于底乘以高,等于对角线乘积的一半.点评:其实只要四边形的对角线互相垂直,其面积就等于对角线乘积的一半.3.菱形的判定判定①:一组邻边相等的平行四边形是菱形.判定②:对角线互相垂直的平行四边形是菱形.判定③:四边相等的四边形是菱形.4.三角形的中位线中位线:连结三角形两边的中点所得的线段叫做三角形的中位线.也可以过三角形一边的中点作平行于三角形另外一边交于第三边所得的线段也是中位线.以上是中位线的两种作法,第一种可以直接用中位线的性质,第二种需要说明理由为什么是中 位线,再用中位线的性质.定理:三角形的中位线平行第三边且长度等于第三边的一半.重点是菱形的性质及判定定理。
菱形是在平行四边形的前提下定义的,首先她是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法。
菱形的这些性质和判定定理即是平行四边形性质与判定的延续,又是以后要学习的正方形的基础。
难点是菱形性质的灵活应用。
由于菱形是特殊的平行四边形,所以它不但具有平行四边形的性质,同时还具有自己独特的性质。
如果得到一个平行四边形是菱形,就可以得到许多关于边、角、对角线的条件,在实际解题中,应该应用哪些条件,怎样应用这些条件,常常让许多学生手足无措,教师在教学过程 中应给予足够重视。
板块一、菱形的性质菱形的两条对角线将菱形分成全等三角形的对数为中点中点中点平行【考点】菱形的性质及判定 【题型】填空 【难度】2星 【关键词】【解析】根据菱形的性质可知:共有对 【答案】在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是 【考点】菱形的性质及判定 【题型】填空 【难度】2星 【关键词】【解析】根据菱形的性质可知:应当旋转至少 【答案】如图2,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距离,则 度.【考点】菱形的性质及判定 【题型】填空 【难度】2星【关键词】2009年,江西中考【解析】由题意可知:构成三角形为等边三角形 【答案】88180︒180︒16cm 16cm AB BC ==1∠=图21CBA120︒如图,在菱形中,,、分别是、的中点,若,则菱形的边长是______.【考点】菱形的性质及判定 【题型】填空 【难度】2星【关键词】2009年,漳州中考 【解析】省略 【答案】如图,是菱形的边的中点,于,交的延长线于,交于,证明:与互相平分.【考点】菱形的性质及判定,平行四边形的性质和判定 【题型】解答 【难度】3星 【关键词】 【解析】省略【答案】连接、、∵菱形中,,∴∥∵∥,∴四边形是平行四边形,∴ ∵,∴ABCD 60A ∠=︒E F AB AD 2EF =ABCD 4E ABCD AD EF AC ⊥H CB F AB P AB EF P HFE DCBABD AF EB ABCD BD AC ⊥EF AC ⊥BD EF AD FC BDEF ED FB =AE ED =AE FB =E F DBCA又∵,∴四边形是平行四边形 ∴与互相平分如图1所示,菱形中,对角线、相交于点,为边中点,菱形的周长为,则的长等于 .【考点】菱形的性质及判定 【题型】填空 【难度】2星【关键词】2009年,本溪中考 【解析】省略 【答案】如图,已知菱形的对角线于点,则的长为【考点】菱形的性质及判定 【题型】填空 【难度】2星 【关键词】 【解析】省略菱形周长为,一条对角线长为,则其面积为 . 【考点】菱形的性质及判定 【题型】填空 【难度】2星 【关键词】AE FB ∥AFBE AB EF ABCD AC BD O H AD ABCD 24OH 图1HO DC BA3ABCD 8cm 4cm AC BD DE BC ==⊥,,E DE 52cm 10cm【解析】菱形的边长为,由勾股数和菱形对角线的性质得另一对角线长为,故面积为 【答案】菱形的周长为,两邻角度数之比为,则菱形较短的对角线的长度为【考点】菱形的性质及判定 【题型】填空 【难度】2星 【关键词】 【解析】省略 【答案】如图2,在菱形中,,,则菱形的边长为( ) A . B . C . D .【考点】菱形的性质及判定 【题型】选择 【难度】2星【关键词】2009年,重庆江津中考【解析】由菱形的对角线互相垂直平分及勾股数可知选A 【答案】A如图3,在菱形中,,、分别是边和的中点,于点,则( )A .B .C .D .()52413cm ÷=()24cm ()2120cm 12020cm 2:15ABCD 6AC =8BD =51068图2DCBAABCD 110A ∠=︒E F AB BC EP CD ⊥P FPC ∠=35︒45︒50︒55︒【考点】菱形的性质及判定 【题型】选择 【难度】2星【关键词】2009年,杭州市中考 【解析】省略 【答案】D如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为的菱形,剪口与折痕所成的角的度数应为( ) A .或 B .或 C .或 D .或【考点】菱形的性质及判定 【题型】选择 【难度】2星【关键词】2009年,绵阳市中考 【解析】省略 【答案】D菱形中,、分别是、的中点,且,,那么等于 .【考点】菱形的性质及判定 【题型】填空 【难度】2星 【关键词】图3E DP CF BA 60︒α15︒30︒30︒45︒45︒60︒30︒60︒ABCD E F BC CD AE BC ⊥AF CD ⊥EAF ∠【解析】省略 【答案】已知菱形的一个内角为,一条对角线的长为则另一条对角线的长为________.【考点】菱形的性质及判定 【题型】填空 【难度】2星【关键词】2009年,辽宁朝阳中考 【解析】省略 【答案】或如图,将一个长为,宽为的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( ) A . B . C . D .【考点】菱形的性质及判定 【题型】选择 【难度】3星【关键词】2009年,南宁市中考 【解析】省略 【答案】A已知菱形的两条对角线的乘积等于菱形的一条边长的平方,则菱形的一个钝角的大小是 【考点】菱形的性质及判定60︒60︒2610cm 8cm 210cm 220cm 240cm 280cm 图1DCBA ABCD AC BD ,【题型】填空 【难度】4星【关键词】希望杯邀请赛 【解析】如图,过点作于,则,又,得,【答案】如图,菱形花坛的周长为,,•沿着菱形的对角线修建了两条小路和,求两条小路的长和花坛的面积.【考点】菱形的性质及判定 【题型】解答 【难度】3星 【关键词】【解析】 ∵四边形是菱形 ∴ ∵∴和都是等边三角形 ∴ 又∵在和中可得A AE BC ⊥E 12AC BD BC AE ⋅=⋅2AC BD AB ⋅=1302AE AB ABC =∠=︒,150BAD ∠=︒EDCBA150︒ABCD 20m 60ABC ∠=︒ACBD 图2ABCD 5AB BC CD DA ====60ABC ∠=︒ABC ∆ADC ∆5AC =AC BD ⊥Rt ABO ∆Rt ADO∆BO DO ==∴∴点评:内角为和的菱形学生必须掌握,这是考试的热点模型. 【答案】见解析如图,在菱形中,在上,点在上,则的最小值为【考点】菱形的性质及判定 【题型】填空 【难度】3星 【关键词】 【解析】关于对称,连交于,且 为最小值 【答案】已知,菱形中,、分别是、上的点,若,求的度数.【考点】菱形的性质及判定 【题型】解答 【难度】4星 【关键词】【解析】∵ ∴BD =12ABCDS AC BD =⋅=60︒120︒ABCD 4AB a E =,BC 2120BE a BAD P =∠=︒,,BD PE PC +DBA C ,BD AE BD P 30AE BC BAE PE PC AE ⊥∠=︒+==,,ABCD E F BC CD AE AF EF AB ===C ∠FEDCBAAE AB =B AEB ∠=∠同理∵四边形是菱形∴,∴ ∵ ∴∵,∴是等边三角形,∴ 设则∵,∴∵,∴,∴∴ ∴ 【答案】已知,菱形中,、分别是、上的点,且,.求:的度数.【考点】菱形的性质及判定 【题型】解答 【难度】4星 【关键词】【解析】连接,∵四边形为菱形 ∴∴和为等边三角形 ∴ ∵ ∴ ∴ ∴ ∵∴为等边三角形D AFD ∠=∠ABCD AD BC B D BAD C ∠=∠∠=∠∥,,AEB AFD ∠=∠B D ∠=∠BAE DAF ∠=∠DE EF AF ==AEF △60EAF ∠=︒BAE x ∠=,602BAD x ∠=︒+180ABE ABE BAE ∠+∠+∠=︒902x ABE ∠=︒-AD BC ∥180B BAD ∠+∠=︒906021802x x ︒-+︒+=︒20x =︒602100C BAD x ∠=∠=︒+=︒100︒ABCD E F BC CD 60B EAF ∠=∠=︒18BAE ∠=︒CEF ∠FEDCBAABCDEFAC ABCD AB BC CD AD ===ABC △ACD △60AB AC B ACD BAC =∠=∠=∠=︒,60EAF ∠=︒BAE CAF ∠=∠ABE ACF △≌△AE AF =60EAF ∠=︒AEF △∴∵ ∴分析:在矩形、菱形的定理题中,有时也常连对角线,把四边形问题转化为三角形问题. 【答案】板块二、菱形的判定如图,如果要使平行四边形成为一个菱形,需要添加一个条件,那么你添加的条件是 .【考点】菱形的性质及判定 【题型】填空 【难度】2星【关键词】2007年,四川成都 【解析】等; 【答案】如图,在中,平分,的中垂线交于点,交于点,求证:四边形是菱形【考点】菱形的性质及判定 【题型】解答 【难度】3星 【关键词】 【解析】省略60AEF ∠=︒AEC B BAE AEF CEF ∠=∠+∠=∠+∠18CEF ∠=︒18︒ABCD DCAB AB AD AC BD =⊥,AB AD AC BD =⊥,ABC ∆BD ABC ∠BD ABE BCF BEDF FEDCBA【答案】∵是的中垂线 ∴∴ ∵∴,所以 同理所以四边形是菱形如图,在中,,是的中点,连结,在的延长线上取一点,连结,.当与满足什么数量关系时,四边形是菱形?并说明理由.【考点】菱形的性质及判定 【题型】解答 【难度】3星【关键词】2009年,娄底中考【解析】当(或或)时,四边形是菱形理由如下:∵,∴又点为中点,∴ ∴四边形为平行四形边 ∵∴四边形为菱形 【答案】见解析已知:如图,平行四边形的对角线的垂直平分线与边、分别相交于 、.求证:四边形是菱形.EF BD BE DE BF DF ==,,DBE BDE ∠=∠EBD DBF ∠=∠DBF EDB ∠=∠BC DE ∥AB DF ∥BEDF ABC ∆AB AC =D BC AD AD E BE CE AE AD ABEC EDCB A2AE AD =AD DE =12DE AE =ABEC 2AE AD =AD DE =D BC BD CD =ABEC AB AC =ABEC ABCD AC AD BC E F AFCE【考点】菱形的性质及判定 【题型】解答 【难度】3星【关键词】2006年,盐城中考 【解析】省略【答案】∵垂直平分, ∴. ∴.又∵平行四边形, ∴. ∴≌. ∴.∴四边形是平行四边形.又由可知,四边形是菱形.如图,在梯形纸片中,,,将纸片沿过点 的直线折叠,使点落在上的点处,折痕交于点,连结.求证:四边形是菱形.【考点】菱形的性质及判定 【题型】解答 【难度】3星【关键词】2007年,云南双柏 【解析】省略【答案】根据题意可知ODEFCABEF AC ,EF AC AO CO ⊥=90AOE COF ∠=∠=oABCD EAO FCO ∠=∠AOE ∆COF ∆OE OF =AECF AC EF ⊥AECF ABCD //AD BC AD CD >D C AD C DE BC E C E 'CDC E 'C'DCB A E'CDE C DE ∆≅∆则. ∵, ∴. ∴, ∴.∴, ∴四边形为菱形.如图,是菱形的边的中点,于,交的延长线于,交于,证明:与互相平分【考点】菱形的性质及判定,平行四边形的性质和判定 【题型】解答 【难度】3星 【关键词】 【解析】省略 【答案】连结,因为菱形中,又因为,所以因为,所以四边形是平行四边形,可得,因为,所以,从而,,因此四边形是平行四边形,所以与互相平分已知:如图,在平行四边形中,是边上的高,将沿方向平移,使点与点重合,得.若,当与满足什么数量关系时,四边形是菱形?证明你的结论.'''CD C D C DE CDE CE C E =∠=∠=,,//AD BC C DE CDE '∠=∠CDE CED ∠=∠CD CE =CD C D C E CE ''===CDC E 'E ABCD AD EF AC ⊥H CB F AB P AB EF AB CDEF P PF EDC B A BD AF EB ,,ABCD BD AC ⊥EF AC ⊥BD EF ∥,AD FC ∥BDEF ED FB =AE ED =AE FB =AE FB ∥AE FB =AFBE AB EF ABCD AE BC ABE ∆BC E C GFC ∆60B ∠=︒AB BC ABFG GF E DCBA【考点】菱形的性质及判定 【题型】解答 【难度】3星【关键词】2009年,山东青岛市 【解析】省略【答案】当时,四边形是菱形.∵,∴四边形是平行四边形 ∵中, ∴ ∴∵,∴∴∴四边形是菱形.如图,在中,,是的中点.分别作于,于,于,于.相交于点.求证:四边形是菱形.【考点】菱形的性质及判定 【题型】解答 【难度】3星 【关键词】 【解析】省略【答案】∵,.∴∥,同理∥,∴四边形是平行四边形32BC AB =ABFC AB GF ∥AG BF ∥ABFG Rt ABE ∆60B ∠=︒30BAE ∠=︒12BE AB =BE CF =32BC AB =12EF AB =AB BF =ABFG ABC ∆AB AC =M BC MD AB ⊥D ME AC ⊥E DF AC ⊥F EG AB ⊥G DF EG 、P DMEP PMF E DG CBA MD AB ⊥EG AB ⊥MD EG ME DF MFPD∵,∴∵,,∴≌ ∴,∴四边形是菱形如图,中,,是的平分线,交于,是边上的高,交于,于,求证:四边形是菱形.【考点】菱形的性质及判定 【题型】解答 【难度】3星 【关键词】 【解析】省略【答案】∵,∴ ∵,∴∵平分,∴,∴ ∵,∴,∴ ∵平分,, ∴,∴ 又∵,∴∥,故四边形是平行四边形 ∵,∴四边形是菱形如图,是矩形内的任意一点,将沿方向平移,使与重合,点移动到点的位置 ⑴画出平移后的三角形;⑵连结,试说明四边形的对角线互相垂直,且长度分别等于的长; ⑶当在矩形内的什么位置时,在上述变换下,四边形是菱形?AB AC =B C ∠=∠BM MC =BDM ∠=90CEM ∠=oBDM ∆CEM ∆DM EM =DMEP ABC ∆90ACB ∠=︒AD BAC ∠BC D CH AB AD F DE AB ⊥E CDEF HF DECBACH AB ⊥90HAF AFH ∠+∠=︒90ACB ∠=︒90CAD ADC ∠+∠=︒AD CAB ∠CAD HAF ∠=∠AFH CDF ∠=∠AFH CFD ∠=∠CDF CFD ∠=∠CF CD =AD CAB ∠DC AC ⊥DE AB ⊥CD DE =CF DE =CH AB ⊥DE AB ⊥CF DE ABCD CD DE =ABCD M ABCD MAB ∆AD AB DC M 'M 'MD MC MM ,,'MDM C AB AD ,M 'MDM C为什么?【考点】菱形的性质及判定 【题型】解答 【难度】3星 【关键词】 【解析】省略【答案】⑴如图,就是所要作的三角形⑵因为平移到,所以且,四边形是平行四边形,所以 ,矩形中,,所以,又因为,,所以四边形的对角线互相垂直,且长度分别等于的长⑶当点是的交点时,四边形是菱形,理由:如图,矩形中,,又因为,可得,所以 四边形是菱形如图,、、均为直线同侧的等边三角形.已知. ⑴ 顺次连结、、、四点所构成的图形有哪几类?直接写出构成图形的类型和相应 的条件.⑵ 当为 度时,四边形为正方形.【考点】菱形的性质及判定 【题型】解答M'M DC BA'DCM ∆AM 'DM 'AM DM ∥'AM DM ='DAMM 'AD MM ∥ABCD AD CD ⊥'MM CD ⊥'AD MM =CD AB ='MDM C AB AD ,M AC BD ,'MDM C ABCD AM BM MC MD ===''AM D M BM CM ==,''MD MC CM DM ==='MDM C ACD ∆ABE ∆BCF ∆BC AB AC =A D F E BAC ∠ADFE FEDCBA【难度】3星【关键词】2008年,佛山市中考改编 【解析】省略【答案】⑴ 构成的图形有两类,一类是菱形,一类是线段.当图形为菱形时,∠ BAC ≠60°(或A 与F 不重合、△ABC 不为正三角形)(若写出图形为平行四边形时,不给分) 当图形为线段时,∠BAC = 60°(或A 与F 重合、△ABC 为正三角形). ⑵ .三、与菱形相关的几何综合题已知等腰中,,平分交于点,在线段上任取一点(点除外),过点作,分别交、于、点,作,交于点,连结. ⑴求证四边形为菱形⑵当点在何处时,菱形的面积为四边形面积的一半?【考点】菱形的性质及判定 【题型】解答 【难度】3星 【关键词】 【解析】省略【答案】⑴∵ ∴四边形为平行四边形 ∵,平分 ∴∵150︒ABC △AB AC =AD BAC ∠BC D AD P A P EF AB ∥AC BC E F PM AC ∥AB M ME AEPM P AEPM EFBM MPFABCDE PM AC EF AB ∥,∥AEPM AB AC =AD CAB ∠CAD BAD ∠=∠AD BC BAD EPA ⊥∠=∠,∴ ∵∴四边形为菱形 ⑵当为中点时, ∵四边形为菱形,∴ ∵ ∴ 又 ∴四边形为平行四边形问题:如图1,在菱形和菱形中,点在同一条直线上,是线段的中点,连结.若,探究与的位置关系及的值.小聪同学的思路是:延长交于点,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题:⑴ 写出上面问题中线段与的位置关系及的值;⑵ 将图1中的菱形绕点顺时针旋转,使菱形的对角线恰好与菱形的边在同一条直线上,原问题中的其他条件不变(如图2).你在⑴中得到的两个结论是否发生变化?写出你的猜想并加以证明.⑶ 若图1中,将菱形绕点顺时针旋转任意角度,原问题中的其他条件不变,求的值(用含的式子表示).【考点】菱形的性质及判定,全等三角形的性质和判定,旋转的性质【题型】解答 【难度】5星CAD EPA ∠=∠EA EP =AEPM P EF 12EFBM AEPMSS =四边形菱形AEPM AD EM ⊥AD BC ⊥EM BC ∥EF AB ∥EFBM ABCD BEFG A B E ,,P DF PG PC ,60ABC BEF ∠=∠=︒PG PC PG PCGP DC H PG PC PG PCBEFG B BEFG BF ABCD AB ()2090ABC BEF αα∠=∠=︒<<︒BEFG B PG PCα图2AB CDEFG P HP G FEDCB A【关键词】2008年,北京中考 【解析】省略【答案】⑴ 线段与的位置关系是;.⑵ 猜想:⑴中的结论没有发生变化.证明:如图,延长交于点,连结. ∵是线段的中点, ∴.由题意可知. ∴.又∵,∴,∴,.∵四边形是菱形,∴,.由,且菱形的对角线恰好与菱形的边在同一条直线上,可得. ∴.∵四边形是菱形, ∴,∴.∴,∴,.∴,即. ∵,,∴,. ∴⑶ .证明过程略.本题是一道探究性的几何综合题,本题的题干是以阅读材料的形式呈现,从而降低了题目的难度,本题应该是在05年大连中考压轴题的基础上改进而来的.PG PC PG PC ⊥PG PCGP AD H CH CG ,P DF FP DP =AD FG ∥GFP HDP ∠=∠GPF HPD ∠=∠GFP HDP ∆∆≌GP HP =GF HD =ABCD CD CB =60HDC ABC ∠=∠=︒60ABC BEF ∠=∠=︒BEFG BF ABCD AB 60GBC ∠=︒HDC GBC ∠=∠BEFG GF GB =HD GB =HDC GBC ∆∆≌CH CG =DCH BCG ∠=∠120DCH HCB BCG HCB ∠+∠=∠+∠=︒120HCG ∠=︒CH CG =PH PG =PG PC ⊥60GCP HCP ∠=∠=︒PG PC=PG PC=()tan 90α︒-四、中位线与平行四边形顺次连结面积为的矩形四边中点得到一个四边形,再顺次连结新四边形四边中点得到一个 ,其面积为 . 【考点】三角形的中位线 【题型】填空 【难度】3星 【关键词】【解析】理由:由中位线得即可.【答案】.如图,在四边形中,,、、、分别是、、、的中点,要使四边形是菱形,四边形还满足的一个条件是 ,并说明理由.【考点】菱形的性质及判定,三角形的中位线 【题型】填空 【难度】3星【关键词】2009年,上海模拟【解析】理由:由中位线得即可.【答案】.在四边形中,,,分别是、的中点,,分别是对角线,中点,证明:与互相垂直.2012EF FG GH HE AD ====AD BC =ABCD AB CD ≠E F G H AB BD CD AC EFGH ABCD HGFE D CBA12EF FG GH HE AD ====AD BC =ABCD AB CD =P Q AD BC M N AC BD PQ MN【考点】菱形的性质及判定,三角形的中位线 【题型】解答 【难度】4星 【关键词】【解析】连接,,,.证明为菱形. 【答案】见解析四边形中,、分别是、上的点,、分别是、的中点,当点在上从向移动而点不动时,那么下列结论成立的是 ( )A .线段的长逐渐增大B .线段的长逐渐减小C .线段的长不变D .线段的长与点的位置有关【考点】三角形的中位线 【题型】选择 【难度】4星 【关键词】【解析】连结,利用三角形的中位线可得与点无关.【答案】C如图,中,是的平分线,于,为的中点,,Q PMNCB D APN NQ MQ PM PNQM ABCD R P BC CD E F AP RP P CD C D R EF EF EF EF P P FREDCBAAR 12EF AR =P ABC ∆AD BAC ∠CE AD ⊥E M BC 14cm AB =,则的长为 .【考点】三角形的中位线 【题型】填空 【难度】3星 【关键词】【解析】延长交于点.利用中位线的性质和直角三角形斜边中线可得.【答案】如图,四边形中,,分别是的中点,连结并延长,分别交的延长线于点,求证:【考点】三角形的中位线 【题型】解答 【难度】4星 【关键词】 【解析】省略【答案】连结,取中点,连结,由条件易得分别是的中位线,所以,且,因为,所以,所以,由可得:,同理可得,所以10cm AC =ME M EDCBAEN M DCBACE AB N ()14102cm 2-=2ABCD AB CD =E F ,BC AD ,EF BA CD ,G H ,BGE CHE ∠=∠PA BCDEF G HH G FED CBABD BD P PE PF ,PE PF ,BDC DBA ∆∆,PE DC PF BA ∥,∥1122PE DC PF BA ==,AB CD =PE PF =PEF PFE ∠=∠PE DC ∥PEF CHE ∠=∠PFE BGE ∠=∠BGE CHE ∠=∠如图,已知、分别为中、的平分线,于,于,求证:.【考点】三角形的中位线 【题型】解答 【难度】4星 【关键词】【解析】延长、交于点、. 由等腰三角形三线合一可得、 再由三角形中位线可得. 【答案】见解析如图,四边形中,分别是边的中点,则和的关系是( )A .B .C .D .【考点】三角形的中位线 【题型】选择 【难度】3星 【关键词】【解析】连结,取的中点,连结,由三角形的中位线可知选B【答案】BBE CF ABC ∆B ∠C ∠AM BE ⊥M AN CF ⊥N MN BC ∥NMEFCBAAM AN BC Q R AM QM =AN RN =MN BC ∥ABCD E F ,AB CD ,AD BC ,EF 2AD BC EF +>2AD BC EF +≥2AD BC EF +<2AD BC EF +≤A BCDEFP FEDCBA BD BD P FP EP ,已知如图所示,、、、分别是四边形的四边的中点,求证:四边形是平行四边形.【考点】平行四边形的性质和判定,三角形的中位线 【题型】解答 【难度】3星 【关键词】【解析】连接.∵、分别为、中点 ∴,∥又∵、分别为、中点∴,∥,∴,∥∴四边形为平行四边形 【答案】见解析如图,在四边形中,为上一点,和都是等边三角形,、、、的中点分别为、、、,证明四边形为平行四边形且.【考点】平行四边形的性质和判定,三角形的中位线 【题型】解答 【难度】4星【关键词】2009年,兰州中考 【解析】如图,连结、.E F G H ABCD EFGH HGFDC BAHGFEDC BAAC H G AD DC 12HG AC =HG AC E F AB BC 12EF AC =EF AC HG EF =HG EF EFGH ABCD E AB ADE ∆BCE ∆AB BC CD DA P Q M N PQMN PQ PN =QEP NMDCBAQ EP NMDCBAAC BD∵为的中位线 ∴且同理且∴且∴四边形为平行四边形. 在和中,, 即 ∴ ∴∴.【答案】见解析如图,四边形中,分别是的中点,求证:相互垂直平分【考点】菱形的性质及判定,三角形的中位线 【题型】解答 【难度】3星 【关键词】 【解析】连结,根据题意,分别是的中位线,所以,同理可证:,因为,所以,则四边形是菱形,所以相互垂直 【答案】见解析的三条中线分别为、、,为边外一点,且为平行四边形,求证:.PQ ABC ∆PQ AC ∥12PQ AC =MN AC ∥12MN AC =MN PQ ∥MN PQ =PQMN AEC ∆DEB ∆AE DE =EC EB =60AED CEB ∠=︒=∠AEC DEB ∠=∠AEC DEB ∆∆≌AC BD =1122PQ AC BD PN ===ABCD AB CD E F G H =,,,,AD BC BD AC ,,,EF GH ,ABCDEFGH H GF EDCBAEG GF FH HE ,,,EG HF ,DAB CAB ∆∆,12EG HF AB ==12GF EH CD ==AB CD =EG HF GF EH ===EGFH EF GH ,ABC ∆AD BE CF H BC BHCF AD EH ∥【考点】平行四边形的性质和判定,三角形的中位线 【题型】解答 【难度】4星 【关键词】【解析】此题解法很多,仅供两种解法参考. 方法一:连结、.(如图1) ∵四边形为平行四边形 ∴且 由中位线可得∴∴四边形为平行四边形 ∴且∴四边形为平行四边形 ∴方法二:连结.(如图2)通过中位线和平行四边的性质可得 , ∴ 又∵ 显然 ∴ ∴【答案】见解析在平行四边形的对角线上取一点,使,连接并延长与的延长线交于,则.ABCDE FH图1HFED CBAABCD EFH图2DE DH BHCF CH BF AF ==CH AF ∥12DE AB AF ==CH DE =DECH DH CE ∥DH CE AE ==DHEA AD EH ∥DE DE HC =AB DE HC ∥∥AED ECH ∠=∠AE EC =ADE EHC ∆∆≌DAE HEC ∠=∠AD EH ∥ABCD BD E 13BE DE =AE DC F 2CF AB =【考点】三角形的中位线 【题型】解答 【难度】5星 【关键词】【解析】法1:如图2,取之中点,由引交于,再由引交于.∵,,,∴,,则为的中点, ∴.又∵,∴,即、是的三等分点. ∵,∴、是的三等分点,有. 而,∴.法2:如图3,连接交于,则为、的中点,取的中点,连接交于,则为、的中点,取的中点,连接,则.∵,图1CAEDBFBD O O OM AF ∥DF M C CG FE ∥BD G 图2FBD E ACMOG AB CD =ABE CDG ∠=∠BAE DCG ∠=∠ABE CDG ∆∆≌BE DG =O EG EO OG =13DG BE DE ==13EO OG DE ==G O DE CG OM AF ∥∥C M DF 2CF CD =CD AB =2CF AB =AC BD O O AC BD AF R AC BD O O AC BD AF R OR 12OR CF =∥图3FBD E ACROOR CD AB ∥∥∴,.又∵,,由此可得,,∴,, ∴.即,∴.法3:如图1,∵, ∴,即. 又∵,∴, 即.【答案】见解析如图,中,、分别是、的中点,、是的三等分点,连结并延长、交于点.求证:四边形是平行四边形.【考点】平行四边形的性质和判定,三角形的中位线 【题型】解答 【难度】4星 【关键词】【解析】连接、、,设与相交与点∵、分别是、的中点,∴∥,同理∥ ∴四边形是平行四边形,∴, ∵,∴∴四边形是平行四边形 【答案】见解析ABE ROE ∠=∠BAE ORE ∠=∠BE OE OD +=11()33BE DE OE OD ==+12BE OD =13OE DE =BE OE =ABE ROE ∆∆≌AB OR =12AB OR CF ==2CF AB =AB DF ∥13AB BE DFDE==3DF AB =AB CD =3CF DF CD AB AB =-=-2CF AB =ABC ∆E F AB BC G H AC EG FH D ABCD HGFEDCBABG BH BD BD AC O E F AB BC EG BH FH BG BHDG OB OD =OG OH =AG HC =OA OC =ABCD如图,在四边形中,、分别为、的中点,,和相交于点,分别与、相交于、,求证:.【考点】三角形的中位线 【题型】解答 【难度】3星 【关键词】【解析】取中点,连结、. 利用中位线可得∴ ∵, ∴ ∴【答案】见解析如图,线段相交于点,且,连结,分别是的中点,分别交于,求证:【考点】三角形的中位线 【题型】解答 【难度】4星 【关键词】ABCD M N AD BC BD AC =BD AC O MN AC BD E F OE OF =FEONM D CBAPF EO NM DCBAAB P MP NP 1122MP BD NP AC ===PMN PNM ∠=∠MP BD ∥NP AC ∥OFE OEF ∠=∠OE OF =AB CD ,O AB CD =AD BC ,E F ,AD BC ,EF AB CD ,M N ,OM ON =P A BCD M N OEF FEO N M DCBA【解析】连结,取中点,连结,由条件易得分别是的中位线,所以,且,因为,所以,所以,由可得,同理可得,所以,所以 【答案】见解析如图,梯形中,,对角线相交于点,,分别是的中点,求证:是等边三角形【考点】三角形的中位线,直角三角形斜边上的中线等于斜边的一半,等腰梯形的性质和判定 【题型】解答 【难度】4星 【关键词】 【解析】省略【答案】连结,由等腰梯形对角线相等,且,可证是等边三角形,因为是中点,所以,在中,是中点,所以,同理可证,因为分别是的中点,所以,因为,所以,即是等边三角形如图,求证:四边形两组对边中点连线与两对角线中点连结这三条线共点.BD BD P PE PF ,PE PF ,DBA BDC ∆∆,PE BA PF DC ∥,∥1122PE BA PF DC ==,AB CD =PE PF =PEF PFE ∠=∠PE BA ∥PEF OMN ∠=∠PFE ONM ∠=∠OMN ONM ∠=∠OM ON =ABCD AD BC AB CD =∥,AC BD ,O 60AOD ∠=︒E F G ,,OA OB CD ,,EFG ∆A BCDEFG OO GFE DCBA DE 60AOD ∠=︒AOD ∆E OA DE AC ⊥Rt DCE ∆G DC 12EG DC =12FG DC =E F ,OA OB ,12EF AB =AB DC =EG FG EF ==EFG ∆【考点】三角形的中位线 【题型】解答 【难度】5星 【关键词】 【解析】方法一:设分别为的中点,要证明及三线共点.因为且,所以且,且,从而四边形为平行四边形,故与互相平分.设与的交点为,则经过中点(当然也是中点).同理,也过中点.所以,,,三线共点于.说明:本题证明的关键是平行四边形的获得(它是通过三角形中位线定理来证明的).由此可见,在某些四边形的问题中,通过构造平行四边形去解题是一种常用的技巧. 请看下例.方法二:应用中点公式法可设, 那么线段的中点坐标为,线段的中点坐标为那么线段的中点坐标为 同理可得:的中点坐标也为 所以可知:,,三线共点于【答案】见解析OE FLHNMDB A N H M L F E ,,,,,AB BC CD DA AC BD ,,,,,EF LH ,,MN LF DC ∥12LF DC =EF DC ∥12EF DC =LF EH ∥LF EH =EHFL LH EF LH EF O LH EF O LH MN EF O EF LH MN O EHFL ()11A x y ,()()()223344B x y C x y D x y ,,,,,AC 131322x x y y F ++⎛⎫⎪⎝⎭,BD 242422x x y y E ++⎛⎫⎪⎝⎭,EF 1234123422xx x x y y y y ++++++⎛⎫⎪⎝⎭,MN LH ,1234123422xx x x y y y y ++++++⎛⎫⎪⎝⎭,EF LH MN O如图,是平行四边形内任意一点,分别是的中点.若,交于,,交于,,交于,,交于,求证:.【考点】平行四边形的性质和判定,三角形的中位线 【题型】解答 【难度】6星 【关键词】【解析】设法证明四边形为平行四边形. 因为,分别为,的中点,所以,且,,且,从而是中点.同理可证,是的中点(是的中位线).所以四边形为平行四边形, ,.同理,.因此 ,即四边形为平行四边形,故 .说明 本题证明显示了用平行四边形证题的技巧,平行四边形,,像三座互相连接的桥梁一样沟通了条件与结论之间的道路. 事实上,由于为平行四边形,我们还可得到,,,与互相平分等等一系列结论.为的中点(同样为的中点)的断言可以证明于下: 取中点,连,则且,所以四边形为平行四边形,.因此为的中点.O ABCD E F G H ,,,OA OB OC OD ,,,DE CF P DG AF Q AH BG R BE CH S PQ SR =SR QPH GOEFDCB A PORS F G OB OC FG BC ∥12FG BC =FG AD ∥12FG AD =F AQ F PC EF PCD ∆APQC PQ AC ∥PA AC =RS AC RS AC ,∥=PQ RS PQ RS ,∥=PQRS PQ RS =PQRS APQC ACRS PQRS PQ SR ∥PS QR ∥PS QR =SQ PR F AQ G DQ AD M MF FG MD ∥FG MD =MFGD MF DG ∥F AQ。
