Maxima官方教程
Maxima快速参考手册

3.1.4 对角矩阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.1.5 单一非零元素矩阵 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
∗Maxima快速参考手册 by Huan Ma is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
†Copyright ⃝c 2010–2011 Huan Ma. 欢迎反馈:yusufma77@
3.2 矩阵运算 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.2.1 加减乘除 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.2.2 幂运算 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.2.3 矩阵乘法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.3 行(列)操作 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Байду номын сангаас . 19
rim包的使用说明:与Maxima计算机代数系统的接口说明书

Package‘rim’August24,2023Type PackageTitle Interface to'Maxima',Enabling Symbolic ComputationVersion0.6.4Date2023-08-24Description An interface to the powerful and fairly complete computer algebra system'Maxima'.It can be used to start and control'Maxima'from within R by entering'Maxima'commands.Results from'Maxima'can be parsed and evaluated in R.It facilitates outputting results from'Maxima'in'LaTeX'and'MathML'.2D and3D plots can be displayed directly.This package also registers a'knitr'-engine enabling'Maxima'code chunksto be written in'RMarkdown'documents.URL https://rcst.github.io/rim/BugReports https:///rcst/rim/issuesSystemRequirements Maxima(https:///projects/maxima/,tested with versions5.42.0-5.46.0),needs to be on PATHLicense GPL(>=3)Imports methods,Rcpp,R6,knitr,GlobalOptionsLinkingTo RcppRoxygenNote7.2.3Suggests testthat(>=3.0.0),rmarkdownConfig/testthat/edition3Encoding UTF-8NeedsCompilation yesAuthor Eric Stemmler[aut,cre],Kseniia Shumelchyk[aut],Hans W.Borchers[aut]Maintainer Eric Stemmler<***********************>Repository CRANDate/Publication2023-08-2412:00:02UTC1R topics documented:rim-package (2)maxima.engine (5)maxima.options (6)Index8 rim-package rimDescriptionProvides an interface to Maxima,a computer algebra system.Usagemaxima.start(restart=FALSE)maxima.stop(engine=FALSE)maxima.get(command)maxima.load(module)maxima.apropos(keystring)maxima.version()maxima.isInstalled()iprint(x)##S3method for class maximaprint(x,...)maxima.eval(x,code=FALSE,envir=globalenv())Argumentsrestart if FALSE(default),then Maxima is started provided it is not running already.If TRUE starts or restarts Maxima.engine if FALSE(default),quits the(running)maxima instance and closes the connec-tion,otherwise quits and closes the(running)maxima instance used for the knitrengine.command character string containing the Maxima command.module character vector naming the Maxima module(typically a*.mac or*.lispfile)to be loaded.keystring character vector containing a search term.x Either a character vector of length1L or an S3object of class"maxima"...other arguments(ignored).code A logical vector of length1L,whether to attach the original expression(TRUE) or not(FALSE,default)envir A environment object.globalenv()(default),is passed to eval().DetailsNote:You need to install the Maxima software separately in order to make use of this package.Maxima is set up automatically on attachment via library(rim)and automatically started whena command is send(if it isn’t running already)using maxima.get().If environment variableRIM_MAXIMA_PATH is not set,rim will search for the Maxima executable,or use the former ing maxima.start()and maxima.stop(),one can stop and(re-)start the current Maxima session if needed,e.g.to clear Maxima command and output history.To send a single command to Maxima and receive the corresponding output use maxima.get().This function returns a S3object of class"maxima".The output is printed by printing the object and will be printed in a format currently set by maxima.options(format).The output format can be changed by setting it,e.g.maxima.options(format="ascii").Output labels are printed according to option maxima.options(label).Valueinvisibly returns NULL.Character vector of length1of the input command.Depending on whether option"label"is set to TRUE,the corresponding input reference label is printed preceding the input command.The evaluated R-objectFunctions•maxima.start():(re-)starts Maxima.•maxima.stop():Quits Maxima.•maxima.get():Executes a single Maxima command provided by command.If no command ending character(;or$is provided,;is appended.•maxima.load():A wrapper to load a Maxima module named by module•maxima.apropos():A wrapper to the Maxima helper function apropos to lookup existing Maxima functions that match keystring.•maxima.version():Returns the version number of Maxima that is used•maxima.isInstalled():Returns TRUE when an installation of Maxima has been detected, otherwise FALSE•iprint():Prints the input command of an maxima S3-object returned by maxima.get()•print(maxima):Prints the maxima output part of an S3object returned by maxima.get()•maxima.eval():Evaluates the parsed and quoted R-expression which is part of an S3object returned by maxima.get()Author(s)Maintainer:Eric Stemmler<***********************>Authors:•Kseniia Shumelchyk<********************>•Hans W.Borchers<*************************>See AlsoUseful links:•https://rcst.github.io/rim/•Report bugs at https:///rcst/rim/issues maxima.engine,maxima.optionsExamplesif(maxima.isInstalled())maxima.start(restart=TRUE)if(maxima.isInstalled()){maxima.start(restart=TRUE)maxima.stop()}if(maxima.isInstalled())maxima.get("2+2;")if(maxima.isInstalled())maxima.load("abs_integrate")if(maxima.isInstalled())maxima.apropos("integrate")maxima.version()maxima.isInstalled()if(maxima.isInstalled()){a<-maxima.get("2+2;")iprint(a)}if(maxima.isInstalled()){a<-maxima.get("2+2;")print(a)}if(maxima.isInstalled()){a<-maxima.get("2+2;")maxima.eval(a)#samemaxima.eval("2+2;")#evaluate with data.framedf<-data.frame(x=seq(0,1,by=0.1))maxima.eval("integrate(1/(1+x^4),x);",code=TRUE,envir=df) maxima.stop()}maxima.engine5 maxima.engine knitr maxima engineDescriptionFunctions to process Maxima code chunks by knitr.Usagemaxima.engine(options)maxima.inline(command)Argumentsoptions named list of knitr options.Supported options are echo,eval,includeand output.var.To change the output format of the Maxima engine set the op-tion maxima.options(engine.format)to either"linear"(default),"ascii","latex"or"mathml".command character string containing the Maxima command to be executed.DetailsUpon attachment,i.e.library(rim)function maxima.engine is registered as a knitr engine.Thus,maxima.engine()is called by knit()to evaluate Maxima code chunks.When called uponthefirst code chunk of a document it starts Maxima in a separate process in server mode.Thismeans that a single Maxima session is used for all Maxima code chunks of an RMarkdown docu-ment.Inputs and outputs can thus be used across chunks(e.g.by using Maxima reference labels).maxima.options(engine.format=...,bel=...)configures the output format andwhether or not output reference labels should be printed.The purpose of maxima.inline is to insert Maxima results as inline text,i.e.on the same lineof the preceding text,if it is actually written on the same line of the RMarkdownfile.It uses thesame running Maxima process as maxima.engine.The output format for inline results can beconfigured separately from the settings of maxima.engine,i.e.maxima.options(inline.format=...,bel=...).ValueThis functions prints the resulting output from maxima together with it’s codecharacter string containing the maxima result printed according options set by maxima.options(inline.format =...,bel=...).Functions•maxima.inline():This function can be used to insert maxima outputs as inline.Examplesif(maxima.isInstalled()){maxima.inline("2+2;")maxima.stop(engine=TRUE)}maxima.options maxima.optionsDescriptionFunction for globally setting and retrieving options.Usagemaxima.options(...,RESET=FALSE,READ.ONLY=NULL,LOCAL=FALSE,ADD=FALSE)Arguments...options to be accessed by using name=value.Options can be added by setting ADD=TRUE,but only those mentioned below will be used my rim.RESET logical of length1,whether to reset all options to default values.READ.ONLY logical of length1,can be used to output all options that are read-only.LOCAL logical of length1,to output all options that are defined locally.ADD logical of length1,whether to add the specified option in...(TRUE),default is FALSE.Detailsformat:character vector of length1setting the output format for maxima.get().Can be one of "linear","ascii","latex"or"mathml".engine.format:same as option format,but for outputs in RMarkdown documents.inline.format:character string setting the output format for maxima.inline(),for knitting outputs inline into RMarkdown documents.Can be one of"linear","latex"or"mathml", but not"ascii".label:logical of length1,whether reference labels should be printed for returned S3objects from maxima.get()(TRUE,default),or not(FALSE).This also applies to printing of input commands using iprint().bel:same as label,but for outputs in RMarkdown documents.bel:same as label,but for inline outputs in RMarkdown documents.Examplesmaxima.options(format="latex")maxima.options(label=FALSE)maxima.options(label=TRUE,format="ascii") #reset to defaultmaxima.options(label=TRUE,format="linear")Indexiprint,6iprint(rim-package),2maxima.apropos(rim-package),2maxima.engine,4,5maxima.eval(rim-package),2maxima.get,3,6maxima.get(rim-package),2maxima.inline(maxima.engine),5 maxima.isInstalled(rim-package),2 maxima.load(rim-package),2maxima.options,3,4,6maxima.start,3maxima.start(rim-package),2maxima.stop,3maxima.stop(rim-package),2maxima.version(rim-package),2print.maxima(rim-package),2rim(rim-package),2rim-package,28。
【word版本】AIM2000简明使用教程

AIM2000 ver2.0简明使用教程文/Sobereva Lastupdate: 2010-MAR-13本文主要介绍AIM2000的基本使用,关于AIM理论就不多谈了。
相对于其它AIM软件,AIM2000的优点是界面友好,简单易用,缺点是原子盆积分速度偏慢(AIMALL快得多)。
建议用ver 2.0,相对于ver 1.0作了一些改进,因此更好用,比如界面、默认设置等等,尤其是新加入envelope图的支持。
官方网站上有demo版(http://www.aim2000.de),用起来和正式版在功能上没区别,但是最多只能载入8个核、14个轨道、128个高斯函数的体系,没太大实用价值。
安装后在aim2000hlp目录下有一个手册aim2000.chm,介绍每一个选项的功能;有一个教程tutor.chm,以C4H4为例图文并茂地介绍做各种图;在AIM2000目录下还有个aim2000V2UsersGuide.pdf ,罗列了AIM2000具备的功能,并对程序中涉及的每个函数进行了简略介绍。
下文示例的波函数是自带的C4h4.wfn。
1. 预备知识1.1 窗口主界面左上角是控制窗口。
可以选择感兴趣的原子,被选择的原子在3D窗口中会显示以这个原子为中心的坐标轴,原子盆积分也将对这个原子积分;可以选择原子间面用作原子间面积分;可以选择函数,默认是电子密度,如果想对别的函数进行分析则选择相应函数,此教程的示例都是对电子密度进行讨论。
如果之前已经对某些函数做了一些图,选择相应函后,在Plots for this density function里面就可以选择对这个函数已做过的图,同时显示在2D窗口中。
主界面右上方是记录窗口。
Record菜单中选其中一项,就会在这里显示已计算的项目的细节信息,然后可在file-print preview里面看到这些内容的打印预览。
主界面下方是2D窗口,通过Plot菜单的功能做的图,即分子图、等值线/梯度线图、Relief图,都显示在这个区域。
马克西马多 工具 型号:工具手册说明书

Medium Pressureto 22,500 psi (1,550 bar)High Pressureto 65,000 psi (4,500 bar)Ultra High Pressureto 152,000 psi (10,500 bar)Valve ActuatorsCustomized SolutionsBall Valvesto 21,000 psi (1,500 bar)Adapters and CouplingsAccessoriesToolsTechnicalInformation1Tools IndexPage:Coning and Threading Tools 2Reseating and Deburr Tools3MAXIMATORGmbH,LangeStraße6,99734Nordhausen,Telefon+49(0)36319533–0,Telefax+49(0)36319533–5010,www.maximator.de,*****************All technical and dimensional information subject to change. All general Terms and Conditions of sale, including limitations of our liability, apply to all products and services sold.Tools feature:• Manual Coning and Threading Coning tools are designed to threadup to 9/16” OD tubing.• One size Coning and Threading tool with interchangeable bushingsand thread dies eliminates multiple tool inventories.• Internal needle bearings and high strength materials offers ease ofoperation and extended tool life.• Coning blades are designed to cut both the angle and straight areasto insure good concentricity between the sealing surfaces.• Precision Reseating Tools to repair damaged female high pressureconnections without full disassembly of components.MAXIMATOR offers manual Coning and Threading tools that are designed to prepare accurate tubing ends to accept the medium, high and ultra high pressure connections.MAXIMATOR offers a complete line of manual tools for the proper preparation of medium, high and ultra high pressure connections up to 9/16” OD tubing. For complete coning and threading instruc-tions see MAXIMATOR’s website at www.maximator.de.Note: When selecting multiple items, the pressure rating would be that of the lowest rated component.3999.1830 | 04/2017Medium Pressureto 22,500 psi (1,550 bar)High Pressureto 65,000 psi (4,500 bar)Ultra High Pressureto 152,000 psi (10,500 bar)Valve ActuatorsCustomizedSolutionsBall Valvesto 21,000 psi (1,500 bar)Adapters and CouplingsAccessoriesToolsTechnical InformationAll technical and dimensional information subject to change. All general Terms and Conditions of sale, including limitations of our liability, apply to all products and services sold.3999.1830 | 04/2017Maximator offers tools for coning and threading tubing up to 9/16” O.D. These are precise tools that allow manual coning and threading of medium, high and ultra high pressure tubing. Please refer to the Maximator website, www.maximator.de and click on the VFT button to find detailed instructions for the coning and threading process.The coning tool comes complete with blades, collet and tools. The blades and tool feed nut allow the user to control the cutting feed rate and face the end of the tube when complete. The blades and collet can be changed for other sizes, while using the same base tool.Coning ToolsThe threading tool comes complete with the threading dieand bushing. The thread is a left hand type. The thread die and bushing can be changed for other sizes, while using the same base tool.Threading ToolsTubing Size Tubing Pressure Connection Type Coning Tool CompleteReplacement Part InformationO.D. x I.D. psi (bar) @ R.T. Catalog Number Collet Coning Blades HSS Coning Blades in. (mm) Part Number Part Number Part Number 1/4 x .109 (6.35 x 2.77) 22,500 (1,550) 4M CT4M 3781.1009 3781.1014 3781.1810 3/8 x .203 (9.53 x 5.17) 22,500 (1,550) 6M CT6M 3781.1010 3781.1013 3781.1811 9/16 x .312 (14.29 x 7.93) 22,500 (1,550) 9M CT9M 3781.1011 3781.1012 3781.1812 9/16 x .359 (14.29 x 9.13)15,200 (1,050)9M CT9M.359 3781.1011 3781.1179 3781.1813 1/4 x .083 (6.35 x 2.11) 65,000 (4,500) 4H / 4U CT4H 3781.1009 3781.0843 3781.1814 3/8 x .125 (9.53 x 3.17) 65,000 (4,500) 6H / 6U CT6H 3781.1010 3781.1017 3781.1808 9/16 x .188 (14.29 x 4.77) 65,000 (4,500) 9H / 9U CT9H 3781.1011 3781.1016 3781.1809 5/16 x .062 (7.94 x 1.58)152,000 (10,500)5UCT5U3781.08463781.08433781.1814Tubing Size Tubing Pressure Connection Type Left HandThreading Tool Replacement Part Information O.D. x I.D. psi (bar) @ R.T. Thread Size CompleteDie Bushing in. (mm) (UNF class 2) Catalog Number Part Number Part Number 1/4 x .109 (6.35 x 2.77) 22,500 (1,550) 4M 1/4-28-LH TT4 3781.1061 3781.1055 3/8 x .203 (9.53 x 5.17) 22,500 (1,550) 6M 3/8-24-LH TT6 3781.1059 3781.1053 9/16 x .312 (14.29 x 7.93) 22,500 (1,550) 9M 9/16-18-LH TT9 3781.1060 3781.1054 9/16 x .359 (14.29 x 9.13)15,200 (1,050)9M 9/16-18-LH TT9 3781.1060 3781.1054 1/4 x .083 (6.35 x 2.11) 65,000 (4,500) 4H / 4U 1/4-28-LH TT4 3781.1061 3781.1055 3/8 x .125 (9.53 x 3.17) 65,000 (4,500) 6H / 6U 3/8-24-LH TT6 3781.1059 3781.1053 9/16 x .188 (14.29 x 4.77) 65,000 (4,500) 9H / 6U 9/16-18-LH TT9 3781.1060 3781.1054 5/16 x .062 (7.94 x 1.58)152,000 (10,500)5U5/16-24-LHTT53781.10583781.1052Medium Pressureto 22,500 psi (1,550 bar)High Pressureto 65,000 psi (4,500 bar)Ultra High Pressureto 152,000 psi (10,500 bar)Valve ActuatorsCustomizedSolutionsBall Valvesto 21,000 psi (1,500 bar)Adapters and CouplingsAccessoriesToolsTechnical Information2 | 33999.1830 | 04/2017All technical and dimensional information subject to change. All general Terms and Conditions of sale, including limitations of our liability, apply to all products and services sold.The reseating tool is designed to rework an existing damaged coned and threaded connection without full disassembly of the component. The reseating tool will resurface the sealing surfaces of the medium, high, and ultra high pressure connections up to 9/16” tubing.Reseating ToolsThe deburring tool is designed to remove the metal burr onthe inside diameter of the tubing after the cutting process. The reseating tool will work on all medium, high, and ultra high pressure connections up to 9/16” tubing.Deburring ToolsTubing Size Tubing Pressure Connection Type Reseating ToolReplacement Part Information O.D. x I.D. psi (bar) @ R.T. CompleteCutter Bushing Gland in. (mm) Catalog Number Part Number Part Number Part Number 1/4 x .109 (6.35 x 2.77) 22,500 (1,550) 4M RT4M 3781.0647 n/a 3781.0649 3/8 x .203 (9.53 x 5.17) 22,500 (1,550) 6M RT6M 3781.0650 n/a 3781.06519/16 x .312 (14.29 x 7.93) 22,500 (1,550) 9M RT9M 3781.0656 n/a 3781.0655 9/16 x .359 (14.29 x 9.13) 15,200 (1,050) 9M RT9M 3781.0656 n/a 3781.0655 3/4 x .438 (19.05 x 11.13)22,500 (1,550)12M RT12M 3781.3557 n/a 3781.3558 1/4 x .083 (6.35 x 2.11) 65,000 (4,500) 4H / 4U RT4H 3781.0647 1700.0719 3781.06483/8 x .125 (9.53 x 3.17) 65,000 (4,500) 6H / 6U RT6H 3781.0645 1700.0718 3781.0646 9/16 x .188 (14.29 x 4.77) 65,000 (4,500) 9H / 9U RT9H 3781.0532 1700.0613 3781.0533 5/16 x .062 (7.94 x 1.58)152,000 (10,500)5URT5U3781.0532n/a3781.0652Tubing Size Tubing Pressure Connection Type Deburring Tool CompleteReplacement PartO.D. x I.D. psi (bar) @ R.T. Catalog Number Informationin. (mm) Bushing Part Number 1/4 x .109 (6.35 x 2.77) 22,500 (1,550) 4M DT4 3781.1381 3/8 x .203 (9.53 x 5.17) 22,500 (1,550) 6M DT4 3781.1381 9/16 x .312 (14.29 x 7.93) 22,500 (1,550) 9M DT4 3781.1381 9/16 x .359 (14.29 x 9.13)15,200 (1,050)9M DT5 3781.1380 1/4 x .083 (6.35 x 2.11) 65,000 (4,500) 4H / 4U DT4 3781.1381 3/8 x .125 (9.53 x 3.17) 65,000 (4,500) 6H / 6U DT4 3781.1381 9/16 x .188 (14.29 x 4.77) 65,000 (4,500) 9H / 9U DT4 3781.1381 5/16 x .062 (7.94 x 1.58)152,000 (10,500)5UDT43781.1381。
MAXQDA 2022 入门指南 (简体中文)说明书

入门指南Free Guide简体中文 Chinese SimplifiedMAXQDA 2022 入门指南简体中文技术支持与销售:VERBI软件. 德国(柏林)社会研究咨询有限责任公司./china版权所有·侵权必究MAXQDA is a registered trademark of VERBI Software. Consult. Sozialforschung. GmbH,Berlin/Germany; Mac is a registered trademark of Apple Computer, Inc. in the United States and/or other countries; Microsoft Windows, Word, Excel, and PowerPoint are registered trademarks of Microsoft Corporation in the United States and/or other countries; SPSS is a registered trademark of IBM Corporation in the United States and/or other countries; Stata is a registered trademark of Stata Corp LLC. in the United States and/or other countries.All other trademarks or registered trademarks are the property of their respective owners, and may be registered in the United States and/or other jurisdictions.© VERBI软件. 德国(柏林)社会研究咨询有限责任公司. 2022目录 5目录目录 (5)引言 (7)MAXQDA概述 (8)项目启动 (8)用户界面 (9)有关数据存储和保存的几条说明 (11)重要概念 (12)数据输入和探索 (13)数据输入 (13)数据探索 (14)数据搜索 (17)颜色编码和备忘录 (18)数据编码 (20)数据片段编码 (20)数据分析 (23)文件激活 (23)检索使用相同代码编码的文件片段 (24)可视化的使用 (25)6混合方法分析的实施 (26)定义文件变量 (26)变量值的输入 (27)将代码频率转化为变量 (28)文件变量在分析中的使用 (29)推荐文献 (30)结束语 (31)引言7引言欢迎使用MAXQDA入门指南!鉴于当下几乎无人喜欢阅读冗长的介绍性文本或使用手册,我们努力为您提供一份尽可能精短的指南。
Chimera-开始教程 - Menu Version

ChimeraUCSF Chimera是一个可高度延伸的程序,用于分子结构和相关数据的交互式可视化和分析。
主要包括:密度图,超分子组合,顺序排列,对接结果,轨迹和构象ensemble。
也可以生成高质量图像和动画。
Chimera包括完整的程序说明书和几个教程。
学术,政府和非营利机构和个人使用者可以免费下载。
Chimera由Resource for Biocomputing, Visualization, and Informatics发展,由National Center for Research Resources资助(grant P41-RR001081)教程开始教程 - Menu VersionChimera的很多工作都可以用多种方法完成。
例如:颜色和显示模式(display style)可以用动作菜单(actions)或者输入命令行(commands)。
一般来说, 命令行更详细,功能更强大,而菜单操作则不需要命令行知识和它们的语法规则就可以易于掌握软件特征。
本教程中,在开始教程-命令行 Version中,采用命令行执行的很多相同任务在此使用菜单代替。
为了继续进行下去,请先下载本教程需要的PDB文件到你电脑中的方便位置。
•1zik.pdb - leucine zipper•1d86.pdb - DNA and 纺锤菌素菜单, Part 1 –操作,选择和链Windows/Mac系统, 点击chimera图标; UNIX系统, 从系统提示符开启Chimera:unix: chimera然后,闪现一个欢迎界面,几秒后被Chimera主窗口取代。
如果你喜欢,通过拖拽窗口右下角来改变Chimera的大小。
现在打开一个结构。
从菜单中选择File... Open,用产生的file browser 找出并打开以前下载的(previously downloaded)文件1zik.pdb (文件类型设为all (guess type)或者PDB). 此结构是一个由两个肽链形成的Leucine zipper。
maxima入门

六、 返回值与附带作用
有的时候我们并不问题特别关心返回值,而更关注于语句的附带作用。比如 kill(all) 的返回值 done 对于我们来说并没有什么意义。我们要的是它的附带作用――清除自定义的变量或函数。因此 我们在语句的末尾加 $ 以避免返回结果。所有的语句都有返回值,但并非所有的语句都有附带作用, 比如 sqrt(2) axim 入门 (%o3)
庚寅年二月廿六
八、
在特定环境下求值
bd + ad + bc + ac
4 等式
一般情况下,冒号起赋值作用,等号起比较作用。但是在环境函数内部,等号起了代换作用 (%i1) x+y,x=a+y; (%o1) 2y + a (%i2) (%o2) %,y=2; a+4 (%i3) (%o3) x+y,x=a+y,y=2; y+a+2 (%i4) (%o4) x+y,[x=a+y,y=2]; y+a+2 可以看出,代换是并行的。 下面的例子展示了如何验证方程解的正确性 (%i5) eqns:[-2*x-3*y=3,-3*x+2*y=-4]$ (%i6) solns:solve(eqns); (%o6) ]] [[ 6 17 y = − ,x = 13 13 (%i7) (%o7) eqns,solns; [3 = 3, −4 = −4]
下面的例子展示了对 -1 的四次方根进行直角化和分式简化 (%i1) (%o1) solve(a^4+1); [ ] 1 1 1 1 a = (−1) 4 i, a = − (−1) 4 , a = − (−1) 4 i, a = (−1) 4 %,rectform,ratsimp;
maxima画图0.1

Maxima画图笔记wangyunqing1平面图1.1显函数命令:plot2d();例如:y=x3输入:plot2d(xˆ3,[x,-30,30]);用plot2d或draw2d用draw命令先输入load(draw)$,例如draw2d(explicit(x^3,x,-1,1));1.2隐函数命令:load(implicit_plot)$implicit_plot();例如:蔓叶线implicit_plot(y^2*(2-x)=x^3,[x,0,3],[y,-10,10]); draw2d(implicit(y^2*(2-x)=x^3,x,0,3,y,-10,10));1.3参数方程例如摆线方程:x=θ−sinθ,y=1−cosθplot2d([parametric,t-sin(t),1-cos(t),[t,0,2*%pi],[nticks,2000]])$ draw2d(parametric(t-sin(t),1-cos(t),t,0,2*%pi));1.4极坐标画心形线r=1−cosθdraw2d(nticks=300,polar(1-cos(t),t,0,3*%pi));2立体图用draw3d,其余与平面图形类似。
12.1空间曲线的参数方程螺旋线x=cos t,y=sin t,z=tdraw3d(parametric(cos(t),sin(t),t,t,0,2*%pi));2.2空间曲面的参数方程螺旋曲面的参数方程x=r cosϕ,y=r sinϕ,z=ϕdraw3d(parametric_surface(r*cos(t),r*sin(t),t,r,0,1,t,0,2*%pi));2.3球面坐标方程draw3d(spherical(1,a,0,2*%pi,z,0,%pi));2.4柱面坐标方程柱面坐标变换为x=r cosθ,y=r sinθ,z=z.抛物面x2+y2=zdraw3d(cylindrical(sqrt(z),z,0,5,theta,0,2*%pi));或draw3d(tube(0,0,z,sqrt(z),z,0,5));3其他设置3.1终端输出可以输出png,jpg,eps,pdf,pdfcairo,gif等格式。
max+plus2教程

EDA(VHDL & FPGA)实验指导教程编者林海波长春工程学院电子信息教研室前言本实验指导教程是EDA(VHDL & FPGA)上机实验指导教材,上机实验前,学生应依照教师指定的实验项目,认真预习实验内容,提前确定实验方案、初步设计实验项目的逻辑电路图或编写、设计VHDL程序,编制VHDL程序清单。
上机实验是一个验证和调试过程,只有充分的预习才能最大的发挥学习效果。
学生在实验教学中要认真依据要求完成每个实验项目,并按照要求详细撰写本书中指定实验项目的实验报告。
教师批阅后,将报告发回。
学生所获得的成绩将作为平时上机实验成绩的一部分,记入期末的考核成绩。
在期末必须上交全部实验报告,并装订存档,不及时交回者,实验成绩记为零分。
本实验指导教程可以作为《VHDL与数字系统设计》课程的实验指导书使用,也可以作为《EDA(VHDL)课程设计》的参考书使用。
《VHDL与数字系统设计》课程组2009年5月第一章 MAX+PLUS Ⅱ EDA 软件操作第一节 逻辑设计的输入方法逻辑设计的输入方法有图形输入、文本输入等。
输入方法不同,生成的文件格式也有所不同。
我们分别以图形输入法和文本输入法介绍MAX+plus II 软件的使用方法。
1.1 图形设计输入法我们将用一简单的实例介绍该输入法。
启动MAX+plus II ,该管理器窗口被打开。
1. 项目的建立用户的每个独立设计都对应一个项目,每个项目可包含一个或多个设计文件,其中有一个是顶层文件,顶层文件的名字必须与项目名相同。
编译器时对项目中的顶层文件进行编译,所以必须确定一个文件作为当前项目。
对于每个新的项目应该建立一个单独的子目录,当指定项目名称时,也就同时指定了保存该设计项目的子目录名。
建立项目名称的步骤如下:1.在File 菜单中选择Project 的Name 项(图1.1),将出现图1.2对画框。
图1.1图1.22.在Project Name 框内,键入设计项目名(注意:一定是英文名)和所选的路径,单击OK 。
Maxima快速参考手册

3.4.6 本征值和本征向量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
4 微积分
23
4.1 微分 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1
2.7.1 常用变换 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 2.7.2 控制变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.8 解方程 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.8.1 单个方程 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.8.2 方程组 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.8.3 数值解 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 2.9 复数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 2.9.1 实部与虚部 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 2.9.2 复共轭 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 2.9.3 复数模和辐角 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 2.9.4 直角形式和极坐标形式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Maxima官方教程

MAXIMAMini manual to study maths functionsMaxima is a computer algebra system that manipulate symbolic and numerical expressions, including differentiation, integration, systems of linear equations, and vectors, matrices, and so on. Maxima produces high precision results by using exact fractions and arbitrarily long floating pointrepresentations, and can plot functions and data in 2D and 3D.Picture n.1 : y =sin(x) Picture n.2 : f(x,y)= 2^(x 2-y 2) The Maxima source code can be compiled on many systems, including Windows, Linux, and MacOS X. The source code for all systems and precompiled binaries for Windows and Linux are available atthe /index.shtml 1You can find Maxima also into the Xplora DVD, a live bootable DVD – Xplora Knoppix, based on the Linux Debian distribution and completely contained on a self booting DVD. This Knoppix version allow you to work in Linux OS without installing it on your PC. The DVD contains software applications focused on science education. As it is open source software it can be given away freely and be copied aswell. (you can read more /shared/data/pdf/xploraknoppix.pdf ) The last version Maxima 5.9.3 was released March 19, 2006. The SourceForge file manager has source and binary files, including a self-contained.Windows installer. Maxima is constantly updating, to fix bugs and improve the code and the documentation. Most discussion and help you can find on the Maxima mailing list. /maximalist.html1 / is the world's largest Open Source software development web site,hosting more than 100,000 projects and over 1,000,000 registered users with a centralized resource for managing projects, issues, communications, and code. has the largest repository of Open Source code and applications available on the Internet, and provides a wide variety of services to projects we host, and to the Open Source community.Running Maxima the prompt like is (%i1) where the "i" represent "input".If you input a simple calculation(%i1) ((2*5)^3 - 100)/3 ;you will get the result as(%o1) 300where the "o" represent "output".When we use a "expand",(%i2) expand((x+y)^2);(%o2) y2 + 2 x y + x2or if you use “factor”(%i4) factor(4!);(%o4) 23 3And(%i1) factor (x^3 - 1);(%o1) (x - 1) (x + x + 1)2NOTE : end each Maxima command with a semicolon ;end the session with the command (%in)quit(); if you don't want a result showed, you can finish your command with $ instead of ;.Variables and parametersA variable can be defined by(%i1) x:1;which will put the value "1" into the variable "x".(%o2) 1This variable is accessible everywhere (even in functions) unless it is redefined in a BLOCK statement. Since the variable is accessable "everywhere", it is advisable to use BLOCK in a functions or else temporary variables inside the function might affect your results.Or you can introduce a parameter “a”;(%i1) a:100;(%o1) 100(%i2) sqrt(a);(%o2) 10Where sqrt (x), is the square root of x. It is represented internally by x^(1/2).ConstantsThere are several constants such as•%e - 2.71828•%inf - infinity•%i - square-root of -1, complex number•%pi - pi (3.14159265)Their value can be obtained usingbfloat(%e);and with the precision set by changing the variablefpprec:150;in the order below:(%i1) fpprec:150;(%o1) 150(%i2) bfloat(%e);(%o2) 2.7182818284590452353602874713526624977572470936999595749669676277240766\ 303535475945713821785251664274274663919320030599218174135966290435729003342952\6b0Maxima knows about complex numbers and numerical constants:(%i1) cos(%pi);(%o1) - 1(%i2) exp(%i*%pi);(%o2) - 1Introduction to Help - Maxima can search the info pages. Use the describe command to show all the commands and variables containing a string, and optionally their documentation. The question mark ? is an abbreviation for describe:(%in) ? function0: ()Special Functions.1: Introduction to Special Functions.2: Definitions for Special Functions.3: Elliptic Functions.4: Introduction to Elliptic Functions and Integrals.5: Definitions for Elliptic Functions.6: Function Definition.7: Introduction to Function Definition.8: Function.9: Definitions for Function Definition.10: Function and Variable Index.11: functions :Definitions for Function Definition.12: remfunction :Definitions for Command Line.13: tr_bound_function_applyp :Definitions for Function Definition.14: tr_function_call_default :Definitions for Function Definition.15: tr_warn_bad_function_calls :Definitions for Function Definition.16: ()Function and variable index.17: mat_function :Definitions for diag.18: ()Function and variable index.19: ()Function and variable index.20: ()Function and variable index.21: ()Function and variable index.22: (solve_)Function and variable index.23: ()Function and variable index.24: ()Function and variable index.25: ()Function and variable index.26: ()Function and variable index.Enter space-separated numbers, `all' or `none': 840.2 Function=============To define a function in Maxima you use the := operator. E.g. f(x) := sin(x);defines a function `f'.An example regarding function and its zeroes:(%i1) f(x):= x^3-4*x^2+3*x;(%o1) f(x) := x - 4 x + 3 x(%i2) f(x)=0;(%o2) x3 - 4 x2 + 3 x = 0(%i3) solve(f(x)=0,x);(%o3) [x = 3, x = 1, x = 0]Maxima calculate differential and integral of functions:(%i4) diff (f(x), x);(%o4) 3 x2 - 8 x + 3(%i5) f1(x):= 3* x^2 - 8* x + 3;(%o5) f1(x) := 3 x2 - 8 x + 3(%i6) integrate(f1(x),x);(%o6) x3 - 4 x2 + 3 xMaxima can solve linear and nonlinear sets of equations:(%i1) eq_1: x+ 3*y = 0$(%i2) eq_2: 3*x + y = 1$(%i3) solve ([eq_1, eq_2]);1 3(%o3) [[y = - -, x = -]]88(%i4) float(%o3);(%o4) [[y = - 0.125, x = 0.375]]Maxima can display a plot of one or more functions of one variable.plot2d ([expr_1, ..., expr_n], x_range, y_range)plot2d ([expr_1, ..., expr_n], x_range)To get the graphics in picture 1 at page 1(%i1) plot2d(sin(x), [x, 0, 2*%pi]);To get a PNG file:plot2d(sin(x), [x, 0, 2*%pi],[gnuplot_preamble,"set terminal png;set out 'sin.png'"])$To get an EPS file:plot2d(sin(x), [x, 0, 2*%pi],[gnuplot_preamble,"set terminal postscript eps;set out 'sin.eps'"])$With Gimp, you can convert then the png to jpg and other bitmat formats, but there are lots of programs to make file conversions.To get a 3D graph: a torus(%i1) expr_1: cos(y)*(10.0+6*cos(x));(%i2) expr_2: sin(y)*(10.0+6*cos(x));(%i3) expr_3: -6*sin(x);(%i4)plot3d ([expr_1, expr_2, expr_3],[x, 0, 2*%pi],[y, 0,2*%pi],['grid, 40, 40]);To get a PNG file that allowed you to insert it in a document like a image the command line is : (%i5) plot3d ([expr_1, expr_2, expr_3], [x, 0, 2*%pi], [y, 0, 2*%pi], ['grid, 40, 40],[gnuplot_preamble,"set terminal png; set out 'torus.png'"])$Maxima can generate several plot_formats: OPENMATH, GEOMVIEW, GNUPLOT and IZIC. "OPENMATH" is the default plot_format and "GNUPLOT" ( a most advanced, plotting package) is very in general.(%i4) set_plot_option([plot_format,openmath]);(%o4) [[x, - 1.75555970201398E+305, 1.75555970201398E+305],[y, - 1.75555970201398E+305, 1.75555970201398E+305], [t, - 3, 3],[grid, 30, 30], [view_direction, 1, 1, 1], [colour_z, false],[transform_xy, false], [run_viewer, true], [plot_format, openmath],[gnuplot_term, default], [gnuplot_out_file, false], [nticks, 10],[adapt_depth, 10], [gnuplot_pm3d, true], [gnuplot_preamble, ],[gnuplot_curve_titles, [default]], [gnuplot_curve_styles,[with lines 3, with lines 1, with lines 2, with lines 5, with lines 4,with lines 6, with lines 7]], [gnuplot_default_term_command, ],[gnuplot_dumb_term_command, set term dumb 79 22], [gnuplot_ps_term_command, se\t size 1.5, 1.5;set term postscript eps enhanced color solid 24],[logx, false], [logy, false]]and after that, every plot command will be handled by Openmath using the Xmaxima graphic console, by default:(%i5) plot2d (sin(x), [x, 0, 2*%pi]);In that way you get a embedded graphic function sin(x).NOTE: at page n. 6Option: gnuplot_preambleInserts gnuplot commands before the plot is drawn. Multiple commands should be separated with a semi-colon. The example shown produces a PNG file. The default value for gnuplot_preamble is the empty string "".Option: gridSets the number of grid points to use in the x- and y-directions for three-dimensional plotting. Composition of Functions:(%i1) f(x):=-x^2$(%i2) g(y):= %e^y$(%i3) h(x):=g(f(x))$(%i4) plot2d(h(x), [x, -3, 3], [x, -5, 5]);Maxima trigonometric functions definedThe trigonometric functions and simplification routines are in Maxima, below yo can read the list of some of them:acos (x) – Arc cosineacot (x) - Arc Cotangentacoth (x) - Hyperbolic Arc Cotangent.acsc (x) - Arc Cosecant.asec (x) - Arc Secantasin (x) - Arc Sine.atan (x) - Arc Tangent.cos (x) - Cosine.cot (x) - Cotangent.csc (x) - Cosecant.sec (x) - Secant.sin (x) – Sinetan (x) - Tangent.Introducing the command lineplot2d ([sin(x),cos(x)], [x, 0,2*%pi],[y, -1,1]); you get both the graphics.Read data from fileThere are several mechanisms to store data in files and retrieve it.•save writes data to a file as Lisp expressions. load retrieves the data written by save. Execute ?save and ? load for more information.•stringout writes data to a file as Maxima expressions. load retrieves the data written by stringout. Execute ? stringout for more information.•writefile creates a console log (a so-called "dribble" file) which records the interactions between the user and Maxima. This file cannot be reloaded into Maxima. Execute ? writefile for moreinformation.The study function 122−+=x x y using MAXIMA(%i1) f(x):= (x+2)/(x^2 - 1)$(%i2) plot2d (f(x), [x, -10,10],[y, -10,10],[gnuplot_preamble,"set xzeroaxis; set yzeroaxis"])$MAXIMA computes the function limit(%in) limit (expr , x , val , dir );expr as the real variable x approaches the value val from the direction dir .dir may have the value plus for a limit from above, minus for a limit from below, or may be omitted (implying a two-sided limit is to be computed).Maxima limit uses the following special symbols: inf (positive infinity) and minf (negative infinity). On output it may also use und (undefined), ind (indefinite but bounded) and infinity (complex infinity).(%i3) limit(f(x),x,-1,plus); (%o3) minf(%i4) limit(f(x),x,-1,minus); (%o4) inf(%i5) limit(f(x),x,1,plus); (%o5) inf(%i6) limit(f(x),x,-1,minus); (%o6) inf(%i7) limit(f(x),x,inf); (%o7) 0First Derivative(%i8) diff(f(x),x);1 2 x (x + 2)(%o8) ------ - -----------x2 - 1 (x2 - 1)2 Expression can be simplified by ratsimp:(%i9) Deriv1:ratsimp(diff(f(x),x));x2 + 4 x + 1(%o9) - -------------x4- 2 x2 + 1(%i10) solve (Deriv1=0,x);(%o10) [x = - sqrt(3) - 2, x = sqrt(3) - 2](%i11) float(%o10);(%o11) [x = - 3.732050807568877, x = - 0.26794919243112]We use theFunction: ev (<expr>, <arg_1>, ..., <arg_n>) to calculate the coordinates of the point .Evaluates the expression <expr> in the environment specified by the arguments <arg_1>, ...,<arg_n>. The arguments are (assignments, equations, and functions. `ev' returns the result (another expression) of the evaluation.(%i12) ev(f(- 3.732050807568877),float);(%o12) - 0.13397459621556(%i13) ev(f(- 0.26794919243112),float);(%o13) - 1.866025403784439You can read below the command line to get of the graphics of first derivative: (%i14) plot2d (Deriv1, [x, -5,5],[y, -5,5],[gnuplot_preamble,"set xzeroaxis; set yzeroaxis"])$and in the next page its picture.Second Derivative(%i15) Deriv2:ratsimp(diff(Deriv1,x));2 x3 + 12 x2 + 6 x + 4(%o15) ------------------------x6 - 3 x4 + 3 x2 - 1(%i16) fpprec:2$(%i17) solve (Deriv2=0,x);………………………(%i19) float(%o17);(%o19) [x = - 2.1 (0.9 %i - 0.5) - 1.4 (- 0.9 %i - 0.5) - 2.0, x = - 1.4 (0.9 %i - 0.5) - 2.1 (- 0.9 %i - 0.5) - 2.0, x = - 5.5]You can read below the command line to get of the graphics of second derivative:(%i20) plot2d (Deriv2, [x, -5,5],[y, -5,5],[gnuplot_preamble,"set xzeroaxis; set yzeroaxis"])$and in the next page its picture.wx Maxima release (0.6.5-1)A very interesting related project about Maxima is wxMaxima release (0.6.5-1) (author Andrej Vodopivec et al) a wxWidgets / graphical user interface for the computer algebra system Maxima.Wxmaxima (free download at / ) provides a wxWindows interface for Maxima, including a menu system, browsable help and formated output (see picture below in this page). Features as symbolic manipulation of polynomials, rational functions, matrices, integration and graphics are as easy as point and click.Wxmaxima should be installed in a subdirectory of Maxima installation directory. This way, wxMaxima can find the Maxima binary automatically.Example: - Maxima installation directory C:\Program Files\ maxima-5.9.3- wxMaxima installation directory C:\Program Files\ maxima-5.9.3\wxMaxima.If you install it in a different directory, you will have to configure it with Maxima->Configure.WEB RESOURCESwxMaxima material to download by Johann WeilharterIntroduction to Maxima by Richard Rand (PDF)/docs/intromax/intromax.pdfThe Computer Algebra Program Maxima by Boris Gaertner(Entire tutorial in one file: gaertner-tutorial-revision.zip)Micro introduction into Maxima at Harvard UK /computing/maxima/ Minimal Maxima by Robert Dodier (PDF) /docs/tutorial/en/minimal-maxima.pdf/manuals/math/maxima-5.9.2/index.html Document generated by Joshua David Goldstein on December, 6 2005。
数学软件Mathematica详解教程

23
自定义函数
Mathematica 允许用户自定义函数,一般格式为
函数名[自变量名1_, 自变量名2_, ...]:= 表达式
这里函数名与变量名的规定相同 方括号中的每个自变量名后都要有一个下划线 “_” 中间的 “:=” 为定义号 注意符号表达式与函数的区别
f[x_]:=2*x-3
② 大多数函数名与数学中的名称相同 ③ 当函数名分为几段时,每一段的头一个字母大写,后面 的用小写字母,如:ArcSin[x]
寻求帮助: ??函数名
In[1]:= ?? Sign[x] Power[x,y] Sqrt[x] Exp[x] Log[x], Log[b,x] 绝对值 符号函数 幂函数 x y 平方根 以 e 为底的指数函数 以 e 和 b 为底的对数函数
m 除以 n 的整数商 三角函数 反三角函数 双曲函数
ArcSinh, ArcCosh, ...
Prime[k] PrimeQ[n] Binomial[n,m]
反双曲函数
第 k 个素数 判断 n 是否为素数 m Cn 二项式系数
20
随机函数
Random[]
Random[Real, a] Random[Real, {a,b}]
定义一个一元函数
f[x_,y_]:=Log[x/y]-Power[x,y]
Clear[f]
定义一个二元函数
清除自定义的函数
自定义函数前,最好先清除自变量的值,否则可能会 出现意想不到的错误
24
自定义函数
In[1]:= f=2*x+y In[2]:= g[x_,y_]:=2*x+y In[3]:= f[2,3] (* 符号表达式 *) (* 函数 *)
Methematica基础教程

Methematica基础教程Mathematica基础教程第1章Mathematica概述1.1 运行和启动:介绍如何启动Mathematica软件,如何输入并运行命令1.2 表达式的输入:介绍如何使用表达式1.3 帮助的使用:如何在mathematica中寻求帮助第2章Mathematica的基本量2.1 数据类型和常量:mathematica中的数据类型和基本常量2.2 变量:变量的定义,变量的替换,变量的清除等2.3 函数:函数的概念,系统函数,自定义函数的方法2.4 表:表的创建,表元素的操作,表的应用2.5 表达式:表达式的操作2.6 常用符号:经常使用的一些符号的意义第3章Mathematica的基本运算3.1 多项式运算:多项的四则运算,多项式的化简等3.2 方程求解:求解一般方程,条件方程,方程数值解以及方程组的求解3.3 求积求和:求积与求和第4章函数作图4.1 二维函数作图:一般函数的作图,参数方程的绘图4.2 二维图形元素:点,线等图形元素的使用4.3 图形样式:图形的样式,对图形进行设置4.4 图形的重绘和组合:重新显示所绘图形,将多个图形组合在一起4.5 三维图形的绘制:三维图形的绘制,三维参数方程的图形,三维图形的设置第5章微积分的基本操作5.1 函数的极限:如何求函数的极限5.2 导数与微分:如何求函数的导数,微分5.3 定积分与不定积分:如何求函数的不定积分和定积分,以及数值积分5.4 多变量函数的微分:如何求多元函数的偏导数,微分5.5 多变量函数的积分:如何计算重积分5.6 幂级数:幂级数的展开及其计算第6章微分方程的求解6.1 微分方程的解:微分方程的求解6.2 微分方程的数值解:如何求微分方程的数值解第7章Mathematica程序设计7.1 模块:模块的概念和定义方法7.2 条件结构:条件结构的使用和定义方法7.3 循环结构:循环结构的使用7.4 流程控制:简单介绍控制函数第8章Mathematica中的常用函数8.1 运算符和一些特殊符号:常用的和不常用一些运算符号8.2 系统常数:系统定义的一些常量及其意义8.3 代数运算:表达式相关的一些运算函数8.4 解方程:和方程求解有关的一些操作8.5 微积分相关函数:关于求导,积分,泰勒展开等相关的函数8.6 多项式函数:多项式的相关函数8.7 随机函数:能产生随机数的函数函数8.8 数值函数:和数值处理相关的函数,包括一些常用的数值算法8.9 表相关函数:创建表,表元素的操作,表的操作函数8.10 绘图函数:二维绘图,三维绘图,绘图设置,密度图,图元,着色,图形显示等函数8.11 流程控制函数第1章Mathematica概述1.1 Mathematica的启动和运行Mathematica是美国Wolfram研究公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
maxima 使用

自己做的翻译,不好之处望大家见谅.Maxima简介目录1.概述2.关键字3.计算4.代数5.微积分6.矩阵计算7.Maxima编程8.Maxima的一部分函数列表1.概述在linux下打开Maxima的方法1.maxima <enter>在电脑上会显示下列介绍:Distributed under the GNU Public License. See the file COPYING. Dedicated to the memory of William Schelter.This is a development version of Maxima. The function bug_report() provides bug reporting information.(%i1)这个(%i1)是一个标签,每一个输入输出在它的前面都会有一个标签,i表示你所输入进去的代码(input),o表示电脑对代码作业的响应(output).不要用像%i1或者是%o2这样的变量名,因为这样很容易与标签混淆了.maxima分辩大小写.所有的内建函数都只有一个小写的函数名如(sin,cos,save,load,etc).内建的常值也有一个小写的名字(%e,%pi,inf,etc).如果你键入SIN(x)或者是Sin(x),Maxima会把它当作和sin(x)不同的函数来处理.用户自己定义函数和变量名的时候大写小写都可以选择.foo(XY),Foo(xy),FOO(xy)都是不同的函数.2.关键字1.结束maxima时,键入quit();2.中断maxima而不离开时,用快捷键Ctrl+c.知道怎样使用这种中断的方法很重要,举个例子,如果你在做一个要费很长时间的计算 ,如(%i)sum(1/x^2,x,1,100000);maxima encountered a lisp error:console interrupt.Automatically continuing.to reenable the lisp debugger set *debugger-hook* to nil.(%i2)3.用符号;告诉maxima你输入的命令结束,然后点回车.4.另外一个结束的命令符是$,但是它不在屏幕显示出maxima计算的结果.这对于有很长的中间过程变量的计算来说是很有用的,因为你不需要花费很长的时间让它显示在屏幕上.5.如果你不想输入刚才你已经输入的命令,打个比方你想输入你刚才输入的第五行(%i5),你只要在前面加上一对单引号,如,''%i5.6.如果你想得到maxima当前运行的结果,你可以用它的O标签,也可以用特特殊的显示符号(%);7.标准量,e,i,pi在maxima中用%e,%i,%pi,来表示.3.计算一般运算符+ 加- 减* 乘/ 除^ 幂. 矩阵计算sqrt(x) x的平方根maxima的输出用精确有理数表达出来:(%i1) 1/100 + 1/101;201(%o1) -----10100如果计算中出现了一些无理的数,那么它会用符号表示出来 :u%i2) (1 + sqrt(2))^5;5(%o2) (sqrt(2) + 1)(%i3) expand (%);(%o3) 29 sqrt(2) + 41但是,它也常常表达为十进制数,这个方法的表达了",numer":(%i4) %, numer;(%o4) 82.01219330881976注意这里用到的%是指先前计算的那个值.这个版本的maxima,number显示了一个16位的值,后面几位常常是不可靠的.但是用bfloat能够提供一个任意高的精度.(%i5) bfloat (%o3);The number of significant figures displayed is controlled by the Maxima variable fpprec, which hasthe default value of 16:值的显示精度是由maxima的fpprec来控制的,它的默认值是16(%i6) fpprec;(%o6) 16这里我们可以重新设定它的值:3(%i7) fpprec: 100;(%o7) 100(%i8) ’’%i5;(%o8) 8.20121933088197564152489730020812442785204843859314941221# 2371240173124187540110412666123849550160561B1没有近似估计的大数:(%i9) 100!;(%o9) 9332621544394415268169923885626670049071596826438162146859# 2963895217599993229915608941463976156518286253697920827223758251# 1852109168640000000000000000000000004代数Maxima’s importance as a computer tool to facilitate analytical calculations becomes more evidentwhen we see how easily it does algebra for us. Here’s an example in which a polynomial is expanded:maxima作为一个计算工具的重要性是它能使方便的分析和计算更加现实。
maxima教程

10分钟教程:用Maxima解决数学问题译者: jizecn发表时间:2008-07-30浏览量:12517评论数:3挑错数:4大约有5万人读了我的另一篇叫做“3 swesome free math programs”的文章。
其中一部分人大概已经下载并安装了Maxima。
如果你是其中一人,但是却不太擅长这类CAS(计算机代数系统)软件的话,Maxima可能让你感觉很复杂,并且很难掌握,甚至仅仅是简单的高中代数问题都会无从下手。
事实上,Maxima用起来没有那么可怕,10分钟的教程足以让你明白它的用法,找到正确的方向。
一旦你开始了第一步,对于实际问题中的特定的功能,你只要去搜寻它的文档就可以了。
或者,你可以用以下这种形式(问号+一个字符串)去得到相应帮助(比如 ? integrate)。
这个教程将会结合实际动手,使用一些简单的例子来讲解怎么去计算一些常见的问题。
当然,这仅仅是冰山一脚。
Maxima能做很多很多的其他事情,但是在开头阶段,接触这些问题足以帮助你明白并且让你能够使用。
并且,最后一点,你不会牺牲超过10分钟的时间。
大约有5万人读了我的另一篇叫做“3 swesome free math programs”的文章。
其中一部分人大概已经下载并安装了Maxima。
如果你是其中一人,但是却不太擅长这类CAS(计算机代数系统)软件的话,Maxima可能让你感觉很复杂,并且很难掌握,甚至仅仅是简单的高中代数问题都会无从下手。
事实上,Maxima用起来没有那么可怕,10分钟的教程足以让你明白它的用法,找到正确的方向。
一旦你开始了第一步,对于实际问题中的特定的功能,你只要去搜寻它的文档就可以了。
或者,你可以用以下这种形式(问号+一个字符串)去得到相应帮助(比如 ? integrate)。
这个教程将会结合实际动手,使用一些简单的例子来讲解怎么去计算一些常见的问题。
当然,这仅仅是冰山一脚。
Maxima能做很多很多的其他事情,但是在开头阶段,接触这些问题足以帮助你明白并且让你能够使用。
Maxima使用教程

Maxima使⽤教程说起数学软件,我们很多⼈脑⼦⾥浮现出的第⼀个就是 matlab,不可否认,matlab 确实是⼀个优秀的数学软件,但是它需要付费啊(这⾥不讨论盗版问题)。
那么有没有⼀个同样强⼤但免费的数学软件呢?答案是肯定的,那就是本⽂所要说的 Maxima,当然了,不只是有这⼀个。
预备知识在正式介绍其使⽤⽅法之前,想先介绍 Maxima ⾥⾯⼀些规则。
1. 在求极限的时候,如果极限不存在,范围值可能为 und(极限不存在),ind(极限不存在但是有界),infinity(发散)2. ⾃然常数 e ⽤ %e 表⽰3. 圆周率π⽤ %pi 表⽰4. 注释:⽅法与 C 语⾔相同,/*...*/⼀、求极限在 Maxima 中⽤ limit 函数来进⾏极限求解。
limit (expr, x, val) /*计算 x 趋近于 val 时 expr 的极限*/limit (expr, x, val, dir) /*dir 为 plus 时求的是右极限,为 minus 时求的是左极限。
*/例如:limit(sin(x)/x,x,0);limit((1+1/x)^x,x,inf);limit((2^(1/x)+1)/(2^(1/x)-1),x,0);limit((2^(1/x)+1)/(2^(1/x)-1),x,0,minus);limit((2^(1/x)+1)/(2^(1/x)-1),x,0,plus);limit((2*x^2+x)/(x^2-2),x,inf);⼆、求和与求积运算可以使⽤ sum 和 product 函数进⾏求和以及求积操作。
sum (expr, i, i_0, i_1) /*求和*/product (expr, i, i_0, i_1) /*求积*/例如:sum (i^2, i, 1, 7);sum (a[i], i, 1, 7);sum(1/k^2,k,0,inf);sum (1/3^i, i, 1, inf), simpsum;product (x + i*(i+1)/2, i, 1, 4);product (a(i), i, 1, n);product (k, k, 1, n), simpproduct;三、taylor 级数展开函数f(x)的在 x = a 附近的幂级数可以通过 powerseries (f(x), x, a) 获得。
Maximo 7.5安装文档
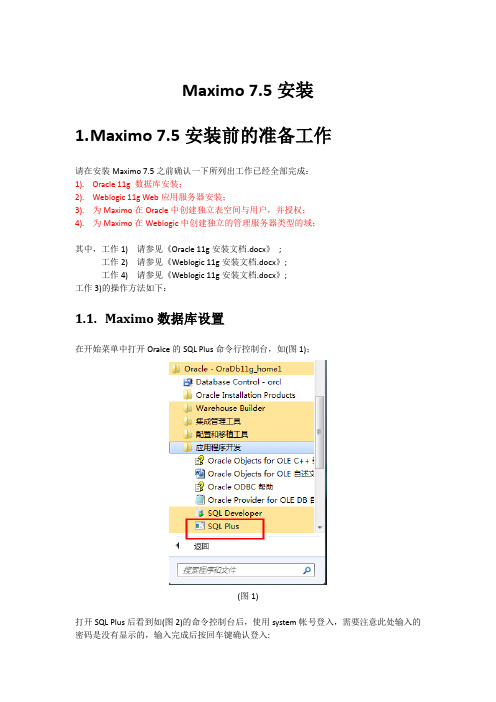
Maximo 7.5安装1.M aximo 7.5安装前的准备工作请在安装Maximo 7.5之前确认一下所列出工作已经全部完成:1). Oracle 11g 数据库安装;2). Weblogic 11g Web应用服务器安装;3). 为Maximo在Oracle中创建独立表空间与用户,并授权;4). 为Maximo在Weblogic中创建独立的管理服务器类型的域;其中,工作1) 请参见《Oracle 11g安装文档.docx》;工作2)请参见《Weblogic 11g安装文档.docx》;工作4)请参见《Weblogic 11g安装文档.docx》;工作3)的操作方法如下:1.1.Maximo数据库设置在开始菜单中打开Oralce的SQL Plus命令行控制台,如(图1);(图1)打开SQL Plus后看到如(图2)的命令控制台后,使用system帐号登入,需要注意此处输入的密码是没有显示的,输入完成后按回车键确认登入:(图2)成功登入后会看到如(图3)的窗口,我们需要在该处执行Oracle的SQL文件导入命令,将maximo_*.sql文件导入即可;该sql文件中已经写好用于创建Maximo表空间用户以及授权更改的SQL代码,成功导入后即完成Maximo表空间、用户以及授权等操作。
(图3)具体的Oralce的SQL文件导入命令如(图4)所示,该命令构成格式为:@+磁盘绝对路径+SQL文件名(即文件maximo_*.sql),其中不应有空格,磁盘绝对路径为非中文磁盘路径,且同样不能含有空格。
(图4)导入命令输入好了后,按回车键,确认并执行该命令。
稍等片刻,程序执行完成后,将看到如(图5)所示的窗口,可以清楚看到各项任务成功执行:(图5)还需要提醒一点的是,在执行导入之前,需要确认maximo.sql文件中如(图6)所示的红线框内的磁盘路径是否存在,建议将其修改为Oralce11g安装目录下的”oradata”目录下。
Magic xpa_入门_教程_New

•
All Right Reserved, Copyrights(C) Magic Software China
修改界面:打开界面编辑器
打开程序编辑器 • • • 点击窗体选项卡 选择一个界面进行编辑 按F5键→打开界面编辑器
All Right Reserved, Copyrights(C) Magic Software China
经常使用的快捷键
以下包括Magic xpa经常用到的快捷键
键 ESC Enter Tab F3 F4
其他的操作 窗口上的‘×’按钮
作用 关闭窗口。(会弹出确 认对话框) 保存/选择结束 向下一个项目移动 删除行 添加行
F5
F7 Ctrl+F2 Alt+Enter
双击
拓展
运行程序 取消 特性(属性)编辑显示
All Right Reserved, Copyrights(C) Magic Software China
Magic xpa 的数据类型
数据类型 Alpha Unicode Numeric 类型说明 字符串 通用字符串,可避免特 殊字符乱码 数字类型 整数 小数 备注 最大32K
Logical
Date
• • 在Database一栏双击(或按F5键)→打开对应的数据库列表对话框。 将光标移到你要选择的数据库上,点击‘选择’按钮→ 在数据库一栏上选定数据库。
All Right Reserved, Copyrights(C) Magic Software China
定义MSSQL SERVER表模型(4)
项目文件
如下图所示,项目名称在此位置被创建。(Magic的程序文件是基于元数据的描述文件,都已xml文件的形式保存)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MAXIMAMini manual to study maths functionsMaxima is a computer algebra system that manipulate symbolic and numerical expressions, including differentiation, integration, systems of linear equations, and vectors, matrices, and so on. Maxima produces high precision results by using exact fractions and arbitrarily long floating pointrepresentations, and can plot functions and data in 2D and 3D.Picture n.1 : y =sin(x) Picture n.2 : f(x,y)= 2^(x 2-y 2) The Maxima source code can be compiled on many systems, including Windows, Linux, and MacOS X. The source code for all systems and precompiled binaries for Windows and Linux are available atthe /index.shtml 1You can find Maxima also into the Xplora DVD, a live bootable DVD – Xplora Knoppix, based on the Linux Debian distribution and completely contained on a self booting DVD. This Knoppix version allow you to work in Linux OS without installing it on your PC. The DVD contains software applications focused on science education. As it is open source software it can be given away freely and be copied aswell. (you can read more /shared/data/pdf/xploraknoppix.pdf ) The last version Maxima 5.9.3 was released March 19, 2006. The SourceForge file manager has source and binary files, including a self-contained.Windows installer. Maxima is constantly updating, to fix bugs and improve the code and the documentation. Most discussion and help you can find on the Maxima mailing list. /maximalist.html1 / is the world's largest Open Source software development web site,hosting more than 100,000 projects and over 1,000,000 registered users with a centralized resource for managing projects, issues, communications, and code. has the largest repository of Open Source code and applications available on the Internet, and provides a wide variety of services to projects we host, and to the Open Source community.Running Maxima the prompt like is (%i1) where the "i" represent "input".If you input a simple calculation(%i1) ((2*5)^3 - 100)/3 ;you will get the result as(%o1) 300where the "o" represent "output".When we use a "expand",(%i2) expand((x+y)^2);(%o2) y2 + 2 x y + x2or if you use “factor”(%i4) factor(4!);(%o4) 23 3And(%i1) factor (x^3 - 1);(%o1) (x - 1) (x + x + 1)2NOTE : end each Maxima command with a semicolon ;end the session with the command (%in)quit(); if you don't want a result showed, you can finish your command with $ instead of ;.Variables and parametersA variable can be defined by(%i1) x:1;which will put the value "1" into the variable "x".(%o2) 1This variable is accessible everywhere (even in functions) unless it is redefined in a BLOCK statement. Since the variable is accessable "everywhere", it is advisable to use BLOCK in a functions or else temporary variables inside the function might affect your results.Or you can introduce a parameter “a”;(%i1) a:100;(%o1) 100(%i2) sqrt(a);(%o2) 10Where sqrt (x), is the square root of x. It is represented internally by x^(1/2).ConstantsThere are several constants such as•%e - 2.71828•%inf - infinity•%i - square-root of -1, complex number•%pi - pi (3.14159265)Their value can be obtained usingbfloat(%e);and with the precision set by changing the variablefpprec:150;in the order below:(%i1) fpprec:150;(%o1) 150(%i2) bfloat(%e);(%o2) 2.7182818284590452353602874713526624977572470936999595749669676277240766\ 303535475945713821785251664274274663919320030599218174135966290435729003342952\6b0Maxima knows about complex numbers and numerical constants:(%i1) cos(%pi);(%o1) - 1(%i2) exp(%i*%pi);(%o2) - 1Introduction to Help - Maxima can search the info pages. Use the describe command to show all the commands and variables containing a string, and optionally their documentation. The question mark ? is an abbreviation for describe:(%in) ? function0: ()Special Functions.1: Introduction to Special Functions.2: Definitions for Special Functions.3: Elliptic Functions.4: Introduction to Elliptic Functions and Integrals.5: Definitions for Elliptic Functions.6: Function Definition.7: Introduction to Function Definition.8: Function.9: Definitions for Function Definition.10: Function and Variable Index.11: functions :Definitions for Function Definition.12: remfunction :Definitions for Command Line.13: tr_bound_function_applyp :Definitions for Function Definition.14: tr_function_call_default :Definitions for Function Definition.15: tr_warn_bad_function_calls :Definitions for Function Definition.16: ()Function and variable index.17: mat_function :Definitions for diag.18: ()Function and variable index.19: ()Function and variable index.20: ()Function and variable index.21: ()Function and variable index.22: (solve_)Function and variable index.23: ()Function and variable index.24: ()Function and variable index.25: ()Function and variable index.26: ()Function and variable index.Enter space-separated numbers, `all' or `none': 840.2 Function=============To define a function in Maxima you use the := operator. E.g. f(x) := sin(x);defines a function `f'.An example regarding function and its zeroes:(%i1) f(x):= x^3-4*x^2+3*x;(%o1) f(x) := x - 4 x + 3 x(%i2) f(x)=0;(%o2) x3 - 4 x2 + 3 x = 0(%i3) solve(f(x)=0,x);(%o3) [x = 3, x = 1, x = 0]Maxima calculate differential and integral of functions:(%i4) diff (f(x), x);(%o4) 3 x2 - 8 x + 3(%i5) f1(x):= 3* x^2 - 8* x + 3;(%o5) f1(x) := 3 x2 - 8 x + 3(%i6) integrate(f1(x),x);(%o6) x3 - 4 x2 + 3 xMaxima can solve linear and nonlinear sets of equations:(%i1) eq_1: x+ 3*y = 0$(%i2) eq_2: 3*x + y = 1$(%i3) solve ([eq_1, eq_2]);1 3(%o3) [[y = - -, x = -]]88(%i4) float(%o3);(%o4) [[y = - 0.125, x = 0.375]]Maxima can display a plot of one or more functions of one variable.plot2d ([expr_1, ..., expr_n], x_range, y_range)plot2d ([expr_1, ..., expr_n], x_range)To get the graphics in picture 1 at page 1(%i1) plot2d(sin(x), [x, 0, 2*%pi]);To get a PNG file:plot2d(sin(x), [x, 0, 2*%pi],[gnuplot_preamble,"set terminal png;set out 'sin.png'"])$To get an EPS file:plot2d(sin(x), [x, 0, 2*%pi],[gnuplot_preamble,"set terminal postscript eps;set out 'sin.eps'"])$With Gimp, you can convert then the png to jpg and other bitmat formats, but there are lots of programs to make file conversions.To get a 3D graph: a torus(%i1) expr_1: cos(y)*(10.0+6*cos(x));(%i2) expr_2: sin(y)*(10.0+6*cos(x));(%i3) expr_3: -6*sin(x);(%i4)plot3d ([expr_1, expr_2, expr_3],[x, 0, 2*%pi],[y, 0,2*%pi],['grid, 40, 40]);To get a PNG file that allowed you to insert it in a document like a image the command line is : (%i5) plot3d ([expr_1, expr_2, expr_3], [x, 0, 2*%pi], [y, 0, 2*%pi], ['grid, 40, 40],[gnuplot_preamble,"set terminal png; set out 'torus.png'"])$Maxima can generate several plot_formats: OPENMATH, GEOMVIEW, GNUPLOT and IZIC. "OPENMATH" is the default plot_format and "GNUPLOT" ( a most advanced, plotting package) is very in general.(%i4) set_plot_option([plot_format,openmath]);(%o4) [[x, - 1.75555970201398E+305, 1.75555970201398E+305],[y, - 1.75555970201398E+305, 1.75555970201398E+305], [t, - 3, 3],[grid, 30, 30], [view_direction, 1, 1, 1], [colour_z, false],[transform_xy, false], [run_viewer, true], [plot_format, openmath],[gnuplot_term, default], [gnuplot_out_file, false], [nticks, 10],[adapt_depth, 10], [gnuplot_pm3d, true], [gnuplot_preamble, ],[gnuplot_curve_titles, [default]], [gnuplot_curve_styles,[with lines 3, with lines 1, with lines 2, with lines 5, with lines 4,with lines 6, with lines 7]], [gnuplot_default_term_command, ],[gnuplot_dumb_term_command, set term dumb 79 22], [gnuplot_ps_term_command, se\t size 1.5, 1.5;set term postscript eps enhanced color solid 24],[logx, false], [logy, false]]and after that, every plot command will be handled by Openmath using the Xmaxima graphic console, by default:(%i5) plot2d (sin(x), [x, 0, 2*%pi]);In that way you get a embedded graphic function sin(x).NOTE: at page n. 6Option: gnuplot_preambleInserts gnuplot commands before the plot is drawn. Multiple commands should be separated with a semi-colon. The example shown produces a PNG file. The default value for gnuplot_preamble is the empty string "".Option: gridSets the number of grid points to use in the x- and y-directions for three-dimensional plotting. Composition of Functions:(%i1) f(x):=-x^2$(%i2) g(y):= %e^y$(%i3) h(x):=g(f(x))$(%i4) plot2d(h(x), [x, -3, 3], [x, -5, 5]);Maxima trigonometric functions definedThe trigonometric functions and simplification routines are in Maxima, below yo can read the list of some of them:acos (x) – Arc cosineacot (x) - Arc Cotangentacoth (x) - Hyperbolic Arc Cotangent.acsc (x) - Arc Cosecant.asec (x) - Arc Secantasin (x) - Arc Sine.atan (x) - Arc Tangent.cos (x) - Cosine.cot (x) - Cotangent.csc (x) - Cosecant.sec (x) - Secant.sin (x) – Sinetan (x) - Tangent.Introducing the command lineplot2d ([sin(x),cos(x)], [x, 0,2*%pi],[y, -1,1]); you get both the graphics.Read data from fileThere are several mechanisms to store data in files and retrieve it.•save writes data to a file as Lisp expressions. load retrieves the data written by save. Execute ?save and ? load for more information.•stringout writes data to a file as Maxima expressions. load retrieves the data written by stringout. Execute ? stringout for more information.•writefile creates a console log (a so-called "dribble" file) which records the interactions between the user and Maxima. This file cannot be reloaded into Maxima. Execute ? writefile for moreinformation.The study function 122−+=x x y using MAXIMA(%i1) f(x):= (x+2)/(x^2 - 1)$(%i2) plot2d (f(x), [x, -10,10],[y, -10,10],[gnuplot_preamble,"set xzeroaxis; set yzeroaxis"])$MAXIMA computes the function limit(%in) limit (expr , x , val , dir );expr as the real variable x approaches the value val from the direction dir .dir may have the value plus for a limit from above, minus for a limit from below, or may be omitted (implying a two-sided limit is to be computed).Maxima limit uses the following special symbols: inf (positive infinity) and minf (negative infinity). On output it may also use und (undefined), ind (indefinite but bounded) and infinity (complex infinity).(%i3) limit(f(x),x,-1,plus); (%o3) minf(%i4) limit(f(x),x,-1,minus); (%o4) inf(%i5) limit(f(x),x,1,plus); (%o5) inf(%i6) limit(f(x),x,-1,minus); (%o6) inf(%i7) limit(f(x),x,inf); (%o7) 0First Derivative(%i8) diff(f(x),x);1 2 x (x + 2)(%o8) ------ - -----------x2 - 1 (x2 - 1)2 Expression can be simplified by ratsimp:(%i9) Deriv1:ratsimp(diff(f(x),x));x2 + 4 x + 1(%o9) - -------------x4- 2 x2 + 1(%i10) solve (Deriv1=0,x);(%o10) [x = - sqrt(3) - 2, x = sqrt(3) - 2](%i11) float(%o10);(%o11) [x = - 3.732050807568877, x = - 0.26794919243112]We use theFunction: ev (<expr>, <arg_1>, ..., <arg_n>) to calculate the coordinates of the point .Evaluates the expression <expr> in the environment specified by the arguments <arg_1>, ...,<arg_n>. The arguments are (assignments, equations, and functions. `ev' returns the result (another expression) of the evaluation.(%i12) ev(f(- 3.732050807568877),float);(%o12) - 0.13397459621556(%i13) ev(f(- 0.26794919243112),float);(%o13) - 1.866025403784439You can read below the command line to get of the graphics of first derivative: (%i14) plot2d (Deriv1, [x, -5,5],[y, -5,5],[gnuplot_preamble,"set xzeroaxis; set yzeroaxis"])$and in the next page its picture.Second Derivative(%i15) Deriv2:ratsimp(diff(Deriv1,x));2 x3 + 12 x2 + 6 x + 4(%o15) ------------------------x6 - 3 x4 + 3 x2 - 1(%i16) fpprec:2$(%i17) solve (Deriv2=0,x);………………………(%i19) float(%o17);(%o19) [x = - 2.1 (0.9 %i - 0.5) - 1.4 (- 0.9 %i - 0.5) - 2.0, x = - 1.4 (0.9 %i - 0.5) - 2.1 (- 0.9 %i - 0.5) - 2.0, x = - 5.5]You can read below the command line to get of the graphics of second derivative:(%i20) plot2d (Deriv2, [x, -5,5],[y, -5,5],[gnuplot_preamble,"set xzeroaxis; set yzeroaxis"])$and in the next page its picture.wx Maxima release (0.6.5-1)A very interesting related project about Maxima is wxMaxima release (0.6.5-1) (author Andrej Vodopivec et al) a wxWidgets / graphical user interface for the computer algebra system Maxima.Wxmaxima (free download at / ) provides a wxWindows interface for Maxima, including a menu system, browsable help and formated output (see picture below in this page). Features as symbolic manipulation of polynomials, rational functions, matrices, integration and graphics are as easy as point and click.Wxmaxima should be installed in a subdirectory of Maxima installation directory. This way, wxMaxima can find the Maxima binary automatically.Example: - Maxima installation directory C:\Program Files\ maxima-5.9.3- wxMaxima installation directory C:\Program Files\ maxima-5.9.3\wxMaxima.If you install it in a different directory, you will have to configure it with Maxima->Configure.WEB RESOURCESwxMaxima material to download by Johann WeilharterIntroduction to Maxima by Richard Rand (PDF)/docs/intromax/intromax.pdfThe Computer Algebra Program Maxima by Boris Gaertner(Entire tutorial in one file: gaertner-tutorial-revision.zip)Micro introduction into Maxima at Harvard UK /computing/maxima/ Minimal Maxima by Robert Dodier (PDF) /docs/tutorial/en/minimal-maxima.pdf/manuals/math/maxima-5.9.2/index.html Document generated by Joshua David Goldstein on December, 6 2005。
