统计计算练习
统计计算练习题
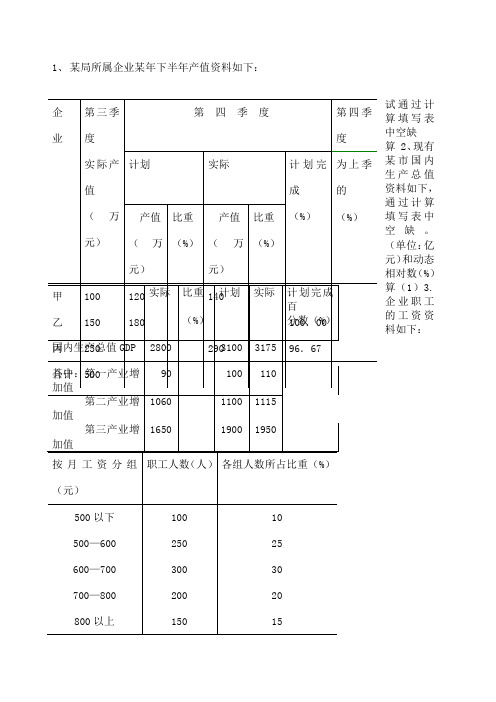
5、该企业工人平均劳动生产率为件/人(组中值:55 65 75 85 95。8250/55+6500/65+5250/75+2550/85+1520/95=366。24070/366)
6、各道工序的平均合格率为
7、(1)甲、乙两企业的平均工资分别为1875元、2420元,所以乙企业职工工资偏高
计算:
(1)建立以商品销售额为因变量的直线回归方程,并解释回归系数的含义
(2)若1996年人均收为400元,试推算该年商品销售额
13、某公司三种商品销售额及价格变动资料如下:
商品
名称
商品销售额(万元)
价格变动率(%)
基期
报告期
甲
乙
丙
500
200
1000
650
200
1200
2
-5
10
计算三种商品价格总指数和销售量总指数。
11、某校甲、乙两班学生的统计学原理考试成绩分组情况如下:
按成绩分组(分)
学生人数
甲 班
乙 班
60以下
2
4
60——70
6
8
70——80
21
17
80——90
16
12
90以上
5
9
合 计
50
50
要求:(1)计算各班学生的平均成绩
(2)通过计算说明哪个班学生平均成绩的代表性强
12、某公司所属40个企业资金利润及有关资料如下表:
2002
430
60
2003
438
8
2、年平均递增率= -1
统计学计算题练习

第四章统计资料整理一、单选题1.某连续变量组距数列,其末组为500以上,又知其邻组组中值为480,则其末组组中值为( ).A.510B.520C.500 D。
4903.对某一总体同时选择三个标志进行复合分组,各个标志所分组数分别分2、4、3,则最后所得组数为().A。
3 B。
9 C.24 D。
27二、操作题某班50名学生的统计学考试成绩如下:50 70 71 72 73 73 72 71 60 6869 70 70 81 82 75 76 78 78 8181 83 84 86 91 92 96 86 88 8489 90 92 93 95 78 79 80 76 7456 72 69 70 80 81 84 48 53 68要求:1、按考试成绩分组编制组距式变量数列,并计算出各组频率和组中值。
2、绘制频数分布直方图、折线图、曲线图和径叶图.第五章统计比较分析法一、单选题1.某厂劳动生产率计划比上年提高8%,实际仅提高4%,则其计划完成百分数为( )。
A。
4% B.50%C。
96.30% D.103。
85%2.某企业某型号电视机,上年实际成本每台6000元,本年计划降低4%,实际降低了5%,则该产品成本计划的完成程度为()。
A。
1%B。
104.0% C.98.96% D.95%二、计算或分析题1。
某企业2010年某产品单位成本为4200元,计划规定2010年成本降低5%,实际降低6%,试确定2011年该产品单位成本的计划数与实际数,并计算该产品单位成本的计划完成程度指标。
2。
(1)某企业2011年产品销售计划为上年的110%,实际为上年的114%,试计算该企业2011年度产品销售计划完成百分数。
(2)某企业2011年劳动生产率增长计划完成102%,这一年劳动生产率为2010年的107%,试计算该企业2011年劳动生产率计划比2010年增长百分数。
要求:计算某省城镇居民各年生活消费的恩格尔系系数,并依据联合国粮农组织提出的贫富标准,指同到2010年底,该城镇居民的生活整体上已达到什么水平。
小学四年级简单统计运算练习题

小学四年级简单统计运算练习题一、选择题(每题2分,共20分)1. 下面哪个是统计数据?A. 2 + 2 = 4B. 苹果、香蕉、橙子C. 计算器D. 运动会接力比赛2. 根据下面的数据,回答问题。
某班同学参加了一次足球比赛,以下是他们进球数:3, 2, 4, 1, 2, 3, 2, 1, 1, 4这些同学进球的总数是几个?A. 4B. 10C. 15D. 203. 根据下面的数据,回答问题。
以下是小明一周内每天早上起床的时间(单位:小时): 7, 8, 7, 7.5, 6, 8.5, 7.5这些数据中,哪个时间出现的次数最多?A. 7小时B. 8小时C. 7.5小时D. 6小时4. 根据下面的数据,回答问题。
以下是小明放学后每天做的不同活动数:2, 1, 3, 2, 4, 1, 2这些数据中,做1个活动的天数有几天?A. 0天B. 1天C. 2天D. 3天5. 根据下面的数据,回答问题。
以下是小华家一周内每天用电视机的时间(单位:小时): 1, 2, 1.5, 0.5, 0, 3, 2.5这些数据中,用电视机时间最少的是哪一天?A. 第一天B. 第三天C. 第五天D. 第六天二、填空题(每题2分,共20分)1. 对于以下数据集合,求平均数:6, 8, 2, 4, 9, 7, 3平均数是_______。
2. 对于以下数据集合,求中位数:2, 3, 4, 5, 6中位数是_______。
3. 对于以下数据集合,求众数(出现次数最多的数): 2, 3, 4, 2, 5, 2, 3, 4, 2众数是_______。
4. 对于以下数据集合,求范围:1, 3, 7, 5, 2范围是_______。
5. 对于以下数据集合,求中位数:5, 6, 3, 2, 1中位数是_______。
三、解答题(每题10分,共30分)1. 根据下面的数据,回答问题。
以下是小明参加游泳比赛的成绩(单位:秒):30, 32, 31.5, 29.7, 32.3这些数据中,哪个成绩是最好的?是多少秒?2. 假设小明和小华一起玩了10把游戏,他们每把游戏获胜的次数如下:小明:3, 5, 4, 2, 3, 4, 3, 5, 2, 3小华:4, 3, 1, 4, 2, 3, 4, 5, 3, 1他们谁赢得的次数更多?分别赢了多少次?3. 全班同学参加了一次考试,以下是他们的分数:72, 85, 90, 68, 78, 82, 79, 87, 94, 81请你编写一个程序来统计分数超过80分的同学人数。
统计练习计算题答案

第四章综合指标四、计算题1.2.某企业统计分析报告中写道:“我厂今年销售收入计划规定2 500万元,实际完成了2 550万元,超额完成计划2%;(对)销售利润率计划规定8%,实际为12%,超额完成计划4%(错,应为超额完成计划50%);劳动生产率计划规定比去年提高5%,实际比去年提高5.5%,完成计划110%(错,应为完成计划100.476%);产品单位成本计划规定比去年下降3%,实际比去年下降2.5%,实际比计划多下降0.5个百分点(错,应为实际比计划少下降0.5个百分点)。
”3.甲企业的总平均成本=19.41乙企业的总平均成本=18.294.该地区个体工商户注册资本金的平均数=61万元一般情况下不同,只有当各组数据的分布为对称或均匀分布时才相同。
5.(1)该公司的本期利润计划平均完成程度=105.74%(2)该公司的本期利润计划平均完成程度=105.74%(3)由于掌握的资料不同使用了不同的方法。
(1)中用了加权算术平均法,(2)中使用了加权调和平均法。
6.所有户型的平均价格=6178.73(¥/m2)7. 该车间三批产品的平均废品率=1.55%8. 单利下:年利率=13%,五年末实际存款=3300复利下:年利率=12.93%,五年末实际存款=3674.129.某次歌唱比赛,共有9位评委,其中歌手A和歌手B得分分别如下:评委 1 2 3 4 5 6 7 8 9歌手A 歌手B 8.99.48.38.48.58.38.68.47.97.98.68.28.28.18.78.78.18.5试用度量资料集中趋势的统计指标,对歌手A和歌手B来进行排名。
通常情况下这种比赛的评委会对歌手的最终评分是去掉歌手得分中的一个最高分和一个最低分,然后再取平均数作为其最终得分。
你认为这种做法是否合理。
合理,因为这样可以去除极端值的影响。
提示:可以通过分别计算一下指标比较说明理由。
没去最大最小之前的和去掉之后的各位歌手的均分各位歌手得分的众数和中位数及标准差10.中位数更好。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标4.1:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少?(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少?4.2:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少?4.3:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
4.4:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少?比计划超额完成多少?(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少?比计划超额完成多少?第四章-----第二部分平均指标与变异指标4.5:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、4.6:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
统计计算练习题

统计计算练习题在统计学中,计算是不可或缺的一部分,它可以帮助我们分析和理解数据。
下面是一些统计计算的练习题,通过解答这些问题,可以增进对统计学的理解,并提升计算能力。
1. 均值计算一家超市有10种商品的价格如下:5元,6元,7元,8元,10元,12元,15元,18元,20元,21元。
计算这些商品的价格均值。
解答:将所有商品的价格相加,得到5+6+7+8+10+12+15+18+20+21=122,然后将总和除以商品的数量10,即122/10=12.2,所以这些商品的价格均值为12.2元。
2. 中位数计算某班级10位学生的考试成绩如下:80,85,88,90,92,95,97,98,99,100。
计算这些分数的中位数。
解答:首先将分数从小到大排列:80,85,88,90,92,95,97,98,99,100。
由于班级人数为10,是一个偶数,所以中位数是第5位和第6位分数的平均值。
即 (92+95)/2 = 93.5,所以这些分数的中位数为93.5。
3. 众数计算一组数据中出现次数最多的数称为众数。
某个班级10个学生的考试成绩如下:85,90,75,90,88,90,92,90,75,90。
计算这些分数的众数。
解答:将分数按照出现的次数从多到少排列:90,90,90,90,90,85,88,92,75,75。
由于90出现的次数最多,所以90是这些分数的众数。
4. 方差计算方差是度量数据集中值与其平均值偏离程度的一种统计量。
某支股票过去5天的收盘价分别为10元,12元,15元,11元,13元。
计算这些收盘价的方差。
解答:首先计算这些收盘价的平均值:(10+12+15+11+13)/5 = 12.2。
然后计算每个收盘价与平均值的差值,分别为-2.2,-0.2,2.8,-1.2,0.8。
将差值的平方相加并除以数据的数量5,即((-2.2)^2+(-0.2)^2+(2.8)^2+(-1.2)^2+(0.8)^2)/5 = 3.12,所以这些收盘价的方差为3.12。
统计计算练习题
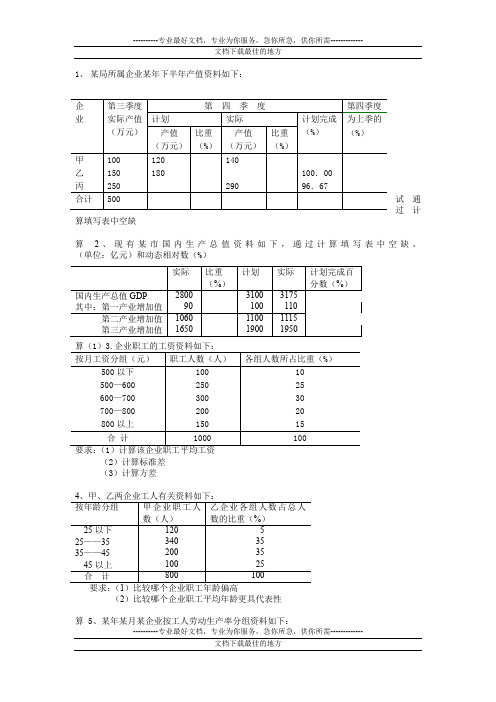
----------专业最好文档,专业为你服务,急你所急,供你所需-------------1、 某局所属企业某年下半年产值资料如下:试通过计算填写表中空缺算 2、现有某市国内生产总值资料如下,通过计算填写表中空缺。
(单位:亿元)和动态相对数(%)(2)计算标准差 (3)计算方差(2)比较哪个企业职工平均年龄更具代表性算 5、某年某月某企业按工人劳动生产率分组资料如下:7、甲、乙两企业工人有关资料如下:要求:(1)比较哪个企业职工工资偏高(2)比较哪个企业职工平均工资更具代表性10、甲、乙两钢铁生产企业某月上旬的钢材供货量资料如下:----------专业最好文档,专业为你服务,急你所急,供你所需-------------11、某校甲、乙两班学生的统计学原理考试成绩分组情况如下:要求:(1)计算各班学生的平均成绩(2)通过计算说明哪个班学生平均成绩的代表性强12求平均利润率。
13、设甲乙两公司进行招员考试,甲公司用百分制记分,乙公司用五分制记分,有关资料如问哪一个公司招员考试的成绩比较整齐?(用标准差)----------专业最好文档,专业为你服务,急你所急,供你所需-----------------------专业最好文档,专业为你服务,急你所急,供你所需-------------3、(1)平均工资=655元 (组中值:450 550 650 750 850。
450*100+550*250+650*300+750*200+850*150=655000。
655000/1000) (2)标准差=120.3元 (3)方差=144754、(1)甲、乙两企业的平均年龄分别为34元、38元,乙企业职工年龄偏高(2)甲、乙两企业的平均差系数分别为22.35%、19.47%,所以乙企业职工的平均年龄更具代表性5、该企业工人平均劳动生产率为67.6件/人 (组中值:55 65 75 85 95。
8250/55+6500/65+5250/75+2550/85+1520/95=366。
小学六年级数学统计简便运算练习题

小学六年级数学统计简便运算练习题练1
某班级学生的身高数据如下:120cm、130cm、135cm、125cm、140cm、128cm、130cm、133cm、132cm、129cm。
请你计算:
1. 这个班级学生的身高平均值是多少?并用文字简单叙述这个
平均数代表的意义。
2. 将这些身高按从小到大排序,并把它们写在下方横线上。
答案:
1. 这个班级学生的身高平均值是:129.2cm。
这个平均数代表
了这个班级学生身高的集中程度和趋势。
2. 120cm、125cm、128cm、129cm、130cm、130cm、132cm、133cm、135cm、140cm
练2
小明连续三天测量自己上学花费的时间(每天的时间是相同的)。
他得到了下面的数据:25分钟、22分钟、23分钟。
请你回答以下问题:
1. 这三天小明平均上学花费了多长时间?
2. 用文字解释这三天的平均数所表达的意义。
答案:
1. 这三天小明平均上学花费了:23.33分钟。
2. 这三天的平均数代表了小明上学花费时间的集中程度和趋势。
练3
某班级学生的数学成绩如下:90分、95分、85分、90分、85分、87分、90分、92分、95分、93分。
请你计算:
1. 这个班级学生的数学成绩平均值是多少?并解释这个平均数
的意义。
2. 这个班级中有多少名学生数学成绩高于90分?
答案:
1. 这个班级学生的数学成绩平均值是:90.2分。
这个平均数代表了这个班级学生数学成绩的集中程度和趋势。
2. 有4名学生数学成绩高于90分。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少比计划超额完成多少(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少比计划超额完成多少第四章-----第二部分平均指标与变异指标:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
:对某车间甲、乙两工人当日产品中各抽取10件产品进行质量检查,得资料如下:试比较甲乙两工人谁生产的零件质量较稳定。
小学数学统计练习题

小学数学统计练习题1. 统计班级学生人数:班级共有45名学生,其中男生23名,女生22名。
请计算男生和女生各占班级总人数的百分比。
2. 统计图书种类:图书室有图书300本,其中故事书80本,科普书70本,教科书50本,其他类型100本。
请计算每种图书占图书总数的比例。
3. 统计一周天气情况:一周内,晴天3天,多云2天,雨天1天,雪天1天。
请列出晴天、多云、雨天和雪天各占一周天数的百分比。
4. 统计水果店苹果和橙子的销售情况:水果店一天内卖出苹果120个,橙子80个。
请计算苹果和橙子各占总销售量的百分比。
5. 统计学校运动会参赛人数:学校运动会共有200名学生参加,其中田径项目100人,球类项目50人,其他项目50人。
请计算各项目参赛人数占总参赛人数的百分比。
6. 统计家庭一周内用电情况:一周内,家庭用电总量为350度,其中照明用电100度,电视用电50度,冰箱用电50度,其他电器用电150度。
请计算各电器用电占总用电量的百分比。
7. 统计商店一天内营业额:商店一天内营业额为5000元,其中食品销售2000元,服装销售1500元,其他商品销售1500元。
请计算各商品类别营业额占总营业额的百分比。
8. 统计学校图书馆借书情况:学校图书馆一天内借出图书200本,其中文学类50本,历史类30本,科学类40本,艺术类30本,其他类50本。
请计算各类图书借出量占总借出量的百分比。
9. 统计一个月内家庭用水情况:一个月内,家庭用水量为30吨,其中饮用水5吨,生活用水15吨,其他用水10吨。
请计算各用水类别占总用水量的百分比。
10. 统计学校一周内学生出勤情况:学校一周内有500名学生,其中周一至周五每天出勤人数分别为450人、460人、470人、480人、490人。
请计算每天出勤率,并计算一周平均出勤率。
统计学练习题——计算题总
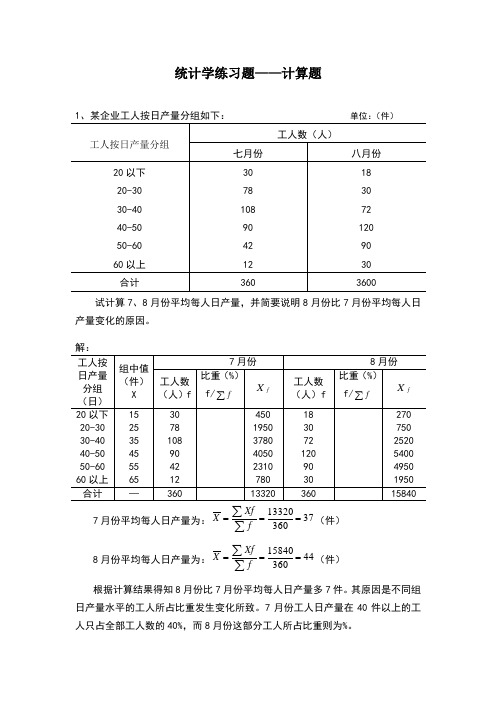
统计学练习题——计算题1、某企业工人按日产量分组如下: 单位:(件)试计算7、8月份平均每人日产量,并简要说明8月份比7月份平均每人日产量变化的原因。
7月份平均每人日产量为:3736013320===∑∑fXf X (件) 8月份平均每人日产量为:4436015840===∑∑fXf X (件) 根据计算结果得知8月份比7月份平均每人日产量多7件。
其原因是不同组日产量水平的工人所占比重发生变化所致。
7月份工人日产量在40件以上的工人只占全部工人数的40%,而8月份这部分工人所占比重则为%。
2、某纺织厂生产某种棉布,经测定两年中各级产品的产量资料如下:解:2009年棉布的平均等级=25010 34022001⨯+⨯+⨯=(级)2010年棉布的平均等级=3006 32422701⨯+⨯+⨯=(级)可见该厂棉布产品质量2010年比2009年有所提高,其平均等级由级上升为级。
质量提高的原因是棉布一级品由80%上升为90%,同时二级品和三级品分别由16%及4%下降为8%及2%。
3、甲乙两企业生产同种产品,1月份各批产量和单位产品成本资料如下:试比较和分析哪个企业的单位成本高,为什么?解:甲企业的平均单位产品成本=×10%+×20%+×70%=(元)乙企业的平均单位产品成本=×30%+×30%+×40%=(元)可见甲企业的单位产品成本较高,其原因是甲企业生产的3批产品中,单位成本较高(元)的产品数量占70%,而乙企业只占30%。
4、有四个地区销售同一种产品,其销售量和销售额资料如下:解:总平均价格=23010600=销售总量销售总额=5根据上表计算该商店售货员工资的全距,平均差和标准差,平均差系数和标准差系数。
解:⑴2010200==∑∑f Xf X =510(元); ⑵全距=690-375=315(元)⑶156020X X fA D f-⋅==∑=78(元); ⑷)(202085002==∑∑-ffXX σ=(元)⑸%10051078%100⨯=⨯⋅=⋅XD A V D A =%; ⑹%1005101.102%100⨯=⨯=XV σσ=% 6、某班甲乙两个学习小组某科成绩如下: 甲小组乙小组试比较甲乙两个学习小组该科平均成绩的代表性大小。
小学数学数据统计练习题

小学数学数据统计练习题一、选择题(每题2分,共20分)1. 下面哪个是统计中的参数?A. 总体B. 样本C. 均值D. 中位数2. 在一个班级中,学生的身高是以下几个值:130 cm,140 cm,145 cm,156 cm,166 cm,174 cm,172 cm,177 cm。
请问,这些数据的众数是多少?A. 156 cmB. 145 cmC. 172 cmD. 177 cm3. 下面哪个图形可以用来表示离散数据?A. 条形图B. 折线图C. 散点图D. 帕累托图4. 假设小明在一场考试中得了以下成绩:70,80,85,90,95。
请问小明的平均成绩是多少?A. 82B. 84C. 85D. 865. 如果一组数据的中位数比众数小,那么这组数据的分布形状是什么样的?A. 对称分布B. 左偏分布C. 右偏分布D. 偏态分布6. 所有学生的成绩从高到低排序后,第25%的学生的成绩位于以下的范围内:A. 0-25%B. 25-50%C. 50-75%D. 75-100%7. 以下哪个不是统计中的变量类型?A. 名义变量B. 顺序变量C. 单变量D. 数值变量8. 在一次调查中,有100人回答了一个问题,其中80人选择了选项A,10人选择了选项B,5人选择了选项C,5人选择了选项D。
请问,选择选项B的人所占比例是多少?A. 10%B. 20%C. 50%D. 80%9. 以下哪个图形可以用来表示连续数据?A. 饼图B. 条形图C. 直方图D. 散点图10. 下列哪个值不是有序数列 {3, 5, 7, 9, 1, 2, 4} 的中位数?A. 3B. 4C. 5D. 7二、填空题(每空2分,共20分)1. 在一个班级中,学生的体重分别为40kg,42kg,44kg,48kg,50kg。
请计算这些数据的平均数。
平均数:______________2. 在一次投票中,100人中有75人选择了候选人A,15人选择了候选人B,10人选择了候选人C,请计算选择候选人B的比例。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标4.1:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少?(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少?4.2:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少?4.3:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
4.4:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少?比计划超额完成多少?(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少?比计划超额完成多少?第四章-----第二部分平均指标与变异指标4.5:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、4.6:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
统计学计算练习题及解答1

统计学计算练习题及解答试计算该集团公司职工的平均工资。
解: ==750×0.2+850×0.25+950×0.3+1050×0.15+1150×0.1=920(元)该局职工的平均工资为920元。
二、试计算三个车间生产该产品的平均废品率。
解:x =xf fåå=3%702%204%90702090???++= 3.4%三、 2006年某月甲、乙两市场某商品价格、销售量和销售额资料如下:试分别计算该商品在两个市场上的平均价格。
解:在甲市场上的平均价格:???===åå7001059001201100137123.04(元/件)2700xf x f在乙市场上的平均价格为:====++åå317900317900117.74(元/件)126009600959002700105120137m x m x 四、根据上述资料计算两车间工人的平均日产量,并说明哪一个车间的平均日产量更具有代表性。
解:??创创==创创创==åååå甲乙4545581.(件/人)件/人)655+7527+857+953x 64=7031405+6010+8024+10015+1202+1401x 57=80.7(xf fxf fs s ======甲乙11.7220.85s n s n n n =创=创á甲甲甲乙乙乙甲乙11.7210010016.6770.3120.8510010025.8480.7%=%=%x %=%=%x所以甲车间工人的平均日产量比乙车间工人的平均日产量更具有代表性。
五、从某学校参加英语等级考试的学生中随机抽取100名,考试成绩分组资料如下:试以95.45%的可靠程度估计该校学生英语等级考试在75分以上的学生所占比重的范围。
(z =2) 解:352055%100p +==0497.010045.055.0)1(=⨯=-=np p p μ20.04970.0994p p z m D ==?0.550.0994pp 盌=?75分以上的学生所占比重的范围为(45.06%,64.94%)六、从某年级学生中按简单随机抽样方式抽取40名学生,对高等数学课程的考试成绩进行检查,得知其平均分数为73.45分,样本标准差为9.25分,试以95.45%的概率保证度推断全年级学生考试成绩的区间范围。
统计计算练习
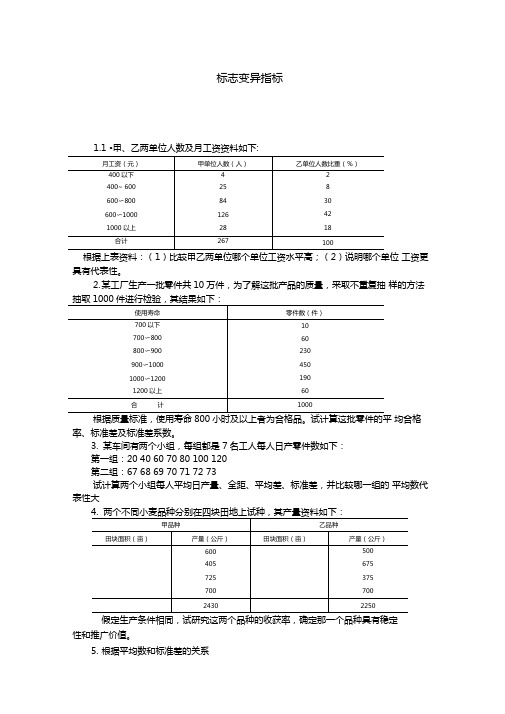
标志变异指标1.1 •甲、乙两单位人数及月工资资料如下:根据上表资料:(1)比较甲乙两单位哪个单位工资水平高;(2)说明哪个单位工资更具有代表性。
2.某工厂生产一批零件共10万件,为了解这批产品的质量,采取不重复抽样的方法均合格率、标准差及标准差系数。
3.某车间有两个小组,每组都是 7名工人每人日产零件数如下:第一组:20 40 60 70 80 100 120第二组:67 68 69 70 71 72 73试计算两个小组每人平均日产量、全距、平均差、标准差,并比较哪一组的平均数代表性大假定生产条件相同,试研究这两个品种的收获率,确定那一个品种具有稳定性和推广价值。
5.根据平均数和标准差的关系(1) (1) 设x 600,V 25%,则标准差为多少(2) (2) 设x 20,卩450,则标准差系数为多少(3) (3) 设236, x2360,则平均数为多少(4) (4) 设V 17.2%, 7174,则平均数为多少第七章时间数列计算题1•某仓库1月1日某产品库为1800吨,3月1日为2000吨,6月1日为 2100吨,6月30日为1940吨。
问该产品上半年平均库存是多少2•某企业试计算该企业年度计划平均完成程度指标。
3•已知某企业1995年各月总产值资料如下:单位:万元试计算每季的月平均总产值和全年的月平均总产值。
4•根据下表中已知资料,运用时间数列指标的相互关系,推算发展水平、累计增长量、定基发展速度和定基增长速度指标。
5.我国28000亿元,则平均发展速度应为多少如果按年平均增长速度为灿算,到1990年我国工农业总产值可达多少亿元6.已知某地区2000年各月月初人口资料如下:1月初230万人,2月初230 万人,3月初240万人,4月初250万人,6月初250万人,8月初260万人,12 月初260万人,次年1月初260万人。
试计算该地区全年平均人口数。
7 •某管理局所属两个企业1月份产值及每日在册人数资料如下:试计算各企业月劳动生产率,并综合计算两个企业的月劳动生产率8 •某公司某产品1997年至2000年各月销售量如下:试用同月平均法计算季节指数,进行季节变动分析。
统计计算题练习

练习27、已知几个地区的工农业增加值和财政收入资料如下, 练习 、已知几个地区的工农业增加值和财政收入资料如下, (1)根据相关系数判断工农业增加值与财政收入之间相关关 )根据相关系数判断工农业增加值与财政收入之间相关关 系的密切程度。 系的密切程度。 的意义。 (2)建立回归方程并说明回归系数 的意义。 )建立回归方程并说明回归系数b的意义 万元时的财政收入预测额。 (3)预测工农业增加值为 万元时的财政收入预测额。 )预测工农业增加值为35万元时的财政收入预测额
练习6 某公司2008年四个季度销售额资料如下, 2008年四个季度销售额资料如下 练习6、 某公司2008年四个季度销售额资料如下,计算 该公司平均每季的销售额。 该公司平均每季的销售额。 时 期 第一季度 450 第二季度 400 第三季度 第四季度 480 500
销售额
练习7 某公司业务一科9月上旬每日出勤人数分别为:14, 练习7、某公司业务一科9月上旬每日出勤人数分别为:14, 15,14,13,15,14,14,13,15,13。计算9 15,14,13,15,14,14,13,15,13。计算9月上旬平均 每日出勤人数。 每日出勤人数。 练习8 某企业2005年 练习8、某企业2005年6月成品库存变动资料记录如下所示 2005 时间 10日 15日 25日 1日 10日 15日 25日 400 300 26日 26日 200 28日 28日 200
(2)若已知各年的发展速度为104%、102%、105%、 若已知各年的发展速度为104%、102%、105%、 104% 107%、104%, 2001—2005年平均每年发展速度 年平均每年发展速度。 107%、104%,求2001—2005年平均每年发展速度。 (3)已知2005年是2000年的123%,求2001—2005年 已知2005年是2000年的123%, 2001—2005年 2005年是2000年的123% 平均每年发展速度
统计计算练习题

统计计算练习题
本文将提供统计计算练题,以帮助读者巩固统计学知识并提高
练能力。
1. 某公司5月份的销售额分别为:1000元、1500元、1200元、1100元、1300元,求该公司5月份销售总额和平均销售额。
2. 某品牌牛仔裤样本的长度如下(单位:厘米):62、64、66、68、70、70、70、70、72、72、72、74、76、78、80,请计算样本
均值、中位数、众数。
3. 某市场调查机构通过对1000位市民做的一项调查得到以下
结果:
- 其中男性有600人,女性有400人;
- 男性中有250人喜欢看电影,350人喜欢看电视剧;
- 女性中有280人喜欢看电影,120人喜欢看电视剧。
请回答以下问题:
- 调查期间看电影的受访者人数占总受访者人数的比例分别是
多少?
- 被调查者中喜欢看电视剧的人数占女性受访者的比例是多少?
4. 某商品在1月份、2月份、3月份的销售量分别为1200件、1400件、1800件,请问3月份销售量比1月份销售量增加了多少
百分比?如果3月份销售量减少了20%,销售量是多少?
以上练习题只是统计学习中的基础题目,希望读者可以在掌握
了基础知识的基础上多练习,不断提高。
统计专题训练经典练习题(含答案)

统计专题训练经典练习题(含答案)统计专题训练经典练题(含答案)以下是一些统计学的经典练题,附带答案供参考。
1. 对于一个班级的学生成绩,已知平均分为75分,标准差为5分。
如果班级总人数为100人,问有多少学生的成绩在65分以上?答案:根据正态分布的性质,我们可以应用标准正态分布表,计算得到 z 值为 (65-75)/5 = -2,查表得到对应的累积概率为 0.0228,因此在65分以上的学生人数约为0.0228 * 100 ≈ 2.28,即约有 2 名学生的成绩在65分以上。
2. 一家工厂生产的产品长度服从正态分布,平均长度为10cm,标准差为0.5cm。
若从该工厂中随机抽取50个产品,问有多少产品的长度在9.5cm至10cm之间?答案:由于从该工厂中抽取的产品长度服从正态分布,我们可以计算出抽样分布的均值和标准差为 10cm 和0.5cm/sqrt(50) ≈0.0707cm。
然后,我们可以将区间 [9.5cm, 10cm] 转化为 z 值计算区间内的概率。
计算得到 z 值为 (10-9.5)/0.0707 ≈ 7.07,查表得到对应的累积概率为 0.9999。
因此,在9.5cm至10cm之间的产品数量约为0.9999 * 50 ≈ 49.995,即约有 50 个产品的长度在9.5cm至10cm之间。
3. 某次调查发现,两种不同品牌的汽车在某一地区的市场占有率的估计值分别为 0.60 和 0.40,并且总样本量为 5000。
现在需要对这一地区汽车市场占有率的差异进行检验。
问如何构建零假设和备择假设?并说明该检验的类型。
答案:对于差异检验,我们可以构建如下的零假设和备择假设:零假设(H0):两个品牌的汽车市场占有率没有差异,即 p1= p2。
备择假设(H1):两个品牌的汽车市场占有率存在差异,即p1 ≠ p2。
该检验属于双侧检验,因为备择假设是双向的,即可能两个品牌的市场占有率存在大于和小于的差异。
统计计算课堂作业练习题

统计计算课堂作业一练习1:用均匀分布生成100 次筛子点数,并画出直方图。
x<-sample.int(6, size=100, replace=TRUE)hist(x,prob=T,col=gray(0.3),main="uniform on [0,1]") #直方图练习2:产生1000个分布律为以下的随机数。
并画出直方图及相应的饼图。
x <- sample(4, size=1000, replace=TRUE, prob=c(0.2, 0.3, 0.4,0.1))hist(x,prob=T,col=gray(0.3),main="uniform on [0,1]") #直方图pie(table(x))练习3:从100个同学中随机抽取10个人参与啦啦队,请模拟该随机过程。
sample.int(100, size=10)练习4:已知汽车通过10个红绿灯是独立随机的,现已知一汽车通过某一路段时,遇到红灯的概率是0.4,一直到汽车停下,通过的路口情况,请模拟该随机过程。
rgeom(10, 0.4)练习5:请模拟射击随机过程,已知一次试验中击中概率是0.2,射击100次的二项分布。
round(dbinom(0:100, size=100, prob=0.2)*100)作业分析:1.给出生成密度函数为(),0xf x xe x-=≥的随机变量的两种方法,并比较二者的效率(system.time).2.给出生成密度为234()30(2),01f x x x x x=-+≤≤的随机变量的方法.rng.beta24<-function(n){xvec<-numeric(n)for(i in1:n){repeat{U1<-runif(1)U2<-runif(1)X<-U1Y<-15U2if(Y<=30*(X^2-2*X^3+X^4))break}xvec[i]<-X}xvec}#测试:x<-rng.beta24(1000)hist(x,freq=FALSE,ylim=c(0,2.5))curve(dbeta(x,2,4),0,1,col="red",add=TRUE)统计计算课堂作业二任务一练习1:的投点法模拟求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标志变异指标
工资更具有代表性。
2.某工厂生产一批零件共10万件,为了解这批产品的质量,采取不重复抽均合格率、标准差及标准差系数。
3.某车间有两个小组,每组都是7名工人每人日产零件数如下: 第一组:20 40 60 70 80 100 120 第二组:67 68 69 70 71 72 73
试计算两个小组每人平均日产量、全距、平均差、标准差,并比较哪一组的平均数代表性大?
性和推广价值。
5.根据平均数和标准差的关系。
(1)(1)设%25,600==σV x ,则标准差为多少?
(2)(2)设450,202==x x ,则标准差系数为多少? (3)(3)设360,3622==x σ,则平均数为多少? (4)(4)设174%,2.172==x V σ,则平均数为多少?
第七章 时间数列
计算题
1.某仓库1月1日某产品库为1800吨,3月1日为2000吨,6月1日为2100吨,6月30日为1940吨。
问该产品上半年平均库存是多少?
4.根据下表中已知资料,运用时间数列指标的相互关系,推算发展水平、累计增长量、定基发展速度和定基增长速度指标。
年翻两翻,达到28000亿元,则平均发展速度应为多少?如果按年平均增长速度为7.2%计算,到1990年我国工农业总产值可达多少亿元?
6.已知某地区2000年各月月初人口资料如下:1月初230万人,2月初230万人,3月初240万人,4月初250万人,6月初250万人,8月初260万人,12月初260万人,次年1月初260万人。
试计算该地区全年平均人口数。
第八章统计指数
计算题
1.1.某百货公司2000年商品销售额为5600万元,2001年比2000年增加500万元,零售价格指数上涨3.6%。
试计算该百货公司零售额变动中由于零售价格和零售量变动的影响程度和影响绝对额。
2.2.某企业生产三种产品有关数据如下表所示:
3.3.下面是某家计调查得到的数据,试利用可变构成指数体系进行因素分析。
4.4.
示。
试建立指数体系,分析原材料消耗总额的变动及各因素的影响水平。
第九章抽样调查基础
计算题
1.某商店有20名职工,现从中抽取5名职工进行调查。
采用简单随机抽样,试计算各种抽样方法的样本可能数目。
2.对某产品进行重量测试,被抽中的10袋产品其重量如下(单位:克):48,47,49,50,51,48,46,45,46,49 试计算产品重量的抽样平均误差。
3.某灯泡厂生产一批灯泡共8000只,随机抽选400只进行耐用时间的试验。
测试结果平均寿命5000小时,总体标准差为300小时。
求抽样误差。
4.某市在家庭平均人数调查中,采用不重置简单随机抽样得到样本的每户平均人数为3.2人,标准差为1.378人。
①如果总户数为1000户,调查户数为80户,试计算抽样的平均误差;
②在①条件下,如果极限误差为0.2956,试估计户平均人数;
③在①的条件下,如果可靠程度为0.95,试计算户平均人数;
④如果要求可靠程度为95.45%,极限误差为0.35,试计算重置和不重置抽样各需抽取多少户进行调查(总户数仍为1000户)。
5.某机械厂生产一批零件共6000件,随机抽查300件,发现其中有9件不合格,求合格率的抽样误差。
6.某服装厂对当月生产的20000件衬衫进行质量检查,结果在抽查的200件衬衫中有10件是不合格品,要求:
(1)(1)以95.45%概率推算该产品的合格范围;
(2)该月生产的产品是否超过规定的8%的不合格率(概率不变)。
7.某地农村种植小麦150亩,在麦收前随机不重置抽取了100个平方公尺的小麦样本,测得每平方公尺小麦产量为0.5公斤,标准差为0.05公斤。
试计算极限抽样误差,并以95.45%的概率保证,推断该地区小麦平均亩产量和总产量。
8.某茶叶公司销售一批茗茶,规定每包规格重量不低于150克,现抽取1%
要求。
试以95.45%的可靠性:(1)估计平均每月看电影的次数;(2)确定每月看电影在4次以上的比重,其误差不超过3%。
10.年终在某乡镇储蓄所中按定期储蓄存款账号进行抽样调查,得到如下资
);
(2)估计定期存款额在2000元以上的比重。
11.工商部门对某超市经销的小包装休闲食品进行重量合格抽查,规定每包
(1)(1)这批食品平均每包重量是否符合规定要求;
(2)(2)若每包食品重量低于30克为不合格,求合格率的范围。
12.对某居委会30户家庭的月收支情况进行抽样调查,发现平均每户每月用于书报费支出为45元,抽样平均误差为2元,试问应以多少概率才能保证每户每月书报费支出在41.08元至48.92元之间。
计算题
1.在2000名工人中,采取重复抽样方式,随机抽取144个工人的土方工程进行测量,测量结果为每一工人的平均工作量为5.32立方米。
(1)试以95%的概率保证程度(t=1.96)来推算抽样极限误差;(2)根据上述条件,若要求极限误差不超过0.1立方米,t=1,应抽多少个工人进行调查。
2.某日化工厂用机械大量连续包装洗衣粉,要求每袋按1公斤包装,为保证质量,生产过程中每隔8小时检查1小时的产品,共检验20次,算出平均重量为1.005公斤,抽样总体各群间方差平均数为0.002公斤。
试计算:(1)抽样平
10.03公斤为标准,问上述均误差;(2)要求概率99.73%,使产品重量不低于
检验的产品是否合格?
(3)概率为0.95时,职工月平均收入的可能范围。
4.某市有职工100000人,其中职员40000人,工人60000人。
现拟进行职工收入抽样调查,并划分职员和工人两类进行选择。
事先按不同类型抽查40名
型抽样调查组织形式计算必要抽样数目。
5.某商店对购进的一批大衣的质量进行检查,抽样结果有1.2%的不合格品,若抽样平均误差为0.02%,试分别在以下各条件下估计不合格品率。
(1)抽样极限误差为0.04%;(2)可靠程度为68.27%。
6.为调查农民的生活水平,在某地5000户农民中采用不重复简单随机抽样抽取了400户进行调查,得知这400户中有彩色电视机的为87户,试以95%的把握估计该区全部农户中拥有彩色电视机的农户所占的比率。
又,若要求抽样允许误差不超过0.02,
问至少应抽取多少户作样本?
7.要对全及总体1000个单位进行5%的机械抽样。
(1)全及总体要划分为多少部分?(2)每部分的单位数为多少?(3)中选单位间隔是多少?(4)如果第一组抽到第5号单位,其他中选单位的号码是多少?
8.某工厂对1000箱入库产品进行抽检。
现从中抽取100箱(每箱装100个(2)(2)试以95%的把握估计这批产品的废品数为多少; (3)生产车间称这批产品的不合格率在1%以下,试根据抽样结果说明这一说法是否可信?
9.某院有30个教学班,每班40名学生。
从中抽取8个班,再从中选班中各
计算题
计算本期与前期存栏头数的相关系数;
②②列出正规方程组求单位成本倚产量的回归方程并解释回归方程中各系数的经济意义;
③③试估计产量为3千件的单位成本;
④④计算估计标准误差。
3.已知:n=6 ∑x=21 ∑y=426 ∑xx=79 ∑yy=30268
∑xy=1481
要求:
①计算相关系数
②建立回归方程
③计算估计标准误差
(1)以人均收入为自变量,商品销售额为因变量,建立直线回归方程;
(2)用最小平方法求人均收入数列的直线趋势方程,并估计2000年该市的人均收入;
(3)根据2000年的人均收入的估计值,利用回归方程推算2000年该市的商品销售额。
根据上表资料:
(1)计算相关系数;(2)建立回归直线方程;(3)计算估计的标准误差;(4)估计生产性固定资产为1100万元时的工业总产值。
b 待定系数的经济意义;若新建一企业,其年设备能力为6.5千瓦/人,估计劳动生产率将为多少?
误差;(4)若个人收入为213亿元时,估计个人消费支出。
)建立直线回归方程;(4)若某商店每人月平均销售额为2千元,估计其利润率;(5)计算估计的标准误差。
准误差;(3)计算相关系数,判断相关程度。
