人教版初中数学分式知识点总复习有答案
人教版八年级数学上册《分式》知识点复习及典例解析

人教版八年级数学上册《分式》知识点复习及典例解析《分式》知识点复习及典例解析一、复习目标1.理解并记住分式的乘法法则、除法法则,会进行简单的分式乘除法计算.能解决一些与分式的乘除运算有关的简单的实际问题.2.了解同分母分式的加减法法则,会进行同分母分式的加减运算,理解通分的意义,会通过通分把异分母的分式加减转化为同分母的分式加减.3.能熟练地进行分式的加减乘除混合运算,提高类比的能力和代数化归的能力.4.了解分式方程的概念,掌握解一元一次方程的分式方程的方法,了解产生增根的原因,会检捡一个数是不是分式方程的增根.5.能够列出可化为一元一次方程的分式方程解简单实际问题.二、重点难点重点:分式乘除法、加减法法则的应用. 分式方程的概念,分式方程的解法难点:异分母分式加减法. 解分式方程时,去分母可能会出现增根。
三、知识概要1. 分式的乘除乘法法则:分式乘分式时,分子的积作积的分子,分母的积作积的分母. 除法法则:分式除以分式,把除式的分子和分母颠倒位置后与被除式相乘. 式子表示:.;bcad c d b a d c b a bd ac d c b a =?=÷=? 2. 分式的加减(1)分式的通分:把几个异分母的分式化成与原来的分式相等的同分母的分式叫通分.(2)法则:同分母分式相加减,分母不变,分子相加减.异分母分式相加减,先通分,变为同分母的分式,再加减.式子表示:;c b a c b c a ±=±.bdbc ad bd bc bd ad d c b a ±=±=± 3.分式方程的概念分式是一种表示具体情境中数量的模型,分式方程则是表示这些数量关系之间相等关系的模型,分式方程是分母中含有未知数的方程.4.分式方程的解法分式方程是转化为一元一次方程来求解,它是通过去分母实现转化的.主要步骤:去分母,去括号,移项,合并同类项,系数化为1,检验.因为分式方程可能产生增根,所以解分式方程最后一步“检验”,检查所解整式方程的根到底是不是分式方程的根.5.去分母的技巧解分式方程的基本思路是“转化”,即把分式方程化为我们熟悉的整式方程,转化的途径是“去分母”,即方程两边都乘以最简公分母.去分母是解分式方程的第一步,也是关键的一步,当分式方程中分式的分母是一次式时,可直接确定最简公分母,方程两边同乘以最简公分母后实现去分母,当各分式的分母中有二次式时,要先进行因式分解,再确定最简公分母,然后再去分母.6.验根的方法因为解分式方程可能出现增根,所以验根是必要的,验根的方法有两种,一种是把求得的未知数的值代入原方程进行检验,这种方法道理简单,而且可以检查解方程时有无计算错误,另一种是把求得的末知数的值代入最简公分母,看分母的值是否为零,这种方法比较简便,但不能检查解方程过程中出现的计算错误.7.列分式方程解决实际问题的方法步骤(1)、审:分析问题,寻找已知、未知及相相等关系,(2)、设:设恰当的未知数(3)、列:根据相等关系列出分式方程(4)、解:求出所列方程的解(5)、验:首先检验所求的解是不是分式方程的解,然后检验所求的解是否与实际符合(6)、答:写出答案.四、典例解析考点一、分式概念的运用例1.若分式||33x x --的值为零,则x 的值等于。
2024中考数学复习核心知识点精讲及训练—分式(含解析)

2024中考数学复习核心知识点精讲及训练—分式(含解析)1.了解分式、分式方程的概念,进一步发展符号感;2.熟练掌握分式的基本性质,会进行分式的约分、通分和加减乘除四则运算,发展学生的合情推理能力与代数恒等变形能力;3.能解决一些与分式有关的实际问题,具有一定的分析问题、解决问题的能力和应用意识;4.通过学习能获得学习代数知识的常用方法,能感受学习代数的价值。
考点1:分式的概念1.定义:一般地,如果A、B表示两个整式,并且B中含有字母,那么式子AB叫做分式.其中A叫做分子,B叫做分母.2.最简分式:分子与分母没有公因式的分式;3.分式有意义的条件:B≠0;4.分式值为0的条件:分子=0且分母≠0考点2:分式的基本性质分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,这个性质叫做分式的基本性质,用式子表示是:A A M A A MB B M B B M⨯÷==⨯÷,(其中M是不等于零的整式).考点3:分式的运算考点4:分式化简求值(1)有括号时先算括号内的;(2)分子/分母能因式分解的先进行因式分解;(3)进行乘除法运算(4)约分;(5)进行加减运算,如果是异分母分式,需线通分,变为同分母分式后,分母不变,分子合并同类项,最终化为最简分式;(6)带入相应的数或式子求代数式的值【题型1:分式的相关概念】【典例1】(2022•怀化)代数式x,,,x2﹣,,中,属于分式的有()A.2个B.3个C.4个D.5个【答案】B【解答】解:分式有:,,,整式有:x,,x2﹣,分式有3个,故选:B.【典例2】(2023•广西)若分式有意义,则x的取值范围是()A.x≠﹣1B.x≠0C.x≠1D.x≠2【答案】A【解答】解:∵分式有意义,∴x+1≠0,解得x≠﹣1.故选:A.1.(2022•凉山州)分式有意义的条件是()A.x=﹣3B.x≠﹣3C.x≠3D.x≠0【答案】B【解答】解:由题意得:3+x≠0,∴x≠﹣3,故选:B.2.(2023•凉山州)分式的值为0,则x的值是()A.0B.﹣1C.1D.0或1【答案】A【解答】解:∵分式的值为0,∴x2﹣x=0且x﹣1≠0,解得:x=0,故选:A.【题型2:分式的性质】【典例3】(2023•兰州)计算:=()A.a﹣5B.a+5C.5D.a 【答案】D【解答】解:==a,故选:D.1.(2020•河北)若a≠b,则下列分式化简正确的是()A.=B.=C.=D.=【答案】D【解答】解:∵a≠b,∴,故选项A错误;,故选项B错误;,故选项C错误;,故选项D正确;故选:D.2.(2023•自贡)化简:=x﹣1.【答案】x﹣1.【解答】解:原式==x﹣1.故答案为:x﹣1.【题型3:分式化简】【典例4】(2023•广东)计算的结果为()A.B.C.D.【答案】C【解答】解:==.故本题选:C.1.(2023•河南)化简的结果是()A.0B.1C.a D.a﹣2【答案】B【解答】解:原式==1.故选:B.2.(2023•赤峰)化简+x﹣2的结果是()A.1B.C.D.【答案】D【解答】解:原式=+==,故选:D.【题型4:分式的化简在求值】【典例5】(2023•深圳)先化简,再求值:(+1)÷,其中x=3.【答案】,.【解答】解:原式=•=•=,当x=3时,原式==.1.(2023•辽宁)先化简,再求值:(﹣1)÷,其中x=3.【答案】见试题解答内容【解答】解:原式=(﹣)•=•=x+2,当x=3时,原式=3+2=5.2.(2023•大庆)先化简,再求值:,其中x=1.【答案】见试题解答内容【解答】解:原式=﹣+====,当x=1时,原式==.3.(2023•西宁)先化简,再求值:,其中a,b是方程x2+x﹣6=0的两个根.【答案】,6.【解答】解:原式=[﹣]×a(a﹣b)=×a(a﹣b)﹣=﹣=;∵a,b是方程x2+x﹣6=0的两个根,∴a+b=﹣1ab=﹣6,∴原式=.1.(2023春•汝州市期末)下列分式中,是最简分式的是()A.B.C.D.【答案】C【解答】解:A、=,不是最简分式,不符合题意;B、==,不是最简分式,不符合题意;C、是最简分式,符合题意;D、==﹣1,不是最简分式,不符合题意;故选:C.2.(2023秋•岳阳楼区校级期中)如果把分式中的x和y都扩大2倍,那么分式的值()A.不变B.扩大2倍C.扩大4倍D.缩小2倍【答案】B【解答】解:∵==×2,∴如果把分式中的x和y都扩大2倍,那么分式的值扩大2倍,故选:B.3.(2023•河北)化简的结果是()A.xy6B.xy5C.x2y5D.x2y6【答案】A【解答】解:x3()2=x3•=xy6,故选:A.4.(2023秋•来宾期中)若分式的值为0,则x的值是()A.﹣2B.0C.2D.【答案】C【解答】解:由题意得:x﹣2=0且3x﹣1≠0,解得:x=2,故选:C.5.(2023秋•青龙县期中)分式的最简公分母是()A.3xy B.6x3y2C.6x6y6D.x3y3【答案】B【解答】解:分母分别是x2y、2x3、3xy2,故最简公分母是6x3y2;故选:B.6.(2023春•沙坪坝区期中)下列分式中是最简分式的是()A.B.C.D.【答案】A【解答】解;A、是最简二次根式,符合题意;B、=,不是最简二次根式,不符合题意;C、==,不是最简二次根式,不符合题意;D、=﹣1,不是最简二次根式,不符合题意;故选:A.7.(2023春•原阳县期中)化简(1+)÷的结果为()A.1+x B.C.D.1﹣x【答案】A【解答】解:原式=×=×=1+x.故选:A.8.(2023•门头沟区二模)如果代数式有意义,那么实数x的取值范围是()A.x≠2B.x>2C.x≥2D.x≤2【答案】A【解答】解:由题意得:x﹣2≠0,解得:x≠2,故选:A.9.(2023春•武清区校级期末)计算﹣的结果是()A.B.C.x﹣y D.1【答案】B【解答】解:﹣==.故答案为:B.10.(2023春•东海县期末)根据分式的基本性质,分式可变形为()A.B.C.D.【答案】C【解答】解:=﹣,故选:C.11.(2023秋•莱州市期中)计算的结果是﹣x.【答案】﹣x.【解答】解:÷=•(﹣)=﹣x,故答案为:﹣x.12.(2023秋•汉寿县期中)学校倡导全校师生开展“语文阅读”活动,小亮每天坚持读书.原计划用a天读完b页的书,如果要提前m天读完,那么平均每天比原计划要多读的页数为(用含a、b、m的最简分式表示).【答案】.【解答】解:由题意得:平均每天比原计划要多读的页数为:﹣=﹣=,故答案为:.13.(2023春•宿豫区期中)计算=1.【答案】1.【解答】解:===1,故答案为:1.14.(2023•广州)已知a>3,代数式:A=2a2﹣8,B=3a2+6a,C=a3﹣4a2+4a.(1)因式分解A;(2)在A,B,C中任选两个代数式,分别作为分子、分母,组成一个分式,并化简该分式.【答案】(1)2a2﹣8=2(a+2)(a﹣2);(2)..【解答】解:(1)2a2﹣8=2(a2﹣4)=2(a+2)(a﹣2);(2)选A,B两个代数式,分别作为分子、分母,组成一个分式(答案不唯一),==.15.(2023秋•思明区校级期中)先化简,再求值:(),其中.【答案】,.【解答】解:原式=÷(﹣)=÷=•=,当x=﹣1时,原式==.16.(2023秋•长沙期中)先化简,再求值:,其中x=5.【答案】,.【解答】解:原式=(﹣)•=•=,当x=5时,原式==.17.(2023•盐城一模)先化简,再求值:,其中x=4.【答案】见试题解答内容【解答】解:原式=(+)•=•=•=x﹣1,当x=4时,原式=4﹣1=3.18.(2022秋•廉江市期末)先化简(﹣x)÷,再从﹣1,0,1中选择合适的x值代入求值.【答案】﹣,0.【解答】解:原式=(﹣)•=﹣•=﹣,∵(x+1)(x﹣1)≠0,∴x≠±1,当x=0时,原式=﹣=0.1.(2023秋•西城区校级期中)假设每个人做某项工作的工作效率相同,m个人共同做该项工作,d天可以完成若增加r个人,则完成该项工作需要()天.A.d+y B.d﹣r C.D.【答案】C【解答】解:工作总量=md,增加r个人后完成该项工作需要的天数=,故选:C.2.(2023秋•长安区期中)若a=2b,在如图的数轴上标注了四段,则表示的点落在()A.段①B.段②C.段③D.段④【答案】C【解答】解:∵a=2b,∴=====,∴表示的点落在段③,故选:C.3.(2023秋•东城区校级期中)若x2﹣x﹣1=0,则的值是()A.3B.2C.1D.4【答案】A【解答】解:∵x2﹣x﹣1=0,∴x2﹣1=x,∴x﹣=1,∴(x﹣)2=1,∴x2﹣2+=1,∴x2+=3,故选:A.4.(2023秋•鼓楼区校级期中)对于正数x,规定,例如,,则=()A.198B.199C.200D.【答案】B【解答】解:∵f(1)==1,f(1)+f(1)=2,f(2)==,f()==,f(2)+f()=2,f(3)==,f()==,f(3)+f()=2,…f(100)==,f()==,f(100)+f()=2,∴=2×100﹣1=199.故选:B.5.(2023秋•延庆区期中)当x分别取﹣2023,﹣2022,﹣2021,…,﹣2,﹣1,0,1,,,…,,,时,计算分式的值,再将所得结果相加,其和等于()A.﹣1B.1C.0D.2023【答案】A【解答】解:当x=﹣a和时,==0,当x=0时,,则所求的和为0+0+0+⋯+0+(﹣1)=﹣1,故选:A.6.(2022秋•永川区期末)若分式,则分式的值等于()A.﹣B.C.﹣D.【答案】B【解答】解:整理已知条件得y﹣x=2xy;∴x﹣y=﹣2xy将x﹣y=﹣2xy整体代入分式得====.故选:B.7.(2023春•铁西区月考)某块稻田a公顷,甲收割完这块稻田需b小时,乙比甲多用0.3小时就能收割完这块稻田,两人一起收割完这块稻田需要的时间是()A.B.C.D.【答案】B【解答】解:乙收割完这块麦田需要的时间是(b+0.3)小时,甲的工作效率是公顷/时,乙的工作效率是公顷/时.故两人一起收割完这块麦田需要的工作时间为=(小时).故选:B.8.(2023春•临汾月考)相机成像的原理公式为,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离.下列用f,u表示v正确的是()A.B.C.D.【答案】D【解答】解:∵,去分母得:uv=fv+fu,∴uv﹣fv=fu,∴(u﹣f)v=fu,∵u≠f,∴u﹣f≠0,∴.故选:D.9.(2023•内江)对于正数x,规定,例如:f(2)=,f()=,f(3)=,f()=,计算:f()+f()+f()+…+f()+f()+f(1)+f(2)+f(3)+…+f(99)+f(100)+f(101)=()A.199B.200C.201D.202【答案】C【解答】解:∵f(1)==1,f(2)=,f()=,f(3)=,f()=,f(4)==,f()==,…,f(101)==,f()==,∴f(2)+f()=+=2,f(3)+f()=+=2,f(4)+f()=+=2,…,f(101)+f()=+=2,f()+f()+f()+…+f()+f()+f(1)+f(2)+f(3)+…+f(99)+f(100)+f(101)=2×100+1=201.故选:C.10.(2023春•灵丘县期中)观察下列等式:=1﹣,=﹣,=﹣,…=﹣将以上等式相加得到+++…+=1﹣.用上述方法计算:+++…+其结果为()A.B.C.D.【答案】A【解答】解:由上式可知+++…+=(1﹣)=.故选A.11.(2023秋•顺德区校级月考)先阅读并填空,再解答问题.我们知道,(1)仿写:=,=,=.(2)直接写出结果:=.利用上述式子中的规律计算:(3);(4).【答案】(1),;;(2);(3);(4).【解答】解:(1),=;=,故答案为:,;;(2)原式=1﹣+++...++=1﹣=;故答案为:;(3)==1﹣+﹣+﹣+⋯⋯+=1﹣=;(2)原式=×()+×()+×()+...+×()=()==.12.(2023秋•株洲期中)阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数.如:.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如,这样的分式就是假分式;,这样的分式就是真分式.类似地,假分式也可以化为带分式(即:整式与真分式的和的形式).如:,;解决下列问题:(1)分式是真分式(填“真”或“假”);(2)将假分式化为带分式;(3)如果x为整数,分式的值为整数,求所有符合条件的x的值.【答案】(1)真;(2)x﹣2+;(3)﹣1或﹣3或11或﹣15.【解答】解:(1)分式是真分式;故答案为:真;(2);(3)原式=,∵分式的值为整数,∴x+2=±1或±13,∴x=﹣1或﹣3或11或﹣15.13.(2023秋•涟源市月考)已知,求的值.解:由已知可得x≠0,则,即x+.∵=(x+)2﹣2=32﹣2=7,∴.上面材料中的解法叫做“倒数法”.请你利用“倒数法”解下面的题目:(1)求,求的值;(2)已知,求的值;(3)已知,,,求的值.【答案】(1);(2)24;(3).【解答】解:(1)由,知x≠0,∴.∴,x•=1.∵=x2+=(x﹣)2+2=42+2=18.∴=.(2)由=,知x≠0,则=2.∴x﹣3+=2.∴x+=5,x•=1.∵=x2+1+=(x+)2﹣2+1=52﹣1=24.∴=.(3)由,,,知x≠0,y≠0,z≠0.则=,=,y+zyz=1,∴+=,+=,+=1.∴2(++)=++1=.∴++=.∵=++=,∴=.14.(2022秋•兴隆县期末)设.(1)化简M;(2)当a=3时,记M的值为f(3),当a=4时,记M的值为f(4).①求证:;②利用①的结论,求f(3)+f(4)+…+f(11)的值;③解分式方程.【答案】(1);(2)①见解析,②,③x=15.【解答】解:(1)=====;(2)①证明:;②f(3)+f(4)+⋅⋅⋅+f(11)====;③由②可知该方程为,方程两边同时乘(x+1)(x﹣1),得:,整理,得:,解得:x=15,经检验x=15是原方程的解,∴原分式方程的解为x=15.15.(2023春•蜀山区校级月考)【阅读理解】对一个较为复杂的分式,若分子次数比分母大,则该分式可以拆分成整式与分式和的形式,例如将拆分成整式与分式:方法一:原式===x+1+2﹣=x+3﹣;方法二:设x+1=t,则x=t﹣1,则原式==.根据上述方法,解决下列问题:(1)将分式拆分成一个整式与一个分式和的形式,得=;(2)任选上述一种方法,将拆分成整式与分式和的形式;(3)已知分式与x的值都是整数,求x的值.【答案】(1);(2);(3)﹣35或43或﹣9或17或1或7或3或5.【解答】解:(1)由题知,,故答案为:.(2)选择方法一:原式==.选择方法二:设x﹣1=t,则x=t+1,则原式=====.(3)由题知,原式====.又此分式与x的值都是整数,即x﹣4是39的因数,当x﹣4=±1,即x=3或5时,原分式的值为整数;当x﹣4=±3,即x=1或7时,原分式的值为整数;当x﹣4=±13,即x=﹣9或17时,原分式的值为整数;当x﹣4=±39,即x=﹣35或43时,原分式的值为整数;综上所述:x的值为:﹣35或43或﹣9或17或1或7或3或5时,原分式的值为整数.16.(2023春•兰州期末)阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可以化为带分数,如:.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如,这样的分式就是假分式;再如:这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:.解决下列问题:(1)分式是真分式(填“真分式”或“假分式”);(2)将假分式化为整式与真分式的和的形式:=2+.若假分式的值为正整数,则整数a的值为1,0,2,﹣1;(3)将假分式化为带分式(写出完整过程).【答案】(1)真分式;(2)2+;1,2,﹣1;(3)x﹣1﹣.【解答】解:(1)由题意得:分式是真分式,故答案为:真分式;(2)==2+,当2+的值为正整数时,2a﹣1=1或±3,∴a=1,2,﹣1;故答案为:2+;1,2,﹣1;(3)原式===x﹣1﹣.1.(2023•湖州)若分式的值为0,则x的值是()A.1B.0C.﹣1D.﹣3【答案】A【解答】解:∵分式的值为0,∴x﹣1=0,且3x+1≠0,解得:x=1,故选:A.2.(2023•天津)计算的结果等于()A.﹣1B.x﹣1C.D.【答案】C【解答】解:====,故选:C.3.(2023•镇江)使分式有意义的x的取值范围是x≠5.【答案】x≠5.【解答】解:当x﹣5≠0时,分式有意义,解得x≠5,故答案为:x≠5.4.(2023•上海)化简:﹣的结果为2.【答案】2.【解答】解:原式===2,故答案为:2.5.(2023•安徽)先化简,再求值:,其中x=.【答案】x+1,.【解答】解:原式==x+1,当x=﹣1时,原式=﹣1+1=.6.(2023•广安)先化简(﹣a+1)÷,再从不等式﹣2<a<3中选择一个适当的整数,代入求值.【答案】;﹣1.【解答】解:(﹣a+1)÷=•=.∵﹣2<a<3且a≠±1,∴a=0符合题意.当a=0时,原式==﹣1.7.(2023•淮安)先化简,再求值:÷(1+),其中a=+1.【答案】,.【解答】解:原式=÷(+)=÷=•=,当a=+1时,原式==.8.(2023•朝阳)先化简,再求值:(+)÷,其中x=3.【答案】,1.【解答】解:原式=[+]•=•=,当x=3时,原式==1.。
人教版初中数学分式知识点总复习附答案解析

人教版初中数学分式知识点总复习附答案解析一、选择题1.下列计算正确的是()A.2236a ab b⎛⎫=⎪⎝⎭B.1a ba b b a-=--C.112a b a b+=+D.1x yx y--=-+【答案】D【解析】【分析】根据分式的乘方、分式的加减运算法则及分式的性质逐一判断即可得答案.【详解】A.22222()3(3)9a a ab b b==,故该选项计算错误,不符合题意,B.a b a b a ba b b a a b a b a b+-=+=-----,故该选项计算错误,不符合题意,C.11b a a ba b ab ab ab++=+=,故该选项计算错误,不符合题意,D.()1x y x yx y x y---+==-++,故该选项计算正确,符合题意,故选:D.【点睛】本题考查分式的运算,分式的乘方,要把分式的分子、分母分别乘方;同分母分式相加减,分母不变,分子相加减;异分母分式相加减,先通分,变为同分母的分式,再加减;熟练掌握分式的运算法则是解题关键.2.下列运算中,不正确的是()A.a b b aa b b a--=++B.1a ba b--=-+C.0.55100.20.323a b a ba b a b++=--D.()()221a bb a-=-【答案】A【解析】【分析】根据分式的基本性质分别计算即可求解.【详解】解:A. a b b aa b b a--=-++,故错误.B、C、D正确.【点睛】此题主要考查分式的基本性质,熟练利用分式的基本性质进行约分是解题关键.3.已知11m n -=1,则代数式222m mn n m mn n --+-的值为( ) A .3B .1C .﹣1D .﹣3【答案】D【解析】【分析】 由11m n -=1利用分式的加减运算法则得出m-n=-mn ,代入原式=222m mn n m mn n--+-计算可得. 【详解】 ∵11m n -=1, ∴n m mn mn -=1, 则n m mn-=1, ∴mn=n-m ,即m-n=-mn ,则原式=()22m n mn m n mn---+=22mn mn mn mn ---+=3mn mn -=-3, 故选D .【点睛】 本题主要考查分式的加减法,解题的关键是掌握分式的加减运算法则和整体代入思想的运用.4.若(x ﹣1)0=1成立,则x 的取值范围是( )A .x =﹣1B .x =1C .x≠0D .x≠1【答案】D【解析】试题解析:由题意可知:x-1≠0,x≠1故选D.5.在等式[]209()a a a ⋅-⋅=中,“[]”内的代数式为( )A .6aB .()7a -C .6a -D .7a【答案】D【分析】首先利用零指数幂性质将原式化简为[]29a a ⋅=,由此利用同底数幂的乘除法法则进一步进行分析即可得出答案.【详解】()01a -=Q ,则原式化简为:[]29a a ⋅=,∴[]927a a -==,故选:D .【点睛】本题主要考查了零指数幂的性质与同底数幂的乘除法运算,熟练掌握相关概念是解题关键.6.在下列四个实数中,最大的数是( )A .B .0C .12-D .13【答案】C【解析】【分析】根据实数的大小比较法则即可得.【详解】 1122-=则四个实数的大小关系为11023-<<< 因此,最大的数是12-故选:C .【点睛】本题考查了实数的大小比较法则,掌握大小比较法则是解题关键.7.若化简22121b a b b a a a -⎛⎫-÷ ⎪+++⎝⎭W 的结果为1a a -,则“W ”是( ) A .a - B .b - C .a D .b【答案】D【解析】【分析】根据题意列出算式,然后利用分式的混合运算法则进行计算.【详解】解:由题意得:()()()()222111=1211111111b a a b a b a b b a b a b ab b a a a a a a a a a a W +-+--⋅=-⋅=+==+++-+-++++,故选:D .【点睛】本题考查了分式的混合运算,熟练掌握运算法则是解题的关键.8.如果2220m m +-=,那么代数式2442m m m m m +⎛⎫+⋅ ⎪+⎝⎭的值是()n n A .2-B .1-C .2D .3【答案】C【解析】 分析:先把括号内通分,再把分子分解后约分得到原式22m m =+,然后利用2220m m +-=进行整体代入计算. 详解:原式2222244(2)(2)222m m m m m m m m m m m m m +++=⋅=⋅=+=+++, ∵2220m m +-=,∴222m m ,+= ∴原式=2.故选C.点睛:考查分式的混合运算,掌握运算法则是解题的关键.注意整体代入法的应用.9.下列运算中,正确的是( )A .2+=B .632x x x ÷=C .122-=-D .325a a a ⋅= 【答案】D【解析】【分析】根据实数的加法对A 进行判断;根据同底数幂的乘法对B 进行判断;根据负整数指数幂的意义对C 进行判断;根据同底数幂的除法对D 进行判断.【详解】解:A 、2不能合并,所以A 选项错误;B 、x 6÷x 3=x 3,所以B 选项错误;C 、2-1=12,所以C 选项错误; D 、a 3•a 2=a 5,所以D 选项正确.故选:D .【点睛】此题考查实数的运算,负整数指数幂,同底数幂的乘法与除法,解题关键在于掌握先算乘方,再算乘除,然后进行加减运算;有括号先算括号.10.测得某人一根头发的直径约为0.000 071 5米,该数用科学记数法可表示为( ) A .0.715×104B .0.715×10﹣4C .7.15×105D .7.15×10﹣5【答案】D【解析】11.计算21133x x x ⎛⎫-•⎪+⎝⎭的结果是( ) A .13x x - B .13x x -- C .13x x + D .13x x+- 【答案】A【解析】【分析】先计算括号内的运算,然后根据分式乘法的运算法则进行计算,即可得到答案.【详解】 解:21133x x x ⎛⎫-• ⎪+⎝⎭ =22133x x x x ⎛⎫-• ⎪+⎝⎭=2(1)(1)3(1)x x x x x +-•+ =13x x-; 故选:A .【点睛】本题考查了分式的化简,以及分式的混合运算,解题的关键是熟练掌握运算法则进行计算.12.0000005=5×10-7故答案为:B.【点睛】本题考查的知识点是科学计数法,解题的关键是熟练的掌握科学计数法.13.056用科学记数法表示为:0.056=-25.610⨯,故选B.14.下列各分式中,是最简分式的是( ).A .22x y x y++ B .22x y x y -+ C .2x x xy + D .2xy y 【答案】A【解析】【分析】 根据定义进行判断即可.【详解】解:A 、22x y x y++分子、分母不含公因式,是最简分式; B 、22x y x y-+=()()x y x y x y +-+=x -y ,能约分,不是最简分式; C 、2x x xy+=(1)x x xy +=1x y +,能约分,不是最简分式; D 、2xy y =x y,能约分,不是最简分式. 故选A .【点睛】本题考查分式的化简,最简分式的标准是分子,分母中不含有公因式,不能再约分,判断的方法是把分子、分母分解因式,然后对每一选项进行整理,即可得出答案.15.下列各式中,正确的是( )A .1a b b ab b++= B .()222x y x y x y x y --=++ C .23193x x x -=-- D .22x y x y -++=- 【答案】B【解析】【分析】根据分式的基本性质分别进行化简即可.【详解】解:A 、1b a+ab =b ab+ ,错误; B 、222x y x y =x y (x y )--++ ,正确;C 、2x 31=x 3x 9-+- ,错误; D 、x y x y =22-+-- ,错误. 故选:B .【点睛】本题主要考察了分式的基本性质,分式运算时要同时乘除和熟练应用约分是解题的关键.16.计算211a a a ---的正确结果是( ) A .11a -- B .11a - C .211a a --- D .211a a -- 【答案】B【解析】【分析】 先将后两项结合起来,然后再化成同分母分式,按照同分母分式加减的法则计算就可以了.【详解】 原式()211a a a =-+- 22111a a a a -=--- 11a =-. 故选B .【点睛】 本题考查分式的通分和分式的约分的运用,解题关键在于在解答的过程中注意符号的运用及平方差公式的运用.17.一种微生物的直径约为0.0000027米,用科学计数法表示为( )A .62.710-⨯B .72.710-⨯C .62.710-⨯D .72.710⨯【答案】A【解析】【分析】绝对值小于1的正数科学记数法所使用的是负指数幂,指数由原数左边起第一个不为0的数字前面的0的个数所决定.【详解】解:0.0000027的左边第一个不为0的数字2的前面有6个0,所以指数为-6,由科学记数法的定义得到答案为62.710-⨯.故选A.【点睛】本题考查了绝对值小于1的正数科学记数法表示,一般形式为10n a -⨯.18.若x 取整数,使分式6321x x +-的值为整数的x 值有( ) A .2个B .4个C .6个D .8个 【答案】B【解析】【分析】 把分式转化为6321x +-,即可转化为讨论621x -的整数值有几个的问题. 【详解】 解:6363663212121x x x x x +-+==+---, 当2x−1=±6或±3或±2或±1时,621x -是整数,即原式是整数, 当2x−1=±6或±2时,x 的值不是整数,当2x−1=±3或±1时满足条件, 故使分式6321x x +-的值为整数的x 值有4个, 故选:B .【点睛】 本题主要考查了分式的性质,把原式化简为6321x +-的形式是解决本题的关键.19.化简2x xy y x y x---=( ) A .﹣xB .y ﹣xC .x ﹣yD .﹣x ﹣y【答案】A【解析】【分析】根据分式的运算法则即可求出答案.【详解】 原式=()2x x y x xy x y x y x--==---, 故选A .【点睛】本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.20.若ba b-=14,则ab的值为()A.5 B.15C.3 D.13【答案】A 【解析】因为ba b-=14,所以4b=a-b.,解得a=5b,所以ab=55bb=.故选A.。
人教版初中八年级数学上册第十五章《分式》知识点(含答案解析)(1)

一、选择题1.使分式21xx -有意义的x 的取值范围是( )A .x ≠1B .x ≠0C .x ≠±1D .x 为任意实数2.若关于x 的一元一次不等式组()()1112232321x x x a x ⎧-≤-⎪⎨⎪-≥-⎩恰有3个整数解,且使关于y 的分式方程3133y ayy y++=--有正整数解,则所有满足条件的整数a 的值之和是( ) A .4B .5C .6D .33.若关于x 的分式方程3211m x x =---有非负实数解,且关于x 的不等式组102x x m +≥⎧⎨+≤⎩有解,则满足条件的所有整数m 的和为( ) A .9-B .8-C .7-D .6-4.如果关于x 的分式方程6312233ax x x x--++=--有正整数解,且关于y 的不等式组521510yy a -⎧≥-⎪⎨⎪+->⎩至少有两个整数解,则满足条件的整数a 的和为( ) A .2 B .3C .6D .115.已知分式34x x -+的值为0,则x 的值是( ) A .3B .0C .-3D .-46.如图,若x 为正整数,则表示3211327121(1)(1)543x x x x x x x x x--++--÷++++的值的点落在( ).A .段①B .段②C .段③D .段④7.下列各式中,正确的是( )A .22a a b b =B .11a ab b +=+ C .2233a b a ab b= D .232131a ab b ++=--8.已知2340x x --=,则代数式24xx x --的值是( )A .3B .2C .13D .129.若2x 11x x 1+--的值小于3-,则x 的取值范围为( ) A .x 4>- B .x 4<-C .x 2>D .x 2<10.若分式()22222x y x y a x a yax ay+-÷-+的值等于5,则a 的值是( )A .5B .-5C .15D .15-11.2222x y x y x y x y -+÷+-的结果是( ) A .222()x y x y ++B .222()x y x y +-C .222()x y x y -+D .222()x y x y ++12.020*******)(0.125)8+⨯的结果是( )A B 2C .2D .013.下列各式中,无论x 取何值,分式都有意义的是( ). A .132x - B .213x + C .231x x+ D .21xx + 14.当1x 0-<<时, 1x -,0x ,2x 的大小顺序是( ) A .102x x x -<< B .012x x x -<<C .021x x x -<<D .120x x x -<<15.计算a ba b a÷⨯的结果是() A .aB .2aC .2b aD .21a二、填空题16.已知5a b +=,6ab =,b aa b+=______. 17.已知3m n +=.则分式222m n m n n m m ⎛⎫+--÷- ⎪⎝⎭的值是_________. 18.已知5,3a b ab -==,则b aa b+的值是__________. 19.新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店抓住商机购进甲、乙、丙三种口罩进行销售.已知销售每件甲种口罩的利润率为30%,每件乙种口罩的利润率为20%,每件丙种口罩的利润率为5%.当售出的甲、乙、丙口罩件数之比为1:3:2时,药店得到的总利润率为20%;当售出的甲、乙、丙口罩件数之比为3:2:2时,药店得到的总利润率为24%.因丙种口罩利润较低,现药店准备只购进甲、乙两种口罩进行销售,若该药店想要获得的总利润率为28%,则该药店应购进甲、乙两种口罩的数量之比是______.20.某班在“世界读书日”当天开展了图书交换活动,第一组同学共带图书24本,第二组同学共带图书27本.已知第一组同学比第二组同学平均每人多带1本图书,第二组人数是第一组人数的1.5倍,则第一组的人数为_________人.21.某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品.甲型机器人比乙型机器人每小时多搬运10kg ,甲型机器人搬运800kg 所用时间与乙型机器人搬运600kg 所用时间相等.问乙型机器人每小时搬运多少kg 产品? 根据以上信息,解答下列问题.(1)小华同学设乙型机器人每小时搬运xkg 产品,可列方程为______小惠同学设甲型机器人搬运800kg 所用时间为y 小时,可列方程为____________. (2)乙型机器人每小时搬运产品_______________kg .22.计算:2120192-⎛⎫-= ⎪⎝⎭______. 23.如图,将形状大小完全相同的“□”按照一定规律摆成下列图形,第1幅图中“□”的个数为1a ,第2幅图中“□”的个数为2a ,第3幅图中“□”的个数为3a ,……,以此类推,若123201922222020n a a a a +++⋅⋅⋅+=(n 为正整数),则(1)5a =________;(2)n 的值为________.24.已知(3)1a a -=,则整数a 的值为______. 25.方程11212x x =+-的解是x =_____. 26.方程22020(1)1x x x ++-=的整数解的个数是_____.三、解答题27.雪梨是石家庄市某地的特色时令水果.雪梨上市后,水果店的老板用2400元购进一批雪梨,很快售完;老板又用3750元购进第二批雪梨,所购件数是第一批的32倍,但进价比第一批每件多了5元.(1)求第一批雪梨每件进价是多少元?(2)老板以每件225元的价格销售第二批雪梨,售出80%后,为了尽快售完,剩下的决定打折促销,要使得第二批雪梨的销售利润为2460元,剩余的雪梨每件售价应该打几折?(利润=售价-进价) 28.计算:(1)化简:()()22n m n m n -++;(2)解分式方程:2132163x x x -=---. 29.分式计算与解方程:(1)21211a a a a ----; (2)121221xx x +=-+. 30.先化简,再求值:22214244x x x x x x x x +--⎛⎫-÷ ⎪--+⎝⎭,其中5x =.。
初二数学上册(人教版)第十五章分式15.1知识点总结含同步练习及答案

x+1 2x + 3 ;(2) . 2x 3x − 5 x+1 解:(1) 要使 有意义,则分母 2x ≠ 0,即 x ≠ 0; 2x 2x + 3 5 (2) 要使 有意义,则分母 3x − 5 ≠ 0,即 x ≠ . 3x − 5 3 x+2 的值为 0 ? 2x − 3 x+2 解: = 0 ,即 x + 2 = 0 , 2x − 3 解得 x = −2 且 2x − 3 ≠ 0 . 所以当 x = −2 时,该分式值为 0 .
① 在分式 分式的基本性质 分式的分子与分母同乘(或除以)一个不等于 0 的整式,分式的值不变,即
约分 约去分式的分子和分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分(reduction of a fraction). 一个分式的分子与分母没有公因式时,叫做最简分式.化简分式时,通常要使结果成为最简分式 或者整式. 通分 把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分(reduction of fractions to a common denominator). 各分式分母中的系数的最小公倍数与所有字母(或因式)的最高次幂的积,叫做最简公分母.
当 x 取何值时,分式
5xy . 20y 2 5xy 5y ⋅ x x 解: . = = 2 5y ⋅ 4y 4y 20y
化简
2a c x , , . b ab 2ab 解:最简公母为 2ab . 2a 4a2 , = b 2ab c 2c , = ab 2ab x x . = 2ab 2ab
通分
四、课后作业
1. 使分式
(查看更多本章节同步练习题,请到快乐学)
2 有意义的 x 的取值范围是 ( x−2 A.x ⩽ 2 B.x ⩽ −2
人教版初中数学分式知识点总复习有答案解析

人教版初中数学分式知识点总复习有答案解析一、选择题1.下列各式从左到右变形正确的是( )A .13(1)223x y x y ++=++ B .0.20.03230.40.0545a b a d c d c d --=++ C .a b b a b c c b--=-- D .22a b a b c d c d --=++ 【答案】C【解析】【分析】依据分式的基本性质进行变化,分子分母上同时乘以或除以同一个非0的数或式子,分式的值不变.【详解】 A 、该式子不是方程,不能去分母,故A 错误;B 、分式中的分子、分母的各项没有同时扩大相同的倍数,故B 错误;C 、a-b b-a =d-c c-d故C 正确; D 、分式中的分子、分母的各项没有同时除以2,故D 错误.故选C .【点睛】本题考查了分式的基本性质,解题的关键是熟练运用性质.2.下列计算正确的是( ).A 2=-B .2(3)9--=C .0( 3.14)0x -=D .2019(1)|4|5---=- 【答案】D【解析】【分析】直接利用二次根式的性质以及负指数幂的性质、零指数幂的性质分别化简得出答案.【详解】A 2=,故此选项错误;B 、(-3)-2=19,故此选项错误; C 、(x-3.14)0=1,故此选项错误;D 、(-1)2019-|-4|=-5,正确.故选:D .【点睛】此题考查二次根式的性质以及负指数幂的性质、零指数幂的性质,正确化简各数是解题关键.3.若a=-0.22,b=-2-2,c=(-12)-2,d=(-12)0,则它们的大小关系是()A.a<c<b<d B.b<a<d<c C.a<b<d<c D.b<a<c<d【答案】B【解析】【分析】根据正整数指数幂、负整数指数幂以及零次幂的意义分别计算出a,b,c,d的值,再比较大小即可.【详解】∵a=-0.22=-0.04,b=-2-2=14-,c=(-12)-2=4,d=(-12)0=1,-0.25<-0.04<1<4∴b<a<d<c故选B.【点睛】此题主要考查了负整数指数幂,正整数指数幂、零次幂,熟练掌握它们的运算意义是解题的关键.4.若式子2x-有意义,则x的取值范围为().A.x≥2B.x≠2C.x≤2D.x<2【答案】D【解析】【分析】根据被开方式大于且等于零,分母不等于零列式求解即可.【详解】解:∵式子2x-有意义∴2x0 x20-≥⎧⎨-≠⎩∴x<2故选:D【点睛】本题考查了代数式有意义时字母的取值范围,代数式有意义时字母的取值范围一般从几个方面考虑:①当代数式是整式时,字母可取全体实数;②当代数式是分式时,考虑分式的分母不能为0;③当代数式是二次根式时,被开方数为非负数.5.要使分式81x -有意义,x 应满足的条件是( ) A .1x ≠-B .0x ≠C .1x ≠D .2x ≠【答案】C【解析】【分析】 直接利用分式有意义的条件得出答案.【详解】 要使分式81x -有意义, 则x-1≠0,解得:x≠1.故选:C .【点睛】此题考查分式有意义的条件,正确把握分式的定义是解题关键.6.x 的取值范围为( ) A .5x ≠-B .0x >C .5x ≠- 且0x >D .0x ≥【答案】D【解析】【分析】根据分式有意义的条件可得x+5≠0,再根据二次根式有意义的条件可得x≥0,由此即可求得答案.【详解】由题意得:x+5≠0,且x≥0,解得:x≥0,故选D .【点睛】本题考查了分式有意义的条件 二次根式有意义的条件,关键是掌握分式有意义的条件是分母不等于零,二次根式中的被开方数是非负数.7.生物学家发现了一种病毒的长度约为0.00000432毫米.数据0.00000432用科学记数法表示为( )A .0.432×10-5B .4.32×10-6C .4.32×10-7D .43.2×10-7【答案】B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为10n a -⨯,这里1<a <10,指数n 是由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解: 0.00000432=4.32×10-6,故选B .【点睛】本题考查科学记数法.8.数字0.00000005m ,用科学记数法表示为( )m .A .70.510-⨯B .60.510-⨯C .7510-⨯D .8510-⨯ 【答案】D【解析】【分析】科学记数法的表示形式为n a 10⨯的形式,其中1a 10≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值1>时,n 是正数;当原数的绝对值1<时,n 是负数.【详解】将0.00000005用科学记数法表示为8510-⨯.故选D .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为n a 10⨯的形式,其中1a 10≤<,n 为整数,表示时关键要正确确定a 的值以及n 的值.9.当式子2||323x x x ---的值为零时,x 等于( ) A .4B .﹣3C .﹣1或3D .3或﹣3【答案】B【解析】【分析】根据分式为零,分子等于0,分母不等于0列式进行计算即可得解.【详解】 解:根据题意得,30x -=,解得3x =或3-.又2230x x --≠解得121,3x x ≠-≠,所以,3x =-.故选:B.【点睛】本题考查了分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.10.下列计算正确的是( )A .2236a a b b ⎛⎫= ⎪⎝⎭B .1a b a b b a -=--C .112a b a b +=+D .1x y x y --=-+ 【答案】D【解析】【分析】根据分式的乘方、分式的加减运算法则及分式的性质逐一判断即可得答案.【详解】 A.22222()3(3)9a a a b b b ==,故该选项计算错误,不符合题意, B.a b a b a b a b b a a b a b a b +-=+=-----,故该选项计算错误,不符合题意, C.11b a a b a b ab ab ab ++=+=,故该选项计算错误,不符合题意, D.()1x y x y x y x y---+==-++,故该选项计算正确,符合题意, 故选:D.【点睛】本题考查分式的运算,分式的乘方,要把分式的分子、分母分别乘方;同分母分式相加减,分母不变,分子相加减;异分母分式相加减,先通分,变为同分母的分式,再加减;熟练掌握分式的运算法则是解题关键.11.下列运算中,正确的是( )A .236x x x ⋅=B .333()ab a b =C .33(2)6a a =D .239-=- 【答案】B【解析】【分析】分别根据同底数幂的乘法法则,积的乘方法则以及负整数指数幂的运算法则逐一判断即可.【详解】x 2•x 3=x 5,故选项A 不合题意;(ab )3=a 3b 3,故选项B 符合题意;(2a )3=8a 6,故选项C 不合题意;3−2=19,故选项D 不合题意.故选:B.【点睛】此题考查同底数幂的乘法,幂的乘方与积的乘方以及负整数指数幂的计算,熟练掌握幂的运算法则是解题的关键.12.把实数36.1210-⨯用小数表示为()A.0.0612 B.6120 C.0.00612 D.612000【答案】C【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】13.计算11-+xx x的结果是()A.2xx+B.2xC.12D.1【答案】D 【解析】原式=11xx-+=xx=1,故选D.【点睛】本题考查了同分母分式的加减法,熟记法则是解题的关键.14.世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为()A.5.6×10﹣1B.5.6×10﹣2C.5.6×10﹣3D.0.56×10﹣1【答案】B【解析】【详解】15.下列各数中最小的是()A.22-B.C.23-D【答案】A【解析】【分析】先根据有理数的乘方、算术平方根、立方根、负整数指数幂进行计算,再比较数的大小,即可得出选项.【详解】解:224-=-,2139-=2=-, 14329-<-<-<Q , ∴最小的数是4-,故选:A .【点睛】本题考查了实数的大小比较法则,能熟记实数的大小比较法则的内容是解此题的关键.16.下列方程中,有实数根的方程是( )A .x 4+16=0B .x 2+2x +3=0C .2402x x -=-D 0= 【答案】C【解析】【分析】利用在实数范围内,一个数的偶数次幂不能为负数对A 进行判断;利用判别式的意义对B 进行判断;利用分子为0且分母不为0对C 进行判断;利用非负数的性质对D 进行判断.【详解】解:A 、因为x 4=﹣16<0,所以原方程没有实数解,所以A 选项错误;B 、因为△=22﹣4×3=﹣8<0,所以原方程没有实数解,所以B 选项错误;C 、x 2﹣4=0且x ﹣2≠0,解得x =﹣2,所以C 选项正确;D 、由于x =0且x ﹣1=0,所以原方程无解,所以D 选项错误.故选:C .【点睛】此题考查判别式的意义,分式有意义的条件,二次根式,解题关键在于掌握运算法则17.下面是一名学生所做的4道练习题:①224-=;②336a a a +=;③44144mm -=;④()3236xy x y =。
人教版初中八年级数学上册第十五章《分式》知识点复习(含答案解析)(1)

一、选择题1.化简221x x x ++÷(1-11x +)的结果是( ) A .11x + B .11x - C .x+1 D .x-12.下列命题中,属于真命题的是( )A .如果0ab =,那么0a =B .253x x x -是最简分式C .直角三角形的两个锐角互余D .不是对顶角的两个角不相等 3.若关于x 的方程121m x -=-的解为正数,则m 的取值范围是( ) A .1m >-B .1m ≠C .1mD .1m >-且1m ≠ 4.若关于x 的方程1044m x x x --=--无解,则m 的值是( ) A .2-B .2C .3-D .3 5.PM2.5是大气压中直径小于或等于0.0000025m 的颗粒物,将0.0000025用科学记数法表示为( )A .50.2510-⨯B .60.2510-⨯C .72.510-⨯D .62.510-⨯ 6.若a 与b 互为相反数,则22201920212020a b ab+=( ) A .-2020 B .-2 C .1 D .27.计算2m m 1m m-1+-的结果是( ) A .m B .-m C .m +1 D .m -18.大爱无疆,在爆发新冠病毒疫情后,甲,乙两家单位分别组织了员工捐款.已知甲单位捐款7500元,乙单位捐款9800元,甲单位捐款人数比乙单位少10人,且甲单位人均捐款额比乙单位多20元,若设甲单位的捐款人数为x ,则可列方程为( )A .7500980020x x 10-=- B .9800750020x 10x -=-C .7500980020x x 10-=+D .9800750020x 10x-=+ 9.小红用15元买售价相同的软面笔记本,小丽用24元买售价相同的硬面笔记本(两人的钱恰好用完)已知每本硬面笔记本比软面笔记本贵3元,且小红和小丽买到相同数量的笔记本.设硬面笔记本每本售价为x 元,根据题意可列出的方程为( )A .1524x x 3=+B .1524x x 3=-C .1524x 3x =+D .1524x 3x=- 10.若数a 关于x 的不等式组()()11223321x x x a x ⎧-≤-⎪⎨⎪-≥-+⎩恰有三个整数解,且使关于y 的分式方程13y 2a 2y 11y--=---的解为正数,则所有满足条件的整数a 的值之和是( ) A .2B .3C .4D .5 11.若数a 使关于x 的分式方程2311a x x+=--的解为非负数,且使关于y 的不等式组213202y y y a +⎧->⎪⎪⎨-⎪≤⎪⎩的解集为2y <-,则符合条件的所有整数a 的个数为( ) A .5B .6C .7D .8 12.计算23211x x x x +-++的结果为( ) A .1 B .3 C .31x + D .31x x ++ 13.下列计算正确的是( )A .1112a a a+= B .2211()()a b b a +--=0 C .m n a -﹣m n a+=0 D .11a b b a +--=0 14.下列各式中错误的是( ) A .2c d c d c d c d d a a a a -+-----== B .5212525a a a +=++ C .1x y x y y x-=--- D .2211(1)(1)1x x x x -=--- 15.化简214a 2a 4---的结果为( ) A .1a 2+ B .a 2+ C .1a 2- D .a 2-二、填空题16.计算2216816a a a -++÷428a a -+=__________. 17.对于两个不相等的实数a ,b ,我们规定符号{}min ,a b 表示a ,b 中的较小的值,如{}min 2,42=.(1){}min 2,3--=__________________.(2)方程{}3min 2,322x x x --=---的解为_________________. (3)方程131min ,2222x x x x -⎧⎫=-⎨⎬---⎩⎭的解为_________________. 18.若关于x 的分式方程233x m x x=---的解为正数,则常数m 的取值范围是______. 19.已知关于x 的分式方程239133x mx x x ---=--无解,则m 的值为______. 20.若分式方程13322a x x x--=--有增根,则a 的值是________. 21.已知2510m m -+=,则22125m m m -+=____. 22.关于x 的分式方程3122m x x -=--无解,则m 的值为_____. 23.化简分式:2121211a a a a +⎛⎫÷+= ⎪-+-⎝⎭_________. 24.化简:(﹣2y x)3÷(223⋅y x x y )=_______________. 25.若分式2221x x --的值为正整数,则x =_____________. 26.方程11212x x =+-的解是x =_____. 三、解答题27.已知点()0,A y 在y 轴正半轴上,以OA 为边作等边OAB ,其中y 是方程31222y +-31y =-的解. (1)求点A 的坐标;(2)如图1,点P 在x 轴正半轴上,以AP 为边在第一象限内作等边APQ ,连QB 并延长交x 轴于点C ,求证:OC BC =;(3)如图2,若点M 为y 轴正半轴上一动点,点M 在点A 的上边,连MB ,以MB 为边在第一象限内作等边MBN △,连NA 并延长交x 轴于点D ,当点M 运动时,DN AM -的值是否发生变化?若不变,求出其值;若变化,求出其变化的范围.28.新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有7人不能到厂工作,为了应对疫情,在每个工人每小时完成的工作量不变的前提下,已复工的工人加班生产,每天的工作时间由原来8个小时增加到10个小时.该公司原来每天能生产防护服800套,现在每天能生产防护服650套.(1)求该公司原来生产防护服的工人有多少人?(2)复工10天后,未到的7名工人到岗且同时加入了生产,每天生产时间仍然为10小时.为了支援灾区,公司复工后决定生产15500套防护服,问至少还需要多少天才能完成任务?29.鄂州市2020年被评为“全国文明城市”.创文期间,甲、乙两个工程队共同参与某段道路改造工程.如果甲工程队单独施工,恰好如期完成;如果甲、乙两工程队先共同施工10天,剩下的任务由乙工程队单独施工,也恰好能如期完成;如果乙工程队单独施工,就要超过15天才能完成.(1)求甲、乙两工程队单独完成此项工程各需多少天?(2)若甲工程队单独施工a 天,再由甲、乙两工程队合作______天(用含有a 的代数式表示)可完成此项工程.(3)现在要求甲、乙两个工程队都必须参加这项工程.如果甲工程队每天的施工费用为2万元,乙工程队每天的施工费用为1.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,能使施工费用不超过61.5万元?30.观察下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯. 将以上三个等式左、右两边分别相加得:1111111131122334223344++=-+-+-=⨯⨯⨯ (1)若n 为正整数,猜想并填空:1(1)n n =+______. (2)计算111111223344520202021+++++⨯⨯⨯⨯⨯的结果为______. (3)解分式方程:11122(2)(3)(3)(4)1x x x x x x ++=------.。
最新最新初中数学—分式的知识点总复习有答案解析
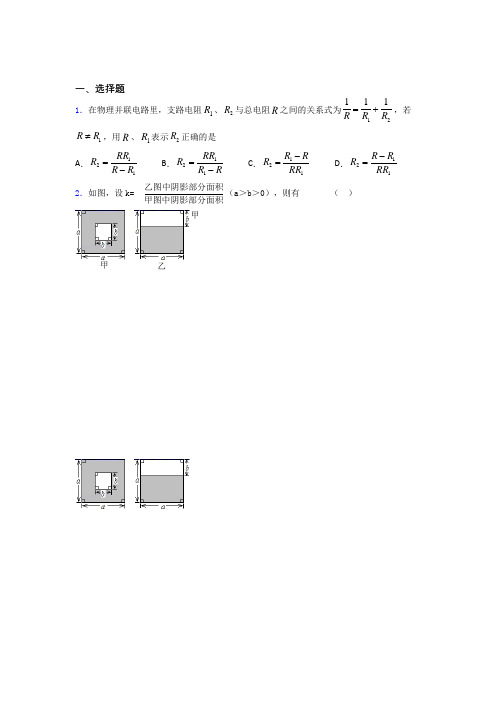
一、选择题1.在物理并联电路里,支路电阻1R 、2R 与总电阻R 之间的关系式为12111R RR =+,若1R R ≠,用R 、1R 表示2R 正确的是A .121RR R R R =- B .121RR R R R=- C .121R RR RR -=D .121R R R RR -=2.如图,设k=甲图中阴影部分面积乙图中阴影部分面积(a >b >0),则有 ( )甲 乙甲(A )k >2 (B )1<k <2 (C )121<<k (D )210<<k 3.若xy y x =+,则yx 11+的值为 ( ) A 、0 B 、1 C 、-1 D 、2 4.下列分式约分正确的是( )A .236a a a =B .1-=-+y x y xC .316222=b a abD .m mn m n m 12=++5.已知,则的值是( )A .B .﹣C .2D .﹣26.化简:(a-2)·22444a a a --+的结果是( )A .a-2B .a +2C . 22-+a aD .22+-a a 7.下列运算正确的是( ) A .(2a 2)3=6a 6 B .-a 2b 2•3a b 3=-3a 2b 5 C . D .乙甲8.分式(a 、b 均为正数),字母的值都扩大为原来的2倍,则分式的值( )A .扩大为原来的2倍B .缩小为原来的C .不变D .缩小为原来的9.若分式23x x --有意义,则x 满足的条件是( ) A .x ≠0 B .x ≠2 C .x ≠3 D .x ≥310.下列算式,计算正确的有( )①10-3=0.0001; ②(0.0001)0=1; ③3a -2=213a; ④(-2)3÷(-2)5=-2-2. A .1个 B .2个 C .3个 D .4个 11.若分式211x x -+的值为零,则x 的值为( ) A .0 B .1C .1-D .±112.在2x ,1()3x y +,3ππ-,5a x -,24x y -中,分式的个数为( ) A .1 B.2 C.3 D .413.如果把分式22a bab+中的a 和b 都扩大了2倍,那么分式的值( ) A .扩大2倍B .不变C .缩小2倍D .缩小4倍14.雾霾已经成为现在生活中不得不面对的重要问题,PM2.5是大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( ) A .2.5×10﹣6B .0.25×10﹣6C .2.5×10﹣5D .0.25×10﹣515.在式子31x - 、2xy π 、2334a b c、2x x 中,分式的个数是( )A .1个B .2个C .3个D .4个16.H7N9禽流感病毒的直径大约是0.000 000 076米,用科学记数法可表示为( )米.A .7.6×10﹣11B .7.6×10﹣8C .7.6×10﹣9D .7.6×10﹣5 17.若分式的值为0,则x 的值为A .B .C .D .不存在18.已知空气的单位体积质量是0.001239g /cm 3,则用科学记数法表示该数为( )g /cm 3. A .1.239×10﹣3 B .1.2×10﹣3C .1.239×10﹣2D .1.239×10﹣419.函数22y x x =+--的自变量x 的取值范围是( ) A .2x ≥B .2x >C .2x ≠D .2x ≤20.(2015秋•郴州校级期中)下列计算正确的是( )A .B .•C .x÷y•D .21.在代数式,,+,,中,分式有( )A .1个B .2个C .3个D .4个 22.式子①,②,③,④中,是分式的是( )A .①② B.③④ C.①③ D.①②③④23.在式子x y 3,πa ,13+x ,31+x ,a a 2中,分式有A .1个B .2个C .3个D .4个24.在函数中,自变量的取值范围是( ) A .>3B .≥3且≠4C .>4D .≥325.下列各式12x y +,52a b a b --,2235a b -,3m ,37xy中,分式共有( )个.A .2B .3C .4D .5【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】试题解析:12111R R R =+, 21111R R R =- 1211R R R RR -=得R 2═11RR R R-. 故选B .2. C解析: C 【解析】试题分析:甲图中阴影部分的面积=22a b -,乙图中阴影部分的面积= ()a a b -,22()1a a b a b k a b a b a b -===--++,∵a >b >0∴0<b a b +<12,∴ 121<<k . 考点:分式的约分. 3.B解析:B 【解析】试题分析:先被求的代数式通分,在根据已知整体带入即可. y x 11+=1==+xyxy xy y x 考点:分式的通分,整体带入.4.D解析:D 【解析】试题分析:A.约分的结果为a3;B.不能进行约分;C.约分的结果为ab3。
初二分式所有知识点总结和常考题提高难题压轴题练习(含答案解析)

初二分式所有知识点总结和常考题知识点:1.分式:形如AB,A B 、是整式,B 中含有字母且B 不等于0的整式叫做分式.其中A 叫做分式的分子,B 叫做分式的分母. 2.分式有意义的条件:分母不等于0. 3.分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变.4.约分:把一个分式的分子和分母的公因式(不为1的数)约去,这种变形称为约分.5.通分:异分母的分式可以化成同分母的分式,这一过程叫做通分.6.最简分式:一个分式的分子和分母没有公因式时,这个分式称为最简分式,约分时,一般将一个分式化为最简分式.7.分式的四则运算:⑴同分母分式加减法则:同分母的分式相加减,分母不变,把分子相加减.用字母表示为:a b a bc c c±±=⑵异分母分式加减法则:异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.用字母表示为: a c ad cb b d bd±±= ⑶分式的乘法法则:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.用字母表示为:a c acb d bd⨯=⑷分式的除法法则:两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘.用字母表示为:a c a d adb d bc bc÷=⨯=⑸分式的乘方法则:分子、分母分别乘方.用字母表示为:nn n a a b b ⎛⎫= ⎪⎝⎭8.整数指数幂:⑴m n m n a a a +⨯=(m n 、是正整数) ⑵()nm mn aa =(m n 、是正整数)⑶()nn n ab a b =(n 是正整数)⑷m n m n a a a -÷=(0a ≠,m n 、是正整数,m n >)⑸nn n a a b b ⎛⎫= ⎪⎝⎭(n 是正整数)⑹1nnaa-=(0a≠,n是正整数)9.分式方程的意义:分母中含有未知数的方程叫做分式方程.10.分式方程的解法:①去分母(方程两边同时乘以最简公分母,将分式方程化为整式方程);②按解整式方程的步骤求出未知数的值;③验根(求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根).常考题:一.选择题(共14小题)1.在式子、、、、、中,分式的个数有()A.2个 B.3个 C.4个 D.5个2.化简的结果是()A.x+1 B.x﹣1 C.﹣x D.x3.如果把分式中的x和y都扩大2倍,则分式的值()A.扩大4倍B.扩大2倍C.不变D.缩小2倍4.把分式方程的两边同时乘以(x﹣2),约去分母,得()A.1﹣(1﹣x)=1 B.1+(1﹣x)=1 C.1﹣(1﹣x)=x﹣2 D.1+(1﹣x)=x﹣25.化简÷(1+)的结果是()A.B. C.D.6.计算的结果为()A.B. C. D.7.已知关于x的分式方程+=1的解是非负数,则m的取值范围是()A.m>2 B.m≥2 C.m≥2且m≠3 D.m>2且m≠38.下列运算正确的是()A.a2•a3=a6 B.()﹣1=﹣2 C.=±4 D.|﹣6|=69.某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为()A.B.C.D.10.货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是()A.B.C.D.11.如图,设k=(a>b>0),则有()A.k>2 B.1<k<2 C.D.12.A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程()A.B.C.+4=9 D.13.计算的结果为()A.1 B.x+1 C. D.14.若分式(A,B为常数),则A,B的值为()A.B.C.D.二.填空题(共13小题)15.计算:=.16.若分式有意义,则实数x的取值范围是.17.分式方程的解x=.18.若代数式的值为零,则x=.19.化简的结果是.20.化简:=.21.计算÷(1﹣)的结果是.22.若关于x的方程=+1无解,则a的值是.23.已知关于x的方程的解是正数,则m的取值范围是.24.a、b为实数,且ab=1,设P=,Q=,则P Q(填“>”、“<”或“=”).25.如果实数x满足x2+2x﹣3=0,那么代数式的值为.26.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,现在平均每天生产台机器.27.杭州到北京的铁路长1487千米.火车的原平均速度为x千米/时,提速后平均速度增加了70千米/时,由杭州到北京的行驶时间缩短了3小时,则可列方程为.三.解答题(共13小题)28.先化简,再求值:,其中.29.先化简代数式,然后选取一个使原式有意义的a值代入求值.30.已知x﹣3y=0,求•(x﹣y)的值.31.解方程:.32.先化简,再求值:,其中x是不等式3x+7>1的负整数解.33.先化简÷(a+1)+,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.34.解分式方程:+=1.35.已知A=﹣(1)化简A;(2)当x满足不等式组,且x为整数时,求A的值.36.甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.(1)甲、乙两队单独完成此项任务需要多少天?(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?37.某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)该商家购进的第一批衬衫是多少件?(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?38.从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.(1)求普通列车的行驶路程;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.39.学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.(1)甲、乙两种图书的单价分别为多少元?(2)若学校计划购买这两种图书共40本,且投入的经费不超过1050元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?40.某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.(1)今年5月份A款汽车每辆售价多少万元?(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a 值应是多少?此时,哪种方案对公司更有利?初二分式所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共14小题)1.(2012春•潜江期末)在式子、、、、、中,分式的个数有()A.2个 B.3个 C.4个 D.5个【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.【解答】解:、、9x+这3个式子的分母中含有字母,因此是分式.其它式子分母中均不含有字母,是整式,而不是分式.故选:B.【点评】本题考查的是分式的定义,在解答此题时要注意分式是形式定义,只要是分母中含有未知数的式子即为分式.2.(2014•南通)化简的结果是()A.x+1 B.x﹣1 C.﹣x D.x【分析】将分母化为同分母,通分,再将分子因式分解,约分.【解答】解:=﹣===x,故选:D.【点评】本题考查了分式的加减运算.分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.3.(2012•岳麓区校级自主招生)如果把分式中的x和y都扩大2倍,则分式的值()A.扩大4倍B.扩大2倍C.不变D.缩小2倍【分析】把分式中的x和y都扩大2倍,分别用2x和2y去代换原分式中的x和y,利用分式的基本性质化简即可.【解答】解:把分式中的x和y都扩大2倍后得:==2•,即分式的值扩大2倍.故选:B.【点评】根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项.4.(2005•扬州)把分式方程的两边同时乘以(x﹣2),约去分母,得()A.1﹣(1﹣x)=1 B.1+(1﹣x)=1 C.1﹣(1﹣x)=x﹣2 D.1+(1﹣x)=x﹣2【分析】分母中x﹣2与2﹣x互为相反数,那么最简公分母为(x﹣2),乘以最简公分母,可以把分式方程转化成整式方程.【解答】解:方程两边都乘(x﹣2),得:1+(1﹣x)=x﹣2.故选:D.【点评】找到最简公分母是解答分式方程的最重要一步;注意单独的一个数也要乘最简公分母;互为相反数的两个数为分母,最简公分母为其中的一个,另一个乘以最简公分母后,结果为﹣1.5.(2013•临沂)化简÷(1+)的结果是()A.B. C.D.【分析】首先对括号内的式子通分相加,然后把除法转化成乘法,进行约分即可.【解答】解:原式=÷=•=.故选A.【点评】本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.6.(2008•黄冈)计算的结果为()A.B. C. D.【分析】先算小括号里的,再把除法统一成乘法,约分化为最简.【解答】解:==,故选A.【点评】分式的四则运算是整式四则运算的进一步发展,在计算时,首先要弄清楚运算顺序,先去括号,再进行分式的乘除.7.(2014•黑龙江)已知关于x的分式方程+=1的解是非负数,则m的取值范围是()A.m>2 B.m≥2 C.m≥2且m≠3 D.m>2且m≠3【分析】分式方程去分母转化为整式方程,求出整式方程的解表示出x,根据方程的解为非负数求出m的范围即可.【解答】解:分式方程去分母得:m﹣3=x﹣1,解得:x=m﹣2,由方程的解为非负数,得到m﹣2≥0,且m﹣2≠1,解得:m≥2且m≠3.故选:C【点评】此题考查了分式方程的解,时刻注意分母不为0这个条件.8.(2009•潍坊)下列运算正确的是()A.a2•a3=a6 B.()﹣1=﹣2 C.=±4 D.|﹣6|=6【分析】幂运算的性质:①同底数的幂相乘,底数不变,指数相加;②一个数的负指数次幂等于这个数的正指数次幂的倒数,算术平方根的概念:一个正数的正的平方根叫它的算术平方根,0的算术平方根是0.绝对值的性质:正数的绝对值等于它本身,负数的绝对值等于它的相反数,0的绝对值是0.【解答】解:A、a2•a3=a5,故A错误;B、()﹣1=2,故B错误;C、=4,故C错误;D、根据负数的绝对值等于它的相反数,故D正确.故选D.【点评】本题涉及知识:负指数为正指数的倒数;任何非0数的0次幂等于1;绝对值的化简;二次根式的化简.9.(2013•本溪)某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为()A.B.C.D.【分析】关键描述语为:“共用了18天完成任务”;等量关系为:采用新技术前用的时间+采用新技术后所用的时间=18.【解答】解:采用新技术前用的时间可表示为:天,采用新技术后所用的时间可表示为:天.方程可表示为:.故选:B.【点评】列方程解应用题的关键步骤在于找相等关系.找到关键描述语,找到等量关系是解决问题的关键.本题要注意采用新技术前后工作量和工作效率的变化.10.(2014•黔南州)货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是()A.B.C.D.【分析】题中等量关系:货车行驶25千米与小车行驶35千米所用时间相同,列出关系式.【解答】解:根据题意,得.故选:C.【点评】理解题意是解答应用题的关键,找出题中的等量关系,列出关系式.11.(2013•杭州)如图,设k=(a>b>0),则有()A.k>2 B.1<k<2 C.D.【分析】分别计算出甲图中阴影部分面积及乙图中阴影部分面积,然后计算比值即可.【解答】解:甲图中阴影部分面积为a2﹣b2,乙图中阴影部分面积为a(a﹣b),则k====1+,∵a>b>0,∴0<<1,∴1<+1<2,∴1<k<2故选B.【点评】本题考查了分式的乘除法,会计算矩形的面积及熟悉分式的运算是解题的关键.12.(2016•本溪一模)A,B两地相距48千米,一艘轮船从A地顺流航行至B 地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程()A.B.C.+4=9 D.【分析】本题的等量关系为:顺流时间+逆流时间=9小时.【解答】解:顺流时间为:;逆流时间为:.所列方程为:+=9.故选A.【点评】未知量是速度,有速度,一定是根据时间来列等量关系的.找到关键描述语,找到等量关系是解决问题的关键.13.(2005•武汉)计算的结果为()A.1 B.x+1 C. D.【分析】先算括号里的通分,再进行因式分解,将除号换为乘号,最后再进行分式间的约分化简.【解答】解:===,故选C.【点评】注意:当整式与分式相加减时,一般可以把整式看作分母为1的分式,与其它分式进行通分运算.14.(2004•十堰)若分式(A,B为常数),则A,B的值为()A.B.C.D.【分析】对等式右边通分加减运算和,再根据对应项系数相等列方程组求解即可.【解答】解:.所以,解得.故选B.【点评】此题考查了分式的减法,比较灵活,需要熟练掌握分式的加减运算.二.填空题(共13小题)15.(2014•陕西)计算:=9.【分析】根据负整数指数幂的运算法则进行计算即可.【解答】解:原式===9.故答案为:9.【点评】本题考查的是负整数指数幂,即负整数指数幂等于该数对应的正整数指数幂的倒数.16.(2014•衢州)若分式有意义,则实数x的取值范围是x≠5.【分析】由于分式的分母不能为0,x﹣5为分母,因此x﹣5≠0,解得x.【解答】解:∵分式有意义,∴x﹣5≠0,即x≠5.故答案为:x≠5.【点评】本题主要考查分式有意义的条件:分式有意义,分母不能为0.17.(2013•梅州)分式方程的解x=1.【分析】本题的最简公分母是x+1,方程两边都乘最简公分母,可把分式方程转换为整式方程求解.结果要检验.【解答】解:方程两边都乘x+1,得2x=x+1,解得x=1.检验:当x=1时,x+1≠0.∴x=1是原方程的解.【点评】(1)解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解.(2)解分式方程一定注意要代入最简公分母验根.18.(2013•临夏州)若代数式的值为零,则x=3.【分析】由题意得=0,解分式方程即可得出答案.【解答】解:由题意得,=0,解得:x=3,经检验的x=3是原方程的根.故答案为:3.【点评】此题考查了分式值为0的条件,属于基础题,注意分式方程需要检验.19.(2013•凉山州)化简的结果是m.【分析】本题需先把(m+1)与括号里的每一项分别进行相乘,再把所得结果相加即可求出答案.【解答】解:=(m+1)﹣1=m故答案为:m.【点评】本题主要考查了分式的混合运算,在解题时要把(m+1)分别进行相乘是解题的关键.20.(2013•衢州)化简:=.【分析】先将x2﹣4分解为(x+2)(x﹣2),然后通分,再进行计算.【解答】解:===.【点评】本题考查了分式的计算和化简.解决这类题关键是把握好通分与约分.分式加减的本质是通分,乘除的本质是约分.21.(2015•黄冈)计算÷(1﹣)的结果是.【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.【解答】解:原式=÷=•=,故答案为:.【点评】此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.22.(2013•绥化)若关于x的方程=+1无解,则a的值是2或1.【分析】把方程去分母得到一个整式方程,把方程的增根x=2代入即可求得a的值.【解答】解:x﹣2=0,解得:x=2.方程去分母,得:ax=4+x﹣2,即(a﹣1)x=2当a﹣1≠0时,把x=2代入方程得:2a=4+2﹣2,解得:a=2.当a﹣1=0,即a=1时,原方程无解.故答案是:2或1.【点评】首先根据题意写出a的新方程,然后解出a的值.23.(2013•德阳)已知关于x的方程的解是正数,则m的取值范围是m .>﹣6且m≠﹣4【分析】首先求出关于x的方程的解,然后根据解是正数,再解不等式求出m的取值范围.【解答】解:解关于x的方程得x=m+6,∵方程的解是正数,∴m+6>0且m+6≠2,解这个不等式得m>﹣6且m≠﹣4.故答案为:m>﹣6且m≠﹣4.【点评】本题考查了分式方程的解,是一个方程与不等式的综合题目,解关于x 的方程是关键,解关于x的不等式是本题的一个难点.24.(2009•枣庄)a、b为实数,且ab=1,设P=,Q=,则P =Q(填“>”、“<”或“=”).【分析】将两式分别化简,然后将ab=1代入其中,再进行比较,即可得出结论.【解答】解:∵P==,把ab=1代入得:=1;Q==,把ab=1代入得:=1;∴P=Q.【点评】解答此题关键是先把所求代数式化简再把已知代入即可.25.(2013•达州)如果实数x满足x2+2x﹣3=0,那么代数式的值为5.【分析】先根据分式混合运算的法则把原式进行化简,再根据实数x满足x2+2x ﹣3=0求出x2+2x的值,代入原式进行计算即可.【解答】解:原式=×(x+1)=x2+2x+2,∵实数x满足x2+2x﹣3=0,∴x2+2x=3,∴原式=3+2=5.故答案为:5.【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.26.(2013•呼和浩特)某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,现在平均每天生产200台机器.【分析】根据现在生产600台机器的时间与原计划生产450台机器的时间相同.所以可得等量关系为:现在生产600台机器时间=原计划生产450台时间.【解答】解:设:现在平均每天生产x台机器,则原计划可生产(x﹣50)台.依题意得:=.解得:x=200.检验:当x=200时,x(x﹣50)≠0.∴x=200是原分式方程的解.∴现在平均每天生产200台机器.故答案为:200.【点评】此题主要考查了分式方程的应用,重点在于准确地找出相等关系,这是列方程的依据.而难点则在于对题目已知条件的分析,也就是审题,一般来说应用题中的条件有两种,一种是显性的,直接在题目中明确给出,而另一种是隐性的,是以题目的隐含条件给出.本题中“现在平均每天比原计划多生产50台机器”就是一个隐含条件,注意挖掘.27.(2013•舟山)杭州到北京的铁路长1487千米.火车的原平均速度为x千米/时,提速后平均速度增加了70千米/时,由杭州到北京的行驶时间缩短了3小时,则可列方程为﹣=3.【分析】先分别求出提速前和提速后由杭州到北京的行驶时间,再根据由杭州到北京的行驶时间缩短了3小时,即可列出方程.【解答】解:根据题意得:﹣=3;故答案为:﹣=3.【点评】此题考查了由实际问题抽象出分式方程,关键是读懂题意,找出题目中的等量关系并列出方程.三.解答题(共13小题)28.(2013•眉山)先化简,再求值:,其中.【分析】这道求代数式值的题目,不应考虑把x的值直接代入,通常做法是先把代数式去括号,把除法转换为乘法化简,然后再代入求值.【解答】解:原式=+(x﹣2)(3分)=x(x﹣1)+(x﹣2)=x2﹣2;(2分)当x=时,则原式的值为﹣2=4.(2分)【点评】分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.29.(2005•徐州)先化简代数式,然后选取一个使原式有意义的a值代入求值.【分析】本题考查的化简与计算的综合运算,关键是正确进行分式的通分、约分,并准确代值计算.此题要注意的是a≠1.【解答】解:原式===,∵a﹣1≠0,∴a≠1,当a=2时,原式=2.【点评】此题考查了分式的化简求值,取合适的值代入原式求值时,要特注意原式及化简过程中的每一步都有意义.30.(2015•甘南州)已知x﹣3y=0,求•(x﹣y)的值.【分析】首先将分式的分母分解因式,然后再约分、化简,最后将x、y的关系式代入化简后的式子中进行计算即可.【解答】解:=(2分)=;(4分)当x﹣3y=0时,x=3y;(6分)原式=.(8分)【点评】分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.31.(2013•普洱)解方程:.【分析】观察可得2﹣x=﹣(x﹣2),所以可确定方程最简公分母为:(x﹣2),然后去分母将分式方程化成整式方程求解.注意检验.【解答】解:方程两边同乘以(x﹣2),得:x﹣3+(x﹣2)=﹣3,解得x=1,检验:x=1时,x﹣2≠0,∴x=1是原分式方程的解.【点评】(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.(3)去分母时有常数项的不要漏乘常数项.32.(2013•重庆)先化简,再求值:,其中x是不等式3x+7>1的负整数解.【分析】首先把分式进行化简,再解出不等式,确定出x的值,然后再代入化简后的分式即可.【解答】解:原式=[﹣]×,=×,=×,=,3x+7>1,3x>﹣6,x>﹣2,∵x是不等式3x+7>1的负整数解,∴x=﹣1,把x=﹣1代入中得:=3.【点评】此题主要考查了分式的化简求值,以及不等式的整数解,关键是正确把分式进行化简.33.(2013•巴中)先化简÷(a+1)+,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.【分析】先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.【解答】解:原式=•+=+=,当a=2(a≠﹣1,a≠1)时,原式==5.【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.34.(2013•陕西)解分式方程:+=1.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:2+x(x+2)=x2﹣4,解得:x=﹣3,经检验x=﹣3是分式方程的解.【点评】此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.35.(2015•广州)已知A=﹣(1)化简A;(2)当x满足不等式组,且x为整数时,求A的值.【分析】(1)根据分式四则混合运算的运算法则,把A式进行化简即可.(2)首先求出不等式组的解集,然后根据x为整数求出x的值,再把求出的x 的值代入化简后的A式进行计算即可.【解答】解:(1)A=﹣=﹣=﹣=(2)∵∴∴1≤x<3,∵x为整数,∴x=1或x=2,①当x=1时,∵x﹣1≠0,∴A=中x≠1,∴当x=1时,A=无意义.②当x=2时,A==.【点评】(1)此题主要考查了分式的化简求值,注意化简时不能跨度太大,而缺少必要的步骤.(2)此题还考查了求一元一次不等式组的整数解问题,要熟练掌握,解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件求得不等式组的整数解即可.36.(2013•哈尔滨)甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.(1)甲、乙两队单独完成此项任务需要多少天?(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?【分析】(1)设乙队单独完成此项任务需要x天,则甲队单独完成此项任务需要(x+10)天,根据甲队单独施工45天和乙队单独施工30天的工作量相同建立方程求出其解即可;(2)设甲队再单独施工a天,根据甲队总的工作量不少于乙队的工作量的2倍建立不等式求出其解即可.【解答】解:(1)设乙队单独完成此项任务需要x天,则甲队单独完成此项任务需要(x+10)天,由题意,得,解得:x=20.经检验,x=20是原方程的解,∴x+10=30(天)答:甲队单独完成此项任务需要30天,乙队单独完成此项任务需要20天;(2)设甲队再单独施工a天,由题意,得,解得:a≥3.答:甲队至少再单独施工3天.【点评】本题是一道工程问题的运用,考查了工作时间×工作效率=工作总量的运用,列分式方程解实际问题的运用,分式方程的解法的运用,解答时验根是学生容易忽略的地方.37.(2015•成都)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)该商家购进的第一批衬衫是多少件?(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?【分析】(1)可设该商家购进的第一批衬衫是x件,则购进第二批这种衬衫是2x件,根据第二批这种衬衫单价贵了10元,列出方程求解即可;(2)设每件衬衫的标价y元,求出利润表达式,然后列不等式解答.【解答】解:(1)设该商家购进的第一批衬衫是x件,则购进第二批这种衬衫是2x件,依题意有+10=,解得x=120,经检验,x=120是原方程的解,且符合题意.答:该商家购进的第一批衬衫是120件.(2)3x=3×120=360,设每件衬衫的标价y元,依题意有(360﹣50)y+50×0.8y≥(13200+28800)×(1+25%),解得y≥150.答:每件衬衫的标价至少是150元.【点评】本题考查了分式方程的应用和一元一次不等式的应用,弄清题意并找出题中的数量关系并列出方程是解题的关键.38.(2014•广州)从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.(1)求普通列车的行驶路程;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.【分析】(1)根据高铁的行驶路程是400千米和普通列车的行驶路程是高铁的行驶路程的1.3倍,两数相乘即可得出答案;(2)设普通列车平均速度是x千米/时,根据高铁所需时间比乘坐普通列车所需时间缩短3小时,列出分式方程,然后求解即可;【解答】解:(1)根据题意得:400×1.3=520(千米),答:普通列车的行驶路程是520千米;(2)设普通列车平均速度是x千米/时,则高铁平均速度是2.5x千米/时,根据题意得:﹣=3,解得:x=120,。
初二数学上册(人教版)第十五章分式15.2知识点总结含同步练习及答案

四、课后作业
1. 计算
(查看更多本章节同步练习题,请到快乐学)
x2 − 4 ,结果是 ( x−2
)
B.x + 2 C.
A.x − 2
答案: B 解析:
x−4 2
D.
x+2 x
(x + 2) (x − 2) x2 − 4 = = x+2 x−2 x−2 1 1 的值为 ( = 3 ,则 a2 + a a2 B.7 )
解析:
1 3 (x − 2y)2 = 0.
B.−
1 3y
x−y = ( x+y 1 C. 3
)
D.
1 3y
答案: C
高考不提分,赔付1万元,关注快乐学了解详情。
② (
负整数次幂 an 的意义亦可视为 an = 1 ⋅ a ⋅ a ⋅ ⋯ ⋅ a ,起始值为 1 (乘法的单位元)乘上 n 个 a ,这 样就很容易得到: 指数是负整数时就等于重复除以底数(或底数的倒数自乘指数这么多次),即
ห้องสมุดไป่ตู้
n个
a−n =
1 1 1 1 1 1 = 1 ⋅ ⋅ ⋅ ⋯ ⋅ = n = ( )n ( a ≠ 0,n 为正整数),例如: a a a⋅a⋅⋯⋅a a a a
n个 n个
(
为正整数),例如:
a−1
1 1 . = (a ≠ 0);2 −3 = a 8
n个
n个
例题: 计算:
3b 2 a 2x3 z 4xz 2 a + 2b b 2a ;(2) ;(3) . ⋅ ÷ + − 2 2 6b y b−a a−b b−a 4a −3y 3b 2 a b 解:(1) ; ⋅ = 2 6b 8a 4a −3y 2 3x2 y 2x3 z 4xz 2 2x 3 z (2) ; ÷ = ×( )=− y y 2z −3y 2 4xz 2 a + 2b b 2a b−a (3) + − = = 1. b−a a−b b−a b−a
(word完整版)新人教版八年级数学下册第十六章分式知识点总结,文档

一、分式的定义: 若是 A 、 B 表示两个整式,并且B 中含有字母,那么式子A叫做分式。
B例 1. 以下各式 a ,1, 1x+y ,a 2b 2 ,-3x 2,0?中,是分式的有〔 〕个。
x 15ab二、 分式有意义的条件是分母不为零; 【B ≠0】分式没有意义的条件是分母等于零; 【B=0】分式值为零的条件分子为零且分母不为零。
【B ≠0 且 A=0 即子零母不零】例 2. 以下分式,当 x 取何值时有意义。
〔 1〕2x1 ;〔 2〕 3 x2。
3x 22x 3例 3. 以下各式中,无论 x 取何值,分式都有意义的是〔 〕。
A .1 B . xC .3x 1D .x 212x 12x 1x 22x 2例 4.当 x______时,分式2x1没心义。
当 x_______时,分式x 21 的值为零。
3x 4x 2x 2例 5. 1 - 1 =3,求5x3xy 5 y的值。
x y x2xyy三、分式的根本性质: 分式的分子与分母同乘或除以一个不等于0 的整式,分式的值不变。
〔 CA A C A A C0 〕B C B B CB四、分式的通分和约分:要点先是分解因式。
1 x 1 y例 6. 不改变分式的值,使分式510的各项系数化为整数,分子、分母应乘以〔 ? 〕。
1 x 1 y3 9例 7. 不改变分式2 3x 2 x 的值,使分子、分母最高次项的系数为正数,那么是〔 ?〕。
5x 3 2x 3分式 4 y 3x , x2 1 , x2xy y 2, a22ab2中是最简分式的有〔例 8. 4x 〕。
4ax1 y ab 2b例 9. 约分:〔1〕x 26x9 ; 〔2〕 m 23m 2x29m2m例 10. 通分:〔 1〕x ,y;〔2〕a 1,66ab 29a 2bc22a 2a 1 a 1例 11. x 2 +3x+1=0,求 x 2+12 的值. x例 12. x+ 1=3,求x 4x 2 2 的值. xx 1五、分式的运算:分式乘法法那么:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
最新初中数学—分式的知识点总复习含答案

一、选择题1.若分式55x x -+的值为0,则x 的值为( )A .0B .5C .-5D .±5 2.计算: ()332xy ?-一 的结果是A .398x y --B .398x y ---C .391x y 2---D .361x y 2---3.下列关于分式的判断,正确的是( ) A .当x =2时,12x x +-的值为零 B .无论x 为何值,231x +的值总为正数 C .无论x 为何值,31x +不可能得整数值 D .当x ≠3时,3x x-有意义 4.下列各式从左到右的变形正确的是( )A .221188a a a a ---=-++B .()()221a b a b -+=-C .22x y x y x y+=++ D .052520.11y yx x++=-++5.下列各式中,正确的是( ). A .1122b a b a +=++B .22142a a a -=-- C .22111(1)a a a a +-=-- D .11b ba a ---=- 6.计算32-的结果是( ) A .-6B .-8C .18-D .187.下列变形正确的是( ). A .1a b bab b++= B .22x y x y-++=- C .222()x y x y x y x y --=++ D .23193x x x -=-- 8.若 a =20170,b =2015×2017﹣20162,c =(﹣23)2016×(32)2017,则下列 a ,b ,c 的大小关系正确的是( ) A .a <b <c B .a <c <b C .b <a <c D .c <b <a 9.生物学家发现一种病毒的长度约为0.00 004mm ,0.00 004用科学记数法表示是( )A .40.410-⨯B .5410-⨯C .54010-⨯D .5410⨯10.如果把分式2xx y-中的x 与y 都扩大2倍,那么分式的值( )A .不变B .扩大2倍C .缩小2倍D .扩大4倍11.下列各式:2116,,4,,235x y xx y x π++-中,分式有( ) A .1个B .2个C .3个D .4个12.下列关于分式的判断,正确的是( ) A .当x=2时,12x x +-的值为零 B .当x≠3时,3x x-有意义 C .无论x 为何值,31x +不可能得整数值 D .无论x 为何值,231x +的值总为正数 13.化简:32322012220122010201220122013-⨯-+-,结果是( ) A .20102013 B .20102012 C .20122013 D .20112013 14.下列分式是最简分式的是( ) A .2426a a -+B .1b ab a++C .22a ba b +-D .22a ba b ++15.纳米是一种长度单位,1纳米=10-9米,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示该种花粉的直径为( ) A .43.510⨯米 B .43.510-⨯米C .53.510-⨯米D .93.510-⨯米16.已知12x y-=3,分式4322x xy y x xy y +-+-的值为( )A .32 B .0C .23D .9417.甲、乙两人分两次在同一粮店内买粮食,两次的单价不同,甲每次购粮100千克,乙每次购粮100元.若规定:谁两次购粮的平均单价低,谁的购粮方式就合算.那么这两次购粮( ) A .甲合算 B .乙合算C .甲、乙一样D .要看两次的价格情况18.下列计算正确的是( )A .3x x=xB .11a b ++=abC .2÷2﹣1=﹣1D .a ﹣3=(a 3)﹣119.下列说法:①在一个装有2白球和3个红球的袋中摸3个球,摸到红球是必然事12a =--,则12a ≥-; 22a ba b-+是最简分式;其中正确的有()个. A .1个 B .2个 C .3个 D .4个 20.若(1-x )1-3x =1,则x 的取值有( )个.A .1个B .2个C .3个D .4个21.若a =-0.32,b =-3-2,c =(-13)-2,d =(-13)0,则它们的大小关系是( ) A .a<c<b<d B .b<a<d<cC .a<b<d<cD .b<a<c<d22.如果把分式2+mm n中的m 和n 都扩大2倍,那么分式的值 ( ) A .扩大4倍B .缩小2倍C .不变D .扩大2倍23.下列运算错误的是( )A 4=B .12100-=C 3=-D 2=24.计算21424m m ++-的结果是( ) A .2m +B .2m -C .12m + D .12m - 25.当x =1时,下列分式中值为0的是( ) A .11x - B .222x x -- C .31x x -+ D .11x x --【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】要使分式的值为0,必须分式分子的值为0并且分母的值不为0. 【详解】由式子x -5=0,解得x 5=±. 而x =5时分母5x +≠0,x =-5时分母5x +=0,分式没有意, 即x =5, 故选B.【点睛】要注意分母的值一定不能为0,分母的值是0时分式没有意义.2.B解析:B 【解析】3333939(2)=(-2)8xy x y x y -------=-.故选B.3.B解析:B 【解析】A 选项中,因为当2x =时,分式12x x +-无意义,所以本选项错误; B 选项中,因为无论x 取何值,21x +的值始终为正数,则分式231x +的值总为正数,所以本选项正确;C 选项中,因为当2x =时,分式311x =+,所以本选项说法错误; D 选项中,因为0x ≠时,分式3x x-才有意义,所以本选项说法错误; 故选B.4.B解析:B 【解析】 解:A .原式=22(1)1(8)8a a a a -++=--- ,错误;B .原式=1,正确;C .原式为最简结果,错误;D .原式=520110yx+-+,错误.故选B .点睛:此题考查了分式的基本性质,熟练掌握分式的基本性质是解本题的关键.5.C解析:C 【解析】解;A .分式的分子分母都乘或除以同一个不为零的整式,故A 错误; B .分子除以(a ﹣2),分母除以(a +2),故B 错误;C .分式的分子分母都乘或除以同一个不为零的整式,分式的值不变,故C 正确;D .分式的分子分母都乘或除以同一个不为零的整式,分式的值不变,故D 错误; 故选C .6.D解析:D 【解析】3311228-==. 故选D. 7.C解析:C 【解析】 选项A.a bab+ 不能化简,错误. 选项B.22x y x y-+-=-,错误. 选项C.()222x y x y x y x y --=++ ,正确. 选项D. 23193x x x -=-+,错误. 故选C.8.C解析:C 【解析】 【详解】解:a =20170=1,b =2015×2017﹣20162=(2016﹣1)(2016+1)﹣20162=20162﹣1-20162=﹣1,c =(﹣23)2016×(32)2017=(﹣23×32)2016×32=32,则b <a <c .故选C . 点睛:本题考查了平方差公式,幂的乘方与积的乘方,以及零指数幂,熟练掌握运算法则及公式是解答本题的关键.9.B解析:B 【解析】解:0.00 004=5410-⨯.故选B .10.A解析:A 【解析】分析:解答此题时,可将分式中的x ,y 用2x ,2y 代替,然后计算即可得出结论. 详解:依题意得:2222x x y ⨯-=222xx y ⋅⋅-()=原式.故选A .点睛:本题考查的是对分式的性质的理解和运用,扩大或缩小n 倍,就将原来的数乘以n或除以n .11.A解析:A 【解析】分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式. 详解:216,,4,,23x y xx y π++的分母中均不含有字母,因此它们是整式,而不是分式.15x -的分母中含有字母,因此是分式. 故选A .点睛:本题主要考查分式的定义,注意π不是字母,6xπ是常数,所以不是分式,是整式.12.D解析:D 【解析】A 选项:当x =2时,该分式的分母x -2=0,该分式无意义,故A 选项错误.B 选项:当x =0时,该分式的分母为零,该分式无意义. 显然,x =0满足x ≠3. 由此可见,当x ≠3时,该分式不一定有意义. 故B 选项错误.C 选项:当x =0时,该分式的值为3,即当x =0时该分式的值为整数,故C 选项错误.D 选项:无论x 为何值,该分式的分母x 2+1>0;该分式的分子3>0. 由此可知,无论x 为何值,该分式的值总为正数. 故D 选项正确. 故本题应选D. 点睛:本题考查了与分式概念相关的知识. 分式有意义的条件是分式的分母不等于零,并不是分母中的x 的值不等于零. 分式的值为零的条件是分式的分母不等于零且分式的分子等于零. 在分式整体的符号为正的情况下,分式值的符号由分子与分母的符号共同确定:若分子与分母同号,则分式值为正数;若分子与分母异号,则分式值为负数.13.A解析:A 【分析】将所求式子的分子分母前两项提取20122,整理后分子提取2010,分母提取2013,约分后即可得到结果,选出答案. 【详解】原式=32322012220122010201220122013-⨯-+-=2220122012220102012201212013--⨯+-()()=22201220102010201220132013⨯-⨯-=22201020121201320121--()()=20102013,故答案选A. 【点睛】本题主要考查了因式分解的应用,是一道技巧性较强的题,熟练掌握因式分解的方法是解本题的关键.14.D解析:D【解析】【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.【详解】A、该分式的分子、分母中含有公因数2,则它不是最简分式.故本选项错误;B、分母为a(b+1),所以该分式的分子、分母中含有公因式(b+1),则它不是最简分式.故本选项错误;C、分母为(a+b)(a-b),所以该分式的分子、分母中含有公因式(a+b),则它不是最简分式.故本选项错误;D、该分式符合最简分式的定义.故本选项正确.故选D.【点睛】本题考查了对最简分式,约分的应用,关键是理解最简分式的定义.15.C解析:C【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】35000纳米=35000×10-9米=3.5×10-5米.故选C.【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.16.A解析:A【解析】【分析】先根据题意得出2x-y=-3xy,再代入原式进行计算即可.【详解】解:∵12x y-=3,∴2x-y=-3xy,∴原式=()()2232x y xyx y xy-+-+,=633xy xyxy xy-+-+,=32xyxy --,=32,故选A.【点睛】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.17.B解析:B【解析】【分析】分别算出两次购粮的平均单价,用做差法比较即可.【详解】解:设第一次购粮时的单价是x元/千克,第二次购粮时的单价是y元/千克,甲两次购粮共花费:100x+100y,一共购买了粮食:100+100=200千克,甲购粮的平均单价是:1001002002x y x y++=;乙两次购粮共花费:100+100=200元,一共购买粮食:()100100100x yx y xy++=(千克),乙购粮的平均单价是:2xyx y+;甲乙购粮的平均单价的差是:()()()()22420 222x y xy x yx y xyx y x y x y>+--+-==+++,即22x y xyx y ++>,所以甲购粮的平均单价高于乙购粮的平均单价,乙的购粮方式更合算,故选B.【点睛】本题考查的知识点是做差法,解题关键是注意一个数的平方为非负数.18.D解析:D【解析】 【分析】分子和分母同乘以(或除以)一个不为0的数,分数值不变. 【详解】A 、3x x=x 2,错误;B 、11a b ++=+1+1a b ,错误; C 、2÷2﹣1=4,错误; D 、a ﹣3=(a 3)﹣1,正确; 故选D . 【点睛】此题考查分式的基本性质,关键是根据把分式的分子和分母扩大还是缩小相同的倍数,分式的值不变解答.19.C解析:C 【解析】 【分析】根据必然事件的定义,二次根式的性质,最简分式的定义以及同类二次根式的定义进行判断. 【详解】①在一个装有2白球和3个红球的袋中摸3个球,摸到红球是必然事件,正确.②12a =--,则12a ≤-,错误;4== ④分式22a ba b-+是最简分式,正确; 故选:C . 【点睛】本题主要考查了随机事件、二次根式以及命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.20.B解析:B 【分析】利用零指数幂,乘方的意义判断即可. 【详解】解:∵(1-x )1-3x =1,∴1-x≠0,1-3x=0或1-x=1,解得:x=13或x=0,则x的取值有2个,故选B【点睛】本题考查了零指数幂,以及有理数的乘方,熟练掌握运算法则是解题的关键.21.B解析:B【解析】【分析】首先根据一个数的平方的计算方法,负整数指数幂的运算方法,以及零指数幂的运算方法,分别求出a、b、c、d的大小;然后根据实数大小比较的方法,判断出它们的大小关系即可.【详解】∵20 221110.30.09,3,9,1933a b c d--⎛⎫⎛⎫=-=-=-=-=-==-=⎪ ⎪⎝⎭⎝⎭,∴10.0919 9-<-<<,∴b<a<d<c.故选:B.【点睛】考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=1pa(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.22.C解析:C【解析】【分析】根据分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变,可得答案.【详解】分式2+mm n中的m和n都扩大2倍,得4222m mm n m n=++,∴分式的值不变,故选A.【点睛】本题考查了分式的基本性质,分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变.23.B解析:B【解析】【分析】分别根据立方根及算术平方根的定义对各选项进行逐一解答即可.【详解】A 、∵42=16=4,故本选项正确;B 、12100-110,故本选项错误;C 、∵(-3)3=-273=-,故本选项正确;D =2,故本选项正确.故选B .【点睛】本题考查的是立方根及算术平方根,熟知立方根及算术平方根的定义是解答此题的关键.24.D解析:D【解析】【分析】 先通分,再加减.注意化简.【详解】21424124(2)(2)2m m m m m m -++==+-+-- 故选:D【点睛】考核知识点:异分母分式加减法.通分是关键.25.B解析:B【分析】考虑将x=1代入,使分式分子为0,分母不为0,即可得到结果. 【详解】解:当x=1时,下列分式中值为0的是222x x --. 故选B .【点睛】此题考查了分式的值,熟练掌握运算法则是解本题的关键.。
人教版八年级数学上册第十五章 分式知识点总结和题型归纳

人教版八年级数学上册第十五章分式知识点总结和题型归纳分式知识点总结和题型归纳第一部分分式的运算一)分式的定义及有关题型考查分式的定义:一般地,如果A,B表示两个整数,并且B中含有字母,那么式子A/B为分式。
例1:下列代数式中是分式的有:(x- y)/(2x+ y),π/(2x- y),(x+ y)/(a+ b)。
考查分式有意义的条件:分式有意义:分母不为0 (B≠0)分式无意义:分母为0 (B=0)例1:当x有何值时,下列分式有意义:1) (x-4)/(13x2-6x)2) 2/x3) 2/(x-4)4) (x+4|x|-3x+2)/(x-1)5) x/(x2-2x-3)考查分式的值为的条件:分式值为:分子为A且分母不为0 (A/B) 例1:当x取何值时,下列分式的值为0.1) (x-1)/(x+3)2) |x|-23) (x2-2x-3)/(x-5)(x+6)例2:当x为何值时,下列分式的值为零:1) 5-|x-1|/(x+4)2) (25-x2)/(x-6)(x+5)考查分式的值为正、负的条件:分式值为正或大于0:分子分母同号 (A/B>0) 分式值为负或小于0:分子分母异号 (A/B<0) 例1:(1) 当x为何值时,分式4/(8-x)为正;2) 当x为何值时,分式5-x/(5+x)为负;3) 当x为何值时,分式(x-2)/(x+3)为非负数.例2:解不等式|x|-2≤(x+1)/(x+5)考查分式的值为1,-1的条件:分式值为1:分子分母值相等 (A/B=1)分式值为-1:分子分母值互为相反数 (A+B=0)例1:若分式|x-2|/(x+2)的值为1,-1,则x的取值分别为3和-1.思维拓展练题:1、若a>b>0,a2+b2-6ab=0,则(a+b)/(a-b)=9/5.2、一组按规律排列的分式:-b/2.5/b。
-8/b。
11/b。
则第n 个分式为(3n-1)/b。
人教版初中八年级数学上册第十五章《分式》知识点总结(含答案解析)

一、选择题1.将分式2+x x y中的x ,y 的做同时扩大到原来的3倍,则分式的值( )A .扩大到原来的3倍B .缩小到原来的13C .保持不变D .无法确定2.下列命题中,属于真命题的是( )A .如果0ab =,那么0a =B .253xx x-是最简分式 C .直角三角形的两个锐角互余 D .不是对顶角的两个角不相等3.若关于x 的分式方程3211m x x =---有非负实数解,且关于x 的不等式组102x x m +≥⎧⎨+≤⎩有解,则满足条件的所有整数m 的和为( ) A .9-B .8-C .7-D .6-4.2020年新冠肺炎疫情影响全球,各国感染人数持续攀升,医用口罩供不应求,很多企业纷纷加入生产口罩的大军中来,重庆某企业临时增加甲、乙两个厂房生产口罩,甲厂房每天生产的数量是乙厂房每天生产数量的2倍,两厂房各加工6000箱口罩,甲厂房比乙厂房少用5天.设乙厂房每天生产x 箱口罩.根据题意可列方程为( )A .6000600052x x -= B .6000600052x x -= C .6000600052x x -=+ D .6000600052x x-=+ 5.如果a ,b ,c ,d 是正数,且满足a +b +c +d =2,11a b c b c d ++++++11a c d ab d+++++=4,那么d a a b c b c d ++++++b ca c d ab d+++++的值为( )A .1B .12C .0D .46.如果分式11m m -+的值为零,则m 的值是( ) A .1m =- B .1m = C .1m =±D .0m =7.下列说法:①解分式方程一定会产生增根;②方程4102x -=+的根为2;③方程11224=-x x 的最简公分母为2(24)-x x ;④1111x x x+=+-是分式方程.其中正确的个数是( ) A .1B .2C .3D .48.若x 2y 5=,则x y y+的值为( ) A .25 B .72C .57D .759.计算2m m 1m m-1+-的结果是( ) A .mB .-mC .m +1D .m -110.大爱无疆,在爆发新冠病毒疫情后,甲,乙两家单位分别组织了员工捐款.已知甲单位捐款7500元,乙单位捐款9800元,甲单位捐款人数比乙单位少10人,且甲单位人均捐款额比乙单位多20元,若设甲单位的捐款人数为x ,则可列方程为( ) A .7500980020x x 10-=- B .9800750020x 10x-=- C .7500980020x x 10-=+D .9800750020x 10x-=+ 11.下列式子的变形正确的是( )A .22b b a a=B .22+++a b a b a b=C .2422x y x yx x --=D .22m nn m-=- 12.3333x a a y x y y x+--+++等于( ) A .33x y x y-+B .x y -C .22x xy y -+D .22xy +13.当1x 0-<<时, 1x -,0x ,2x 的大小顺序是( )A .102x x x -<<B .012x x x -<<C .021x x x -<<D .120x x x -<<14.计算a ba b a÷⨯的结果是() A .a B .2aC .2b aD .21a 15.化简214a 2a 4---的结果为( ) A .1a 2+ B .a 2+C .1a 2- D .a 2-二、填空题16.已知5,3a b ab -==,则b aa b+的值是__________. 17.席卷全世界的新型冠状病毒是个肉眼看不见的小个子,它的身高(直径)约为0.0000012米,将数0.0000012用科学记数法表示为_________.18.已知13x x-=,则21x x ⎛⎫+= ⎪⎝⎭________.19.若关于x 的方程1322m x x x-+=--的解是正数,则m =____________. 20.101()()2π-+-=______,011(3.14)2--++=______. 21.化简分式:2121211a a a a +⎛⎫÷+= ⎪-+-⎝⎭_________.22.下列计算:①3100.0001-=;②()00.00011=;③()()352x x x --÷-=-;④22133a a-=;⑤()()321m m mm a a a -÷=-.其中运算正确的有______.(填序号即可)23.对于两个不相等的实数a ,b ,我们规定符号Min{,}a b 表示a ,b 中的较小的值,如Min{3,4}3=,按照这个规定,方程135Min ,2222x x x x -⎧⎫=-⎨⎬---⎩⎭的解为_____________.24.计算:11|1|3-⎛⎫-= ⎪⎝⎭______. 25.计算3224423y x x y⎛⎫-⋅ ⎪⎝⎭的结果是________.26.某工人现在平均每天比原计划多做20个零件,现在做4000个零件和原来做3000个零件的时间相同,问现在平均每天做______个零件.三、解答题27.某社区为了落实“惠民工程”,计划将社区的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的3倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需10天. (1)这项工程的规定时间是多少天?(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?28.某快餐店欲购进A ,B 两种型号的餐盘,每个A 种型号的餐盘比每个B 种型号的餐盘费用多5元,且用120元购进的A 种型号的餐盘与用90元购进的B 种型号的餐盘的数量相同.(1)问A ,B 两种型号的餐盘单价为多少元?(2)若该快餐店决定在成本不超过1900元的前提下购进A ,B 两种型号的餐盘100个,则最多购进A 种型号餐盘多少个?29.鄂州市2020年被评为“全国文明城市”.创文期间,甲、乙两个工程队共同参与某段道路改造工程.如果甲工程队单独施工,恰好如期完成;如果甲、乙两工程队先共同施工10天,剩下的任务由乙工程队单独施工,也恰好能如期完成;如果乙工程队单独施工,就要超过15天才能完成.(1)求甲、乙两工程队单独完成此项工程各需多少天?(2)若甲工程队单独施工a 天,再由甲、乙两工程队合作______天(用含有a 的代数式表示)可完成此项工程.(3)现在要求甲、乙两个工程队都必须参加这项工程.如果甲工程队每天的施工费用为2万元,乙工程队每天的施工费用为1.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,能使施工费用不超过61.5万元? 30.计算 (1)2152224-⨯+÷; (2)()()30201821 3.14413π-⎛⎫-⨯---+- ⎪⎝⎭;(3)()2222322xy x y x y xy ⎡⎤---⎣⎦; (4)()()()3323231333xx x x ⎛⎫-+--⋅ ⎪⎝⎭.。
初中数学总复习-分式
2
2.(2018·重庆中考A卷)计算:
x2 x 2 4x 4 ( x 2) . x 3 x 3
ac a d a c bd g ___. b c b d an a ( ) n __. bn b
【自我诊断】(打“√”或“×”)
x 1 x 3 1.若分式 有意义,则x≠-2,-3,-4. ( √ ) x2 x4 2x y 2.将分式 中的x,y值均扩大为原来的10倍, 2 3x y
第三讲
分 式
一、分式的概念和基本性质
整式 1.分式的概念:一般地,如果A,B表示两个_____,
A 字母 并且B中含有_____,那么式子 叫做分式. B
2.分式的基本性质:分式的分子与分母同乘(或除以) 整式 分式的值_____. 不变 同一个不等于0的_____,
AM AM A 用式子表示: =_______=______ B M (其中M为不等于0 B M B
【自主解答】当x+2≠0时,分式 1 有意义,即当
x2
x≠-2时, 1
x2
有意义.
答案:x≠-2
【跟踪训练】 (2018·贵港中考)若分式 2 ________. 【解析】若分式 2 的值不存在,说明分式无意义,因
x 1 x 1
的值不存在,则x的值为
此x+1=0,解得x=-1. 答案:-1
则分式的值不变. ( × )
3.分式
3a 2(a+b), 的分母经过通分后变成 2(a-b) a 2 b2
那么分子应变为6a(a-b).(√ )
4. c c 1 1 1 .
a a a a
(√)
2 x 1 5.当x=-1时,分式 2 的值为.( √ ) 3 2x 1
人教版八年级数学下册第十六章分式知识点总结

一、分式的定义:如果A 、B 表示两个整式,并且B 中含有字母,那么式子BA叫做分式。
例1.下列各式aπ,11x +,15x+y ,22a b a b --,-3x 2,0•中,是分式的有( )个。
答:本题考查学生对分式的概念的理解,从题目中我们知道11x + 和22a b a b--是分式,所以本题的答案是2个。
二、 分式有意义的条件是分母不为零;【B ≠0】 分式没有意义的条件是分母等于零;【B=0】分式值为零的条件分子为零且分母不为零。
【B ≠0且A=0 即子零母不零】例2.下列分式,当x 取何值时有意义。
(1)2132x x ++; (2)2323x x +-。
答:本题考查学生对分式的分母不为0的掌握,因为分母为0分式无意义。
所以,(1)中我们知道3x+2≠0,得到x ≠- 2/3,(2)中我们知道2x-3≠0,得到x ≠ 3/2. 例3.下列各式中,无论x 取何值,分式都有意义的是( )。
A .121x +B .21x x +C .231x x +D .2221x x +答:本题考察学生对分母不为0的掌握,A 、B 选项当x=-1/2的时候分母为0,故排除,C 选项当X=0时分母为0 。
所以此题只能选D 。
例4.当x______时,分式2134x x +-无意义。
当x_______时,分式2212x x x -+-的值为零。
答:当X= 4/3时分母为0,分式无意义。
有题目得,x ²-1=0且x ²+x-2≠0,解得x=-1.所以此空填-1.例5.已知1x -1y =3,求5352x xy yx xy y+---的值。
答:由已知得y-x=3xy,原式=-12xy/-5xy=12/5.三、分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
(0≠C )四、分式的通分和约分:关键先是分解因式。
C B C A B A ⋅⋅=CB C A B A ÷÷=例6.不改变分式的值,使分式115101139x yx y -+的各项系数化为整数,分子、分母应乘以(•90 )。
八年级初二数学-【分式的复习知识点、】练习和答案-全面详细易懂

试问:在不耽误工期的情况下,你觉得哪一种施工方案最节省工程款?请说明理由。
8、一个分数的分母比分子大 数的倒数,求原分数。
7,如果把此分数的分子加
17,分母减 4,所得新分数是原分
9、今年某市遇到百年一遇的大旱,全市人民齐心协力积极抗旱。某校师生也行动起来捐款 打井抗旱, 已知第一天捐款 4800 元,第二天捐款 6000 元, 第二天捐款人数比第一天捐款人 数多 50 人,且两天人均捐款数相等,那么两天共参加捐款的人数是多少?
400 千
克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?
11.( 2009 年孝感)关于 x 的方程
的解是正数,则 a 的取值范围是
A .a>- 1 C. a<- 1
B. a>- 1 且 a≠ 0 D. a<- 1 且 a≠- 2
(2)
(3)
随堂练习
( 4) -8xy
计算 (1) (3)
(5)
(6)
16. 2.1 分式的乘除 ( 二 )
(2) (4)
16. 2.1 分式的乘除 ( 三 )
1.判断下列各式是否成立,并改正 .
(1)
=
(2)
=
(3) 2.计算
(1)
= (2)
(4)
=
(3)
( 4) (6)
5) 16. 2. 2 分式的加减(一)
1 个,结果比李刚少用半小时
7、某一项工程在招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队款
1.5
万元,乙工程队款 1.1 万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方
案:
方案一:甲队单独完成这项工程刚好如期完成;
方案二:乙队单独完成这项工程要比规定日期多用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本题考查分式的化简,熟练掌握分式的运算法则是解题关键.
17. 的相反数是()
A.9B.-9C. D.
【答案】B
【解析】
【分析】
先根据负指数幂的运算法则求出 的值,然后再根据相反数的定义进行求解即可.
【详解】
=9,
9的相反数为-9,
故 的相反数是-9,
故选B.
【点睛】
本题考查了负整数指数幂、求一个数的相反数,熟练掌握负整数指数幂的运算法则是解题的关键.
6.若式子 有意义,则x的取值范围为().
A.x≥2B.x≠2C.x≤2D.x<2
【答案】D
【解析】
【分析】
根据被开方式大于且等于零,分母不等于零列式求解即可.
【详解】
解:∵式子 有意义
∴
∴x<2
故选:D
【点睛】
本题考查了代数式有意义时字母的取值范围,代数式有意义时字母的取值范围一般从几个方面考虑:①当代数式是整式时,字母可取全体实数;②当代数式是分式时,考虑分式的分母不能为0;③当代数式是二次根式时,被开方数为非负数.
【答案】A
【解析】
【分析】
先根据有理数的乘方、算术平方根、立方根、负整数指数幂进行计算,再比较数的大小,即可得出选项.
【详解】
解: , , ,
,
最小的数是 ,
故选: .
【点睛】
本题考查了实数的大小比较法则,能熟记实数的大小比较法则的内容是解此题的关键.
13.下列各式:① ;② ;③ ;④ ;⑤ ;其中运算正确的个数有()个.
A.1B.2C.3D.4
【答案】B
【解析】
【分析】
分别利用负整数指数幂、零指数幂、积的乘方、同底数幂的除法等对各式进行运算,即可做出判断.
【详解】
解:① ,故①正确;
② ,故②错误;
③ ,故③错误;
④ ,故④错误;
⑤ ,故⑤正确;
∴运算正确的个数有2个,
故选:B.
【点睛】
本题主要考查了负整数指数幂、零指数幂、积的乘方和同底数幂的除法,熟练掌握相关的运算法则是解题的关键.
A. B. C. D.
【答案】B
【解析】
【分析】
利用幂次方计算公式即可解答.
【详解】
解:原式= .
答案选B.
【点睛】
本题考查幂次方计算,较为简单.
16.化简 的结果是()
A.-a-1B.–a+1C.-ab+1D.-ab+b
【答案】B
【解析】
【分析】
将除法转换为乘法,然后约分即可.
【详解】
解: ,
故选B.
14.计算 的正确结果是( )
A. B. C. D.
【答案】B
【解析】
【分析】
先将后两项结合起来,然后再化成同分母分式,按照同分母分式加减的法则计算就可以了.
【详解】
原式
.
故选B.
【点睛】
本题考查分式的通分和分式的约分的运用,解题关键在于在解答的过程中注意符号的运用及平方差公式的运用.
15.计算 的结果为()
【详解】
2.乐乐所在的四人小组做了下列运算,其中正确的是()
A. B.
C. D.
【答案】B
【解析】
【分析】
根据负整数指数幂计算法则,积的乘方计算法则,同底数幂除法法则,单项式乘以单项式计算法则依次判断.
【详解】
A、 ,故错误;
B、 正确;
C、 ,故错误;
D、 ,
故选:B.
【点睛】
此题考查整式的计算,正确掌握负整数指数幂计算法则,积的乘方计算法则,同底数幂除法法则,单项式乘以单项式计算法则是解题的关键.
18.老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给来自一人,最后完成化简.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A.只有乙B.甲和丁C.乙和丙D.乙和丁
【答案】D
【解析】
【分析】根据分式的乘除运算步骤和运算法则逐一计算即可判断.
x2•x3=x5,故选项A不合题意;
(ab)3=a3b3,故选项B符合题意;
(2a)3=8a6,故选项C不合题意;
3−2= ,故选项D不合题意.
故选:B.
【点睛】
此题考查同底数幂的乘法,幂的乘方与积的乘方以及负整数指数幂的计算,熟练掌握幂的运算法则是解题的关键.
12.下列各数中最小的是()
A. B. C. D.
人教版初中数学分式知识点总复习有答案
一、选择题
1.把实数 用小数表示为()
A.0.0612B.6120C.0.00612D.612000
【答案】C
【解析】
【分析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
3.下列运算中,不正确的是()
A. B.
C. D.
【答案】A
【解析】
【分析】
根据分式的基本性质分别计算即可求解.
【详解】
解:A. ,故错误.
B、C、D正确.
故选:A
【点睛】
此题主要考查分式的基本性质,熟练利用分式的基本性质进行约分是解题关键.
4.若化简 的结果为 ,则“ ”是( )
A. B. C. D.
A. B.
C. D.
【答案】C
【解析】
【分析】
根据幂的乘方法则、分式的基本性质及同底数幂除法法则计算即可得答案.
【详解】
,
故选:C.
【点睛】
本题考查幂的乘方及分式的基本性质,幂的乘方,底数不变,指数相乘;分式的分子、分母同时乘以(或除以)一个不为0的整式,分式的值不变;同底数幂相除,底数不变,指数相减;熟练掌握分式的基本性质是解题关键.
【详解】∵
=
=
=
=
= ,
∴出现错误是在乙和丁,
故选D.
【点睛】本题考查了分式的乘除法,熟练掌握分式乘除法的运算法则是解题的关键.
19.化简 =()
A.﹣xB.y﹣xC.x﹣yD.﹣x﹣y
【答案】A
【解析】
【分析】
根据分式的运算法则即可求出答案.
【详解】
原式= ,
故选A.
【点睛】
本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
C、 ,故C符合题意;
D、 ,故D不符合题意;
故选:C.
【点睛】
此题考查同底数幂的乘除法,平方差公式,熟记法则并根据法则计算是解题关键.
11.下列运算中,正确的是()
A. B. C. D.
【答案】B
【解析】
【分析】
分别根据同底数幂的乘法法则,积的乘方法则以及负整数指数幂的运算法则逐一判断即可.
【详解】
7.若分式 在实数范围内有意义,则 的取值范围是()
A. B. C. D.
【答案】D
【解析】
【分析】
根据分式有意义的条件即可求出答案.
【详解】
由题意可知:x-2≠0,
x≠2,
故选:D.
【点睛】
本题考查分式的有意义的条件,解题的关键是熟练运用分式有意义的条件,本题属于基础题型.
8.下列运算中正确的是()
【点睛】
此题考查二次根式的性质以及负指数幂的性质、零指数幂的性质,正确化简各数是解题关键.
10.下列运算正确的是()
A. B. C. D.
【答案】C
【解析】
【分析】
根据同底数幂的乘除法,积的乘方,负整数指数幂,平方差公式,可得答案.
【详解】
解:A、不是同底数幂的乘法指数不能相加,故A不符合题意;
B、 ,故B不符合题意;
【答案】D
【解析】
【分析】
根据题意列出算式,然后利用分式的混合运算法则进行计算.
【详解】
解:由题意得: ,
故选:D.
【点睛】
本题考查了分式的混合运算,熟练掌握运算法则是解题的关键.
5.计算(a2)3+a2·a3-a2÷a-3的结果是( )
A.2a5-aB.2a5- C.a5D.a6
【答案】D
【解析】
20.0000036=3.6×10-6;
故选:A.
【点睛】
本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
9.下列计算正确的是().
A. B.
C. D.
【答案】D
【解析】
【分析】
直接利用二次根式的性质以及负指数幂的性质、零指数幂的性质分别化简得出答案.
【详解】
A、 ,故此选项错误;
B、(-3)-2= ,故此选项错误;
C、(x-3.14)0=1,故此选项错误;
D、(-1)2019-|-4|=-5,正确.
故选:D.
【分析】先分别进行幂的乘方、同底数幂的乘法、同底数幂的除法运算,然后再进行合并同类项即可.
【详解】原式=a2×3+a2+3-a2-(-3)
=a6+a5-a5
=a6,
故选D.
【点睛】本题考查了有关幂的运算,熟练掌握“幂的乘方,底数不变,指数相乘”、“同底数幂的乘法,底数不变,指数相加”、“同底数幂的除法,底数不变,指数相减”是解题的关键.
