第五章机械振动(1)

合集下载

机械振动(1)

ω
=
∆Φ 2π
T
即得x2的曲线
若
∆φ < o 时
说明振动2比振动1落后，将x1曲线右移 ∆φ T 距离为 ∆ t = 即得x2的曲线 2π
19
四简谐振动表示法-解析法由给定振动系统，可求出ω ； 1 取平衡位置为原点;
2
建立坐标,分析任一位置时物体受力;
d2x 3 写出动力学方程： + ω2x = 0 dt 2
*两个振动同频率、同一时刻间的相位差：
∆Φ = (ϕ 20 − ϕ 10 ) 初相位的差！
17
同一时刻两个同频率的简谐振动相位差
∆Φ = ϕ 20 − ϕ 10
位移 x
x2 x1
x 1 = A1 cos( ω t + ϕ 10 )
x 2 = A2 cos( ω t + ϕ 20 )
位移 x
x1 x2
……
26
由初始条件求初相
初态一
o
ϕ
x
v=0
x = A
⇒ ϕ = 0
初态二
X=o
⇒ ϕ =
π
2
O
X
初态三
V=0
x = −A
⇒ ϕ = π
v
初态四
x=0
π 3π ⇒ ϕ = 或 − 2 2
27
水平谐振子例1：由初始条件求初相 ϕ ; k 1 由平衡位置右拉0.1m放手; x o 2 由平衡位置左推0.1m放手; 3 在A/2处给一个向右的速度; − 2 A 4 在处给一个向左的速度。 2 分别求出初相。 ϕ =0 1 X0=0.1, v0=0 A=0.1 0 x x
ω
由给定初始条件可求出A、ϕ; 已知 A、ϕ 、ω

机械振动答案

机械振动答案（1）选择题1解析：选D.如图所示，设质点在A 、B 之间振动，O 点是它的平衡位置，并设向右为正．在质点由O 向A 运动过程中其位移为负值；而质点向左运动，速度也为负值．质点在通过平衡位置时，位移为零，回复力为零，加速度为零，但速度最大．振子通过平衡位置时，速度方向可正可负，由F ＝－kx 知，x 相同时F 相同，再由F ＝ma 知，a 相同，但振子在该点的速度方向可能向左也可能向右．2．解析：选B.据简谐运动的特点可知，振动的物体在平衡位置时速度最大，振动物体的位移为零，此时对应题图中的t 2时刻，B 对．3．解析：选BD.质点做简谐运动时加速度方向与回复力方向相同，与位移方向相反，总是指向平衡位置；位移增加时速度与位移方向相同，位移减小时速度与位移方向相反．4解析：选C.因为弹簧振子固有周期和频率与振幅大小无关，只由系统本身决定，所以f 1∶f 2＝1∶1，选C.5解析：选B.对于阻尼振动来说，机械能不断转化为内能，但总能量是守恒的．6.解析：选B.因质点通过A 、B 两点时速度相同，说明A 、B 两点关于平衡位置对称，由时间的对称性可知，质点由B 到最大位移，与由A 到最大位移时间相等；即t 1＝0.5 s ，则T2＝t AB ＋2t 1＝2 s ，即T ＝4 s ，由过程的对称性可知：质点在这2 s 内通过的路程恰为2 A ，即2A ＝12 cm ，A ＝6 cm ，故B 正确．7.解析：选A.两球释放后到槽最低点前的运动为简谐运动且为单摆模型．其周期T ＝2πR g，两球周期相同，从释放到最低点O 的时间t ＝T4相同，所以相遇在O 点，选项A 正确．8．解析：选C.从t ＝0时经过t ＝3π2L g 时间，这段时间为34T ，经过34T 摆球具有最大速度，说明此时摆球在平衡位置，在给出的四个图象中，经过34T 具有负向最大速度的只有C 图，选项C 正确．9.解析：选CD.单摆做简谐运动的周期T ＝2πlg，与摆球的质量无关，因此两单摆周期相同．碰后经过12T 都将回到最低点再次发生碰撞，下一次碰撞一定发生在平衡位置，不可能在平衡位置左侧或右侧．故C 、D 正确．10．解析：选D.通过调整发生器发出的声波就能使酒杯碎掉，是利用共振的原理，因此操作人员一定是将声波发生器发出的声波频率调到500 Hz ，故D 选项正确．二、填空题(本题共2小题，每小题8分，共16分．把答案填在题中横线上)11答案：(1)B (2)摆长的测量、漏斗重心的变化、液体痕迹偏粗、阻力变化……12答案：(1)ABC (2)①98.50 ②B ③4π2k计算题13．(10分)解析：由题意知弹簧振子的周期T ＝0.5 s ，振幅A ＝4×10－2m. (1)a max ＝kx max m ＝kA m＝40 m/s 2. (2)3 s 为6个周期，所以总路程为s ＝6×4×4×10－2m ＝0.96 m.答案：(1)40 m/s 2(2)0.96 m14．(10分)解析：设单摆的摆长为L ，地球的质量为M ，则据万有引力定律可得地面的重力加速度和高山上的重力加速度分别为：g ＝G M R 2，g h ＝G M R ＋h2据单摆的周期公式可知T 0＝2πLg ，T ＝2πL g h由以上各式可求得h ＝(T T 0－1)R . 答案：(T T 0－1)R15．(12分解析：球A 运动的周期T A ＝2πl g，球B 运动的周期T B ＝2π l /4g ＝πl g. 则该振动系统的周期T ＝12T A ＋12T B ＝12(T A ＋T B )＝3π2l g. 在每个周期T 内两球会发生两次碰撞，球A 从最大位移处由静止开始释放后，经6T ＝9πlg，发生12次碰撞，且第12次碰撞后A 球又回到最大位置处所用时间为t ′＝T A /4. 所以从释放A 到发生第12次碰撞所用时间为t ＝6T －t ′＝9πl g －2T 2l g ＝17π2lg. 答案：17π2l g16．(12分解析：在力F 作用下，玻璃板向上加速，图示OC 间曲线所反映出的是振动的音叉振动位移随时间变化的规律，其中直线OC 代表音叉振动1.5个周期内玻璃板运动的位移，而OA 、AB 、BC 间对应的时间均为0.5个周期，即t ＝T 2＝12f＝0.1 s ．故可利用匀加速直线运动的规律——连续相等时间内的位移差等于恒量来求加速度．设板竖直向上的加速度为a ，则有：s BA －s AO ＝aT 2①s CB －s BA ＝aT 2，其中T ＝152 s ＝0.1 s ②由牛顿第二定律得F －mg ＝ma ③ 解①②③可求得F ＝24 N. 答案：24 N机械振动（2）机械振动（3）1【解析】如图所示，图线中a 、b 两处，物体处于同一位置，位移为负值，加速度一定相同，但速度方向分别为负、正，A 错误，C 正确．物体的位移增大时，动能减少，势能增加，D 错误．单摆摆球在最低点时，处于平衡位置，回复力为零，但合外力不为零，B 错误．【答案】 C2【解析】质量是惯性大小的量度，脱水桶转动过程中质量近似不变，惯性不变，脱水桶的转动频率与转速成正比，随着转动变慢，脱水桶的转动频率减小，因此，t 时刻的转动频率不是最大的，在t 时刻脱水桶的转动频率与机身的固有频率相等发生共振，故C 项正确．【答案】 C3【解析】摆球从A 运动到B 的过程中绳拉力不为零，时间也不为零，故冲量不为零，所以选项A 错；由动能定理知选项B 对；摆球运动到B 时重力的瞬时功率是mg v cos90°＝0，所以选项C 错；摆球从A 运动到B 的过程中，用时T /4，所以重力的平均功率为P ＝m v 2/2T /4＝2m v 2T ，所以选项D 错．【答案】 B4【解析】由振动图象可看出，在(T 2－Δt )和(T2＋Δt )两时刻，振子的速度相同，加速度大小相等方向相反，相对平衡位置的位移大小相等方向相反，振动的能量相同，正确选项是D.【答案】 D5【解析】据受迫振动发生共振的条件可知甲的振幅较大，因为甲的固有频率接近驱动力的频率．做受迫振动物体的频率等于驱动力的频率，所以B 选项正确．【答案】 B6【解析】由题意知，在细线未断之前两个弹簧所受到的弹力是相等的，所以当细线断开后，甲、乙两个物体做简谐运动时的振幅是相等的，A 、B 错；两物体在平衡位置时的速度最大，此时的动能等于弹簧刚释放时的弹性势能，所以甲、乙两个物体的最大动能是相等的，则质量大的速度小，所以C 正确，D 错误．【答案】 C题号 1 2 3 4 5 6 7 8 9 10答案 ACBADACBDACADD(T 2-T 1)R/T 17【答案】 C8【解析】根据题意，由能量守恒可知12kx 2＝mg (h ＋x )，其中k 为弹簧劲度系数，h 为物块下落处距O 点的高度，x 为弹簧压缩量．当x ＝x 0时，物块速度为0，则kx 0－mg ＝ma ，a ＝kx 0－mg m ＝kx 0m －g ＝2mg (h ＋x 0)mx 0－g ＝2g (h ＋x 0)x 0－g >g ，故正确答案为D.【答案】 D9【解析】由题中条件可得单摆的周期为T ＝0.30.2s ＝1.5s ，由周期公式T ＝2πlg可得l＝0.56m.【答案】 A10【解析】当摆球释放后，动能增大，势能减小，当运动至B 点时动能最大，势能最小，然后继续摆动，动能减小，势能增大，到达C 点后动能为零，势能最大，整个过程中摆球只有重力做功，摆球的机械能守恒，综上可知只有D 项正确．【答案】 D机械振动（4）1解析：选A.周期与振幅无关，故A 正确．2解析：选C.由单摆周期公式T ＝2π lg知周期只与l 、g 有关，与m 和v 无关，周期不变频率不变．又因为没改变质量前，设单摆最低点与最高点高度差为h ，最低点速度为v ，mgh ＝12m v 2.质量改变后：4mgh ′＝12·4m ·(v 2)2，可知h ′≠h ，振幅改变．故选C.3解析：选D.此摆为复合摆，周期等于摆长为L 的半个周期与摆长为L2的半个周期之和，故D 正确．4解析：选B.由简谐运动的对称性可知，t Ob ＝0.1 s ，t bc ＝0.1 s ，故T4＝0.2 s ，解得T ＝0.8s ，f ＝1T＝1.25 Hz ，选项B 正确．5解析：选D.当单摆A 振动起来后，单摆B 、C 做受迫振动，做受迫振动的物体的周期(或频率)等于驱动力的周期(或频率)，选项A 错误而D 正确；当物体的固有频率等于驱动力的频率时，发生共振现象，选项C 正确而B 错误．6解析：选BD.速度越来越大，说明振子正在向平衡位置运动，位移变小，A 错B 对；速度与位移反向，C 错D 对．7解析：选AD.P 、N 两点表示摆球的位移大小相等，所以重力势能相等，A 对；P 点的速度大，所以动能大，故B 、C 错D 对．8解析：选BD.受迫振动的频率总等于驱动力的频率，D 正确；驱动力频率越接近固有频率，受迫振动的振幅越大，B 正确．9解析：选B.读图可知，该简谐运动的周期为4 s ，频率为0.25 Hz ，在10 s 内质点经过的路程是2.5×4A ＝20 cm.第4 s 末的速度最大．在t ＝1 s 和t ＝3 s 两时刻，质点位移大小相等、方向相反．。

大学物理振动

第二象限
P
A
M
第三象限
第一象限
x
第四象限
注意：旋转矢量在第3象限速度V〉0
第二象限
P
A
第三象限 M
第一象限
x
第四象限
注意：旋转矢量在第3象限速度V〉0
第二象限
P
A
第三象限
M
第一象限
x
第四象限
注意：旋转矢量在第3象限速度V〉0
第二象限
P
第三象限
A
M
第一象限
x
第四象限
注意：旋转矢量在第3象限速度V〉0
第二象限
第三象限
第一象限
P
A
x
M
第四象限
注意：旋转矢量在第4象限速度V〉0
第二象限
第三象限
第一象限
P
A
x
M
第四象限
注意：旋转矢量在第4象限速度V〉0
第二象限
第三象限
第一象限
A
M Px
第四象限
注意：旋转矢量在第4象限速度V〉0
第二象限
第三象限
第一象限
A
M Px
第四象限
第二象限第三象限
t=t
51
一、同方向同频率的简谐振动的合成
1、解析法
x1=A1cos( t+ 1) x2=A2cos( t+ 2)
合振动 :
x x1 x2 A1 cos( t 1) A2 cos( t 2 )
(A1 cos1 A2 cos2) cos t (A1 sin1 A2 sin2)sin t
Acos
d 2t l
令 g l 2 则有：
d 2 2 0

第五、六章作业解答

x(m)
4.0
x(m)
0.10 0.05
P
B
t (s)
P
4.0

O
o0
B

AB
O
AO
o0
B
t (s)
1

由比例关系求振动的周期T
(2) 画出P点对应的旋转矢量AP，可知P点相位： P

0
t BO BO 5 6 5 T 2 2 12
T

PO P O 0 ( 3) 3 OP两点的相位差：
2
(1) 由振动曲线可知振动的振幅：解： A 0.10m

BO B O 2 ( 3) 5 6

画出t =0时刻的旋转矢量AO，可知振动的初相：
OB两点的时间间隔：t BO 4.0s
x(m)
AO
x(m)
0.10 0.05
O 5 3 或 3
Ex5-20
3 2k 1 2k 0.75

x2+x3振幅最小的条件是： 32 3 2 ( 2k 1)
两个同频率简谐运动1和2的振动曲线如图所示，求：(1)两简谐运动的运动方程；(2) 在同一图中画出两简谐运动的旋转矢量； (3) 若两简谐运动叠加，求合振动方程。
o0
t (s)

2 rad s 1 T
2

画出两个简谐运动在初始时刻的旋转矢量A1和A2。由矢量图可知两个简谐运动的初相分别为： 1 2 因此两简谐运动方程分别为：
2

两简谐运动的相位差： 21 2 1 合振动振幅： A
2 1 2 2

物理学教程(第二版)[上册]第五章课后习题答案解析详解

物理学教程第二版第五章课后习题答案第五章机械振动5-1 一个质点作简谐运动，振幅为A ，在起始时刻质点的位移为2A，且向x 轴正方向运动，代表此简谐运动的旋转矢量为（）题5-１图分析与解（B ）图中旋转矢量的矢端在x 轴上投影点的位移为－A /2，且投影点的运动方向指向Ox 轴正向，即其速度的x 分量大于零，故满足题意．因而正确答案为（B ）．5-2 一简谐运动曲线如图（a ）所示，则运动周期是（）(A) 2.62 s (B) 2.40 s (C) 2.20 s（D ）2.00 s题5-２图分析与解由振动曲线可知，初始时刻质点的位移为A /2，且向x 轴正方向运动．图（ｂ）是其相应的旋转矢量图，由旋转矢量法可知初相位为-3/π2．振动曲线上给出质点从A /2 处运动到x =0处所需时间为1 s ，由对应旋转矢量图可知相应的相位差65232πππϕ=+=∆，则角频率1s rad 65Δ/Δ-⋅==πϕωt ，周期s 40.22==ωπT .故选（B ）． 5-3 两个同周期简谐运动曲线如图（a ）所示， x 1的相位比x 2的相位（）（A ）落后2π（B ）超前2π（C ）落后π（D ）超前π分析与解由振动曲线图作出相应的旋转矢量图（b ）即可得到答案为（B ）．题5 -３图5-4 两个同振动方向、同频率、振幅均为A 的简谐运动合成后，振幅仍为A ，则这两个简谐运动的相位差为（）（A ）60 （B ）90 （C ）120 （D ）180分析与解由旋转矢量图可知两个简谐运动1和2的相位差为120 时，合成后的简谐运动3的振幅仍为A .正确答案为（C ）．题5-4图5-5 若简谐运动方程为⎪⎭⎫ ⎝⎛+=4ππ20cos 10.0t x ，式中x 的单位为m ，t 的单位为s.求：（1）振幅、频率、角频率、周期和初相；（2）s 2=t 时的位移、速度和加速度．分析可采用比较法求解．将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量．运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果．解（1）将()()m π25.0π20cos 10.0+=t x 与()ϕω+=t A x cos 比较后可得：振幅A ＝0.10m ，角频率1s rad π20-⋅=ω，初相ϕ＝0.25π，则周期s 1.0/π2==ωT ，频率Hz /1T =v ．（２）s 2=t 时的位移、速度、加速度分别为()m 1007.7π25.0π40cos 10.02-⨯=+=t x()-1s m 44.4π25.0π40sin π2d /d ⋅-=+-==t x v()-22222s m 1079.2π25.0π40cos π40d /d ⋅⨯-=+-==t x a5-6 一远洋货轮，质量为m ，浮在水面时其水平截面积为S ．设在水面附近货轮的水平截面积近似相等，水的密度为ρ，且不计水的粘滞阻力，证明货轮在水中作振幅较小的竖直自由运动是简谐运动，并求振动周期．分析要证明货轮作简谐运动，需要分析货轮在平衡位置附近上下运动时，它所受的合外力F 与位移x 间的关系，如果满足kx F -=，则货轮作简谐运动．通过kx F -=即可求得振动周期k m ωT /π2/π2==．证货轮处于平衡状态时［图（a ）］，浮力大小为F ＝mg ．当船上下作微小振动时，取货轮处于力平衡时的质心位置为坐标原点O ，竖直向下为x 轴正向，如图（b ）所示．则当货轮向下偏移x 位移时，受合外力为∑'+=F P F其中F '为此时货轮所受浮力，其方向向上，大小为gSx mg gSx F F ρρ+=+='题5-6图则货轮所受合外力为kx gSx F P F -=-='-=∑ρ式中gS k ρ=是一常数．这表明货轮在其平衡位置上下所作的微小振动是简谐运动．由∑=t x m F 22d d /可得货轮运动的微分方程为0d d 22=+m gSx t x //ρ令m gS /ρω=2，可得其振动周期为gS ρm πωT /2/π2==5-7 如图（a ）所示，两个轻弹簧的劲度系数分别为1k 、2k ．当物体在光滑斜面上振动时．（1）证明其运动仍是简谐运动；（2）求系统的振动频率．题5-7图分析从上两题的求解知道，要证明一个系统作简谐运动，首先要分析受力情况，然后看是否满足简谐运动的受力特征（或简谐运动微分方程）．为此，建立如图（b ）所示的坐标．设系统平衡时物体所在位置为坐标原点O ，Ox 轴正向沿斜面向下，由受力分析可知，沿Ox 轴，物体受弹性力及重力分力的作用，其中弹性力是变力．利用串联时各弹簧受力相等，分析物体在任一位置时受力与位移的关系，即可证得物体作简谐运动，并可求出频率υ．证设物体平衡时两弹簧伸长分别为1x 、2x ，则由物体受力平衡，有2211sin x k x k mg ==θ（1）按图（b ）所取坐标，物体沿x 轴移动位移x 时，两弹簧又分别被拉伸1x '和2x '，即21x x x '+'=．则物体受力为 ()()111222sin sin x x k mg x x k mg F '+-='+-=θθ（２）将式（1）代入式（2）得1122x k x k F '-='-=（３）由式（3）得11k F x /-='、22k F x /-='，而21x x x '+'=，则得到()[]kx x k k k k F -=+-=2121/式中()2121k k k k k +=/为常数，则物体作简谐运动，振动频率 ()m k k k k πm k ωv 2121/21/π21π2/+=== 讨论（1）由本题的求证可知，斜面倾角θ对弹簧是否作简谐运动以及振动的频率均不产生影响．事实上，无论弹簧水平放置、斜置还是竖直悬挂，物体均作简谐运动．而且可以证明它们的频率相同，均由弹簧振子的固有性质决定，这就是称为固有频率的原因．（2）如果振动系统如图（c ）（弹簧并联）或如图（d ）所示，也可通过物体在某一位置的受力分析得出其作简谐运动，且振动频率均为()m k k v /π2121+=，读者可以一试．通过这些例子可以知道，证明物体是否作简谐运动的思路是相同的．5-8 一放置在水平桌面上的弹簧振子，振幅A ＝2.0 ×10-2 m ，周期T ＝0.50ｓ．当t ＝0 时，（1）物体在正方向端点；（2）物体在平衡位置、向负方向运动；（3）物体在x ＝-1.0×10-2m 处，向负方向运动；（4）物体在x ＝-1.0×10-2 m 处，向正方向运动．求以上各种情况的运动方程．分析在振幅A 和周期T 已知的条件下，确定初相φ是求解简谐运动方程的关键．初相的确定通常有两种方法．（1）解析法：由振动方程出发，根据初始条件，即t ＝0 时，x ＝x 0和v ＝v 0来确定φ值．（2）旋转矢量法：如图（a ）所示，将质点P 在Ox 轴上振动的初始位置x 0和速度v 0的方向与旋转矢量图相对应来确定φ．旋转矢量法比较直观、方便，在分析中常采用．题5-8图解由题给条件知A ＝2.0 ×10-2 m ，1s π4/2-==T ω，而初相φ可采用分析中的两种不同方法来求．解析法：根据简谐运动方程()ϕω+=t A x cos ，当0t =时有()ϕω+=t A x cos 0，sin 0ϕωA -=v ．当（1）A x =0时，1cos 1=ϕ，则01=ϕ；（2）00=x 时，0cos 2=ϕ，2π2±=ϕ，因00<v ，取2π2=ϕ；（3）m 100120-⨯=.x 时，50cos 3.=ϕ，3π3±=ϕ，由00<v ，取3π3=ϕ；（4）m 100120-⨯-=.x 时，50cos 4.-=ϕ，3ππ4±=ϕ，由00>v ，取3π44=ϕ．旋转矢量法：分别画出四个不同初始状态的旋转矢量图，如图（b ）所示，它们所对应的初相分别为01=ϕ，2π2=ϕ，3π3=ϕ，3π44=ϕ．振幅A 、角频率ω、初相φ均确定后，则各相应状态下的运动方程为（1）()m t πcos4100.22-⨯=x（2）()()m /2πt π4cos 100.22+⨯=-x（3）()()m /3πt π4cos 100.22+⨯=-x（4）()()m0.22+10=-xcos⨯/3π44tπ5-9有一弹簧，当其下端挂一质量为m的物体时，伸长量为9.8 ×10-2 m．若使物体上、下振动，且规定向下为正方向．（1）当t＝0 时，物体在平衡位置上方8.0 ×10-2ｍ处，由静止开始向下运动，求运动方程．（2）当t＝０时，物体在平衡位置并以0.6ｍ·s-1的速度向上运动，求运动方程．分析求运动方程，也就是要确定振动的三个特征物理量A、ω和φ．其中振动的角频率是由弹簧振子系统的固有性质（振子质量m及弹簧劲度系数k）决定的，即k mω=/，k可根据物体受力平衡时弹簧的伸长来计算；振幅A和初相φ需要根据初始条件确定．题5-9图解物体受力平衡时，弹性力F与重力P的大小相等，即F＝mg．而此时弹簧的伸长量Δl＝9.8 ×10-2m．则弹簧的劲度系数k＝F／Δl ＝mg／Δl．系统作简谐运动的角频率为1ωmk//g=s=l10-∆=（1）设系统平衡时，物体所在处为坐标原点，向下为x轴正向．由初始条件t ＝0 时，x10＝8.0 ×10-2m、v10＝0 可得振幅()m 10082210210-⨯=+=./ωv x A ；应用旋转矢量法可确定初相π1=ϕ［图（a ）］．则运动方程为()()m π10t cos 100.821+⨯=-x（2）t ＝０时，x 20＝0、v 20＝0.6 ｍ·s -1，同理可得()m 100622202202-⨯=+=./ωv x A ；2/π2=ϕ［图（b ）］．则运动方程为 ()()m π5.010t cos 100.622+⨯=-x5-10 某振动质点的x -t 曲线如图（a ）所示，试求：（1）运动方程；（2）点P 对应的相位；（3）到达点P 相应位置所需的时间．分析由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题．本题就是要通过x －t 图线确定振动的三个特征量A 、ω和0ϕ，从而写出运动方程．曲线最大幅值即为振幅A ；而ω、0ϕ通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比较方便．解（1）质点振动振幅A ＝0.10 ｍ．而由振动曲线可画出t 0＝0 和t 1＝4 ｓ时旋转矢量，如图（b ）所示．由图可见初相3/π0-=ϕ（或3/π50=ϕ），而由()3201//ππω+=-t t 得1s 24/π5-=ω，则运动方程为()m 3/π24π5cos 10.0⎪⎭⎫ ⎝⎛-=t x题5-10图（2）图（a ）中点P 的位置是质点从A ／2 处运动到正向的端点处．对应的旋转矢量图如图（c ）所示．当初相取3/π0-=ϕ时，点P 的相位为()000=-+=p p t ωϕϕ（如果初相取成3/π50=ϕ，则点P 相应的相位应表示为()π200=-+=p p t ωϕϕ．（3）由旋转矢量图可得()3/π0=-p t ω，则s 61.=p t ．5-11 质量为10 g 的物体沿x 的轴作简谐运动，振幅A =10 cm ，周期T =4.0 s ，t =0 时物体的位移为，cm 0.50-=x 且物体朝x 轴负方向运动，求（1）t =1.0 s 时物体的位移；（2）t =1.0 s 时物体受的力；（3）t =0之后何时物体第一次到达x =5.0 cm 处；（4）第二次和第一次经过x =5.0 cm 处的时间间隔.分析根据题给条件可以先写出物体简谐运动方程)cos(ϕω+=t A x .其中振幅A ，角频率Tπ2=ω均已知，而初相ϕ可由题给初始条件利用旋转矢量法方便求出. 有了运动方程，t 时刻位移x 和t 时刻物体受力x m ma F 2ω-==也就可以求出. 对于（3）、（4）两问均可通过作旋转矢量图并根据公式t ∆=∆ωϕ很方便求解.解由题给条件画出t =0时该简谐运动的旋转矢量图如图（a ）所示，可知初相3π2=ϕ.而A =0.10 m ，1s 2ππ2-==T ω.则简谐运动方程为m )3π22πcos(10.0+=t x (1)t =1.0 s 时物体的位移m 1066.8m )3π22π0.1cos(10.02-⨯-=+⨯=x（2）t =1.0 s 时物体受力N1014.2N)1066.8()2π(101032232---⨯=⨯-⨯⨯⨯-=-=x m F ω （3）设t =0时刻后，物体第一次到达x =5.0 cm 处的时刻为t 1，画出t =0和t =t 1时刻的旋转矢量图，如图（b ）所示，由图可知，A 1与A 的相位差为π，由t ∆=∆ωϕ得s 2s 2/ππ1==∆=ωϕt （4）设t =0时刻后，物体第二次到达x =5.0 cm 处的时刻为t 2,画出t =t 1和t = t 2时刻的旋转矢量图，如图（c ）所示，由图可知，A 2与A 1的相位差为3π2，故有 s 34s 2/π3/π212==∆=-=∆ωϕt t t题 5-11 图5-12 图（a ）为一简谐运动质点的速度与时间的关系曲线，且振幅为2cm ，求（1）振动周期；（2）加速度的最大值；（3）运动方程．分析根据v -t 图可知速度的最大值v max ，由v max ＝Aω可求出角频率ω，进而可求出周期T 和加速度的最大值a max ＝Aω2．在要求的简谐运动方程x ＝A cos （ωt ＋φ）中，因为A 和ω已得出，故只要求初相位φ即可．由v －t 曲线图可以知道，当t ＝0 时，质点运动速度v 0＝v max /2 ＝Aω/2，之后速度越来越大，因此可以判断出质点沿x 轴正向向着平衡点运动．利用v 0＝－Aωsinφ就可求出φ．解（1）由ωA v =max 得1s 51-=.ω，则s 2.4/π2==ωT（2）222max s m 1054--⋅⨯==.ωA a（3）从分析中已知2/sin 0ωA ωA =-=v ，即21sin /-=ϕ6/π5,6/π--=ϕ因为质点沿x 轴正向向平衡位置运动，则取6/π5-=，其旋转矢量图如图（b ）所示．则运动方程为()cm 6π55.1cos 2⎪⎭⎫⎝⎛-=t x题5-12图5-13 有一单摆，长为1.0m ，最大摆角为5°，如图所示．（1）求摆的角频率和周期；（2）设开始时摆角最大，试写出此单摆的运动方程；（3）摆角为3°时的角速度和摆球的线速度各为多少？题5-13图分析单摆在摆角较小时（θ＜5°）的摆动，其角量θ与时间的关系可表示为简谐运动方程()ϕωθθ+=t cos max ，其中角频率ω仍由该系统的性质（重力加速度g 和绳长l ）决定，即l g /=ω．初相φ与摆角θ，质点的角速度与旋转矢量的角速度（角频率）均是不同的物理概念，必须注意区分．解（1）单摆角频率及周期分别为s 01.2/π2;s 13.3/1====-ωT l g ω（2）由0=t 时o max 5==θθ可得振动初相0=ϕ，则以角量表示的简谐运动方程为t θ13.3cos 36π=（３）摆角为3°时，有()60cos max ./==+θθϕωt ，则这时质点的角速度为()()1max 2max max s2180800cos 1sin /d d --=-=+--=+-=..ωθϕωωθϕωωθθt t t线速度的大小为1s m 218.0/d d -⋅-==t l v θ讨论质点的线速度和角速度也可通过机械能守恒定律求解，但结果会有极微小的差别．这是因为在导出简谐运动方程时曾取θθ≈sin ，所以，单摆的简谐运动方程仅在θ较小时成立．*5-14 一飞轮质量为12kg ，内缘半径r ＝0.6ｍ，如图所示．为了测定其对质心轴的转动惯量，现让其绕内缘刃口摆动，在摆角较小时，测得周期为2.0s ，试求其绕质心轴的转动惯量．题5-14图分析飞轮的运动相当于一个以刃口为转轴的复摆运动，复摆振动周期为c /π2mgl J T =，因此，只要知道复摆振动的周期和转轴到质心的距离c l ，其以刃口为转轴的转动惯量即可求得．再根据平行轴定理，可求出其绕质心轴的转动惯量．解由复摆振动周期c /π2mgl J T =，可得22π4/m g r TJ =（这里r l C ≈）．则由平行轴定理得222220m kg 83.2π4⋅=-=-=mr mgrT mr J J 5-15 如图（a ）所示，质量为 1.0 ×10-2kg 的子弹，以500m·s -1的速度射入木块，并嵌在木块中，同时使弹簧压缩从而作简谐运动，设木块的质量为4.99 kg ，弹簧的劲度系数为8.0 ×103 N·m -1，若以弹簧原长时物体所在处为坐标原点，向左为x 轴正向，求简谐运动方程．题5-15图分析可分为两个过程讨论．首先是子弹射入木块的过程，在此过程中，子弹和木块组成的系统满足动量守恒，因而可以确定它们共同运动的初速度v 0，即振动的初速度．随后的过程是以子弹和木块为弹簧振子作简谐运动．它的角频率由振子质量m 1＋m 2和弹簧的劲度系数k 确定，振幅和初相可根据初始条件（初速度v 0和初位移x 0）求得．初相位仍可用旋转矢量法求．解振动系统的角频率为()121s 40-=+=m m k /ω由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度v 0为12110s m 0.1-⋅=+=m m v m v又因初始位移x 0＝0，则振动系统的振幅为()m 105.2//202020-⨯==+=ωωx A v v图（b ）给出了弹簧振子的旋转矢量图，从图中可知初相位2/π0=ϕ，则简谐运动方程为()()m π0.540cos 105.22+⨯=-t x5-16 如图（a ）所示，一劲度系数为k 的轻弹簧，其下挂有一质量为m 1的空盘．现有一质量为m 2的物体从盘上方高为h 处自由落入盘中，并和盘粘在一起振动．问：（1）此时的振动周期与空盘作振动的周期有何不同？（2）此时的振幅为多大？题5-16图分析原有空盘振动系统由于下落物体的加入，振子质量由m 1变为m 1 + m 2，因此新系统的角频率（或周期）要改变．由于()2020/ωx A v +=，因此，确定初始速度v 0和初始位移x 0是求解振幅A 的关键．物体落到盘中，与盘作完全非弹性碰撞，由动量守恒定律可确定盘与物体的共同初速度v 0，这也是该振动系统的初始速度．在确定初始时刻的位移x 0时，应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置．因此，本题中初始位移x 0，也就是空盘时的平衡位置相对新系统的平衡位置的位移．解（1）空盘时和物体落入盘中后的振动周期分别为k m ωT /π2/π21== ()k m m ωT /π2/π221+='='可见T ′＞T ，即振动周期变大了．（2）如图（b ）所示，取新系统的平衡位置为坐标原点O ．则根据分析中所述，初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移，即g kmg k m m k g m l l x 2211210-=+-=-= 式中k g m l 11=为空盘静止时弹簧的伸长量，l 2＝g km m 21+为物体粘在盘上后，静止时弹簧的伸长量．由动量守恒定律可得振动系统的初始速度，即盘与物体相碰后的速度gh m m m m m m 22122120+=+=v v 式中gh 2=v 是物体由h 高下落至盘时的速度．故系统振动的振幅为()gm m khk g m x A )(21/2122020++='+=ωv 本题也可用机械能守恒定律求振幅A ．5-17 质量为0.10kg 的物体，以振幅1.0×10-2 m 作简谐运动，其最大加速度为4.0 ｍ·s -1求：（1）振动的周期；（2）物体通过平衡位置时的总能量与动能；（3）物体在何处其动能和势能相等？（4）当物体的位移大小为振幅的一半时，动能、势能各占总能量的多少？分析在简谐运动过程中，物体的最大加速度2max ωA a =，由此可确定振动的周期T ．另外，在简谐运动过程中机械能是守恒的，其中动能和势能互相交替转化，其总能量E ＝kA 2/2．当动能与势能相等时，E k ＝E P ＝kA 2/4．因而可求解本题．解（1）由分析可得振动周期s 314.0/π2/π2max ===a A ωT（2）当物体处于平衡位置时，系统的势能为零，由机械能守恒可得系统的动能等于总能量，即J 100221213max22k -⨯====.mAa mA E E ω （3）设振子在位移x 0处动能与势能相等，则有42220//kA kx =得m 100772230-⨯±=±=./A x（４）物体位移的大小为振幅的一半（即2x A =/）时的势能为4221212P /E A k kx E =⎪⎭⎫⎝⎛==则动能为43P K /E E E E =-=5-18 一劲度系数k =312 1m N -⋅的轻弹簧，一端固定，另一端连接一质量kg 3.00=m 的物体，放在光滑的水平面上，上面放一质量为kg 2.0=m 的物体，两物体间的最大静摩擦系数5.0=μ.求两物体间无相对滑动时，系统振动的最大能量.分析简谐运动系统的振动能量为2p k 21kA E E E =+=.因此只要求出两物体间无相对滑动条件下，该系统的最大振幅max A 即可求出系统振动的最大能量.因为两物体间无相对滑动，故可将它们视为一个整体，则根据简谐运动频率公式可得其振动角频率为mm k+=0ω.然后以物体m 为研究对象，它和m 0一起作简谐运动所需的回复力是由两物体间静摩擦力来提供的.而其运动中所需最大静摩擦力应对应其运动中具有最大加速度时，即max 2max A m ma mg ωμ==，由此可求出max A . 解根据分析，振动的角频率mm k+=0ω 由max 2max A m ma mg ωμ==得kgm m g A μωμ)(02max +=则最大能量J1062.92)(])([212132220202max max -⨯=+=+==kg m m kg m m k kA E μμ5-19 已知两同方向、同频率的简谐运动的运动方程分别为()()m π75.010cos 05.01+=t x ；()()m π25.010cos 06.02+=t x ．求：（1）合振动的振幅及初相；（2）若有另一同方向、同频率的简谐运动()()m 10cos 07033ϕ+=t x .，则3ϕ为多少时，x 1＋x 3的振幅最大？又3ϕ为多少时，x 2＋x 3的振幅最小？题5-19图分析可采用解析法或旋转矢量法求解.由旋转矢量合成可知，两个同方向、同频率简谐运动的合成仍为一简谐运动，其角频率不变；合振动的振幅()12212221cos 2ϕϕ-++=A A A A A ，其大小与两个分振动的初相差12ϕϕ-相关．而合振动的初相位()()[]22112211cos cos sin sin arctan ϕϕϕϕϕA A A A ++=/解（1）作两个简谐运动合成的旋转矢量图（如图）．因为2/πΔ12-=-=ϕϕϕ，故合振动振幅为()m 1087cos 2212212221-⨯=-++=.ϕϕA A A A A合振动初相位()()[]rad1.48arctan11cos cos sin sin arctan 22112211==++=ϕϕϕϕϕA A A A /（2）要使x 1＋x 3振幅最大，即两振动同相，则由π2Δk =ϕ得,...2,1,0,π75.0π2π213±±=+=+=k k k ϕϕ要使x 1＋x 3的振幅最小，即两振动反相，则由()π12Δ+=k ϕ得(),...2,1,0,π25.1π2π1223±±=+=++=k k k ϕϕ5-20 两个同频率的简谐运动1 和2 的振动曲线如图（a ）所示，求（1）两简谐运动的运动方程x 1和x 2；（2）在同一图中画出两简谐运动的旋转矢量，并比较两振动的相位关系；（3）若两简谐运动叠加，求合振动的运动方程．分析振动图已给出了两个简谐运动的振幅和周期，因此只要利用图中所给初始条件，由旋转矢量法或解析法求出初相位，便可得两个简谐运动的方程．解（1）由振动曲线可知，A ＝0.1 ｍ，T ＝2ｓ，则ω＝2π／T ＝πｓ-1．曲线1表示质点初始时刻在x ＝0 处且向x 轴正向运动，因此φ1＝－π／2；曲线2 表示质点初始时刻在x ＝A /2 处且向x 轴负向运动，因此φ2＝π／3．它们的旋转矢量图如图（b ）所示．则两振动的运动方程分别为()()m 2/ππcos 1.01-=t x 和()()m 3/ππcos 1.02+=t x（2）由图（b ）可知振动2超前振动1 的相位为5π／6．（3）()ϕω+'=+=t A x x x cos 21其中()m 0520cos 212212221.=-++='ϕϕA A A A A()12π0.268arctan cos cos sin sin arctan22112211-=-=++=ϕϕϕϕϕA A A A则合振动的运动方程为 ()()m π/12πcos 052.0-=t x题5-20 图5-21 将频率为348 Hz 的标准音叉振动和一待测频率的音叉振动合成，测得拍频为3.0Hz ．若在待测频率音叉的一端加上一小块物体，则拍频数将减少，求待测音叉的固有频率．分析这是利用拍现象来测定振动频率的一种方法．在频率υ1和拍频数Δυ＝|υ2－υ1|已知的情况下，待测频率υ2可取两个值，即υ2＝υ1 ±Δυ．式中Δυ前正、负号的选取应根据待测音叉系统质量改变时，拍频数变化的情况来决定．解根据分析可知，待测频率的可能值为υ2＝υ1 ±Δυ＝（348 ±3） Hz因振动系统的固有频率mkπ21=v ，即质量m 增加时，频率υ减小．从题意知，当待测音叉质量增加时拍频减少，即｜υ2－υ1｜变小．因此，在满足υ2与Δυ均变小的情况下，式中只能取正号，故待测频率为υ2＝υ1＋Δυ＝351 Hz*5-22 图示为测量液体阻尼系数的装置简图，将一质量为m 的物体挂在轻弹簧上，在空气中测得振动的频率为υ1，置于液体中测得的频率为υ2，求此系统的阻尼系数．题5-22图分析在阻尼不太大的情况下，阻尼振动的角频率ω与无阻尼时系统的固有角频率ω0及阻尼系数δ有关系式220δωω-=．因此根据题中测得的υ1和υ2（即已知ω0、ω），就可求出δ．解物体在空气和液体中的角频率为10π2v =ω和2π2v =ω，得阻尼系数为2221220π2v v -=-=ωωδ。

大学物理第五章机械振动习题解答和分析

5-1 有一弹簧振子，振幅m A 2100.2-⨯=，周期s T 0.1=，初相.4/3πϕ=试写出它的振动位移、速度和加速度方程。

分析根据振动的标准形式得出振动方程，通过求导即可求解速度和加速度方程。

解：振动方程为：]2cos[]cos[ϕπϕω+=+=t TA t A x 代入有关数据得：30.02cos[2]()4x t SI ππ=+ 振子的速度和加速度分别是：3/0.04sin[2]()4v dx dt t SI πππ==-+ 2223/0.08cos[2]()4a d x dt t SI πππ==-+5-2若简谐振动方程为m t x ]4/20cos[1.0ππ+=，求：（1）振幅、频率、角频率、周期和初相；（2）t=2s 时的位移、速度和加速度.分析通过与简谐振动标准方程对比，得出特征参量。

解：(1)可用比较法求解.根据]4/20cos[1.0]cos[ππϕω+=+=t t A x 得：振幅0.1A m =，角频率20/rad s ωπ=，频率1/210s νωπ-==，周期1/0.1T s ν==，/4rad ϕπ=（2）2t s =时，振动相位为：20/4(40/4)t rad ϕππππ=+=+ 由cos x A ϕ=，sin A νωϕ=-，22cos a A x ωϕω=-=-得 20.0707, 4.44/,279/x m m s a m s ν==-=-5-3质量为kg 2的质点，按方程))](6/(5sin[2.0SI t x π-=沿着x 轴振动.求：（1）t=0时，作用于质点的力的大小；（2）作用于质点的力的最大值和此时质点的位置.分析根据振动的动力学特征和已知的简谐振动方程求解，位移最大时受力最大。

解：（1）跟据x m ma f 2ω-==，)]6/(5sin[2.0π-=t x 将0=t 代入上式中，得： 5.0f N =（2）由x m f 2ω-=可知，当0.2x A m =-=-时，质点受力最大，为10.0f N =5-4为了测得一物体的质量m ，将其挂到一弹簧上并让其自由振动，测得振动频率Hz 0.11=ν；而当将另一已知质量为'm 的物体单独挂到该弹簧上时，测得频率为Hz 0.22=ν.设振动均在弹簧的弹性限度内进行，求被测物体的质量.分析根据简谐振动频率公式比较即可。

机械振动的检测

下一页返回
5.2 机械振动的类型
1.简谐振动简谐振动的振动量随时间的变化规律如图5-3所示，其位移
表达式为:
上一页下一页返回
5.2 机械振动的类型
将式(9-1)求导可得振动速度和振动加速度的表达式:
上一页下一页返回
5.2 机械振动的类型
由此可知，简谐振动的位移、速度和加速度的波形和频率都为一定，其速度和加速度的幅值与频率有关，在相位上，速度超前位移π/2，加速度又超前速度π/2。对于简谐振动，只要测定出位移、速度、加速度和频率这四个参数中的任意两个，便可推算出其余两个参数。
而且其振动量与时间也无一定的联系。诸如路面的不平对车辆的激励;加工工件表面层几何物理状况的不均匀对机床刀具的激励;波浪对船舶的激励;大气湍流对飞行器的激励等，都将会产生随机振动。随机振动的统计参数通常有均值、方均值、方差、相关函数和功率谱密度函数等，与一般随机信号的处理一样。
上一页下一页返回
上一页下一页返回
5.2 机械振动的类型
3.准周期振动准周期振动是由频率比不全为有理数的简谐振动迭加而成，
如
这种振动如果忽略其相位角，也可用离散频谱来表征，如图5-5所示。因而称之为准周期振动。
实际工作中遇到的两个或几个不相关联的周期振动混合作用时，便会产生这种振动状态。
上一页下一页返回
第五章机械振动的检测
5.1 概述 5.2 机械振动的类型 5.3 振动的激励和激振器 5.4 测振传感器 5.5 振动的测量
5.1 概述
机械振动是自然界、工程技术和日常生活中普遍存在的物理现象。各种机器、仪器和设备在其运行时，由于诸如回转件的不平衡、负载的不均匀、结构刚度的各向异性、润滑状况的不良及间隙等原因而引起力的变化、零部件之间的碰撞和冲击，以及由于使用、运输和外界环境条件下能量的传递、存储和释放等都会诱发或激励机械振动。所以说，任何一台运行着的机器、仪器和设备都会存在着振动现象。

5-1简谐运动简谐运动的振幅周期频率和相位讲解

四相位和初相
相位 (t ) ：决定简谐
初相位：
运动状态的物理量。
t =0 时的相位。 1）t ( x , v)存在一一对应的关系;
例： t x 0, v A 设有两个同频率的谐 2 2 A 振动，表达式分别为： t x , v 3 A 2 3 2
4 t 3
3 A A x , v 2 2
第五章机械振动 5-1 简谐运动简谐运动
19
的振幅周期频率和相位
2）相位在 0 ~ 2 内变 x1 A1 cos t 1 化，质点无相同的运动 x A cos t 2 2 2 状态；相位差为 2n 质二者的相位差为： t 2 t 1 2 1 点运动状态全同.（周 (a) 当 2k 时，称两个振期性）动为同相； 3）相位概念可用于比较两个谐振动之间在振 (b) 当 2k 1 时，称两个振动为反相；动步调上的差异。 (c) 当 0 时,称第二个振动超设有两个同频率的谐前第一个振动；振动，表达式分别为： (d) 当 0 时,称第二个振动落后第一个振动；
14
x A cos(t )
二振幅物体离开平衡位置的最大位移的绝对值。三周期、频率周期：物体作一次完全运动所经历的时间。
A xmax
A
x x t 图
T 2
T
o
A
t
x A cos(t )
T 2
周期
A cos[( t T ) ]
2 T 2 T
a
A
x
v
v
x t 图

第五章机械振动

当 t =0时,(1)物体在正方向端点；(2)物体在平衡位置,
并且向负方向运动; (3)物体在x0=1.0×10-2m处，向负方向运动，求以上各种情况的振动方程．
解 2 4 s1 x Acos(t )
T
(1) 0 x 2.0102 cos 4tm
(2) x 2.0102 cos(4t )m
确的?
（C ）
(A)物体处在运动正方向的端点时.速度和加速度
都达到最大值．
(B)物体位于平衡位置且向负方向运动时, 速度和加速度都为零．
(C)物体位于平衡位置且向正方向运动时, 速度最
大, 加速度为零．
(D)物体在负方向端点时,速度最大, 加速度为零.
第五章机械振动
课后练习九
3．已知一弹簧振子，物体处在运动正方向的端
0
解取竖直向下为正,以平衡位置为原点
A 0.1m F kx k 9.8N m1
0.5
0.6 O k 98s1 9.9s1
m
x / m x Acos(t ) 0.1cos(9.9t )m
第五章机械振动
课后练习十
7．图中a、b表示两个同方向同频率的简谐运动的
x-t曲线，求它们合振动运动方程为多少?
amax
(2)
Ek
E
1 mA2 2
2
1 2
mAamax
8.0103 J
(3)
Ek
Ep
1 2
E
1 2
kx02
1 4
kA2
x 2 2 10-2 m
第五章机械振动
课后练习九
8. 一质点作简谐振动，振幅为A，在起始时刻质点的位移为A/2，且向ox轴的正方向运动，画出此简谐运动的旋转矢量图。

大学物理第5章习题解答

第五章机械振动5-1一远洋货轮，质量为t M 4102⨯=，浮在水面对其水平截面积为23102m S ⨯=。

设在水面附近货轮的截面积与货轮高度无关，试证明此货轮在水中的铅直自由运动是简谐振动，并求其自由振动的周期。

解：取固定坐标xOy ，坐标原点O 在水面上（图题所示）设货轮静止不动时，货轮上的A 点恰在水面上，则浮力为S ρga .这时 ga s Mg ρ= 往下沉一点时，合力 )(y a g s Mg F +-=ρ gy s ρ-=. 又 22d d t yMMa F == 故0d d 22=+gy s t y M ρ022=+y M gs dt dy ρ 故作简谐振动 M gs ρω=2)(35.68.910102101022223334s g s M T =⨯⨯⨯⨯⨯===πρπωπ5-2 重物A 的质量M=1kg ，放在倾角030=θ的光滑斜面上，并用绳跨过定滑轮与劲度系数149-⋅=m N k 的轻弹簧连接，如习题5-2图所示，将物体由弹簧未形变的位置静止释放，并开始计时，试求:（1）不计滑轮质量，物体A 的运动方程;（2）滑轮为质量M ，半轻r 的均质圆盘，物体A 的运动方程。

解：取物体A 为研究对象，建立坐标Ox 轴沿斜面向下，原点取在平衡位置处，即在初始位置斜下方距离l 0处，此时：)(1.0sin 0m kmg l ==θ(1) 习题5-1图(1) A 物体共受三力；重mg, 支持力N, 张力T.不计滑轮质量时，有 T =kx列出A 在任一位置x 处的牛顿方程式220d d )(sin sin txm x l k mg T mg =+-=-θθ将（1）式代入上式，整理后得0d d 22=+x mkt x 故物体A 的运动是简谐振动，且)rad/s (7==mkω 由初始条件,000⎩⎨⎧=-=v l x 求得,1.00⎩⎨⎧===πϕml A 故物体A 的运动方程为x =(7t+π)m(2) 当考虑滑轮质量时，两段绳子中张力数值不等，如图所示，分别为T 1、T 2,则对A 列出任一位置x 处的牛顿方程式为:221d d sin txm T mg =-θ (2)对滑轮列出转动方程为：22221d d 2121t x Mr r a Mr J r T r T =⎪⎭⎫ ⎝⎛==-β (3)式中,T 2=k (l 0+x ) （4）由式（3）、(4)知2201d d 21)(t xM x l k T ++=代入(2)式知22021)(sin dtxd m M x l k mg ⎪⎭⎫ ⎝⎛+=+-θ又由（1）式知0sin kl mg =θ故0d d )21(22=++kx txm M即0)2(d d 22=++x m M ktx 习题5-2图m M k +=22ω可见，物体A 仍作简谐振动，此时圆频率为：rad/s)(7.52=+=m M k ω由于初始条件：0,000=-=v l x可知，A 、ϕ不变，故物体A 的运动方程为:m t x )7.5cos(1.0π+=由以上可知：弹簧在斜面上的运动，仍为简谐振动，但平衡位置发生了变化，滑轮的质量改变了系统的振动频率.5-3质点作简谐振动的振动曲线如习题5-3图所示，试根据图得出该质点的振动表达式。

第五章机械振动

cos 2 (t
0)
3、总能
E
Ek
EP
1 2
kA2
1 2
m 2 A2
1 2
mv
2 max
4、动能和势能在一个周期内的平均值
cos 2 1 (1 cos 2 )
2
sin2 1 1 cos 2
2
32
在一个周期 T 内的平均动能
Ek
1 T
T 0
1 2
kA 2
sin 2
(t
0
)dt
1
T
A A; B A; C 3 A; D 2 A
4
2
2
2
解： 1 mv 2 1 kx 2 1 kA2
2
2
2
而题知 1 mv 2 1 kx 2
2
2
1 kx 2 1 1 kA2
2
22
于是 x 2 A,即应选D
2
34
例：一物体质量为0.25kg，在弹性力作用下作简谐振
动，弹簧的倔强系数k=25Nm-1，如果起始振动具有势
3过阻尼541弱阻尼谐振子系统谐受迫振动微分方程ptdtdt452受迫振动ptdtdt不讨论随机外力cospt只讨论谐和策动力f周期性外力用下的新平衡点将坐标原点移至恒力作恒力作用552方程的解及其物理意义由微分方程理论上述方程的解为1自由振动的能量是外界一次性输入减幅振动有能量损耗有阻尼等幅振动能量守恒无阻尼2受迫振动过程中外界在不断地向振动系统补充能量的稳定受迫振动是由谐和策动力所维持也就不存在了与初始条件相关的a当其衰减完毕时的固有项就是由初始能量所维持563稳定的受迫振动说明此时振动方程的位相与初始条件无关其表示振动位移的位相与策动力位相的位相差

机械振动基础第五章随机振动教材

第五章随机振动
——对于确定性振动，以相同的条件重现振动时，在预定的时刻将出现预计的振动。因此，确定性振动中的物理量在将来某一时刻的值是可以预测的。比如：单自由度系统的简谐强迫振动，只要系统不变，初始条件不变，激励不变，则系统响应是确定的，也不变。
——对于随机振动，以相同的条件重现振动时，会发现振动的物理量没有重复性，即无法预测其在将来某一时刻究竟取什么值。
xr
xr
(t)
lim
T
1 T
T /2
T / 2 xr (t)dt
随机过程X(t)在时域的平均值
样本函数时域描述样本平均随机变量集合描述集合平均
2．方差
a) 方差的集合定义（随机变量的方差）
2 x
(t1
)
D[
X
(t1)]
E[{X
(t1
)
x
(t1
)}2
]
{x
x
(t1
)}2
p(
x,
t1
)dx
x减均值的二次方与一维概率密度函数的乘积
任何一个随机过程X(t)是一系列(一般是无穷多个)样本函数的集合，记为：
X (t) {xr (t)}
还可从另外的角度去看随机过程X(t)：给定一个时刻t1， X(t1)是一个随机变量，它的取值范围是随机过程X(t)所有的样本函数xr(t)在t1时刻的值的全体{xr(t1)}。称随机变量 X(t1)为随机过程X(t)在t1时刻的截口或状态。
§5.2 随机过程的数字特征
1) 随机过程是样本函数的集合，因此可以逐个描述样本函数，从而得到随机过程的性质，这种描述称为时域描述。又称为样本平均。
2) 随机过程既然是随机变量系，就可以用描述随机变量的方法来描述随机过程。称为集合描述；或者集合平均。

大学物理第五章机械振动

A0 B C
提交
例题2. 弹簧振子放在光滑的水平面上，已知k=1.60N/m，m=0.4kg.
试就下列两种情形分别求运动方程. (1)将物体从平衡位置向右移到
x=0.10m处后释放; (2)将物体从平衡位置向右移到x=0.10m处后并给
物体以向左的速度0.20m/s.
解： k m 1.6 0.4 2rad s1
k
m
(1) t 0， x0 0.10m， v0 0
o
x
A
x02
v02
2
x0 0.10m
cos x0 1
A
0
x 0.1cos2t (m)
(2)
t
0，
x0
0.10m，
v0
0.20m/s
cos
x0
1
A
x02
v02
2
0.1
2m
A2
sin v0 0
A
x 0.1 2 cos(2t ) (m)
设弹簧振子在任一时刻 t 的位移为x，速度为v，则
振动系统所具有的弹性势能Ep和动能Ek分别为：
Ep
1 kx2 2
x Acos( t )
Ep
1 2
kA2
cos2 (
t
)
Ek
1 2
mv2
v A sin( t )
Ek
1 2
m 2 A2
sin2 (
t
)
2 k /m
1 kA2 sin2 ( t )
大加速度为 4.0 ms-2. 求：(1) 振动的周期；(2) 通过平衡位置的动
能；(3) 总能量；(4) 物体在何处其动能和势能相等？
解: (1) amax A 2

机械振动学第五章_两自由度系统振动(讲)

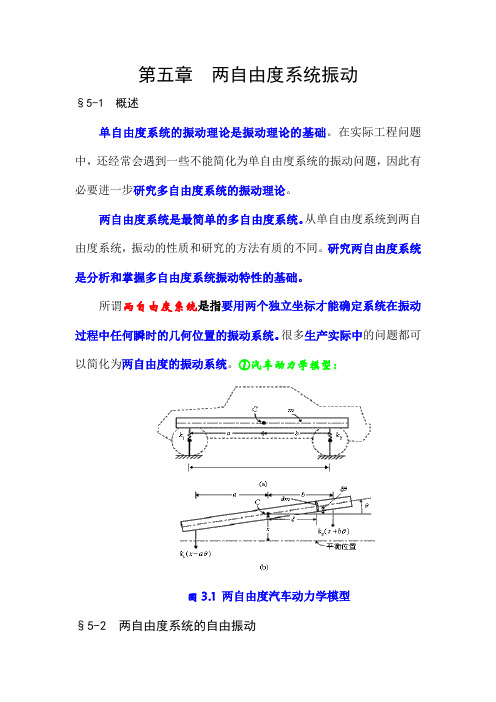
第五章两自由度系统振动§5-1 概述单自由度系统的振动理论是振动理论的基础。

在实际工程问题中，还经常会遇到一些不能简化为单自由度系统的振动问题，因此有必要进一步研究多自由度系统的振动理论。

两自由度系统是最简单的多自由度系统。

从单自由度系统到两自由度系统，振动的性质和研究的方法有质的不同。

研究两自由度系统是分析和掌握多自由度系统振动特性的基础。

所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。

很多生产实际中的问题都可以简化为两自由度的振动系统。

①汽车动力学模型：图3.1两自由度汽车动力学模型§5-2 两自由度系统的自由振动一、系统的运动微分方程②以图3.2的双弹簧质量系统为例。

设弹簧的刚度分别为k 1和k 2，质量为m 1、m 2。

质量的位移分别用x 1和x 2来表示，并以静平衡位置为坐标原点，以向下为正方向。

(分析)在振动过程中的任一瞬间t ，m 1和m 2的位移分别为x 1及x 2。

此时，在质量m 1上作用有弹性恢复力()12211x x k x k -及，在质量m 2上作用有弹性恢复力()122x x k -。

这些力的作用方向如图所示。

应用牛顿运动定律，可建立该系统的振动微分方程式：()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm （3.1）令2212121,,m k c m k b m k k a ==+=则（3.1）式可改写成如下形式：()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm⎭⎬⎫=+-=-+00212211cx cx xbx ax x（3.2）这是一个二阶常系数线性齐次联立微分方程组。

(分析)在第一个方程中包含2bx -项，第二个方程中则包含1cx -项，称为“耦合项”（coupling term ）。

这表明，质量m 1除受到弹簧k 1的恢复力的作用外，还受到弹簧 k 2的恢复力的作用。

大学物理学-机械振动教案

第五章机械振动前言1. 振动是一种重要的运动形式2. 振动有各种不同的形式——机械振动:位移 x 随t 变化；电磁振动；微观振动广义振动:任一物理量(如位移、电流等)在某一数值附近反复变化。

3. 振动分类§5.1 简谐振动的动力学特征一、弹簧振子的振动二、谐振动方程 f = - k x x mk m f a -==令 2ω=m k 则有x dtxd a 222ω-== 即 0x dtx d 22=+2ω 其解为()()0t Acos t x ϕω+=振动受迫自由阻尼无阻尼自由非谐自由谐动mo x X 0 = 0 A x m o X 0 = Ax m o -A X 0 = -Aωt+ϕ解：选平板位于正最大位移处t=0(00=ϕ)，由πππω4212T2===则 t Acos4x π= t Acos4-16a 2ππ= （1）对物体 ma N -mg = t mAcos416mg ma -mg N2ππ+==物体对平板压力 t m Acos416--m g -N F 2ππ== （SI ）t cos41.28--19.62ππ=（N ）负号表示向上（2） N=0 时，物体离开平板。

即0t m Acos416m g 2=+ππ时，由（1）知当 -1t cos4=π时，N 最小，（即当 x = -A 时）∴ 6.2116gm 16mg A 22≈==ππ（cm ）六单摆如图所示，m 受合外力沿轨道切线方向分力θsin mg f t -=,负号表示力的方向与θ角的方向相反。

当 5<θ时θθmg mg f t -≈-=sin 有θθβmg dtd ml ml ma t -===22 即 022=θ+θlgdt d 令 l g =ω20222=θω+θdtd 所以，在角位移很小（ 5<θ）情况下，单摆的振动才是近似的简谐振动。

l g =ω ，gl T π=2 ，lgπ=ν21 。

第五章机械振动(1)

机械振动(1)

机械振动答案

大学物理 振动

第五、六章作业解答

物理学教程(第二版)[上册]第五章课后习题答案解析详解

大学物理第五章机械振动习题解答和分析

机械振动的检测

5-1简谐运动 简谐运动的振幅 周期 频率和相位讲解

第五章 机械振动

大学物理第5章习题解答

第五章 机械振动

机械振动基础 第五章 随机振动教材

大学物理第五章机械振动

机械振动学 第五章_两自由度系统振动(讲)

大学物理学-机械振动教案

大学物理振动

5-1简谐运动简谐运动的振幅周期频率和相位讲解

第五章机械振动

第五章机械振动

机械振动基础第五章随机振动教材

机械振动学第五章_两自由度系统振动(讲)