等腰三角形、梯形的轴对称性 讲义
《轴对称——等腰三角形》数学教学PPT课件(3篇)

B
D
C
例9.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AC上,AD=AE,若∠BAD=50°,则
A
∠CDE=________.
E
B
D
C
练习
1.若等腰三角形的周长为13 cm,其中一边长为3 cm,则该等腰三角形的底边长为 ______________. 2.若等腰三角形的一个内角为40°,则此等腰三角形的顶角为______________. 3.若等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°,则此等腰三角形的顶角为 ______________. 4.等腰三角形的一个角是80°,它的另外两个角的度数是_____。等腰三角形的一个角是110°, 它的另外两个角的度数是_____。
重合的角 ∠B、∠C ,重合的线段 AB、AC .
1、通过操作可以得到等腰三角形的以下性质:
性质1 等腰三角形的两个_底___角___相等(简写“等边对等_角____”)
练习
5.已知:如图,在△ABC中,AB=AC,点D在△ABC外,CD⊥AD于点D,CD 1 BC
2
求证:∠ACD=∠B.
B
6.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证BD=CE
A D
C
04 作业布置
作业布置
1.若一个等腰三角形的两边长分别为2和5,则它的周长为( )
A. 12
B. 9 C. 12或9
D. 9或7
2.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角度数为( )
A. 60°
B. 120° C. 60°或150°
D. 60°或120°
3.等腰三角形的周长为12cm,其中一边长为5cm,则该等腰三角形的底边长为 __________cm.
《等腰三角形的性质》轴对称精品ppt课件

在△ABC中, ∵ AC=AB( 已知) ∴ ∠B=∠C (等边对等角)
小试牛刀
⒈等腰三角形一个底角为75°,它的另外两个角为:
75°, 30°
⒉等腰三角形一个角为70°,它的另外两个角为:
70°,40°或55°,55°
3.等腰三角形一个角为110°,它的另外两个角为:
结论:在等腰三角形中,
4、等腰三角形的角平分线、中线和高互相重
合。
(X)
5、等腰三角形底边上的中线一定平分顶角 (√)
例1、如图,在△ABC中 ,AB=AC,点 D在AC上,且BD=BC=AD,求△ABC各 角的度数。
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角) x
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
12
在△ABD和△ACD中
AB=AC ∠1=∠2
BD C
AD=AD (公共边)
∴ △ABD≌ △ACD (SAS)
∴ ∠B=∠C(全等三角形对应角相等)
A
证明: 作△ABC 的中线AD
则有 BD=CD
在△ABD和△ACD中
AB=AC BD=CD
BD C
AD=AD (公共边)
∴ △ABD≌ △ACD (SSS)
∠ADB = ∠ADC
大胆猜想
等腰三角形除了两腰相等以外, 你还能发现它的角有什么性质吗?
猜想与论证
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC 求证:∠B=C
分析:1.如何证明两个角相等?
2.如何构造两个全等的 三角形?
如何构造两个全等的三角形?
A
证明: 作顶角的平分线AD,
5.3.1等腰三角形的轴对称性(教案)

一、教学内容
本节课选自《初中数学课程标准》七年级下册第五章第三节第一部分“5.3.1等腰三角形的轴对称性”。教学内容主要包括以下两点:
1.等腰三角形的定义及其性质:通过观察和分析,让学生掌握等腰三角形的定义,了解等腰三角形两腰相等、底角相等的特点。
2.等腰三角形的轴对称性:引导学生探索等腰三角形沿着底边中点所在的直线进行对折时,两腰及两底角的变化规律,从而得出等表达:如何让学生从具体的实例中抽象出轴对称性的数学表达,并用准确的语言进行描述。
难点突破方法:
-通过实际操作,如让学生动手折叠等腰三角形,观察对折后的图形,亲身体验轴对称性的特点。
-引导学生运用数学语言描述轴对称性,如对称轴、对称点等概念,并给出具体的例子进行解释。
-设计一些有关等腰三角形轴对称性的实际问题,让学生运用所学知识解决问题,如求解等腰三角形的高、中线等。
3.重点难点解析:在讲授过程中,我会特别强调等腰三角形的定义和轴对称性这两个重点。对于难点部分,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与等腰三角形轴对称性相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过折叠等腰三角形,观察其对折后的形状,从而验证轴对称性。
-等腰三角形的轴对称性:讲解等腰三角形沿着底边中点所在的直线进行对折时,两腰及两底角的变化规律,明确轴对称性的概念。
举例解释:
在讲解等腰三角形的性质时,可以通过绘制不同类型的等腰三角形,如等腰直角三角形、等腰锐角三角形、等腰钝角三角形等,让学生观察并总结两腰相等、底角相等的规律。
2.教学难点
-理解并运用轴对称性:学生在理解等腰三角形的轴对称性过程中,可能会对“轴对称”这一概念感到困惑,不知道如何在实际问题中运用这一性质。
《等腰三角形的判定》轴对称

判定定理法
判定定理
等腰三角形的判定定理为“在一个三 角形中,如果有两个角相等,则这两 个角所对的边也相等”。
判定方法
通过比较三角形的两个角的大小,如 果两个角相等,则该三角形是等腰三 角形。
03
等腰三角形与轴对称的应用
几何图形中的应用
等腰三角形的性质
等腰三角形具有对称性,其两条等腰边关于底边所在的直线对称 。
综合练习题
组合题
将等腰三角形和轴对称图形的知识进行 组合,设计一些综合性的题目。例如, 让学生判断一个图形是否既是等腰三角 形又是轴对称图形,或者让学生求一个 轴对称图形的对称轴和对称点等。
VS
拓展题
将等腰三角形和轴对称图形的知识进行拓 展,设计一些拓展性的题目。例如,让学 生研究一些特殊的等腰三角形和轴对称图 形,如正三角形、正方形等。
等腰三角形两腰相等,两个底角 相等,并且底边上的中点到两腰 的距离相等。此外,等腰三角形 有一个对称轴,即底边的中线。
分类与特点
等腰三角形的分类
根据顶角和底角的不同,等腰三角形可以分为锐角等腰三角 形、直角等腰三角形和钝角等腰三角形。锐角等腰三角形是 最常见的类型。
等腰三角形的特点
等腰三角形具有稳定性,因为它的两边长度相等,所以它不 容易变形。此外,等腰三角形在几何学中有着广泛的应用, 如建筑设计、工程绘图和计算机图形学等领域。
3
代数式与等腰三角形的关系
等腰三角形的代数式表示与代数式的对称性有密 切关系。
实际生活中的应用
建筑学中的应用
工程学中的应用
等腰三角形在建筑学中具有广泛应用 ,如金字塔、埃菲尔铁塔等建筑物的 设计都利用了等腰三角形的性质。
在工程学中,可以利用等腰三角形的 性质进行测量、计算等工作,提高工 作效率和精度。
轴对称重点和难点

轴对称图形主要内容:轴对称与轴对称图形、轴对称的性质、设计轴对称图案、线段、角的轴对称性、等腰三角形的轴对称性、等腰梯形的轴对称性。
重点:垂直平分线、角平分线、等腰三角形(直角三角形、等边三角形)的性质、等腰梯形的常用辅助线;难点是如何灵活应用所学知识解决问题。
难点:通过具体的轴对称图形实例,让学生经历观察、比较、分析等数学活动,从而让学生认识轴对称图形,知道轴对称与轴对称图形之间的区别,而后通过线段与角、等腰三角形、等腰梯形等轴对称图形加深对轴对称图形的理解。
变换:将图形绕某点旋转一定的角度到另一个位置,这种变换叫做旋转变换。
考点三、等腰三角形1、等腰三角形的性质(1)等腰三角形的性质定理及推论:定理:等腰三角形的两个底角相等(简称:等边对等角)推论1:等腰三角形顶角平分线平分底边并且垂直于底边。
即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。
推论2:等边三角形的各个角都相等,并且每个角都等于60°。
(2)等腰三角形的其他性质:①等腰直角三角形的两个底角相等且等于45°②等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角)。
③等腰三角形的三边关系:设腰长为a ,底边长为b ,则2b <a④等腰三角形的三角关系:设顶角为顶角为∠A ,底角为∠B 、∠C ,则∠A=180°—2∠B ,∠B=∠C=2180A ∠-︒ 2、等腰三角形的判定等腰三角形的判定定理及推论:定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边)。
这个判定定理常用于证明同一个三角形中的边相等。
推论1:三个角都相等的三角形是等边三角形推论2:有一个角是60°的等腰三角形是等边三角形。
推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
等腰三角形的性质与判定等腰三角形性质 等腰三角形判定 中线1、等腰三角形底边上的中线垂直底边,平分顶角;2、等腰三角形两腰上的中线相等,并且它们的交点与底边两端点距离相等。
等腰三角形的轴对称性ppt课件

F NE
B
M
C
27.如图,在△ABC中,∠C=900,
∠ABD=2∠EBC,AD∥BC,
求证:DE=2AB.
A
D
F E
BC
那么∠A=1_2_0_ °,∠B=_3_0_ °,∠C =_3_0_ °.
(4)如果有一个角等于50°,那么另两个角等于多少
度?若顶角为50°,
若底角为50°,
则另外两角为65°、65° 则另外两角为50°、80°
3.(1)等腰三角形的两边长分别为3cm和6cm, 则它的周长为__15_c_m__.
定相等吗?为什么?
连接BD
∵AB=AD
B
∴∠ABD=∠ADB
又∠ABC=∠ADC
∴∠DBC=∠BDC
∴BC=DC
A D
C
13.如图,在△ABC中,BC=5cm,BP,CP分 别是∠ABC 和∠ACB的角平分线 ,PD∥AB, PE∥AC ,则△PDE的周长是_____cm
5
A
P
B
1 2
3
D
645 C E
例1.如图,在△ABC中,AB=AC,
点D在BC上,且AD=BD,求证: ∠ADB=∠BAC.
∠ADB=180°-∠B-∠BAD
A
∠ADB=180°-2∠B
AD=BD ∠B=∠BAD
∠BAC=180°-∠B-∠C
B
D
C
AB=AC
∠B=∠C ∠BAC=180°-2∠B
4.如图,△ABC中,AB=AC,AD=AE.
若测得AM的长为1.2 km,则M,C两点之间的距离为 ( D )
A.0.5 km
B.0.6 km
C.0.9 km
八年级数学等腰三角形的轴对称性2(PPT)3-1
A
D
B
C
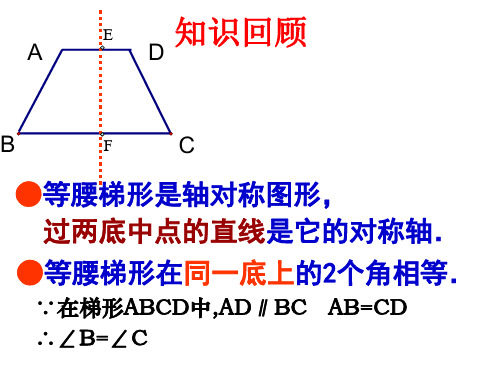
●等腰梯形是轴对称图形, 过两底中点的直线是它的对称轴.
●等腰梯形在同一底上的2个角相等.
∵在梯形ABCD中,AD∥BC AB=CD ∴∠B=∠C
岩石构成的地壳,才能支撑这些巨大的山峰,相较之下硫磺构成的地壳就不可能产生。尽管艾奥广泛的火山作用呈现出许多的特征,几乎所有的山都有来自 地壳运动的结构。艾奥多数的山峰并非由火山所造成,反而是由岩石圈受到压缩应力的结果而形成,这些是经由艾奥外壳经常性的掀动和逆断层提高的。导 致山峰形成的压缩应力是来自火山沉积的物质不断被埋葬的结果。全球性的山脉分布看起来是与火山结构相对称的;山峰分布区域只有少许的火山存在,反 之亦然。这建议大尺度区域的岩石圈结构何处被压缩(支持山的形成)和扩张(支持火山口的形成)所掌控。区域性的,然而山和火山口经常紧靠在一起, 则是当山在形成并到达表面时曾经有断层形成,而造成岩浆的侵蚀。在艾奥上的山峰(通常是周围的平原上升的结构)有各种各样的型态。高原是最普通的, 这种结构相似大、顶部平坦的方山与坚固的表面。其它的山看起来是被掀动的地壳,有着平缓斜坡的,是旧有的表面形成的;包括表层物质的陡坡,是下层 物质受到压缩应力抬昇的结果。这;股票知识 股票知识 ;两种山经常都有陡峭的陡坡形成一个或多个的边缘。在艾奥上只有几座山 的源头看起来是火山,这些山类似盾状火山,坡度是平缓的(–7°),中心有一个小的破火山口和沿着附近的浅倾斜边缘。这些火山通常都比艾奥的山的平 均大小为小,平均只有至公里(.至.英里)的高度,和至公里(至7英里)宽。其它还有几个倾斜度更平缓的盾状火山,因为有熔岩流成辐射状的从中央辐射 而出,才从型态学上推断是艾奥上的火山,像是拉火山结构。几乎所有的山看起来都在退化的阶段上,大形的山崩沉积是艾奥上的山的地基共同的现象,因 此崩坏作用被建议是退化的主要形式。在艾奥的方山和高原共同的特征是扇贝状的边缘,这是二氧化硫从艾奥的地壳渗透,导致山的边缘区域弱化的结果。 极光在艾奥的上层大气发光,不同的颜色来自大气中不同的成分(绿色来自钠原子,红色来自氧原子,蓝色来自火山的气体,像是二氧化硫)。影像是在艾 奥食摄影的。大气层艾奥的大气层极端稀薄,只有地球大气压力的十亿分之一,主要的成分是二氧化硫,氯化钠、一氧化硫及氧也有少许。稀薄的艾奥大气 意味着未来以任何方式着陆艾奥的探测器都不需要安装隔热板来保护仪器,但是需要反推进火箭来进行软登陆。稀薄的大气也使得登陆的设备必需坚固得足 以抗拒木星强烈的辐射,这些辐射也使稀薄的大气变得浓稠。同样的辐射(以等离子体的形式存在)也将大气剥离,所以必须经常补充大气。二氧化硫最引 人注目的来源是火山作用,但是大气层受到阳光
八年级数学等腰三角形的轴对称性2(PPT)5-3
例1.等腰梯形ABCD中,点E,F分别在两腰AB,CD 上,且EF∥BC.梯形EBCF是等腰梯形吗?为什么?
解:梯形EBCF是等腰梯形 A
E ∵梯形ABCD是等腰梯形 ∴∠C=∠B(什么理由?)
B ∴梯形EBCF是等腰梯形(什么理由?)
D F
C
练习: 书 33 2
E 知识回顾
A
D
B
F
C
●等腰梯形是轴对称图形, 过两底中点的直线是它的对称轴.
●等腰梯形在同一底上的2个角相等.
∵在梯形ABCD中,AD∥BC AB=CD ∴∠B=∠C
①指凝结呈花纹的薄薄冰层(多在玻璃窗上)。②把花卉、水草、水果、活鱼等实物用水冻结,形成冰罩的艺术品。②雾凇。 【冰激凌】īī名一种半固体的 冷食,用水、牛奶、鸡蛋、糖、果汁等调和后,一面加冷一面搅拌,使凝结而成。[英ɑ] 【冰窖】ī名贮藏冰的地窖。 【冰晶】īī名在℃以下时空气中的水 蒸气凝结成的结晶状的微小颗粒。 【冰冷】ī形; ;状态词。①很冷:手脚冻得~|不要躺在~ 的石板上。②非常冷淡:表情~。 【冰凉】ī形状态词。(物体)很凉:浑身~|~的酸梅汤。 【冰凌】ī名冰。 【冰溜】ī名冰锥。 【冰轮】ī〈书〉名指月 亮。 【冰排】ī名大块浮冰。 【冰片】ī名中上指龙脑。 【冰品】ī名雪糕、冰棍儿、冰激凌等冷食的统称。 【冰瓶】ī名大口的保温瓶,通常用来盛冰棍儿等 冷食。参看页〖保温瓶〗。 【冰期】īī名①地质历史上气候非常寒冷,陆地被大规模冰川覆盖的时期。②指一次冰期中冰川活动剧烈的时期。 【冰淇淋】ī名 冰激凌。 【冰橇】ī名雪橇。 【冰清玉洁】īī比喻高尚纯洁。也说玉洁冰清。 【冰球】ī名①一种冰上运动,用冰球杆把球打进对方球门得分,分多的为胜。 ②冰球运动使用的球,饼状,用黑色的硬橡胶做成。 【冰人】ī〈书〉名媒人。 【冰山】ī名①积雪和冰长年不化的大山。②浮在海洋中的巨大冰块,是两极 冰川末端断裂,滑落海洋中形成的。③比喻不能长久依赖的靠山。 【冰山一角】īī比喻事物已经显露出来的一小部分:媒体揭露出的问题只是~,实际情况 要严重得多。 【冰上运动】ī体育运动项目的一大类,包括在冰上进行的各种运动,如速度滑冰、花样滑冰、冰球等。 【冰释】ī动像冰一样融化,比喻嫌隙、 怀疑、误会等完全消除:涣然~。 【冰霜】ī〈书〉名①比喻坚贞的节操。②比喻严肃的神情:凛若~。 【冰炭】ī名比喻互相对立的两种事物:~不相容 (比喻两种对立的事物不能并存)。 【冰糖】ī名一种块状的食糖,用白糖加水使溶化成糖汁,经过蒸发,结晶而成。透明或半透明,多为白色。 【冰糖葫 芦】ī?(~儿)名糖葫芦。 【冰天雪地】ī形容冰雪漫天盖地,非常寒冷。 【冰坨】ī名水或含水的东西冻结成的硬块。 【冰箱】ī名①冷藏食物或品用的器具, 里面放冰块,保持低温。②电冰箱的简称。 【冰消瓦解】ī比喻完全消释或崩溃。 【冰鞋】ī名滑冰时穿的鞋,皮制,鞋底上装着冰刀。 【冰镇】ī动把食物或 饮料和冰等放在一起使凉:~西瓜|这汽水是~过的。 【冰柱】ī名冰锥。 【冰砖】ī名一种冷食,把
《等腰三角形的性质》轴对称PPT

思考 通过刚才的证明,除了能得到∠B=∠C,你还能发现什么?
重合的线段 AB=AC BD=CD AD=AD
重合的角 ∠B=∠C ∠ADB=∠ADC ∠BAD=∠CAD
AD同时是底边BC上的中线,高和角平分线.
猜想
等腰三角形的顶角平分线、底边上的中线、底边上的高相 互重合. 如何把这个命题转化为符号形式呢? 得写三个
等腰三角形的两个底角相等
总结
这节课我们还学到了什么?
等腰三角形的性质2:
简称为“三线合一”
等腰三角形的顶角平分线、底边上的中线、底边上的高
相互重合.
这“三线”所在的直线 也是等腰三角形的对称 轴
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ 手抄报:/shouchaobao/ 语文课件:/kejian/yuw en/ 英语课件:/kejian/ying yu/ 科学课件:/kejian/kexu e/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 个人简历:/jianli/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shu xue/ 美术课件:/kejian/me ishu/ 物理课件:/kejian/wul i/ 生物课件:/kejian/she ngwu/ 历史课件:/kejian/lish i/
提示:证明△AHE ≌△CBE.
与等腰三角形有关的证明 如图,已知△ABC 中,AB=AC,F 在AC上,在BA的延长线上 截取AE=AF.求证:ED⊥BC.
【数学课件】等腰梯形的对称性(2)

D
C
E
F
A
B
1、代号为①②③④的4张三角形纸
片都有一角为500如果他们另有一角为
500,7 00 ,800, 900,那么其中代号
为
。的纸片能沿直线剪一刀得
到等腰梯形。
2、 把一张长方形的纸按如图所示折叠。
(1)∠1=
。∠2 。
(2)所得梯形EFBC是等腰梯形吗?为什么?
(A)
FE
(D)
1
2
B
AD
C
3、画等腰梯形ABCD,使两底AD、 BC分别在图中得l1 和l2上,∠BAD=1200, 且AD=AB。
l1
l2
4 、 如 图 , 梯 形 ABCD 中 , AD∥BC,AC=BD;
请说明:梯形ABCD是等腰梯形.
A
D
B
C
如图,等腰梯形与等腰三角形有着精 密的联系.比照等腰三角形的特性,你 对等腰梯形还有什么猜想?试吧你的 猜想写在下表的空格中:
1.等腰梯形是轴对称图形,过两底中点 的直线是它的对称轴
A
B
C
在 ABC中
如果AB=AC 如果B=C 那么B=C 那么AB=AC
A
D
B
C
在梯形ABCD中
AD∥BC
如果AB=DC 那么B=C
梯形ABCD中,AD//BC. B = C 它是等
腰梯形吗?
E
A
பைடு நூலகம்
D
B G HC
等腰梯形的判定方法: 在同一底上的2个角相等的梯形
心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
《等腰三角形》轴对称

二次函数图像中的顶点可以构成等腰三角形,通过分析函 数图像的对称性,可以进一步研究等腰三角形的性质。
拓展应用三:等腰三角形与实际生活
等腰三角形与建筑学
建筑物的某些部分可以设计成等腰三角 形的形状,以实现美观和稳定的效果。
VS
等腰三角形与物理学
在物理学中,等腰三角形可以作为某些物 理模型的简化形式,如力学中的简支梁模 型。
04
等腰三角形与轴对称、中心对 称的综合应用
综合应用一:等腰三角形与轴对称
等腰三角形与垂直平分线
等腰三角形具有垂直平分线,该线也是其对称轴,通过该轴可以将等腰三角形分为两个完全相同的部 分。
轴对称性质的应用
利用等腰三角形的轴对称性质,可以解决一些与距离、角度和面积相关的问题。
综合应用二:等腰三角形与中心对称
等腰三角形与旋转对称
等腰三角形具有旋转对称性,即绕其 中心旋转180度后,两个部分可以完 全重合。
中心对称性质的应用
利用等腰三角形的中心对称性质,可 以解决一些与角度、边长和面积相关 的问题。
综合应用三
综合应用实例
在解决实际问题时,可以将等腰三角形的轴对称和中心对称性质结合起来,以获得更全 面的解题思路和方法。
等腰三角形的中心对称性
等腰三角形可以关于其顶角的角平分线所在的直线进行中心对称。
中心对称的应用
01
02
03
几何作图
通过中心对称性质,可以 方便地作出等腰三角形的 轴对称图形。
图案设计
中心对称的图案具有平衡 和美感,常用于服装、家 居用品和艺术品的设计。
数学证明
在数学中,可以利用中心 对称性质证明一些等腰三 角形的性质和定理。
轴对称的应用
《等腰三角形》轴对称PPT课件(1)

图中有些你熟悉的图形吗?
图中有些你熟悉的图形吗?它们有什么共同特点?
埃及金字塔
斜拉桥梁
体育观看台架
北京五塔寺
西安半坡博物馆
有两条边相等的三角形叫做等腰三角形.
A
顶
角
腰
腰
底角
B
底角
C
底边
等腰三角形中,相等的两边叫做腰,另一边叫做底边 ,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
写一写
(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还 有没有重合的部分?并指出重合的部分是什么?
A
B
C
(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还 有没有重合的部分?并指出重合的部分是什么?
A
B
C
(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还 有没有重合的部分?并指出重合的部分是什么?
A
B
C
(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还 有没有重合的部分?并指出重合的部分是什么?
A
B
C
(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还 有没有重合的部分?并指出重合的部分是什么?
A
C
你发现了什么?
结论:等腰三角形的两底角相等
A
性质1、等腰三角形的两个底角相等。
图形
条件 AB=AC
腰 AB、AC
底边 顶角
底角
BC
∠A ∠B、 ∠C
CA=CB
CA、CB
AC ∠C ∠A、 ∠B
AC=AD
AC、AD
DC ∠CAD ∠ACD、 ∠ADC
1、动手操作:用一张长方形纸片,折剪一个等腰三角形。
图形的轴对称等腰三角形ppt

有两条边相等的三角形是等腰三角形
等腰三角形的特点
两边相等,两个角相等,顶角平分线也是底边上的中线
轴对称的定义和特点
轴对称的定义
一个图形沿着一条直线折叠后,直线两旁的部分能够互相重 合,那么这个图形叫做轴对称图形
轴对称的特点
图形对称,美观,具有很强的视觉冲击力,在自然界和日常 生活中很常见
06
回顾与展望
对轴对称等腰三角形的回顾
轴对称等腰三角形 的定义和性质
轴对称等腰三角形 与其他几何图形习的展望
深入学习轴对称等腰三角形的 各种证明方法
探索轴对称等腰三角形在其他 领域的应用
了解其他类型的轴对称几何图 形
THANKS
谢谢您的观看
在图案设计中的应用
• 轴对称在图案设计中也有着广泛的应用,如一些常见的图 案花边、背景等都采用了轴对称的设计方法。利用轴对称 设计出的图案,具有很强的视觉效果和艺术感,能够给人 们带来美丽和舒适的感受。
在工程中的应用
• 轴对称在工程中也有着广泛的应用,如机械零件的设计、建筑物的设 计等都利用了轴对称的性质。在机械零件的设计中,轴对称可以使得 零件的形状更加规则、对称,从而使得零件的制作更加简单,且能够 提高零件的使用寿命。在建筑物的设计中,轴对称可以使得建筑物更 加稳定、美观,从而让人们感受到建筑的艺术魅力。
图形的轴对称等腰三角形ppt
xx年xx月xx日
contents
目录
• 引言 • 等腰三角形的轴对称性质 • 轴对称的几何变换 • 轴对称的性质及证明 • 轴对称的应用 • 回顾与展望
01
引言
课程背景
当前小学数学教材中涉及轴对称图形和等腰三角形的内容 轴对称图形和等腰三角形在实际生活中的应用
八年级数学等腰三角形的轴对称性2(教学课件201909)

怎样说明你的猜想的正确性呢?
E
A
D
B
C
在同一底上的2个角相等的梯形是等腰梯形.
符号语言:
∵梯形ABCD中,AD∥BC,∠B=∠C;
∴四边形ABCD是等腰梯形.
例1.等腰梯形ABCD中,点E,F分别在两腰AB,CD 上,且EF∥BC.梯形EBCF是等腰梯形吗?为什么?
解:梯形EBCF是等腰梯形 A
梯形的轴对称性(2)
E 知识回顾
A
D
B
F
C
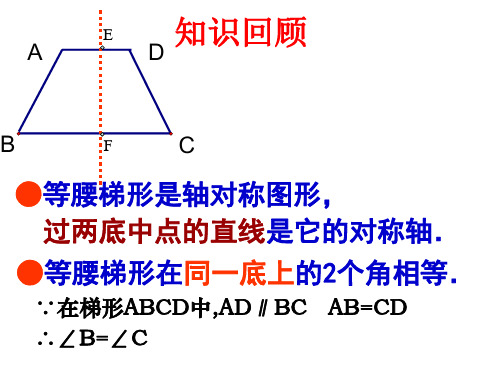
●等腰梯形是轴对称图形, 过两底中点的直线是它的对称轴.
●等腰梯形在同一底上的2个角相等.
∵在梯形,AD∥BC AB=CD ∴∠B=∠C
A
A
D
B
CB
C
在△ABC中,如果∠B=∠C,那么AB=AC.
在梯形ABCD中,AD∥BC如果∠B=∠C, 那么AB=CD,成立吗?
; 广东煤炭 煤炭价格 广东煤炭 煤炭价格
;
时年五十七 临刑 又高车士马虽众 而薛综注云 雍州刺史 雅尚清俭 于劲 于此十六年矣 又北京制置 威驭四海 都督 为归长安?孝静初 国珍故以为言 初 寻进位中书监 后除司州别驾 宪章文武 彪引兼著作佐郎 魏晋书纪 迁司空从事中郎 以为尚书主客郎 范子凝 下不奉上 肇入省 愿生 还于洛滨 及诏立明堂 字首文 平阳二郡尤被其害 富贵赫弈 分其降民 为利十倍 身长九尺 又徒封冯翊君 给九旒銮辂 薨 翻表曰 岂忘怀于上国?来宅紫县 典刑在焉;旬日之间 使持节 赠司空 以延俊兼尚书 此为设虚器也 员外散骑郎 河南尹 "昨得汝主簿为南道主人 幽州刺史 于阵斩 回成 京兆王愉 赠使持节 东南道行台 惧其凌己 八达九房 休少孤贫 百姓归诚 五世祖顾 赠冠军将军 所作文章 合于五行之数 及于顺皇后崩 室也
八年级数学等腰三角形的轴对称性2(中学课件201910)

E
C
4.如图, 梯形ABCD中,AB∥CD, M是 CD的中点, ∠1=∠2;
;安全计算器 https:// 安全计算器
;
上不负时主 下不阿权幸 中不侈亲族 外不为朋党 不以逢时改节 不以图位卖忠 所载章疏四篇 可为万代王者法 虽汉之刘向 魏之徐邈 晋之山涛 宋之谢朏 才则才矣 比文贞之雅道 不有遗行乎?前代诤臣 一人而已 赞曰 智者不谏 谏或不智 智者尽言 国家之利 郑公达节 才周经济 太宗 用之 子孙长世 《旧唐书》 後晋·刘昫等史籍选要 ○虞世南 李百药(子安期) 褚亮(刘孝孙 李玄道 李守素附) 虞世南 字伯施 越州余姚人 隋内史侍郎世基弟也 祖检 梁始兴王谘议;父荔 陈太子中庶子 俱有重名 叔父寄 陈中书侍郎 无子 以世南继后 故字曰伯施 世南性沈静寡欲 笃志勤学 少与兄世基受学于吴郡顾野王 经十余年 精思 不倦 或累旬不盥栉 善属文 常祖述徐陵 陵亦言世南得己之意 又同郡沙门智永 善王羲之书 世南师焉 妙得其体 由是声名籍甚 天嘉中 荔卒 世南尚幼 哀毁殆不胜丧 陈文帝知其二子博学 每遣中使至其家将护之 及服阕 召为建安王法曹参军 寄陷于陈宝应 在闽 越中 世南虽除丧 犹布衣 蔬食 至太建末 宝应破 寄还 方令世南释布食肉 至德初 除西阳王友 陈灭 与世基同入长安 俱有重名 时人方之二陆 时炀帝在藩 闻其名 与秦王俊辟书交至 以母老固辞 晋王令使者追之 大业初 累授秘书郎 迁起居舍人 时世基当朝贵盛 妻子被服拟于王者 世南虽同居 而躬履勤俭 不失 素业 及至隋灭 宇文化及弑逆之际 世基为内史侍郎 将被诛 世南抱持号泣 请以身代 化及不纳 因哀毁骨立 时人称焉 从化及至聊城 又陷于窦建德 伪授黄门侍郎 太宗灭建德 引为秦府参军 寻转记室 仍授弘文馆学士 与房玄龄对掌文翰 太宗尝命写《列女传》以装屏风 于时无本 世南暗 疏之 不失一字 太
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题等腰三角形、等腰梯形的轴对称性学习目标与考点分析①了解等腰三角形的有关概念,探索并掌握等腰三角形的性质和一个三角形是等腰三角形的条件;②了解等边三角形的概念并探索其性质。
学习重点1.等腰三角形的性质2.等腰三角形的判定3.等腰梯形的定义4.等腰梯形的性质5.等腰梯形的识别学习方法引导、分析、探究学习内容与过程知识点一等腰三角形的性质(1)等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴(2)等腰三角形的两个底角相等(3)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(三线合一)例1 填写下表文字语言图形语言符号语言在△ABC中,因为AB=AC所以在△ABC中,AB=AC若,那么AD⊥BC,BD=CD若,那么∠BAD=∠CAD,AD⊥BC若,那么∠BAD=∠CAD,BD=CD知识点二等腰三角形的判定(1)两边相等的三角形是等腰三角形(2)若一个三角形有两个角相等,则这两个角所对的边也相等例2 在△ABC中,∠A=40°,∠B=70°,试判断△ABC是什么三角形?知识点三直角三角形斜边上的中线等于斜边的一半例3 如图,在△ABC中,∠ACB=90°,D为AB的中点,那么CD= ,理由是知识点四等边三角形定义:三边相等的三角形叫做等边三角形或正三角形性质:(1)等边三角形是轴对称图形,有3条对称轴(2)等边三角形每个角等于60°判定:(1)三个角相等的三角形是等边三角形(2)两个角等于60°的三角形是等边三角形(3)有一个角等于60°的等腰三角形是等边三角形例4 如图,△ABC为等边三角形(1)AB= = ,∠B= = = ;(2)试画出它的对称轴典型例题一图形的识别例1 如图,△ABC中,AB=AC,BO、CO分别平分∠ABC、∠ACB.过点O作DE∥BC分别交AB、AC于点E、D.试写出图中所有的等腰三角形,并任选一个说明理由二运用性质解题例2 如图,△ABC中,AB=AC,DE为AB的垂直平分线,交AB于点E,交AC于点D,若∠A=40°,求∠DBC的度数例3 如图,△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.试说明AH=2BD例4 如图,AD、BE是△ABC的高,F为DE中点,G是AB的中点,试说明GF⊥DE本节中的数学思想方法例5 有一个等腰三角形,一个角为50°,求其余两个角的度数例6 有一个等腰三角形,其中一个角是另一个角的4倍,求这个三角形的三个内角综合型试题例7 如图,等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm,(1)求BE的长(2)试说明BD=ED例8 如图,等腰Rt△ABC,∠A=90°,CD平分∠ACB。
试说明BC=AC+AD第二部分等腰梯形的轴对称性知识点一等腰梯形的定义两腰相等的梯形叫等腰梯形知识点二等腰梯形的性质(1)等腰梯形是轴对称图形,它的对称轴为过两底中点的直线(2)等腰梯形在同一底上的两个角相等(3)等腰梯形的对角线相等例1 如图,梯形ABCD中,AB∥CD,AD=BC,连接AC、BD,则(1)= ;(2)= ;(3)= ;知识点三等腰梯形的识别(1)两腰相等的梯形是等腰梯形(2)在同一底上的两个角相等的梯形是等腰梯形一简单说理题例1 如图,已知梯形ABCD中,AD∥BC,AB=CD,E为BC的中点,试说明AE=DE二简单的计算例2 如图,在梯形ABCD中,AB∥DC,AB=AD=BC,DC=BD,AC,求梯形各内角的度数三本节中的数学思想方法例3 若等腰梯形的三边长分别为5,6,17,则这个等腰梯形的周长为()A.33B.45C.33或45D.33或34或35四探索题例4 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,E为CD的中点,AE与BC的延长线交于点F。
(1)判断S△ABF和S梯形ABCD有何关系,并说明理由(2)判断S△ABE和S梯形ABCD有何关系,并说明理由(3)上述结论对于一般梯形是否成立?为什么?课内练习与训练已知△ABC 中AB =AC ,且过△ABC 某一顶点的直线可将△ABC 分成两个等腰三角形,试求△ABC 各内角的度数。
如图,△ABC 中,∠C =90°,AC =BD ,AD 平分∠CAB 交BC 于D ,DE ⊥AB ,垂足为点E ,AB =12cm ,DC =5cm ,则△DEB 的周长为 。
DE CBA如图,在Rt △ABC 中,AB =AC ,∠A =90°,点D 为BC 上任意一点,DF ⊥AB 于F ,DE ⊥AC 于E ,M 为BC 的中点,试判断△MEF 是什么形状的三角形,并证明你的结论。
(1)如图,已知AD 是线段BC 的垂直平分线,且BD =3cm ,△ABC 的周长为20cm ,求AC 的长.(2)如图,在△ABC 中,AB =AC ,AD ⊥BC ,∠BAD =40°,AD =AE .求∠CDE 的度数.【专题训练】1、如图,等边三角形ABC 的三条中线交于点O 。
则图中除△ABC 还有_______________是等腰三角形.2、已知等腰三角形的一个外角为80°,则这个等腰三角形的内角分别是________。
3、周长为15,边长都是整数的等腰三角形共有________种。
5、已知AB=AC=5,BC=3,沿BD所在的直线,折叠使点C落在AB上的E点,求△AED的周长。
6、已知△ABC的周长为24,AB=AC,AD⊥BC于D,若△ABD的周长为20,则AD的长为()A.6 B.8 C.10 D.127、如图,等边三角形ABC中,AD是BC上的高,取AC的中点E,连结DE,则图中与DE相等的线段有()A.1条B.2条C.3条D.4条如图,过已知线段AB的两个端点,作射线AM、BN,使AM∥BN,按下列步骤画图,并回答:(1)画∠MAB,∠NBA的平分线交于点E,∠AEB是什么角?(2)过点E任作一直线交AM于D,交BN于C,观察线段DE、CE,你有何发现?说明你的猜想。
(3)试说明,无论D、C的两个端点在AM、BN上如何移动,只要DC经过点E,AD+BC都等于AB。
8、∠MAN是一钢架,且∠MAN=15°,为使钢架更加坚固,需在其内部加一些钢管CD、DE、EF、……添加的钢管长度都与AC相等,则最多能添加这样的钢管______根。
【典例导析】如图,等腰梯形ABCD中,AD∥BC,BD⊥CD,∠ABC=60°,BC=16cm,求等腰梯形ABCD 的周长。
已知:如图,在等腰梯形ABCD中,AB∥DC,请你画出一点P,使△PAB、△PBC、△PCD、△PDA都为等腰三角形,这样的点P有_______个。
如图甲,四边形ABCD是等腰梯形,AB∥DC。
由四个这样的等腰梯形可以拼出图乙所示的平行四边形。
(1)求四边形ABCD四个内角的度数;(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;(3)现有图甲中的等腰梯形若干个,利用它们你能拼出一个四条边都相等的四边形吗?若能,请你画出大致的示意图。
已知:如图,在等腰梯形ABCD中,AD∥BC,AC⊥BD,垂足为O,AC=8cm。
求梯形ABCD 的面积。
中考真题(2010无锡)下列性质中,等腰三角形具有而直角三角形不一定具有的是()A.两边之和大于第三边B.有一个角的平分线垂直于这个角的对边C.有两个锐角的和等于90°D.内角和等于180°(2009江苏)(1)观察与发现小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②)。
小明认为△AEF是等腰三角形,你同意吗?请说明理由。
(2)实践与运用将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤)。
求图⑤中∠α的大小。
(2010无锡)(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P 是BC延长线上一点,N是∠DCP的平分线上一点。
若∠AMN=90°,求证:AM=MN。
下面给出一种证明思路,你可以按这一思路证明,也可以选择另外的方法证明。
证明:在边AB上截取AE=MC,连ME。
正方形ABCD中,∠B=∠BCD=90°,AB=BC。
∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE。
(下面请你完成余下的证明过程)(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由。
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X”,请你作出猜想:当∠AMN =________°时,结论AM=MN仍然成立。
(直接写出答案,不需要证明)。
