2发电机基本方程
《电力系统分析理论》课件第6章 同步发电机的基本方程

第六章 同步发电机的基本方程
用傅里叶系数表示,取基波:
LabLba[m0 m2co2s(a300)] LbcLcb[m0 m2co2s(a900)] LcaLac[m0 m2co2s(a1500)]
d q
i 0
32cso1iansa
coas(120)
sina(120)
1
coas(120)
sina(120)
1
ia ib ic
2
2
2
或缩记为:
id0 qPaibc
(61)7
第六章 同步发电机的基本方程
利用逆变换,可以得到:
coas coas(120)
sina sina(120)
电流的正方向与磁链的正方向符
a
dy
+
a
+
D
Q
D
ω
fQ
c +D +x
合右手螺旋定则,定子各绕组中 b
D
c
电流的正方向与磁链的正方向符
+z
b
合右手螺旋定则
q
第六章 同步发电机的基本方程
➢ 感应电势:与电流正方向 一致
➢ 定子电流:中性点流向机 v f 端
➢ 定子电压:电流流出端为 正
➢ 转子电压:提供正向电流 的励磁电压是正的
vf
f
Rf
0
0
if
00
D Q
0
0 0
RD 0
0 RQ
iD iQ
v为各绕组端电i为 压各 ;绕组电流;
(61)
电力系统分析第七章 同步发电机的基本方程

maD 0 0
0 maQ 0
3 2maf LRS P 1 3 2maD 0
0 0 3 2maQ
0 0 0
16
郑州航空工业管理学院
• Park方程:磁链方程
L0 m0 3 l2 2 d 0 q 0 0 f 3 maf 2 D 3 m 2 aD Q 0
2017/4/16 郑州航空工业管理学院 12
一. 派克变换 4. 物理意义: 将观察者的立场由静止的定子转移 至旋转的转子,原来定子三个静绕组 abc由两个与转子同步旋转的dq绕组代 替,实现交直流变换。 结论:经派克变换后的同步发电机的原 始方程就是一组常系数微分方程。
二. dq0坐标下的同步发电机的 等效结构 d轴方向: d(定子)、f(励磁)、D q轴方向: q(定子)、Q d轴方向相当于一个三卷变; q轴方向相当于一个双卷变; 0轴方向相当于一个单匝线圈;
7
郑州航空工业管理学院
磁链方程可记为:
abc LSS fDQ RS
LSR iabc LRR i fDQ
LSS :定子绕组间自感、互感系数矩阵
LRR :转子绕组间自感、互感系数矩阵
LRS , LSR :定转子绕组间互感系数矩阵
18
郑州航空工业管理学院
四. 电压方程的坐标变换
• Park方程:电压方程
vabc abc Rs v fDQ fDQ 0
vabc abc Rsiabc vdq 0 Pvabc P abc PRsiabc P abc Rsidq 0 dq 0 P P 1 dq 0 Rsidq 0
直流电机的基本方程式

直流电机的基本方程式一.直流发电机的基本方程式以并励机为例:(一).电压平衡方程直流发电机发出的电势E a产生电流I a,I a在电枢回路总电阻R a(包括电枢绕组电阻及两个电刷的接触电阻)上产生压降I a R a,则输出电压U=E a-I a R a,可见发电机E a>U。
电路如图:(二).转矩平衡方程式直流发电机是把机械能转变为电能,因此由原动机输入的机械转矩T1是驱动转矩;电磁转矩T是制动转矩;即使电机空转也存在的、对应电机机械摩擦、铁损耗等的空载转矩T0一定是阻转矩,当驱动=制动时,电机恒速旋转。
因此发电机稳定运行时的转矩平衡方程为:T1=T+ T0(三)功率平衡方程式其功率流程图如图:从原动机输入机械功率P1,扣除了机械方面的损耗p机,就是机转变为电的部分称为电磁功率P M,再扣除了电方面的损耗p电,就是输出的电功率P2=UI,对并励发电机I=I a-I f。
额定时的P2就是P N=U N I N。
其中:p机是机械方面的损耗,它也是电机空载运行时就存在的损耗,故称空载损耗p,它包括了机械摩擦损耗mp、铁耗Fe p、附加损耗ad p(≈0.01~0.05P N),即:p 机=0p =m p +Fe p +ad p ;p 电是电方面的损耗称为铜耗,它包括了电枢回路铜耗cua p =2a I R a 和励磁回路铜耗cuf p =UI 2fU R =2f I =f R ,即p 电=cua p +cuf p 由功率流程图可列功率平衡方程:机械方面:10M P P p =+;电方面:2M cua P P p =--cuf p ;把机械方面的功率平衡方程两边除以Ω,就得到了转矩平衡方程。
其中:T 1=1P Ω;T 0=0P Ω;T =M PΩ。
可见电磁功率M P =T Ω——这是用机械量表示的电磁功率。
把电压平衡方程U =E a -I a R a 的两边乘以I a :UI a = E a I a -2a I R a ∵I a =I +I f ,则:UI a = U(I+I f )= E a I a -2a I R a , ∴UI= E a I a -2a I R a -UI f =E a I a -cua p -cuf p其中:UI 就是P 2;对比电方面的功率平衡方程可知:E a I a 就是电磁功率P M 。
第三章 同步发电机的基本方程

第三章同步发电机的基本方程3-1 基本前提3.1 基础假设•电机铁心的导磁系数为常数;•电机定子三相绕组结构对称,磁轴空间相差120o;•电机转子在结构上对纵轴和横轴对称;•转子绕组的磁动势在定子绕组所感应的空载电动势是时间的正弦函数;•电机定、转子表面光滑。
3.1 正方向的规定•定子绕组:磁链正方向:各轴线正方向;电流正方向:产生正向磁连的电流;•转子绕组:横轴落后于纵轴。
同步机磁路结构图3.1 正方向的规定同步机电路结构图•定子绕组:–三相电流的正方向:流出绕组为正;•转子绕组:–励磁电流的正方向:从励磁电源流出为正。
3-2 同步发电机的原始方程3.2.3 同步发电机原始方程的电感系数•定子各绕组的自感系数:的变化规律自感Laa⇓定子绕组的自感系数是以Π为周期是时变的。
3.2.3 同步发电机原始方程的电感系数•定子绕组间的互感系数:⇓定子绕组的互感系数是以Π为周期是时变的。
互感L ab 的变化规律3.2.3 同步发电机原始方程的电感系数•转子绕组间的自感系数:由于定子是个空心的圆柱,转子绕组电流产生的磁通,其磁路的磁导总是不变的。
因此,转子各绕组的自感系数Lff 、LDD和LQQ都是常数。
3.2.3 同步发电机原始方程的电感系数•转子绕组间的互感系数:由于定子是个空心的圆柱,且转子绕组间的相互位置固定不变,从而转子绕组电流产生的磁通,其磁路的磁导总是不变的。
因此,转子各绕组的互感系数都是常数。
3.2.3 同步发电机原始方程的电感系数•转子绕组间的互感系数:•d轴绕组间:励磁绕组f和阻尼绕组D之间的互感系数L fD =LfD=常数。
•d、q轴绕组间:由于d、q轴绕组相互垂直,因此d、q轴绕组间的互感系数LfQ = LQf=LDQ=LQD=0。
3.2.3 同步发电机原始方程的电感系数•定、转子绕组间的互感系数:⇓定、转子绕组间的互感系数是以2Π为周期是时变的。
互感L af 的变化规律3-3 d、q、0坐标系的同步机方程3.3.1 同步发电机原始方程变系数产生的原因•转子的旋转•转子的d、q轴不对称3.3.2 电流相量的分解•采用双反应理论把电流相量分解为和横轴纵轴分量id分量i。
武大电力系统分析第三章同步发电机的基本方程

二、电感系数
1. 定子各相绕组的自感系数
Laa l0 l2 cos 2
Lbb l0 l2 cos 2( 120o ) Lcc l0 l2 cos 2( 120o )
(3-7)~(3-9)
2. 定子绕组间的互感系数
Lab Lba [m0 m2 cos 2( 30o )] Lbc Lcb [m0 m2 cos 2( 90o )] Lca Lac [m0 m2 cos 2( 150o )]
组等效替代
三、 d、q、0坐标系统的磁链方程 和电感系数
将原始磁链方程(3-4)分写成两个式子
ψabc L iSS abc L iSR fDQ
(3 32)
ψfDQ L iRS abc L i RR fDQ
经过P变换,得
(3 33)
Ld
0
0 maf
d
0
Lq 0 0
q
0
0 L0 0
ψabc ψfDQ
LSS LRS
LSR iabc
L RR
i fDQ
(3 4)
原始方程分析:
电势、磁链共12个方程
电压、电流、磁链共有18个运行变量
六个绕组的电压是已知的
理论上用12个方程可解出12个变量
问题是: • 转子的d轴和q轴的磁导(或磁阻) 并不相等 • 转子与定子的相对位置又不断变化, 磁链方程中的电感参数也随转子位置变 化而变化,即上述电势、磁链方程是变 系数方程 • 实际解方程是十分困难的
q Lqiq m iaQ Q
0 L0i0 f m ifa d Lf if L ifD D
D
m iDa d
LDf if
LDi
D
Q mQaiq LQiQ
第3章 同步发电机的基本方程

变换由美国工程师派克在1929年首次提出(其后不久,苏联 学者戈列夫也独立地完成了大致相同的工作),一般称为派克变换。
Park 变换就是将
的量经过下列变换,转换成另外三个量。 i 例如对于电流,将 ia 、 ib 、c 变换成另外三个电流, d、i q 、 0 i i q 分别成为定子电流的 d 轴分量、 轴分量、零轴分量。
4)转子各绕组间的互感系数
同上述原因,它们也都是常数,而且绕组Q与绕组D、 f相互垂直,它们的互感为零,即:
M M fD M Df mr ; M fQ M Qf 0 ; DQ M QD 0
转子各绕组的自感系数和互感系数均为常数
5)定子与转子的互感系数
900
或
=2700
0
凸极机时定子绕组互感系数随转子旋转以 二倍频周期性变化, 隐极机时定子绕组互感系数不变。
3)转子绕组的自感系数
转子上各绕组是随着转子一起转动的,无论是凸极 机还是隠极机,转子绕组的磁路中总是不变的,即 转子各绕组的自感系数为常数,令他们表示为: ; LQQ LQ L ff L f ; LDD LD
转子绕组的 自感
定转子绕组间的互感
转子绕组间的互感
四 绕组的自感、互感系数
a相绕组磁路磁阻(磁导)的变化与转子d轴与a相绕组轴线的夹 角 有关 —— a 相轴线与直轴 d 轴的夹角
1)定子绕组的自感系数 900 或 =2700 时,自感为最小值; =00 或 =1800 时,自感为最大值; Laa l0 l2 cos2 Lbb l0 l2 cos2( 1200 )
说明:
u d u q u 0
u a P u b u c
同步发电机的基本方程

39/79
3.3 dq0坐标系的同步电机方程
2) dq0系统的电势方程
vabc vfDQ
ψψfaDbQc
RS
0
0 iabc
RR
ifDQ
vabc ψabc RSiabc
40/79
3.3 dq0坐标系的同步电机方程
量图? 6. 掌握空载电势、同步电抗?
2/79
3.1 基本前提
B,
B
1) 理想同步电机
磁路:忽略饱和、磁滞、涡流。
认为导磁系数为常数。叠加原理。 O
H
定子结构:结构相同,空间相差120º。
转子结构:纵轴和横轴分别对称。
转子和定子表面光滑,忽略导体槽和通风槽影响。
空载电动势是正弦函数。
0
ψD
0
0
RD
0
iD
0 ψQ
0 0 RQ iQ
8/79
3.2 同步发电机的原始方程
1) 电势方程
vabc vfDQ
ψψfaDbQc
RS
0
0 iabc RR ifDQ
转子在磁路上只是分别对于d轴和q轴对称而 不是随意对称的;定子各绕组电感系数作周期 性变化。
27/79
3.2 dq0坐标系的同步电机方程
1) 坐标变换和dq0系统—电枢磁势
同步电机稳态运行时,电枢磁势幅值不变,转 速恒定,对于转子相对静止。
双反应理论 电枢磁势对转子磁场的作用分
解为纵轴分量和横轴分量
0º 90º 180º 270º 360º
电力系统分析第二篇 同步发电机的基本方程

主讲教师:徐 箭 所在单位:电气工程学院
内容提要 本章将根据理想同步发电机内部的各电
磁量的关系,建立同步发电机的较为精确而 完整的数学模型,为电力系统的暂态分析准 备必要的基础知识。
《电力系统分析》 主讲人:电气工程学院 徐箭
3-1 3-2 3-3 3-6
基本前提 同步发电机的原始方程 dq0坐标系的同步发电机方程 同步电机的对称稳态运行
LfD=LDf=常数; 纵轴和横轴阻尼绕组之间的互感系数为零(因为两
绕组相互垂直),即LfQ=LQf= LDQ=LQD=0 。
《电力系统分析》 主讲人:电气工程学院 徐箭
⒋ 定子绕组和转子绕组间的互感系数
无论是凸极机还是隐极机,这些互感系数都与定子绕
组和转子绕组的相对位置有关。下面以励磁绕组和定子a
=
w2
⎡⎢⎣λmσ
+
1 4
(λad
+ λaq )⎤⎥⎦⎬⎫⎪⎪
( ) m2
=
1 2
w2
λad −λaq
⎪ ⎪⎭
《电力系统分析》 主讲人:电气工程学院 徐箭
Lab = Lba = −⎡⎣m0 + m2 cos2(α +30°)⎤⎦
定子各相绕组间的互感系数也是转子位置角的周期 函数,周期为π;
变化部分的幅值与自感系数的相等,即m2=l2; m0恒大于m2,因此定子绕组间的互感系数恒为负
《电力系统分析》 主讲人:电气工程学院 徐箭
3-1 基本前提 一、理想同步电机 二、假定正方向的选取
《电力系统分析》 主讲人:电气工程学院 徐箭
一、理想同步电机
不计磁路饱和、磁滞、涡流等的影响,即假定电机的 导磁系数为常数;
直流电机的的基本方程式和运行特性
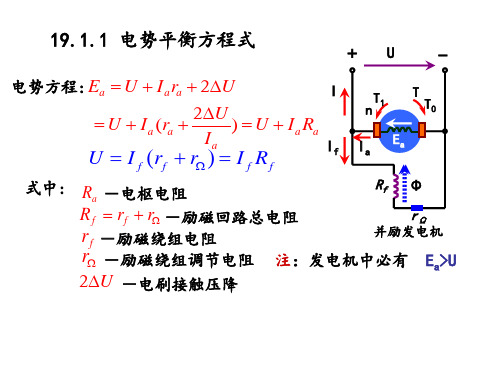
+U -
电势方程: Ea U IaБайду номын сангаасa 2U
I
U
Ia
(ra
2U Ia
)
U
Ia Ra
U I f (rf r ) I f Rf
If
nT1
T T0
Ia Ea
式中: Ra -电枢电阻
Rf Φ
Rf rf r -励磁回路总电阻
rf -励磁绕组电阻
rΩ
并励发电机
r -励磁绕组调节电阻 注:发电机中必有 Ea>U
① 负载特性 n=常数、I=常数时,U=f(If)的关系。其中,当I=0 时的特性U0=f(If)称为发电机的空载特性
② 外特性
n=常数、If=常数(并励时Rf=常数)时,U=f(I) 的关系
③调节特性 n=常数、U=常数时,If=f(I)的关系
19.2.1 它励直流发电机的空载特性 + U
-
定义:n=常数,I=0时,U0=f(If)的关系
P2
其中 p pm pFe pad pCuf pCua
注:额定负载时,直流发电机的效率与容量有关。10kW以下的 小电机,效率为75%~88.5%;10~100kW的电机,效率为85 %~90%;100~1000kW的电机效率为88%~93%
例 一台四极并励直流发电机的额定数据为:PN=6kW, UN=230V,
nN=1450r/min,电枢回路电阻ra=0.92Ω,励磁回路的电阻 Rf=177Ω,2ΔU=2V,损耗pFe+pm=295W。试求额定负载下的 电磁功率、电磁转矩及效率(杂散损耗取输出功率的1%)。
解:额定电流
IN
PN UN
同步发电机的基本方程

P 1 S P ψ dq0
d sin dt d 2 cos dt 3 0
2 3 0 3 d 2 dt 0
sin( 120 )
d dt d cos( 120 ) dt 0
ib I cos( 120 ) ic I cos( 120 )
id I cos( ) iq I sin( )
图2-7 通用电流相量在两种坐标系统上的投影关系
由两种不同的投影可得他们之间的关系
2 i d [i a cos ib cos( 120 ) ic cos( 120 ) 3 2 i q [i a sin ib sin( 120 ) ic sin( 120 ) 3
id iq i 0 cos( 120 ) cos( 120 ) cos 2 sin sin( 120 ) sin( 120 ) 3 1 1 1 2 2 2 ia ib ic
2-2 同步发电机的原始方程
正方向的规定: (1) 绕组轴线的正方 向作为磁链的正方向. (2)定子绕组产生的磁 链方向与轴线方向相 反时的电流为正值. (3)转子绕组产生的磁 链方向与轴线方向相 同时的电流为正值. (4)电压的正方向 如图2-2示。 图2-1 同步发电机各绕组轴线正方向示意图
图2-2
R i v abc ψ abc S abc
左乘P
R i v dq0 Pψ abc S dq 0
由于Ψdq0=Pψabc
所以
P ψ Pψ ψ dq 0 abc abc
直流电机的基本方程式

.直流电机的基本方程式一.直流发电机的基本方程式以并励机为例:(一).电压平衡方程直流发电机发出的电势E产生电流I,I在电枢回路aaa总电阻R(包括电枢绕组电阻及两个电刷的接触电阻)上a产生压降IR,则输出电压U=E-IR,可见发电机E>U。
aaaaaa电路如图:(二).转矩平衡方程式直流发电机是把机械能转变为电能,因此由原动机输入的机械转矩T 是驱动转矩;1电磁转矩T是制动转矩;即使电机空转也存在的、对应电机机械摩擦、铁损耗等的空载转矩T一定是阻转矩,当驱动=制动时,电机恒速旋转。
因此发电机稳定运行时的转矩0平衡方程为:T=T+ T 01(三)功率平衡方程式其功率流程图如图:从原动机输入机械功率P,扣除了机械方面的损耗,就是机转变为电的部分称为电磁p1机功率P,再扣除了电方面的损耗,就是输出的电功率P=UI,对并励发电机p2M电I=I-I。
额定时的P就是P=UI。
Na2fNN其中:是机械方面的损耗,它也是电机空载运行时就存在的损耗,故称空载损耗,pp0机它包括了机械摩擦损耗、铁耗、附加损耗(≈0.01~0.05P),即:ppp N adFem..==++;ppppp adFe0m机是电方面的损耗称为铜耗,它包括了电枢回路铜耗=R和励磁回路铜耗2ppI a acua电2U=UI,即=+pppp2R I==cufcuacuf由功率流程图可列功率平衡方程:电ff R f机械方面:;电方面:-;pP?P?pP?P?p cuaM201Mcuf P;T=把机械方面的功率平衡方程两边除以Ω,就得到了转矩平衡方程。
其中:11?PP TΩ——这是用机械量表示的电磁功率。
;T=。
可见电磁功率==T0M P0 M把电压平衡方程U=E-IR的两边乘以I:UI= EI-R 2I aaaaaaaa a∵I =I+I,则:UI = U(I+I)= EI-R,2I aaaaaff a∴UI= EI-R -UI=EI--其中:UI就是P;对比电方面的功率平衡方程可知:EI 2ppI afaaaa cuacufa就是电磁功率P。
同步发电机的基本方程

VS
详细描述
同步发电机的电压方程是描述发电机端电 压与内部电势、电流和阻抗之间关系的数 学表达式。这个方程通常采用三相坐标系 或同步坐标系来表示。在三相坐标系中, 电压方程可以表示为三个一阶微分方程, 而在同步坐标系中,电压方程可以简化为 一个二阶微分方程。
同步发电机的电流方程
总结词
描述同步发电机内部电流与电压、磁链和阻 抗之间的关系。
工业领域
在工业领域中,同步发电机可用于驱动各种电动 机、压缩机、泵等设备。
交通领域
在交通领域中,同步发电机可用于驱动列车、地 铁、船舶和飞机等交通工具。
02
同步发电机的基本原理
同步发电机的电磁原理
总结词
描述同步发电机如何通过磁场和电流相互作用产生电力的过程。
详细描述
同步发电机的基本原理是利用磁场和电流的相互作用产生电能。在发电机中,磁场由励磁系统产生,而转子上的 导线则会在旋转过程中切割磁力线,从而产生感应电动势。这个电动势的大小与磁场强度、导线切割磁力线的速 度以及导线与磁场的相对角度有关。
详细描述
功率控制的主要目标是确保发电机输出的有功功率和 无功功率满足电网的需求,同时保持电网的稳定运行 。为实现这一目标,功率控制器需要监测电网的有功 功率和无功功率需求,以及发电机的输出功率,通过 调节发电机的励磁电流和气门开度等参数,实现有功 功率和无功功率的解耦控制。常用的功率控制策略包 括恒功率控制、恒压控制和下垂控制等。
详细描述
同步发电机的磁链方程是描述发电机内部磁链与电压、电流和极对数之间关系的数学表 达式。这个方程通常采用三相坐标系或同步坐标系来表示。在三相坐标系中,磁链方程 可以表示为三个一阶微分方程,而在同步坐标系中,磁链方程可以简化为一个二阶微分
第二章2.4同步发电机及其基本方程

派克变换及d,q,0坐标系统
原始方程中的定子绕组方程取空间静止不 动,转子各绕组电量取随转子旋转的d.q 两相坐标系统列写。 Park变换是一种坐标变换,它将静止的定 子abc绕组变换到旋转的dq0坐标系统,变 换后定子dd、qq绕组中的等效磁势相对与 转子静止,磁路磁阻不变,相应的电感系 数也就变为常数。
LSR iabc LRR i fDQ
ψ dq 0 P 0 ψ abc P 0 LSS ψ = ψ = 0 U L RS fDQ 0 U fDQ P 0 LSS = 0 U LRS PLSS P 1 = LRS P 1
1
2.4同步发电机及其基本方程
本节知识点:
认识同步发电机的结构 同步电机的电势方程和磁链方程 同步发电机的基本方程 稳态运行模型及相关参数 暂态运行模型及相关参数 同步发电机的序参数
同步发电机的分类
1 隐极机 定子; 转子可以认为各向磁阻相同; 高速旋转的汽轮机。 2 凸轮机 定子同隐极机; 转子磁阻不再随意对称; 水轮机。
M af = maf cos α M bf = mbf cos( α 120 ) M cf = mcf cos( α + 120 )
定子和转子各相绕阻间的互感系数
定子绕组与直轴阻尼绕组间的互感系数
M aD = maD cos α M bD = mbD cos( α 120 ) M cD = mcD cos( α + 120 )
电磁基础
磁动势F = NI F l 磁通φ = ,其中Rm = 磁链ψ = Nφ = NI Rm s F 串联回路φ = Rm1 + Rm 2 E = j 4.44 fNφ
理想同步发电机
1、定子abc三相绕组结构完全相同,互相对称, 空间相隔120度电角度。 2、电机转子在结构上对于d轴与q轴完全对称。 3、定子、转子铁心同轴且表面光滑(忽略定、 转子上的齿槽),忽略齿谐波。 4、定子、转子绕组电流产生的磁动势在气隙中 是正弦分布的,忽略高次谐波。 5、磁路是线性的,无饱和,无磁滞和涡流损耗, 认为电机铁心部分导磁系数为常数,可应用迭 加原理。
第3章同步发电机的基本方程

a
f
f
x
ad
d a
a
ad
d
f a f x
maf wwf ad
f a f x d
ad
a d
(4)定子绕组和转子各绕组间的互感系数—abc--D
a
ad
a
D
D
x
aD wwD iD ad cos
L L m cos Da aD aD LbD LDb maD cos 120 L L m cos 120 Dc aD cD
绕组轴线正向示意图
3-3 dq0坐标系的同步电机方程
1. 坐标变换和 dq0坐标系 2. dq0坐标系下的电势方程
3. dq0坐标系下的磁链方程和电感系数
4. 同步电机标幺值基本方程
1. 坐标变换与dq0坐标系
(1)采用通用相量表示定子三相电流
F
a
I
定子三相对称电流可以用以同 步转速旋转的通用相量I表示;
if rf uf iD rD ec eD iQ rQ eQ rc ua ub uc ic ef ra ea eb rb ib ia
i
abc rS u abc ψ u ψ fDQ fDQ 0
0 i abc i rR fDQ
eQ
i
e
3-2 同步电机的原始方程式
1. 电势方程
ua u b uc u f 0 0 a r b 0 c 0 f D Q 0 0 r 0 0 r 0 rf 0 0 0 0 rD 0 ia ib ic 0 i f 0 iD rQ iQ
发电机电磁功率方程_概述说明以及解释

发电机电磁功率方程概述说明以及解释1. 引言1.1 概述发电机是一种将机械能转化为电能的设备,广泛应用于工业生产和日常生活中。
在发电机的工作过程中,电磁功率方程是一个非常重要的理论工具。
它描述了发电机内部电磁场的特性和与之相关的功率转换过程。
了解和应用电磁功率方程可以对发电机的设计、优化和性能评估提供有效支持。
1.2 研究背景随着社会经济的快速发展以及对清洁能源需求的不断增加,对发电机高效、可靠、环保等方面要求也越来越高。
因此,对发电机内部运行规律进行深入研究并探寻其影响因素成为了当前的热点问题。
而电磁功率方程作为解析性工具,通过建立数学模型来分析和表达电磁场与功率转换之间的关系,可以有效地帮助我们理解并预测发电机的行为。
1.3 目的本文旨在全面概述和解释发电机电磁功率方程,并通过推导过程阐明其物理原理和数学基础。
同时,还将探讨电磁功率方程在实际应用中的意义,包括发电机效率优化、工作状态监测和设计参数优化等方面。
通过对该方程的深入研究,我们可以更好地理解发电机内部的物理过程,从而为不断提升发电机的性能和可靠性提供有力支持。
以上是“1. 引言”部分内容的详细清晰撰写,请参考。
2. 电磁功率方程概述:2.1 电磁场基础知识在讨论发电机的电磁功率方程之前,我们需要了解一些基本的电磁场知识。
电磁场是由带电粒子所产生的带有能量和动量的区域。
根据麦克斯韦方程组,电磁场包括一个静态的电场和一个随时间变化的磁场。
这两个场相互作用,形成了电磁波。
2.2 发电机原理简介发电机是将机械能转化为电能的装置。
它基于法拉第定律和洛伦兹力原理,利用导体在磁场中运动时感应出现的电动势来产生电流。
常见的发电机包括直流发电机和交流发电机。
2.3 电磁功率方程定义在发生感应现象时,我们需要考虑导体中存在的阻抗以及能量转化过程中损耗等因素。
因此,通过引入一些额外的参数和假设,我们可以得到描述发生感应时各种能量转换损失与效率的指标。
在分析功率转换过程中,主要涉及到三个关键参数:电压、电流和功率。
第3章 同步发电机的基本方程

场有了相对运动,就会在这个鼠笼里产生感应电流,形成附加磁 场(起阻尼作用)。
第三章 同步发电机的基本方程
简化前提
一、理想同步电机的简化假设
为了方便分析,常采用以下假设(理想同步机):
1、忽略磁路饱和、磁滞、涡流等影响,假设电机铁心部分导磁系数为常数。 2、电机转子在结构上对于纵轴和横轴分别对称。 3、定子的abc三相绕组空间位置互差120度电角度,在结构上完全对称。 4、电机空载,转子恒速旋转时,转子绕组的词董事在定子绕组所感应的空 载电动势是时间的正弦函数。 5、定子和转子的槽和通风沟不影响转子和定子的电感,即认为定子和转子 有光滑的表面。
(3)机座和端盖等。 (1)转子铁心:
由整块铸(锻)钢制成。 2. 转子 (2)励磁绕组:
工作时施加直流励磁。 (3)阻尼绕组和转轴等。
阻尼绕组
5第.2 三三章相同同步步电机发的电基机本结的构基本方程
二、励磁方式
1. 直流励磁机励磁
励磁绕组由小型直流发电机供电。
2. 静止整流器励磁
交流励磁机→整流→直流电 电刷
第三章 同步发电机的基本方程
第三节 d、q、0坐标系的同步电机方程
一、坐标变换 定子a,b,c三相绕组对转子的影响可考虑为其对转子
d,q轴的影响之效应和,为此我们引入一种数学变换,即: 著名的派克变换。从数学角度考虑,派克变换是一种线性 变换;从物理意义上理解,它将观察者的角度从静止的定 子绕组转移到随转子一同旋转的转子上,从而使得定子绕 组自、互感,定、转子绕组间互感变成常数,大大简化了 同步电机的原始方程。
第三章 同步发电机的基本方程
磁学有关公式
B d
dA
F
Rm
F iw
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
---发电机基本方程
王敏
本节内容:2-4,2-3
同步发电机的基本方程 同步发电机负载下三相短路交流电流初始值
参考书:电机学;
陈珩,同步电机运行基本理论与计算机算法,北京:水利电力出版社,1992 黄家裕、岑文辉,同步电机基本理论及其动态性为分析,上海:上海交通大学出版社,1989 [日]关根泰次著,蒋建民,金基圣,王仁洲译,电力系统暂态解析论,北京:机械工业出版社,1989
定子各相绕组和转子各绕组间的互感系数也是α 的周期 函数(周期为2Л )
例例::定定子子绕绕组组的间自的感变自化感规变律化示规意律图示意图
是α 的余弦函数,周期为Л
例: 定子绕组间的互感变化规律示意图
发电机基本方程
ua
ub
r
r
ia a
b
M
ba
c f
M M
ca fa
D
Q
M Da M Qa
M ab Lbb M cb M fb M Db M Qb
M ac M bc Lcc M fc M Dc M Qc
M af M bf M cf L ff M Df M Qf
Ⅲ. 定子电流中直流分量产生的空间静止的磁场与转子的相对速度 为同步转速;定子电流的倍频交流分量产生的以两倍同步转速旋 转的磁场,与转子的相对速度也是同步转速,这两种电枢反应均 会在励磁回路中感应基频交流电流分量。也可以理解为励磁回路 为保持自身磁链守恒感生基频交流电流,以抵消穿入的交变磁场。
同步发电机在转子有励磁而定子回路开路即空载运行情 况下,定子三相绕组端突然三相短路
补充:
Q阻尼绕组与次暂态过程对应,时间常数很小;g阻尼 绕组与暂态过程对应,时间常数较大,其在暂态过程中 的特点与d轴的励磁绕组f对应,只是没有电源激励。
同步发电机在转子有励磁而定子回路开路即空载运行情 况下,定子三相绕组端突然三相短路
定子中产生同步频率的交流分量。交流分量是逐渐衰减 的,最终衰减至稳态值。其实际衰减过程是按两个时间 常数衰减。
这类方程的求解是颇为困难的。如何解决? ---将变系数的微分方程变为常系数的微分方程
如何完成?
分析:发电机的原始方程的物理特点
(1)定子各电磁变量是按三个绕组也就是对于空间静止不动 的三相坐标系列写的
ib
b
uc
u f
r rf
ic if
c f
0
0
rD
iD
D
rQ iQ Q
三、磁链方程的建立
ad
●
×
(主要是气隙磁阻)
I Id Eq|0| / xd
×
●
●
×
空载情况下短路电流交流分量初始值
从前面的分析看出,走直轴主磁路的电枢反应磁通 和漏磁通 决定了定子回路的等值电抗,乃至短路电流 稳态值的大小。
则短路瞬间电枢反应磁通所走的磁路将决定短路电流初 始值的大小。
I Id Eq|0| / xd
cos0et /Ta
本节学习什么?
同步发电机的原始方程? 派克转换? d、q、0坐标系统的发电机基本方程? 发电机基本方程各种形式? 利用发电机基本方程分析求解短路交流电流初始值?
1、同步发电机的原始方程?
同步发电机结构示意图
定子三相绕组 a、b、c 转子励磁绕组 f 转子阻尼绕组D、Q
短路全电流表达式
如果忽略倍频分量,则直流分量的起始值和基频交流分量的初始瞬时值 大小相等,方向相反,短路全电流表达式为:
ia
2
Eq|0|[(
1 xd
1 )et /Td xd
( 1 xd
1 )et /Td xd
1 xd
] cos( 0
0t)
2 Eq|0| xd
始值的计算?
同步电机的基本结构
定子绕组
客观真实存在的绕组
励磁绕组
阻尼绕组:阻尼条构成的回路和铁芯中涡流回路等效而成。
-----电气上的等值绕组
补充:关于阻尼绕组
阻尼绕组的个数:从理论上讲,等值绕组的个数越多, 模拟的精度就越高。采用较多的等值阻尼绕组,仅从建 立同步机的数学模型的角度而言并不困难。但是采用过 多的等值绕组将带来两个问题,一是使数学模型微分方 程的阶数增高,从而使后续的求解计算量大大增加;二 是很难准确的获取相关的电气参数。因此,除了在电机 设计中采用多个阻尼绕组来研究某些特殊问题的报告, 在目前应用比较广泛的数学模型中,等值阻尼绕组的个 数一般不超高3个。
M aD M aD M cD M fD LDD M QD
M aQ ia
M
bQ
ib
M M
cQ fQ
i
ic
f
M
DQ
iD
LQQ iQ
问题:
由于磁链方程中许多电感系数都是随转子角α 而周期变 化的,Ψ 代入电势方程后,电势方程将成为一组以时间 的周期函数为系数的微分方程。
凸极同步发电机转子磁极两端短接的阻尼条和隐极机实心转子 铁中涡流回路在正常稳态运行时是没有电流的,而在暂态过程 中会感生电流。
短路后D绕组中和励磁绕组一样会产生直流电流和基频交流电 流。
Q绕组中只有基频交流电流而没有直流电流,这是因为假设定 子回路电阻为零,定子基频交流电流只有直轴方向上的电枢反 应。
磁链方程的特点
非对角元素为两绕组间的互感系数,两绕组间的互感系 数是可逆的。
附录A中给出了各类电感系数的表达式。对于凸极机, 大多数电感系数为周期性变化的,隐极机则小部分为周 期性变化。
磁链方程式出现变系数的原因主要是:
(1)转子的旋转使定子、转子绕组间产生相对运动,致 使定、转子绕组间的互感系数发生相应的周期性变化
Im (t) (Im Im )et /Td (Im Im )et /Td Im
为了产生恒定的磁链定子三相中除了大小不变的直流分 量外,还有一个倍频的交流电流,其幅值取决于直轴和 交轴磁阻之差,一般不大。所以在短路电流波形中不易 被观察到。
同步发电机在转子有励磁而定子回路开路即空载运行情 况下,定子三相绕组端突然三相短路
空载情况下短路电流基频交流分量稳态值
短路到稳态后,恒定的励磁电流产生的主磁通 0 在定子
三相绕组感应空载电动势(或励磁电动势 Eq|0| )
忽略定子电阻,三相交流电流是纯感性的,它们在转子
空间合成的同步旋转的电枢反应是纯去磁的,电枢反应
磁通 ad 的路径为主磁路。
转子直轴、气隙和定子铁芯
补充:关于阻尼绕组
阻尼绕组的作用:对水轮发电机等凸极同步电机,阻尼 绕组模拟了分布在转子上的阻尼条的阻尼作用;对汽轮 发电机等隐极同步电机,阻尼绕组则模拟了整块转子铁 芯中的由涡流所产生的阻尼作用。
由于凸极机的转子阻尼条与隐极机的整块转子铁芯比起 来,前者更接近于真实的绕组,以及在磁路上凸极机在 转子的直轴、交轴两个方向的磁阻不同而隐极机相同, 故对于凸极机,一般在转子的直轴和交轴上各采用一个 等值阻尼绕组,分别记为D绕组和Q绕组;而对于隐极 机,出了D、Q绕组外,在交轴上再增加一个等值阻尼 绕组,记为g绕组。g绕组和Q绕组分别用于反映阻尼作 用较强和较弱的涡流效应。
二、电势方程的建立 定子侧:ua iar a
转子侧:u f rf if f
直轴阻尼绕组:0 rDiD D
交轴阻尼绕组:0 rQiQ Q
假设定子三相绕组电阻相同,发电机电势方程写成矩阵的形式
ua
ub
r
r
ia a
不衰减
衰减至零,时间常数 主要决定于转子回路参数
突然短路时
定、转子绕组间产生变压器感应关系
定子电流 急剧变化
电枢反应磁 通随着变化
在转子绕组 中感应电流
影响定子电流的变化
定子和转子绕组电流
的互相影响是同步电机突 然短路暂态过程区别于稳 态短路的显著特点
定子短路电流交流分
量的幅值随时间衰减的现 象是是同步电机突然三相 短路电流与恒压源短路电 流的最基本的差别
(2)对于凸极机,转子在磁路上只是分别对于d轴和q轴 对称而不是随意对称的,转子的旋转也导致定子各绕组 间的自感和互感的周期性变化。
补充:电感系数的变化规律
定子各相绕组的自感和互感均为转子位置角α 的周期函 数(周期为Л )
转子各绕组的自感和互感为常数(转子电流产生的磁通 的磁路的磁导总是不变的)
ib
b
uc
u f
r rf
ic
if
c f
0
0
rD
iD
D
rQ iQ Q
一组变系数的微分方程
a Laa
上节回顾
发电机的基本结构和各绕组等值电路? 同步发电机突然三相短路其电流的变化和恒压源三相电
路的短路电流变化有何不同?为什么? 同步发电机突然三相短路分析过程的基本假设? 同步发电机突然三相短路分析过程所应用的基本原理? 同步发电机突然三相短路后定子绕组、转子绕组以及阻
