第2章随机过程的基本概念
随机过程第二章

4、有限维分布族
定义:设
X t ; t T 为一个 S .P. ,其有限
维分布函数的全体(一维分布函数,二维分布函
数,n维分布函数)。
F Ft1 ,t2 ,,tn x1, x2 ,, xn ; xi R,ti T,n N, i 1,2,, n
称之为 S.P. X t 的有限维分布函数。
2、特点:
独立增量过程在零均值且二阶矩存在时,是正交增量过程。 注:独立增量过程在现实环境中大量存在(例2.10)
3、平稳独立增量过程(定义 2.8)
增量 X(t)-X(s) 的分布律仅依赖于区间长度t-s。(第三章) (三)马尔可夫过程(第四、五章) (四)正态过程 1、定义 2.10: X(t)的有限维分布律是n维正态随机向量的分布律. 2、特点: ①二阶矩过程 ②数字特征成为其参数。
状态空间:S .P. X t 的状态所有可能取值的 集合,称之为状态空间。
小结:
X e, t 是状态与参数的二元函数
若 若
e
t
确定 确定
X e, t 是时间函数
X e, t 是随机变量
是一个确定值 是随机过程 S .P.
r.v.
若 e, t 确定 若 e, t 不定
随机过程的分类
一维正态过程分布律:
X (t ) ~ N u(t ),
2 2
2
(t )
二维正态过程分布律:
X (t1 ), X (t2 ) ~ N u(t1 ),u(t2 ),
这里有5个参数。 其中 1
(t1 ), (t2 ), (t1 , t2 )
(t1 , t2 ) 1 为相关系数或归一化协方差函数
2.2随机过程的分布律和数字特征

2.2随机过程的分布律和数字特征
任 意 有 限 个 时 刻 过 程 各个 状 态 的 联 合 概 率 分 布 : 给定随机过程 { X (t), t T }.
对任意n (1)个不同的时刻 t1, ,tn T , 相应
的状态可由 n维随机变量 X (t1), X (t2), , X (tn)
描述 .
a cost
,t
,
其中a
0,
且P1
2 3
,
P2
1 3
,
试求随机过程 X (t),t (,)
的数字特征。
解
mX
EX t a cos t 1 a cos t 2 1 cos t,
3
33
t (,)
RX s,t EX sX t
a coss a cost 1 a cossa cost 2
示一条固定的曲线。如图蓝色曲线
2.2随机过程的分布律和数字特征
2.称 BX(s,t) = E{[X(s) - mX(s)][X(t) - mX(t)]},s,t T
为 XT 的协方差函数;
3.称 DX (t) BX t,t E[X (t) mX (t)]2 ,t T 为 XT
的方差函数;
4.称 RX (s,t) E[X (s)X (t)],s,t T 为 XT
2019级研究生课程
彭晓华
辽宁工大基础部数学教研室
第2章 随机过程的基本概念
2.1随机过程的基本概念 2.2随机过程的分布律和数字特征 2.3 复随机过程 2.4几种重要的随机过程
本章小结 思考题与作业
复习2.1 1.怎样理解随机过程?它与函数及随机变量有何不同?
2.随机过程的五个要素都是什么?
随机信号分析与处理(第2版)

随机信号分析与处理(第2版)概述本文档介绍了随机信号分析与处理(第2版)的主要内容。
随机信号是一种在时间上或空间上具有随机性质的信号,在诸多领域中都有广泛的应用,如通信、图像处理、控制系统等。
随机信号的分析和处理对于了解其性质、提取有用信息以及设计有效的处理算法都是必不可少的。
主要内容第一章:随机信号的基本概念本章介绍了随机信号的基本概念和特性,包括随机信号的定义、概率密度函数、均值、方差等。
通过对随机信号的特性分析,可以为后续的分析和处理提供基础。
第二章:随机过程本章讨论了随机过程的定义和性质。
随机过程是一类具有随机性质的信号集合,其在时间上的取值不确定,但具有统计规律性。
通过对随机过程的分析,可以了解其演化规律和统计性质。
本章介绍了随机信号的表示与分解方法。
随机信号可以通过不同的数学模型进行表示,如傅里叶级数、傅里叶变换、小波变换等。
通过将随机信号进行分解,可以提取出其中的有用信息。
第四章:随机信号的功率谱密度本章研究了随机信号的功率谱密度。
功率谱密度描述了随机信号在频率域上的分布,通过分析功率谱密度可以获得随机信号的频率特性和频谱信息。
第五章:随机信号的相关与协方差本章讨论了随机信号的相关与协方差。
相关是用来描述随机信号之间的依赖关系,协方差是用来描述随机信号之间的线性关系。
通过分析随机信号的相关与协方差,可以研究信号之间的相关性和相关结构。
本章介绍了随机信号的滤波和平均处理方法。
滤波是用来抑制或增强随机信号中的某些频率分量,平均则是通过对多次采样的随机信号进行求平均来减小随机性。
第七章:随机信号的参数估计本章研究了随机信号的参数估计方法。
参数估计是通过对随机信号进行采样和分析,通过估计参数来了解信号的统计性质和特征。
第八章:随机信号的检测和估计本章讨论了随机信号的检测和估计方法。
检测是用来判断随机信号的存在或不存在,估计是通过对随机信号的采样和分析来估计信号的参数。
第九章:随机信号的最优滤波本章研究了随机信号的最优滤波方法,最优滤波是通过优化设计滤波器来最小化系统误差或最大化输出信噪比。
随机过程课程第二章 随机过程的基本概念

第一节 随机过程的定义及其分类 第二节 随机过程的分布及其数字特征 第三节 复随机过程 第四节 几种重要的随机过程简介
第一节 随机过程的定义及其分类
一、直观背景及例
例1 电话站在时刻t时以前接到的呼叫次数 一般情况下它是一个随机变数X ,并且依赖 时间t,即随机变数X(t),t[0,24]。
首页
(4)平稳随机过程
平稳过程的统计特性与马氏过程不同,它不 随时间的推移而变化,过程的“过去”可以对 “未来”有不可忽视的影响。
首页
返回
第二节 随机过程的分布及其数字特征
一、随机过程的分布函数
设{ X (t) ,t T }是一个随机过程,
一维
分布 对于固定的t1 T ,X (t1) 是一个随机变量,
F (t1,t2;x1, x2 ) =
x1
x2
f (t1, t2;y1, y2 )dy1dy2
则称 f (t1,t2;x1, x2 ) 为 X (t) 的二维概率密度
n维
n 维随机向量(X (t1 ) ,X (t2 ) ,…, X (tn ) )
分布 函数
联合分布函数
F (t1,t2 , ,tn;x1, x2 , , xn )
分布函数
FXY (t1, ,tn ;t1, ,tm ;x1, , xn ; y1, , ym )
P{X (t1) x1, , X (tn ) xn;Y(t1) y1, ,Y(tm ) ym }
称为随机过程和的n + m维联合分布函数
首页
相互 设 X (t) 和Y (t) ,t1,t2 , ,tn ,t1,t2 , ,tm T
首页
2.方差函数
随机过程{ X (t) ,t T }的二阶中心矩
第2章随机过程的基本概念

F ?? { F ?t1 , t2 ,? , tn ; x 1 , x 2 ,? , x n ?:
ti ? T , x i ? Ri , i ? 1,2, ? , n , n ? 0} 称F为XT 的有限维分布函数族. 定义3 过程 { X(t), t的? nT维} 特征函数定义为
φ?t1 , t2 ,? , tn;?1 ,θ 2 ,? ,θ n ?
? E{e i[θ 1 X (t1 )? ? } ?θ n X (tn )]
称 {φ(t1, t2 ,? , tn;θ 1 ,θ 2 ,? ,θ n ) : t1 , t2 ,? , tn ? T, n ? 1}
为XT 的有限维特征函数族. 特征函数和分布函数是相互唯一确定.
定义2 过程 { X(t),对t ?任T给} 的
t1 , t2 ,? , tn ? T ,
随机向量
?X (t1 ), X (t2 ),? , X (tn )?
的联合分布函数
F (t1 , t2 ,? , tn; x1 , x2 ,? , xn ) ?
P{ X (t1 ) ? x1 , X (t2 ) ? x2 ,? , X (tn ) ? xn }
X(t1,ω)
X(t2,ω)
t1
t2
X(t,ω1) X(t,ω2) X(t,ω3) tn
定义 对每一固定 ω?,Ω称 { X(t, ? ), t的? 一T}个样本函数.
X是t ?随ω?机过程
也称轨道, 路径,现实.
Ex.5 利用抛硬币的试验定义一个随机过程,
X(t)
?
?cos? t, ?
?2t
出现正面; 出现反面. t ? R.
过程识别
高等数学中的随机过程相关知识点详解

高等数学中的随机过程相关知识点详解近年来,随机过程被越来越多的人所关注和使用。
作为高等数学的一个分支,随机过程具有广泛的应用领域,包括金融、医学、生物学等等。
在本文中,将详细解析高等数学中的随机过程相关知识点,帮助读者更好地理解和应用这一领域的知识。
一、概率论基础在进行随机过程的学习之前,我们需要了解一些概率论的基础知识。
概率论是确定不确定性的一种科学方法,它研究的是随机事件的发生规律和概率计算方法。
在概率论中,有一些基本概念和公式,包括概率、条件概率、概率分布、随机变量等等。
1.1 概率概率是指一个事件发生的可能性大小。
通常用P来表示,它的取值范围是0到1。
当P=0时,表示这个事件不可能发生;当P=1时,表示这个事件一定会发生。
例如,掷一枚硬币正面朝上的概率为1/2,或者说P=0.5。
1.2 条件概率条件概率是指在已知某些条件下,某个事件发生的概率。
通常用P(A|B)来表示,表示在B发生的情况下,A发生的概率。
例如,从一副牌中摸两张牌,第一张是红桃,第二张是黑桃的概率为P(第二张是黑桃|第一张是红桃)=26/51。
1.3 概率分布概率分布是指所有可能事件发生的概率分布,它是概率论的基础。
在不同的情况下,概率分布也是不同的。
例如,在离散型随机变量中,概率分布通常以概率质量函数的形式给出;而在连续性随机变量中,概率分布通常以概率密度函数的形式给出。
1.4 随机变量随机变量是一种随机事件的数学描述。
它通常用大写字母表示,如X、Y、Z等等。
根据其取值的类型,随机变量可以分为离散型和连续型。
离散型随机变量只能取到有限或可数个值,如掷硬币、扔骰子等等;而连续型随机变量可以取到任意实数值,如身高、体重等等。
二、随机过程的基本概念2.1 随机过程的定义随机过程是一种描述随机事件随时间变化的方法。
它可以看作是有限维随机变量序列的无限集合,其中每个随机变量代表系统在某个时刻的状态。
随机过程的定义包括两个方面:空间(状态集合)和时间(时刻集合)。
第二章 随机过程的基本概念_2.3 2.4

4 2 0 -2 -4 10 5 0 -5 -10
0
50
100
0
50
100
0 1
2015/5/12
0 100
14
两个不同相关时间随机过程的样本函数
2.3.4 循环平稳的概念
广义循环平稳:
如果随机过程X(t)的均值和自相关函数满足下列关系
2T
0
(1
2T
2 )[ RX ( ) mX ]d 0
平稳随机过程X(t)具有相关函数遍历性的充要条件
1 lim T T
2T
0
(1
2T
2 )[ R ( ) RX ( )]d 0
(t ) X (t ) X (t )
2015/5/12 22
第二章随机过程的基本概念
mX mX
其中
RX ( ) RX ( )
RX ( )
1 lim T 2T
T T
x(t
) x(t )dt
则X(t)为遍历(各态历经)过程。
2015/5/12 19
2.3.5 随机过程的各态历经性
X (t ) X (t )
t
t
(a)
(b)
各态历经过程与非各态历经过程示意图 各态历经过程的一个样本函数经历了随机过程 所有可能的状态
如果
f XY ( x1 ,..., xN , t1 ,..., t N , y1 ,..., yM , t '1 ,..., t 'M ) f X ( x1 ,..., xN , t1 ,..., t N ) fY ( y1 ,..., yM , t '1 ,..., t 'M )
随机过程 第2章

随机变量 随机变量族
e → x(e) (e, t) → xt(e)=x(e, t)
x=xt(ei)
x
e1 e2 e3
e
概率空间和随机对象
样本空间
概率空间
随机变量
随机向量
随机过程
2.1 随机过程的基本概念
定义:设(Ω, ö,P)为概率空间,T是参数集。 若对任意 t ∈T ,有随机变量X(t, e)与之 对应,则称随机变量族{X(t, e), t ∈T } 是(Ω, ö,P)上的随机过程,简记为 {X(t),t ∈T }或{Xt,t ∈T }。 ★ X(t)的所有可能的取值的集合称为状态空 间或相空间,记为I。
由此可将随机过程分为以下四类:
a. 离散参数离散型随机过程; b. 离散参数连续型随机过程; c. 连续参数离散型随机过程; d. 连续参数连续型随机过程。
2. 以随机过程的统计特征或概率特 征分类:
a. 独立增量过程; b. Markov过程; c. d. e. f. g. 二阶矩过程; 平稳过程; 鞅; 更新过程; Poission过程;
称之为随机过程X(t) 的二维概率密度。
2.3 随机过程的分布律
随机过程的二维分布函数比一维分布函数包含了随 机过程变化规律更多的信息,但它仍不能完整地反 映出随机过程的全部特性及变化规律。用同样的方 法,我们可以引入随机过程 X(t) 的 n 维分布函数和 n 维概率密度。
FX ( x1 , x2 , , xn ; t1 , t2 , tn )
• 又如移动某基站每天的通话次数,X 显然不 能确定,即为随机变量,进一步分析知这 个 X 还和时间 t 有关,即 X(t),所以 X(t) 也构成一个过程,即随机过程;类似地, 气温、气压、商店每天的顾客流量等都构 成一个随机过程。
2-1+随机过程的定义与分类

t
e
可变 固定 固定 可变
固定 固定 可变 可变
X(t) 确定的时间函数; 随机变量; 确定值 随机过程
2.1-2 随机过程的分类 根据时间和状态的不同,可以将随机过程划分为四类:
连续时间随机过程 随机序列
离散随机过程 离散随机序列
时间 连续 离散 连续 离散
状态 连续 连续 离散 离散
2.1-2 随机过程的分类
函数空间 X (t, e1)
样本函数
t
X (t, e2 )
t
X (t, e3)
t
随机过程是从样本空间到函数空间的映射 是t和e的二维函数,X(t,e)
2.1-1 随机过程的定义
X (t1, e) 是一个随机变量
● ●
●
X
●
(t1,
e2 ) ●
●
S
X (t1, e3)
●
●
t1
t2
2.1-2 随机过程的分类
y(n 1) (11y(n) 11117)(mod M )
x(n) y(n) / M
1
0.8
0.6
0.4
0.2
0
0
50
100
150
200
伪随机序列
本节小结:
随机过程的定义 随机过程是样本函数的集合 随机过程是随时间变化的随机变量的集合
随机过程的分类 根据时间和状态的不同可分为四类 其中离散型随机过程的分析是课程学习的难点 随机过程的分解:任意随机过程都可以分解为 一个可预测过程与一个不可预测过程之和。
不可预测过程
5 0 -5
0 5 0 -5
0 5 0 -5 50 0 -5
0
02_03第二章 随机过程的基本概念汇总

即Z(t)的三阶矩就与时间t有关,故Z(t)不是 狭义平稳随机过程。
2.3.1 平稳随机过程的定义
★ 平稳随机过程的例题(续)
[例2.13]设随机过程X(t)=X (k) ,k=…-2, -1,0,1,2…, X (k)为相互独立且具有相同分布 的随机变量序列,已知E[X (k)]=0, E[X2 (k)] = σ2X。试证X(t)既是广义平稳随机过程,又 是狭义平稳随机过程。
E[ X (t )] xf X ( x, t )dx xf X ( x)dx mX
D[ X (t )] [ X (t ) mX (t )]2 f X ( x)dx 2 X
2.3.1 平稳随机过程的定义
★ 狭义平稳随机过程的定义(续) 同理,狭义平稳随机过程的二维概率密度仅与时
间间隔τ= t1 - t2有关,即有
fX(x1,x2,t1,t2)= fX(x1,x2,t1+ △t ,t2 + △t) △t =-t2
fX(x1,x2,t1 - t2,0)= fX(x1,x2,τ)
由此可以求得X(t)的相关函数也只是τ的函数,即
RX (t1 , t2 )
0 rX ( )d
0
物理意义
相关时间 0 越小,就意味着相关系数 rX ( ) 随 增加而降落的越快,这表明随机过程随时 间变化越剧烈。反之,相关时间 0 越大, 则表时随机过程随时间变化越慢。
K x ( ) Rx ( ) E ( X ( ))
2
性质4
如果平稳随机过程中含有周期分量,那么其 自相关函数中也含有周期分量 例2.10可知, X (t ) A cos(wt + F) + N (t ) 相关函数为: A2 RX ( ) cos w + R N ( ) 2
随机过程随机过程的基本概念ppt课件

6
2.1 随机过程的定义
例2.1.2 电子元件或器件由于内部微观粒子 (电子)的随机热噪声引起的端电压称为热 噪声电压,它在任一确定时刻的值是随机变 量,记为V(t). 如果t 从0变到+∞,t 时刻的热 噪声电压需要用一族随机变量{V(t), t ∈[0, +∞]}来表示,则该随机变量就是一个随机过 程. 对某种装置做一次试验,便可得到一个 “电压—时间函数”v(t) . 这个“电压—时间 函数”是不可能预先确知的,只有通过测量才 能得到. 如果在相同的条件下独立地再进行一 次测量,则得到的记录是不同的.
; 取V=0,则
x(t)=0;取V3=1,则x(3t)=cosωt. 这些都是 t 的
确定函数,即随机过程的样本函数.
12
2.1 随机过程的定义
(2) 当t=0时,X(0)=V,故X(0)的概率密度函 数就是V的概率密度函数,即
1,0 x 1 fX (0) (x) 0,其他
当 故
1,0 v 1 fV (v) 0,其他
(1) 画出{X(t) ,﹣∞<t<+∞}的几条样本曲线;
(率2)密求度t 函 0数, 4;
,
3 4
,
时随机变量X(t)的概
(3)求
t
2
时X(t)的分布函数
11
2.1 随机过程的定义
解
(1) 取 V 2 则x(t) 2 cost
定义2.1.3 设{X(t), t ∈T }是随机过程,则 当ω ∈ Ω固定时, X(t)是定义在上T不具有 随机性的普通函数,记为x(t), 称为随机过 程的一个样本函数. 其图像成为随机过程 的一条样本曲线(轨道或实现).
《应用随机过程》-课程教学大纲

《应用随机过程》课程教学大纲一、课程基本信息课程代码:16055502课程名称:应用随机过程英文名称:Applied Stochastic Processes课程类别:专业课学时:32学分: 2适用对象:财经类专业本科生考核方式:考试先修课程:微积分、线性代数、概率论二、课程简介中文简介紧抓课程改革核心环节,不断提升教学质量,将“课程思政”作为融合德育与智育的融合主渠道,是逐步实现“立德树人”的综合教育理念的前进方向。
《应用随机过程》是面向经济统计专业三年级学生开设的一门必修课,随机过程通常被视为概率论的动态部分,即研究的是随机现象的动态特征,着重对随时间和空间变化的随机现象提出各种不同的模型并研究其内在的性质与相互联系。
具有较强的理论性。
该学科在社会科学、自然科学、经济和管理等各个领域中都有广泛的应用,培养学生的科学精神,探索自然和人类的奥秘。
英文简介The course Applied Stochastic Processes is one of the compulsory courses for the junior undergraduates majoring in Economic Statistics,which is usually viewed as the dynamic part of probability theories. It focuses on the dynamic feature of stochastic phenomena and emphasizes modeling the stochastic phenomena varying with time and space .Moreover,it explores the inner property and relationship among various models and it is quite theoretical and widely used in social science,natural science,Economic and management science etc.三、课程性质与教学目的本课程是经济统计专业一门应用性很强的专业课。
第二章随机过程基本概念

2随机过程的基本概念§2.1 基本概念随机过程是指一族随机变量.对随机过程的统计分析称为随机过程论,它是随机数学中的一个重要分支,产生于本世纪的初期.其研究对象是随机现象,而它特别研究的是随“时间”变化的“动态”的随机现象.一随机过程的定义1 定义设E为随机试验,S为其样本空间,如果(1)对于每个参数t∈T, X(e,t)为建立在S上的随机变量,(2)对每一个e∈S, X(e,t)为t的函数,那么称随机变量族{X(e,t), t∈T, e∈S}为一个随机过程,简记为{X(e,t), t∈T}或X(t)。
()()()()(){}{}[]()为随机序列。
时,通常称,取可列集合当可以为无穷。
通常有三种形式:参数一般表示时间或空间,或有时也简写为一个轨道。
随机过程的一个实现或过程的样本函数,或称随机的一般函数,通常称为为对于:上的二元单值函数。
为即若用映射来表示注意:t X T T T b a b a T T T T t X t X t e X T t e X S e S T t e X RS T t e X t21321,,,,3,2,1,0,1,2,3,,3,2,1,0T ,.4,.3,,2,:,.1=---==ÎÎ×δ®´L L L为一个随机过程。
则令掷一均匀硬币,例),()(cos )(},{1t e X t X Rt T e t H e t t X T H S =Îîíì====p 2 随机过程举例îíì=====为随机变量的函数均为和解释:T e t He t t e X t t t T X t t H X 000cos ),(),(cos ),((p p 2121cos ),(000p t t t e X p 并且:例2:用X(t)表示电话交换台在(0,t)时间内接到的呼唤的次数,则(1)对于固定的时刻t, X(t)为随机变量,其样本空间为{0,1,2,…..},且对于不同的t,是不同的随机变量.(2)对于固定的样本点n, X(t)=n是一个t的函数.(即:在多长时间内来n个人?)所以{X(t),t>0}为一个随机过程.相位正弦波。
第二章随机过程(函数)

西安电子科技大学 理学院
不相关:2阶联合中心矩
E[(X-E(X) )(Y-E(Y) )] = 0
正交:2阶联合原点矩
E(XY) = 0
独立:f(X,Y,x,y)=f(X,x)f(Y,y)
48
西安电子科技大学 理学院
同样对于离散随机过程有:
49
西安电子科技大学 理学院
西安电子科技大学 理学院
章
序
题目
绪论
学 时 4
主要内容
课程介绍、方法分享、相互熟悉、概率论回顾。
第一章
第二章
随机过程(函 16 数)
随机过程(函数)理解、概念、研究方法。
第三章
随机微积分
6
随机微积分及其求解方法介绍。
第四章
随机场
18
随机过程(函数)理解、概念、研究方法。
无线电物理中 无线电物理中的随机场简单应用,纵横分析、资料 第五章 随机场及简单 2 分析、学习方法升华,作业及课堂情况考核。 应用
西安电子科技大学理学院40西安电子科技大学理学院4133相关函数相关函数均值和方差只描述了随机过程在某个特定时刻的统计特均值和方差只描述了随机过程在某个特定时刻的统计特所用的只是一维概率密度所用的只是一维概率密度能反映随机过程在两个不同能反映随机过程在两个不同时刻状态之间的联系时刻状态之间的联系如图所示的两个随机过程如图所示的两个随机过程x和和yytt大致具有相同的均值和方差大致具有相同的均值和方差但这两个信号还是有明但这两个信号还是有明显的区别的显的区别的yytt随时间随时间t的变化较为剧烈的变化较为剧烈各个不同时刻各个不同时刻状态之间的相关性较弱状态之间的相关性较弱随时间的变化较为缓慢随时间的变化较为缓慢同时刻状态之间的相关性较强同时刻状态之间的相关性较强若只用均值函数和方差函数若只用均值函数和方差函数是不能反映出这些特征的是不能反映出这些特征的相关函数能反映两个不同时刻状相关函数能反映两个不同时刻状态之间相关程度的数字特征态之间相关程度的数字特征
第二章、随机过程的基本概念
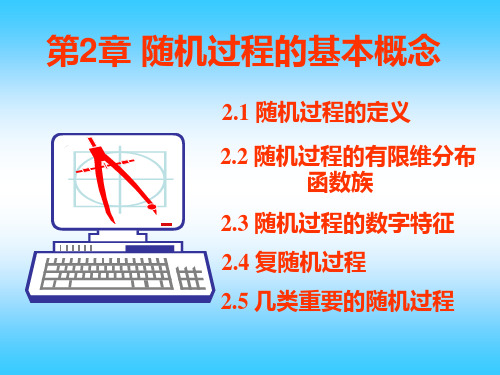
{V (t),t 0}。 1、设已给概率空间(, F, P)及参数集T (,),则称
{X (,t), ,t T},
2020年5月6日星期三
机动 目录 上页 下页 返回 结束
第2页共51页
随机过程(西电版) 2.1 随机过程的定义
第2章 随机过程的基本概念
为该概率空间上的随机过程,简记为 {X (t),t T}。
随机过程(西电版)
2.4 复随机过程
第2章 随机过程的基本概念
设 {X (t),t T},{Y (t),t T}为两个实随机过程,则称
{Z(t) X (t) iY(t),t T}
为复随机过程.
1、复随机过程的数字特征 设复随机过程 {Z (t),t T} 称
(1)均值函数为 mZ (t) E[Z (t)] mX (t) imY (t);
x2
P
A
x1,
A 2
x2
PA x1, A 2x2
3•
x1 2x2
2•
P( P(
A A
x1), x1 2x2 ), x1
2
x2 2x2
1•
•
•
•
1 23
x1
0,
x1
2x2 ,
x1
1或x1
2x2 ,
x2
1 2
F
0,
3
;
x1,
x2
1 3
,
x1
2x2,1
x1
2或x1
2x2 ,
0,
3
;
x1,
x2
.
2020年5月6日星期三
机动 目录 上页 下页 返回 结束
第9页共51页
随机过程2(西.电2版随) 机过程的有限维分布函数族第2章 随机过程的基本概念
第二章 随机过程

图2-1-1 噪声电压的输出波形
定义1 设随机试验E的样本空间为 ,如果 对于每一个样本 ,总可以依某种规则确定 一时间t的函数 (T是时间t的变化范 围 ) 与之对应。于是,对于所有的 来说, 就得到一族时间t的函数,称此族时间的函数为 随机过程(也称随机信号)X,而族中的每一个 函数称为该随机过程的样本函数。 注:随机过程是样本函数的集合 。
决定随机信号的主 要物理条件不变
3、主要性质 (1)、若 是严平稳随机过程,则它的一维概 率密度与时间无关。 证明 令 ,则一维概率密度函数
得证。
(2)、若 是严平稳随机过程,则它的均值、 均方值和方差都是与时间无关的常数。
证明: 根据题意有 (2.3.2) (2.3.3) (2.3.4)
(2)、若 是严平稳随机过程,则它的均值、 均方值和方差都是与时间无关的常数。
2.2.1、随机过程的概率分布
随机过程 ,在每一固定时刻 都是随机变量。 随机事件:
发生概率:
, 和
,
,
1、一维分布函数 与 和 都有直接的关系,是 和 的 二元函数,记为: (2.2.1) 被称为随机过程的一维分布函数。 2、一维概率密度函数 如果存在二元函数 ,使 (2.2.2) 成立,则称 为随机过程的一维概率密度函 数, 是 和 的二元函数,且满足 (2.2.3)
• 研究随机过程的概率密度函数的统计特性是 很困难的; • 随机过程一、二阶矩函数在一定程度上描述 了随机过程的一些重要特性。 (1) 噪声电压是一平稳过程 ,那么一、二阶 矩函数,就是噪声平均功率的直流分量、交 流分量、总平均功率等参数。 (2) 正态随机过程由数学期望和相关函数详 细描述。
1 定义 若随机过程
自协方差函数反映了随机过程 在两个不同 时刻的状态相对于数学均值之间的相关程 度。
通信原理课件(西安电子科技大学版)2

B(t1,t2)=E{[ξ(t1)-a(t1)][ξ(t2)-a(t2)]} =
[ x1 a(t1 )][x2 a(t2 )] f2(x1,x2; t1,t2)dx1dx2
式中,t1与t2是任取的两个时刻;a(t1)与a(t2)为在t1及
t2时刻得到的数学期望;f2(x1,x2; t1,t2)为二维概率密度函 数。相关函数定义为 B(t1, t2)=R(t1, t2)-a(t1)a(t2)
Rξη(t1, t2)=E[ξ(t1)η(t2)]
(2.1 - 12)
2.2平稳随机过程
2.2.1定义
所谓平稳随机过程,是指它的统计特性不随时间的推移而 变化。设随机过程{ξ(t),t∈T},若对于任意n和任意选定t1<t2 <…<tn, tk∈T, k=1, 2, …, n,以及h为任意值,且x1, x2, …, xn∈R,有
则称f2(x1,x2; t1,t2)为ξ(t)的二维概率密度函数。
同理,任给t1, t2, …, tn∈T, 则ξ(t)的n维分布函数被定义为 Fn(x1,x2,…,xn; t1,t2,…,tn)=P{ξ(t1)≤x1,ξ(t2)≤x2,…, ξ(tn)≤xn}
2 Fn ( x1, x2 ...;t1,t2 ...,tn ) f ( x1, x2 ..., xn ; t1, t2 ...,tn ) x1 x2 ...xn
任给两个时刻t1, t2∈T,则随机变量ξ(t1)和ξ(t2)构成一个二 元随机变量{ξ(t1), ξ(t2)},称F2(x1,x2; t1,t2)=P{ξ(t1)≤x1, ξ(t2)≤x2} (2.1 - 3) 为随机过程ξ(t)的二维分布函数。 如果存在
第二章随机过程基本概念.

为称使可积
}: ({ , ( , ( , (, 0 , (1111T t t X t x f dx
t x f t x F t x f x
Î=³ò¥-(2若有的一维概率分布。
为称满足}: ({}{1
, 0} ({T t t X p p
p p x t X P k k k k k
k Î=³==å
¥¥-k k iux X k k iux X p e
u t p x t X P t X dx t x f e u t t x f t X k , ( (( ( 2 , ( , ( , ( (111jj则有分布列若(,则
有密度若(
有时也需要利用常用的一些特征函数来求随机变量的分布函数,由特征函数与分布函数的一一对应性有:
cos(
(Q
+
=t
a
t
X w
的均值函数,方差函数和自相关函数。其中, a , w为常数, Q是在(0, 2p上均匀分布的随机变量。例4试求随机相位余弦波
2随机过程的特征函数
的一维特征函数。
为称为随机变量,记
由于给定( , ( ( ( , ( (, ( (t X u t u e
E u t t X T t X t X t iuX X jjjÙ==Îåò====
为X (t的有限维分布函数族。
为随机过程的n维分布函数。称关于随机过程X (t的所有有限维分布函数的集合
注意:随机过程的n维分布函数描述了随机过程在任意n不同时刻的状态之间的联系。
随机过程X (t的有限维分布函数族的意义何在?随机过程的n维分布函数(或概率密度能够近似地描述随机过程的统计特性,而且, n越大,则n维分布函数越趋完善地描述随机过程的统计特性。
随机过程随机过程的基本概念

2.2 随机过程的分类和举例
随机过程可以根据参数集 T 和状态空间 S 是离散集还是
连续集分为四大类.
1、离散参数、离散状态的随机过程 这类过程的特点是参数集是离散的,同时固定t ∈T, X(t)是离散型随机变量即其取值也是离散的。
例 2.2.1(贝努利过程)考虑抛掷一颗骰子的试验,设Xn
是第n(n≥1)次抛掷的点数,对于n=1,2,…的不同值, Xn是
,它不能用一个或几个随机变量来刻画,而要用一族无穷多
个随机变量来描绘,这就是随机过程. 随机过程是概率论的继续和发展. 被认为是概率论的“动力学
”部分. 它的研究对象是随时间演变的随机现象.
事物变化的过程不能用一个(或几个)时间t 的确定的函数 来加以描述. 对事物变化的全过程进行一次观察得到的结果是一个时间t 的 函数,但对同一事物的变化过程独立地重复进行多次观察所 得的结果是不同的,而且每次观察之前不能预知试验结果.
(3) 当 t
的分布函数为
1, x 0 F ( x) X( ) 0, x 0 2
第2章 随机过程的基本概念
2.1 随机过程的定义 2.2 随机过程的分类和举例 2.3 随机过程的有限维分布函数族 2.4 随机过程的数字特征 2.5 两个随机过程的联合分布和数字特征 2.6 复随机过程 2.7 几类重要的随机过程
“电压—时间函数”是不可能预先确知的,只有通过测量
才能得到. 如果在相同的条件下独立地再进行一次测量, 则得到的记录是不同的.
2.1 随机过程的定义
所谓一族随机变量,首先是随机变量,从而是该试验样
本空间上的函数;其次形成一族,因而它还取决于另一
个变量,即还是另一参数集上的函数. 所以,随机过程 就是一族二元函数. 定义2.1.1 设(Ω, F , P)是一个概率空间,T 是一个实的参 数集,定义在Ω 和T 上的二元函数 X(ω,t),如果对于任
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定义在T上的普通函数.
X(t1,ω)
X(t2,ω)
X(t,ω1) X(t,ω2) X(t,ω3)
t1
t2
tn
定义 对每一固定ω Ω,称 X t ω是随机过程 { X ( t , ), t T } 的一个样本函数. 也称轨道, 路径,现实.
研究该城市气温有无以年为周期的变化规律?
随机过程的 谱分析问题
Ex.2 从杂乱电讯号的一段观察{Y(t),0< t< T}
中,研究是否存在某种随机信号S(t )?
过程检测
Ex.3 监听器上收到某人的话音记录{Z(t),α<t <β} 试问他是否确实是追踪对象?
过程识别
二、随机过程定义 定义 设(Ω,F, P)是概率空间, T R ,若对每个 t T , X t ,ω 是概率空间(ΩF,P)上的随机变量, 则称这族随机变量
的联合分布函数
F (t1 , t 2 ,, t n ; x1 , x2 ,, xn )
P{ X (t1 ) x1 , X (t 2 ) x2 ,, X (t n ) xn }
称为过程的n 维分布函数.记
F ˆ { F t1 , t 2 ,, t n ; x1 , x 2 , , x n : t i T , x i Ri , i 1,2,, n, n 0}
当T=(1,2, … ,n,…),
随机时间序列
随机过程是n 维随机变量,随机变量序列的
一般化,是随机变量X(t), t T 的集合. 用 E表示随机过程X T X t , t T 的值域,称E为 过程的状态空间. Ex.4 设(Ω,F, P)是对应于抛均匀硬币的概率
空间:
Ω ω1 ,ω2 ,
F s, t ; x , y ˆ PX ( s ) x, X (t ) y
称为XT 的二维分布函数族. 定义2 过程{ X ( t ), t T } 对任给的 t1 , t 2 ,, t n T , 随机向量
X (t1 ), X (t 2 ),, X (t n )
的互相关函数。
Ex.1 设p,q是两个随机变量, 构成随机过程
X (t ) p qt ,
t T R
均值函数为m( t ) E[ X ( t )] E ( p) E (q )t , 自相关函数为
R( s, t ) E{( p qs )( p qt )}
E[ P 2 ] E[ pq]( s t ) E[q 2 ]st ,
( s, t ) R2 .
若p,q相互独立,且均服从分布N(0,1),则 R( s, t ) E{( p qs )( p qt )}
E[ P ] E[ pq ]( s t ) E[ q ]st 1 st , ( s , t ) R . 2 2 2
Ex.2 设随机过程
s, t E X (t ) X (s) m s m t
D t t , t E X t m t
2
定义 给定随机过程X T X (t ), t T ,称
R( s, t ) ˆ E[ X ( s) X (t )]
为过程XT的自相关函数.
有 s, t R(s, t ) m s m t
特别当 mt 0 时 称
( s, t ) R( s, t )
XT是零均值过程
(s, t ) ˆ σ s σ t
s ,t
为过程XT的自相关系数.
定义 给定两个随机过程 X T X (t ), t T YT Y (t ), t T 称
m t ˆ E[ X ( t )]
xdF
t , x ,
t T
为过程XT的均值函数.
称 定义 给定随机过程 X T X (t ), t T,
D t ˆ D X ( t ) E X t mt
2
为过程XT的方差函数. 称σ t Dt 为过程XT的均方差函数. 需要描述不同时刻过程状态的关联关系. 定义 给定随机过程X T X (t ), t T ,称 s, t ˆ Cov X ( s ), X (t ) E X ( s) m s X (t ) m t 为过程XT的协方差函数. 有
注 因事件乘积满足交换律. (2)相容性 对任意固定的自然数m<n,均有
F t1 , t 2 ,, t m ; x1 , x2 ,, xm
F t1 , t 2 ,, t m ,, t n ; x1 , x2 ,, xm , lim F t1 , t 2 ,, t n ; x1 ,, xm , xn
X ( t ) Acos( t )
其中β是正常数, 随机变量A 与Θ相互独立, A~ N(0,1), Θ~U(0, 2π).试求过程的均值函数和相关 函数. 解 m X ( t ) E ( X ( t )) E[ Acos(t )]
E ( A) E[cos(t )] 0;
RX ( s, t ) E[ X ( s ) X (t )] E[ A cos( t )cos( s )]
2
E ( A2 ) E[cos( t )cos( s )] 1 2π cos ( t θ ) cos ( s θ ) d θ 2π 0 1 2π 随机变量函 [ cos ( t s ) cos ( ( t s ) 2θ )dθ 0 4π 数的数学期 望公式 1 cos( t s ). 2
2、复随机过程 定义 设 X (t ), t T 和 Y ( t ), t T 是两个实随 机过程,称 Z (t ) ˆ X ( t ) iY ( t ), T , i 1 为复随机过程. 复随机过程Z (t ), t T 的均值函数为 m Z t ˆ E[ X (t )] iE[Y(t )], t T ; 方差函数为 2 DZ ( t ) ˆ E{ Z ( t ) mZ ( t ) } DX ( t ) DY ( t ),
其参数集T ={0,1,2,…}, 状态空间E={0,1}.
随机过程的理解 为集合T 与Ω的积集. 称 T Ω t ,ω : t T ,ω Ω
随机过程 X t ,ω 可看成定义在积集 T Ω 上的二 元函数
Ω
T
1)当固定 t T ,X t ω X (t , ) 是一个随机变量;
XY (s, t ) E[( X (s) mX (s))(Y (t ) mY (t ))]
为 X T X (t ), t T 和 YT Y (t ), t T
的互协方差函数。称
RXY (s, t ) E[ X (s)Y (t )]
为 X T X (t ), t T 和 YT Y (t ), t T
称F为XT 的有限维分布函数族.
定义3 过程{ X ( t ), t T } 的n 维特征函数定义为
φ t1 , tn
E {e
i [θ 1 X ( t1 ) θ n X ( t n )]
}
称
{φ ( t1 , t 2 ,, t n ;θ 1 ,θ 2 ,,θ n ) : t1 , t 2 ,, t n T , n 1}
{ X t ,ω, t T }
为(ΩF,P)上的一个随机过程.
注
1) 称T是参数集(或参数空间) 当T=(1,2, …,n),
随机向量
{ X t ,ω, t T } ( X 1 , X 2 ,, X n )
{ X t ,ω, t T } ( X 1 , X 2 ,, )
PX (t1 ) x1 ,, X (t n ) xn .
三、随机过程的数字特征
在实际应用中,很难确定出随机过程的有限维 分布函数族,过程的数字特征能反映其局部统计性 质. 需确定各类数字特征随时间的变化规律.
1、均值函数、方差函数及相关函数
定义 给定随机过程X T X (t ), t T ,称
个随机过程 X T X (t ), t T ,其有限维分布函 数族恰为 F { F t1 , t 2 ,, t n ; x1 , x 2 , , x n : 即有 F t1 , t 2 ,, t n ; x1 , x2 ,, xn
t i T , x i Ri , i 1,2,, n, n 0}
第二章 随机过程的基本概念
§2.1 基本概念
§2.2 有限维分布与柯尔莫哥洛夫定理
§2.3 随机过程的数字特征
§2.1 基本概念
一、实际背景
在许多实际问题中,不仅需要对随机现象做特 定时间点上的一次观察,且需要做多次的连续不 断的观察,以观察研究对象随时间推移的演变过 程. Ex.1 对某城市的气温进行n年的连续观察, 记录得 { X ( t ), a t b},
2) 对任意固定的自然数m<n,均有
φ t1 , t 2 ,, t m ;θ 1 ,θ 2 ,,θ m
φt1 , t 2 ,, t m ,, t n ;θ 1 ,θ 2 ,,θ m ,0,,0
3、随机过程存在定理(柯尔莫哥罗夫) 如果分布函数族 {F t1 , t 2 ,, t n ; x1 , x2 ,, xn , t1 , t 2 ,, t n T , n 1} 满足条件(1)和(2),则存在一个概率空间上的一
ω1 正 , ω2 反,
1 P ω1 P ω2 , F ω1 ,ω2 , ,Ω. 2 做无穷多次抛硬币独立试验,引入随机变量
