3第三讲最优风险资产组合
风险厌恶与风险资产的最优组合(ppt 46页)

• 多元化:同时持有多种资产可以减少总体 风险而不降 低期望收益率
收益率的概率分布
• 投资的收益率是不确定的(有风险) • 我们用如下指标来刻划不确定性
– 期望收益率:你预期将获得的平均收益率 – 波动率(标准差):未来收益率的分散程度 – 股票的波动率越大,可能的收益率区间越宽,
方差与相关系数
协方差:衡量两种证券的收益率如何共同变化以及共
同变化的幅度
co R ~ A ,R ~ v B niR A i E R ~ A R B iE R ~ B i 1
经济的状态 概率
• 对损失比收益更加敏感,也即满足厌恶损 失(loss aversion)的特征
• 权重函数:非线性的概率变换
前景理论(Prospect Theory)
Kahneman和Tversky(1979)
前景理论(Prospect Theory)
Kahneman和Tversky(1979)
风险管理
• 套期保值:减少不利的风险暴露,同时也 丧失了获利的机会
i 1
ER~ :投资的期望收益率
i:第i种状态发生的概率 R i:第i种状态发生时的收益率估计值 n:可能的状态的数量
计算期望收益率的例子
经济的状态
概率
Risco的收益率 Genco的收益率
强
0.20
50%
30%
正常
0.60
10%
10%
弱
0.20
30%
10%
E R ~ Ri s 0 .c 2 o 0 0 .5 0 0 .6 0 0 .1 0 0 .2 0 0 .3 0
收益率出现极端情况的可能性越大
第三章 最优风险资产组合 复习资料

配置资产的收益与风险分布状态及其相关 性
找出风险资产配置的可行集与有效集 结合资本配置线寻找最优资本配置 思路:由简单到复杂,现有两种风险资产
组合发展到多种资产组合
4-2
资产组合风险的来源:
◦ 可分散风险独特风险,或特有公司风险、非系统性风险或 可分散风险、非系统风险
◦ 不可分散风险,或系统风险、市场风险
最小方差组合由具有最小标准差的风险资产组成,这 一组合的风险最低。
当相关系数小于 +1时, 资产组合的标准差可能小于 任何单个组合资产。
当相关系数是 -1时, 最小方差组合的标准差是0.
718
2 p
wD2
2 D
wE2
2 E
2wD wE Cov
rD , rE
2 p
wD2
2 D
(1
4-9
完全正相关的两种资产构成的可行集是一条直线。
Er p
(σE, rE)
(σD,rD)
p
2 p
wD2
2 D
wE2
2 E
2wD wE D E
DE
2 P
(wD
D
-wE
E
2
)
P wE E - wD D 特别的: -1,可以通过选择资产组合来实现组合资产
标准差趋于零。即完全套期头寸。
令: P wE E - wD D wE E (- 1- wE) D 0
4-5
开始研究有效分散风险,构建任意给定期望收益条件下的 最低风险的资产组合。
两种风险资产组合易于分析,它体现的原则和思考可以适 用于多种资产的资产组合。
4-6
长期债券的资产组合D:债券基金 股权证券的资产组合E:股票基金 数据如下:
投资学第七章最优风险资产组合PPT课件

投资组合理论
介绍现代投资组合理论, 包括马科维茨投资组合理 论和夏普资本资产定价模 型。
投资组合优化
阐述如何通过优化技术来 寻找最优风险资产组合。
学习目标
01
理解最优风险资产组合 的概念及其重要性。
02
掌握现代投资组合理论 的基本原理和模型。
03
学习如何运用优化技术 来构建最优风险资产组 合。
04
风险和回报的关系
风险和回报之间存在正相关关系,即高风险的证券组合可能会带来更高的预期回 报,而低风险的证券组合则可能带来较低的预期回报。投资者应该根据自己的风 险承受能力和预期回报要求来选择适合自己的证券组合。
04 动态最优风险资产组合
时间变化对最优组合的影响
时间变化对市场环境、投资者偏好和风险资产价格波动都有影响,从而影响最优风 险资产组合的构成和权重。
投资学第七章最优风险资产组合 ppt课件
目录
• 引言 • 最优风险资产组合的基本概念 • 最优风险资产组合的构建 • 动态最优风险资产组合 • 投资分散化的重要性 • 最优风险资产组合的实际应用 • 结论
01 引言
主题简介
01
02
03
最优风险资产组合
探讨如何构建在风险和回 报之间达到最佳平衡的投 资组合。
模拟分析
通过模拟不同市场环境和资产类别的变化,可以评估投资分散化策略在不同情 境下的表现,为投资者提供更准确的决策依据。
06 最优风险资产组合的实际 应用
个人投资者的应用
分散风险
个人投资者可以通过分散投资到 不同的资产类别和地区,降低单 一资产的风险,实现最优风险资
产组合。
长期投资
个人投资者应该树立长期投资的理 念,根据自身的风险承受能力和投 资目标,选择合适的投资组合,以 获得稳定的收益。
投资学之最优风险资产组合理论

•3.3 两项风险资产的投资组合
3.3.3 最小方差组合
最小方差组合:相关系数不为-1时,如何求最小方差组合? 2 P w2 D 2 D w2 E 2 E 2wD wE cov(rD , rE ) 投资组合收益率的方差: 代入: wE 1 wD 同样利用导数为零求解最小方差组合:
2 P w2 D 2 D w2 E 2 E 2wD wE D E corr (rD , rE )
corr (rD , rE ) 1
corr (rD , rE ) 0
corr (rD , rE ) 1
P (wD D wE E )2 wD D wE E
此时:
E (rC ) rf ( E (rP ) rf ) 0.07 0.41 (0.15 0.07) 0.1028
C P 0.41 0.22 0.0902
•3.3 两项风险资产的投资组合
3.3.1 风险的类型
不可分散风险:对所有资产都存在影响的风险,如商业周期、 通货膨胀、利率、汇率等,又称为市场风险或系统性风险。 可分散风险:只影响某个具体资产的风险,如管理层变动、合 同纠纷等,又称为公司特有风险或非系统风险。 当风险均来自于公司层面时,分散化可以降低该类风险,特别地 ,当所有风险来源都相互独立时,通过资产组合可将该类风险降 低到可忽视水平。
E (rP ) rf A P 2
•3.2 风险资产与无风险资产的投资组合
3.2.2 最优风险资产配置比例的精确解
对于组合C,风险厌恶系数为4的投资者的最优风险资产比例: E (rP ) rf A P 2
0.15 0.07 0.08 0.413 2 4 0.22 0.1936
第三章投资者风险偏好与最优资产组合

0.59
WE* 1WD* 0.41
(3)最优风险资产组合的期望收益:rP
rP WD* rD WE* rE 0.141
P2 WD*2 D2 WE*2 E2 2WD* WE* cov(rD , rE ) 0.054
报酬-波动比率为:
SP
rP rf
P
0.1415% 0.39 0.054
请思考
最优资产组合确定的基本步骤是?
现实中投资组合的构建: 年轻人如何构建有效的基金组合? 如何设计出适合自己的基金投资组合?
风险厌恶型
E(R)
U 标准差或方差
风险偏好型
E(R)
U 标准差或方差
风险中性型
E(R)
U 标准差或方差
三、最优资产组合的选择
前提:风险厌恶型投资者
分离定理:投资者决定持有无风险资产与风险资产 组合的份额
➢ 投资者对风险和收益的偏好状况与该投资者最优风 险资产组合的构成是无关的。
风险厌恶型投资者的最有资产组合的确定思路
1元钱不投资,最终得到确定的收益1元。 (无风险)
投资者的态度决定方案的选择,其态度即为 风险偏好或厌恶。
风险偏好 风险厌恶
Hale Waihona Puke U(0)U(1)U(2)
比较2U(1) 与 U(0) +U(2)
风险中性型效用函数,如:
U (W ) 5W U W 5为常数
2U W 2 0
风险厌恶型效用函数,如:(类似于边际报酬递减规律)
第三章 投资者风险偏好与最优资产组合
第一节 投资者的效用函数
一、投资者的效用
经济学的效用:人们从某事物中获得的主观满足程 度。
苹果、梨子的故事
投资学的效用:投资者对各种不同投资方案的主观 上的偏好指标。
风险厌恶与风险资产的最优组合PPT课件( 46页)

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 Standard Deviation
由两种风险证券构成的组合
• 假设我们将比例为w的财富投资于证券 1,1-w的财 富投资于证券2
• 证券1的期望收益率为 ,证券2的期望收益率为
• 证券1的标准差为 ,r证1 券2的标准差为
i :第i种状态发生的概率 R i :第i种状态发生时的收益率估计值 n :可能的状态的数量
资产组合的收益率和风险
经济的状态 概率 A的收益率 B的收益率 组合收益率
1
0.20
5%
19%
4.6%
2
0.60
10%
10%
10%
3
0.20
35%
4%
19.4%
12%
9%
10.8%
E R ~ P 0 . 2 4 . 6 % 0 . 6 1 % 0 . 2 1 0 . 4 % 1 . 8 9 %
第 五 课(2)
资产组合理论 (均值方差分析)
资产组合理论的形成
• Portfolio selection (Markowitz, 1952) • 1990年Markowitz 被授予诺贝尔经济学奖
无风险资产和一种风险资产构成的组合
• 无风险资产:未来的收益率是确定的 • 假设只有一种风险资产和无风险资产, • 该风险资产在现实世界中是所有风险资产的组合
收益率出现极端情况的可能性越大
Distribution of Returns on Tw o Stocks
3.5
P rob ab ility D en sity
•
3.0
2.5
NORMCO
最优风险资产的风险组合

最优风险资产的风险组合8.1 分散化与资产组合风险分散化(diversification):投资者如果不是进行单一证券的投资,而是投资于由两种以上证券构成的投资组合。
如果构成投资组合的证券不是完全正相关,那么投资组合就会降低风险,在最充分分散条件下还保存的风险是市场风险(market risk),它源于与市场有关的因素,这种风险亦称为系统风险(systematic risk),或不可分散风险(nondiversifiable risk)。
相反,那些可被分散化消除的风险被称为独特风险(unique risk)、特定公司风险(firm-specific risk)、非系统风险(nonsystematic risk)或可分散风险(diversifiable risk)资产组合中股票的个数8.2 两种风险资产的资产组合两种资产的资产组合较易于分析,它们体现的原则与思考可以适用于多种资产的资产组合,我们将考察包括的资产组合,一个为只投资于长期债券的资产组合D,另一个专门投资于股权证券的股票基金E,两个共同基金的数据列表(8-1)如下:债券股权期望收益率E(r)(%)8 13 标准差为σ(%) 12 20 协方差Cov(r D, r E) 72相关系数ρDE 0.3投资于债券基金的份额为w D,剩下的部分为w E=1- w D投资于股票基金,这一资产组合的投资收益r p 为:r p=w D r D,+ w E r E r D为债券基金收益率r E为股权基金的收益率。
资产组合的期望收益:E(r p)=w D E(r D)+ w E E(r E)两资产的资产组合的方差:σ2P =W D2σ2D+ W E2σE2+2W D W E Cov(r D,r E)根据第六章式[6-5]得:ρDE=[Cov(r r D, r E)]/[ σD*σE]Cov(r r D, r E)= ρDE*σD*σE所以:σ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE 当完全正相关时:ρDE=1σ2P =W D2σ2D+ W E2σE2+2W D W E*σD*σE=(W DσD+ W E σE)2资产组合的标准差σP =W DσD+ W EσE当完全负相关时:ρDE=-1σ2P =W D2σ2D- W E2σE2+2W D W E*σD*σE=(W DσD- W E σE)2资产组合的标准差σP =︱W DσD- W EσE︱当完全负相关时:ρDE=-1 则W DσD- W EσE=0 因为w E=1- w D 两式建立联立方程得运用表(8-1)中的债券与股票数据得:E(r p)=w D E(r D)+ w E E(r E)= 8w D+ 13w Eσ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE=122 W D2+ 202W E2+2*12*20*0.3*W D W E=144 W D2+400 W E2+144 W D W E表8-3 不同相关系数下的期望收益与标准差给定相关性下的资产组合的标准差W D We E(rp) ρ=-1ρ=0ρ=0.3ρ=1 0113202020200.10.912.516.818.0399618.3956519.20.20.81213.616.17916.8760218.40.30.711.510.414.4554515.4660917.60.40.6117.212.924414.1985916.80.50.510.5411.661913.11488160.60.4100.810.762912.2637715.20.70.39.5 2.410.3227911.6961514.40.80.29 5.610.411.4542613.60.90.18.58.810.9836211.5585512.810812121212图8-3中,当债券的投资比例从0-1(股权投资从1-0)时,资产组合的期望收益率从13%(股票的收益率)下降到8%(债券的收益率)1.0 0 -1.0 债券如果w D〉1,w E〈0时,此时的资产组合策略是做一股权基金空头,并把所得到的资金投入到债券基金。
第7章-最优风险资产组合(投资学,上海财经大学)
16
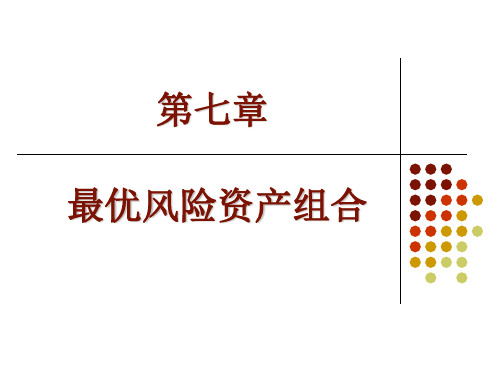
若有A、B两个股票,则可行组合在其连线 上,并视ρ的值而为直线、折线或曲线。若 有A、B、C三个股票,则可行组合一般为 一区域。
ρ=1 ρ= -1 A Z C B A
B
17
相关效应的结论:
资产相关性越小,分散化就更有效,组合风 险也就越低。 随着相关系数接近于-1,降低风险的可能性 也在增大。
t 1
5
n
2、两个资产构成的资产组合: 收益
rp rP Portfolio Return 资产组合的收益率
wr
D
D
wE r E
wD Bond Weight 债券的权重 rD Bond Return 债券的收益率 wE Equity Weight 股票的权重 rE Equity Return 股票的收益率
一、分散化和组合风险 (一)投资决策
1. 2. 3.
决策过程可以划分为自上而下的3步: 风险资产与无风险资产之间的资本配置 各类资产间的配置 每类资产内部的证券选择
2
(二)投资组合风险构成
市场风险 系统性风险或不可分散风险 公司特有风险 非系统风险或可分散风险
P128图7.1 组合风险关于股票数量的函数
25
(三)资本配置和分离特性
每个人都投资于P,而不考虑他们的风险厌恶 程度。
大多数风险厌恶者更多的投资于无风险资产。 少数的风险厌恶者在P上投资的更多。
分离特性阐明组合决策问题可以分为两个独立 的步骤。
决定最优风险组合,这是完全技术性的工作。 整个投资组合在无风险短期国库券和风险组合 之间的配置,取决于个人偏好。
3第三讲 最优风险资产组合

债券和股票基金的投资可行集、最优资本配置线和最优风险资产组合
决定最优组合
最优组合的成分
构造整个组合的步骤
确定所有证券的特征(期望收益率、方差、协方差) 建立风险资产组合
计算最优风险组合P 在此基础上计算组合P的期望收益和标准差
在风险资产和无风险资产之间配置资金
需解以下问题
max S P
wi
E (rP ) rf
P
s.t.
2 E 2 D
w 1
i
最优风险组合的解
E ( RD ) E ( RE )Cov( RD , RE ) wD 2 E ( RE ) ( E ( RD ) E ( RE ))Cov( RD , RE ) E ( RD ) E
风险资产的最小方差边界
马科维茨模型
min s.t.
1 n n wi w j Cov(ri , rj ) 2 i 1 j 1
w E (r ) E (r )
i 1 n i i p
n
w 1
i 1 i
方差前面的系数1/2只是为了计算方便而已,它使得最后得出的 结果更加整齐
马科维茨模型(续)
传统理念认定风险集合降低风险,并成为保险行业风险管理的 背后推动力
但是,增加一个独立的赌局怎么会降低整个风险敞口呢?
风险集合
假设一个富有的投资者沃伦,持有10亿美元的组合P,其中风险 资产组合A的比例为y,无风险资产为1-y
A的风险溢价为R,标准差为σ 则P的风险溢价RP=yR,标准差σP=yσ,夏普比率SP=R/σ 沃伦发现另一个风险资产组合B和A具有相同的风险溢价和标准 差,且A和B相关系数为0,于是他认为可以通过分散化来降低 风险,决定持有B,且与A的头寸相同
最优风险资产组合公式

最优风险资产组合公式
1、rr=β* v
rr为风险收益率;
β为风险价值系数;
v为标准离差率。
2、rr=β*(km-rf)
rr为风险收益率;
β为风险价值系数;
km为市场组合平均收益率;
rf为无风险收益率;
(km-rf)为市场组合平均风险报酬率。
风险收益率,就是由投资者承担风险而额外建议的风险补偿率为。
风险收益率包含偿付风险收益率,流动性风险收益率和期限风险收益率。
影响因素:
风险大小和风险价格。
在风险市场上,风险价格的多寡依赖于投资者对风险的偏好程度。
风险收益率包括违约风险收益率,流动性风险收益率和期限风险收益率。
风险收益就是指乘以当时基本的市场收益后的投资收益。
风险收益就是无风险证券与其他证券间存有的利差,它充分反映了投资者出售非财政证券所遭遇的额外风险。
风险收益额是指投资者因冒风险进行投资而获得的超过资金时间价值的那部分额外收益。
风险就是指人们事先能确实实行某种犯罪行为所有可能将的后果,以及每种后果发生可能性的状况。
风险报酬是指投资者因承担风险而获得的超过时间价值的那部分额外报酬。
【大学课件】最优风险资产组合

当 ρDE = 1, 不受相关性影响
Pw E Ew D D
当 ρDE = -1, 完全对冲
wED DE1wD
表 7.2 从协方差矩阵计算的 资产组合的方差
713
ppt课件
三种资产的组合
714
ppt课件
E(rp ) w1E(r1) w2E(r2 ) w3E(r3)
p 2w 1 2 1 2w 2 2 2 2w 3 2 3 2
当相关系数小于 +1时, 资产组合的标准差可 能小于任何单个组合 资产。
当相关系数是 -1时, 最小方差组合的标准 差是0.
图
7.5
组合期望收益关于标准差的函数
718
ppt课件
7-
相关效应
19
ppt课件
资产相关性越小,分散化就更有效,组合风 险也就越低。
随着相关系数接近于-1,降低风险的可能性 也在增大。
ppt课件
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
大多数风险厌恶者更多的投资于无风险资产。 少数的风险厌恶者在P上投资的更多。
资本配置和分离特性
730Βιβλιοθήκη ppt课件分离特性阐明组合决策问题可以分为两个 独立的步骤。
决定最优风险组合,这是完全技术性的 工作。
整个投资组合在无风险短期国库券和风 险组合之间的配置,取决于个人偏好。
图 7.13 有效集组合与资本配置线
风险集合和保险原理
736
ppt课件
风险集合: 互不相关的风险项目聚合在一起来降低 风险。
通过增加额外的不相关资产来增加风险投资的规模。
保险原理: 风险增长速度低于不相关保单数量的增 长速度。
夏普比率升高
最优风险资产风险组合
最优风险资产的风险组合8.1 分散化与资产组合风险分散化(diversification):投资者如果不是进行单一证券的投资,而是投资于由两种以上证券构成的投资组合。
如果构成投资组合的证券不是完全正相关,那么投资组合就会降低风险,在最充分分散条件下还保存的风险是市场风险(market risk),它源于与市场有关的因素,这种风险亦称为系统风险(systematic risk),或不可分散风险(nondiversifiable risk)。
相反,那些可被分散化消除的风险被称为独特风险(unique risk)、特定公司风险(firm-specific risk)、非系统风险(nonsystematic risk)或可分散风险(diversifiable risk)资产组合中股票的个数8.2 两种风险资产的资产组合两种资产的资产组合较易于分析,它们体现的原则与思考可以适用于多种资产的资产组合,我们将考察包括的资产组合,一个为只投资于长期债券的资产组合D,另一个专门投资于股权证券的股票基金E,两个共同基金的数据列表(8-1)如下:债券股权期望收益率E(r)(%)8 13 标准差为σ(%) 12 20 协方差Cov(r D, r E) 72相关系数ρDE 0.3投资于债券基金的份额为w D,剩下的部分为w E=1- w D投资于股票基金,这一资产组合的投资收益r p 为:r p=w D r D,+ w E r Er D为债券基金收益率r E为股权基金的收益率。
资产组合的期望收益:E(r p)=w D E(r D)+ w E E(r E)两资产的资产组合的方差:σ2P =W D2σ2D+ W E2σE2+2W D W E Cov(r D,r E)根据第六章式[6-5]得:ρDE=[Cov(r r D, r E)]/[ σD*σE]Cov(r r D, r E)= ρDE*σD*σE所以:σ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE 当完全正相关时:ρDE=1σ2P =W D2σ2D+ W E2σE2+2W D W E*σD*σE=(W DσD+ W E σE)2资产组合的标准差σP =W DσD+ W EσE当完全负相关时:ρDE=-1σ2P =W D2σ2D- W E2σE2+2W D W E*σD*σE=(W DσD- W E σE)2资产组合的标准差σP =︱W DσD- W EσE︱当完全负相关时:ρDE=-1 则W DσD- W EσE=0 因为w E=1- w D 两式建立联立方程得运用表(8-1)中的债券与股票数据得:E(r p)=w D E(r D)+ w E E(r E)= 8w D+ 13w Eσ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE=122 W D2+ 202W E2+2*12*20*0.3*W D W E=144 W D2+400 W E2+144 W D W E表8-3 不同相关系数下的期望收益与标准差给定相关性下的资产组合的标准差W D We E(rp) ρ=-1ρ=0ρ=0.3ρ=1 0113202020200.10.912.516.818.0399618.3956519.20.20.81213.616.17916.8760218.40.30.711.510.414.4554515.4660917.60.40.6117.212.924414.1985916.80.50.510.5411.661913.11488160.60.4100.810.762912.2637715.20.70.39.5 2.410.3227911.6961514.40.80.29 5.610.411.4542613.60.90.18.58.810.9836211.5585512.810812121212图8-3中,当债券的投资比例从0-1(股权投资从1-0)时,资产组合的期望收益率从13%(股票的收益率)下降到8%(债券的收益率)LcbcW6f1.0 0 -1.0 债券如果w D〉1,w E〈0时,此时的资产组合策略是做一股权基金空头,并把所得到的资金投入到债券基金。
最优风险资产投资组合

大摩增强债券型基金選擇原因分析
长期业绩稳定,债市节奏把握较好。 成立以来大幅跑赢业绩基准及中证债基指数。 基金自2009年12月成立以来,其净值累计收益率分 别为26.17%,远超过同期业绩比较基准12.09%, 以及中证债券基金指数13.62%的涨幅。 债券配置顺势而为,债市节奏把握能力较强。基 金目前实质为纯债基金,一季度基金加大可转债 配置,期间涨幅较好,不过二季度转债下跌,拖 累了期间基金业绩。二季度、三季度基金逐步加 大短融配置,为基金收益作出较大贡献。此外基 金从二季度开始少量配置利率债(金融债),目前 利率债收益率处于高位,安全边际较高。整体来 看,基金经理对债市节奏把握能力较强。
大摩增强债券型基金選擇原因分析
基金公司固收整体业绩较好。
摩根士丹利华鑫基金公司固收产品规模不大但整体业绩较 好,大摩增强债收益债券今年以来取得了较好的收益,排 名靠前。
基金经理投研经验丰富。基金经理洪天阳先生曾于 2005年9月至2007年7月任职于摩根大通银行投资银行部, 2007年10月至2012年8月任职于中银保险北京总公司, 历任外汇投资经理、固定收益投资经理、权益类投资经理 和组合投资经理等职。
基金行業分析
我国基金当前的问题:
• • • • • 我国基金公司治理结构制度存在缺陷 相关的法律法规制度还不够完善 基金监督管理体系不健全 民众的投资意识有待提高 证券市场缺乏做空机制,基金的风险难以 规避
基金行業分析
我国基金业发展的必要性及建议:
通过分析基金的风险和收益,获得有关基金投资操作的准 确信息,避免投资者盲目投资而遭受损失,也有利于提升 基金行业的公信力,增强基金投资者的信心。 通过完整的评价指标体系可以定量评价基金经理的业绩水 平,基金管理公司也可以据此分析投资结果是否达到或超 过了投资目标,总结基金管理成功的经验,从而促进基金 管理公司提高经营管理水平。 完善基金的投资运作的监管机制,加大基金的内部治理, 健全基金立法,防止其操作行为对市场可能产生的巨大波 动以及存在的其它负面影响,引导其活跃市场增加市场弹 性的积极作用。 维护市场的“生物多样化”与生态平衡。
最优风险资产风险组合

最优风险资产的风险组合8.1 分散化与资产组合风险分散化(diversification):投资者如果不是进行单一证券的投资,而是投资于由两种以上证券构成的投资组合。
如果构成投资组合的证券不是完全正相关,那么投资组合就会降低风险,在最充分分散条件下还保存的风险是市场风险(market risk),它源于与市场有关的因素,这种风险亦称为系统风险(systematic risk),或不可分散风险(nondiversifiable risk)。
相反,那些可被分散化消除的风险被称为独特风险(unique risk)、特定公司风险(firm-specific risk)、非系统风险(nonsystematic risk)或可分散风险(diversifiable risk)资产组合中股票的个数8.2 两种风险资产的资产组合两种资产的资产组合较易于分析,它们体现的原则与思考可以适用于多种资产的资产组合,我们将考察包括的资产组合,一个为只投资于长期债券的资产组合D,另一个专门投资于股权证券的股票基金E,两个共同基金的数据列表(8-1)如下:债券股权期望收益率E(r)(%) 8 13标准差为σ(%) 12 20 协方差Cov(r D, r E) 72相关系数ρDE 0.3投资于债券基金的份额为w D,剩下的部分为w E=1- w D投资于股票基金,这一资产组合的投资收益r p 为: r p=w D r D,+ w E r E r D为债券基金收益率r E为股权基金的收益率。
资产组合的期望收益:E(r p)=w D E(r D)+ w E E(r E)两资产的资产组合的方差:σ2P =W D2σ2D+ W E2σE2+2W D W E Cov(r D,r E)根据第六章式[6-5]得:ρDE=[Cov(r r D, r E)]/[ σD*σE]Cov(r r D, r E)= ρDE*σD*σE所以:σ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE当完全正相关时:ρDE=1σ2P =W D2σ2D+ W E2σE2+2W D W E*σD*σE=(W DσD+ W EσE)2资产组合的标准差σP =W DσD+ W EσE当完全负相关时:ρDE=-1σ2P =W D2σ2D- W E2σE2+2W D W E*σD*σE=(W DσD- W EσE)2资产组合的标准差σP =︱W DσD- W EσE︱当完全负相关时:ρDE=-1 则W DσD- W EσE=0 因为w E=1- w D两式建立联立方程得运用表(8-1)中的债券与股票数据得:E(r p)=w D E(r D)+ w E E(r E)= 8w D+ 13w Eσ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE=122 W D2+ 202W E2+2*12*20*0.3*W D W E=144 W D2+400 W E2+144 W D W E表8-3 不同相关系数下的期望收益与标准差给定相关性下的资产组合的标准差 W D We E(rp) ρ=-1ρ=0ρ=0.3ρ=1 0113202020200.10.912.516.818.0399618.3956519.20.20.81213.616.17916.8760218.40.30.711.510.414.4554515.4660917.60.40.6117.212.924414.1985916.80.50.510.5411.661913.11488160.60.4100.810.762912.2637715.20.70.39.5 2.410.3227911.6961514.40.80.29 5.610.411.4542613.60.90.18.58.810.9836211.5585512.810812121212图8-3中,当债券的投资比例从0-1(股权投资从1-0)时,资产组合的期望收益率从13%(股票的收益率)下降到8%(债券的收益率)1.0 0 -1.0 债券如果w D〉1,w E〈0时,此时的资产组合策略是做一股权基金空头,并把所得到的资金投入到债券基金。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲最优风险资产组合投资决策⏹投资决策可以看做为自上而下的过程⏹资本配置:风险资产与无风险资产之间的资本配置⏹资产配置:各类风险资产间的配置⏹证券选择:每类资产内部的证券选择分散化与组合风险⏹市场风险⏹系统性风险或不可分散风险⏹公司特有风险⏹可分散风险或非系统风险组合风险关于股票数量的函数组合分散化:应用纽约证券交易所股票数据协方差和相关性⏹投资组合的风险取决于投资组合中各资产收益率的相关性⏹协方差和相关系数提供了衡量两种资产收益变化的方式两个资产构成的资产组合: 收益与方差⏹组合的收益率⏹组合的期望收益⏹组合的方差p D D E Er w r w r =+()()()p D D E E E r w E r w E r =+222222(,)p D D E ED E D E w w w w Cov r r σσσ=++协方差与相关系数⏹协方差⏹相关系数:可能的值⏹如果ρ= + 1.0,资产间完全正相关⏹如果ρ= -1.0,资产间完全负相关(,)D E DE D E Cov r r ρσσ=1.0 1.0ρ+≥≥-相关系数⏹当ρDE = +1,不受相关性影响⏹当ρDE = -1,可完全对冲1DE DD E w w σσσ==-+p D D E E w w σσσ=+22()σσσ=-p D D E E w w 0σσ-=D D E E w w σσσ=+E D D Ew组合方差的计算组合期望收益关于投资比例的函数组合标准差关于投资比例的函数最小方差组合⏹最小方差组合由具有最小标准差的风险资产组成,这一组合的风险最低⏹当相关系数小于+1时,资产组合的标准差可能小于任何单个组合资产⏹当相关系数是-1时,最小方差组合的标准差是0组合期望收益关于标准差的函数相关效应⏹资产相关性越小,分散化就更有效,组合风险也就越低⏹随着相关系数接近于-1,降低风险的可能性也在增大⏹如果r = +1.0,不会分散任何风险⏹如果r = 0,σP可能低于任何一个资产的标准差⏹如果r = -1.0,可以出现完全对冲的情况债券和股票基金的投资可行集和两条资本配置线夏普比率⏹使资本组合P 的资本配置线的斜率最大化⏹斜率的目标方程是⏹这个斜率就是夏普比率()P f P P E r r S σ-=计算最优风险组合P⏹对于两个风险资产的组合P ,期望收益和标准差为⏹需解以下问题⏹最优风险组合的解()max σ-=iP f P w P E r r S ()()()p D D E E E r w E r w E r =+22221/2(2(,))σσσ=++p D D E E D E D E w w w w Cov r r ..1=∑i s t w 222()()(,)()()(()())(,)σσσ-=+-+D EE D E D D E E D D E D E E R E R Cov R R w E R E R E R E R Cov R R 1=-E Dw w债券和股票基金的投资可行集、最优资本配置线和最优风险资产组合决定最优组合最优组合的成分构造整个组合的步骤⏹确定所有证券的特征(期望收益率、方差、协方差)⏹建立风险资产组合⏹计算最优风险组合P⏹在此基础上计算组合P的期望收益和标准差⏹在风险资产和无风险资产之间配置资金⏹计算投资风险资产组合P的比例⏹计算整个组合中各资产的比例马科维茨资产组合选择模型⏹证券选择(多个风险资产和一个无风险资产的情况)⏹第一步,确定风险资产的最小方差边界⏹第二步,确定无风险资产下的最优风险资产组合⏹第三步,确定最优风险资产组合和无风险资产一定比例的最终组合风险组合组合边界⏹马科维茨资产组合选择模型是组合管理的第一步:确认有效的组合集,即风险资产有效边界⏹任意风险组合的期望收益和方差,都可以通过计算下式得到⏹核心原理:对于任意期望收益率水平,我们只关注风险最低的组合。
对于任意风险水平,我们只关注期望收益率最高的组合1211()()(,)n p i i i n n Pi j i j i j E r w E r w w Cov r r σ=====∑∑∑风险资产的最小方差边界马科维茨模型方差前面的系数1/2只是为了计算方便而已,它使得最后得出的结果更加整齐11111min (,)2..()()1n ni j i j i j ni i p i ni i w w Cov r r s t w E r E r w ======∑∑∑∑马科维茨模型(续)⏹构造拉格朗日函数⏹然后对每个变量wi 求导,并令导数值等于011111(,)(()())(1)2n nn n i j i j i i p i i j i i L w w Cov r r w E r E r w λμ=====----∑∑∑∑111(,)()0(1,2,,)()()1n j i j ij n i i pi n ii w Cov r r E r i n w E r E r w λμ===--==⋅⋅⋅==∑∑∑风险资产有效边界和最优资本配置线最优组合有效集组合与资本配置线资本配置和分离特性⏹分离特性阐明组合决策问题可以分为两个独立的步骤⏹决定最优风险资产组合,这是完全技术性的工作。
给定所有证券的数据,最优风险组合对所有客户都是一样的⏹整个投资组合在无风险资产和最优风险资产组合之间的配置,取决于个人偏好。
这里客户是决策者⏹不同风险厌恶程度的投资者会满足于两个共同基金构成的市场⏹一个基金在货币市场进行无风险投资⏹一个持有资产配置线与有效边界切点的最优风险资产组合P⏹职业投资管理更有效率且成本更低资本配置和分离特性(续)⏹在实际中,不同的投资经理对证券估计的数据是不一样的,因此得到不同的有效边界,提供不同的“最优组合”⏹这种偏差来自于证券分析的差异。
如果证券分析质量很差,那么被动的市场指数基金生成的资本配置线都会优于用低质量证券分析生成的资本配置线(垃圾进-垃圾出)⏹最优化技术是组合构造问题中最容易的部分,基金经理间真正的竞争在于证券分析精确性上的角逐分散化的威力⏹因为⏹如果定义平均方差和平均协方差为⏹可以得出组合的方差211(,)n n P i j i j i j w w Cov r r σ===∑∑2211111(,)(1)n i i n n i j j i j in Cov Cov r r n n σσ===≠==-∑∑∑2211Pn Cov n n σσ-=+相关性和无相关性的证券等权重构造组合的风险减少风险集合、风险共享与长期投资风险⏹分散化意味着把投资预算分散到各类资产中以降低投资组合的风险⏹有人提出时间上的分散化想法,这样平均收益率反映了不同投资期限的收益,类比得出“时间分散化”的概念,长期投资比短期投资更安全⏹这一对“分散化”的概念拓展有意义吗?风险集合和保险原理⏹风险集合:将互不相关的风险项目聚合在一起来降低风险⏹应用到保险行业,风险集合为销售风险不相关的保单,即众所周知的保险原理⏹传统理念认定风险集合降低风险,并成为保险行业风险管理的背后推动力⏹但是,增加一个独立的赌局怎么会降低整个风险敞口呢?风险集合⏹假设一个富有的投资者沃伦,持有10亿美元的组合P,其中风险资产组合A的比例为y,无风险资产为1-y⏹A的风险溢价为R,标准差为σ⏹则P的风险溢价R P=yR,标准差σP=yσ,夏普比率S P=R/σ⏹沃伦发现另一个风险资产组合B和A具有相同的风险溢价和标准差,且A和B相关系数为0,于是他认为可以通过分散化来降低风险,决定持有B,且与A的头寸相同⏹这一策略是纯粹的风险机会。
整个组合Z构成如下:A比例为y,B比例为y,无风险资产比例为1-2y风险集合(续)⏹好消息是Z 的夏普率提升倍,坏消息是标准差也增长倍⏹当n 种资产时,夏普率提升倍,坏消息是标准差也增长倍⏹这一简单分析说明,单纯的风险集合带来了机会,但同时因为增加了风险投资的规模,风险机会并不降低总体风险22222222(12)02022/2/22/σσσσσσσσσσ=++-==++======Z Z Z Z Z Z Z R yR yR y yR y y y y S R yR y R (R P 的2倍)(S P 的1.41倍)(σP 的1.41倍)(σP 2的2倍)22n n保险原理⏹保险原理:风险增长速度低于不相关保单数量的增长速度,风险集合的获利能力(夏普比率)才能增长,但这并不足以降低风险⏹这可能会限制大型保险公司持续增长的组合潜在的规模效应,可以把分析中的资产看做保单。
每一笔保单要求保险公司设置保证金弥补或有损失,保险公司投资这些资金直至有索赔发生⏹卖出更多的保险意味着增加风险投资的头寸,当投资于更多收益不相关的资产时,夏普比率升高,但是因为风险资产比例上升,整体风险也会上升保险原理(续)保险原理解释为“风险集合后损失的概率会降低”,从数学上是正确的,因为夏普比率上升,但是将损失概率的降低和总风险的降低混为一谈却是错误的风险共享⏹风险共享:随着风险资产增加到资产组合中, 一部分资产需要被卖掉以保持固定的投资比例⏹考虑组合V,构成如下:A和B的比例均为y/2,无风险资产比例仍为1-y组合V组合Z 2/σ=Z S R 2σσ=Z y 2222σσ=Z y 2=Z R yR 2/σ=Z S R /2σσ=Z y 222/2σσ=Z y =Z R yR⏹风险共享和风险集合构成了保险行业的关键核心⏹投资于多种风险资产,但是风险资产比例保持不变,这才是真正的分散化⏹当n 种资产时,组合的标准差为,夏普比率为/σy n /σnR长期投资⏹第一年收益和第二年收益无关⏹短期投资决策:第一年投资于风险组合,第二年投资于无风险组合⏹长期投资决策:投资于一项两年期的风险组合⏹长期投资决策的风险更大⏹卖出一部分两年期的风险组合来降低风险⏹“时间分散化”并不是真正的分散化作业⏹第7章,习题:第12题⏹第7章,CFA考题:第1~4题。
