定理(Theorem)引理(Lemma)推论(Corollary)

合集下载

数学中定义英文

数学中定义英文
在数学中，有很多定义，这里提供一些常见数学术语的英文翻译：
1. 定义(Definition): 定义是对一个概念或对象的明确定义，通常以确保理解一致性和精确性为目的。

2. 定理(Theorem): 定理是在一定的公理或前提条件下，通过逻辑推理得出的结论或命题。

3. 引理(Lemma): 引理是用于证明定理的辅助命题或结论。

4. 推论(Corollary): 推论是在一个定理或引理的基础上直接得出的结论。

5. 公理(Axiom): 公理是在某个理论或系统中作为基础而不需要证明的基本假设或原理。

6. 证明(Proof): 证明是通过逻辑推理和演绎过程，以严格的步骤和论证来验证一个命题的过程。

7. 假设(Hypothesis): 假设是在证明或推理中作为前提条件的未经证实的陈述或假定。

8. 数学模型(Mathematical Model): 数学模型是用数学语言和符号来描述现实世界问题或系统的抽象表示。

9. 方程(Equation): 方程是一个包含未知数和数学运算符的数学表达式，通常用于描述相等关系。

10. 不等式(Inequality): 不等式是一个包含不等号的数学表达式，用于表示两个数之间的大小关系。

11. 函数(Function): 函数是一个将每个输入值映射到唯一输出值的关系。

12. 导数(Derivative): 导数是描述函数变化率的概念，表示函数在某一点的变化速率。

13. 积分(Integral): 积分是对函数在一定区间上的累积或总和的操作。

数学常用英文词汇

数学常用英文词汇这是一篇关于数学常用英文词汇的文章，主要介绍了一些基本的数学概念、符号、函数、图形等的英文表达方式，以及一些常见的数学术语的中英文对照。

文章的目的是帮助读者提高数学英语的阅读和写作能力，以及了解一些数学文化背景。

文章的结构如下：1. 数学基本概念数学是一门研究数量、结构、空间、变化等抽象对象的科学，它具有严密的逻辑和推理，以及广泛的应用¹。

数学可以分为不同的分支，如代数、几何、微积分、概率统计等，每个分支都有自己的特点和方法。

下面是一些数学基本概念的英文词汇：中文英文例句数量quantity数量可以用数字或字母表示。

Quantity can be expressed by numbers or letters.数字number 数字有不同的类型，如自然数、整数、有理数等。

Numbers have different types, such as natural numbers, integers, rational numbers, etc.字母letter 字母可以用来表示未知或变量的数量。

Letters can be used to represent unknown or variable quantities.符号symbol 符号是一种约定俗成的表示方式，如加号、等号、括号等。

Symbols are conventional ways of expression, such as plus sign, equal sign, parentheses, etc.表达式expression表达式是由数字、字母和符号组成的有意义的组合。

Expression is a meaningful combination ofnumbers, letters and symbols.等式equation 等式是两个表达式之间用等号连接的关系。

Equation is a relation between two expressions connected by an equal sign.不等式inequality不等式是两个表达式之间用不等号连接的关系。

Latex学习笔记

Latex学习笔记Latex 学习笔记Chap2 Typing text1.多个空⾏等于⼀个空⾏，没有空⾏表⽰连接着写。

所以要表⽰有回车新起⼀⾏，最好还是在script⾥⾯空出⼀⾏写。

2.正⽂中的语句有三种：text, math(formulas) and instructions3.\begin {}\end {}表⽰环境environment, {} ⾥⾯可以填写flushright, flushleft, or center。

2.1 The keyword(1) 合法的key：a-z, A-Z 0-9 + = * / ( ) [ ]其它的标点：, ；. ? !: ?‘–以及空格键，Table键和回车键Enter(2) ⼗三个常⽤的special keys in LATEX commands:# $ % & ~ _ ^ \ { } @ ―|对这些特别键要显⽰它们，要在之前加上\, 其中@除外。

2.2 your first note(1) 不区分多空⾏，不区分多个空格，不区分多个TABLE，即这些都当作⼀个。

(2) 双引号的⽤法：``something‘‘也就是前⾯是两个``, 后⾯是两个单引号‘‘(3) 强制连接符, ⽤~ ，⽐如Prof. ~Tian, 答应效果就是Prof. Tian。

这不同于直接加空格，直接加空格会⽐⽤~的字距⼤些。

2.3 Lines too wide当字段太长时需要加\- 来强制加短横-，⼜因为系统会⾃动在有短横处换⾏。

某⼀⾏太长的情况⼀般是不会出现的，系统会⾃动切成两边都对齐的情况，可是当该段中已经含有连字符时，系统会认为该连字符就是被要求的切断符号，所以是误导了系统。

这个时候就需要在之前就加连字符\-, 以使得系统提前得到连字符⽽换⾏。

⽽在不该有连字符的地⽅强制放⼊\-是没有效果的。

只能加直接加-才有效果。

2.4 More text features(1) \ today 表⽰插⼊⽇期，如February 9, 2010(2) environments to right justify, or left justify, or center即flushright, flushleft, center\begin {flushright}。

英语单词博览060欧拉定理

英语单词博览060欧拉定理欧拉30多岁时右眼失明，晚年时双眼完全失明，但他却是最多产的数学家。

1911年起数学界整理出版4开84卷本《欧拉全集》，至今已完成80卷，整套书将重达300磅。

下面第一张是瑞士法郎10元的正面图案，画面中的人物就是欧拉。

第二张是邮票中的欧拉和他的定理。

记忆theorem [?θi?r?m]（n.定理）＝theor(y)理论＋em后缀。

词根theoretical [θi??retikl]（a.理论上的）＝theor(y)理论＋etical形容词后缀。

补充mathematics [?m?θ??m?tiks]（n.数学）≈mat垫子＋he他＋mat垫子＋ics后缀表“学科”。

联想：数学就是把垫子(mat)数来数去的学问。

美国口语简称math；英国口语简称maths。

mathematical [?m?θ??m?tikl]（a.数学的）。

数学归纳法（mathematical induction）其实是一种严谨的演绎法（deduction）。

mathematician [?m?θ?m??ti?n]（n.数学家）＝mathemat(ics)＋ician后缀表“专家”。

arithmetic [??riθm?tik]（n.算术 a.算术的）。

直接记。

初级算术（elementary arithmetic）指“（加、减、乘、除）四则运算”。

algebra [??ld?ibr?]（n.代数）。

直接记。

geometry [d?i??m?tri]（n.几何）＝geo词根“地”＋metr词根“测量”＋y后缀表“学科”。

几何学本来就是“测地术”。

cube [kju:b]（n.立方）。

下图是电影The Cube的海报。

cubic [?kju:bik]（a.立方的）＝cub(e)立方＋ic形容词后缀。

sphere [sfi?]（n.球体；球面；范围）≈sp(a)＋here这里。

“在球体里做spa”。

戴森球（Dyson sphere）是一种设想中的包围恒星以图获得其几乎所有辐射能量的巨大人造天体。

latex笔记

latex笔记2007-11-07 14:34文档文档模式字号中文书籍一般使用基本字号为五号字（10.5pt），故在article中一般选用11pt，若不选默认为10pt。

空格中文与英文之间一般加入小空隙排出来才好看，可以加"\,"或者"~"。

中文与行内公式之间也要加。

如果"."不表示句子的结束，应加入"\空格"，如"Mr. Wang"应输入为"Mr.\空格Wang"。

因为当"."表示句号时，TeX会加入一段额外的空隙。

TeX遇到一个单词以大写字母结束时会自动认为这并不是句子的结束，故这种情况不必加入\空格。

但如果确实是句子的结束，就需要在"."前加上"\@”，如“I study in SJTU\@.”。

分行\\[*]，*为指定的行间距。

mbox{文本}可以将文本保持在同一行内。

数学模式中一般以此加入中文。

而且mbox里也可以出现数学模式。

标题在用\author定义作者时可使用\and命令，来包含多个作者的信息。

如\author{作者1\\单位1\\地址1\and 作者2\\单位2\\地址2}在\title、\author、\date中均可出现thanks命令来实现脚注。

对齐左对齐、居中对齐、右对齐的环境分别为flushleft、center和flushright。

也可以使用命令\raggedright、\centering和\raggedleft使以后的文本按指定方式对齐引用quotation环境：有段首缩进(正常段落有缩进的话)，有正常段间距。

quote环境：无首行缩进，增大段间距。

verse环境：类似quote，但换行时为左端悬挂。

抄录verbatim环境可原样输出其中的文本，忽视TeX命令。

verbatim*会将空格以└┘的形式输出。

北美数学学术英语

北美数学学术英语在北美数学学术领域，学术英语的使用具有一定的规范和特点。

以下是一些在数学学术写作和交流中常见的术语和表达方式：●数学概念和操作：1.Theorem (定理): A statement that has been proven to be true.2.Lemma (引理): A smaller result that is often used in the proof of a larger theorem.3.Corollary (推论): A result that follows directly from a theorem.4.Conjecture (猜想): A statement believed to be true, but not yet proven.●证明和推理：1.Proof (证明): A logical argument that demonstrates the truth of a statement.2.Lemma Proof (引理证明): A proof specifically for a lemma.3.Contradiction (反证法): A proof technique where the assumption of the statement beingfalse leads to a contradiction.4.Induction (归纳法): A proof technique that involves proving a statement for a base case andshowing that if it holds for one case, it holds for the next.●方程和符号：1.Equation (方程): A mathematical statement that asserts the equality of two expressions.2.Variable (变量): A symbol that can represent any element from a set.3.Function (函数): A relation between a set of inputs and a set of possible outputs.4.Integral (积分): The concept of an antiderivative.●统计和概率：1.Probability (概率): The likelihood of a particular event occurring.2.Random Variable (随机变量): A variable whose value is subject to variations due to chance.3.Distribution (分布): A function or curve that describes the likelihood of different outcomes.●图论和几何：1.Graph (图): A collection of nodes and edges connecting pairs of nodes.2.Vertex (顶点): A point in a graph.3.Edge (边): A line connecting two vertices in a graph.4.Geometric (几何): Related to the properties and relations of points, lines, surfaces, andsolids.●学术写作风格：1.Precision (精准性): Clear and precise language is highly valued in mathematical writing.2.Rigor (严谨性): Mathematical arguments and proofs should be logically sound and rigorous.3.Conciseness (简洁性): Expressing ideas in a clear and concise manner is important inmathematical writing.以上是一些在北美数学学术领域中常见的英语术语和表达方式。

微积分双语词汇

MATHEMATICAL TERMS (Part 1)calculus 微积分definition 定义theorem 定理lemma 引理corollary推论prove 证明proof 证明show 证明solution 解formula 公式if and only if ( iff ) 当且仅当x X for all x X x X there exists an x Xsuch that 使得given 已知set集合finite set有限集infinite set 无限集interval区间open interval开区间closed interval 闭区间neighborhood 邻域number 数natural number 自然数integer 整数odd number 奇数even number 偶数real number 实数rational number 有理数irrational number 无理数positive number 正数negative number 负数mapping 映射function 函数monotone function 单调函数increasing function 增函数decreasing function 减函数bounded function 有界函数odd function 奇函数even function 偶函数periodic function 周期函数composite function 复合函数inverse function 反函数domain 定义域range 值域variable 变量independent variable自变量dependent variable因变量sequence 数列convergent sequence收敛数列divergent sequence 发散数列bounded sequence 有界数列decreasing sequence 递减数列increasing sequence 递增数列limit极限one-sided limit 单侧极限left-hand limit 左极限right-hand limit 右极限The Squeeze Theorem 夹逼定理infinity 无穷大infinitesimal 无穷小equivalent infinitesimal 等价无穷小infinitesimal of higher order 高阶无穷小order of infinitesimal 无穷小的阶infinitesimals of the same order 同阶无穷小increment 增量continuous function 连续函数continuity 连续性f(x) is continuous at x 在x连续f(x) is discontinuous at x 在x间断discontinuity 间断点discontinuity of the first (second) kind 第一（二）类间断点removable discontinuity 可去间断点jump discontinuity 跳跃间断点infinite discontinuity 无穷间断点intermediate value 介值The Intermediate Value Theorem 介值定理zero point 零点The Zero Point Theorem 零点定理root 根equation 方程uniform continuity 一致连续derivative 导数rate of change 变化率velocity 速度instantaneous velocity 瞬时速度tangent (line) 切线normal (line) 法线slope 斜率left-hand derivative 左导数right-hand derivative 右导数f(x) is differentiable at x f(x) 在x处可导(可微) differentiation 求导The Chain Rule 链式法则differentiation formulas 求导公式implicit function 隐函数explicit function 显函数implicit differentiation 隐函数求导logarithm 对数Logarithmic differentiation 对数求导法parameter 参数parametric equation 参数方程parametric curve 参数曲线hyperbolic function 双曲函数hyperbolic sine 双曲正弦hyperbolic cosine 双曲余弦hyperbolic tangent 双曲正切hyperbolic cotangent 双曲余切MATHEMATICAL TERMS (Part 2)differential 微分differential quotient 微商approximate value 近似值error 误差relative error 相对误差absolute error 绝对误差invariance of differential form 微分形式不变性higher derivative 高阶导数first derivative 一阶导数second derivative 二阶导数third derivative 三阶导数nth derivative n阶导数twice differentiable 二阶可导acceleration 加速度mean value 中值The Mean Value Theorem 中值定理Rolle’s Theorem 罗尔定理Lagrange’s Mean Value Theorem 拉格朗日中值定理Cauchy’s Mean Value Theorem 柯西中值定理equality 等式inequality 不等式indeterminate form 不定型(未定式) indeterminate form of type ( ) ( )型未定式L’Hospital’s Rule 洛必达法则Taylor’s formula 泰勒公式polynomial 多项式nth-degree polynomial n次多项式remaind 余项Lagrange’s form of remainder 拉格朗日型余项Peano’s form of remainder 皮亚诺型余项Maclaurin formula 麦克劳林公式Taylor polynomial 泰勒多项式Mauclaurin polynomial 麦克劳林多项式polynomial approximation 多项式逼近accuracy 精确度margin 边际marginal cost 边际成本marginal revenue 边际收益elasticity 弹性density 密度mass 质量extreme value 极值local maximum value 极大值local minimum value 极小值(absolute) maximum 最大值(absolute) minimum 最小值stationary point 驻点（稳定点）critical point 临界点The First (Second) Derivative Test （极值的）一（二）阶判别法convex 凸的convex curve 凸曲线concave 凹的concave curve 凹曲线convex function 凸函数point of inflection 拐点asymptote 渐近线horizontal asymptote 水平渐近线vertical asymptote 垂直渐近线slant asymptote 斜渐近线curve sketching 作图sketch a curve 作图curvature 曲率The bisection method 二分法The secant method 弦位法Newton’s method 牛顿（切线）法The tangent method 切线法differential calculus 微分学integral 积分integral calculus 积分学definite integral 定积分indefinite integral 不定积分partition 分割Riemann sum 黎曼和integral sign 积分符号integrand 被积函数upper (lower) limit of integration 积分上（下）限integration 积分（求积）integrable 可积的f(x) is integrable on [a, b] integrable function 可积函数integrability 可积性sufficient condition 充分条件necessary condition 必要条件piecewise continuous 分段连续property 性质The mean value theorem of integral 积分中值定理The fundamental theorem of calculus 微积分基本定理Newton-Leibniz formula primitive function (anti-derivative) 原函数（反导数）The substitution rule for integration 换元积分法The inverse of the chain rule 反链式法（凑微分法）integration by parts 分部积分法rational function 有理函数fraction 分式irreducible fraction 最简分式partial fraction 部分分式partial fraction decomposition 部分分式分解MATHEMATICAL TERMS (Part 3)vector 矢量free vector 自由矢量zero vector 零矢量magnitude of a vector 矢量的模unit vector 单位矢量scalar product 数量积dot product 点积vector product 矢量积cross product 叉积a is perpendicular (orthogonal) tob a与b 垂直coordinate 坐标coordinate system 坐标系coordinate axis 坐标轴x-axis x轴coordinate plane 坐标面direction angle 方向角direction cosine 方向余弦rectangular coordinate system 直角坐标系octant 卦限the first octant 第一卦限variable 变量function of two (three) variables 二（三）元函数function of several variables 多元函数independent variable 自变量dependent variable 因变量domain 定义域range 值域set of points 点集neighborhood 邻域interior point 内点boundary point 边界点bound 边界open set 开集closed set 闭集connected set 连通集region 区域open region 开区域closed region 闭区域bounded region 有界区域unbounded region 无界区域cluster point 聚点double limit 二重极限iterated limit 累次极限continuity 连续性increment 增量total increment 全增量partial increment 偏增量partial derivative 偏导数partial derivative of f(x,y) with respect to x ( y ) f(x,y)关于x（y）的偏导数higher partial derivative 高阶偏导数mixed partial derivative 混合偏导数Laplace equation 拉普拉斯方程total differential 全微分differentiable 可微chain rule 链式法则implicit function 隐函数implicit differentiation 隐函数微分法Jacobian determinant 雅可比行列式curve 曲线space curve 空间曲线tangent vector 切矢tangent line 切线normal plane 法平面surface 曲面normal vector 法矢normal line 法线tangent plane 切平面sphere 球面cylinder 柱面cone 锥面directional derivative 方向导数gradient 梯度gradient vector 梯度矢量Ñf delf level curve 等值线level surface 等值面local extremum 极值local maximum 极大值local minimum 极小值extreme value 最值absolute maximum (minimum) 最大（最小）值stationary point (critical point) 驻点（临界点）conditional extremum 条件极值Lagrange multiplier 拉格朗日乘数method of Lagrange multiplier 拉格朗日乘数法objective function 目标函数constraint 约束条件method of least square 最小二乘法field 场scalar field 数量场vector field 矢量场gradient field 梯度场potential field 势场potential function 势函数conservative field 保守场gravitational field 引力场force field 力场velocity field 速度场MATHEMA TICAL TERMS(Part 4)multiple integral 重积分double integral 二重积分iterated integral 累次积分region 区域region of integration 积分区域type X (Y) region X（Y）型区域order of integration 积分秩序reverse the order of integration 交换积分秩序polar coordinates 极坐标double integrals in polar coordinates 极坐标下的二重积分volume 体积lamina 平面薄片mass 质量density 密度moment about x-axis 关于x轴的（静）力矩center of mass 重心moment of inertia 转动惯量surface 曲面area of a surface 曲面的面积triple integral 三重积分rectangle 矩形rectangular coordinates 直角坐标系cylinder 柱面cylindrical coordinates 柱面坐标系sphere 球面spherical coordinates 球面坐标系change of variables in multiple integrals 重积分的变量替换Jacobian determinant 雅可比行列式line integral 曲线积分line integral with respect to arc length 对弧长的曲线积分（第一型）line integral with respect to x ( y ) 对坐标x（y）曲线积分（第二型）line integral of a vector field 向量场的曲线积分smooth curve 光滑曲线piecewise smooth curve 逐段光滑曲线oriented curve 有向曲线orientation of a curve 曲线的方向work 功the line integral is independent of path 曲线积分与路径无关connected region 连通区域simply-connected region 单连通区域closed curve 闭曲线Green’s theorem 格林定理（公式）positive orientation of a curve 曲线的正向Fundamental theorem for line integrals 曲线积分的基本定理surface integral 曲面积分surface integral of a scalar field 数量场的曲面积分（第一型）surface integral of a vector field 向量场的曲面积分（第二型）orientable surface 可定向曲面oriented surface 有向曲面Möbius strip 莫比乌斯带Klein bottle 克莱因瓶one-sided surface 单侧曲面two-sided surface 双侧曲面closed surface 闭曲面flux 流量、通量electric flux 电通量divergence 散度rotation (curl) 旋度Gauss’theorem 高斯定理（公式）The divergence theorem 散度定理（公式）Stokes’theorem 斯托克斯定理（公式）curl theorem 旋度定理（公式）circulation of v around L v沿L的环流量Hamilton operator 哈密顿算子harmonic field 调和场。

图论课件

鸽巢原理（鸽舍原理、抽屉原理）
平均值总是介于最大值和最小值之间
如果对象多于kn的一个集合被划分为n个
类，则必有一个包含的对象多于k个
等价关系与同余（1）
集合S上的一个等价关系是S上的一个关系
R,它对不同元素
满足 a) 自反性 ( x, x) R b) 对称性
x, y, z S
图论及其应用 Graph Theory and Its Applications
主要内容
图论前言
数学预备知识
前言
课程目标
学时和学分教学大纲
教材和主要参考资料
课程考核
图论学科简介（1）
图论是研究点与线组成的“图形”问题
的一门科学。图论是组合数学的一个分支，它交叉运用了拓扑学、群论、数论等学科，有时将其归为离散数学的一个分支属于应用数学分支哥尼斯堡七桥问题欧拉（1707~1782）：根据几何位置的解题方法，这是图论领域的第一篇论文， 1736年，被尊称为图论和拓扑之父
31
(5) 考试时间安排问题一个教授需要对期末考试时间进行安排，使得学生们不会有相互冲突的考试。如何解决？该问题可以建立一个图论模型来解决：待考的课程可抽象为图的顶点，连接两个顶点的边表示至少有一个学生同时选择了这两门课程。问题归结于在模型图中求所谓的“顶点着色方案”问题，该问题将在第六章讨论。例如：有a, b, c ,d, e, f 六门课程。按照上面方法建立的模型图如下：
学习方法
目的明确
态度端正理论和实践相结合
充分利用资源
逐步实现从知识到能力到素质的深化和
升华
课程考核
平时成绩（30%-40%）

数学证明英语表达路例子(一)

数学证明英语表达路例子(一)数学证明英语表达路本文将针对数学证明中的英语表达路进行详细讲解，并提供一些例子来说明。

引言在进行数学证明时，准确和清晰的英语表达是非常重要的。

以下是一些常见的数学证明中使用的英语表达方式。

1. 假设和定义在数学证明中，我们经常需要引入假设和定义。

以下是一些常用的表达方式：•假设 (Suppose): 假设某个条件成立。

–Example: Suppose that x is a positive real number. •定义 (Define): 给出一个术语的定义。

–Example: Define a prime number as a natural number greater than 1 that is divisible only by 1 anditself.2. 命题和定理在进行数学证明时，我们需要使用命题和定理。

以下是一些常见的表达方式：•命题 (Proposition): 需要证明的陈述或命题。

–Example: Proposition: The sum of two even numbers is always even.•定理 (Theorem): 已经被证明成立的陈述或命题。

–Example: Theorem: The square of any real number is non-negative.3. 证明结构在进行数学证明时，我们需要用到一些特定的结构和词汇来说明证明的过程。

以下是一些常见的表达方式：•证明 (Proof): 用来证明一个命题或定理的推理和逻辑过程。

–Example: Proof: By contradiction, assume that the sum of two even numbers is odd.•引理 (Lemma): 可以帮助证明一个更大命题或定理的中间结果。

–Example: Lemma: If a and b are positive realnumbers, then the product ab is also positive. •推论 (Corollary): 从一个已证明的定理中推导出的结论。

费马引理,罗尔定理,拉格朗日中值定理,洛必达法则,柯西定理

费马引理，罗尔定理，拉格朗日中值定理，洛必达法则，柯西定理费马引理，罗尔定理，拉格朗日中值定理，洛必达法则，柯西定理是微积分中的五个重要定理，它们在解决数学问题中起着至关重要的作用。

费马引理是微积分中的一个基本定理，它指出在函数的极值点处，函数的导数为零。

这个定理是微积分中的一个基本定理，它在求解函数的最大值和最小值时非常有用。

罗尔定理是微积分中的一个重要定理，它指出如果一个函数在两个端点处取相同的值，并且在这两个端点之间的某个点处导数为零，那么这个函数在这个区间内至少有一个极值点。

拉格朗日中值定理是微积分中的一个重要定理，它指出如果一个函数在一个区间内连续并且可导，那么在这个区间内至少存在一个点，使得这个点的导数等于这个函数在这个区间内的平均变化率。

洛必达法则是微积分中的一个重要定理，它指出如果一个函数在某个点处的导数为零，那么这个函数在这个点处的极值点就是这个函数的导数为零的点。

柯西定理是微积分中的一个重要定理，它指出如果一个函数在一个区间内连续并且可导，那么在这个区间内至少存在两个点，使得这两个点的导数相等。

这五个定理在微积分中起着非常重要的作用，它们可以帮助我们解决各种数学问题。

在实际应用中，我们可以根据这些定理来求解函数的最大值和最小值，找到函数的极值点，计算函数的平均变化率等等。

因此，掌握这些定理对于学习微积分和解决实际问题都非常重要。

总之，费马引理，罗尔定理，拉格朗日中值定理，洛必达法则，柯西定理是微积分中的五个重要定理，它们在解决数学问题中起着至关重要的作用。

我们应该认真学习这些定理，并在实际应用中灵活运用它们，以便更好地解决各种数学问题。

怎么区分原理、定理、定律、理论、概念、效应这些烧脑词？

怎么区分原理、定理、定律、理论、概念、效应这些烧脑词？原理（ principles）原理是某一学说或学科“理论”的某个具体问题领域的阐释。

著名的原理：彼得原理卡姆剃刀原理定理（Theorem）定理是经过受逻辑限制的证明为真的陈述。

——梁启超《近世文明初祖倍根笛卡儿之学说》：“凡一现象之定理，既一旦求而得之，因推之以徧，按其同类之现象，必无差谬，其有差谬者，非定理也。

”基本概念。

在数学里，定理是指在既有命题的基础上证明出来的命题，这些既有命题可以是别的定理，或者广为接受的陈述，比如公理。

数学定理的证明即是在形式系统下就该定理命题而作的一个推论过程。

定理的证明通常被诠释为对其真实性的验证。

由此可见，定理的概念基本上是演绎的，有别于其他需要用实验证据来支持的科学理论。

几何中的著名定理费马大定理大数定理中心极限定理高斯-马尔科夫引理尼科梅彻斯定理公理系统，通过有限的公理来证明所有的“真命题”。

真命题（true statement）是一种逻辑学术语。

一般的，在数学中把用语言、符号或式子表达的，可以判断真假的陈述句叫做命题。

命题真值只能取两个值：真或假。

真对应判断正确，假对应判断错误。

定律出处来自古希腊泰勒斯定律，目的是为相关理论提供数据实践证明。

定律是一种理论模型，是由不变的事实规律所归纳出的结论，是对客观事实的一种表达形式，通过大量具体的客观事实经验累积归纳而成的结论。

定律的适用范围非常广泛，它揭示了一种独特的社会及自然现象。

•举例：墨菲定律爱德华·墨菲(Edward A. Murphy)是一名工程师，他曾参加美国空军于 1949年进行的MX981实验。

这个实验的目的是为了测定人类对加速度的承受极限。

其中有一个实验项目是：将16个火箭加速度计悬空装置在受试者上方，当时有两种方法可以将加速度计固定在支架上。

不可思议的是，竟然有人有条不紊地将16个加速度计全部装在错误的位置。

墨菲通过这个事件，作出了这一著名的论断（论断：指推论判断）：If there are two or more ways to do something, and one of those ways can result in a catastrophe, then someone will do it.（如果有两种选择，其中一种将导致灾难，则必定有人会作出这种选择。

数学名词解释

數學名詞解釋絕對值(absolute)：數線上任何一個數點到零點的距離。

例如：- 4的絕對值是4；4的絕對值是4。

算則(algorithm)：為了執行一個特定形式的計算或解某類的問題，而進行組織化的程序。

例如：長除法。

等差數列(arithmetic sequence)：有 a 1 , a 2, a 3, ….元素的數列，連續項的差都是一個常數，也就是：對每一個i ，k a a i i =--1；例如：數列{2,5,8,11,14,….}，其公差是3。

漸近線(asymptotes)：當變數從原點增加到無窮大時，函數的曲線會非常靠近某些直線；例如：x 軸是函數sin(x)/x 圖形的唯一漸近線。

公理(axiom)：數學系統的基本假設，它可以推導出定理；例如：這系統可以是平面上的點與直線，則公理可以是「平面上任意二個相異點，存在唯一直線穿過這二點」。

二項式(binomial)：由二個單項式（monomial ）的和或差所組成的代數式（關於單項式，請參閱單項式的定義）。

例如：4a-8b 。

二項式的係數(binomial coefficient)：當n 是任一正整數，k 是介於0到n 的任一整數（可以是0或n ），二項式係數B(n , k)是!)!(!k k n n -。

對於B(n , k)的常用記法是n C k 或⎪⎭⎫⎝⎛k n 。

除了0！之外，符號n ！（n 階乘）代表1到n 所有整數的乘積（例如：5！＝5×4×3×2×1＝120）；0！是特例定義成1（也就是0！＝1）。

二項分配(binomial distribution)：機率名詞，兩種結果的n 次獨立試驗裡，出現k 次結果的機率為A(或出現n-k 次結果的機率為B)，可能出現的這個結果就記作A 和B 。

二項式定理(binomial theorem)：對於每個正整數n ，n b a )(+是一個多項式，二項式係數 n C k 為單項式（monomial ）k n k b a -的係數。

Latex简单用法一分钟搞定Word版

用LATEX对数学类文章编辑的方法，现将下面的程序运行，再根据需要对照PDF文件与源文件的相应项，就可以一分钟搞定。

\documentclass[12pt,a4paper]{article}\usepackage{CJK}\usepackage{subfigure} %%插入并列图片宏包\usepackage{graphicx} %%一般插入图片宏包\usepackage{amsmath}\usepackage[sort]{natbib}\newtheorem{theorem}{定理}\newtheorem{definition}{定义}\newtheorem{lemma}{引理}\newtheorem{corollary}{推论}\newtheorem{proposition}{性质}\newtheorem{example}{例}\newtheorem{remark}{注}\renewcommand\figurename{\rm 图}\renewcommand\tablename{\bf 表}%%----------------------------------------------------------------------\begin{CJK*}{GBK}{song}\title{“孤立子“方向用到的诸多公式的编写方法,对照PDF文件和源文件,LATEX学习分钟搞定}\author{SUNLEY FORWARD}\date{2011/4/28}\begin{document}\maketitle\section{Darboux变换}\indent 已知谱问题$\psi_x=U\psi$和相应的辅谱问题$\psi_t=V\psi$,其中\\\begin{align*}U=\left(\begin{array}{cccc}0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\u+\lambda & \upsilon & 0 & 0 \\\omega & u-\lambda & 0 & 0 \\\end{array}\right),\end{align*}\begin{align*}V=\left(\begin{array}{cccc}\frac{1}{2}u_x & -v_x & -u+2\lambda & 2v \\-\omega_x & \frac{1}{2}u_x & 2\omega & -u-2\lambda \\\frac{1}{2}u_{xx}+2\omega u-u^2+\lambda u+2\lambda^2 & -v_{xx}+uv & -\frac{1}{2}u_x & v_x \\-\omega_{xx}+u\omega & \frac{1}{2}u_{xx}+2\omega u-u^2-\lambda u-2\lambda^2 & \omega_x & \frac{1}{2}u_x \\\end{array}\right)\end{align*}\indent 引入相应谱问题的规范变换$T:\psi\mapsto\bar{\psi}$,即$\bar{\psi}=T\psi$,其中$\Phi$是Lax对的基解矩阵，在T的作用下，有$\bar{\Phi}=T\Phi$.\section{达布变换的应用-精确解}\ \ \ \ \ 根据达布变换的显式表达式，当我们给定已知的平凡解时，根据线性代数系统可以计算出T和其他相关的参数，最终得到方程的新解。

数学名词解释

數學名詞解釋絕對值(absolute)：數線上任何一個數點到零點的距離。

例如：- 4的絕對值是4；4的絕對值是4。

算則(algorithm)：為了執行一個特定形式的計算或解某類的問題，而進行組織化的程序。

例如：長除法。

漸近線(asymptotes)：當變數從原點增加到無窮大時，函數的曲線會非常靠近某些直線；例如：x 軸是函數sin(x)/x 圖形的唯一漸近線。

二項式(binomial)：由二個單項式（monomial ）的和或差所組成的代數式（關於單項式，請參閱單項式的定義）。

例如：4a-8b 。

二項式的係數(binomial coefficient)：當n 是任一正整數，k 是介於0到n 的任一整數（可以是0或n ），二項式係數B(n , k)是!)!(!k k n n -。

對於B(n , k)的常用記法是n C k 或⎪⎭⎫ ⎝⎛k n 。

除了0！之外，符號n ！（n 階乘）代表1到n 所有整數的乘積（例如：5！＝5×4×3×2×1＝120）；0！是特例定義成1（也就是0！＝1）。

二項分配(binomial distribution)：機率名詞，兩種結果的n 次獨立試驗裡，出現k次結果的機率為A(或出現n-k 次結果的機率為B)，可能出現的這個結果就記作A 和B 。

二項式定理(binomial theorem)：對於每個正整數n ，n b a )(+是一個多項式，二項式係數 n C k 為單項式（monomial ）k n k b a -的係數。

数学相关英语单词

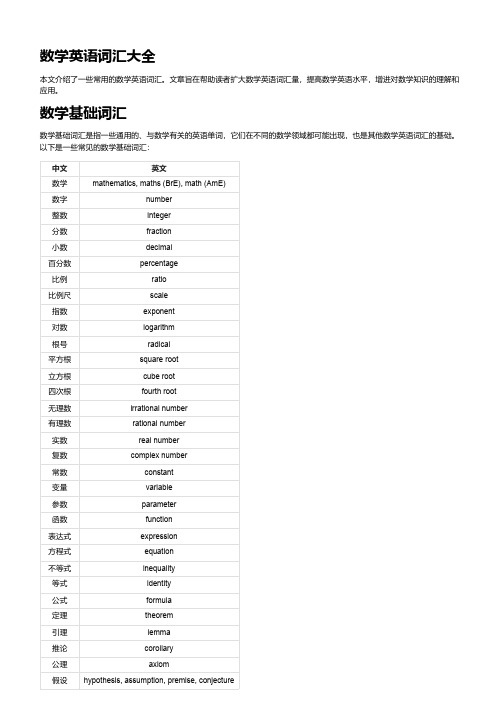
数学英语词汇大全本文介绍了一些常用的数学英语词汇。

文章旨在帮助读者扩大数学英语词汇量，提高数学英语水平，增进对数学知识的理解和应用。

数学基础词汇数学基础词汇是指一些通用的、与数学有关的英语单词，它们在不同的数学领域都可能出现，也是其他数学英语词汇的基础。

以下是一些常见的数学基础词汇：中文英文数学mathematics, maths (BrE), math (AmE)数字number整数integer分数fraction小数decimal百分数percentage比例ratio比例尺scale指数exponent对数logarithm根号radical平方根square root立方根cube root四次根fourth root无理数irrational number有理数rational number实数real number复数complex number常数constant变量variable参数parameter函数function表达式expression方程式equation不等式inequality等式identity公式formula定理theorem引理lemma推论corollary公理axiom假设hypothesis, assumption, premise, conjecture中文英文结论conclusion, result, outcome, consequence证明proof, demonstration, verification反证法proof by contradiction, reductio ad absurdum数值计算numerical computation, numerical analysis符号计算symbolic computation, computer algebra计算器calculator数量和运算数量和运算是指与数字的大小、顺序、关系、组合、变化等有关的英语单词，它们是最基本的数学概念，也是其他数学知识的基础。

数学交流的名词解释

数学交流的名词解释数学是一门严谨而又饱含美感的学科，它以逻辑和推理为基础，通过符号和公式表达出抽象的数学思想。

然而，为了有效地传递数学思想和知识，数学交流起着至关重要的作用。

在数学交流中，一些专用的名词或术语被广泛采用，它们扮演着连接思想和观点之间的桥梁的角色。

本文将对数学交流中常见的一些名词进行解释和探讨。

1. 定义(Definition)在数学中，定义用于确立某个数学概念的含义。

通过定义，我们可以清楚地了解一个概念的内涵和外延。

定义通常由关键词和一系列推导出来的规则组成。

一个好的定义应该准确且无歧义，以便其他人能够理解和运用。

2. 定理(Theorem)定理是在特定的公理或假设下通过严密的证明得出的一个数学命题。

定理往往是对一些数学问题的重要解答，它们是数学体系中的基石。

一个定理通常由前提（假设）、命题表述和证明构成。

3. 证明(Proof)证明是数学中核心的思维活动，它通过逻辑的推导和推理来论证一个数学命题的真实性。

证明由一系列合乎逻辑的步骤组成，其中每一步都基于前面已经得到的结论或已知条件。

在数学交流中，一个结论如果没有得到严密的证明，很难被其他数学家接受。

4. 推论(Corollary)推论是由一个已经证明过的定理得出的新的结论。

推论通常是对定理的一种直接逻辑推导，或是在特定条件下的一个特殊情况。

推论可以帮助我们更好地理解和扩展一个定理的适用范围。

5. 引理(Lemma)引理是为了证明一个更为复杂的定理而设计的一个次要命题。

引理通常是定理证明中的一个中间步骤，用于推动证明的进展。

引理的证明可能相对较简单，但对于定理的整体证明起到了关键的作用。

6. 猜想(Conjecture)猜想是数学家对一个尚未证明的命题的推测和猜测。

猜想往往来自于对大量的实例观察和数学探索的经验。

猜想可以为数学家提供指引，激发他们进一步地研究和探索，在证明过程中扮演了重要的角色。

7. 证明方法(Proof Techniques)在数学交流中，有许多不同的证明方法被广泛应用。

浅谈定义命题定理与推论的学习

浅谈定义命题定理与推论的学习今天来讲讲如何读数学书的问题，一般数学书总是通过定义（definition）、命题（proposition）、定理（theorem）、推论（corollary）等等展开其基本内容，下面我就分别对它们做一个阐述。

先来看定义，这是数学中最基础的部分，如果连定义弄不明白的话，那说明那本书你暂时还看不了。

但不要因为好像很容易，就把定义一带而过，要思考一下这个定义动机的什么，然后举一些简单的例子。

很多书上在定义后面都会附带几个例子，一般而言总是要比你举的例子典型一些，这时你就可以品味一下其中的味道。

假若不幸你举的例子比书上典型，可能是你对此领域非常有天赋，但也可能是这本书的质量太差了，这是可以考虑更换一些高级著作。

定义之后就是命题与定理，它们是区分与自身的重要性和证明的复杂性有关，这里并没有什么绝对的标准。

这里我把证明简明短小的结论称为小命题，而把证明复杂冗长的结论称为大定理，这和书上所标注的情况有所出入。

书上的有些结论可能原先证明比较麻烦，后来引入先进工具之后证明得到简化，但是由于历史原因，我们依然称其为定理；而一些结论的证明比较复杂，却只是重要结论的一个前提铺垫，也就只能被称为命题，假若这样的复杂结论偏离主线的话，那么更加适合的称呼则是引理（lemma）。

对于那些小命题的证明，一般我们在阅读时是容易掌握的，特别是那些比较不乏机智的小证明，非常值得细细品味。

充分理解小命题的证明，对于研究大定理的证明，将是非常关键的。

对于初学者而言，大定理的证明并非一定要读透，假若你觉得自己有能力把它消化掉，那自然是最好不过的了。

但是，这些大定理往往是数学家长时间的研究成果（不用自卑，如果你自己在研究的话，你同样有那么多时间专门考虑那个问题），因此很可能导致初学者消化不良，最方便的办法莫过于记住结论之后，转而研究相应的注记（remark）或评论（comment）。

假若实在要研读证明的话，最好不要像编辑那样就是从头到尾的核对（check），这样除了知道它正确之外，很少能得到额外的收获。

黎曼-勒贝格引理

黎曼-勒贝格引理
，又称为黎曼-勒贝格不等式，是数学家黎曼在1928年提出的
一个有关函数极值的定理。

它指出，如果某函数在某一区域内可导，且在该区域内满足拉格朗日乘子法的一阶导数条件，那么该函数在该区域内的极值点一定满足拉格朗日乘子法中的一阶导数等式。

黎曼-勒贝格不等式可以用来求解最优化问题，即求解某函数
在某一区域内的最小值或最大值。

它提供了一种更有效的方法，可以更快地求解最优化问题，而且可以用来求解多元函数的极值问题。