2016-2017-1西南科技大学线性代数B期末试卷(A卷)
线性代数试题线性代数试卷及答案大全(173页大合集)

属于 对应的特征向量为 ,单位化: ,
属于 对应的特征向量为 ,单位化: ,
取 ,则有 。
八、(本题8分)证明:由
得 的特征值 ,
,
故 的最大特征值是 。
试卷2
闭卷考试时间:100分钟
一、填空题(本题15分,每小题3分)
1、若n阶行列式零元素的个数超过n(n-1)个,则行列式为。
三、(本题8分)解:从第一行开始,每行乘 后逐次往下一行加,再按最后一行展开得:
原式= 。
四、(本题12分)解:由 ,得: ,
可逆,故 ;
由于 , 。
五、(本题14分)解:(1)令 , ,
则 线性无关,故 是向量组 的一个极大无关组;
(2)由于4个3维向量 线性相关,
若 线性无关,则 可由 线性表示,与题设矛盾;
A:矩阵A必没有零行
B:矩阵A不一定是阶梯形矩阵
C:矩阵A必有零行
D:矩阵A的非零行中第一个不等于零的元素都是1
非齐次线性方程组Ax=b中,系数矩阵A和增广矩阵(A b)的秩都等于3,A是3×4矩阵,则▁▁▁。【A】
A:方程组有无穷多解
B:无法确定方程组是否有解
C:方程组有唯一解
D:方程组无解
试卷1
4、若 阶实方阵 , 为 阶单位矩阵,则( )。
(A) (B)
(C) (D)无法比较 与 的大小
5、设 , , , ,其中 为任意常数,则下列向量组线性相关的为( )。
(A) ( B) (C) (D)
三、(10分)计算 阶行列式 , 的主对角线上的元素都为 ,其余位置元素都为 ,且 。
四、(10分)设3阶矩阵 、 满足关系: ,且 ,求矩阵 。
B:Ax=0的基础解系中的解向量的个数不可能为n-r
2016-2017-1西南科大线性代数B期末试卷(B卷)

第 1 页 共 4 页
7、设 B 1 0 , C 3
1 2
1 2 , 且有ABC E , 则A 1 = ______________. 4
a 2 1 2 8、设向量组 1 3 , 2 b , 3 2 , 4 3 的秩为 2,则 a ______, b ______. 1 3 1 1 a11
cos ( A) sin
sin cos
sin cos
cos (C) sin
).
sin (D)A不一定可逆 cos
2、设 A, B 均为 n 阶方阵, AB 0, 且 B 0 ,则必有(
1 . 0
2016-2017-1 学期
《线性代数 B》(B 卷)
第 3 页 共 4 页
14、求向量组 1 (1, 1, 1, 3) , 2 ( 1, 3, 5, 1) , 3
T T
(3, 2, 1, 4)T , 4 (2, 6, 10, 2)T 的一个最
a 23 2 ,则 2a 21
a 31
10、设 a1a2 an 0 ,n 阶行列式 Dn =
1 1
1+a2
三、解答题(每小题 12 分,共 60 分)
4 3 2 1 11、设 A 0 0 0 0 0 0 0 1 ,求 A . 1 2 3 4 0
(D) b 2c 2 a 2 d 2
4、 A, B 均为 n 阶矩阵,且 ( A B ) 2 A 2 2 AB B 2 ,则必有 (
( A) A B
线性代数期末考题1

西南财经大学会计专升本科2003级《线性代数》课程期末考试题1专业 学号 姓名 成 绩 (分) 试 题 全 文一、填空题(请将正确答案直接填在横线上。
每小题2分,共20分): 1. 排列36215784 的逆序数是的逆序数是 ,是,是 排列。
排列。
2.行列式513231412--的代数余子式31A = , 23A = 。
3. 设矩阵úûùêëé=d c b a A ,当满足,当满足______________________________时,时,A 是可逆阵,其逆阵为是可逆阵,其逆阵为___ __________ __________ _______。
4. 分块矩阵úûùêëé00B A ,其中A ,B 都是可逆方阵,则100-úûùêëéBA = = 。
5. n 阶方阵A 满足032=--E A A ,则=-1A。
6.设A 是一个n 阶方阵,则A 非奇异的充分必要条件是R (A )=__________=__________。
7.向量)1,2,2,3()4,2,2,1(-==b a ,,则α+β=____ __,2α-3β=___ _______=___ _______。
8.单独一个非零向量必线性.单独一个非零向量必线性___________。
9.设AX = O 是有6个方程,5个未知数的齐次线性方程组,其系数矩阵A 的秩为2,则方程组AX = O 有____ _____组解,其基础解系含_ ________个解向量。
个解向量。
10.若2是可逆方阵A 的特征值,则的特征值,则___ ______ ______ ___是是2A 的特征值,的特征值, __ ___ __ ___ __ ___ 是是1-A 的特征值。
西南科技大学2009年线性代数(B)期末试题A

证: 设有 k1α + k2 Aα + k3 A2α = 0 ,
则 k1 Aα + k 2 A2α + k3 A3α = 0 ,因 A3α = 0 ,故 k1 Aα + k 2 A2α = 0 -----(3 分)
ww w. zh
A2α ≠ 0 ,求证向量组 α , Aα , A2α 是线性无关的。
in
命题共 5 页 第 4 页
an ch e
1 x = −(λ − 1)2 (λ + 1) −λ
.c
⎛0 0 1⎞ ⎜ ⎟ 6.(10 分)设 矩阵A = ⎜ 1 1 x ⎟ ,问 x 为何值时,矩阵 A 可对角化? ⎜1 0 0⎟ ⎝ ⎠
om
⎛1⎞ ⎛ 2⎞ ⎜ ⎟ ⎜ ⎟ 2⎟ 3 ⎜ ,η 2 + η3 = ⎜ ⎟ η1 = ⎜ 3⎟ ⎜ 4⎟ ⎜ ⎟ ⎜ ⎟ ⎝ 4⎠ ⎝ 5⎠ 求该方程组的通解。 解 : 此 方 程 组 的 导 出 组 的 基 础 解 系 含 有 4−3 =1 个 解 向 量 ( 3 分 ) ,而 ⎛0⎞ ⎜ ⎟ 1 ξ = 2η1 − (η2 + η3 ) = ⎜ ⎟ 是导出组的一个非零解,故 ξ 就是基础解系(4 分) 。所 ⎜ 2⎟ ⎜ ⎟ ⎝ 3⎠ 以,方程组的通解为η = kξ + η1 ( k 为任意常数) (3 分)
(3) λ = −
5. (10 分)设四元非齐次线性方程组的系数矩阵的秩为 3,已知η1 ,η2 ,η3 是它 的三个解向量且
命题共 5 页 第 3 页
ww w. zh
4 ,方程无解---------------------------(2 分) 5
in
⎛ 1 1 λ⎞ ⎜ ⎟ 解: 设方程组的系数矩阵为 A,则 A = ⎜ −1 λ 1 ⎟ --------(2 分) ⎜ 1 −1 2 ⎟ ⎝ ⎠
线性代数期末考试题库及答案

2、n2, 当 n 为偶数时为偶排列,当 n 为奇数时为奇排列. 4、29.
1、12.
2、 x2 y2 .
4
∑ 3、 x = 0 或 − ai . i =1
4、 λ = ±1, 2 .
三、证明题
证明提示: 由于 f(x)是关于 x 的二次多项式,在[0,1]中可导,又可计算出 f (0) = f (1) = 0 ,
3、解方程 D4( x) =
a1 a1
a1 + x
a2 a2 a2 + x a2
a3 a3 + x
a3 a3
a4 + x a4 = 0 . a4 a4
4、已知下列齐次线性方程组有非零解,求参数λ的值。
(5
− λ)x1 −6 x1
−4 x2 +(7 − λ )x2
−7 x3 +11x3
=0 =0
6 x1
(B)若 AX=0有非零解,则 AX=b有无穷多解;
(C)若 AX=b有无穷多个解,则 AX=0仅有零解;
(D)若 AX=b有无穷多个解,则 AX=0有非零解。
(7)非齐次线性方程组 AX=b中未知量个数为 n,方程个数为 m,系数矩阵 A的秩为 r,则
()
(A)r=m时,方程组 AX=b有解; (B)r=n时,方程组 AX=b有唯一解;
《线性代数》补充练习二
一、选择题:
(1)设 n阶方阵 A的秩 r<n,则在 A的 n个行向量中( )
(A)必有 r个行向量线性无关; (B)任意 r个行向量均可构成极大无关组;
(C)任意 r个行向量均线性无关;(D)任一个行向量均可由其他 r个行向量线性表示
(2)若向量组α,β,γ线性无关;α,β,δ线性相关,则( )
线性代数期末考试试卷复习资料合集详解

×××大学线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.矩阵⎪⎪⎪⎭⎫ ⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,,Λ21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,,Λ21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=T A A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,,Λ21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,,Λ21中任意两个向量都线性无关 ② s ααα,,,Λ21中存在一个向量不能用其余向量线性表示 ③ s ααα,,,Λ21中任一个向量都不能用其余向量线性表示④ s ααα,,,Λ21中不含零向量 3. 下列命题中正确的是( )。
西南科技大学线性代数题目网络教育

西南科技大学网络教育线性代数题目解答一、单项选择题1.A.0B.-5C.-6D.7答案:C2.计算排列34125的逆序数后,有( )。
A.逆序数是3, 并为奇排列B.逆序数为4, 并为奇排列C.逆序数为4, 并为偶排列D.逆序数为3, 并为偶排列答案:C3.A.B.C.D.答案:A4.取( )值时齐次线性方程组有非零解。
A.B.C.D.答案:B5.。
A.B.C.D.答案:D6.从给出的线性方程组的增广矩阵可以看出此方程组有几个方程,几个未知数?A.3个方程,3个未知数B.4个方程,4个未知数C.4个方程,3个未知数D.3个方程,4个未知数答案:D7.A.B.C.D.答案:B8.已知向量组计算出这组向量的秩是( )A.1B.2C.3D.4答案:C9.A.B.C.D.答案:D10.A.B.C.D.答案:A11.矩阵的特征值为( ) A.B.C.D.答案:A12.A.1B.-1C.2D.-2答案:B二、判断题13.每一列元素之和为零的n阶行列式D的值等于 0 .答案:正确14.答案:错误15.A为任一方阵,则,均为对称阵。
答案:正确16.答案:正确17.答案:错误18.答案:正确19.答案:错误20.答案:错误三、复合题121.证明:,所以第一步( )(4 分)A.B.C.D.答案:D22.第二步( )(4 分)A.B.C.D.答案:A23.第三步( )(4 分)A.B.C.D.答案:C四、复合题2解:,则24.第一步( )(4 分)A.B.C.D.答案:C25.第二步( )(4 分)A.B.C.D.答案:B26.第三步( )(4 分)A.B.C.D.答案:D五、复合题3解:,则27.第一步( )(4 分)A.B.C.D.答案:B28.第二步( )(4 分)A.B.C.D.答案:A29.第三步( )(4 分) A.B.C.D.答案:D六、复合题4解:30.第一步( )(4 分) A.B.C.D.答案:B31.第二步( )(4 分) A.B.C.D.答案:B32.第三步( )(4 分)A.B.C.D.答案:A。
西南理工大学《线性代数》2017-2018学年第二学期考试试卷

西南理工大学2017-2018学年第二学期《线性代数》期末考试试卷课程代码: 试卷编号: 1-A 命题日期: 2016年 11 月 1 日。
答题时限: 120 分钟 考试形式:闭卷、笔试一、单项选择题(从4 个备选答案中选择最适合的一项,每小题2 分,共20 分)1、下列函数中,( )为x 的指定过程的无穷小(A )x x y 1arctan ⋅= ,0→x (B )6432-+=x x x y ,∞→x(C ) 702050)3()1()4(+-+=x x x y , 4→x (D )xxy sin =,0→x 2. n 阶方阵A 与对角阵相似的充要条件是 ( ).(A) A 是实对称阵 (B) A 有n 个互异特征值 (C) A 有n 个线性无关的特征向量 (D) A 的特征向量两两正交3、设)(x f 是区间I 内的连续函数,)(x f ≠0,()x F 1,()x F 2是)(x f 在区间I 内的两个不同的原函数,则在区间I 内必有( )。
(A )()()121C x F x F =+ (B )()()221C x F x F =⋅ (C )()()x F C x F 231= (D )()()421C x F x F =-4. 已知线性方程组的系数矩阵A 是54⨯矩阵,且A 的行向量组线性无关,则下列结论正确的是( ). (A) A 的列向量组线性无关(B) 线性方程组的增广矩阵的任意四个列向量线性无关(C) 线性方程组的增广矩阵的行向量组线性无关 (D) 线性方程组的增广矩阵的列向量组线性无关5、设{()()t x t y ϕψ==,ϕ,ψ可导,则dxdy =( ). (A )()t ϕ' (B )()t ψ' (C )()()t t ψϕ'' (D )()()t t ϕψ''6. 如果0λ是n 阶矩阵A 的特征值, 那么必有( ).(A) 0||0=-E A λ (B) 0||0≠-E A λ (C) 0=-E A 0λ (D)0≠-E A 0λ7、若lim 0x x →()x f 存在,则( ). (A )()x f 必在0x 的某一领域内有界 (B )()x f 在0x 的某一领域内无界 (C )()x f 必在0x 的任一领域内有界 (D ) ()x f 必在0x 的任一领域内无界8. 已知矩阵x44174147---的特征值为λ1=λ2=3,λ3=12,则x = ( )(A) 4 (B) 3 (C) 2 (D) 19、下列反常积分收敛的是( ).(A )⎰+∞1sin xdx (B )dx x ⎰+∞11 (C )dx x⎰+∞11 (D )dx e x⎰+∞-1 10. 向量组12,,...n ααα线性相关,则( ) (A )1α可由其余向量线性表示; (B )12,,...n ααα至少有一个零向量;(C )12,,...n ααα中至少有一个向量可以由其余向量线性表示; (D )12,,...n ααα任两个向量成比例.二、填空题(每空6分,共30分)1. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=111111111A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=150421321B ,则B A T =( ). 2、lim 0x x →=⎰42sin xtdx x 。
线性代数期末考试试卷+答案合集

×××大学线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,,Λ21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,,Λ21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0100100000010010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=T A A ( )。
① n 2 ② 12-n ③ 12+n ④ 42. n 维向量组 s ααα,,,Λ21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,,Λ21中任意两个向量都线性无关 ② s ααα,,,Λ21中存在一个向量不能用其余向量线性表示 ③ s ααα,,,Λ21中任一个向量都不能用其余向量线性表示 ④ s ααα,,,Λ21中不含零向量 3. 下列命题中正确的是( )。
西南科技大学2014-2015学年第2学期期末考试试卷(附答案)

西南科技大学2014-2015学年第2学期期末考试试卷《高等数学B2》(经管类)A 卷(附答案)一、填空题(每小题3分,共15分)1.函数z ={}____________________(,)D x y =.2.设224(,)(0,0)(,)0(,)=(0,0)xy x y x y f x y x y ⎧⎪⎨⎪⎩≠+=,则(0,0)____________________x f '=.3.函数xy z e =的全微分____________________dz =.4. 设D 是由1,x y =±=±围成的闭区域,则____________________(sin sin )Dy x y dxdy ++=⎰⎰21.5. 若某二阶常系数非齐次线性微分方程的一个特解为3x ,其对应的二阶常系数齐次微分方程的特征方程有两个实根1,2,则该非齐次方程的通解为____________________.二、选择题 (每小题3分,共15分)1.对(,)z f x y =在点,)x y (处下列命题正确的是( ).A .若偏导数存在则一定连续 B. 若偏导数存在则一定可微C. 若连续则一定偏导数存在D. 若可微则一定偏导数存在2. 设函数(,)z f x y =在点00,)x y (的某邻域内连续且有一、二阶连续偏导数,又00(,)0,x f x y '=00(,)0y f x y '=,令000000(,),(,),(,)xxxy yy A f x y B f x y C f x y ''''''===,则下列命题正确的是( ).A. 20AC B -<时具有极值,0A >时有极小值B. 20AC B <-时具有极值,0A <时有极大值C. 20AC B ->时具有极值,0A >时有极大值,0A <时有极小值D. 20AC B ->时具有极值,0A <时有极大值,0A >时有极小值3.若{}22(2)(1)2(,)x y D x y -+-≤=,则下列正确的是( ).A.()()ln()D D D x y dxdy x y dxdy x y dxdy +≤+≤+⎰⎰⎰⎰⎰⎰23 B.()ln()()D D D x y dxdy x y dxdy x y dxdy +≤+≤+⎰⎰⎰⎰⎰⎰23C.ln()()()D D D x y dxdy x y dxdy x y dxdy +≤+≤+⎰⎰⎰⎰⎰⎰23 D. ()()ln()D D D x y dxdy x y dxdy x y dxdy +≤+≤+⎰⎰⎰⎰⎰⎰32 4.微分方程y '=的通解为( ). A. 21arctan 2y x c =+ B. 21arcsin 2y x c =+ C. 21arctan 2y x = D. 21arcsin 2y x = 5. 下列级数收敛的是( ). A. 1123n n n ∞-=∑ B. 1132n n n -∞=∑ C. 12n n ∞=∑ D. 1n n ∞=∑三、解答题(1小题每小题7分,2-8小题每小题9分,共70分)1.求极限00x y →→2. 若f 具有二阶连续偏导数,且(2,)x z f x y =,求22xz ∂∂.3. 设),(y x z z =由方程z e xyz =确定,求yz x z ∂∂∂∂,.4. 某公司可通过电台及报纸两种方式做销售商品的广告,根据统计资料,销售收入R (万元)与电台广告费用x (万元)及报纸广告费用y (万元)之间的关系有如下的经验公式:22(,)1514328210R x y x y xy x y =++---,若提供的广告费用为1.5(万元),求相应的最优广告策略.5.计算二重积分Dσ⎰⎰,其中D 是圆环形闭区域22224x y ππ≤+≤6. 求一阶线性微分方程x y y e -'+=的通解.7. 判断级数1(1)5nnn n ∞=-∑是否收敛?如果收敛,是绝对收敛还是条件收敛?8. 求幂级数13n n n x n ∞=⋅∑的收敛域.(答案详解):一、填空题(每小题3分,共15分)1.22+1x y ≤2.03.xy xy ye dx xe dy +4.4 5. 2312x x y c e c e x =++二、选择题 (每小题3分,共15分)1. D 2. D 3. C 4.B 5.A三、解答题(1小题7分,2-8小题每小题9分,共70分)1. 20016x x y y →→→→==-分分.2. 2112f y f z x '+'='—4分,2221211144f yf y f z xx ''+''+''=''—5分. 3. x x z z yz F z F e xy''=-='-—5分,y y z z xz F z F e xy ''=-='-—4分. 4. 22(,,)()1514328210F x y x y xy x y λ=++---( 1.5)x y λ++-—4分令0x y F F F λ'''===—3分,得唯一驻点及所求(0,1.5)—2分. 5. =I 6分2220sin 6d r rdr πππθπ=-⎰⎰3分.6. 5[]()dx dx x x y e e e dx c e x c ---⎰⎰=+=+⎰分4分.7. 15n n n ∞=∑,1lim 111555n n n n n →∞+=<+,收敛—7分,1(1)5nn n n ∞=-∑绝对收敛—2分. 8. 1(1)lim 311313n n n n n →∞+⋅+=⋅,3R =—5分,3x =-,1(1)n n n∞=-∑收敛,3x =,11n n ∞=∑发散—2分 收敛域[3,3)-—2分.。
线性代数期末试卷及解析(4套全)2016科大
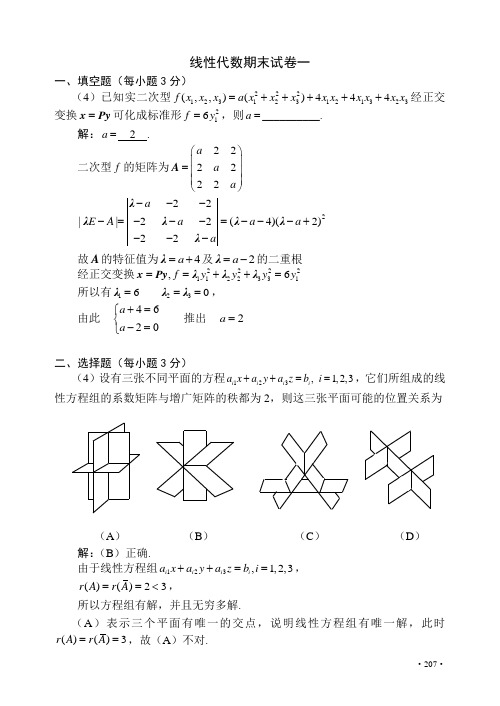
·207·线性代数期末试卷一一、填空题(每小题3分)(4)已知实二次型222123123121323(,,)()444f x x x a x x x x x x x x x =+++++经正交变换=x Py 可化成标准形216f y =,则a =__________. 解:a = 2 .二次型f 的矩阵为222222a a a ⎛⎫⎪= ⎪ ⎪⎝⎭A222||22(4)(2)22a E A a a a a----=---=---+---λλλλλλ 故A 的特征值为4a =+λ及2a =-λ的二重根经正交变换22221122331,6f y y y y ==++=x Py λλλ 所以有12360===λλλ, 由此 4620a a +=⎧⎨-=⎩推出 2a =二、选择题(每小题3分)(4)设有三张不同平面的方程123,1,2,3i i i i a x a y a z b i ++==,它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为(A ) (B ) (C ) (D ) 解:(B )正确.由于线性方程组123,1,2,3i i i i a x a y a z b i ++==, ()()23r A r A ==<,所以方程组有解,并且无穷多解.(A )表示三个平面有唯一的交点,说明线性方程组有唯一解,此时()()3r A r A ==,故(A )不对.·208· (C )表示三个平面两两相交,但三个平面无公共点,说明线方程组无解,此时()2()3r A r A =<=,故(C )不对.(D )表示三个平面中有两个平行平面,与第三个平面相交,但三个平面无公共点,说明线性方程组无解,此时()2()3r A r A =<=,故(D )不对. (B )中三个平面相交于同一直线,说明方程组有解,且无穷多解,因此必有()()3r A r A =≠,又三平面既不是重合平面,又不是平行平面,故()2r =A ,即(B )正确.九、(本题满分6分)已知4阶方阵12341234(,,,),,,,=A αααααααα均为4维列向量,其中234,,ααα线性无关,1232=-ααα,如果1234=+++βαααα,求线性方程组=Ax β的通解.解法1 令1234x x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭x ,则由12123434(,,,)x x x x ⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪⎝⎭Ax ααααβ得112233441234x x x x +++=+++αααααααα,将1232=-ααα代入上式,整理后得12213344(23)()(1)x x x x x +-+-++-=ααα0. 由234,,ααα线性无关,知12134230,0,10.x x x x x +-=⎧⎪-+=⎨⎪-=⎩解此方程组得01320110k ⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭x ,其中k 为任意常数.解法2 由234,,ααα线性无关和123420=-+αααα,故A 的秩为3,因此=Ax 0的基础解系中只包含一个向量.由 12342-++=αααα0·209·知1210⎛⎫ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭为齐次线性方程组=Ax 0的一个解,所以其通解为12,10k k ⎛⎫ ⎪- ⎪= ⎪ ⎪ ⎪⎝⎭x 为任意常数.再由 123412341111(,,,)1111⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=+++== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭βααααααααA知1111⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭为非齐次线性方程组=Ax β的一个特解,于是=Ax β的通解为11121110x k ⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,其中k 为任意常数.十、(本题满分8分) 设,A B 为同阶方阵,(1)如果,A B 相似,试证,A B 的特征多项式相等(2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当,A B 均为实对称矩阵时,试证(1)的逆命题成立. 证:(1)若,A B 相似,那么存在可逆矩阵P ,使1-=P AP B ,故 111|||||λλλ----=-=-=E B E P AP P EP P AP B ,故11|()|||||||λλ--=-=-P E A P P E A P 1||||||||.λλ-=-=-P P E A E A(2)令0100,0000⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭A B ,那么2||||λλλ-==-E A E B ,但,A B 不相似. 否则,存在可逆矩阵P ,使 1-==P AP B 0,·210· 从而1-==A PBP 0,矛盾.(3)由,A B 均为实对称矩阵知,,A B 均相似于对角阵.若,A B 的特征多项式相等,记特征多项式的根为1,,n λλL ,则有A 相似于1n λλ⎛⎫ ⎪⎪ ⎪⎝⎭O , B 也相似于1n λλ⎛⎫ ⎪⎪ ⎪⎝⎭O , 即存在可逆矩阵,P Q 使111n λλ--⎛⎫⎪== ⎪ ⎪⎝⎭P AP Q BQ O. 于是111()()---=PQ A PQ B .由1-PQ 为可逆矩阵知,A 与B 相似.·211·线性代数期末试卷二一、填空题(每小题3分)(5)矩阵022222222--⎛⎫ ⎪- ⎪ ⎪--⎝⎭的非零特征值是__________.解: 4 .设 022222222--⎛⎫ ⎪=- ⎪ ⎪--⎝⎭A232222||2220222222r r +-=--===--λλλI A λλλλλ3222000(4)224c c -====--λλλλλ故非零特征值为4.二、选择题(每小题3分)(5)设向量组123,,ααα线性无关,1β可由123,,ααα线性表示,而向量2β不能由123,,ααα线性表示,则对于任意常数k ,必有 (A )12312,,,k +αααββ线性无关 (B )12312,,,k +αααββ线性相关 (C )12312,,,k +αααββ线性无关 (D )12312,,,k +αααββ线性无关解:(A )正确因为123,,ααα线性无关,1β可由123,,ααα线性表示,所以1231,,,αααβ线性相关;2β不能由123,,ααα线性表示,所以1232,,,αααβ线性无关.取0k =,说明(B )、(C )不对,而仅当0k =时,(D )才成立,故(D )不对,现证(A )正确.易见12k +ββ不能表成123,,ααα的线性组合,如若不然,存在常数123,,l l l 使 12112233k l l l ++++ββααα则 21122331l l l k =++-βαααβ (1) 而1β可由123,,ααα线性表示,即存在常数123,,k k k ,使1112233k k k =++βααα (2) (2)代入(1)2111222333()()()l kk l kk l kk =-+-+-βααα·212· 这与2β不能由123,,ααα线性表示矛盾. 可见12312,,,k +αααββ线性无关,当然也可以用线性无关的定义来证明该结论.十一、(本题满分6分)已知,A B 为3阶矩阵,且满足124-=-A B B E ,其中E 是3阶单位矩阵. (1)证明:矩阵2-A E 可逆;(2)若120120002-⎛⎫ ⎪= ⎪ ⎪⎝⎭B ,求矩阵A .解 (1)由124-=-A B B E 知24--=AB B A 0, 从而 (2)(4)8--=A E B E E ,或 1(2)(4)8-⋅-=A E B E E .故2-A E 可逆,且11(2)(4)8--=-A E B E .(2)由(1)知128(4)-=+-A E B E ,而 111104432013(4)1200,880021002--⎛⎫- ⎪--⎛⎫ ⎪⎪ ⎪-=-=-- ⎪ ⎪ ⎪- ⎪⎝⎭ ⎪- ⎪⎝⎭B E 故 020110002⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭A .十二、(本题满分6分) 同试卷(一)九.·213·线性代数期末试卷三一、填空题(每小题3分)(3)设三阶矩阵122212304-⎛⎫ ⎪= ⎪ ⎪⎝⎭A ,三维列向量T (,1,1)a =α,已知A α与α线性相关,则a =__________.解:1a =-.122212123304134a a a a -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪==+ ⎪⎪ ⎪ ⎪⎪ ⎪+⎝⎭⎝⎭⎝⎭A α由A α与α线性相关,故k =A αα,即2334a ka a k a k ⎛⎫⎛⎫⎪ ⎪+= ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭故1a =-二、选择题(每小题3分)(3)设A 是m n ⨯矩阵,B 是n m ⨯矩阵,则线性方程组()=AB x 0 (A )当n m >时仅有零解. (B )当n m >时必有非零解. (C )当m n >时仅有零解. (D )当m n >时必有非零解. 解:(D )正确因为A 是m n ⨯矩阵,B 是n m ⨯矩阵,所以AB 是m m ⨯方阵,故x 为1m ⨯列向量线性方程组()=AB x 0可写成()=A B x 0,这说明=Bx 0的解一定是()=AB x 0的解.当m n >时,=Bx 0必有非零解,所以()=AB x 0必有非零解,故(D )正确,而(C )错误.当n m >时,取B 为零阵时,x 为任意m 维向量=Bx 0,()=AB x 0故(A )不正确.当n m >时,取10100,0101011⎛⎫⎛⎫ ⎪== ⎪ ⎪⎝⎭ ⎪⎝⎭A B 时,2,()==AB E AB x 0仅有零解,故(B )错误.事实上只要选择,A B 使AB 满秩阵即知(B )不对. (4)设A 是n 阶实对称矩阵,P 是n 阶可逆矩阵,已知n 维列向量α是A 的属于特征值λ的特征向量,则矩阵1T ()-P AP 属于特征值λ的特征向量是·214· (A )1-P α. (B )T P α. (C )P α. (D )1T ()-P α. 解:(B )正确.由已知条件=A αλα因A 是对称阵,故1T T T 1T T T 1()()()---==P AP P A P P A P . 因此有T T 1T T T T ()()()-⋅===P A P P αP AαP λαλP α这说明T P α是1T ()-P AP 属于特征值λ的特征向量,故(B )正确. 本题的关键是与向量α左乘的矩阵是T P 才能与T 1()-P 消掉,(A )、(C )、(D )不具备此形式. 九、(本题满分8分) 设齐次线性方程组1231231230,0,0.n nn ax bx bx bx bx ax bx bx bx bx bx ax ++++=⎧⎪++++=⎪⎨⎪⎪++++=⎩L L L L L L其中0,0,2a b n ≠≠≥. 试讨论,a b 为何值时,方程组仅有零解、有无穷多组解?在有无穷多组解时,求出全部解,并用基础解系表示全部解. 解:方程组的系数行列式1||[(1)]()n a b b bb a b ba nb a b b b a b b b b a-==+--A L LLM M M M L. (1)当a b ≠且(1)a n b ≠-时,方程组仅有零解. (2)当a b =时,对系数矩阵A 作行初等变换,有111100000000a a a a aa a a a a a a ⎛⎫⎛⎫⎪ ⎪⎪ ⎪=→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A L K L L M M M M M M M M LL. 原方程组的同解方程组为120,n x x x +++=L其基础解系为T T T 121(1,1,0,,0),(1,0,1,,0),,(1,0,0,,1)n -=-=-=-αααL L L L . 方程组的全部解是·215·112211n n c c c --=+++x αααL (121,,,n c c c -L 为任意常数).(3)当(1)a n b =-时,对系数矩阵A 作行初等变换,有(1)(1)(1)(1)n bb b b b b n b b b b b b n b b b b b b b n b -⎛⎫ ⎪- ⎪⎪=→- ⎪⎪ ⎪-⎝⎭A L L L M M M M M L100011111101001111110010111111000111111100000nn n n -⎛⎫-⎛⎫ ⎪- ⎪ ⎪- ⎪ ⎪- ⎪→-⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪-⎝⎭ ⎪⎝⎭L L L L L L M M MM M M M M M M L L L 原方程组的同解方程组为121,,.n nn n x x x x x x -=⎧⎪=⎪⎨⎪⎪=⎩L L 其基础解系为T (1,1,,1)=βL . 方程组的全部解是c =x β(c 为任意常数).十、(本题满分8分)设A 为三阶实对称矩阵,且满足条件22+=A A 0,已知A 的秩()2r =A . (1)求A 的全部特征值;(2)当k 为何值时,矩阵k +A E 为正定矩阵,其中E 为三阶单位矩阵. 解法1 (1)设λ为A 的一个特征值,对应的特征向量为α,则 ()λ=≠A ααα0 22λ=A αα. 于是22(2)(2)λλ+=+A A αα. 由条件2(2)+=A A α0推知 2(2)λλ+=α0. 又由于≠α0,故有·216· 220λλ+=, 解得2,0λλ=-=.因为实对称矩阵A 必可对角化,且()2r =A ,所以2~20-⎛⎫ ⎪-= ⎪ ⎪⎝⎭A Λ. 因此,矩阵A 的全部特征值为1232,0λλλ==-=.(2)矩阵k +A E 仍为实对称矩阵. 由(1)知,k +A E 的全部特征值为 2,2,k k k -+-+.于是,当2k >时矩阵k +A E 的全部特征值大于零. 因此,矩阵k +A E 为正定矩阵.解法2 (1)同解法1.(2)实对称矩阵必可对角化,故存在可逆矩阵P ,使得 1-=P AP Λ, 1-=A P ΛP . 于是11k k --+=+A E P ΛP PP 1()k -=+P ΛE P , 所以~k k ++A E ΛE . 而22k k k k -⎛⎫ ⎪+=- ⎪ ⎪⎝⎭ΛE .k +ΛE 为正定矩阵,只需其顺序主式式均大于0,即k 需满足 2220,(2)0,(2)0k k k k ->->->. 因此,当2k >时,矩阵k +A E 为正定矩阵.·217·线性代数期末试卷四一、填空题(每小题3分)(3)设矩阵211,3223-⎛⎫==-+ ⎪⎝⎭A B A A E , 则1-=B __________解:1-=B 10211⎛⎫ ⎪ ⎪ ⎪--⎝⎭. (2)()=--B A E A E110121212220-----⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭所以||2=B*110101222||211-⎛⎫⎛⎫ ⎪=== ⎪ ⎪-- ⎪⎝⎭--⎝⎭B B B . (4)设向量组123(,0,),(,,0),(0,,)a c b c a b ===ααα线性无关,则,,a b c 必满足关系式__________.解:0abc ≠因为123,,ααα线性无关,故123|,,|0≠ααα00200a cb c abc a b=≠. 即0abc ≠.二、选择题(每小题3分)(3)设,A B 为n 阶矩阵,**,A B 分别为,A B 对应的伴随矩阵,分块矩阵⎛⎫= ⎪⎝⎭A CB 00,则C 的伴随矩阵*=C (A )**||||⎛⎫ ⎪⎝⎭A A B B 00. (B )**||||⎛⎫ ⎪⎝⎭B B A A 00. (C )**||||⎛⎫ ⎪⎝⎭A B B A 00. (D )**||||⎛⎫ ⎪⎝⎭B A A B 00. 解:(D )正确*||=AA A I·218· *||=BB B I||||||⎛⎫== ⎪⎝⎭A C A B B 00,设*,⎛⎫= ⎪⎝⎭G C G H 00、H 是n 阶方阵 *⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭A G AG CCB H BH 000000 2|||||||||||n n n ⎛⎫== ⎪⎝⎭A B I A B I A B I 00 因此有 ||||||||n n =⎧⎨=⎩AG A B I BH A B I 所以应有*||=G B A*||=H A B于是***||||⎛⎫= ⎪⎝⎭B AC A B 00,恰为(D ) 故(D )正确当然此题通过直接计算选择正确答案也是一种行之有效的作法.九、(本题满分8分)设四元齐次线性方程组(I )为123123230,20.x x x x x x +-=⎧⎨++=⎩ 由已知另一四元齐次线性方程组(II )的一个基础解系为 T T 12(2,1,2,1),(1,2,4,8)a a =-+=-+αα.(1)求方程组(I )的一个基础解系;(2)当a 为何值时,方程组(I )与(II )有非零公共解?在有非零公共解时,求出全部非零公共解.解法1 (1)对方程组(I )的系数矩阵作行初等变换,有2310105312110132--⎛⎫⎛⎫=→ ⎪ ⎪--⎝⎭⎝⎭A . 得方程组(I )的同解方程组13423453,32.x x x x x x =-⎧⎨=-+⎩ 由此可得方程组(I )的一个基础解系为T T 12(5,3,1,0),(3,2,0,1).=-=-ββ·219·(2)由题设条件,方程组(II )的全部解为112212112231212422(2)4(8)x k k x k k k k x a k k k a k x -⎛⎫⎛⎫ ⎪ ⎪-+ ⎪ ⎪=+= ⎪ ⎪++ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭αα ① (12,k k 为任意常数).将上式代入方程组(I ),得112(1)0,(1)(1)0.a k a k a k +=⎧⎨+-+=⎩ ② 要使方程组(I )与(II )有非零公共解,只需关于12,k k 的方程组②有非零解. 因为210(1)1(1)a a a a +=-++-+,所以,当1a ≠-时,方程组(I )与(II )无非零公共解. 当1a =-时,方程组②有非零解,且12,k k 为不全为零的任意常数. 此时,由①可得方程组(I )与(II )的全部非零公共解为12123421121417x x k k x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(12,k k 为不全为零的任意常数).解法2 (1)对方程组(I )的系数矩阵作行初等变换,有23102310.12113501---⎛⎫⎛⎫=→ ⎪ ⎪---⎝⎭⎝⎭A 得方程组(I )的同解方程组31241223,35.x x x x x x =+⎧⎨=+⎩ 由此可得方程组(I )的一个基础解系为T T 12(1,0,2,3),(0,1,3,5)==ββ.(2)设方程组(I )与(II )的公共解为η,则有数1234,,,k k k k ,使得 11223142k k k k =+=+ηββαα.由此得线性方程组·220· (III )1342341234123420,20,23(2)40,35(8)0.k k k k k k k k a k k k k k a k -+==⎧⎪--+=⎪⎨--+++=⎪⎪--+++=⎩ 对方程组(III )的系数矩阵作行初等变换,有10211021011201122324001035180001a a a a ---⎛⎫⎛⎫ ⎪ ⎪--- ⎪ ⎪→ ⎪ ⎪--++ ⎪ ⎪ ⎪ ⎪--++⎝⎭⎝⎭由此可知,当1a ≠-时,方程组(III )仅有零解,故方程组(I )与(II )无非零公共解.当1a =-时,方程组(III )的同解方程组为1342342,2,k k k k k k =-⎧⎨=-+⎩ 令3142,k c k c ==,得方程组(I )与(II )的非零公共解为1221121417c c -⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭η (12,c c 为不全为零的任意常数).十、(本题满分8分)设实对称矩阵 111111a a a ⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A ,求可逆矩阵P ,使1-P AP 为对角形矩阵,并计算行列式||-A E 的值. 解:矩阵A 的特征多项式211||11(1)(2)11aa a a aλλλλλλ----=--=---+--E A . 由此得矩阵A 的特征值1231,2a a λλλ==+=-. 对于特征值121a λλ==+,可得对应的两个线性无关的特征向量 T T 12(1,1,0),(1,0,1)==αα.·221· 对于特征值32a λ=-,可得对应的特征向量 T 1(1,1,1)=-α.令矩阵1231111(,,)101,10112a a a -+⎛⎫⎛⎫⎪ ⎪===+ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭P αααΛ,则1112a a a -+⎛⎫⎪==+ ⎪ ⎪-⎝⎭P AP Λ.11||||---=-A E P ΛP PP 1||||||-=⋅-⋅P ΛE P0000003a a a =-2(3).a a =-。
线性代数期末考试试卷合集(共十一套)

线性代数期末考试试卷合集(共十一套)目录线性代数期末试卷及参考答案(第一套) .............................................................................. 1 线性代数期末试卷及参考答案(第二套) .............................................................................. 9 南京工程学院期末试卷(第一套) ........................................................................................ 17 南京工程学院期末试卷(第二套) ........................................................................................ 24 南京工程学院期末试卷(第三套) ........................................................................................ 30 线性代数 期末试卷(A 卷) .................................................................................................. 36 线性代数 期末试卷(B 卷) .................................................................................................. 41 线性代数 期末试卷(C 卷) .................................................................................................. 46 线性代数 期末试卷(D 卷) .................................................................................................. 51 线性代数 期末试卷(E 卷) .................................................................................................. 57 线性代数 期末试卷(F 卷) (62)线性代数期末试卷及参考答案(第一套)一、单项选择题(本大题共5小题,每小题3分,共15分)1、设矩阵⎪⎪⎭⎫ ⎝⎛=3223A 满足B AB =,则矩阵=B ( )(A ) ⎪⎪⎭⎫⎝⎛21k k ; (B )⎪⎪⎭⎫ ⎝⎛11; (C ) ⎪⎪⎭⎫ ⎝⎛--2121k k k k ; (D ) ⎪⎪⎭⎫ ⎝⎛-2111k k .(21k k ,为任意常数) 2、设n 阶方阵A ,B 满足E AB =,则下列一定成立的是 ( ) (A )E B A == ; (B )E B A =+ ; (C )1=A 或1=B ; (D )1=⋅B A .3、设矩阵,⎪⎪⎪⎭⎫ ⎝⎛=001010100A 则 =-++)()(E A R E A R ( )(A ) 2; (B ) 3; (C ) 4; (D ) 5 .4、设向量组A :r a a a,,,21可由向量组B :s b b b ,,,21线性表示,则正确的是 ( )(A )当s r >时,向量组A 必线性相关; (B ) 当s r <时,向量组A 必线性相关; (C )当s r >时,向量组B 必线性相关; (D ) 当s r <时,向量组B 必线性相关.5、设A 为n m ⨯的矩阵,0=x A 是非齐次线性方程组b x A =所对应的齐次线性方程组,则下列结论正确的是( )(A ) 若0=x A 仅有零解,则b x A =有唯一解;(B ) 若b x A =有无穷多解,则0=x A 有非零解;(C ) 若n m =,则b x A=有唯一解;(D ) 若A 的秩m A R <)(,则b x A=有无穷多解.二、填空题(本大题共5小题,每小题3分,共15分)1、设方阵⎪⎪⎪⎭⎫⎝⎛=010002cb a A ,当c b a ,,满足 时,A 为可逆方阵.2、若可逆方阵A 的有一个特征值3,则13-)(A 必有一个特征值为 .3、设A 为54⨯的矩阵,且秩2=)(A R ,则齐次方程组0=x A 的基础解系所含向量个数是 .4、若三阶行列式222023z y x =1,则行列式1117110111------z y x = . 5、设向量组⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛13232121,,x 线性相关,则常数x= .三、计算题(本题共6小题,共50分)1、(6分)设矩阵⎪⎪⎪⎭⎫ ⎝⎛-=b a a A 140132121的秩2=)(A R , 求常数b a ,及一个最高阶非零子式.2、(8分)求矩阵⎪⎪⎪⎭⎫ ⎝⎛--=314020112A 的特征值和特征向量. 3、(8分)设3阶方阵A 与B 满足BA A BA A 22+=*, 其中,⎪⎪⎪⎭⎫⎝⎛=400030001A 求B .4、(10分)设向量组A :.,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=77103 1301 3192 01414321αααα 求: (1) 向量组A 的秩; (2) 向量组A 的一个最大线性无关组; (3) 将此最大无关组之外的其它向量用最大无关组线性表示.5、(8分)计算行列式aa a a D ++++=4321432143214321,其中0≠a .6、(10分)设线性方程组⎪⎩⎪⎨⎧=+-=--=--532403321321321x x x b ax x x x x x , 问:当参数b a ,取何值时,(1)此方程组有唯一解? (2)此方程组无解? (3)此方程组有无穷多解? 并求出通解.四、判断题(本大题共5小题,每小题2分,共10分) 1、设矩阵B A ,为3阶方阵,且42==B A ,,则121=-AB.( )2、由3维向量构成的向量组4321a a a a,,,中必有一个可由其余向量线性表示. ( ) 3、对任意n 阶方阵C B A ,,,若AC AB =,且O A ≠,则一定有C B =.( )4、设向量21ηη ,是线性方程组b x A =的解,则212ηη -也是此方程组的一个解.( ) 5、正交向量组321a a a ,,线性无关.( )五、证明题(本题共2小题,每小题5分,共10分) 1、设n 阶对称矩阵A 满足关系式O E A A =++862,证明:(1)E A 3+是可逆矩阵,并写出逆矩阵; (2) E A 3+是正交矩阵.2、若3210a a a a,,,是n 元非齐次线性方程组b x A =的线性无关解,且,)(3-=n A R证明:030201a a a a a a---,,是其对应的齐次线性方程组0 =x A 的基础解系.参考答案一、选择题(本题5小题, 每小题3分, 共15分)1. C ;2. D ;3. B ;4. A ;5. B .二、填空题(本题5小题, 每小题3分, 共15分)1. c ab 2≠;2.91; 3. 3; 4. 23- ; 5. 5. 三、计算题(本题6小题, 共50分)1. 解: A →⎪⎪⎪⎭⎫ ⎝⎛------210022170121b a a a (2分), 由R (A ) = 2知,⎩⎨⎧=-=--0201b a , ⎩⎨⎧=-=∴21b a ,一个最高阶非零子式3221-. 2.解: 由λλλλ-----=-314020112E A (),)(0212=-+-=λλ 得A 的特征值为.,21321==-=λλλ当11-=λ时, 解 ().0=+x E A,⎪⎪⎪⎭⎫ ⎝⎛-−→−⎪⎪⎪⎭⎫ ⎝⎛--=+000010101414030111r E A得基础解系:,⎪⎪⎪⎭⎫⎝⎛=1011p 对应11-=λ的全部特征向量为)(0111≠k p k当232==λλ时, 解().02=-x E A,⎪⎪⎪⎪⎪⎭⎫⎝⎛--−→−⎪⎪⎪⎭⎫⎝⎛--=-000000414111140001142r E A 得基础解系:,⎪⎪⎪⎭⎫ ⎝⎛=401 2p ,⎪⎪⎪⎭⎫ ⎝⎛=041 3p对应232==λλ的特征向量为)0,(323322不全为k k p k p k+ 3. 解: B= 2(|A |E -2A ) -1 A |A |=12(|A |E -2A ) -1 =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛4100061000101, B=2⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛410061000101⎪⎪⎪⎭⎫⎝⎛400030001 =⎪⎪⎪⎪⎪⎭⎫⎝⎛20001000514. 解: ),,,(4321αααα=A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------71307311100943121→⎪⎪⎪⎪⎪⎭⎫⎝⎛--0000110024103121 → ⎪⎪⎪⎪⎪⎭⎫⎝⎛-0000110020102001 所以,秩3=A R , (1分)一个最大线性无关组为,,,321ααα(2分)且321422αααα++-=5. 解:aa a a D ++++=43214321432143214321c c c c +++aa a a a a a +++++++432104321043210432101r r i -aa a a 00000000043210+=)(103+a a 6. 解: 增广矩阵⎪⎪⎪⎭⎫⎝⎛-----==5312410131b ab A B ),( →⎪⎪⎪⎭⎫⎝⎛+---120011100131b a(1) 当12-≠=b a ,时, 32=<=)()(B R A R ,此时方程组无解. (2) 当b a ,2≠取任意数时, 3==)()(B R A R ,此时方程组有唯一解. (3) 当12-==b a ,时, 32<==)()(B R A R ,此时方程组有无穷多解.B →⎪⎪⎪⎭⎫ ⎝⎛--000011100131 →⎪⎪⎪⎭⎫ ⎝⎛000011103201即⎩⎨⎧+-=+-=1323231x x x x 原方程组的通解为)(R c c ∈⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛--013112.四、判断题(本题5小题, 每小题2分, 共10分)1. ×;2. √;3. ×;4. √;5. √.五、证明题(本题2小题, 每小题5分, 共10分)1.证明: (1)由O E A A =++862得E E A A =++962,即E E A E A =++))((33 所以E A 3+可逆,且E A E A 331+=+-)(.(2)由A 为n 阶对称矩阵知,E A E A E A TT T 333+=+=+)()(,故()()()E E A E A E A E A T=++=++333)3(,所以E A 3+是正交矩阵.2. 证明: 3210a a a a,,,是n 元非齐次线性方程组b x A =的解,030201a a a a a a---∴,,是对应齐次方程组0 =x A 的解;又,)(3-=n A R 所以0 =x A 的基础解系中含向量个数为3)(=-A R n 个; 下证 030201a a a a a a---,,线性无关即可.设0033022011 =-+-+-)()()(a a k a a k a a k 即00321332211=++-++a k k k a k a k a k )(又 3210a a a a ,,,线性无关, 故⎪⎪⎩⎪⎪⎨⎧=++-===0000321321)(k k k k k k 有唯一解0321===k k k所以030201a a a a a a---,, 线性无关,从而030201a a a a a a---,,是其对应的齐次方程组0 =x A 的基础解系线性代数期末试卷及参考答案(第二套)一、填空题(本大题共7小题,每小题3分,共21分)1、设向量⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=123,321βα ,则当k = 时,.正交与βαα +k2、设方阵A 满足关系式O A A =+322,则1)(-+E A = .3、若三阶行列式930021-=x xxx ,则 =x . 4、设矩阵⎪⎪⎭⎫⎝⎛-=0211A ,多项式x x x f 2)(2+=,则=)(A f . 5、设向量组⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-13,032,101λ线性相关,则常数λ= .6、n 元非齐次线性方程组b x A=有无穷多解的充要条件是 .7、设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=2135212b a A 的对应特征值λ的一个特征向量为⎪⎪⎪⎭⎫ ⎝⎛-111,则 ._______________,______,===b a λ二、单项选择题(本大题共5小题,每小题3分,共15分)1、设A ,B 是任意n 阶方阵(2≥n ),则下列各式正确的是 ( )(A ) B A B A +=+; (B ) 22B A B A B A -=-⋅+; (C ) B A B A ⋅=; (D ) A B AB T⋅= .2、下列4个条件中,①A 可逆 ; ②A 为列满秩(即A 的秩等于A 的列数); ③A 的列向量组线性无关; ④ O A ≠ ;可使推理“ 若O AB =, 则O B = ”成立的条件个数是 ( )(A ) 1个 ; (B ) 2个; (C ) 3个; (D ) 4个.3、向量组s ααα,,,21)2(≥s 线性无关,且可由向量组s βββ ,,,21线性表示, 则下列结论中不成立的是( )(A ) 向量组s βββ,,,21线性无关;(B ) 对任一个j α )1(s j ≤≤,向量组s j βββα,,,,21线性相关;(C ) 存在一个j α )1(s j ≤≤,向量组s j βββα,,,,21线性无关;(D ) 向量组s ααα,,,21与向量组s βββ ,,,21等价. 4、设A ,B 均为3阶方阵, 3)(=A R ,2)(=B R , 则=)(AB R( )(A ) 1; (B ) 2; (C ) 3; (D ) 6 .5、设A 为n m ⨯的矩阵,r A R =)(,则非齐次线性方程组b x A=( )(A ) 当n r = 时有唯一解; (B ) 当n m r == 时有唯一解;(C ) 当n m = 时有唯一解; (D ) 当n r < 时有无穷多解. 三、计算题(本题共6小题,共54分)1、(7分)设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=61011152121λλA 的秩2)(=A R , 求常数λ及一个最高阶非零子式.2、(9分)求矩阵⎪⎪⎪⎭⎫ ⎝⎛=320230001A 的全部特征值和特征向量.3、(8分)设3阶方阵C B A ,,满足方程 A B A C =-)2(,试求矩阵A ,其中 ⎪⎪⎪⎭⎫ ⎝⎛=100010301B , ⎪⎪⎪⎭⎫ ⎝⎛=300020001C .4、(10分)设向量组A :.6721 ,11313 ,5652 ,21214321⎪⎪⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=αααα 求: (1) 向量组A 的秩; (2) 向量组A 的一个最大线性无关组; (3) 将此最大无关组之外的其它向量用最大无关组线性表示.5、(8分)计算行列式cc b b a a x x x x D ---=000000, 其中x c b a ,,,全不为0.6、(12分)设线性方程组⎪⎩⎪⎨⎧=++=++=++bx x x x a x x x x x 3213213214231202, 问:当参数b a ,取何值时,(1)此方程组有唯一解? (2)此方程组无解? (3)此方程组有无穷多解? 并求出通解.四、证明题(本题共2小题,每小题5分,共10分)1、若向量321,,ααα线性无关, 求证 2132αα +,324αα +,135αα + 也线性无关.2、设矩阵T E A ηη -=, 其中E 是3阶单位矩阵,⎪⎪⎪⎭⎫⎝⎛=321x x x η 是单位向量,证明:(1) A A =2; (2) A 不可逆.参考答案一、填空题(本题7小题, 每小题3分, 共21分)1. 75-; 2. E A +2; 3. 3±; 4. ⎪⎪⎭⎫ ⎝⎛--2631 ; 5. 6 ; 6. n b A R A R <=),()(; 7. -1 ,-3 ,0 .二、选择题(本题5小题, 每小题3分, 共15分)1. D ;2. C ;3. C ;4. B ;5. B .三、计算题(本题6小题, 共54分)1. 解: A →⎪⎪⎪⎭⎫⎝⎛--+---3390022110121λλλλλ(3分), 由R (A ) = 2知,⎩⎨⎧=-=-03039λλ,3=∴λ (2分), 一个最高阶非零子式5221 .2.解: 由λλλλ---=-32230001E A (),01)5(2=--=λλ得A 的特征值为.1,5321===λλλ当51=λ时, 解 ().05=-x E A,0001100012202200045⎪⎪⎪⎭⎫⎝⎛-−→−⎪⎪⎪⎭⎫ ⎝⎛---=-r E A得基础解系:,1101⎪⎪⎪⎭⎫⎝⎛=p 对应51=λ的全部特征向量为)(0111≠k p k当132==λλ时, 解().0=-x E A,000000110220220000⎪⎪⎪⎭⎫ ⎝⎛−→−⎪⎪⎪⎭⎫ ⎝⎛=-r E A 得基础解系:,001 2⎪⎪⎪⎭⎫ ⎝⎛=p ,110 3⎪⎪⎪⎭⎫ ⎝⎛-=p对应132==λλ的特征向量为)0,(323322不全为k k p k p k+.3. 解: CB A E C =-)2( ;⎪⎪⎪⎭⎫ ⎝⎛=-5000300012E C ; ⎪⎪⎪⎪⎭⎫ ⎝⎛=--51000310001)2(1E C ; ⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛=⋅-=-5300032030110001030130002000151000310001)2(1CB E C A . 4. 解: ),,,(4321αααα =A →⎪⎪⎪⎪⎪⎭⎫⎝⎛---00210045101321 → ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000021********001 (初等变换步骤不一,请酌情给分)所以,秩3=A R , (1分) 一个最大线性无关组为,,,321ααα(2分)且32142617αααα--=5. 解:)1,2,3(1=++i c c i i Dcb a xx x x---0000000234=xabc 4- .6. 解: 增广矩阵⎪⎪⎪⎭⎫⎝⎛==b a b A B 4231120211),( →⎪⎪⎪⎭⎫⎝⎛----120014100211b a a , (1) 当b a ,2≠取任意数时, 3)()(==B R A R , 此时方程组有唯一解; (2). 当1,2≠=b a 时, 3)(2)(=<=B R A R ,此时方程组无解;(3) 当1,2==b a 时, 32)()(<==B R A R ,此时方程组有无穷多解.B →⎪⎪⎪⎭⎫ ⎝⎛-000012100211 →⎪⎪⎪⎭⎫⎝⎛-000012101001 即⎩⎨⎧--==121321x x x原方程组的通解为)(011120R c c ∈⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-.四、证明题(本题2小题, 每小题5分, 共10分)1.证明: 由题意 ⎪⎪⎪⎭⎫⎝⎛=+++540013102),,()5,4,32(321133221ααααααααα , 记 AK B = .K K ∴≠=,022 可逆, 又321,,ααα线性无关,所以)5,4,32(133221αααααα +++R 3),,(321==αααR , 即 2132αα +,324αα +,135αα+ 也线性无关.2. 证明: (1) η为单位向量,1=∴ηηT ,A E E E E A T T T T T T T =-=+--=--=∴ηηηηηηηηηηηηηη)())((2.(2) 由(1)知,A A =2, 即 O E A A =-)(,3)()(≤-+∴E A R A R ,η为单位向量,O E A T ≠-=-∴ηη , 1)(≥-E A R ,从而32)(<≤A R , 所以0=A , 故A 不可逆.另一证法: 0)(=-=-=-=ηηηηηηηηηηT T E A ,的非零解,为线性方程组0=∴ηηA所以0=A , 故A 不可逆.南京工程学院期末试卷(第一套)共6 页第1页课程所属部门:基础部课程名称:线性代数A 考试方式:闭卷(A卷)使用班级:工科本科南京工程学院试卷共 6 页第 4 页南京工程学院期末试卷(第二套)共6 页第1页课程所属部门:基础部课程名称:线性代数A 考试方式:闭卷(A卷)使用班级:工科本科南京工程学院期末试卷(第三套)共6 页第1页课程所属部门:数理部课程名称:线性代数A 考试方式:闭卷(A卷)使用班级:工科本科线性代数 期末试卷(A 卷)一、(本大题共8小题,每题3分,共24分)1. 设B A ,均为n 阶方阵,则下面各式正确的是----------------------------------( C ) (A)TTTB A AB =)( (B) 222)(B A AB = (C) || ||AB BA = (D)AB BA = 2. 下列命题正确的是--------------------------------------------------------------------( C ) (A) 若02=A ,则0=A (B) 若A A =2,则0=A 或E A = (C) 若E A =,则E A n = (D) 若E A =2,则E A ±=3. 若行列式的所有元素都变号,则--------------------------------------------------( D ) (A) 行列式一定变号 (B) 行列式一定不变号 (C) 偶阶行列式变号 (D) 奇阶行列式变号4. 设k c c c b b b a a a =321321321,则112311231123232323a a a a b b b b c c c c ++=+-------------------------------( B ) (A) k 6 (B) k 3 (C) k 2 (D) k5. 若某线性方程组的系数行列式为零,则该方程组------------------------------( D ) (A) 有唯一解 (B) 有非零解 (C) 无解 (D) 有非零解或无解6.已知TT T t ),3,1(,)3,2,1(,)1,1,1(321===ααα线性相关的,则t =-----( B )(A) 4 (B) 5 (C) 6 (D) 77. 设方阵A 相似于(1,1,1)diag -,则10A =---------------------------------------- ( A )(A) E (B) 10E (C) E - (D) 10E - 8. 设A 为n 阶方阵,则下列说法中正确的是--------------------------------------( B ) (A) 若A 可对角化,则A 为实对称阵 (B) 若A 为实对称阵,则A 可对角化 (C) 若A 可对角化,则A 必可逆 (D) 若A 可逆,则A 可对角化二、填空题(本大题共4小题,每题4分,共16分)1.设2110A ⎛⎫=⎪-⎝⎭,则*A =0112-⎛⎫ ⎪⎝⎭,1A-=0112-⎛⎫ ⎪⎝⎭。
线性代数期末考试试卷合集

×××大学线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每题 2 分,共 10 分)131 1.若05x 0,则__________。
122x1x2x302.若齐次线性方程组x1x2x30 只有零解,则应知足。
x1x2x303.已知矩阵A,B,C( c ij ) s n,知足AC CB ,则 A与 B 分别是阶矩阵。
a11a124.矩阵Aa21a22的行向量组线性。
a31a325.n阶方阵A知足A23A E0,则A1。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每题 2 分,共 10 分)1.若队列式 D 中每个元素都大于零,则 D 0。
()2.零向量必定能够表示成随意一组向量的线性组合。
()3.向量组 a1, a2,, a m中,假如 a1与 a m对应的重量成比率,则向量组a1, a2,, a s线性有关。
()01004.A 1 000,则A1A。
()000100105.若为可逆矩阵 A 的特点值,则 A 1 的特点值为。
( )三、单项选择题 (每题仅有一个正确答案,将正确答案题号填入括号内。
每题 2 分,共 10 分)1.设 A 为n阶矩阵,且 A2,则 AA T()。
① 2n② 2 n 1③ 2n 1④ 42.n 维向量组1,2,,s(3s n )线性没关的充要条件是()。
①1,2,,s中随意两个向量都线性没关②1,2,,s中存在一个向量不可以用其他向量线性表示③ 1,2,,s中任一个向量都不可以用其他向量线性表示④1,2,,s 中不含零向量3. 以下命题中正确的选项是 ( )。
① 随意 n 个 n 1维向量线性有关 ② 随意 n 个 n 1维向量线性没关 ③ 随意 n 1个 n 维向量线性有关④ 随意 n 1个 n 维向量线性没关4. 设 A , B 均为 n 阶方阵,下边结论正确的选项是( )。
① 若 A , B 均可逆,则 A B 可逆② 若 A , B 均可逆,则 AB 可逆③ 若 A B 可逆,则A B 可逆④ 若 AB 可逆,则A ,B 均可逆5. 若 1, 2,3,4 是线性方程组A0 的基础解系,则1 2 34 是 A0 的( )① 解向量② 基础解系 ③ 通解④ A 的行向量四、计算题 (每题 9 分,共 63 分)x a b c d1. 计算队列式a xbcd 。
2016-2017-1西科研究生矩阵分析期末考试参考答案及评分细则(A)

西南科技大学2016-2017-1学期《线性代数与矩阵分析》研究生期末考试试卷(A 卷)参考答案及评分细则一、单项选择题(每小题5分,共15分) 1、C ;2、B ;3、A 。
二、填空题(每小题5分,共15分)1、()22100010001λλ⎛⎫ ⎪ ⎪ ⎪ ⎪-⎝⎭;2、2;3、1000101012⎛⎫ ⎪- ⎪- ⎪ ⎪-- ⎪⎝⎭。
三、解答题(每小题10分,共70分) 1、解:4max||||311==∑=i ijjaA ;7max ||||31==∑=∞j ij ia A ;1322,1||||()F ij i j A a ===∑5||||22===A A A T A λλ;3})(max{)(==A A λρ。
2、解:(1)因为OA AO =,所以φ≠V ;假设V Y X ∈,,那么Y AY X AX λλ==,,于是)()(Y X Y X AY AX Y X A +=+=+=+λλλ,所以V Y X ∈+;假设R k V X ∈∈,,那么X AX λ=,所以)()()()(kX X k AX k kX A λλ===,所以V kX ∈。
所以V 是nn R⨯的一个线性子空间。
(2)当1≠λ并且2≠λ时,则}{o V=。
没有基,0dim =V 。
当1=λ时,方程组0)(=-X E A 的解为032==X X ,所以一个基为⎪⎪⎪⎭⎫ ⎝⎛001,1dim =V 。
当2=λ时,方程组0)(=-X E A 的解为01=X ,所以一个基为⎪⎪⎪⎭⎫ ⎝⎛010、⎪⎪⎪⎭⎫ ⎝⎛100,2dim =V 。
3、解:(1)3R x ∈∀,因为A 为3阶矩阵,所以3R Ax ∈,所以33:R R T →。
3,R y x ∈∀,Ty Tx Ay Ax y x A y x T +=+=+=+)()(; R k R x ∈∀∈∀,3,kTx Ax k kx A kx T ===)()()(。
所以T 是3R 上的线性变换。
(完整word版)线性代数期末考试试题 答案解析合集

×××大学线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=T A A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示④ s ααα,,, 21中不含零向量 3. 下列命题中正确的是( )。
线性代数期末考试试卷 答案合集

2
0
10 0
1 0
4 16
2
16
0 3 1 7
0 3 1
7
0 0 13 13
1 0 0 2
0 1 0
2
0 0 1 1
0 0 0
0
则 ra1, a2, a3, a4 3 ,其中 a1, a2, a3 构成极大无关组, a4 2a1 2a2 a3
7.
1 0 0 E A 0 1 0 ( 1)3 0
1. ×
2. √
三、单项选择题
1. ③
2. ③
四、计算题
1.
3. s s , n n
4. 相关
3. √ 3. ③
4. √ 4. ②
5. × 5. ①
共 3 页第 4页
大学生校园网— 线性代数 综合测试题
xa b c d xabcd b c d
a xb c
d xabcd xb c
五、解答题(本题共 3 小题,每小题 12 分,满分 32 分。解答应写出文字说明或演算步骤)
2 0 0
13、设
A
0
3
2
,求一个正交矩阵
P
使得
P
1
AP
为对角矩阵。
0 2 3
14、已知方程组
x1 x2 x1 2x2
x3 ax3
x1 4x2 a 2 x3
0 0 与方程组 x1 2x2 x3 a 1有公共解。 0
1 x 1 1 1
9、计算行列式 D 1 1 x 1
1
1 1 1 y 1
1 1 1 1 y
10、计算 n 阶行列式
x1 3 x2 xn
Dn
x1
x2 3 xn
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西南科技大学2016-2017-1学期
⎩=λ++0
321
x x x
8、设向量组12,A αα:向量组123,,B ααα:向量组124,,C ααα:的秩分别为2,3===A B C R R R , 则向量组1234,,23-D αααα:的秩=D R ______________.
9、设A 为3阶方阵,1,2
A =则1(2)5-*
-=A A ______________.
10、.设⎪⎪⎪
⎭
⎫ ⎝⎛-=30511132a A ,且秩(A )=2,则=a ______________.
三、解答题(每小题12分,共60分)
11、计算n 阶行列式a
b b b
a b b
b a D n =.
12、设12312323-⎛⎫ ⎪
=-- ⎪ ⎪-⎝⎭
k A k k ,问k 为何值时,可使(1)()1;(2)()2;(3)() 3.R A R A R A ===
13、已知向量组⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-=769,103,321321ααα和⎪⎪⎪
⎭
⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-=01,12,110321b a βββ;已知3β可以
由321,,ααα线性表示, 且321,,ααα与321,,βββ具有相同的秩,求,a b 的值。
.
14、已知向量组⎪⎪⎪⎪
⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=02
21,8451,6352,2130,421154321ααααα (1)求向量组54321,,,,ααααα的秩以及它的一个极大线性无关组;
………密……………封……………线……………以……………内……………答……………题……………无……………效……………
(2)将其余的向量用所求的极大线性无关组线性表示。
.
15、已知线性方程组⎪⎩⎪
⎨⎧=+--=+++=+++a
x x x x x x x x x x x x 4321
432143219105363132
(1)a 为何值时方程组有解?
(2)当方程组有解时求出它的全部解(用解的结构表示).。
