相交线(2)PPT课件

合集下载

7.7相交线(2)

• • • • •
垂直定义；垂线的多种画法；垂直的表示方法；垂直的性质；点到直线的距离。
小试牛刀！
C
A
D
B
如图， ∠ ACD与∠ BCD互余， ∠ CDA与互余，如图，与互余与相等且互补． ∠ CDB相等且互补．相等且互补 CD的长的长则点C到的距离是线段＿＿＿＿＿, 的距离是线段＿＿＿＿＿则点到AB的距离是线段＿＿＿＿＿的长的距离是线段＿＿＿＿＿，点A到BC的距离是线段＿＿＿＿＿，到的距离是线段 AC的长 BC的长的长的距离是线段＿＿＿＿＿点B到AC的距离是线段＿＿＿＿＿到的距离是线段＿＿＿＿＿.
A O D
n C
B
m
互相垂直的两条直线的交点叫做垂足互相垂直的两条直线的交点叫做垂足。垂足。
注意
“⊥”是“垂直”的记号，垂直”的记号，是图形中“垂直” 直角)的标记。是图形中“垂直”(直角)的标记。而“ ”
随堂练习
随堂练习
找出下图中互相垂直的直线，找出下图中互相垂直的直线，并用符号表示。表示。 A
7.7 相交线（2）
(1)
(2)
(3)
(4)
如果两条直线相交所构成的四个角中有一个是直角，个角中有一个是直角，那么这两条直线互相垂直垂直。条直线互相垂直。
图中，直线AB与直线CD垂直 AB与直线CD垂直图中，直线AB与直线CD 记作： AB⊥CD；记作： AB⊥CD；直线 m 与直线 n 垂直记作：记作：m⊥n ；
a
C
b
D B
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7

《相交线》_精品课件

解：因为∠DOB=∠ AOC ，（对顶角相等）且 ∠AOC =80°（已知）
所以∠DOB= 80 °（等量代换）又因为∠1=30°（已知）
所以∠2= ∠DOB -∠ 1 = 80°- 30°= 50 ° 则∠2的度数是 50° 。
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
∠2和∠4
两边互为反向延长线
对顶角
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
1、下列各图中∠1、∠2互为邻补角吗？为什么？
1
2
2 1
1
2
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
象∠1和∠3有一个公共顶点O，并且∠1的两边分别是∠3的两边的反向延长线，具有这种位置关系的两个角，互为对顶角。
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
【获奖课件ppt】《相交线》_精品课件1-课件分析下载【获奖课件ppt】《相交线》_精品课件1-课件分析下载
同学们再见
（ ×）
可见：当两个角位置关系确定时，必有相应的数量关系；而当数量关系确定时，并不一定有相应的位置关系。
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
【获奖课件ppt】《相交线》_精品课件1-课件分析下载
如图，直线AB和直线CD相交于点O, ∠21+==∠964∠0403˚=˚=210000˚，˚，则∠2 = 140 ˚ 、∠3 = 140 ˚ 、∠4 = 40 ˚ 。
1.通过前面的学习，像∠1和∠2这样互为邻补角的两个角有怎样的数量关系？

人教版七年级数学下册课件相交线2

）3
• 变式1：若∠2是∠1的3倍，求∠3的度数？ • 变式2：若∠2-∠1=400, 求∠4的度数？
用代数的方法(列方程）解决几何问题是比较有效的!
两直线相交分类
位置关系
名称大小关系
C
2O
1
3
4
A
∠1和∠2、1、有公共顶点
邻
∠2和∠3、 2、有一条公共边
邻补
B ∠3和∠4、 3、另一边互为反向延长线 ∠4和∠1
∴∠3=40° （对顶角相等）
1∴、∠下1列+∠各2的图=1中80邻，° ∠补1 、角∠2是有邻补_∠角_吗_2？_、__∠__4___.
∴∠4=∠2=140° （邻补角定义） 3、如图,直线AB,CD相交于点O， ∠EOC=70°,
C
∴∠DOB= °（等量代换）
练习2：下列图中，∠1与∠2是对顶角吗？为什么？
用代数的方法(列方程）解决几何问题是比较有效的!
（1） ∠ 1=400，求∠2，∠3，∠4的度数。
3、另一边互为反向延长线
解：（1）由邻补角的定义，可得
3、两边互为反向延长线
A
3、图中是对顶角量角器，你能说出用它测量角的原理吗？
12 O3
B
∠2+∠3=180°，又∵∠1=30°（）
4
同理可得：∠2=∠4.
（A）80；（B）100；（C）130（D）150。
A
D
O
C
E
B
8：如图,直线a、b相交。（1） ∠ 1=400，求∠2，∠3，∠4的度数。（2） ∠1:∠2=2:7 ，求各角的度数。
解：（1）由邻补角的定义，可得
a
∠2＝180°－∠1 ＝180°－ 40°

人教版七年级上学期数学课件5.1相交线(共21张PPT)

a b
l
（2）两条直线被第三条直线所截．
a b
E A
1 O3 4 6 5 7 8 2
C
B D
F
两直线AB、CD被第三条直线EF所截，构成8个角，简称“三线八角”. 直线AB、CD是被截直线，EF是截线.
问题3 观察图中的∠1和∠5，它们与截线及两条被截直线在位置上有什么特点？你能给它们起个名字吗？
布置作业
E A
1 O3 4 6 5 7 8 2
B
F
总结归纳
1.同位角、内错角、同旁内角的位置特征及结构特征. 2.识别同位角、内错角、同旁内角的方法.
1.习题5.1第12题. 2.在下图中，如果直线AB绕着与截线EF 的交点O 旋转（转动时直线AB不与截线EF重合）, ∠1与∠5的同位角关系是否发生改变？两条被截直线有没有不相交的位置？
错角的图形特征吗？
F
问题6：（1）你能找出图中还有哪几对角构成内错角？（2）两条直线被第三条直线所截构成的八个角中，共有几对内错角？（1）除了∠3和∠5是内错角，还有∠4和∠6 也构成内错角．（2）共有2对内错角．
角的名称同位角
位置特征在两条被截直线同旁，的______ 同侧在截线的______ 在两条被截直线之间，的______ 两侧在截线的______ 在两条被截直线的______，在截线的_____
角的名称同位角
位置特征在两条被截直线同旁，的______ 同侧在截线的______ 在两条被截直线之间，的______ 两侧在截线的______
基本图形图形结构特征 “ F” 形如字母 ___
内错角
“ Z” 形如字母 ___

七年级上册数学课件_7.7 相交线(2)

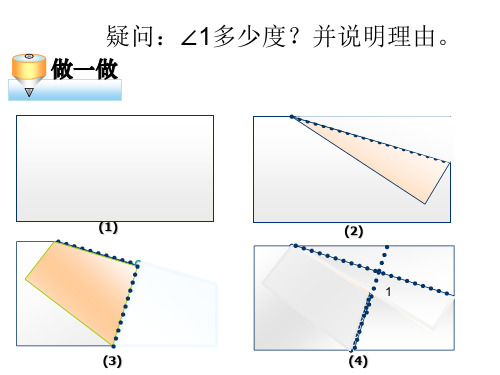
(1)做一做(2)1疑问：∠1多少度？并说明理由。

浙教版七年级上册——数学如果两条直线相交成直角，那么这两条直线互相垂直。

O D CB A mn 图中，直线AB 与直线CD 垂直记作：AB ⊥CD ；直线m 与直线n 垂直记作：m ⊥n ；互相垂直的两条直线的交点叫做垂足。

注意 “⊥”是“垂直”的记号，“两直线”互相垂直的事物在生活中随处可见，设计者是如果做到的？你有哪些方法能画出两条互相垂直直线？思考作一条直线l ，l 在l 外取一点B ，A 在直线l 上取一点A ，试分别过点A 、B 用三角尺、量角器作直线的垂线。

B 疑问：分别能作几条？垂线的性质在同一平面内，过一点有且只有一条直线与已知直线垂直。

如图，CD ⊥EF ，∠1=∠2，则AB ⊥EF ，请说明理由(补全解答过程).解: ∵CD ⊥EF, ∴∠1=_________ ( ) ∵∠2=∠1=_______ , ∴AB___EF. ( ) 12C E BFA RT ∠两条直线互相垂直的意义两条直线互相垂直的意义RT ∠⊥垂直在解题中的应用•例如图直线AB 与直线CD 相交于点O ，OE ⊥AB 。

已知∠BOD=45°，求∠COE 的度数。

ABO DCE小明家P河流小明家住点P，小明每天都要去河边打水，他每天几乎都是到同一个地方打水，你知道他是在哪打的水吗？提示：我们可以把河流近似看作是直线点到直线的距离直线l 的垂线段PO 的长度叫做点P 到直线l 的距离。

直线外一点与直线上各点连接的所有线段中，垂线段最短。

P 是直线外一点，P 与直线上所有点之间的距离中，哪一条距离最小？l本节课你的收获是什么？•垂直定义；•垂线的多种画法；•垂直的表示方法；•垂直的性质；•点到直线的距离。

1.课本作业题2.作业本。

《相交线》课件

利用平行线性质作图
总结词
操作复杂，适用于特定情况
详细描述
利用平行线的性质，通过平移、旋转等方法进行作图。这种方法操作较为复杂，适用于需要绘制特定形状的相交线。
05
相交线的定理与证明
对顶角相等定理
总结词
对顶角相等定理是相交线的基本定理之一，它表明在两条相交的直线中，相对的两个角是相等的。
VS
要点二
详细描述
在两条相交的直线中，除了对顶角外，还会形成一些相邻的角。这些相邻的角被称为邻补角。根据邻补角互补定理，这些邻补角的和总是等于180度。这个定理对于证明其他相交线定理和解决几何问题也非常重要。
同位角相等定理和内错角相等定理
总结词
同位角相等定理和内错角相等定理是相交线定理中的重要组成部分，它们分别表明在两条平行线和被截线相交的情况下，同位角和内错角是相等的。
详细描述
交通信号灯利用相交线的原理，通过不同颜色的灯光来控制交通流量的方向和速度。红灯表示停止，绿灯表示通行，黄灯则作为警告信号，提醒行人和车辆注意安全。交通信号灯的设置有效地减少了交通事故的发生，保障了交通秩序。
剪刀的交线
总结词
剪刀的交线是相交线在机械制造中的实例，通过两片剪刀的交线形成剪切力，实现材料的剪切。
详细描述
根据两条直线相交形成的角度，可以将相交线分为垂直相交和平行相交两种类型。此外，根据两条直线的位置关系，还可以将相交线分为一般位置和特殊位置两种类型。这些分类有助于我们更好地理解和应用相交线的性质和特点。
02
相交线的角度关系
对顶角
对顶角
证明
如果两条直线相交，相对的两个角就是对顶角。
可以通过全等三角形的性质来证明对顶角相等。

沪科版七年级下10.1.2相交线(2)垂线ppt课件

∠AOD=_9_0_°_,
∠BOD=_9_0_°_.
2
探究---两条直线垂直的定义
一如图，直线AB与直线CD相交于点O,若∠AOC=90°则
类特
直线AB与直线CD 互_相_垂_ 直
.
C
殊
的记作__ABCD.
相
交读作 AB垂直于CD .
关
A
O
B
系交点O叫做__垂__足_ .
垂直
直线AB叫做直线CD的__垂_线__.
请
思
考
生一活中类特殊相的
交相线交关的系
特殊垂性直
龙扬中学七（2）
最新版整理ppt
1
情景引入---在观察中感受：
一
如图2，如果∠AOC= 90°，
类
那么其它3个角的度数各是
特
多少?为什么？ A
殊
的
相
交
C
O
D
关
系
B
图2
垂
直我们将十字路口的两条道路看作两条直线相交最新。版整理ppt
∠BOC=_9_0_°_,
类
特
殊的
【操作】
相 1、过直线L上一点画已知直线的垂线
交关
2、过直线L外一点画已知直线的垂线
系 3、你能通过折纸的方法画垂线吗？
垂直
最新版整理ppt
6
活动探究---在实践中收获：
一
类问题：
特
殊这样过一点画L的垂线可以画几条？
的
相
交
关 1条
系
注意：在连接直线外一点与直线上个点的所
垂直
连线中垂线段最短
垂线段：连接直线最外新版整一理p点pt 与垂足形成的线段。7

《相交线》课件 (2)

大桥上的钢梁和钢索
棋盘上的横线和竖线
• 学校操场上的双杠,教室中课桌面、学校操场上的双杠,教室中课桌面、黑板面相邻的两边与相对的两条边……都给我们以相交线平行线的都给我们以相交线平行线的形象
有一个公共点的两条直线形成相交直线. 有一个公共点的两条直线形成相交直线. 问题:两条相交直线.形成的小于平角的角问题:两条相交直线. 有几个? 有几个? 请你画出任意两条相交直线. 请你画出任意两条相交直线.看看这四个角有什么关系? 四个角有什么关系?
） 3
∴∠2=180°—∠1=140° 邻补角的定义） ° ∠ ∴∠ ° 邻补角的定义）（
二、填空
1、一个角的对顶角有一个，邻补角最多有、两个，而补角则可以有无数个。 2、右图中∠AOC的对顶角是 ∠DOB , 、右图中∠ 的对顶角是 ∠AOD和邻补角是 ∠AOD和∠COB . D A 3、如图，直线、CD相交于、如图，直线AB、相交于 )1 )2 E O，∠AOC=80°∠1=30°；， ° ° O 的度数. 求∠2的度数的度数 C
解：∵∠DOB=∠ AOC ，（对顶角相等） ∵∠ ∠ ∠AOC =80°（已知） ° 已知） ∴∠DOB= 80 °（等量代换）等量代换） ∴∠ ∵∠1=30°（已知）又∵∠ ° ° ° = ∴∠2=∠ ∠ ∴∠ ∠ DOB -∠ 1 = 80° 30° 50 ° B
一、判断题 1、有公共顶点且相等的两个角是对顶角。（ × ）、有公共顶点且相等的两个角是对顶角。（ 2、两条直线相交，有两组对顶角。、两条直线相交，有两组对顶角。（ √ ） 3、两条直线相交所构成的四个角中有一个角是直角，、两条直线相交所构成的四个角中有一个角是直角，那么其余的三个角也是直角。那么其余的三个角也是直角。（ √ ）二、选择题 1、如右图直线、CD交于点，OE为射线，那么（C）交于点O，为射线那么（为射线，、如右图直线AB、交于点 A。∠AOC和∠BOE是对顶角；是对顶角；。和是对顶角 B。∠COE和∠AOD是对顶角；是对顶角；。和是对顶角 A D C。∠BOC和∠AOD是对顶角；是对顶角；。和是对顶角 O D。∠AOE和∠DOE是对顶角。是对顶角。。和是对顶角 2、如右图中直线、CD交于，交于O，、如右图中直线AB、交于 C B E OE是∠BOC的平分线且∠BOE=50度，的平分线且∠ 是的平分线且度那么∠ 那么∠AOE=（ C）度（；（B）；（C）（A）80；（）100；（）130（D）150。）；（；（（）。

【新】人教版七年级数学下册《相交线》公开课课件.ppt

知
并把它们想象成两条直线，就得到一个相交
识
线的模型.你能说出其中的一些邻补角与对顶
点二
角吗？两根木条所成的角中，如果∠α=35°，其他三个角各等于多少度？如果∠α等于 90°，115°，m°呢？
四、归纳小结
1、两个角有一条___公_共__边，且它们的另一边互为 __反__向_延__长__线，这样的两个角称作互为邻补角. 2、两个角有一个__公__共__顶点，且其中一个角的两边分别是另一个角的两边的___反__向__延_长____线，这样的两个角称作互为对顶角.
角
的
性
质
1、互为邻补角的两个角的和等于180°. 2、如图， ∵∠1+∠2 = 180，° ∠2+∠3 = 180.° （邻补角的定义） ∴∠1=180°－ ∠，2 ∠3=180°－ ∠2，（等式的性质）
∴∠1=∠3 (等量代换) 由上面推理可知，对顶角的性质：对顶角相等 .
三、研读课文
例1 如图,直线a、b相交,∠1=40°,求
∠2,∠3,∠4的度数.
知
解：∵∠1+∠2=___1_8_0_°
识点二
（邻补角的定义） ∠1=40° ∴∠2=180°- __∠_1 =180°- _4_0_°
=140°；
∴∠3=∠ 1= 40，°
∠4=∠ 2= 140.°
（对顶角相等）
三、研读课文
练一练
如图，取两根木条a、b，将它们钉在一起，
其中互为邻补角的有 ___∠_1_与__∠_2___、 __∠__2_与_∠__3___、 __∠_3_与__∠_4___、 __∠_4_与__∠_1___；
互为对顶角的有 ___∠_1_与__∠_3__、 __∠__2_与_∠__4__.

《相交线》参考课件2

如图两堵墙围一个角AOB,但人不能进入围墙，我们如何去测量这个角的大小呢？
O
C AOB=180°-∠AOC AOB=∠COD
D （邻补角互补) （对顶角相等)
如图，直线AB、CD、EF相交于O，
A F
C O
D )1 )2 E
(1)∠AOC的对顶角是 ∠DOB , ∠1邻补角是∠DOF和∠EOC .
2.平面上三条直线交于一点，有几对对顶角？有几对邻补角？
6对对顶角，12对邻补角
b c
3.平面上n条直线交于一点，有几对对顶角？有几对邻补角？
C
2 1
B
o4
3
A
D
3、类比∠1和∠2，看∠1和∠3有怎样的位置关系？
两直线相交分类位置关系大小关系
C 1 A
2 4
B 3 D
∠1 ∠2 ∠3 ∠4
和∠2 和∠ 3 和∠4 和∠1
邻补角
∠1 和∠3 ∠2 和∠4
C
2 1
B
o
4
3
A
D
1.下列各图中∠1、∠2是邻补角吗？为什么？
1
2
1
2
1
∠1 和∠2
C 1 A 2 4 B ∠2 和∠ 3 ∠3 和∠4 ∠4 和∠1
3
D
∠1 和∠3 ∠2 和∠4
2、观察∠1和∠2的顶点和两边，有怎样的位置关系？
两直线相交分类位置关系大小关系
∠1 和∠2
C 1 A 2 4 B ∠2 和∠ 3 ∠3 和∠4 ∠4 和∠1
3
D
∠1 和∠3 ∠2 和∠4
B
D
4、你能得到对顶角∠1和∠3的大小关系吗？猜猜看：若直线CD绕点O转动时，∠1和∠3 同时缩小或增大，你

相交线PPT课件PPT课件

若两个角不是对顶角，则这两个角不相等．
A．1个
B．2个
Hale Waihona Puke C．3个D．4个知1－练
感悟新知
知识点 2 同位角
知2－讲
如图,直线AB，CD与EF相交(也可以说两条直线
AB，CD被第三条直线EF所截)，构成八个角. 我们
看那些没有公共顶点的
两个角的关系.
感悟新知
没同位角
1、都在被截直线AB、CD 知2－讲
D 的角叫内错角.
F ∠4和∠6
感悟新知
特别解读：
知3－讲
1. 内错角是成对出现的，并且是由三条直线组成的，即一对边
共线，另一对边不共线.
2. 内错角的顶点不是公共的.
3.“内”可理解为夹在两直线之间，“错”可理解为交错，即位
于第三条直线的两侧. 内错角的位置关系具有“同内、异侧”
的特征.
感悟新知
感悟新知
4. 如图，图中共有( B )对同位角． A．2 B．4 C．6 D．8
知2－练
感悟新知
知识点 3 内错角
知3－讲
感悟新知
没
有
公A 共
顶
点
的
角
的
位
置关
C
系
E
内错角
知3－讲
之间(之内)
21
2、在截线EF的
34
B
_两__侧__(_交__错__)_.
65
我们把具有∠3和 ∠5这种位置关系
78
指名朗读片段，听评朗读效果。 1.生字、多音字读音是否正确。 2.朗读是否做到正确、流利。 3.朗读课文，读出感情。
我会读
xiù
绣花
xiāo

5.1.1相交线（共35张ppt）

所以 ∠1 =∠3（同角的补角相等）.
同理 ∠2 =∠4 ．
例如图，直线 a，b 相交，∠1 = 40°，求 ∠2 ，∠3 ，∠4 的度数．
解：由邻补角定义，可得
∠2 = 180°- ∠1
b
= 180°- 40°
= 140°；
a
由对顶角相等，得
12 43
∠3 = ∠1 = 40°，∠4 = ∠2 = 140°.
如果把剪子的构造抽象成一个几何图形，会是什么样的图形？请你在笔记本上画出．
探究
仔细观察你所画的图形，当两条直线相交时，所形成的四个角中，∠1 与∠2 有怎样的位置关系？
C
∠1 与∠2 的顶点所在的位置有什么特点？ A
23
1 4O
B
D
探究
仔细观察你所画的图形，当两条直线相交时，所形成的四个角中，∠1 与∠2 有怎样的位置关系？
（5）对顶角有__∠__1_和__∠__3_，__∠__2_和__∠__4_，_
_∠__5_和__∠__7_，__∠__6__和__∠__8__.
2.如图，直线AB、CD 相交于点O，∠AOE＝ 90°，如果∠1＝20°，那么∠2＝__2_0_°__，∠3＝ __7_0_°__，∠4＝_1_6_0_°__.
（2）当 a 与 b 所成角 α 为 90° 时，其余的
角分别为多少？均为90°
误区一不能准确判断对顶角 1.下列图形中，∠1 与∠2 是对顶角的是（）
错解 A或C或D 正解 B
错因分析不理解互为对顶角的条件：（1）有公共顶点；（2）角的两边互为反向延长线. A，C 或 D 中的∠1 和∠2 不符合对顶角的条件.判断对顶角一定要抓住对顶角形成的前提条件是两直线相交.