群论与化学练习题
群论课后习题答案

群论课后习题答案群论是数学中的一个分支,研究的是群的性质和结构。
在学习群论的过程中,习题是不可或缺的一部分,通过解答习题可以加深对群论概念和定理的理解。
本文将给出一些群论课后习题的答案,希望能对读者在学习群论时有所帮助。
1. 证明:对于任意群G和H,如果存在同构映射f: G→H,则G和H具有相同的群性质。
证明:假设f: G→H是一个同构映射。
由同构的定义可知,f是一个双射,并且满足对于任意的g1, g2∈G,有f(g1g2) = f(g1)f(g2)。
首先证明G和H具有相同的单位元。
设eG和eH分别是G和H的单位元,则有f(eG) = eH。
对于任意的h∈H,存在g = f^(-1)(h)∈G,因此有f(g) = h。
由此可得f(eG) = f(geG) = f(g)f(eG) = hf(eG),即eH = hf(eG)。
同理可证hf(eG) = eH,因此G和H具有相同的单位元。
其次证明G和H具有相同的逆元。
设g∈G,对应的元素f(g)∈H。
由于f是双射,存在g' = f^(-1)(f(g))∈G,使得f(g') = f(g)^(-1)。
因此有f(g)f(g') = f(gg') = eH。
同理可证f(g')f(g) = eH。
由此可知g' = g^(-1),即G和H具有相同的逆元。
最后证明G和H具有相同的封闭性。
设g1, g2∈G,对应的元素f(g1), f(g2)∈H。
由于f是双射,存在g' = f^(-1)(f(g1)f(g2))∈G,使得f(g') = f(g1g2)。
因此有f(g') = f(g1)f(g2)。
由此可知g' = g1g2,即G和H具有相同的封闭性。
综上所述,如果存在同构映射f: G→H,则G和H具有相同的群性质。
2. 设G是一个有限群,证明:G的任意子群的阶数必整除G的阶数。
证明:设H是G的一个子群,记|G|为G的阶数,|H|为H的阶数。
《量子化学与群论》课程第七、八两章作业题-09修[1]
![《量子化学与群论》课程第七、八两章作业题-09修[1]](https://img.taocdn.com/s3/m/4b4fbda2eefdc8d377ee3207.png)
第七-八章 群论基础及初步应用7-1 假定2-4CuCl 原来属于d T 点群,四个Cl 原子的标号见7-2题图()a 。
当出现以下情况时,它所属的点群如何变化: (1)(1)Cu-Cl 键长缩短, (2)键长(1)Cu-Cl 和键长(2)Cu-Cl 缩短同样的长度, (3)键长(1)Cu-Cl 和(2)Cu-Cl 缩短不同长度, (4)(1)(2)Cl -Cl 距离缩短,(5)(1)(2)Cl -Cl 和(3)(4)Cl -Cl 间距离缩短相同长度。
(徐光宪《量子化学》上册 P 383 19) 7-2 一个正立方体,如果把互相错开的顶角都锯掉同样的一个小正三棱锥体,得到的多面体属哪个点群?如果在它的每个面上如图()b 所示刻上沟槽,它将属于哪个点群?如果这些沟槽都以表面的外向法线为轴旋转θ角(04)θπ<<,将得到哪个点群?如果045θ=呢? (徐光宪《量子化学》上册 P 383 20)()a 24CuCl -()b 立方体7-3 对4h D 群,计算下列直积,并将其约化成不可约表示1g g A E ⨯ 11g u B B ⨯ g u E E ⨯ (厦大P141 题6-11)7-4 5PCl 分子属3h D 点群,将P Cl -形成的5个σ键的可约表示约化成不可约表示。
(厦大P141 题6-13)7-5 环己三烯 为2h D 点群,试写出π电子z p 轨道形成的可约表示,并将其约化成不可约表示。
(厦大P141 题6-15)8-1 作出4MnO -中氧原子轨道的对称性匹配的线性组合。
(徐光宪《量子化学》上册 P 503 39)8-2 甲烷分子属于点群d T ,不可约表示维数3≤,当以4个H 原子上的1s 轨函:1,1,1,1A B C D s s s s 为基时,所得群表示必是可约的,试通过计算特征标,确认哪些不可约表示会出现。
(江元生《结构化学》P 125 15)8-3 苯分子属于点群6h D ,但对6个H 上的1s 轨函的分类,只需用子群6D ,(1)试根据点群6D ,给出以6个1s 轨函为基的群表示的约化结果; (2)对6个C 原子的2s 轨函,群表示的约化结果是否相似; (3)若认为6个C-H 键是这两组轨道组合成的,试给出对应的能级图。
群论在化学中的应用习题集
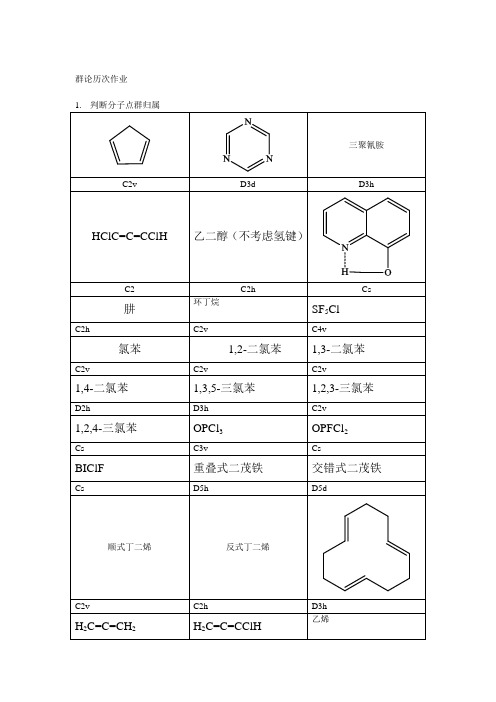
群论历次作业
假定CuCl42-原来属于T d点群,四个Cl原子的标号如图所示,当
出现以下情况是,它所属的点群如何变化:
1 Cu—Cl(1)键长缩短;
2键长Cu—Cl(1)和Cu—Cl(2)缩短相同长度;
3键长Cu—Cl(1)和Cu—Cl(2)缩短不同长度;
4 Cl(1)—Cl(2)和Cl(3)—Cl(4)间距离缩短不同的长度;
5 Cl(1)—Cl(2)和Cl(3)—Cl(4)间距离缩短相同的长度。
操作矩阵方面
1.物体绕原点与(X 0,Y 0,Z 0)的直线旋转θ角,求D(ˆR
(θ))=? 答:可以吧绕任意轴的旋转分解为绕x ,y ,z 轴分别旋转α,β,γ角的乘积。
=
2. 证明:同一类操作矩阵的特征标相等。
提示:1若R 和R ’是同类操作矩阵,则操作R 可由操作R ’经相似变换得到
(R=S -1R’S )
2 Trace (AB )=Trace (BA )
群的定义方面
1.判断下列集合是否够成群
(1) {除零以外的全部有理数}结合规则是乘法 是 (2) {1,0,-1 },结合规则是加法 否 (3) {1,0,-1 },结合规则是乘法 否 (4) {1,-1,i ,-i},结合规则是乘法 是
广义正交定理方面
cos sin 0cos 0sin 100sin cos 00100cos sin 001sin 0cos 0sin cos ααββααγγββγγ--⎛⎫⎛⎫⎛⎫ ⎪⎪⎪- ⎪⎪⎪ ⎪⎪⎪-⎝⎭⎝⎭⎝⎭。
群论在化学中的应用

17.01.2020
5
2. Molecular chirality (分子手性)
A chiral molecule (手性分子) is a molecule that is distinguished from its mirror image in the same way that left and right hands are distinguishable
xz
B2 1 1 1 1 y,Rx
yz
用Mulliken记号,对称类型用大写字母表示(见表),而轨
17.01.2020
13
3-2 特征标表在判断轨道对称性中的应用
以H2S分子为例,分析特征标与分子轨道的对称性。 H2S分 子属于C2v点群,其特征标表表示如下。
C2v Eˆ Cˆ2(z) sˆXZ sˆYZ
A1 1 1
11
z x2,y2,z2
A2 1 1 1 1 Rz
xy
B1 1 1 1 1 x,Ry
17.01.2020
群的不可约表示的特征标,它 具体说明右边列出的表示的基 向量的变换方式。
9
A. 群的不可约表示的Mulliken符号
a. 一维不可约表示 A或B
二维不可约表示 E (不是恒等操作!) 三维不可约表示 T (用于电子问题)
或 F(用于振动问题) 四维不可约表示 G 五维不可约表示 H b. 同为一维不可约表示时
17.01.2020
3
Exercises: Which of the following molecules are polar?
17.01.2020
4
第一章 分子的对称性
二、分子的对称性和旋光性 旋光性的判据:
群论第五章

k
= 4Ν (σ1 + σ 2 + σ 3 )
归一化后:1( A1) = φ ' 再求E’的基:
φ2 ( E ' ) = Ν ∑ x j ( Rk ) Rk σ1
1 3
(σ1 + σ 2 + σ 3 )
= Ν(2⋅σ1 +(−1)⋅σ2 +(−1)⋅σ3 +0⋅σ1 +0⋅σ3 +0⋅σ2 +2⋅σ1 +(−1)⋅σ2 +(−1)⋅σ3 +0⋅σ1 +0⋅σ3 +0⋅σ2)
z = r cos φ
b、对p、d的下标x、y、z等怎么来的,就与其表示有关,即: sin 在r不变的情况下, θ cos φ 和 cos φ。必与y和z有位同的变换操 作,所以p下面加上x、y、z。 同样对d轨道下标: 3cos 2θ − 1 = 2 cos 2 θ − sin 2 θ
(x / r ) 2 = sin 2 θ cos 2 φ
第三章 群论的应用(A)

O 原子的轨道 2s 2pz 2px 2py
H 原子的轨道 -1
(2) 2 (1sa +1sb )
—
-1
(2) 2 (1sa 1sb )
分子轨道 1a1,2a1,3a1
1b1 1b2, 2b2
分子的能级图概括于图3.1.2所示
图3.1.2 H2O 分子能级图概况
由图可见,有两个成键轨道(1a1和1b2),两个实际上是非键轨道(2a1 和1b1)。这四个轨道均填满电子,其基态的电子组态为
+1sb
1sc
1sd
)
3.1.15
方程3.1.11+3.1.13=
1 2
(1sa
1sb
+1sc
1sd
)
3.1.16
方程3.1.11+3.1.14=
1 2
(1sa
1sb
1sc
+1sd
)
3.1.17
由方程3.1.11到3.1.14组合得到具有T2对称性的三者组合可以 有许多途径,这里选择的一种是由方程3.1.15到3.1.17分别和C 原子的2pz,2px和2py轨道有效的叠加的函数,如图3.1.7所示。
=4(1sa +1sb +1sc ) (3)1/2 (1sa +1sb +1sc ) (归一化之后)
3.1.5
PE' (1sa )=2(1sa ) 1(1sb +1sc )+2(1sa ) 1(1sb +1sc )
=4(1sa ) 2(1sb +1sc )
(6)1/2[2(1sa ) 1sb 1sc ] (归一化之后)
对于具有oh对称性的八面体羰基配合物mco6则为由于羰基配合物的结构和co伸缩振动谱带的数目间有着直接的联系当用群论方法对每个可能的结构计算出羰基配合物中co伸缩谱带的数目并和它们的光谱进行比较通常可以直接推断在配合物中co基团的排列
群论.期末考试及参考答案

群论.期末考试及参考答案对称元素,象转轴⼀、指出下列分⼦的对称元素及基于这些对称元素的所有对称操作ONCl, H2O, NH3, CFClBrI1. ONCl {E, σ}2. H2O {E, C2 σv σv’}3. NH3 {E, C3 C32 σv σV’’}4. 具有畸变的四⾯体结构 {E}⼆、任何⼀个集合,如果按照某⼀个乘法的定义,满⾜如下的四个性质,就是⼀个群。
1。
封闭性2。
结合律3。
单位元素4。
逆元素三、⽤对称元素和他们的某种组合的符号,熊⾥夫符号1、只有⼀个n 次对称轴的分⼦为Cn, 如C1, C2, C3, 如果是直线型异核分⼦,有n 为⽆穷⼤,⽽且有任意多的通过主轴的对称⾯,所以叫做2、有⼀个最⾼n 次轴,⽽且有N 个经过主轴的对称⾯,这样的Cnv, 如果是没有2次以上的转动轴,只有⼀个对称⾯的,如ONCl ,则是C1v,C1h 或Cs3、⼀个分⼦除了有Cn 以外,还有n 个垂直于主轴的C2轴,是Dn4、如果除此之外,分⼦中还有σh ,所以也有Cn σh=Sn 轴,分⼦点群为Dnh5、同核双原⼦分⼦或具有对称中⼼的直线形多原⼦分⼦,为具有⽆穷多的C2和σv ⾯6 、如果在含有Cn 轴和n 个C2轴的分⼦中,具有n 个包含Cn 轴并且平分相邻两个C2轴的平⾯叫做σd 平⾯,这样的点群是DndE C S C C S C C S σC S n E C S C C S C C S C C C C S C C C C S C σσC S n E C EC C C C C C C C S i C C S n C S n h h h h h h h h h h h h h h h h h h h h h h h h h h h====================================444443433434222424446636323553533443433333332323223332333322222222222222224 32 1σσσσσσσσσσσσσσσσσσσσσσσσσσ7、构型为正四⾯体的分⼦Td, 对称元素为与x,y,z轴重合的3个C2,3个S4, 4个化学键⽅向的C3, 6个σd8、构型AB6的分⼦Oh,四、判断下列分⼦有没有偶极距H2O, CO2, SO3和PH3有没有没有有五、从分⼦的⾓度看,有旋光活性的充分必要条件是看分⼦不能与他的镜像重合.如果这个条满⾜,那么分⼦以两种形式存在,并且具有相等⽽⽅向相反的旋光活性.这两种分⼦叫做对映异构体。
结构化学:第四章 分子对称性和群论基础 (3)

1.对称操作和对称元素 2.对称操作群及对称元素的组合 3.分子的点群 4.分子的偶极矩和极化率 5.分子的手性和旋光性 6.群的表示
4.4. 分子的偶极矩和极化率
Dipole Moment: µ = qr
r
q
-q
分子的对称性可以判断偶极矩是否存在。
1. 只有分子的电荷中心不重合,才有偶极矩。 2. 偶极矩方向是由正电中心指向负电中心。
矢量表达式:
µx α xx α xy α xz Ex
µ y = α yx α yy α yz Ey
µz
α
zx
α zy
α zz Ez
极化率的计算-由折光率算极化率
α
=
3ε 0 (n2
N A(n2
−1)M + 2)d
293K时水n=1.3330;ε0=8.854×10-12J-1·C2·m2
分子的对称性
分子有无偶极矩
分子偶极矩的大小
分子的结构性质
分子的偶极矩和分子结构
例如:Pauling 用µ/er值作为键的离子性的判据
分子 CO
µ/(1030C·m)
0.39
r/(10-10m) 1.1283
µ/er 0.02
强共价键
共 离 HF
价 子 HCl 性性 增 减 HBr
强 弱 HI
6.37
但是,现代科学中一直有一个未解之谜:为什么组成我们机体的重 要物质——蛋白质都是由L-氨基酸构成?而构成核糖核酸的糖又都是D 型?大自然这种倾向性选择的根源何在——它是纯粹的偶然因素还是有 着更深刻的原因?
许多科学家都关注着自然界这一类对称性破缺. 1937年,Jahn与 Teller指出,非线型分子不能稳定地处于电子简并态,分子会通过降低 对称性的畸变解除这种简并. 例如,MnF3中Mn3+周围虽然有6个F-配位 ,却不是标准的正八面体,而是形成键长为0.179、0.191、0.209 nm的3 种Mn-F键. 在线型分子中,类似地也有Renner-Teller效应. 1956年,李政 道、杨振宁提出弱相互作用下宇称不守恒假说,同年由吴健雄等证实. 到了21世纪, 物理学提出了五大理论难题,其中之一就是对称性破缺问题.
群论与化学

I 2 S1 s I 3 S 6 C3 i
I 4 S4 I 5 S10 C5 i
S 2 I1 i S3 I 6 C3 s
S4 I 4 S5 I10 C5 s
应—— 环烯烃开环成多烯烃的一类反应。例如:
电环化反应的成键过程取决于反应物中开链异构物的HOMO轨道的对称性。
31
(1)含4n个π电子体系的化时,起反应的前线轨道HOMO是ψ 2, 环化时,顺旋 允许,对旋禁阻。在激发态(光照)环化时,起反应的前线轨道HOMO是ψ3 , 对旋允许,顺旋是禁阻的 其他含有π电子数为4n的共轭多烯烃体系的电环化反应的方式也基本相同
4. 对称操作的代数
多个对称操作的结合本身就是一个对称操作。PQ=R
逆运算 PQ=R, PQR-1=RR-1=E
E, Cn, s, Sn, i 的逆操作分别为E, Cn-1,s, Sn-1, i.
28
四、偶极矩和旋光性的判别
1.偶极矩 若分子中只要有两个对称元素仅仅相交于一点时,则分子就不存在偶极矩。
s,sh,sv, sd ,s2=E
C 4C 2C 43
sh
sd
19
?Question:此处sv是否sd?
20
4. 旋转反映 绕轴转2π/ n,接着被垂直于该轴的平面反映(反之亦可) 非真轴Sn
?Question:一个转动5x2p/3 (或2x2p/3)后反映是
S32 吗?
S 35 C 35s h C 32s h
六、特征标表和构造
第八章 群的表示与量子力学
一、Schrödinger方程 二、群的直积表示 三、零积分
4
量子化学与群论习题

量子化学与群论习题1. 证明xP ˆ为厄米算符. 2. 验证xx P x x P ˆˆˆˆ≠. 3. 证明x P ˆ和yP ˆ可对易. 4. 试求在一维无限深势阱中运动的电子在基态时的.,,,,,,22x x x x P x x P P x P x ∆∆∆∆5. 证明在一维深势阱中运动的质点的不同波函数互相正交. (证明)0*=⎰dx m n ψψ 6. 函数ax aaxax ππψ2sin23sin22)(⋅-⋅=是否是一维势箱中粒子的一种可能状态?若是,其能量有无确定值?若有,其值为多少?若无,求其平均值.7. 用变分函数2x xL -=ψ, 求一维势箱中(0;0)(,0≤=<<x x V L x 或∞=≥)(,x V L x )粒子的基态能级. 8. 假定rc e r c c 3)1(21-+=ψ是氢原子Schrödinger 方程的一个解,求出.,,,321E c c c9. 推导2222222zyx∂∂+∂∂+∂∂=∇在球坐标系和柱坐标系中的表达式.10. 设2crAe -=ψ为氢原子1s 态波函数的试探函数,计算归一化常数A , 确定变分参数c 及能级E .11. 对一维势箱中的粒子用变分法求解. 在11<<-x 时,;0=V 其他情况下,.∞=V 设,1,14221x x -=-=φφ构造试探函数,2211φφψc c +=求2221121122211211,,,,,,,S S S S H H H H 以及能级.,21E E12. 假定氢原子的1s 波函数的特解为,rNeαψ-=用待定系数法求.,,1N E s α13. 一粒子在有一个小势坑的一维盒中运动,;,0,L x x V ≥≤∞=;2/0,L x b V <<-= .2/,0L x L V <≤= 将势坑视为一个“规则的”刚性盒)0,0;,0,(L x V L x x V <<=≥≤∞=的一个微扰, 求出基态的第一级能级.EV =0 x =0 2/L x = x =L 0 x14. 若粒子从左边入射,求上图所示一维阶梯势(E >V 0)的反射系数和透射系数. 15. 上题这若4/30E V =, 计算在0=x 处被反射的粒子的几率(反射系数为多少). 16. 设G 一切不等于零的有理数集合, 证明G 对于数的乘法构成一个群.17. 设}1,0,1{-=G ,对于加法是否构成一个群?对于乘法是否构成一个群?为什么? 18. 构造C 2V 点群的乘法表.19. 验证点群},,,{342444C C C E C =和α},,1,1{i i U --=及β},,,{→←↓↑=V 同构. (α为数的乘法, β为动作,↑ 立正, ↓ 向后转, ← 向左转, →向右转) 20. 将下列C 3V 的可约表示Г分解为不可约表示.21. 将下列C 2V 的可约表示Г分解为不可约表示.22. 以CH 4分子中的4个氢原子的1s 轨道为基, 求该可约表示的特征标表, 并将它分解为不可约表示.23. 将CH 4分子中的4个氢原子的1s 轨道组合成为对称性匹配函数.24. 用对称操作的表示矩阵证明)(ˆˆˆ:));(ˆ)(ˆ)(ˆ:);ˆˆ)(ˆ:)22222z C c z C y C x C b i z C a xz yz xy ===σσσ. 25. 求反式二氯乙烯分子中以2个氢原子的1s 轨道为基的表示的特征标, 并将其分解为不可约表示.26. 写出下列点群以(x ,y ,z )为基的表示矩阵.:);:);:);:)424d h h T d D c D b C a 27. 氢原子处于基态时, 1s 波函数为0/231)1(1a r s ea -=πψ,求1)r 平均值r ; 2)位能reV 2-=的平均值; 3)动能的平均值T .。
群论考试试题及答案

1、 一个集合构成群必须具备哪四个要素?什么是群的子群,陪集群和类。
本题书上可找到,略。
2、 试写出平面正三角形对称群即二面体群D3群的所有群元。
类分割和所含的所有子群,并且用其中一个子群写出D3群的左右陪集分割串。
解:D3={E,A,B,C,D,F} 其中,E :恒等操作 A :绕轴1旋转pai B :绕轴2旋转pai C :绕轴3旋转pai D :绕Z 轴旋转2pai/3 F :绕Z 轴放置4pai/3子群:{E}、{E ,A}、{E ,B}、{E ,C}、{E ,D ,F}、{E ,A ,B ,C ,D ,F} 类:{E}、{A ,B ,C}、{D ,F} 取H1={E ,A},则DH1={D ,C},FH1={F ,B},故左陪集分割串为:{D ,C}、{F ,B} H1D={D ,B},H1F={F ,C},故右陪集分割串为:{D ,B}、{F ,C}3、 证明所有实数在数的加法运算下构成的群与所有正实数在数的乘法运算下构成的群同构。
首先,设所有实数S 的集合为G ,于是,集合对元素的加法运算是封闭的,数的加法满足结合律,实数0是此集合的恒元,-S 仍是实数,它是S 的逆元,因此,集合G 构成群,称为实数加法群;其次,设所有正实数R 的集合为H ,于是,集合对元素的乘积是封闭性的,数的乘积满足结合律,正实数1是此集合的恒元,R 的倒数1/R 仍为正实数,它是R 的逆元,因此,集合H 构成群,称为正实数乘法群;最后,通过指数函数建立群H 与G 的元素一一对应关系,且这种关系对元素的乘积保持不变。
R=e S R ’=e S ’ RR ’=e S+S ’因此,群H 与G 同构。
4、 证明由满足232()A B AB E ===的A,B 二元素生成的一个群,并写出其乘法表。
本题,老师课件上有原题,略。
5、 简述什么是群表示,等价表示和不可约表示。
教材中有原述,略。
6、 写出3阶置换群S3的所有群元,将每个群元写成相邻数码对换的乘积形式,并求出S3的所有共轭类所包含的元素(即S3的类分割)。
第8章 群论参考答案

第8章群论习题解答提示1. 仅平凡群{e}有零元,独异点(单位半群)的幂等元不一定惟一,但群的幂等元惟一。
3. (P170) 由于变换(映射)的复合运算ο是可以结合的,恒等变换I=f1,0∈G,显然I为G 单位元。
下面只证明复合运算ο在G上是封闭的,且G中每个元素有单位元。
事实上,a,b,c,d∈Q,且a,c≠0,对于x∈Q,有(fab οfcd)(x)=fab(fcd(x))=a(cx+d)+b=acx+(ad+b),又ac≠0,ac,ad+b∈Q,故=fac,ad+b∈G,所以,复合运算在G上是封闭的。
f a,b∈G,a≠0,a,b∈Q,取f1/a,-b/a∈G,有fa,b οf1/a,-b/a=fa(1/a),a(-b/a)+b=f1,0所以,fab存在逆元f。
综上,G关于变换的复合运算ο构成群。
4. 设<S;*>是单位半群,e是单位元,H是S中所有可逆元素的集合。
显然单位元e是可逆元,所以e∈H,H非空。
若a,b∈H,则存在a-1,b-1∈S,使得a-1*a=a*a-1=e,b-1*b=b*b-1=e,于是,(b-1*a-1)*(a*b)=(a*b)*(b-1*a-1)=e,因此a*b也是可逆元,故a*b∈H,<H;*>是一代数结构。
因为H是S的子集,所以运算*在H上也是可结合的,e是<H;*>的单位元。
∀a∈H,必有a-1∈S,使得a-1*a=a*a-1=e,所以a是a-1的逆元,因此a-1∈H。
由上证得,<H;*>是一个群。
6. 在等式两边同时左乘x-1,有axba=bc,再在等式两边同时左乘a-1,右乘a-1b-1,有x=a-1bca-1b-1故方程存在解。
再证惟一性。
若方程存在两解,设为x,y,即有axba=bc=ayba,由于G是群,满足消去律,有x=y。
故解是惟一的。
7. 必要性显然。
下面证明充分性。
设|G|=n,G={a1,a2,…,an}。
化学中的群论-1

D
C
AB
A
A
C
B
E
FD
B
B
A
C
D
EF
C
C
B
A
F
DE
找出子群:{E,A} , {E,D,F}的左右陪集,并判 断此子群是否正规子群。
子群{E,A}的左陪集有两个:{D,B}和{F,C},右陪集也有两个: {D,C}。左右陪集不对应相等,因此,此子群不是不变子群。 另一个子群{E,D,F} 是不变子群,陪集是{A,B,C}
3.{立定,向左转,向后转,向右转}对于连续动作构成四阶群。 单位元:立定 逆元:立定↔立定 向左转↔ 向右转 向后转↔向后转 封闭性:满足 结合律:满足
4.所有n维空间Rn中的向量X=(x1,x2,…,xn)的集合对于向量的加法构成群。 恒元:零向量 逆元:a=(a1,a2,…an) ↔-a=(-a1,-a2,…,-an) 封闭性:满足 结合律:满足
abc aabc bbca ccab
3.证明下列四个方阵A、B、C、D对于矩阵的乘法 构成一个群V:
A 1 01 0 ,B 1 0 0 1 ,C 0 11 0 ,D 0 1 0 1
写出V的乘法表。V是否循环群?V是否Abel群?
循环群的乘法表:当表中元素按生成元的幂次排列时,表 的每一行都可由前一行向左移动一格得到,而最左面的元 素移到最右面去。
例 G={E=R4,R,R2,R3}, R1~4分别表示在一平面内绕一点顺时针 旋转π/4~π的操作。其乘法表如下
E R R2 R3 E E R R2 R3 R R R2 R3 E R2 R2 R3 E R R3 R3 E R R2
3.集合中存在恒元E(单位元),用它左乘集合中的任意元素,
北师大 结构化学 第4章 分子对称性和群论

北师大 结构化学 课后习题第4章 分子对称性和群论习题与思考题解析1. 以H 2O 为例说明对称操作和对称元素的含义。
解:H 2O 分子为V 型结构,若将该分子经过O 原子且平分H-O-H 键角的直线旋转1800便可得到其等价图形,该直线称为对称元素-对称轴,其轴次为2,即为二重轴,用2C 表示。
绕2C 轴的对称操作叫旋转,用2ˆC 表示。
2. 写出HCN ,CO 2,H 2O 2,CH 2==CH 2和C 6H 6分子的对称元素,并指出所属对称元素系。
答:HCN 分子的对称元素:1个C ∞轴、∞个v σ面,属于'v C ∞对称元素系。
CO 2分子的对称元素:1个C ∞轴、∞个2C 轴、1个h σ、∞个v σ面和i 对称中心;属于'h D ∞对称元素系。
H 2O 2分子的对称元素:只有1个2C 轴,属于'2C 对称元素系。
CH 2==CH 2分子的对称元素:3个相互垂直的2C 轴、3个对称面(1个h σ、2个v σ),对称中心i ;属于'2h D 对称元素系。
C 6H 6分子的对称元素:1个6C 轴、6个垂直于6C 轴的2C 轴、1个h σ面、6个v σ面、和对称中心i ,属于'6hD 对称元素系。
3. 试证明某图形若兼有2C 轴和与它垂直的h σ对称面,则必定存在对称中心i 。
证明:假设该图形的2C 轴与z 轴重合,则与它垂直的h σ对称面为xy 平面。
则对称元素2()C z 和()h xy σ对应的对称操作2ˆˆ(),()h C z xy σ的矩阵表示为: 2100ˆ()010001C z -=- 和 100ˆ()010001h xy σ=- 则 210010100ˆˆˆ()()010010010010011h C z xy i σ--=-=-=--由此得证。
4. 写出xy σ和通过原点并与x 轴重合的2()C x 轴的对称操作的表示矩阵。
解:空间有一点(x , y , z ),经过对称面xy σ作用后得到点(x , y , -z ),经过2()C x 对称轴作用后得到点(x , -y , -z ),所以xy σ和2()C x 对应对称操作2ˆˆ,()xy C x σ的矩阵为: 100ˆ010001xy σ=- 和 21ˆ010001C =-- 5. 用对称操作的表示矩阵证明:(1) 2ˆˆˆ()xy C z i σ= (2) 222ˆˆˆ()()()C x C y C z = (3) 2ˆˆˆ()yz xz C z σσ= 证明:(1) 因为对称操作2ˆˆ(),xy C z σ的矩阵为: 21ˆ()010001C z -=- 和 10ˆ010001xy σ=- 所以210010100ˆˆˆ()010010010010011xy C z i σ--=-=-=--,由此得证。
第六章 群论

所以,三个对称面等价。
7
量子化学
3 对称点群
分子点群:对称操作的完全集合构成的群——对称点群。 例1: G = {v, v2 = E} 逆元素 v-1 = v 例2: G = {E, C2, v(1), v(2)} H2O: C2V 点群 FONO: Cs 点群
单位元: E; 封闭性. v v = v2 = E, vE = v
1+2=3 1 + 2 + 3 = ( 1 + 2 ) + 3 = 1+ ( 2 + 3 ) = 6
满足封闭性 满足结合律 0是单位元素 n有逆元素-n
0+3=3+0=3
n + ( -n ) = 0
乘法表
由于所有对称元素 都经过一个共同点, 因此把这种群称为 点群
2
量子化学
2 群的乘法表 a. 重排定理: 群的乘法表中每一行或每一列中每个元素都出现一 次,只是排列次序有所不同,这称为重排定理。 b. 构造乘法表
F F S F F
21
F F
量子化学
4 分子对称性的分类
c. Ih 群:正三角形二十面体或正五边 形十二面体的对称操作的 集合构成这个群。
22
量子化学
6.3 群的表示
1 群的表示矩阵
C2V 点群
选择x, y, z 为基 ——— 三维表示 在对称操作下,点的变换
23
量子化学
6.3 群的表示
1 群的表示矩阵
Sn仅当n为偶数时存在,对于n为 奇时恒等于Cnh群。
S4
1,3,5,7-四甲基环辛四稀
S2 = I
16
量子化学
4 分子对称性的分类
结构化学_第四章习题(周公度)_群论

10、联苯 C6H5—C6H5 有三种不同的构象,两苯环的二面角(a)分别为:a=0 (2) a=90o 种构想的点群 2
解:(1) a=0
两个苯环在一个平面内,联苯分子属于 D 2h 点群
(2) a=90o 两个苯环相互垂直,分子含有 1 个通过两个苯环相连的 C-C 键轴方向的 C2 轴,两个通过两个苯环二 面角 45o 方向的 C2 轴,2 个σ v,分子属于 D 2d 点群。 (3) 0< a <90o 分子含有 1 个通过两个苯环相连的 C-C 键轴方向的 C2 轴,分子属于 C2 点群。 11、SF5 分子的形状和 SF 6 相似,试指出它的点群 解 SF 5 分子为四方锥构型;SF6 分子为八面体构型。 SF 5 分子属于 C4v 点群,SF6 分子属于 O h 点群 12、画一立方体,在 8 个顶角上放 8 个相同的球,写明编号。若(1)去掉 2 个球,(2)去掉 3 个球。分别列表指出所 去掉的球的号数,指出剩余的球构成的图形属于什么点群
NO 2
Br
(6)
N
(7)
C CH3 Cl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
群论与化学复习题
1、确定下列分子所属的点群
(1) CH2ClF; (2) 丙二烯;(3)1,3,5—三氯代笨;
(4) 反—Pt(NH3)2Cl2 (看成正四边行, 忽略H) ; (5) 反—CoN4A2;
(6) 交错—C2H6; (7) 顺式--C2H4; (8) SF5Cl;
(9) N2F2; (10) O3;
2、写出C2v群的矩阵表示
C
C
Cl Cl H
H
3、考虑位于下图的SO2分子诸核上的基向量组(e3, e6, e9垂直于纸面),构造一个SO2所属点群的9维矩阵表示。
并求出C2v点群的每个不可约表示在该9维表示中出现的次数。
e4
4、根据广义正交定理及其推论,推导C2v群的特征标表。
、
5、试画出笛卡尔坐标系的原基矢( e1, e2, e3 )及其经过中心反演作用后的新基矢( e1’, e2’, e3’ ), 并求出相应的表示矩阵.
6、试画出笛卡尔坐标系的原基矢( e1, e2, e3 )及其经过非真转动S3 作用后的新基矢( e1’, e2’, e3’ ), 并求出相应的表示矩阵. ( 已知S3 = σ C3 , 其中C3 绕e1 轴转动, σ为垂直与该转轴的镜面)
7、将D3
χ5
3 1 0 8、试分别利用(和不利用)约化系数公式(a j = ∑g i χ*( C i ) χ ( C i ) / h ) 对 D 2d 群的六维表示 D 6 进行约化, 已知该六维表示 D 6 的特征标和群 D 2d 不可约表示
9、Γ1 、Γ2 和33v a b 3v 示
试将Γa 和Γb 10、请给出H 2O, NH 3和CH 4的全部对称元素,列出每个分子对易操作。
11、确定下列分子所属的点群
(a) CoN 6; (b) CoN 5A; (c) 顺-CoN 4A 2; (d) 反-CoN 4A 2; (e) 顺,顺-CoN 3A 3; (f) 反,顺-CoN 3A 3;
12、确定下列化合物的点群 (a) 椅式环己烷(不管H 原子); (b) 船式环己烷(不管H 原子); (c) 交错 C 2H 6; (d) 重叠 C 2H 6; (e) 交错与重叠之间的 C 2H 6。
13、确定下列点群
(a) 四方角锥; (b) 正圆锥; (c) 四方薄板; (d) 上边、下边涂不同色彩的四方薄板; (e) 正圆柱体;(f)两底面涂饰不同的圆柱体; (g)平行于轴的条纹彩色正圆柱体。
14、求出下列矩阵的逆矩阵
(a) a ib c id c id
a i
b ++⎡⎤
⎢
⎥-+-⎣⎦
; (b) 1000010000100001⎡⎤
⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦
; (c) 000000a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦
; (d) a b b a -⎡⎤⎢⎥⎣⎦; (e) 00i i -⎡⎤⎢⎥⎣⎦; (f) 231352002⎡⎤
⎢⎥⎢⎥⎢⎥⎣⎦
15、试证下列矩阵是正交矩阵
(a) ⎥⎥⎦
; (b) ⎤⎥
⎥; (c) cos sin sin cos θ
θθθ⎡⎤
⎢⎥-⎣⎦
16
、若1
022102200
2A ⎡⎤--
⎢⎥⎢⎥⎢⎥=-
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣
⎦
及1022102200
1Q ⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣
⎦
试证:Q -1AQ 是对角矩阵
17、对于 D 2h 点群:
(a) 用三个实数p 轨道作为基函数建立一个三维矩阵表示 (三个实p 轨道可以用笛卡尔坐标x 1, x 2, x 3 表示成 p 1 = F(r)x 1 p 2 = F(r)x 2
p 3 = F(r)x 3 )
(b) 用五个实数d 轨道作为基函数建立一个五维矩阵表示 (五个实数d 轨道:
22
112
()/2d x x =- 212d x x = 313d x x = 423d x x =
2
253(3)/d x r =-18、考虑平面三乙烯基基团具有七个π轨道的位置如下图所示:
2
3
用这些π轨道作为基函数,建立一个C 3点群的七维表示。
19、请写出NaCl 、CsCl 、ZnS 、ZnF 2和金刚石晶胞中原子的分数坐标。
20、请解释立方晶胞所属的点群
423h O m m
-
各符号所表示的意义。
