公开课《锐角三角函数复习》课件
合集下载
锐角三角函数复习课.ppt

(2)一个锐角的余弦值随着角度的增大而减小 。
5、解直角三角形必须要已知 两 个条件,且其中一个条件必
是边。
6、解直角三角形的应用:
(1)在测量时,视线与水平线所成的角中,规定:视线在水平线 上方的角叫做 仰 角,视线在水平线下方的角叫做 俯 角。
(2)坡面的铅重高度(h)与水平长度(L)的比叫做 坡度 ,用字
母
i
表示,即i=
h L
。坡面与水平面的夹角叫做 坡 角,坡
角越大,坡度就越大,坡面就越 陡 。
达标检测
1、在Rt△ABC中,∠C=90°,sinA= 12,则∠B= 60°
3
4
2、在Rt△ABC中,∠C=90°,tanA=
3 4
,则sinA=
5 ,cosA= 5 。
3、已知α为锐角,且cosα=0.8,则锐角α的大致范围是( A ) A、45°<α<60° B、α>30° C、30°<α<45° D、α>45°
(1)互为余角的三角函数关系: ①sin(90°-A)= cosA ②cos(90°-A)= sinA
(2)同角的锐角三角函数关系:
① sin2 A cos2 A 1
③ tanAtanB= 1
② tan A sin A
cos A
4、三角函数的增减性:
(1)一个锐角的正弦、正切值随着角度的增大而增大 。
答:A、B两点的距离是100( 3 +1)米。
学习目标
1、理解锐角三角函数的定义,掌握特殊锐 角的三角函数值,并进行计算;
2、掌握直角三角形三边之间的关系,会解 直角三角形;
3、运用解直角三角形的知识解决简单的实 际问题。
《锐角三角函数》PPT教学课件(第1课时)

BC AC
= 12 =
AC
34,所以AC=9.故填9.
随堂训练
AB 6.如图,在Rt△ABC中,∠C=90°,BC
17 15
,则tan
15 A=_8__.
由正切定义可知tan A=BACC , 因为 AB 17 , 可设BC=15a,AB=17a,从而可
BC 15
用勾股定理表示出第三边AC=8a,再用正切的定义求解得 tan A= BC 15 .
由勾股定理可得 AB= BC2 AC2 122 162 =20.
∴AB的长为20.
课堂小结
1.正切的定义: 如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻
边的比便随之确定,这个比叫做 ∠A的正切,记作tan A, 即tan A= A的对边
A的邻边
2.tanA的值越大,梯子(坡)越陡
图①
图②
新课导入
问题引入
如图所示,轮船在A处时,灯塔B位于它 的北偏东35°的方向上.轮船向东航行5 km 到达C处时,轮船位于灯塔的正南方,此时轮 船距灯塔多少千米?(结果保留两位小数)
该实际问题中的已知和所求为图中的哪些角和线段?
(事实上,求轮船距灯塔的距离,就是在Rt△ABC中,已知 ∠C=90°,∠BAC=55°,AC=5 km,求BC长度的问题)
C,C'.
BC AC
与BACC
具有怎样的关系?
在两个直角三角形中,当一对锐角相等
时,这两个直角三角形相似,从而两条对应直
角边的比相等,即当∠A(小于90°)确定时,以 ∠A为锐角的Rt△ABC的两条直角边的比 BC
AC
是确定的.
知识讲解
1.正切的定义
如图所示,在Rt△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫
《锐角三角函数》课件

锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
锐角三角函数复习课课件

90度角
总结词
正弦值和余弦值不存在,正切值为无穷大
详细描述
在90度角时,正弦函数值和余弦函数值都不存在,因为无法定义与x轴的角度;正切函数值为无穷大 ,因为在直角三角形中,对边长度可以无限小而保持与斜边的比值不变。
03
锐角三角函数的图像与性质
正弦函数图像
总结词
正弦函数图像是一个周期函数,其图像在直角坐标系中呈波 浪形。
用三角函数来处理角度和旋转。
05
常见题型解析与解题技巧
选择题
• 题型特点:选择题通常考察学生对锐角三角函数基础知识的理 解和应用,题目会给出一些具体的数值或图形,要求选择正确 的答案。
选择题
排除法
根据题目给出的选项,逐一排除明显 错误的答案,缩小选择范围。
代入法
对于涉及数值计算的题目,可以将选 项中的数值代入题目中,通过计算验 证答案的正确性。
在研究磁场和电场时,我们经常需要使用锐 角三角函数来描述场的方向和强度。
日常生活中的问题
建筑和设计
在建筑设计、工程规划和土木工程中,锐角 三角函数用于计算角度、高度和距离等参数 ,以确保结构的稳定性和安全性。
游戏和娱乐
在许多游戏和娱乐活动中,锐角三角函数也 起着重要作用。例如,在制作动画、设计游 戏关卡或创建虚拟现实环境时,我们需要使
总结词
正弦值为0,余弦值和正切值不存在
详细描述
在0度角时,正弦函数值为0,表示射线与x轴重合;余弦函数值不存在,因为无 法定义与x轴的角度;正切函数值也不存在,因为没有对边形成直角三角形。
30度角
总结词
正弦值为0.5,余弦值为0.866,正切值为1/3
详细描述
在30度角时,正弦函数值为0.5,表示对边长度为斜边长度的一半;余弦函数值 为0.866,表示邻边长度为斜边长度的一半的平方根;正切函数值为1/3,表示对 边长度与邻边长度的比值。
第16讲锐角三角函数复习课件(共42张PPT)

解:原式= 3+ 2× 22+ 3--3-2 3+1= 3+1+ 3 +3-2 3+1=5.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
4.在△ABC 中,若|cos A-12|+(1-tan B)2=0,则∠C 的
度数是
(C )
A.45°
B.60°
C.75°
D.105°
5.式子 2cos 30°-tan 45°- (1-tan 60°)2的值是
∵CE=EF,∴CAEC=
m= 5m
55,
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
∴tan∠CAE= 55. 解法二:∴在 Rt△ABC 中,
tan
B=ABCC=
2m = 5m
2, 5
在 Rt△EFB 中,EF=BF·tan B=2m,∴CE=EF=2m,
5
5
2m
∴在 Rt△ACE 中,tan∠CAE=CAEC=2m5= 55,
∴tan∠CAE= 55.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
7.如图5-16-4,在Rt△ABC中, ∠C=90°,∠A=30°,E为线段AB上 一点且AE∶EB=4∶1,EF⊥AC于F, 连结FB,则tan∠CFB的值等于 ( C )
3 A. 3
53 C. 3
23 B. 3 D.5 3
大师导航 归类探究 自主招生交流平台 思维训练
第五章 解直角三角形
第16讲 锐角三角函数
全效优等生
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
月球有多远? 如图,如果从地球上A点看, 月球S刚好在地平线上(即AS和地 球半径OA垂直),而同时从地球上B点看,S刚好在天顶处(即S 在地球半径OB的延长线上),那么∠S就叫做月球S的地平视 差,根据一个天体的地平视差,可以算出这个天体的距离. ∠S可以从∠AOB算出,而∠AOB可以从地球上A,B两点 的经纬度算出. 月球S的地平视差(∠S),就是从月球S看来,垂直于视线 (SA)的地球半径(OA)所对的角.
公开课锐角三角函数复习课件ppt

一.锐角三角函数的概念
ca
正弦:把锐角A的_对__边__与__斜__边_的比叫做∠A
的正弦,记作 sin A a
c
A bC
余弦:把锐角A的_邻__边__与__斜__边_的比叫做∠A的 余弦,记作 cos A b
c
正切:把锐角A的_对__边__与__邻__边_的比叫做∠A的 正切,记作 tan A a
思考:若∠A+∠B=900,那么: sinA = cosB cosA = sinB
在 整堂课 的教学 中,刘 教师总 是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
☆ 应用练习
一.已知角,求值 (1)tan45°-sin60°cos30° (2)2sin30°+3tan30°+tan45° (3)cos245°+ tan60°cos30° (4)2sin60°-3tan30°-(π-cos30°)+(-1)2012
一试. tan22.5 °= 2 1
A
D
D′
B
C
在 整堂课 的教学 中,刘 教师总 是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
☆ 应用练习
三.比较大小
(1)sin250____sin430 (2)cos70____cos80 (3)sin400____cos600 (4)tan480____tan400
B
A
C
4.如图,在Rt△ABC中,∠C=90,b= 2 3 ,c=4.
则a= 2 ,∠B= 60°,∠A= 30°.
5.如果 coAs1+ 3taB n30
锐角三角函数说课稿市公开课一等奖省优质课获奖课件.pptx

注意:sinA不表示“sin”乘以“A”. 正弦常见写法有以下两种形式:
(1)sinA,sin42°,sinβ(省去角符号);
(2)sin∠DEF,sin∠1(不能省去角符号).
第4页
例题精讲 【例1】如图28-1-4,在Rt△ABC中,BC=8, AC=10. 求sinA和sinB值.
第5页
解析 依据正弦定义知sinA= ,sinB= . 因为AB未知,所以应先依据勾股定理求出AB.
(1)求证:DC=BC; (2)若AB=5,AC=4,求 tan∠DCE值.
第36页
第37页
第38页
第17页
锐角三角函数概念:锐角A正弦、余弦、正切都叫 做∠A锐角三角函数.三角函数实质是一个比值,这些 比值只与锐角大小相关,与直角三角形大小无关. 当 一个锐角值给定,它三个三角函数值就对应地确定了 ,另外,并非只有在直角三角形中才有锐角三角函数 值,而是只要有角就有三角函数值.
第18页
2. 各锐角三角函数之间关系: (1)互余关系:sinA=cos(90°-A), cosA= sin(90°-A). (2)平方关系:sin2A+cos2A=1. (3)弦切关系:tanA=
方法规律
第32页
第33页
7. (6分)在Rt△ABC中,∠C=90°,∠A,∠B ,∠C对边分别为a,b,c.已知2a=3b,求∠B三角函 数值.
第34页
第35页
8. (6分)如图KT28-1-2所表 示,△ABC内接于⊙O,AB是⊙O直 径,点D在⊙O上,过点C切线交AD 延长线于点E,且AE⊥CE,连接CD.
解析 作出图形如图28-1-10,可得AB=500 m,∠A=20°,在Rt△ABC中,利用三角函数即可求 得BC长度.
锐角三角函数的复习课.公开课课件

(1) sin2A+cos2A= 1
. 2 tanA
sinA cosA
四、锐角三角函数值的变化:
1.当A为锐角时,各三角函数值均为正数,
且 0 <sinA< 1 ; 0 <cosA< 1 。
当0°<A<90°时,sinA、tanA随角度的增大
而 增大 ,cosA随角度的增大而 减小 .
2.当0°<A<45°时, sinA< cosA, 当45°<A<90°时, sinA> cosA, 当 0°<A<90°时, sinA< tanA.
(填“>”“<”
自主测评
• 1.计算
•
• A. 2
2 sin45°的结果等于(B )
B.1 C. 2 D.1
2
2
• 2.在 △ABC中,已知∠C=90°,
• sinA= 4 ,则tanB的值是(B)
•
5
• A. 4 B. 3 C. 3 D. 4
3
4
5
5
自主测评
• 3.在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的 值是 (C)
位,已知 3 ≈1.732)
60°
A
Hale Waihona Puke C45°∟
D
B
【课堂练习】 一、基础训练
1.计算2sin30°-2cos60°+tan45°1=________.
2.在Rt△ABC中,∠C=90°, AB=5,
B
3
AC=3,则sinB=____5_.
A
C
3.在△ABC中,若BC= 2 ,AB= 7 , AC=3,A
(2)若要使超市采光不受影响,
两楼应相距多少米? (结果保留整数)
锐角三角函数总复习ppt课件.pptx

基础自主导学
1.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的 是( )
A.sin
A=
3 2
C.cos
B=
3 2
答案:D
B.tan A=12 D.tan B= 3
2.在正方形网格中,△ABC的位置如图,则cos B的值为( )
A.
1 2
C.
3 2
答案:B
B.
2 2
D.
┃ 知识归类
解直角三角形
1.三边关系:a2+b2=c2
2.三角关系:∠A=90°-∠B
a
3.边角关系:sinA=cosB= c
;
;
b
,cosA=sinB=c ,tanA
sinA
sinB
= cosA ,tanB= cosB
.
4.面积关系:sABC
1 2
ab
1 2
ch
(2)直角三角形可解的条件和解法
条件:解直角三角形时知道其中的2个元素(至少有一个是边), 就可以求出其余的3个未知元素.
[思路分析]设每层楼高为x m,由MC-CC′求出MC′的 长,进而表示出DC′与EC′的长,在直角三角形DC′A′中, 利用锐角三角函数定义表示出C′A′,同理表示出C′B′, 由 C′B′-C′A′求出 AB 的长即可.
解:设每层楼高为 x m, 由题意,得 MC′=MC-CC′=2.5-1.5=1(m). ∴DC′=5x+1,EC′=4x+1. 在Rt△DC′A′中,∠DA′C′=60°, ∴C′A′=tDanC6′0°= 33(5x+1).
1 2
,sin45°=
2 2
,sin60°=
3 2
公开课锐角三角函数复习课件

特殊角的三角函数值
• 0°、30°、45°、60°、90°等特殊角的三角函数值应熟练掌握, 包括sin、cos、tan、cot、sec、csc等函数。
02
锐角三角函数的图像与 性质
正弦函数的图像与性质
正弦函数的周期性和对称性
正弦函数是周期函数,具有轴对称性和中心对称性。
正弦函数的单调性
在每个周期内,正弦函数在一定区间内单调递增或递减。
正切函数的图像与性质
正切函数的定义域
正切函数只在直角三角形 中定义,表示对边与邻边 的比值。
正切函数的单调性
正切函数在每个区间内单 调递增,无周期性。
正切函数的值域
正切函数的值域为全体实 数,表示任意两个边的比 值。
三角函数图像的变换
平移变换
翻折变换
通过平移正弦、余弦、正切函数的图 像,可以得到其他三角函数图像。
根据数学模型,选择合适的三角 函数公式进行计算。
计算结果
根据选择的公式进行计算,得出 结果。
理解题意
首先需要仔细阅读题目,理解题 目的要求和所给条件,明确解题 的目标。
检验结果
最后需要对计算结果进行检验, 确保结果的正确性。经典Leabharlann 角三角函数综合题解析题型一
求角度问题
题型二
求边长问题
题型三
求面积问题
02
通过已知的边长和角度,利用三角函数可以求出其他边长或角
度,从而解决实际问题。
特殊角的三角函数值
03
对于一些特殊角,如30°、45°、60°等,其三角函数值是已知的
,这些值在解直角三角形时非常有用。
三角函数在实际问题中的应用
测量问题
在建筑、工程和地理测量等领域 ,经常需要使用三角函数来解决 实际问题,如计算距离、高度和
锐角三角函数复习.ppt
又BC-CD=BD
解得x=6
∴CD=6
A
B
C
D
例题解析
(2) BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中z x xk
问题2 要解一个直角三角形,除一个直角的已知元素外,还需要几个元素?为什么这些元素中至少要有一条边?试给出可以求解直角三角形的两个条件.
A
B
C
D
问题3 如果题中给出的图形不是直角三角形而是一个综合图形,我们用什么方法进行处理,就能把它转化为可以解的直角三角形?
问题4 你认为需要具备哪些知识、掌握哪些方法,就能较顺利地解决有关实际问题?请总结实际问题的一般步骤和注意点.
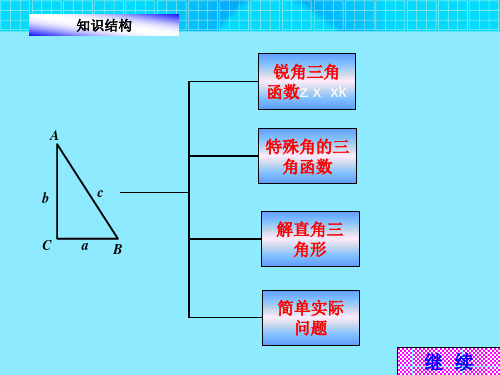
锐角三角 函数z x xk
特殊角的三 角函数
解直角三 角形
简单实际 问题
c
a
b
A
B
C
知识
特殊角的三 角函数
2
1
30°
1
1
45°
2
1
60°
30°+ 60°= 90°
返 回
解直角 三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数 关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
返 回
简单实 际问题
数学模型
直角三角形
等腰梯形
组合图形
等腰三角形
构建
解
作高转化为直角三角形
解
返 回
问题1 已知:如同,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=3,CD= ,怎样求sinA和cos∠BCD的值?怎样求∠B的正切值?
已知:如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求:(1)DC的长;(2)sinB的值.
解得x=6
∴CD=6
A
B
C
D
例题解析
(2) BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中z x xk
问题2 要解一个直角三角形,除一个直角的已知元素外,还需要几个元素?为什么这些元素中至少要有一条边?试给出可以求解直角三角形的两个条件.
A
B
C
D
问题3 如果题中给出的图形不是直角三角形而是一个综合图形,我们用什么方法进行处理,就能把它转化为可以解的直角三角形?
问题4 你认为需要具备哪些知识、掌握哪些方法,就能较顺利地解决有关实际问题?请总结实际问题的一般步骤和注意点.
锐角三角 函数z x xk
特殊角的三 角函数
解直角三 角形
简单实际 问题
c
a
b
A
B
C
知识
特殊角的三 角函数
2
1
30°
1
1
45°
2
1
60°
30°+ 60°= 90°
返 回
解直角 三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数 关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
返 回
简单实 际问题
数学模型
直角三角形
等腰梯形
组合图形
等腰三角形
构建
解
作高转化为直角三角形
解
返 回
问题1 已知:如同,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=3,CD= ,怎样求sinA和cos∠BCD的值?怎样求∠B的正切值?
已知:如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求:(1)DC的长;(2)sinB的值.
锐角三角函数复习课件公开课

锐角三角函数复习课件公 开课
欢迎来到锐角三角函数复习课件公开课! 在本课程中,我们将回顾锐角三角 函数的基本概念,常见公式,性质和图像,解三角方程,以及一些实际应用。
锐角三角函数的基本概念
锐角三角函数是用于描述锐角三角形中角度和边长之间关系的函数。包括正弦、余弦和正切等函 数。
1 正弦函数
描述角的对边与斜边之间的关系。
总结和回顾
在本课程中,我们回顾了锐角三角函数的基本概念、常见公式、性质和图像。学习了如何利用锐角三角 函数求解三角方程,并了解了一些实际应用。希望你已经对锐角三角函数有了更深入的理解!
锐角三角函数在直角三角形的图像中不断变化,并呈现出一些特殊的性质。
单位圆
单位圆是用于可视化锐角三角 函数图像和特殊性质的工具。
正弦函数
正弦函数是一条波浪形曲线, 用于描述周期性变化。
余弦函数
余弦函数是一条类似正弦函数 的波浪形曲线,但相位差90度。
利用锐角三角函数求解三角方程
锐角三角函数可以用于解决涉及三角函数的方程,从而求得角度的值。
2 余弦函数
描述角的邻边与斜边之间的关系。
3 正切函数
描述角的对边与邻边之间的关系。
常见的锐角三角函数公式
锐角三角函数有一些常见的公式用于计算和简化角度的计算。
倍角和半角公式
• 正弦和余弦的倍角和半角公式。 • 正切的双角和半角公式。
和差公式
• 正弦和余弦的和差公式。 • 正切的和差公式。
锐角三角函数的性质和图像
1
方程转化
将方程转化为以三角函数为未知数的
方程求解
2
方程。
利用三角函数的运算特性和解方程的
方法求解得出角度的值。
3
验证解
欢迎来到锐角三角函数复习课件公开课! 在本课程中,我们将回顾锐角三角 函数的基本概念,常见公式,性质和图像,解三角方程,以及一些实际应用。
锐角三角函数的基本概念
锐角三角函数是用于描述锐角三角形中角度和边长之间关系的函数。包括正弦、余弦和正切等函 数。
1 正弦函数
描述角的对边与斜边之间的关系。
总结和回顾
在本课程中,我们回顾了锐角三角函数的基本概念、常见公式、性质和图像。学习了如何利用锐角三角 函数求解三角方程,并了解了一些实际应用。希望你已经对锐角三角函数有了更深入的理解!
锐角三角函数在直角三角形的图像中不断变化,并呈现出一些特殊的性质。
单位圆
单位圆是用于可视化锐角三角 函数图像和特殊性质的工具。
正弦函数
正弦函数是一条波浪形曲线, 用于描述周期性变化。
余弦函数
余弦函数是一条类似正弦函数 的波浪形曲线,但相位差90度。
利用锐角三角函数求解三角方程
锐角三角函数可以用于解决涉及三角函数的方程,从而求得角度的值。
2 余弦函数
描述角的邻边与斜边之间的关系。
3 正切函数
描述角的对边与邻边之间的关系。
常见的锐角三角函数公式
锐角三角函数有一些常见的公式用于计算和简化角度的计算。
倍角和半角公式
• 正弦和余弦的倍角和半角公式。 • 正切的双角和半角公式。
和差公式
• 正弦和余弦的和差公式。 • 正切的和差公式。
锐角三角函数的性质和图像
1
方程转化
将方程转化为以三角函数为未知数的
方程求解
2
方程。
利用三角函数的运算特性和解方程的
方法求解得出角度的值。
3
验证解
锐角三角函数复习课ppt课件

sina cosa tana
1
2
3
2
2
2
3
2
1
2
2
2
3
3
1
3
思考
锐角A的正弦值、余弦 值有无变化范围?
0< sinA<1
0<cosA最<新1 版整理ppt
角度 逐渐 增大
正 弦 值 余弦 也 值逐 增 渐减 大 正小切
值也 随之 增大
14
sin 2 cos2 1 tan sin
cos
1.3m
O
O
10m
方法总结:对于这
样的实际问题,先认真 分析题意,建立直角三
BC
B
角形的模型,将实际问
题转化为数学问题
A
A
最新版整理ppt
19
• 10分:元旦期间,学校的教学楼上AC挂着庆元旦 条幅BC,小明站在点F处,测得条幅顶端B的仰 角为300,再往条幅方向前进20m到达点E处,测 得B的仰角为600,求条幅BC的长。
AC=
√3,
AB=2,Tan
B 2
75° √3 =3
4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( B
)
A,相等 B,互余 C,互补 D,不确定。
5.已知在Rt△ABC中, ∠C=90°,sinA=
1 2
,则
cosB=( A )
A,
1 2
B,√22
C, √最2新3版整理Dp,pt √3
4
6. 计算
(1) tan30°+cos45°+tan60°
3 2 3 32
4 3 2 32
(2) tan30°·tan60°+ cos230°
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)已知 tan( ∠A+20°)= 3 ,求锐角A . (4)在△ABC中, ∠ B、 ∠ C均为锐角,且
1 3 0 sin B + cos C 2 2
2
,求∠A的度数。
第21课时┃锐角三角函数及其应 用 突|破|点|2 特殊角的三角函数值的计算
例 2 [2017·烟台]在 Rt△ABC 中,∠C=90°,AB=2,BC= 3, A 1 则 sin =Leabharlann _______. 2 2b
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
第22课时┃锐角三角函数
例 1 【2018· 原创】如图 22-2,在 Rt△ABC 中,∠BAC =90°,AD⊥BC 于点 D,判断正误:
图 22-2 AD (1)sinB= ;( √ ) AB AD (3)sinB= ;( × ) AC AC (2)sinB= ;( BC CD (4)sinB= .( AC √
B
一.锐角三角函数的概念
对边与斜边的比叫做∠A 正弦:把锐角A的__________ a 的正弦,记作 sin A c A 邻边与斜边的比叫做∠A的 余弦:把锐角A的__________ 余弦,记作 cos A b
c
c
a
b
C
对边与邻边的比叫做∠A的 正切:把锐角A的__________ a 正切,记作 tan A
1. 巩固三角函数的概念,巩固用直角三角形边之 比来表示某个锐角的三角函数. 2. 熟记30°,45°, 60°角的三角函数值.会计 算含有特殊角的三角函数的值,会由一个特殊 锐角的三角函数值,求出它的对应的角度. 3.掌握直角三角形的边角关系,会运用勾股定理, 直角三角形的两锐角互余及锐角三角函数解直 角三角形. 4.会用解直角三角形的有关知识解决简单的实际 问题.
☆
应用练习
三.比较大小
(1)sin250____sin430 (2)cos70____cos80 (3)sin400____cos600 (4)tan480____tan400
三.解直角三角形
1.什么叫解直角三角形? 由直角三角形中,除直角外的已知元素,求出所 有未知元素的过程,叫做解直角三角形. 2.直角三角形中的边角关系:
1 2
3 2
3 3
2 2
2 2
3 2
1 2
1
3
锐角的三角函数值 有何变化规律呢?
正切值和正弦值都随着锐角度数的增大而_____ 增大 ; 余弦值随着锐角度数的增大而_____. 减小
思考:若∠A+∠B=90 ,那么:
sinA = cosB
0
cosA = sinB
☆
应用练习
一.已知角,求值 (1)tan45°-sin60°cos30°
⑶解直角三角形在实际问题中 的应用
1.若
2 sin 2 0 ,则锐角α= 45°
2.若 tan( 20) 3 0 ,则锐角α= 80°
3.计算:
1 2 (1) sin 45 + tan60 2 cos30. 2 2
1 2 6 tan 30 3 sin 60 2cos 45 . 2 2
A
B
C
D 30°
练
习
3.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平 地,如图所示.BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防 夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改 造.经地质人员勘测,当坡角不超过45°时,可确保山体不滑 坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少 是多少米(结果保留根号)?
3 ≈1.73 sin 76°≈ 0.97
北 东
B
76°
cos 76°≈ 0.24
tan 76°≈ 4.01
C
D
60°
F
E l
A
⑴正弦
1.锐角三角函数的定义 ⑵余弦 ⑶正切 2.30°、45°、60°特殊角的三角函数值
⑴定义
①三边间关系
锐 角 三 角 函 数
3.解直角三角形
⑵解直角三角形的依据
②锐角间关系 ③边角间关系
(2)2sin30°+3tan30°+tan45°
(3)cos245°+ tan60°cos30°
(4)2sin60°-3tan30°-(π-cos30°)+(-1)
2012
☆
应用练习
二.已知值,求角
3 (1)已知 sinA= ,求锐角A . 2
(2)已知2cosA - 2 = 0 , 求锐角A.
2 0 0 0
B A
则a= 2 ,∠B=
C
4.如图,在Rt△ABC中,∠C=90,b= 2 3 ,c=4.
60° ,∠A= 30°.
5.如果
1 cos A + 3 tan B 3 0 2
那么△ABC是( D )
A.直角三角形 C.钝角三角形 B.锐角三角形 D.等边三角形
G
F
试一试:(2009年江苏省中考原题)如图,在航线l的两侧分 别有观测点A和B,点A到航线l的距离为2km,点B位于 点A北偏东60°方向且与A相距10km处.现有一艘轮船 从位于点B南偏西76°方向的C处,正沿该航线自西向东 航行,5min后该轮船行至点A的正北方向的D处. (1) 求观测点B到航线l的距离; (2)求该轮船航行的速度(结果精确到0.1km/h ) 参考数据:
h
l
h i tan l
1.在Rt △ ABC中,∠C=90°,∠ A=30°,a=5,
求b、c的大小.
B
5
A
30°
C
2.海中有一个小岛A,它的周围6海里内有暗礁,渔船跟踪鱼群 由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12 海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔 船不改变航线继续向东航行,有没有触礁的危险?
√
)
)
回归教材
考点聚焦
考向探究
1、如图,在Rt△ABC中,∠C=90, AB=5,AC=3,求sinA,cosA及tanA。
B
A
C
例1如图,在Rt△ABC中,∠C=90°,AC=4, B BC=2, 解:在 Rt△ABC中,∠C=90°. 2 求∠ A的正弦、余弦、正切的值. 因为AC=4,BC=2,所以 A AB= AC 2 + BC 2 4 2 + 2 2 2 5.
BC 2 5 sinA= AB 2 5 5 5
2
C
4
AC 4 2 5 AB 2 5 5
BC 2 1 tanA AC 4 2
cosA =
=
2、 在正方形网格中,△ABC的位置如图所示, 则cos∠ABC的值为________。
A
专家指点
作辅助线构造 直角三角形!
B C
二.特殊角的三角函数值
c B
a
(1)三边关系: a 2 + b 2 c 2 (勾股定理)
(2)两锐角的关系:∠A十∠B=90°
A
C b a b a tan A cos A (3)边角的关系:sin A b c c 边 , 归纳:只要知道其中的2个元素(至少有一个是____) 就可以求出其余3个未知元素.
四.解直角三角形的应用
1.仰角和俯角 在进行测量时, 仰角; 从下向上看,视线与水平线的夹角叫做____ 俯角。 从上往下看,视线与水平线的夹角叫做____
视线 铅 直 线
仰角 俯角
水平线
视线
2.坡角、坡度
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
坡度:坡面的铅直高度h和水 平距离l的比叫做坡度,用字 母i表示,即:
60°
3 1 [解析] ∵△ABC 中,∠A,∠B 都是锐角,sinA= ,cosB= ,∴∠A 2 2 =∠B=60°.∴∠C=180°-∠A-∠B=180°-60°-60°=60°.
对接中考
考点过关
突破重难
如图,作边长为1 的正方形ABCD .延长 边CB 到D ′ ,使B D ′= B D,连接D D ′ .你能 利用这个图形求出22 . 5°角的正切的值吗?试 一试. A tan22.5 °= 2 1 D′ B C D
[解析] 在 Rt△ABC 中,∠C=90°,AB=2,BC= 3,∴sinA 3 A 1 = .∴∠A=60°,∴sin =sin30°= . 2 2 2
对接中考
考点过关
突破重难
第21课时┃锐角三角函数及其应 用
2.[2018·中考预测]△ ABC 中,∠A,∠B 都是锐角.若 sinA= 1 = ,则∠C=________. 2 3 ,cosB 2
1 3 0 sin B + cos C 2 2
2
,求∠A的度数。
第21课时┃锐角三角函数及其应 用 突|破|点|2 特殊角的三角函数值的计算
例 2 [2017·烟台]在 Rt△ABC 中,∠C=90°,AB=2,BC= 3, A 1 则 sin =Leabharlann _______. 2 2b
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
第22课时┃锐角三角函数
例 1 【2018· 原创】如图 22-2,在 Rt△ABC 中,∠BAC =90°,AD⊥BC 于点 D,判断正误:
图 22-2 AD (1)sinB= ;( √ ) AB AD (3)sinB= ;( × ) AC AC (2)sinB= ;( BC CD (4)sinB= .( AC √
B
一.锐角三角函数的概念
对边与斜边的比叫做∠A 正弦:把锐角A的__________ a 的正弦,记作 sin A c A 邻边与斜边的比叫做∠A的 余弦:把锐角A的__________ 余弦,记作 cos A b
c
c
a
b
C
对边与邻边的比叫做∠A的 正切:把锐角A的__________ a 正切,记作 tan A
1. 巩固三角函数的概念,巩固用直角三角形边之 比来表示某个锐角的三角函数. 2. 熟记30°,45°, 60°角的三角函数值.会计 算含有特殊角的三角函数的值,会由一个特殊 锐角的三角函数值,求出它的对应的角度. 3.掌握直角三角形的边角关系,会运用勾股定理, 直角三角形的两锐角互余及锐角三角函数解直 角三角形. 4.会用解直角三角形的有关知识解决简单的实际 问题.
☆
应用练习
三.比较大小
(1)sin250____sin430 (2)cos70____cos80 (3)sin400____cos600 (4)tan480____tan400
三.解直角三角形
1.什么叫解直角三角形? 由直角三角形中,除直角外的已知元素,求出所 有未知元素的过程,叫做解直角三角形. 2.直角三角形中的边角关系:
1 2
3 2
3 3
2 2
2 2
3 2
1 2
1
3
锐角的三角函数值 有何变化规律呢?
正切值和正弦值都随着锐角度数的增大而_____ 增大 ; 余弦值随着锐角度数的增大而_____. 减小
思考:若∠A+∠B=90 ,那么:
sinA = cosB
0
cosA = sinB
☆
应用练习
一.已知角,求值 (1)tan45°-sin60°cos30°
⑶解直角三角形在实际问题中 的应用
1.若
2 sin 2 0 ,则锐角α= 45°
2.若 tan( 20) 3 0 ,则锐角α= 80°
3.计算:
1 2 (1) sin 45 + tan60 2 cos30. 2 2
1 2 6 tan 30 3 sin 60 2cos 45 . 2 2
A
B
C
D 30°
练
习
3.我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平 地,如图所示.BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防 夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改 造.经地质人员勘测,当坡角不超过45°时,可确保山体不滑 坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少 是多少米(结果保留根号)?
3 ≈1.73 sin 76°≈ 0.97
北 东
B
76°
cos 76°≈ 0.24
tan 76°≈ 4.01
C
D
60°
F
E l
A
⑴正弦
1.锐角三角函数的定义 ⑵余弦 ⑶正切 2.30°、45°、60°特殊角的三角函数值
⑴定义
①三边间关系
锐 角 三 角 函 数
3.解直角三角形
⑵解直角三角形的依据
②锐角间关系 ③边角间关系
(2)2sin30°+3tan30°+tan45°
(3)cos245°+ tan60°cos30°
(4)2sin60°-3tan30°-(π-cos30°)+(-1)
2012
☆
应用练习
二.已知值,求角
3 (1)已知 sinA= ,求锐角A . 2
(2)已知2cosA - 2 = 0 , 求锐角A.
2 0 0 0
B A
则a= 2 ,∠B=
C
4.如图,在Rt△ABC中,∠C=90,b= 2 3 ,c=4.
60° ,∠A= 30°.
5.如果
1 cos A + 3 tan B 3 0 2
那么△ABC是( D )
A.直角三角形 C.钝角三角形 B.锐角三角形 D.等边三角形
G
F
试一试:(2009年江苏省中考原题)如图,在航线l的两侧分 别有观测点A和B,点A到航线l的距离为2km,点B位于 点A北偏东60°方向且与A相距10km处.现有一艘轮船 从位于点B南偏西76°方向的C处,正沿该航线自西向东 航行,5min后该轮船行至点A的正北方向的D处. (1) 求观测点B到航线l的距离; (2)求该轮船航行的速度(结果精确到0.1km/h ) 参考数据:
h
l
h i tan l
1.在Rt △ ABC中,∠C=90°,∠ A=30°,a=5,
求b、c的大小.
B
5
A
30°
C
2.海中有一个小岛A,它的周围6海里内有暗礁,渔船跟踪鱼群 由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12 海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔 船不改变航线继续向东航行,有没有触礁的危险?
√
)
)
回归教材
考点聚焦
考向探究
1、如图,在Rt△ABC中,∠C=90, AB=5,AC=3,求sinA,cosA及tanA。
B
A
C
例1如图,在Rt△ABC中,∠C=90°,AC=4, B BC=2, 解:在 Rt△ABC中,∠C=90°. 2 求∠ A的正弦、余弦、正切的值. 因为AC=4,BC=2,所以 A AB= AC 2 + BC 2 4 2 + 2 2 2 5.
BC 2 5 sinA= AB 2 5 5 5
2
C
4
AC 4 2 5 AB 2 5 5
BC 2 1 tanA AC 4 2
cosA =
=
2、 在正方形网格中,△ABC的位置如图所示, 则cos∠ABC的值为________。
A
专家指点
作辅助线构造 直角三角形!
B C
二.特殊角的三角函数值
c B
a
(1)三边关系: a 2 + b 2 c 2 (勾股定理)
(2)两锐角的关系:∠A十∠B=90°
A
C b a b a tan A cos A (3)边角的关系:sin A b c c 边 , 归纳:只要知道其中的2个元素(至少有一个是____) 就可以求出其余3个未知元素.
四.解直角三角形的应用
1.仰角和俯角 在进行测量时, 仰角; 从下向上看,视线与水平线的夹角叫做____ 俯角。 从上往下看,视线与水平线的夹角叫做____
视线 铅 直 线
仰角 俯角
水平线
视线
2.坡角、坡度
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
坡度:坡面的铅直高度h和水 平距离l的比叫做坡度,用字 母i表示,即:
60°
3 1 [解析] ∵△ABC 中,∠A,∠B 都是锐角,sinA= ,cosB= ,∴∠A 2 2 =∠B=60°.∴∠C=180°-∠A-∠B=180°-60°-60°=60°.
对接中考
考点过关
突破重难
如图,作边长为1 的正方形ABCD .延长 边CB 到D ′ ,使B D ′= B D,连接D D ′ .你能 利用这个图形求出22 . 5°角的正切的值吗?试 一试. A tan22.5 °= 2 1 D′ B C D
[解析] 在 Rt△ABC 中,∠C=90°,AB=2,BC= 3,∴sinA 3 A 1 = .∴∠A=60°,∴sin =sin30°= . 2 2 2
对接中考
考点过关
突破重难
第21课时┃锐角三角函数及其应 用
2.[2018·中考预测]△ ABC 中,∠A,∠B 都是锐角.若 sinA= 1 = ,则∠C=________. 2 3 ,cosB 2
