第1章、索洛增长模型
索罗增长模型

第一章索洛经济增长模型The Solow Growth Model基本内容1 索洛模型的基本假定2 离散时间的索洛模型3离散时间索洛模型的过渡过程4连续时间的索洛模型5连续时间索洛模型的过渡过程6持久增长7带技术进步的索洛模型8比较动态分析1 索洛模型的基本假定● 一个分析经济增长和各国收入差异的基本框架.● 其核心假定是新古典总的生产函数.家庭与生产 I● 封闭经济,唯一的最终产品.● 离散时间,t = 0, 1, 2, ....● 该经济里有众多的家庭,暂时假定家庭没有优化行为.● 这也是索罗模型与新古典增长模型的主要区别.● 为了简化,假定各个家庭相同,可以用代表性家庭来表示.家庭与生产II● 假定家庭的储蓄率外生● 所有厂商具有相同的生产函数,可以用代表性厂商表示.● 对该经济中的唯一最终产品,生产函数为(1)Y T F K t L t A t()[(),(),()]●假定资本与最终产品相同(比如玉米),用于生产更多的产品.●()A t可以理解为技术.●主要假定: 技术是免费的; 具有非竞争性与非排他性.关键假设1Assumption 1 (连续性, 可微性, 边际产出为正且递减, 规模报酬不变) 生产函数3:F R R ++→ 关于 K 与 L 二阶连续可微, 且满足2222()()(,,)0 (,,)0()()(,,)0 (,,)0K L KK LL F F F K L A F K L A K L F F F K L A F K L A K L ∂⋅∂⋅≡>≡>∂∂∂⋅∂⋅≡<≡<∂∂ 同时, F 关于K 与 L 规模报酬不变.● 假定 F 关于K 与 L 规模报酬不变,即关于这两个变量线性齐次.复习定义 假定K 为整数,如果对任意的R λ+∈与K z R ∈,有(,,)(,,)m g x y z g x y z λλλ=,那么函数2:K g R R ++→为x R ∈与y R ∈的m 次齐次函数.定理 (欧拉定理Euler 's Theorem ) 假定函数2:K g R R ++→为x R ∈与y R ∈的m 次齐次函数,偏导数分别是x g 与y g ,那么对任意的x R ∈,y R ∈以及K z R ∈,有()()(),, ,,,,x y mg x y z g x y z x g x y z y =+同时,,(),x g x y z 与,(),y g x y z 是关于x 与y 的1m -次齐次式.市场结构与市场出清 I●假定市场是竞争的, 因此也可认为是竞争一般均衡模型. ●家庭拥有劳动, 供给无弹性.●经济中的劳动(力),)L t , 无论在什么价格下,劳动的供给量均为()L t .●劳动力市场出清条件:())L t L t =上式对所有的t 均成立 , ()L t 劳动需求 (也可视为就业水平). ●一般来说, 互补松弛条件的表述更为准确.●记 t 时期的工资率为 w (t), 于是劳动力市场出清条件可表示为()()),0(L t L t w t ≤≥ and (()()) (0)L t L t w t =-市场结构与市场出清II●假设 1 与竞争的劳动力市场意味着工资率必须严格为正. ●家庭拥有资本,并将其出租给厂商.●记t 期的资本租赁价格()R t .●资本市场出清条件:()()s d K t K t =LHS-家庭的行为决定;RHS-厂商的行为决定●假定家庭拥有的初始资本存量为()0K●()P t 为t 时期最终产品的价格, 将其标准化为1.●利率r(t)●折旧率δ●家庭得到的实际回报()() r t R t δ=-.厂商优化厂商优化 I●考虑代表性厂商的最大化问题:0)0,()([()()()],()()()(),.L t K t max F K t L t A t w t L t R t K t ≥≥--●注意:●上述最大化问题中的变量是总量.●在F 前面没有系数, 这是因为最终产品的价格已正规化为1.●假定要素市场完全竞争: 在厂商看来,()w t 与()R t 是给定的.●凹的问题,因为F 是凹的.厂商优化 II●由于 F 可微, 一阶条件(FOC )为:()[()()()],,,L w t F K t L t A t = (2)()[()()()] ,.,K R t F K t L t A t = (3)●在(2) 与(3)中, ()K t 与()L t 分别表示厂商对资本和劳动的需求量.●实际上,可以通过(2)与(3)求解()K t 与 ()L t ,它们是资本租赁价格()R t 和工资率()w t 的函数.厂商优化 III命题 假定假设1成立,那么均衡时厂商的利润为0,()()( )()() .Y t w t L t R t K t =+●证明: 可直接从欧拉定理得到(注意到1m =,即规模报酬不变).关键假设2假设2 (Inada conditions) F 满足 Inada 条件0 0 0 ()() K K K K lim F and lim F for all L all A →→∞⋅=∞⋅=> 00 0 ()() L L L L lim F and lim F for all L all A →→∞⋅=∞⋅=> ●保证内点解.生产函数Figure: Production functions and the marginal product of capital. The example in Panel A satisfies the Inada conditions in Assumption 2, while the example in Panel B does not.2 离散时间Solow 模型Solow模型的动态过程描述 I●K的折旧率为 , 于是1 1()((() ),)K t K t I t δ+=-+ (4) 其中, ()I t 是t 阶段的投资.●对于封闭经济, 产出等于消费与储蓄(投资)之和 ,()()()Y t C t I t =+ (5) ●注意,该模型没有家庭效用的最大化问题,因此此处难以讨论社会福利等方面的话题.Solow 模型的动态过程描述II●由于经济是封闭的 (同时不考虑政府支出),于是.()()()()S t I t Y t C t ==-●假定家庭的储蓄率是常数,则()(),S t sY t =(6) 1()()()C t s Y t =-(7) ●于是资本供给(家庭的行为决定储蓄率s )可表示为()()( 1 1 )()()()().s K t K t S t K t sY t δδ=-+=-+Solow 模型的动态过程描述 III●资本的供求相等 ()().s K t K t =●同时也有劳动力市场供求相等 ()().L t L t =●结合 (1) 与 (4), 可得 Solow 增长模型的动态方程: ()[()()1 ,, 1.()]()()K t sF K t L t A t K t δ+=+- (8) ●非线性差分方程.●Solow 增长模型的均衡由该方程以及 ()(())()L t or L t and A t 来刻画.定义均衡 I●没有家庭优化, 但仍然有厂商最大化行为以及要素市场的出清.定义 在Solow 模型中,对于给定的序列 {}0()(),t L t A t ∞= 以及初始资本存量()0K , {}0,,,()()()(,)()t K t Y t C t w t R t ∞=是资本、产出、消费、工资率、租赁价格的均衡路径,其中()K t 满足 (8), ()Y t 由(1)给出, ()C t 由 (7)给出, ()w t 与 ()R t 分别由 (2) 与 (3)给出.●注意,均衡是沿着时间的整条路径,而不是静态的点.不考虑人口增长与技术进步时的均衡不考虑人口增长与技术进步时的均衡I●进一步假定(稍后放松假定):●没有人口增长;假定总人口为常数 L > 0, 即() L t L =. ●假定没有技术进步,即() A t A =.●定义资本-劳动比率(人均资本)为 ((,))K t k t L ≡(9)●利用规模报酬不变, 人均产出) ()(/y t Y t L ≡可表示为,1, ()()(() ).K t y t F A L f k t ⎡⎤=⎢⎥⎣⎦≡ (10)不考虑人口增长与技术进步时的均衡 II ●注意()f k 依赖于A, 本可以将生产函数写成,()f k A ;但由于A 是常数,因此可以假定 A = 1.●由欧拉定理0 ()(())()(())()(())0.R t f k t w t f k t k t f k t -'=>'=> (11) ●由假设1可知(11)中的要素价格均为正.例子: Cobb-Douglas 生产函数 I●一类特殊的生产函数,但应用很广泛:1()[()()()]()( ,,,01)Y t F K t L t A t AK t L t ααα-==<<●满足假设1和 2.●两边同时除以()L t ,()() y t Ak t α=●由 (11)可得(1)()()()()Ak t R t Ak t k t ααα--∂==∂ ●由欧拉定理,()()() 1.()()()w t y t R t k t Ak t αα==--例子: Cobb ‐Douglas 生产函数II●或者直接从 Cobb-Douglas 生产函数有,()111()()() () ,R t AK t L t Ak t ααααα----==()()()()()()1 1 ,w t AK t L t A t k ααααα-=-=-直接可验证满足欧拉定理.不考虑人口增长与技术进步时的均衡 不考虑人口增长与技术进步时的均衡I●将 (8)的两端同时除以 L 可得人均量的表达式:()(()1 1).)(()k t sf k t k t δ+=+- (12) 定义 稳态均衡(steady-state equilibrium )* ()k t k =.该经济将趋于该稳态均衡(但在有限时间不能到达).稳态人均资本不考虑人口增长与技术进步时的均衡 II●上图实线代表 (12),虚线是45 线.●它们的(正的)交点*k 表示稳态人均资本 **.()f k k s δ=(13)●注意到还有另一交点0k =,因为已经假定0(0)f =.●忽略该稳态值:●如果资本不是必不可少的(essential ), ()0f 可能大于0 0k =可能变为稳态均衡点●本交点,即使存在,也不稳定。
Solow-Swan模型
第1章索洛-斯旺模型从本章开始,我们将利用三章的篇幅来探讨增长经济学的内容。
从初、中级的教科书中我们已经知道,增长经济学研究的是经济的长期行为,它重点要阐明一个国家或一个地区中生产能力的变化原因。
具体而言,我们要探讨生产要素的积累和技术的改进是如何导致了生活水平的提高。
在这部分内容中,我们将忽略经济的短期波动,并且假定劳动、资本以及原材料等生产要素都是被充分利用的。
经济的增长率一般是指国内生产总值(GDP)的增长率,这一指标衡量了一个经济的发展水平。
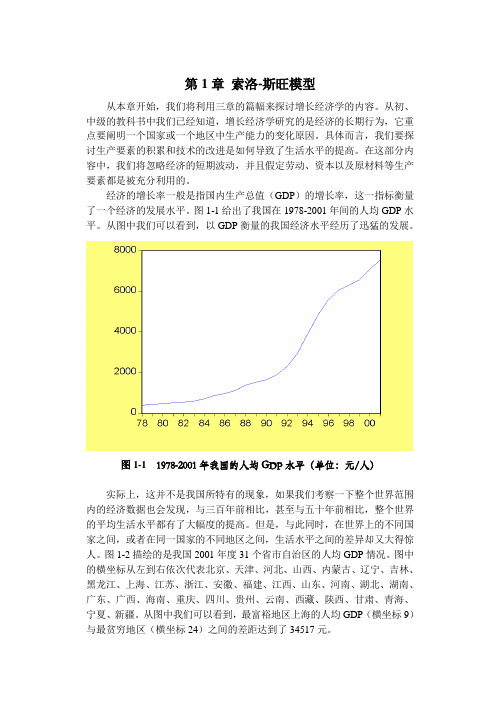
图1-1给出了我国在1978-2001年间的人均GDP水平。
从图中我们可以看到,以GDP衡量的我国经济水平经历了迅猛的发展。
图1-1 1978-2001年我国的人均GDP水平(单位:元/人)实际上,这并不是我国所特有的现象,如果我们考察一下整个世界范围内的经济数据也会发现,与三百年前相比,甚至与五十年前相比,整个世界的平均生活水平都有了大幅度的提高。
但是,与此同时,在世界上的不同国家之间,或者在同一国家的不同地区之间,生活水平之间的差异却又大得惊人。
图1-2描绘的是我国2001年度31个省市自治区的人均GDP情况。
图中的横坐标从左到右依次代表北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、江苏、浙江、安徽、福建、江西、山东、河南、湖北、湖南、广东、广西、海南、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆。
从图中我们可以看到,最富裕地区上海的人均GDP(横坐标9)与最贫穷地区(横坐标24)之间的差距达到了34517元。
图1-2 2001年我国31个省市自治区的人均GDP(单位:元/人)单单只就上面提到的这两个事实(即在纵向上世界整体生活水平的迅速提高和在横向上各国之间或一国内的各个地区之间生活水平的巨大差异),关于经济增长研究的现实意义已不言而喻。
正如卢卡斯(Robert E. Lucas)所言:“印度政府是否可以采取一些手段来使得印度经济像印度尼西亚或埃及一样增长?如果可以,是什么手段?如果不可以,那么使得它之所以如此的印度国情究竟是什么?对于涉及于此类问题之中的人类福利而言,结果是令人惊愕的:一旦你开始考虑它们,就很难再考虑其他的事情了。
5-罗默高级宏观经济学

我们在求导的时候注意 是一个常数, 表示的是家庭在两个时期转换消费的消费意愿, 越小,随着消费的上升边际效用下降的越慢,家庭越愿意跨期消费。
2.2企业行为和家庭行为
资本要素完全竞争---利率=资本的边际产出
工资=劳动的边际产出
宏观经济学的起点——凯恩斯1936年的通论
高级宏观经济学的起点——将我们的动态最优的分析方法,1928年开始提出,196几年的时候才开始运用,现在宏观经济学运用最多的就是这个模型
这样的争论是,资本的所有者是否应该
资本存量的增长率先是增加,然后增加的逐渐下降,
资本存量的变化率
资本存量本身是一定是往上走的,是递减的增加
和资本存量的增长率相对应
劳均资本的增长率和资本存量的增长率是同步的
变动,因为技术进步率是不变的
劳军产出的对数值
每单位劳动的平均消费是怎么变化
取决于产出怎么变
也取决于劳动怎么变
投资先快速下滑,然后回归到新的均衡
我们经济学是先提出假定,然后在这个基础上发展框架
政治经济学中资本对劳动的剥削,只要你进行劳动,就有剩余
资本对劳动存在剥削,
因为只有劳动创造价值,其他因素不占有价值,其他要素获取剩余价值,所以就有对劳动的剥削
劳动者得到工资L——w
资本所有者得到利息K——r(一定是来自于劳动者的贡献)—所以这就应该是剥削
考虑一个变量对另一个变量的影响,
最基本的方式就是求导;
还有一个是弹性的概念总产出增加2%,储蓄增加X%。
有一个基本的方程,如果卡住了,把那个公式写到一遍,就一定能得到启发
如果储蓄率一定的话,经济会收敛到唯一的一个均衡点
考察经济收敛的速度,核心的变量就是资本存量
罗默《高级宏观经济学》【教材精讲+经典考题串讲】讲义(第1~3章)【圣才出品】

罗默《高级宏观经济学》【教材精讲+经典考题串讲】讲义第1章索洛增长模型第一部分重难点解读“一旦人们开始思考(经济增长)问题,他将很难再顾及其他问题。
”——罗伯特·卢卡斯(Robert Lucas,1988)1.1模型假设投入与产出生产函数采取如下形式:()()()()(),Y t F K t A t L t =其中,t :时间,A :有效劳动....——劳动增加型.....的或哈罗德中性.....。
生产函数生产函数是规模报酬不变的:()(),,F cK cAL cF K AL =,对于所有0c ≥规模不变结合两个不同的假设:第一是经济规模足够大,以至于专业化的收益已被全部利用。
第二是除资本、劳动与知识以外的其他投入相对不重要。
把单位有效劳动的产出写成单位有效劳动的函数:()1,1,⎛⎫= ⎪⎝⎭K F F K AL AL AL定义/=k K AL ,/=y Y AL 以及()(),1=f k F k ,得:()=y f k 关于()f k 的假设:(1)()00=f ,()0'>f k ,()0''<f k (如何推导?比较重要!)(2)稻田条件(Inada condition):()0lim →'=∞k f k ,()lim 0→∞'=k f k 柯布一道格拉斯函数:()()1,,01ααα-=<<F K AL K AL 。
根据规模报酬不变假设,整理可得:()α=f k k ,图示如图1.1所示。
图1.1柯布-道格拉斯生产函数生产投入的演化给定资本、劳动与知识的初始水平,劳动与知识以不变的增长率增长:()()∙=L t nL t ()()∙=A t gA t 其中,n 与g 是外生参数。
求解以上两微分方程,可得:()()0=ntL t L e()()0=gtA t A e 假设:用于投资的产出份额s 是外生且不变的,则有资本动态积累方程:()()()δ∙=-K t sY t K t 其中,δ为资本折旧率。
罗默《高级宏观经济学》(第4版)课后习题详解

目录分析
第2章无限期模型 与世代交叠模型
第1章索洛增长模 型
第3章内生增长
第4章跨国收入差距
第5章实际经济周期 理论
第6章名义刚性
第7章动态随机一般 均衡周期模型
1
第8章消费
2
第9章投资
3
第10章失业
4
第11章通货膨 胀与货币政策
5
第12章预算赤 字与财政政策
作者介绍
这是《罗默《高级宏观经济学》(第4版)课后习题详解》的读书笔记模板,暂无该书作者的介绍。
罗默《高级宏观经济学》(第 4版)课后习题详解
读书笔记模板
01 思维导图
03 目录分析 05 读书笔记
目录
02 内容摘要 04 作者介绍 06 精彩摘录
思维导图
本书关键字分析思维导图
解答
名义
教材
罗默
刚性
第章
理论
习题
习题
第版 模型
收入
罗默
差距
消费
经济周期
内生
周期
动态随机
内容摘要
本书是罗默《高级宏观经济学》教材的配套电子书,参考大量相关资料对罗默《高级宏观经济学》(第4版) 教材每章的课后习题进行了详细的解答,并对个别知识点进行了扩展,特别适合应试作答和临考冲刺。
读书笔记
这是《罗默《高级宏观经济学》(第4版)课后习题详解》的读书笔记模板,可以替换为自己的心得。
精彩摘录
这是《罗默《高级宏观经济学》(第4版)课后习题详解》的读书笔记模板,可以替换
索洛增长模型PPT课件

图2-7
中国1978-2009年GDP及人均GDP增长率(%)
.
11
350000 300000 250000 200000 150000 100000
50000 0
1978 1980 1982 1984 1986 1988 1990 1992 1994 1996 1998 2000 2002 2004 2006 2008
29252
21763
21124
18409
12140
33885 22885 19766
0
美国 日本 德国 英国 法国 意大利 加拿大 中国 印度 俄罗斯 巴西
图2-5 2008年按购买力平价法计算的GDP(亿美元)
.
9
50000 46716
45000
40000 35000 30000
34099
35613
.
13
30000 25000 20000 15000 10000
5000 0
图2-10 中国1978-2009年人均GDP(元)
1978 1980 1982 1984 1986 1988 1990 1992 1994 1996 1998 2000 2002 2004 2006 2008
.
14
3.经济增长与经济发展的区别与联系 (二)增长的源泉
35445
34045
30756
36444
25000
20000 15000 10000
5000
16139
5962
2972
10296
0
美国 日本 德国 英国 法国 意大利 加拿大 中国 印度 俄罗斯 巴西
图2-6 2008年按购买力平价法计算的人均GDP(美元)
[经济学]新第一章 索罗增长模型
![[经济学]新第一章 索罗增长模型](https://img.taocdn.com/s3/m/39cc9fe158fb770bf68a5542.png)
h
(2)边际产出递减
f(k)满足f(0)=0,f’(k)>0,f”(k)<0,f’(k)是 资本的边际产品。
【证明】
Y=ALf(k)两边分别对K、L求导数:
资本的边际产品为: YAL'(kf) 1f'(k)
K
AL
有效劳动的边际产品为:
( A Y ) L f(k ) A'(k L ) [ ( fA K )2 ]L f(k ) k'(k f)
f(k)
k1
K*
k2
(n+g+δ)k
f(k)
sf(k)
K1时的
•
k (t)
K2时的
•
k (t)
•
K*时的 k ( t )
k
24
h
•
k (t)
k的走势:不论k从何处开始,它都向k*收敛。
k*
k
反映变量变化率与其本身关系的曲线图
25
h
二、平衡增长路径: 各个主要变量如何变动? 绝对量: L,A, AL, K, Y,C 相对量: K/AL K/L Y/AL Y/L C/AL
11
h
f(k)
(3)稻田条件:
lik m of'(k)
lik m f'(k)0 k
资本存量足够小时,资本的边际产品很大 资本存量足够大时,资本的边际产品很小
12
h
三、一个特殊的生产函数:柯布-道格拉斯
F (K ,A) LK (A)1 L 01
这一生产函数易于应用,并且是对实际生产函数的一个好 的初步近似。 • 规模报酬不变: 生产函数的密集型式 f(k)=kα f’(k)=αkα-1 f’’(k)=α(α -1)kα-2 (小于0)
索洛-斯旺增长模型

比较不同国家或地区的发展水平
通过比较不同国家或地区之间索洛-斯旺模型的参数,可以评估各 国或地区的发展水平和发展阶段。
制定经济发展战略
根据索洛-斯旺模型的结论,政府可以制定针对性的经济发展战略, 优化资源配置,促进经济的持续增长。
引入动态分析,考虑技术进步和资本积累的相互作用;引入制度因素, 分析其对经济增长的影响;考虑非线性生产函数的可能性。
模型的发展方向与未来研究展望
发展方向
将模型与其他经济理论相结合,如内 生增长理论、人力资本理论等,以更 全面地解释经济增长现象。
未来研究展望
探索模型在发展中国家和发达国家的应用, 比较不同国家经济增长的异同;研究全球化 、技术创新等对经济增长的影响;进一步深 化对经济增长机制和动力的理解。
模型的基本假设
假设经济中只存在两种生产要 素:资本和劳动,且资本和劳
动之间可以相互替代。
假设生产函数是规模收益不变 的,即增加投入并不能带来更
大的产出。
假设经济中不存在技术进步和 资本折旧,即经济增长只取决 于资本和劳动的投入。
假设经济中的储蓄率、人口增 长率和技术进步率是外生给定 的,即不受经济系统内部因素 的影响。
06 结论
对索洛-斯旺增长模型的综合评价
01
贡献
索洛-斯旺增长模型为经济增长研究提供了重要的理论基础,它揭示了
资本、劳动和技术进步对经济增长的贡献,并解释了经济增长的源泉。
02
局限性
然而,该模型也存在一些局限性,例如假设条件过于严格,忽略了许多
现实世界中的复杂因素,如经济政策、市场失灵、资源限制等。
罗默《高级宏观经济学》第版课后习题详解第章索洛增长模型

罗默《高级宏观经济学》(第3版)第1章 索洛增长模型跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
增长率的基本性质。
利用一个变量的增长率等于其对数的时间导数的事实证明:(a )两个变量乘积的增长率等于其增长率的和,即若()()()Z t X t Y t =,则(b )两变量的比率的增长率等于其增长率的差,即若()()()Z t X t t =,则(c )如果()()Z t X t α=,则()()()()//Z t Z t X t X t α=证明:(a )因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:因为两个变量的积的对数等于两个变量各自对数之和,所以有下式: 再简化为下面的结果:则得到(a )的结果。
(b )因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:因为两个变量的比率的对数等于两个变量各自对数之差,所以有下式:再简化为下面的结果:则得到(b )的结果。
(c )因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:又由于()()ln ln X t X t αα⎡⎤=⎣⎦,其中α是常数,有下面的结果: 则得到(c )的结果。
假设某变量X 的增长率为常数且在10~t 时刻等于0a >,在1t 时刻下降为0,在12~t t 时刻逐渐由0上升到a ,在2t 时刻之后不变且等于a 。
(a )画出作为时间函数的X 的增长率的图形。
(b )画出作为时间函数的ln X 的图形。
答:(a )根据题目的规定,X 的增长率的图形如图1-1所示。
索洛增长模型

t0
t
但是消费是否会超过s上升之前的原来水平是
不确定的,存在一个实现消费最大化最优增长 路径,即黄金分割率问题。 我们有下面有关消费的表达式:每单位有效劳 动的平均消费等于每单位有效劳动的平均产量 减去每单位有效劳动的平均投资,在平衡增长 路径上,实际投资等于持平投资,因此
c f (k ) (n g )k
索洛增长模型
1、索洛模型的基本假定 投入与产出 索洛模型包括四个变量,产量Y,资本K,劳动
L和知识或者劳动的有效性A,资本劳动和知识 结合起来生产产品,生产函数形式为:
Y (t ) F ( K (t ), A(t ) L(t )) (1.1)
两点解释:时间并不直接进入生产函数,只是通过 K、L、A进入。仅在生产投入变化时,产量才会随 时间变化。A和L以相乘形式进入,AL被称为有效 劳动,以此种形式进入技术进步为劳动增进型或者 哈罗德中性。
3、对索洛模型的评价 索洛模型确定了每工人平均产量变动的两个可
能来源:每工人平均资本的变动和劳动的有效 性的变动。然而只有劳动的有效性的增长才能 导致每工人平均产量的永久性增长,而且在合 理的情形下,每工人平均资本的变动对每工人 平均产量的影响不大。其结果,只有劳动的有 效性的差异才有希望解释财富在不同时期不同 地域的巨大差异。具体而言,索洛模型的基本 结论是如果资本取得的市场收益大体体现了其 对产量的贡献,那么实物资本积累的变动既不 能解释世界经济的增长,也不能很好的解释国 家间的收入差别。
由于K / AL k , L/ L n, A/ A g , K sY (t ) K (t ), 则, k (t )
sY (t ) K (t ) Y (t ) k (t ) n k (t ) g s k (t ) nk (t ) gk (t ) A(t ) L (t ) A(t ) L (t )
索洛增长模型

kmax
资本—劳动比kt
c
cG kG kmax 资本—劳动比kt 劳动—资本黄金律水平
稳态的到达
引入储蓄比例 假定经济体中储蓄和收入成正比, 则:St=sYt (0<s<1) 两部门经济储蓄等于投资, 则:sYt= (n+d)Kt (稳定状态下) 人均储蓄=人均投资 sf(k)= (n+d)k (稳定状态下) 稳态下,人均产出 y*=f(k*) 人均消费 c*=f(k*)-(n+d)k*
索洛模型
1 2
罗伯特·默顿·索洛简介 索洛模型的基本结构
长期生活水准的根本决定因素
3
1
罗伯特·默顿·索洛
罗伯特·默顿·索洛(Robert Merton Solow,1924年 8月23日-),美国经济学 家,麻省理工学院客座教授,1961年被授 予美国经济学会授予青年经济学家的“约 翰·贝茨·克拉克奖”(John Bates Clark Medal),并于1987年获得诺贝尔 经济学奖。
结论:人口增长率n的提高,意 味着需要更多的产出来给工人配 备资本,所以可用来消费或增加 人均资本的产出减少,生活水准 降低 生产率增长
结论:生产率的增长,直接使产 出增加,通过增加收入,它也使 储蓄和资本存量增加,生活水准 提高
人 均 投 资 储 蓄
新稳定状态下的 人均投资(n2+d)Kt 初始稳定状态下的 人均投资(n1+d)Kt 人均储蓄sf(k)
主要观点:长期的经济增长主要依靠技术 进步,而不是依靠资本和劳动力的投入。
2
1 2 3
4
索洛模型的基本结构
基本假设 人均生产函数
稳定状态 稳态的到达
基本假设
《索洛增长模型高宏》课件

人口增长率
总结词
人口增长率是影响经济增长的重要参数,它表示人口数量的变化率。
详细描述
人口增长率对经济增长的影响主要体现在劳动力供给方面。如果人口增长率较高,劳动力供给增加,会促进经济 增长;反之,如果人口增长率较低或为负数,劳动力供给减少,会制约经济增长。在索洛增长模型中,人口增长 率被视为外生变量。
VS
详细描述
折旧率对经济增长的影响主要体现在资本 投入方面。如果折旧率较高,表明固定资 产损耗较快,需要更多的投资来维持生产 能力;如果折旧率较低,则表明固定资产 可以使用较长时间,减少了资本投入的需 求。在索洛增长模型中,折旧率被视为外 生变量。
03
索洛增长模型的应用
对经济增长的预测
总结词
索洛增长模型可以用来预测经济增长,通过 分析影响经济增长的因素,如资本、劳动力 和技术进步,可以预测未来经济增长的趋势 和水平。
的影响而发生波动。
与新经济理论的比较
要点一
内生增长理论
与索洛模型相比,内生增长理论更注重企业内部生产活动 对技术进步和经济增长的影响。内生增长理论认为技术进 步是内生的,即由企业内部的研发投入、人力资本积累等 因素所驱动。这种理论能够更好地解释现实世界中技术进 步和经济增长的复杂关系。
要点二
新古典综合理论
详细描述
索洛增长模型是现代经济增长理论的 重要组成部分,通过比较模型预测的 经济增长率和实际经济增长率,可以 检验经济理论的正确性和可靠性,从 而为经济研究提供支持。
04
索洛增长模型的局限性
假设条件的局限性
技术进步外生
索洛模型假设技术进步是外生的,即技术进步是由市场外部因素决定的,而不是由企业内 部生产活动所驱动。这种假设限制了模型对现实世界中技术进步的描述和预测能力。
罗默《高级宏观经济学》章节题库(索洛增长模型)【圣才出品】

第1章索洛增长模型1.在Solow模型中,假设一个经济体在初始时候处于稳定状态。
现在一场自然灾害夺去了一部分人的生命,但资本总量却在灾害中没有损失。
请问人均资本、人均产出在短期和长期的变化趋势。
答:(1)索洛增长模型的总量生产函数是Y=F(K,L),或者以人均形式来表示为y =f(k)。
在短期,如果自然灾害夺取了部分人的生命,L下降,使k=K/L上升了。
由总量形式的生产函数可知,劳动力减少,则总产出下降。
但是,由于人均资本存量水平上升了,工人人均产出将会增加。
(2)劳动力的减少意味着自然灾害后的人均资本存量高于灾害发生之前,而灾害前的经济处于稳定状态,所以灾害后的人均资本存量水平高于稳定状态水平。
如图1-1所示,灾害发生后的人均资本存量位于k*右边的某一个位置k1。
但是k1不是稳定状态,这时人均储蓄小于资本扩展化水平,所以资本深化为负,人均资本存量会降低,经济逐渐向稳定状态过渡。
因此,在长期中,人均资本存量下降到k*,经济重新达到稳定状态。
在这个过程中,由于人均资本存量一直在下降,所以人均产出也一直在下降。
在稳定状态,技术进步决定人均产出增长率,一旦经济恢复到稳定状态,人均产量仅由技术进步决定。
因此这和灾害发生前是一样的。
图1-1 资本存量恢复稳态水平2.某经济体的生产函数为:Y t=(A t L t)αK t1-α,其中A t L t为效率劳动单位,如参数A t上升,则同样数量的劳动者可提供更多的效率劳动。
在每一期,消费者将s比例的产出投资于新资本,即I t=sY t,资本运动方程为:K t+1=(1-δ)K t+I t,其中δ为折旧率。
设劳动力与劳动生产率均以固定比率增长:L t+1=(1+l)L t,A t+1=(1+μ)A t。
试回答以下问题:(其中前4问反映的是卡尔多指出的经济增长进程的典型化事实)(1)设代表性竞争企业分别按实质工资W t和实质利息R t雇佣劳动和资本,写出企业的最优化问题,证明劳动和资本分配份额W t L t/Y t和R t K t/Y t在该经济中均为常数。
罗默《高级宏观经济学》第4版课后习题详解(索洛增长模型)【圣才出品】

证明:(a)因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:
Z&(t) d ln Z (t) d ln[X (t)Y (t)]
Z (t) dt
dt
因为两个变量的积的对数等于两个变量各自对数之和,所以有下式:
Z&(t) d[ln X (t) ln Y (t)] d ln X (t) d ln Y (t)
圣才电子书 十万种考研考证电子书、题库视频学习平台
因为两个变量的比率的对数等于两个变量各自对数之差,所以有下式:
Z&(t) d[ln X (t) lnY (t)] d ln X (t) d lnY (t)
Z (t)
dt
dt
dt
再简化为下面的结果: 则得到(b)的结果。
Z (t)
dt
dt
dt
再简化为下面的结果:
Z&(t) X&(t) Y&(t) Z (t) X (t) Y (t)
则得到(a)的结果。
(b)因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:
Z&(t) d ln Z(t) d ln[X (t) Y (t)]
Z(t) dt
dt
1 / 38
k
存量水平从 k*上升到 NEW 。
4 / 38
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-3 折旧率下降的影响
(b)技术进步率上升的影响
由于持平投资线的斜率为(n+g+δ),当技术进步率 g 上升后,会使持平投资线的斜
率变大,持平投资线向左旋转,而实际投资线则不受影响。从图 1-4 可以看出,平衡增长
sk 投资线为 sf(k),而 f(k)=kα,因此
罗默《高级宏观经济学》(第3版)课后习题详解(第1章 索洛增长模型)

罗默《高级宏观经济学》(第3版)第1章 索洛增长模型跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.1 增长率的基本性质。
利用一个变量的增长率等于其对数的时间导数的事实证明: (a )两个变量乘积的增长率等于其增长率的和,即若()()()Z t X t Y t =,则(b )两变量的比率的增长率等于其增长率的差,即若()()()Z t X t Y t =,则(c )如果()()Z t X t α=,则()()()()//Z t Z t X t X t α=证明:(a )因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:因为两个变量的积的对数等于两个变量各自对数之和,所以有下式:再简化为下面的结果:则得到(a )的结果。
(b )因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:因为两个变量的比率的对数等于两个变量各自对数之差,所以有下式:再简化为下面的结果:则得到(b )的结果。
(c )因为一个变量的增长率等于对该变量取对数后再对时间求导,那么可得下式:又由于()()ln ln X t X t αα⎡⎤=⎣⎦,其中α是常数,有下面的结果:则得到(c )的结果。
1.2 假设某变量X 的增长率为常数且在10~t 时刻等于0a >,在1t 时刻下降为0,在12~t t 时刻逐渐由0上升到a ,在2t 时刻之后不变且等于a 。
(a )画出作为时间函数的X 的增长率的图形。
(b )画出作为时间函数的ln X 的图形。
答:(a )根据题目的规定,X 的增长率的图形如图1-1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⇒ L(t ) = L(0)e nt ⇒ A(t ) = A(0)e gt
(t ) / X (t ) : 关于增长率的一些有用数学技巧, X
/X +X /X X 1 X 2 的增长率为 X 1 1 2 2
/X −X /X X 1 /X 2 的增长率为 X 1 1 2 2
α K (k * ) , 1 − α K (k * )
α K (k * ) = k * f '(k * ) / f (k * ) 的含义:
k=k*处产出关于资本的弹性。[当为 C—D 生产函数时,α K 的值] 资本份额(资本收入占总收入的比重) 。如果市场是竞争性的,并 且不存在外部性,资本就能获得其边际产出。在平衡增长路径上, 资本(单位有效劳动的资本)所获得的总产出为 k * f '(k * ) ,因而资 本份额为 k * f '(k * ) / f (k * ) 。 例子: 大部分国家α K =1/3, 因此α K /(1- α K )=0.5。 s 增加 10% (从 0.2 增加 到 0.22),将导致 y 只增加 5%。即使 s 增加 50%,y 也只增加 25%。这 说明: 储蓄率的显著变化对平衡增长路径上的人均产出的影响是中度的 (moderate) 。 【含义:1、黄金规则下的储蓄率才是最优的。2、储蓄率的增加虽然可 以增加收入,但是影响不大】
• • •
=>
k K ( AL) = − k K AL • • • K A L = − + K A L sY − δ K = −n−g K sY = −δ − n − g kAL sf (k ) = −δ − n − g k
因此,得到 = k (t ) sf (k (t )) − (n + g + δ )k (t )
简约型(紧凑型,Intensive-form)生产函数: y=f(k) F(cK, cAL) = cF(K, AL), and c =1/AL F(K/AL, 1) = (1/AL)F(K, AL) F(k, 1) = y k=K/AL: 单位有效劳动的资本,capital per unit of effective labor y=Y/AL=F(K, AL)/AL: 单位有效劳动的产出 output per unit of effective labor f(k) = F(k, 1)
• • • • • •
•
•
•
索洛模型意味着,无论其起点在何处,经济总会收敛于平衡增长路 径,在此情形中,模型的每个变量都以不变速度增长。 (注意:r, w 等价格变量增长率为 0) 在平衡增长路径上,人均产出的增长率只取决于技术进步速度 g。
1.4 储蓄率变动的影响 1) 对产出的dvanced Macroeconomics(D. Romer,第 4 版) 。
第 1 章、索洛增长模型
“增长理论”的进一步阅读材料: 1. Weil,经济增长。 2. Barro,经济增长。 1.1 经济增长的一些基本事实 经济体为什么出现增长? 国家之间为什么出现差异? 1.2 假定 索洛模型的提出者:Solow (1956),Swan (1956)。
由 = k (t ) sf (k (t )) − (n + g + δ )k (t )
•
有 sf (k * ( s, n, g , δ )) = (n + g + δ )k * ( s, n, g , δ ) ∂k * ∂k * * sf '(k ) + f (k ) = (n + g + δ ) ∂s ∂s
由于
∂k * ( s, n, g , δ ) > 0 , 所以 ∂s
∂c* = 0⇒ ∂s f '(k * ( s, n, g , δ )) = (n + g + δ )
k*的这个值称为:黄金规则水平的资本。
Y 【含义: f '( k ( s, n, g , δ )) − δ = n + g = ,实际收益率等于实际经济增 Y
2) 关于生产函数的假设 生产函数关于两个自变量是规模报酬不变的:资本和有效劳动 F(cK, cAL) = cF(K, AL) for any positive c 规模报酬不变假设与下面两个假设有关: 经济规模足够大,以至于专业化的收益已被全部利用。 除了资本、劳动与知识以外的其他投入相对不重要。
* •
长率】
相关性不是因果关系!
1.5 定量的含义 以上的定性分析表明:储蓄率的增加具有水平效应,将人均资本和 人均产出将增加到更高的水平。 下面的定量分析将表明:储蓄的显著变化只会对平衡增长路径上的 产出水平产生中度的影响。 1) 长期中对产出的影响 储蓄增加对产出的长期效应为
s ∂y* ∂y* / y* ∂y * = 。下面计算: * ∂s y ∂s ∂s / s
•
问题:为什么有 sf’(k*)<n+g+δ? sf’(k*)<n+g+δ sf’(k*)k*<sf(k*) f’(k*)k*<f(k*)
由于= k (t ) sf (k (t )) − (n + g + δ )k (t ) , • d k = sf '(k ) − (n + g + δ ), dk • d2 k sf ''(k ) < 0 = dk 2 当 k<k*, k > 0 ; 当 k>k*, k < 0 . 当 k=0, = k sf (0) − (n + g + δ )0 = 0 ; 当 k=k*, k = 0 . 据上,得到下面图形
*
∂k * f (k * ) = ∂s (n + g + δ ) − sf '(k * )
因此,由 y* = f (k * ) ,得到
∂y* ∂k * ( s, n, g , δ ) f '(k * ) f (k * ) = f= '(k * ) ∂s ∂s (n + g + δ ) − sf '(k * )
问题:最后的稳态消费是否会超过 t 0 之前的稳态消费?
3) 黄金规则水平的 k 令 c*表示平衡增长路径上的 C/AL,
c*= (1 − s ) f (k * ) = f (k * ) − sf (k * ) = f (k * ) − (n + g + δ )k *
由于 k*取决于 s, n, g, δ, 将 k*记为: k * = k * ( s, n, g , δ ) 有, = c* f (k * ( s, n, g , δ )) − (n + g + δ )k * ( s, n, g , δ ) 得到 ∂c* ∂k * ( s, n, g , δ ) * = f '( k ( s , n , g , δ )) − ( n + g + δ ) ∂s ∂s
f(k)的假设: f(0)=0, f’(k)>0, f’’(k)<0 Inada 条件: lim k->0 f’(k) = ∞, lim k->∞ f’(k) = 0 f’(k)的含义: 资本的边际产出 F(K, AL) = ALf(K/AL), dF(K, AL)/dK=f’(k).
因此,
s ∂y* s f '(k * ) f (k * ) = y* ∂s f (k * ) (n + g + δ ) − sf '(k * ) = = = = = sf (k * ) f '(k * ) f (k * ) (n + g + δ ) − sf '(k * ) (n + g + δ )k * f '(k * ) f (k * ) (n + g + δ ) − sf (k * ) f '(k * ) / f (k * ) (n + g + δ )k * f '(k * ) f (k * ) (n + g + δ ) − (n + g + δ )k * f '(k * ) / f (k * ) k * f '(k * ) / f (k * ) 1 − k * f '(k * ) / f (k * )
Cobb-Douglas 生产函数: F(K, AL)=Kα(AL)1−α, 0<α<1 F(cK, cAL) = cF(K, AL) f(k)=kα f’(k)=αkα−1>0 f’’(k) = −(1−α)αkα−2<0
3) 投入至产出的演化 L(t ) ≡ dL(t ) / dt = nL(t ) A(t ) = gA(t ) n,g 为外生参数 n 是 L 的增长率: dL(t ) / dt =n L(t ) ⇒ L(t + ∆t ) − L(t )= n(∆t ) L(t )
•
• • •
•
稳定点(均衡)是稳定的(The stationary point is stable) 当偏离 k*时,有回到 k*的趋势。
2) 平衡增长路径
当 k=k*, 依据假设, L 和 A 的增长率为 n 和 g
• • •
K A L K = k AL ⇒ = + = g + n K A L
•
因此,得到下面图形。
总长,储蓄率的变化具有水平效应(level effect) ,但不具有增长效应 (growth effect) :它改变了经济的平衡增长路径因而改变了在任何时点 上的人均产出 Y/L, 但这并不影响平衡增长路径上人均产出 Y/L 的增长 率。只有 g 的变化具有增长效应。
