n人合作博弈的模型
博弈类型及其表述形式

1博弈的分类博弈模型一般分为合作博弈( cooperative game )和非合作博弈( non- cooperativegame),如图。
合作博弈是以单个参与者的可能行动集合为基本元素,而非合作博弈是以参与人群的可能联合行动集合为基本元素( Martin and Ariel Rub in stein ,2000, P2),也就是说,在合作博弈中,博弈中所有参与者都独立行动,不存在有约束力的合作、联合或联盟的关系,而在非合作博弈中,在一些参与者之间存在着有约束力的合作、联合或联盟的关系,并因为这种关系影响到博弈的结局。
合作博弈强调的是团体理性( collectiverati on ality )、效率、公正和公平;非合作博弈强调的是个人理性、个人最优决策,其结果可能是有效率的,也可能是低效率或无效率的(张维迎,1996,P5)。
20世纪50年代,合作博弈的研究达到鼎盛期,同时开始出现对非合作博弈的研究,此后,博弈论的研究主流逐步转向在非合作博弈领域。
有些人认为非合作博弈模型比合作博弈更“基本”,但有些人认为两者不相上下(Martin and Ariel Rubinstein ,2000,P2)。
合作博弈,有时也叫做联盟博弈( coalitional game ),一般根据有无转移支付而分为两类:可转移支付联盟博弈( coalitio nal game with tran sferable payoff )和不可转移支付联盟博弈(coalitional game with non-transferable payoff )。
可转移支付也叫有旁支付(side payment ),可转移支付联盟博弈假设博弈中各参与者都用相同的尺度来衡量他们的赢得,且各联盟的赢得可以按任意方式在联盟成员中分摊;否则,就是不可转移支付联盟博弈。
可转移支付合作博弈合作博弈不可转移支付合作博、非合作博弈非合作博弈的分类主要从两个角度进行划分。
第11章博弈模型

总投资
DC (1 )C (2,3)595 3
4)1, 3合作 C ( 1 ,3 ) 7( 5 3 5 )0 .71 0 2 .65 0 6 .51 5 4 8 C(1)C(3)460合作不会实现
5)三城合
DC (1 ,2 ,3 )7(3 535 )0 .71 20 .65 6 0 .512 5
即 B 1 已 , b 1 ( 4 , 5 , 7 ) 知 求 , x ( x 1 , x 2 , x 3 )
(1)协商解 以n-1方合作的获利为下限
模型 x i B
x i
x 1
b 1
x i x n b n
AxT bT,
A0110
A (Sh)a .x p ( 6 .6 l,1 .e 6 7 ,1 . y 6 7 )7
B .b i v ( I \ i ) b , ( 0 , 1 , 1 ) 0 B 0 ,v ( I ) 10
xTA1bT(1,0,0) x(1,00,0)
x i B b i,x (1,0 ,0 0 )
1 Q1=5
2 Q2=3 河流
38km
3 Q3=5
• 污水处理,排入河流. •三城镇可单独建处理厂, 或联合建厂(用管道将污水 由上游城镇送往下游城镇).
Q~污水量,L~管道长度 建厂费用P1=73Q0.712 管道费用P2=0.66Q0.51L
污水处理的5 种方案
1)单独建厂 C ( 1 ) 7 5 0 3 .71 2 2 ,C 3 ( 2 ) 0 1,C 6 ( 3 ) 0 23
非合作博弈
静态、动态 信息完全、不完全
军事、政治、经济、企业管理和社会科学中应用广泛
约翰·纳什

约翰·纳什(JohnF Nash),生于 1928年6月13日。任普林斯顿大学 数学系教授。1950,约翰·纳什获 得美国普林斯顿高等研究院的博 士学位,他那篇仅仅27页的博士 论文中有一个重要发现,这就是 后来被称为“纳什均衡”的博弈 理论。
约翰·福布斯·纳什(John Forbes Nash Jr.) 约翰·纳什生于1928年6月13日。父亲是电子工程师与教师,
第一次世界大战的老兵。纳什小时孤独内向,虽然父母对他照顾 有加,但老师认为他不合群不善社交。 纳什在上大学时就开始从事纯数学的博弈论研究,1948年进 入普林斯顿大学后更是如鱼得水。他在普林斯顿大学读博士时刚 刚二十出头,但他的一篇关于非合作博弈的博士论文和其他相关 文章,确立了他博弈论大师的地位。在20世纪50年代末,他已是 闻名世界的科学家了。特别是在经济博弈论领域,他做出了划时 代的贡献,是继冯·诺依曼之后最伟大的博弈论大师之一。他提 出的著名的纳什均衡的概念在非合作博弈理论中起着核心的作用。 后续的研究者对博弈论的贡献,都是建立在这一概念之上的。由 于纳什均衡的提出和不断完善为博弈论广泛应用于经济学、管理 学、社会学、政治学、军事科学等领域奠定了坚实的理论基础。
Nash平衡是指博弈中这样的局面,对于每个参与者来
说,只要其他人不改变策略,他就无法改善自己的状 况。Nash在证明了在每个参与者都只有有限种策略选 择、并允许混合策略的前提下,Nash平衡一定存在。 以两家公司的价格大战为例,Nash平衡意味着两败俱 伤的可能:在对方不改变价格的条件下,既不能提价, 否则会进一步丧失市场;也不能降价,因为会出现赔 本甩卖。于是两家公司可以改变原先的利益格局,通 过谈判寻求新的利益评估分摊方案,也就是Nash平衡。 类似的推理当然也可以用到选举,群体之间的利益冲 突,潜在战争爆发前的僵局,议会中的法案争执等。
合作博弈代码

合作博弈代码合作博弈(Cooperative game)是博弈论中的一个重要分支,研究的是参与者通过合作来实现组织目标的博弈模型。
在合作博弈中,参与者之间通过协商、合作来达成最优解,共同分享收益或承担风险。
为了解决这类问题,人们开发了各种合作博弈模型和相应的求解方法。
本文将介绍一种常见的合作博弈代码实现方法。
合作博弈模型可以用一个特征函数(characteristic function)来表示。
特征函数描述了博弈参与者之间的合作关系以及相应的收益分配方式。
以合作博弈中的N人问题为例,特征函数可以表示为:v(S):对于任意的联盟S,v(S)表示这个联盟合作所能获得的总收益。
基于这个特征函数,我们可以使用Shapley值(Shapley value)来确定参与者的个人收益。
Shapley值是一个有理分配方式,可以确保参与者之间的收益是公平和合理的。
为了实现合作博弈的代码,我们可以按照以下步骤进行:第一步:定义特征函数根据实际情况,我们可以首先定义特征函数v(S)。
这个函数可以是一个字典或一个矩阵,用来表示各个联盟合作所能获得的总收益。
第二步:计算Shapley值根据定义的特征函数,我们可以使用迭代的方法计算每个参与者的Shapley值。
Shapley值的计算方式如下所示:1. 初始化参与者的Shapley值为0;2. 对于每个参与者i,依次计算他参与所有可能的联盟所能获得的平均边际值;3. 将每个参与者的平均边际值累加到其对应的Shapley值上。
具体而言,我们可以使用以下伪代码来实现Shapley值的计算:```pythondef shapley_value(v):n = len(v) # 参与者的个数shapley = [0] * n # 初始化Shapley值为0for i in range(n):for j in range(2 ** n):if (j >> i) % 2 == 1:coalition = [k for k in range(n) if (j >> k) % 2 == 1]m = len(coalition)marginal_value = (v[coalition + [i]] - v[coalition]) / b(n - 1, m)shapley[i] += marginal_valuereturn shapley```第三步:应用代码在得到了Shapley值之后,我们可以根据实际需要进行进一步的分析和应用。
志愿者困境模型

志愿者困境模型志愿者困境的博弈模型是,有N个参与者,每人都面临要么牺牲自己小部分利益,要么选择搭便车。
威廉·庞士东用如下场景来描述该博弈:有一个社区都停电了,社区里所有居民都知道,只要有一个人花钱给电力公司打电话,电力公司就会修复这个问题。
但是如果没有志愿者,所有人都面临一直没电的情况。
如果有一个人决定做志愿者,其他人都会因为没有做而获益[1]。
该博弈的收益矩阵如下:志愿者困另外至少有一个人合作其他人都不合作境的收益矩阵合作0 0对抗 1 -10该博弈衍生出很多实验,但所有实验的结果都与标准博弈论预测相违背。
志愿者困境实例还是让我们从一个生活中的小故事开始讨论这个问题。
你和一群互不相识的人乘坐飞机旅行,途经一处荒岛飞机出事故迫降了,一切通讯设备都在迫降中损坏,不过好在你们大家人都安然无恙。
所有人聚集在一起讨论如何逃生。
很快有人发现,这个小岛离附近的大陆其实不远,游泳可以勉强到达大陆,从而找到人求救。
唯一的问题是,这附近的海域鲨鱼很多,安全的游过去需要一定的运气。
为了让问题明确,请不要考虑等待路过的轮船发现之类的好运降临或者你竟然不会游泳这类的借口。
你们要做出的选择就是,谁来充当这个志愿者,冒着风险游过去解救大家?在这场博弈中,每个人都企盼出现的对自己最有利的情况,总是由别人站出来游过大海,自己等着被解救。
那个游过大海的人则将要面对巨大的风险,甚至是付出自己的生命。
然而如果每个人都这么想,则最终不会有任何人站出来去求救,大家都得完蛋。
[2]再举一个例子,你上的是管理非常严格的寄宿学校。
为了公然反抗校长,所有学生团结一致,把钟楼上那个古老的钟偷走了。
第二天,校长非常生气。
他把所有学生召集在礼堂里并许诺:如果有人在当天结束前告诉他钟在哪里,这个人或这伙人(他们显然有过失)这学期将被记载为不及格;如果没有人告诉他钟在哪里,那么整个学年的成绩都将被记载为不及格。
学生们心里都很清楚他们每个人都犯有同样的过失,所有人也都知道钟在哪里。
合作博弈_精品文档

哥本哈根气候峰会博弈
1 发达国家 欧、美、日为代表
2 发展中国家 中、印、巴西、印尼
3 气候敏感国家和贫穷国家 图瓦卢、马尔 代夫、斐济等太平洋小岛国 ;非洲
各国的立场
中国,到2020年单位国内生产总值二氧 化碳排放比2005年下降40%-45%
美国将在哥本哈根气候变化大会上承诺 2020年温室气体排放量在2005年基础上 减少17%。
Shapley 值是其中重要的解概念之一
Shapley 值
Shapley公理 Shapley 提出了看上去比较 合理的几个公理假设
在这些假设下,Shapley 证明了任何合 作博弈 (N, v)存在唯一的Shapley值。可 作为合作分配的一个解概念。
Shapley 值
参与人集合N的一个置换 (permutation),是 任一函数π:N N,使得对于N中的每个j, N 中恰好存在一个i, 使得π(i) =j( π是单射,又 是满射)
英国:承诺到2020年和2050年分别减排 2005年的34%和80%,
各国立场
欧盟:通过包括气候与能源一揽子计划和各 种能效措施,无条件承诺到2020年较1990年 减排20%以上。同时承诺抬高减排幅度至30%, 前提是各工业化国家同意相当水平的减排力 度,同时发展中国家做出重大贡献,共同促 成国际条约的签署 。
给定上述置换π和任一联盟博弈v, 令πv为满足 π v ({π (i) | i∈S})=v (S), S为N的任一子集
的联盟博弈。
Shapley 值
Shapley 公理1(对称性)对于合作博弈 (N, v), 在任一参与人的置换映射π(i) 下, 分配结果应保持不变,即有
φπ(i) (πv) = φi(v) 公理1表明:一个参与人在博弈中的角
shapley value 模型

Shapley Value 模型一、什么是 Shapley Value 模型?Shapley Value 模型是一种用于衡量合作博弈中参与者贡献度的方法。
在博弈论中,合作博弈是指多个参与者通过合作来实现共同目标的情况。
Shapley Value 模型通过考虑每个参与者的贡献和合作的次序来确定每个参与者的收益分配。
二、Shapley Value 的计算方法Shapley Value 的计算方法基于合作博弈中的排列组合。
假设有n个参与者,每个参与者都可以与其他参与者进行合作,形成不同的合作组合。
Shapley Value 的计算方法如下:1.对于每个可能的合作组合,计算每个参与者加入该合作组合时的边际贡献。
边际贡献是指参与者加入合作组合后对整个组合带来的额外收益。
2.对于每个参与者,计算其在所有可能的合作组合中的平均边际贡献。
这个平均值即为参与者的 Shapley Value。
3.将计算得到的 Shapley Value 分配给每个参与者,作为其合理的收益分配。
三、Shapley Value 的特点和应用Shapley Value 模型具有以下特点和应用:1. 公平性Shapley Value 模型能够公平地衡量每个参与者的贡献度。
通过考虑每个参与者的边际贡献和合作的次序,确保每个参与者都能够获得合理的收益份额。
2. 稳定性Shapley Value 模型能够保持稳定性,即不会因为新增或减少一个参与者而导致其他参与者的收益发生剧烈变化。
这使得 Shapley Value 模型在实际应用中具有较好的可靠性。
3. 合作博弈分析Shapley Value 模型可以用于分析合作博弈中的参与者的贡献度。
通过计算每个参与者的 Shapley Value,可以了解每个参与者对整个合作博弈的重要程度,从而做出相应的决策。
4. 资源分配Shapley Value 模型可以用于公平地分配资源。
在资源有限的情况下,通过计算每个参与者的 Shapley Value,可以实现资源的合理分配,避免资源的浪费和不公平现象。
合作博弈

I { A, B, C}
v( A) v( B) v(C ) 0
则
1 v( A, B) 1, v( A, C ) 1, v( B, C ) 0 w( 2) 6 1 w(3) v( A, B, C ) 1 3 P 2 / 3; P2 1 / 6; P3 1 / 6 1
v(1) v(2) v(3) v(4) 0
v(1,2) 3, v(1,3) 3, v(1,4) 0 v(2,3) 0, v(2,4) 0, v(3,4) 0 v(1,2,3) 3, v(1,2,4) 6 v(1,3,4) 6, v(2,3,4) 0
非合作博弈是研究人们在利益相互影响的局势中如何选决策 使自己的收益最大,即策略选择问题。(纳什均衡) Shapley 公平三原则 原则1:报酬与名字无关,只与各人的贡献有关; 原则2:利润属于工作者; 原则3:若有二件工作 ,可得二份酬劳。
符号说明
I {1,2,3,, n}
SI
——合作博弈的n方
v(1,2,3,4) 6
按Shapley值计算公式
P 3.25; P2 0.75; P 0.75; P4 1.25 1 3
收益分配模型的应用
权力问题:有ABC三个议员,A有两票,BC各有一票,这三个 人组成一个议会,对某项议题进行投票。假定此时获胜原则 是多数规则,即4票中获3票就通过,假定不存在弃权票,那 么他们各自的权力有多大呢? 分析
——n方的子集合
v(S )
——相应的效益
Pi
——i在合作收益中应得到的一份收入
T
P (P (v), P2 (v),, Pn (v)) 1
分配公式为
——Shapley值
n人合作博弈理论、方法及其在战略联盟上的应用共3篇

n人合作博弈理论、方法及其在战略联盟上的应用共3篇n人合作博弈理论、方法及其在战略联盟上的应用1n人合作博弈理论、方法及其在战略联盟上的应用随着市场经济的发展,产业竞争愈发激烈,如何进行有效的合作,成为企业在发展中不可避免的问题。
为了实现企业之间的合作,在一定范围内建立战略联盟已经成为一种非常有效的方式。
而在战略联盟的建立过程中,n人合作博弈理论及其方法得到了广泛的应用。
本文将探讨n人合作博弈理论、方法及其在战略联盟上的应用。
一、n人合作博弈理论基本概念合作博弈是指在团队合作中,合作方按照协商和约定合作,博弈方根据利益关系精心选择策略的一种博弈。
而当参与者超过两个以上时,则被称为n人合作博弈。
在n人合作博弈中,参与者会协商达成一个关于资源分配的协议,以使得每个参与者都能取得最大的收益。
在n人合作博弈中,有两个基本概念:合作劝诱和核心。
合作劝诱是指每个参与者自己选择策略,使得其他所有参与者都愿意与其合作;而核心则是指在合作劝诱的前提下,不论是哪种策略所得到的结果,都不能被其他合法策略所代替。
可以说,核心是所有参与者所认为的最佳合作方案。
二、n人合作博弈方法要想在n人合作博弈中获得更好的收益,需要采取一些有效的方法。
以下是一些常用的方法:1.契约理论在n人合作博弈中,人们会根据自己的利益选择合作策略。
而契约理论则是基于此而出现的。
契约理论通过设计契约以约束合作方,从而尽可能减少合作方的欺诈行为。
通过契约的设计,可以在双方之间建立起一种有效的信任关系,进而促进有效合作。
2.协议理论协议理论是在双方相互合作达成的共同目标的基础上,协商达成一种更可接受的合作方案。
协议理论的重点在于如何寻求合作方案。
通过协商、妥协和交易,达成一项平衡的协议,以使得每个参与者都能获得最大的收益。
3.奥斯本益格博弈奥斯本益格博弈是一种博弈论游戏,用于研究n人合作博弈可能产生的结果。
在奥斯本益格博弈中,参与者通过自己的策略来逐步优化自身收益,最终达到合作的目的。
合作博弈的解

合作博弈的解合作博弈需要解决的最重要问题就是所有参与者合作时所获得的收益(或节省的费用)如何在个体参与者之间进行分配,显然,联盟的形成是建立在所有参与者对博弈中的建议分配都同意的基础上的,该分配称为合作博弈的解。
根据分配时的采取的方法不同,合作博弈的解有多种求解方案,本文主要讨论核心、核仁和Shapley 值三种合作博弈解。
(1)核心Gillies 于20世纪50年代提出了核心的概念,可以认为核心是最早出现的合作博弈的解,同时它也是其他解出现的基础。
下面首先对核心做定义:在一个n 人合作博弈(,)N V 中,不被任何其他分配向量所支配的分配向量的集合称为核心,记为(,)C N V 或()C V 。
在实际的生产活动中,由于不会存在使自身获利更多的分配方案,核心()C V 中的所有分配方案均会被对应的联盟所认可,即核心的分配使得任何联盟都没有能力推翻它。
在核心中的各参与者都会接受加入该联盟所分配到的收益结果,因此这些参与者只会选择满足核心的联盟。
分配向量x 应当满足的条件为:1()n i i xV N ==∑ (2.6)()i i S xV S ∈≥∑ (2.7)此时,在存在核心的合作博弈中,采用核心作为合作博弈的解时分配给所有参与者的收益之和等于所有参与者合作所得,即能够实现收益的完全分配。
同时,作为一个理性的参与者,在选择分配向量时,都会将加入该联盟所能分配到的收益与脱离联盟不进行合作的获益相比较,由于核心中的分配向量满足个体合理性,故满足条件的参与者会选择核心作为合作博弈的解。
合作博弈的核心解能够为联盟的参与者提供满意的结果,但是核心解在求解时可能会很难实现或者说有时不存在核心解,这是合作博弈的核心解在应用中的最大问题。
具体情况表现为核心为一个区域有多个元素或者合作博弈不存在核心。
以下用反证法对这些情况进行说明。
1)博弈的核心为空对一个n 人合作博弈(,)N V ,常和博弈表示博弈的特征函数有()()()+-=V S V N S V N ,空核心博弈的特征函数满足{}S T φ⋂=,()()()⋃=+V S T V S V T ,此时若x 是该博弈的核心解,则有:()()()∈=≤∑i N V N x N V i (2.8)这不满足常和博弈特征函数的条件,所以该博弈的核心解不存在。
博弈论

博弈论的基本概念1.博弈论:博弈论,又称对策论,是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题。
博弈论的定义可以这样理解:博弈论是指某个个人或是组织,面对一定的环境条件,在一定的规则约束下,依靠所掌握的信息,从各自可选择的行为或策略中进行选择并加以实施,并从中取得相应收益的过程。
2.参与人:参与人指的是博弈中选择行动以最大化自己效用的决策主体(个人、团体)。
3、行动:行动是参与人在博弈的某个时点的决策变量。
一般来讲,把第i个参与人的一个行动为ai,其可供i选择的行动集合表示为Action set: Ai ={ai}。
在一个n人博弈中,n个参与人的行动的有序集为a={a1,…,an},称为行动组合。
根据行动顺序,可以把博弈分为静态博弈、动态博弈。
静态博弈:一般来讲,如果行动时同时发生的或相当于同时发生的,则称之为静态博弈。
动态博弈:如果行动的发生有先后顺序,则称之为动态博弈。
4.信息:信息指的是参与人有关博弈的知识,特别是有关“自然”的选择、其他参与人的特征和行动的知识。
信息集是指参与人在特定时刻所拥有的有关变量的值的知识。
例如:囚徒困境甲不知乙的选择,则甲的信息集为{坦白或者抵赖}乙已经行动,甲观察到乙的选择,则甲的信息集为{坦白}或者是{抵赖}。
5.战略:战略是参与人在给定信息集的情况下的行动规则,是参与人完整的一套行动计划,它规定参与人在什么时候选择什么行动。
战略不同于行动,它是行动的规则,对于战略的表述应该是完备的。
例如:人不犯我,我不犯人;人若犯我,我必犯人”例如:田忌赛马,田忌所选的赛马计划就是一套完整的行动计划,也就是一个战略。
6.战略空间:参与者可以选择的战略的全体组成了战略空间。
田忌赛马,六种行动方案可供选择:上中下,上下中,中上下,中下上,下上中,下中上。
这些可选择的战略的全体组成了战略空间。
任何一人战略的改变都将使结果也随之改变。
7、收益:支付、报酬,指在一个特定的战略组合下参与人得到的效用水平或期望效用水平。
博弈论
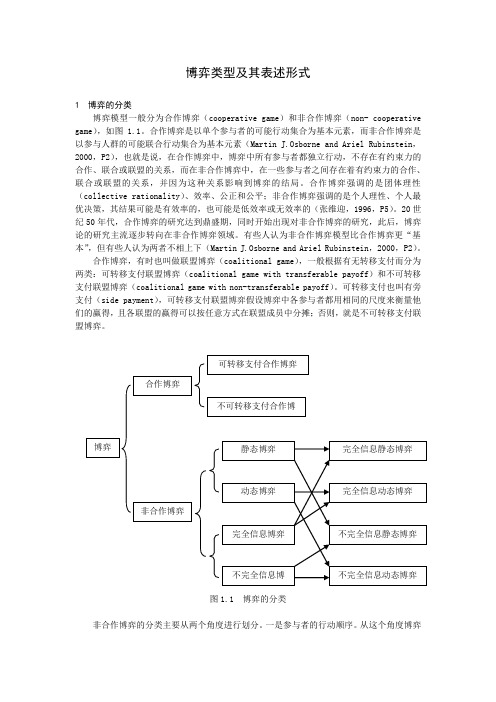
博弈类型及其表述形式1 博弈的分类博弈模型一般分为合作博弈(cooperative game )和非合作博弈(non- cooperative game ),如图1.1。
合作博弈是以单个参与者的可能行动集合为基本元素,而非合作博弈是以参与人群的可能联合行动集合为基本元素(Martin J.Osborne and Ariel Rubinstein ,2000,P2),也就是说,在合作博弈中,博弈中所有参与者都独立行动,不存在有约束力的合作、联合或联盟的关系,而在非合作博弈中,在一些参与者之间存在着有约束力的合作、联合或联盟的关系,并因为这种关系影响到博弈的结局。
合作博弈强调的是团体理性(collective rationality )、效率、公正和公平;非合作博弈强调的是个人理性、个人最优决策,其结果可能是有效率的,也可能是低效率或无效率的(张维迎,1996,P5)。
20世纪50年代,合作博弈的研究达到鼎盛期,同时开始出现对非合作博弈的研究,此后,博弈论的研究主流逐步转向在非合作博弈领域。
有些人认为非合作博弈模型比合作博弈更“基本”,但有些人认为两者不相上下(Martin J.Osborne and Ariel Rubinstein ,2000,P2)。
合作博弈,有时也叫做联盟博弈(coalitional game ),一般根据有无转移支付而分为两类:可转移支付联盟博弈(coalitional game with transferable payoff )和不可转移支付联盟博弈(coalitional game with non-transferable payoff )。
可转移支付也叫有旁支付(side payment ),可转移支付联盟博弈假设博弈中各参与者都用相同的尺度来衡量他们的赢得,且各联盟的赢得可以按任意方式在联盟成员中分摊;否则,就是不可转移支付联盟博弈。
图1.1 博弈的分类非合作博弈的分类主要从两个角度进行划分。
n人博弈的均衡点

N人博弈的均衡点约翰·F·纳什㈠可以这样定义n人博弈(n-person game),n个参与人(player),每个参与人的纯策略(pure strategy)集为有限集,对于每个纯策略的n元组合,n个参与人具有与之对应的明确的支付集,纯策略的n元组合中,一个策略对应一个参与人。
混合策略(mixed strategy)是纯策略上的概率分布,支付函数(pay-off function)是参与人的期望,因此在概率上是多元线性形式的,表示各个参与人采用各个纯策略的概率。
任意的策略n元组合(n-tuple of strategies),一个策略对应一个参与人,可以看作是由参与人的n个策略空间相乘得到的乘积空间(product space)中的一点。
一个这样的n元组合优超(counter)另一个,如果优超的n元组合中的每个参与人的策略,使得该参与人产生最高可得期望。
这是因为给定的优超n元组合中任一参与人都会对抗其他参与人的n-1个策略。
自我优超(self-countering)的策略n 元组合称为均衡点。
每个n元组合与其优超集的对应,都给出了乘积空间到其本身的一个一对多的映射(a one-to-many mapping)。
从优超的定义,我们看到一点的优超点的集合是凸的(convex)。
利用支付函数的连续性,我们得到该映射的图是闭的。
闭性等价于:如果P1,P2,···和Q1, Q2,···,Qn,···是乘积空间中的点列,并且Qn→Q,Pn→P,Qn优超Pn,那么Q优超P。
因为图是闭的,并且每个点在映射下的对应是凸的,由角谷不动点定理(Kakutani`s theorem)㈡我们得到该映射存在不动点(即该点包含在它自已的对应中)。
因此,存在均衡点。
在二人零和博弈中,“主要定理”㈢和均衡点的存在性是等价的。
合作博弈

将此问题转化为三人博弈,其特征函数如下:
S
V(S) 0
{1} {2} {3} {1,2} {1,3} {2,3} 0 0 0 0 0 500
{1,2,3} 1000
局中人2,3,通过合作生产,但由于他们 共有四种原材料只能生产1/2个单位产品,所以 能挣500元。
例3:成本分摊问题(A Cost Game)
I (V ) X (x1, x2, x3) | x1 0, x2 0, x3 0, x1 x2 x3 1
而
X1
(1 2
,
1 3
,
1 ), 6
X2
(1 3
,5 12
,
1) 4
就是其中两合理分配。
2、支配(Domination)
多人结盟博弈求解问题实际是在合理分配集 I(V) 中,按某种准则选择一个或一组合理分配,作为对 策的解。
1)当z1 1,z2 z3 1,则必有z2 1,z3 1则(0,1,1) Z 2)当z1 1,z2 z3 1,则有z2 , z3 1或Z (1,1,0)或Z (1,0,1), 而Z (1,1,0)或Z (1,0,1)时,Z S(v),故有(0,1,1) Z成立。
3
3)当z1 1,z2 , z3之中必有z2 1或z3 1,反之 zi 2矛盾。
1、局中人与结盟
(1) N={1,2,…,n}表示局中人集合。 (2)结盟S,表示一个联盟,即一局多人对
策中,一部份局中人联合成一体像一 个“局中人”一样选择策略,这种联合 称为结盟。显然结盟S是局中人集合N 的子集,SN。 (3)2n是局中人可能形成结盟的个数。
2、特征函数 V(S)
(1)V(S)表示当若干局中人联合成一个结盟S时,在 这局博弈中能获得的最大收益值,即当形成结盟S,只 要S内每一个局中人共同策略,选择相应策略结盟S 能保证获得,而与联盟外局人采用什么策略无关。若
混合策略纳什均衡

目录[隐藏]1 什么是混合策略纳什均衡2 解混合策略纳什均衡的方法3 混合策略纳什均衡的经典博弈——猜谜博弈[1]4 混合策略纳什均衡博弈与其他均衡的关系[1]5 参考文献[编辑][编辑][编辑]混合策略纳什均衡混合策略纳什均衡(Mixed Strategy Nash Equilibrium )什么是混合策略纳什均衡混合策略纳什均衡:在n 个参与人的博弈G={S 1 ,... S n ; u 1,...u n }中,混合策略组合构成一个纳什均衡,如果对于所有的i =1,2...,n 下式成立:也就是说,如果一个策略组合使任何一个参与人的策略都是相对于其他参与人的策略的最佳策略,这个策略就构成一个纳什均衡,不管这个策略是混合策略还是纯策略。
混合策略纳什均衡是面对其他博弈者选择的不确定性的一个理性对策,其主要特征是作为混合策略一部分的每一个纯策略有相同的期望值,否则,一个博弈者会选择那个期望值最高的策略而排除所有其他策略,这意味着原初的状态不是一个均衡。
解混合策略纳什均衡的方法1、最大化支付法:即最大化各个参与人的效用函数。
2、支付相等法:根据前面分析的猜硬币博弈中参与人的策略的思路,每个参与人的混合策略都使其余参与人的任何纯策略的期望支付相等,因此,解混合策略纳什均衡可以令参与人的各个纯策略支付相等,构成方程组求解。
混合策略纳什均衡的经典博弈——猜谜博弈[1]两个局中人A 、B 手里各拿一枚硬币,每人可以选择正面向上或反面向上,然后同时亮出,如果两枚硬币正反面相同,B 付给A1元钱,如果两枚硬币正反面不相同,A 付给B1元钱。
在这种情况下,局中人A 、B 如何选择呢?下图给出这个博弈的双变量收益矩阵。
这是一个两人零和博弈,在每一个结局中一方所得即为另一方所失,即两个局中人的收益之和恰好等于零。
在双变量收益矩阵中采用画线的方法,在这个博弈中找不到纯策略纳什均衡。
那么,猜谜博弈是否存在混合策略纳什均衡呢?1950年纳什证明了任何有限博弈都至少存在一个纳什均衡(包括纯策略纳什均衡和混合策略纳什均衡)。
博弈论的数学模型

博弈论的数学模型作者:竺可桢学院01混合班王大方何霈邹铭摘要博弈论现在得到了广泛的应用,涉及到人的决策问题都可以用博弈论的模型加以解释。
本文首先用数学的方法表述实际生活中的博弈行为,并导出一般情况下的博弈的结果,进而讨论一些不同的外部约束条件对博弈过程的影响。
我们用经济学中的垄断竞争现象作为博弈问题的一个实例,讨论生产者在不同状态下的决策,进而分析双方共谋的动机和可能性。
(一)基本博弈模型的建立一, 博弈行为的表述博弈的标准式包括:1.1.博弈的参与者。
2.2.每一个参与者可供选择的战略集。
3.3.针对所有参与者可能选择的战略组合,每一个参与者获得的利益在n人博弈中,用Si为参与者i的可以选择战略空间,其中任意一个特定的纯战略为s i,其中任意特定的纯战略为s i,s i∈Si,n元函数u i(s1,s2,……s n), 当n个博弈者的决策为s1,s2,……s n时,表示第I各参与者的收益函数。
二, 博弈的解当博弈进入一个稳定状态时,参与者选择的战略必然是针对其他参与者既定战略的最优反应,在此状态下没有人愿意单独背离当前的局势。
这个局势叫纳什均衡:在n个参与者标准式博弈,G={ S1,S2,……S n;u1,u2,……u n}中,若战略组合{s1*,s2*,……s n*}满足对每一个参与者i,s i*是针对{ s1*,s2*,……s i-1*,s i+1*……s n*}的最优反应战略,,目标战略组合{s1*,s2*,……s n*}为该博弈的纳什均衡。
即:u i { s1*,s2*,……s i-1*,s i*,s i+1*……s n*}≥u i { s1*,s2*,……s i-1*,s i,s i+1*……s n*},对一切s i∈Si均成立。
纳什于1950年证明在任何有限个参与者,且每个参与者可选择的纯战略为有限个的博弈中,均存在纳什均衡。
(包括混合战略)混合战略指认某种概率分布来取一个战略空间中的战略,在本文中不加讨论。
专题二合作博弈PPT课件

(1)n个局中人之间是如何构成联盟的。
(2)各个联盟的支付或收益有多大。
(3)局中人最终在联盟中分配到多少。
§1.稳定集 1、联 盟 设局中人集合N={1,2,…..,n},N
的任意子集称为联盟。
注 1:空子集 也称为一个联盟。 记所有的联盟构成的集类为B。
对于 SB,用v(S)表示联盟S中的局中
(5,0,0)
(4,1,0) 3,2,0
0,5,0
有些联盟博弈的核可能是空的。满足非空的条 件:
定理:对于n人的联盟博弈,核心非空的充要条 件是线性规划有解:
n
min xi v( N ) i 1
s.t xi v(S ) S N iS
§ 4 联盟博弈的Shapley值 —n人合作博弈的另一个解
§ 2.核心
定义1: n人联盟博弈<N,v>的所有不被优超的 分配构成的集合称为核心,记为c(v)
定理1:分配方案x=(x1,x2,…xn)在核心c(v)中 的充要条件:
n
(1) xi v(N )
i 1
(2)对S B, x(S) xi v(S)
iS
例3:设有三人联盟对策,其特征函数 v{1}= v{2}= v{3}=0, v{1,2}=4, v{2,3}=1, v{1,3}=3,v{1,2,3}=5 由定理1知:这个博弈的核心由下面不等式组
好)
xi v(S)
iS
(2)
(说明分配中给联盟成员
的支付可由联盟付出)
x y
S
则称对联盟, S,I(分v) 配x优于y,记作
。
如果对于 ,能找到一个联 盟T,使 T ,则称 优于 ,记作 > 。
定义3:对于联盟博弈<N,v>,集合s(V)
纳什均衡

3.加强了经济学研究的深度。纳什均衡理论不回避经济个体之间直接的交互作用,不满足于对经济个体之间复杂经济关系的简单化处理,分析问题时不只停留在宏观层面上而是深入分析表象背后深层次的原因和规律,强调从微观个体行为规律的角度发现问题的根源,因而可以更深刻准确地理解和解释经济问题。
当然,严格来说,每个纯战略都是一个“退化”的混合战略,某一特定纯战略的机率为 1,其他的则为 0。
故“纯战略纳什均衡”,即参与之中的所有玩家都玩纯战略;而相应的“混合战略纳什均衡”,之中至少有一位玩家玩混合战略。并不是每个赛局都会有纯战略纳什均衡,例如“钱币问题"就只有混合战略纳什均衡,而没有纯战略纳什均衡。不过,还是有许多赛局有纯战略纳什均衡(如协调赛局,囚徒困境和猎鹿赛局)。甚至,有些赛局能同时有纯战略和混合战略均衡。
囚徒困境博弈
A╲B 坦白 抵赖
坦白 -8,-8 0,-10
抵赖 -10,0 -1,-1
关于案例,显然最好的策略是双方都抵赖,结果是大家都只被判1年。但是由于两人处于隔离的情况,首先应该是从心理学的角度来看,当事双方都会怀疑对方会出卖自己以求自保、其次才是亚当·斯密的理论,假设每个人都是“理性的经济人”,都会从利己的目的出发进行选择。这两个人都会有这样一个盘算过程:假如他坦白,如果我抵赖,得坐10年监狱,如果我坦白最多才8年;假如他要是抵赖,如果我也抵赖,我就会被判一年,如果我坦白就可以被释放,而他会坐10年牢。综合以上几种情况考虑,不管他坦白与否,对我而言都是坦白了划算。两个人都会动这样的脑筋,最终,两个人都选择了坦白,结果都被判8年刑期。
博弈论的几个经典模型

• 潘天群著,博弈生存(第二版),中央编 译出版社,2004年10月
• 王春永编著,博弈论的诡计,中国发展出 版社,2007年1月
博弈论的几个经典模型
基本术语
• 博弈论研究的对象:是理性的行动者或参与 者如何选择策略或如何作出行动的决定。理 性的人是对现实的人的基本假定,即假定参 与者努力用自己的推理能力使自己的目标最 大化。“理性的”与“道德的”不是一回事, 理性的与道德的有时会发生冲突,但是理性 的人不一定是不道德的。
合作互动是指既存在协调又存在冲突的博弈协调是因为两个参与同时改变行动可以变得更好冲突是因为尽管其他参与人承诺行动也不一定有利于该参与人支付的增加前者可能引起无效率后者则意意味着无效率状态会成为均衡博弈论的几个经典模型猎鹿类型协调博弈由策略不确定性所引起的均衡结果依赖于参与人之间的行为预期博弈支付与策略风险
小猪
大猪
按
不按(等待)
按
(5,1)
(5,3)
不按(等待)
(9,-1)
(0,0)
大猪和小猪分别该如何选择。
博弈论的几个经典模型
模型一、智猪博弈/完全信息静态博弈
选择等待是小猪的占优策略。
大猪的最佳选择取决于小猪的行动,如果小猪 去按,大猪最好选择等待;如果小猪不去按, 则最佳选择是大猪亲自去按。
也就是说,在智猪博弈中,大猪没有占优策略, 而小猪有占优策略,它的最佳选择就是耐心 等待大猪去按钮,才能获得最佳结果。
• 不完全信息博弈:参与者所做的是努力使自 己的期望支付或期望效用最大化。
博弈论的几个经典模型
模型一、智猪博弈/完全信息静态博弈
例:猪圈里有两只猪,一只比较大,一只比较 小。猪圈狭长,猪食槽在一头,猪食按钮在 另一头,按一下会有10个单位的猪食落进槽 里。由于按钮和食槽距离较远,按按钮的体 力耗费相当于2个单位的食物。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2005年得獎
Robert J. Aumann 和Thomas C. Schelling因對 (多人競爭賽局下)合作與衝突性的貢獻,於 2005 年獲獎。其中, Aumann 因對 Folk Theorem 進行正式分析的貢獻, Schelling 因對賽局理論應 用在嚇阻、武器競賽上的貢獻。 Aumann 於 1995 年,以專書“ Repeated Games with Incomplete Information"(co-authored by M.J. Maschler and R.E. Sterns, MIT press, 1995),獲頒美國作業研 究與管理科學學會的Lanchester著作獎、並於2005 年獲頒John von Neumann理論獎。 Aumann 是對民間智慧 Folk Theorem ,進行 正式分析的先驅, Folk Theorem 的主張為:(多 個)個體間重複性的互動,會產生許多具有自我 約束力的行為型態(均衡點),其中之一是,個 體會犧牲短期利益,來維持長久合作關係。個體 犧牲短期利益來維持長久合作關係,這種行為型 態,其實是小朋友在幼稚園階段,便開始學習的 東西:學習分享與輪流承擔。透過非合作賽局模 型, Aumann (或與合著人)在一系列文章: ( 1 ) 視長期目標型式而定,建立那些結果會、那些不 會成為均衡點;(2)對均衡點做進一步的釐清,是 否是Nash均衡點或更強、是否是完美均衡點;(3) 對模型的結構參數,例如,參賽人數、對方動作 的可觀測性、互動頻率、訊息完整性的層次、參 賽人的計算能力等等,進行系統性分析。 破產賽局問題,是 Aumann (與合著人 M.J.
如何策略性互動及其互動行為。由於社會
是由個體(個人、組織)所組成,賽局理論已逐 漸被認為是社會科學的物理學,並逐漸進入及深 化社會科學的各領域。諾貝爾經濟獎,於1994年 首度頒給賽局理論,並於2005年再度頒給這個領 域。
1994年得獎
John F. Nash, John C. Harsanyi 和 Jr. Reinhard Selten三人因對(非合作賽局)均衡性的貢獻,於 1994年獲獎。其中,Nash因對Nash Equilibrium的 貢獻, Harsanyi 因對資訊不完整情況下均衡性的 貢獻,Selten因對Perfect Equilibrium的貢獻。美國 作業研究與管理科學學會最早肯定Nash的貢獻, 於1979年即頒給他John von Newmann理論獎。 Nash 憑藉卡內基美隆大學 R.L. Duffin 教授一 封介紹信,進入普林斯敦大學攻讀數學博士,該 封介紹信只有一句話︰「這個人是個天才。」他 的博士論文指導教授A.W. Tucker回憶說︰「我偶 爾會認為 Duffi是對的。」 Nash的博士論文有27頁,包含三部分,第一 部分(論文前6頁)是關於n人非合作賽局模型的 定義、觀念介紹,及(至少存在一個解的)存在 性証明。第二部分(論文後 6 頁)是研究動機與 解釋(他所證明存在的)均衡解(點),Nash提 供兩種解釋︰第一種解釋,假設參賽者具有完美 的訊息與理性,認為均衡點是完美理性反應的預 期行為,第二種解釋,捨棄完美訊息與理性的假 設,而從群體統計行為的觀點來解釋。第三部分 (其餘 15 頁)被他當時博士班同學 H.W. Kuhn 以 諂媚的口吻譏笑是Nash灌水上去的。實質說來, Nash的博士論文只有12頁,而他之所以獲頒諾貝
屬於S,則(v, u)屬於S),且各自報酬如相等, 則雙方在合議解的值亦相同(如果 u=v ,則 u*=v*)。 關於 Nash 的合議價問題,有三點補充: ( 1 ) 對稱性公設,適用於雙方力量約在伯仲間,若過 於懸殊則不適用;(2)有威脅時,該如何處理呢? Nash 並沒有提出令人滿意的解答,處理威脅情 況,至少有兩個棘手的地方,一是威脅牽涉說與 做到的落差,另一是增加求解的困難度;(3)Ariel Rubinstein(1982)將Nash的一回合問題推廣至n 回合問題。
1960),這本書對於衝突(conflict)、承諾 (commitment)、協調(coordination)的觀念剖 析與洞察力(insights),貢獻顯著,尤其是在嚇 阻( deterrence )與武器競賽的應用上。這本書 沒有使用高深的賽局理論,而是以討論的方式進 行,至多使用兩人非合作賽局的( 2 × 2 )報酬矩 陣來分析,例如膽怯( Chicken )範例,由於該 書的數學障礙低,讀者群廣泛,影響深遠。膽怯 範例是說:兩位參賽者,在一條雙線路寬、中間 沒有分隔線的道路,各自沿著路中間、高速迎面 而來,這時雙方各有兩個選項:讓(閃到路邊) 或不讓(沿路中間繼續高速前進);膽怯範例又 稱鷹鴿(Hawk-Dove)範例,當兩個團體面對衝 突時,各自都有兩個選項:鷹派或鴿派做法。該 書至少有三點貢獻: ( 1 ) 在侵略與嚇阻情境,借 助膽怯賽局範例, Schelling 說明,面對可能侵略 時,承諾反擊的能力若可信,將有嚇阻效果,尤 其該反擊兌現的機率很高時,效果更好;(2)面對 複雜且棘手的(兩造合議)議題時, Schelling 討 論如何,經由一次邁進一步的方式(實質與時間 上)有效地化解該爭議;(3)當協調使得上力時, Schelling的聚焦點(focal point)思維,是一種便 利工具,在某些情境下,有時能解決多均衡點的 問題。 由於 Aumann 是應用數學家,而 Schelling 是 政治學者,兩人不論在背景、研究作品的性質上 差異都很大,人們好奇地問 Schelling ︰你們兩個 人同時獲獎,中間的關連在那裡呢? Schelling 回 答:提名委員將我們倆個人連結在一起,因為 Aumann是賽局理論的生產者,而我是使用者。
管理新知/資源配置管理
從諾貝爾經濟獎漫談 資源配置管理研究(二):互動面
文/賴聰乾
賽
局理論,又稱互動決策理論,乃探討個體間
爾經濟獎,是因為論文前6頁。 Nash 對其均衡點所提供的兩種解釋,第一 種解釋較為世人所熟知,第二種解釋適合生物體 (物種、器官、基因體)間的互動,因生物體不 像人有思考能力去選擇最適反應方式,生物體的 反應方式由基因來調控、在適者生存的回應訓練 下,進行演化,第二種解釋也適合社會規範(例 如,排隊、靠右 ( 左 ) 走、拆分差異、女士優先、 某些地方在餐廳用餐給小費、教授研究室由資深 者先選…)的行為演化分析。 人類在探索新知識,常採用的一項策略是: 站在巨人肩膀上,向前探索。 Nash 的存在性証 明,並不是從頭証起,而是利用已知的固定點定 理,不論使用 Brouwer 或 Kakutani 固定點定理來 証,都能達到目的,Brouwer固定點定理是拓樸學 (Topology)的一個定理,而Kakutani是Brouwer 固定點定理的一個延伸。 Nash 均衡點還有一個 重要意義,自然與社會科學的交流互動,無論從 方法、理論本身來看,一向是從自然流向社會科 學,Nash均衡點是一個例外,它是從社會流向自 然科學,Nash均衡點的發展,原本是用來解決經 濟與其他社會科學的問題,後來才被應用於生物 體的演化分析。 Harsanyi獲獎,主要是因發表在Management Science(1967-68)的那三篇一系列文章 “ Games with Incomplete Information Played by Bayesian Players. I, II, III"。Nash的n人非合作賽 局模型,假設模型結構的訊息完整,但實際情 況,訊息往往不完整( Incomplete ),參賽人各 自所擁有的私有訊息,既無義務、往往也無意願 去揭露,例如,冷戰時期,美蘇的武器競賽,任 一方都不太清楚對方的內部情況(例如,武器研 發進展、數量、威力、準度…),又例如,企業 之間的競爭,一企業往往不清楚其他企業內部的 作業參數值(例如,新產品的研發進展、作業配
(4) 對稱性:可行議價區S必須是對稱(如果(u, v)
臺大校友雙月刊/2010年1月號
91
管理新知/資源配置管理
Maschler )最廣為人知的作品︰有 n 個權益請求 者,各持有權益價值 (i=1,2,…,n),而可分配價值 不足時,如何公平分配呢?Aumann與 Maschler 提出一分配規則,並證明該分配解是n人合作賽局 的核仁。該分配規則,將猶太經典(Talmud)記 載的一則對兩人爭分衣服實例所提出的分配法, 推廣至n人情況,在爭分衣服實例中,一人(甲) 持有1/2、另一人(乙)持有全部,該如何公平分 配呢?猶太傳教士 Shlomo Titzhaki 提出的分配法 如下:對乙而言,1/2是屬於非爭分部分,這部分 應全歸乙,剩下的1/2是屬於兩人爭分部分,這部 分平分,所以甲分得1/4而乙分得3/4。Aumann與 Maschler 的分配法如下︰若可分配值小於權益總 值的一半,依等所得原則分配,但每人可分得的 上限為 ;若可分配值等於權益總值的一半, ;若可分配值大於權益總值的 ,剩餘再依等損失原則分 則每人各分得 配。 核(Core)與核仁(Nucleolus)是n人合作賽 局的兩個重要解觀念,結盟的誘因有兩種︰經濟 與公平。在核中的任一解,n人聯盟沒有瓦解成任 一次聯盟的經濟誘因,而核仁是核中的一個公平 解,核仁所根據的分配思維,是讓一個群體中最 不幸成員的幸福極大化,若有多重選擇時,再次 使不幸成員的幸福極大化,依此類推,直到找出 一個解。這裡所指的成員是n人聯盟中的任一個次 聯盟,不包括 n 人聯盟本身及空集合,共有 個成員。 Schelling獲獎,主要是因他的一本專書 “ The Strategy of Conflict "(哈佛大學出版,
90
NTU Alumni Bimonthly No.67
方、良率、產品作業前置期…)。為克服訊息不 完整這個困擾, Harsanyi 假設參賽者是貝氏型決 策者,並將原來的不完整訊息問題,巧妙地轉化 成不完美(Imperfect)訊息問題,之後,再運用 貝氏理論來處理,由於不完美訊息問題,並不難 處理,這個困擾就這樣被Harsanyi給克服了。 由於 Nash 均衡點不保證唯一,如果有多個 時,該選那一個呢?這個問題,對採用第一種解 釋“均衡點是完美理性反應的預期行為",格外 重要。對這個問題的解決, Selten 跨出重要的一 步,他提出完美均衡點的觀念,將均衡點分成完 美與非完美兩群,完美均衡點是那些有可能被理 性參賽者所選用的、非完美均衡點是那些不被選 用的,不過,Selten仍然沒有解決大家所渴望的唯 一性,因為完美均衡點也可能有多個;唯一性這 個問題,至今仍困擾著人類! 合作性議價問題(合議價問題),向來被大 家所津津樂道,這是Nash留給世人的另一珍貴遺 產。Nash假設合議雙方的訊息透明,包括雙方的 個別效用函數、個別自助報酬,個別自助報酬代 表無需靠合作、各自便能獨立達成的報酬,這是 雙方合議不成(破局)時的各自報酬,它實際上 反應各自的議價籌碼。為方便操作,Nash採用在 效用空間上操作,Nash的合議價問題是:給定雙 方在效用空間上的可行議價區 S 及自助報酬點 (u, v) ,是否唯一存在一個合議(報酬)解 (u*,v*) 。 Nash列出一組公設,來描述理性的合議行為,並 證明唯一存在一個合議解(u*, v*)滿足該組公設。 該組有四個公設: (1) 明顯理性公設:合議解必須大於等於自助報酬 點,亦即(u*, v*) (u, v),合議解必須屬於可行 議價區S,合議解必須是柏拉圖最適解; (2) 不相關解的獨立性:對可行議價區 S 的任一子 集合 T 而言,如果 S 上面的合議解 (u*, v*) 屬於 T,則(u*, v*)必須是T上面的合議解; (3) 效用空間線性轉換的獨立性:如果轉換後的空 間為 解為 ; , 則轉換後的合議
